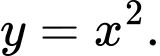Dạng toán: Nhận dạng phương trình đường tròn. Tìm tâm và bán kính đường tròn
Câu 1 [583000]: Phương trình nào sau đây là phương trình của một đường tròn?
A, 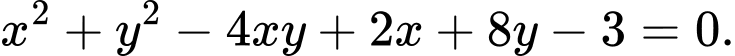
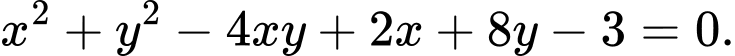
B, 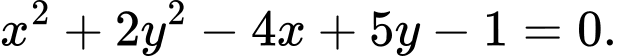
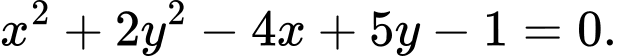
C, 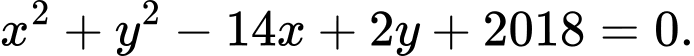
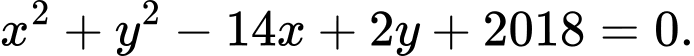
D, 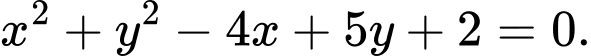
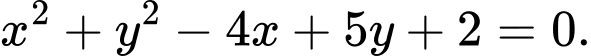
Chọn D
Phương án A: có tích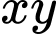 nên không phải là phương trình đường tròn.
nên không phải là phương trình đường tròn.
Phương án B: có hệ số bậc hai không bằng nhau nên không phải là phương trình đường tròn.
Phương án C: ta có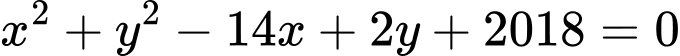
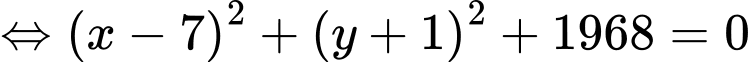 không tồn tại
không tồn tại 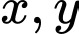 nên cũng không phải phương trình đường tròn. Đáp án: D
nên cũng không phải phương trình đường tròn. Đáp án: D
Phương án A: có tích
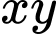 nên không phải là phương trình đường tròn.
nên không phải là phương trình đường tròn.Phương án B: có hệ số bậc hai không bằng nhau nên không phải là phương trình đường tròn.
Phương án C: ta có
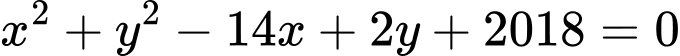
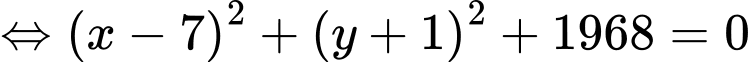 không tồn tại
không tồn tại 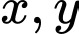 nên cũng không phải phương trình đường tròn. Đáp án: D
nên cũng không phải phương trình đường tròn. Đáp án: D
Câu 2 [583001]: Trong các phương trình sau, phương trình nào biểu diễn đường tròn? Tìm tâm và bán kính nếu có.
a)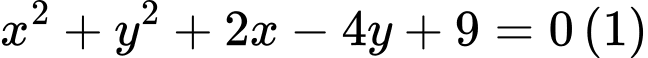
b)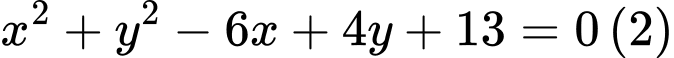
c)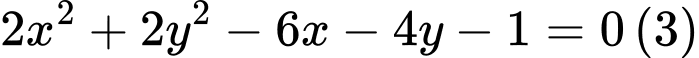
d)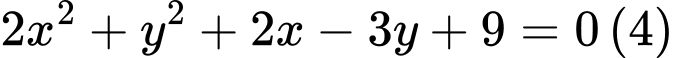
a)
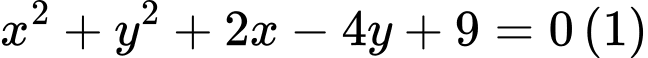
b)
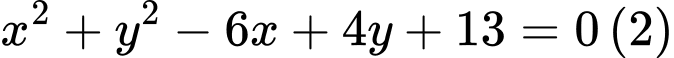
c)
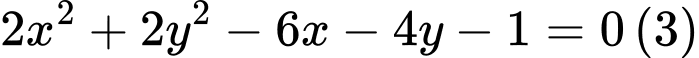
d)
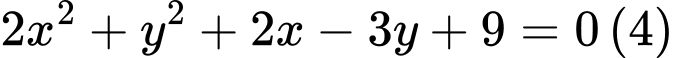
a) Phương trình  có dạng
có dạng 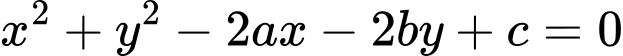 với
với 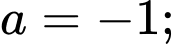
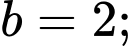
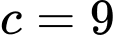
Ta có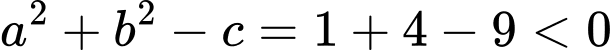
Vậy phương trình không phải là phương trình đường tròn.
không phải là phương trình đường tròn.
b) Ta có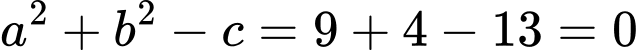
Suy ra phương trình không phải là phương trình đường tròn.
không phải là phương trình đường tròn.
c) Ta có
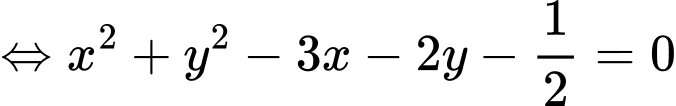
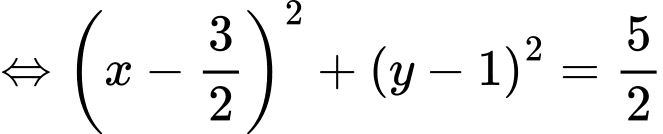
Vậy phương trình là phương trình đường tròn tâm
là phương trình đường tròn tâm 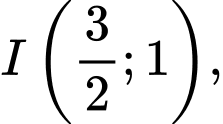 bán kính
bán kính 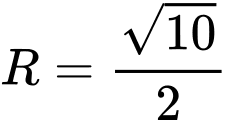
d) Phương trình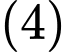 không phải là phương trình đường tròn vì hệ số của
không phải là phương trình đường tròn vì hệ số của 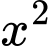 và
và 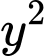 khác nhau.
khác nhau.
 có dạng
có dạng 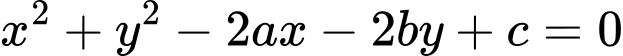 với
với 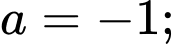
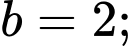
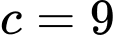
Ta có
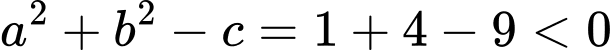
Vậy phương trình
 không phải là phương trình đường tròn.
không phải là phương trình đường tròn.b) Ta có
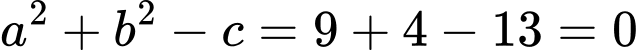
Suy ra phương trình
 không phải là phương trình đường tròn.
không phải là phương trình đường tròn.c) Ta có

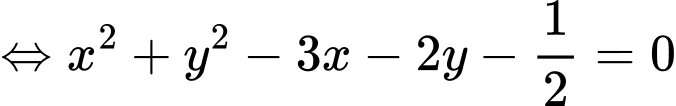
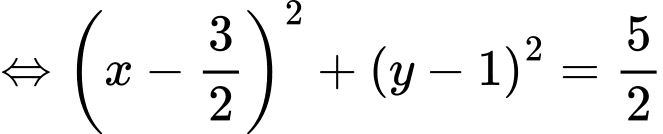
Vậy phương trình
 là phương trình đường tròn tâm
là phương trình đường tròn tâm 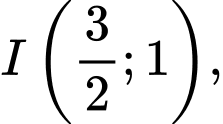 bán kính
bán kính 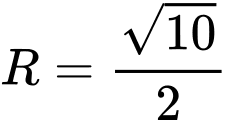
d) Phương trình
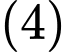 không phải là phương trình đường tròn vì hệ số của
không phải là phương trình đường tròn vì hệ số của 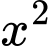 và
và 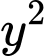 khác nhau.
khác nhau.
Câu 3 [583002]: Cho phương trình 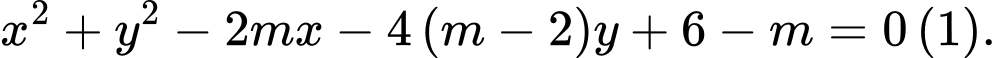 Điều kiện của
Điều kiện của 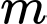 để
để  là phương trình của đường tròn.
là phương trình của đường tròn.
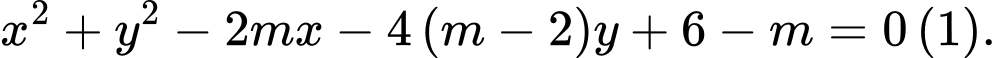 Điều kiện của
Điều kiện của 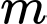 để
để  là phương trình của đường tròn.
là phương trình của đường tròn. A, 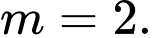
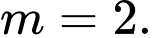
B, 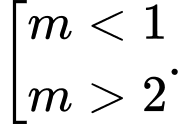
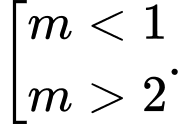
C, 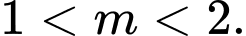
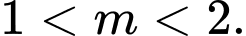
D, 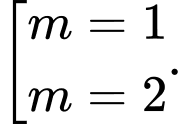
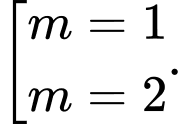
Chọn B
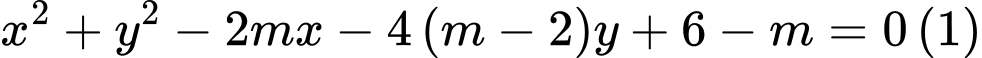 là phương trình của đường tròn khi và chỉ khi
là phương trình của đường tròn khi và chỉ khi 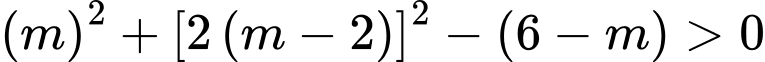
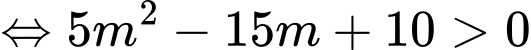
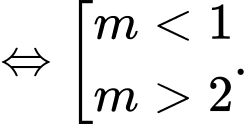 Đáp án: B
Đáp án: B
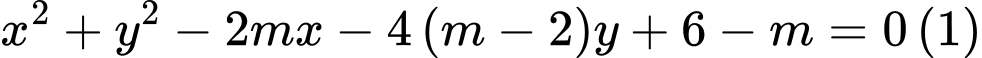 là phương trình của đường tròn khi và chỉ khi
là phương trình của đường tròn khi và chỉ khi 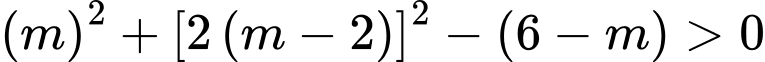
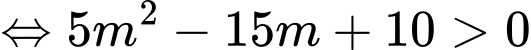
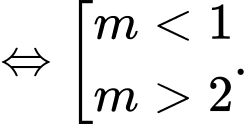 Đáp án: B
Đáp án: B Dạng toán: Viết phương trình đường tròn
Câu 4 [583003]: Trong mặt phẳng với hệ tọa độ 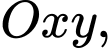 viết phương trình đường tròn
viết phương trình đường tròn  đi qua ba điểm
đi qua ba điểm 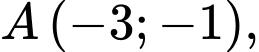
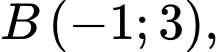
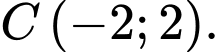
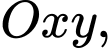 viết phương trình đường tròn
viết phương trình đường tròn  đi qua ba điểm
đi qua ba điểm 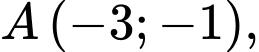
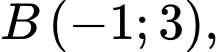
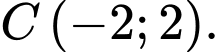
Cách 1. Phương trình đường tròn có dạng 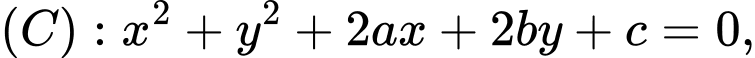 với
với 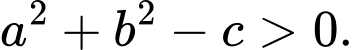
Vì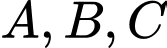 thuộc
thuộc  nên ta có hệ phương trình
nên ta có hệ phương trình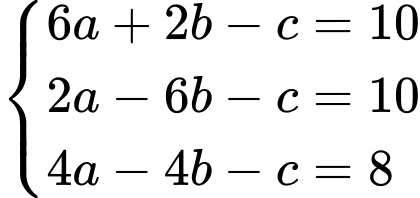
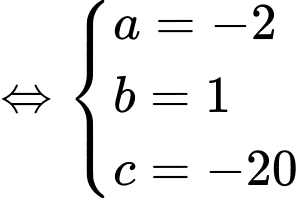
Vậy phương trình đường tròn cần tìm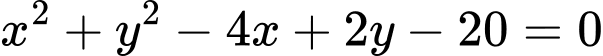
Cách 2. Gọi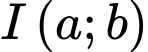 là tâm của
là tâm của 
Vì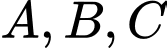 thuộc
thuộc  nên
nên
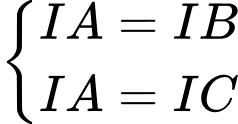
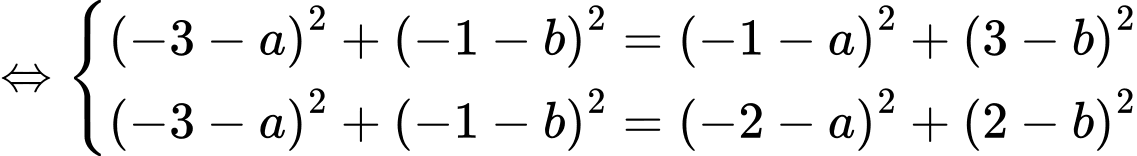
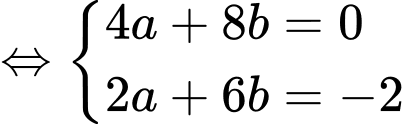
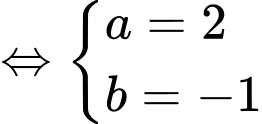
Suy ra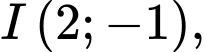 bán kính
bán kính 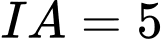
Vậy phương trình đường tròn cần tìm
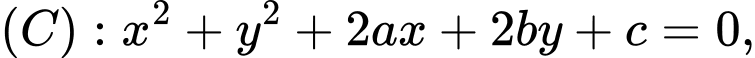 với
với 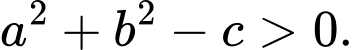
Vì
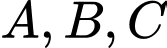 thuộc
thuộc  nên ta có hệ phương trình
nên ta có hệ phương trình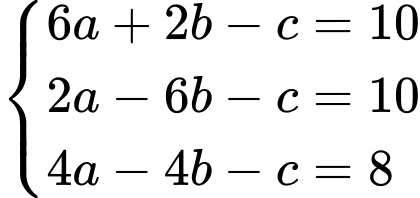
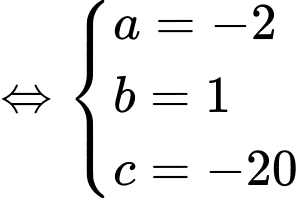
Vậy phương trình đường tròn cần tìm
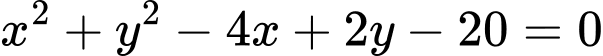
Cách 2. Gọi
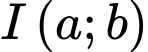 là tâm của
là tâm của 
Vì
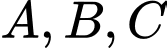 thuộc
thuộc  nên
nên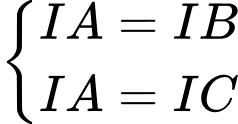
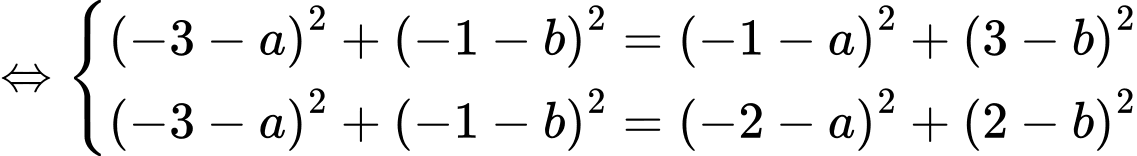
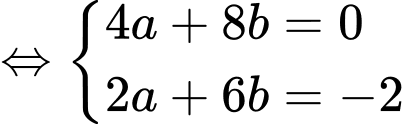
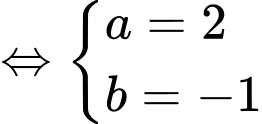
Suy ra
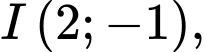 bán kính
bán kính 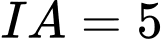
Vậy phương trình đường tròn cần tìm

Câu 5 [583004]: Cho hai điểm 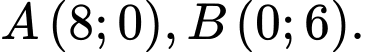
a) Viết phương trình đường tròn ngoại tiếp tam giác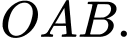
b) Viết phương trình đường tròn nội tiếp tam giác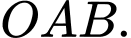
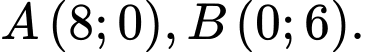
a) Viết phương trình đường tròn ngoại tiếp tam giác
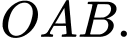
b) Viết phương trình đường tròn nội tiếp tam giác
a) Ta có tam giác 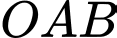 vuông ở
vuông ở  nên tâm
nên tâm 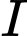 của đường tròn ngoại tiếp tam giác là trung điểm củacạnh huyền
của đường tròn ngoại tiếp tam giác là trung điểm củacạnh huyền  suy ra
suy ra 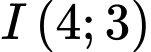 và bán kính
và bán kính 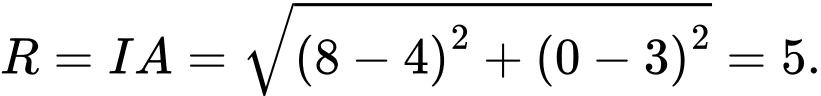
Vậy phương trình đường tròn ngoại tiếp tam giác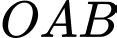 là:
là: 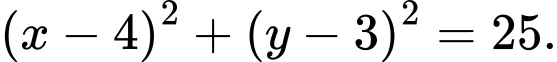
b) Ta có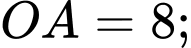
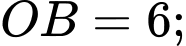
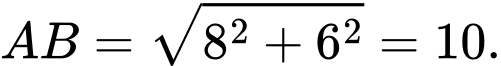
Mặt khác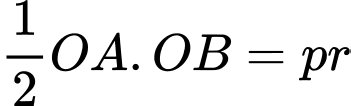 (vì cùng bằng diện tích tam giác
(vì cùng bằng diện tích tam giác 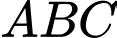 ).
).
Suy ra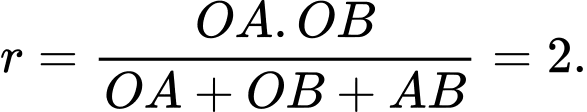
Dễ thấy đường tròn cần tìm có tâm thuộc góc phần tư thứ nhất và tiếp xúc với hai trục tọa độ nên tâm của đường tròn có tọa độ là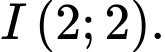
Vậy phương trình đường tròn nội tiếp tam giác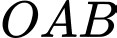 là
là 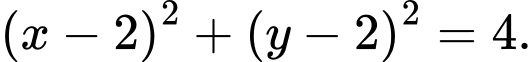
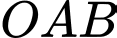 vuông ở
vuông ở  nên tâm
nên tâm 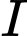 của đường tròn ngoại tiếp tam giác là trung điểm củacạnh huyền
của đường tròn ngoại tiếp tam giác là trung điểm củacạnh huyền  suy ra
suy ra 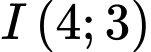 và bán kính
và bán kính 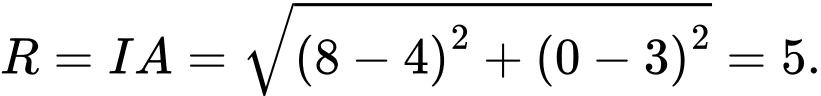
Vậy phương trình đường tròn ngoại tiếp tam giác
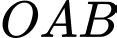 là:
là: 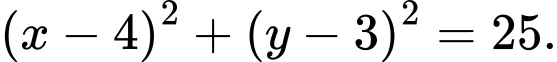
b) Ta có
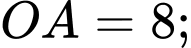
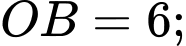
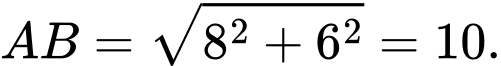
Mặt khác
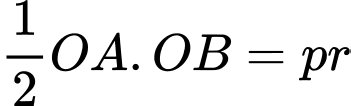 (vì cùng bằng diện tích tam giác
(vì cùng bằng diện tích tam giác 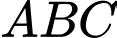 ).
).Suy ra
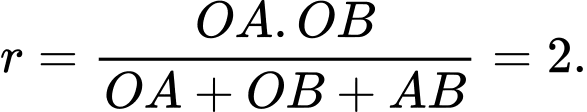
Dễ thấy đường tròn cần tìm có tâm thuộc góc phần tư thứ nhất và tiếp xúc với hai trục tọa độ nên tâm của đường tròn có tọa độ là
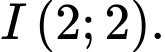
Vậy phương trình đường tròn nội tiếp tam giác
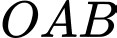 là
là 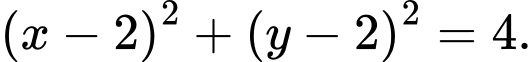
Câu 6 [583005]: Trong mặt phẳng 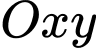 cho 2 điểm
cho 2 điểm 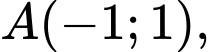
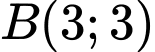 và đường thẳng
và đường thẳng 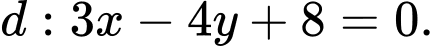 Viết phương trình đường tròn (C) qua
Viết phương trình đường tròn (C) qua 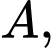
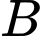 và tiếp xúc
và tiếp xúc 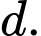
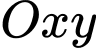 cho 2 điểm
cho 2 điểm 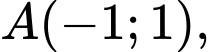
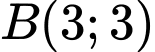 và đường thẳng
và đường thẳng 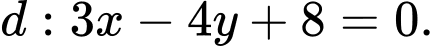 Viết phương trình đường tròn (C) qua
Viết phương trình đường tròn (C) qua 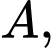
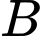 và tiếp xúc
và tiếp xúc 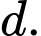
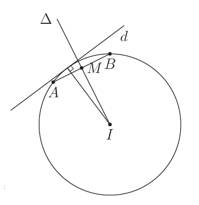
Đường trung trực
 của
của  đi qua
đi qua 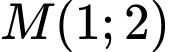 là trung điểm
là trung điểm  có phương trình là
có phương trình là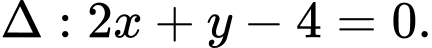
Gọi tâm
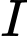 của
của  thuộc
thuộc  là
là 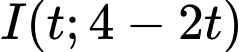
Ta có
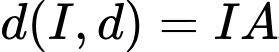
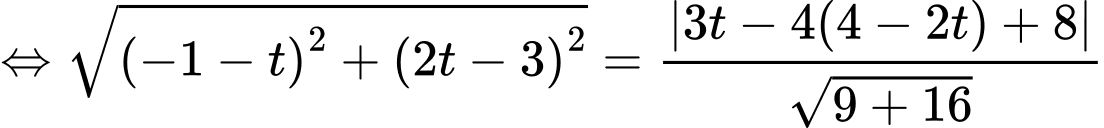
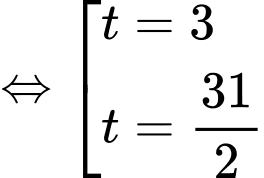
• Với
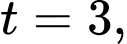 suy ra tâm
suy ra tâm 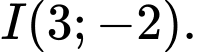 Bán kính
Bán kính 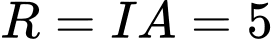
Phương trình
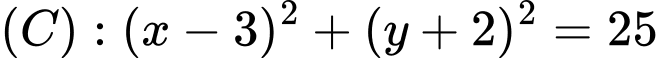
• Với
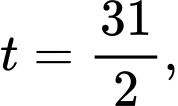 suy ra tâm
suy ra tâm 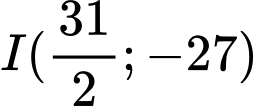 và
và 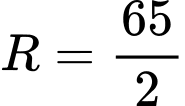
Phương trình
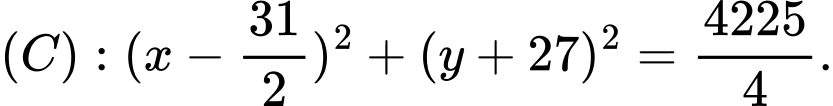
Dạng toán: Vị trí tương đối của đường thẳng, đường tròn với đường tròn
Câu 7 [583006]: Trong mặt phẳng tọa độ 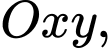 cho đường thẳng
cho đường thẳng 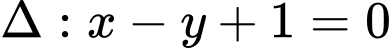 và đường tròn
và đường tròn 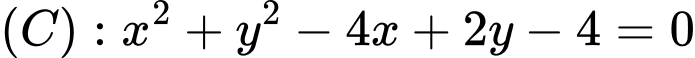
a) Chứng minh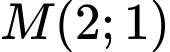 nằm trong đường tròn
nằm trong đường tròn
b) Xét vị trí tương đối của và
và 
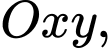 cho đường thẳng
cho đường thẳng 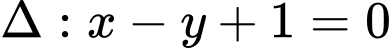 và đường tròn
và đường tròn 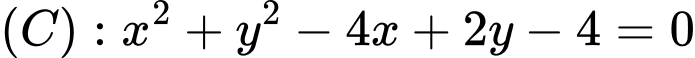
a) Chứng minh
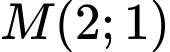 nằm trong đường tròn
nằm trong đường trònb) Xét vị trí tương đối của
 và
và 
a) Đường tròn  có tâm
có tâm 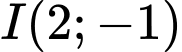 và bán kính
và bán kính  Ta có
Ta có
 Do đó
Do đó 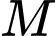 nằm trong
nằm trong 
b)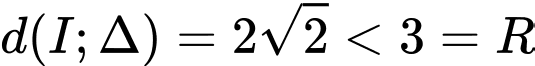 nên
nên  cắt
cắt  tại 2 điểm phân biệt.
tại 2 điểm phân biệt.
 có tâm
có tâm 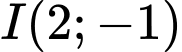 và bán kính
và bán kính  Ta có
Ta có Do đó
Do đó 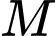 nằm trong
nằm trong 
b)
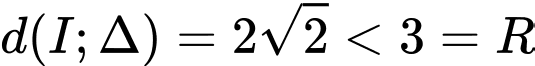 nên
nên  cắt
cắt  tại 2 điểm phân biệt.
tại 2 điểm phân biệt.
Câu 8 [583007]: Trong mặt phẳng tọa độ 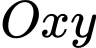 cho đường tròn
cho đường tròn 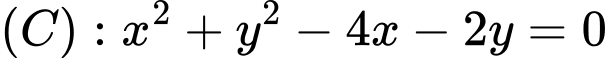 và đường thẳng
và đường thẳng 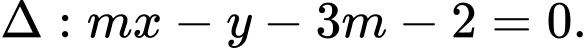 Biện luận theo
Biện luận theo 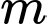 số giao điểm của
số giao điểm của  và
và 
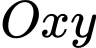 cho đường tròn
cho đường tròn 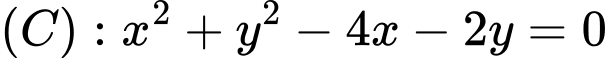 và đường thẳng
và đường thẳng 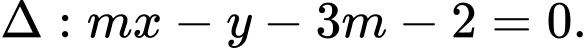 Biện luận theo
Biện luận theo 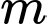 số giao điểm của
số giao điểm của  và
và 
Đường tròn  có tâm
có tâm 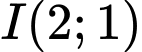 và bán kính
và bán kính 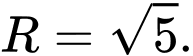
Ta có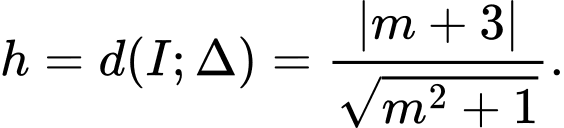
• Nếu hoặc
hoặc 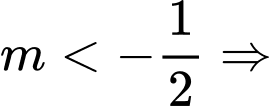
 cắt
cắt  tại 2 điểm phân biệt.
tại 2 điểm phân biệt.
• Nếu hoặc
hoặc 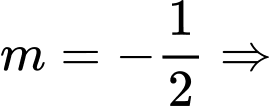
 tiếp xúc
tiếp xúc 
• Nếu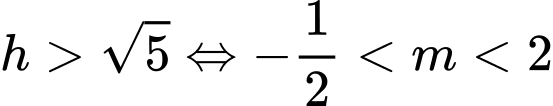
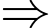
 không cắt
không cắt 
 có tâm
có tâm 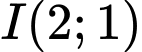 và bán kính
và bán kính 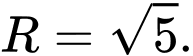
Ta có
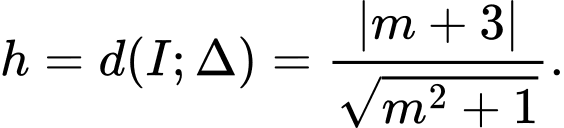
• Nếu
 hoặc
hoặc 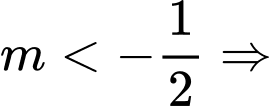
 cắt
cắt  tại 2 điểm phân biệt.
tại 2 điểm phân biệt.• Nếu
 hoặc
hoặc 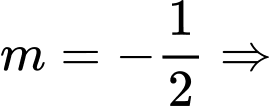
 tiếp xúc
tiếp xúc 
• Nếu
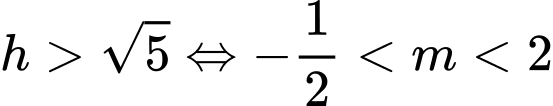
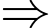
 không cắt
không cắt 
Câu 9 [583008]: Trong mặt phẳng 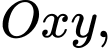 cho hai đường tròn:
cho hai đường tròn: 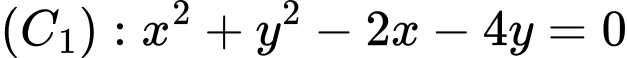 và
và 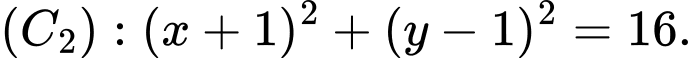 Viết phương trình đường thẳng đi qua giao điểm của hai đường tròn đó.
Viết phương trình đường thẳng đi qua giao điểm của hai đường tròn đó.
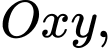 cho hai đường tròn:
cho hai đường tròn: 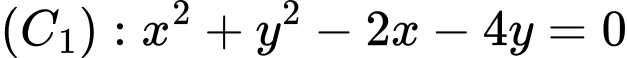 và
và 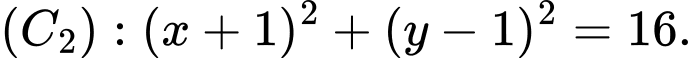 Viết phương trình đường thẳng đi qua giao điểm của hai đường tròn đó.
Viết phương trình đường thẳng đi qua giao điểm của hai đường tròn đó. 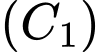 có tâm
có tâm 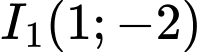 và bán kính
và bán kính 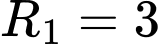
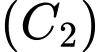 có tâm
có tâm 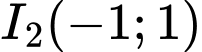 và bán kính
và bán kính 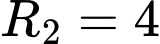
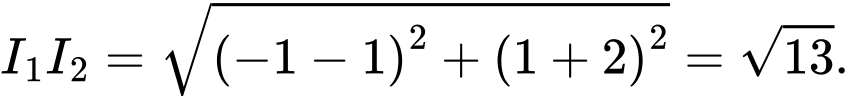
Ta thấy
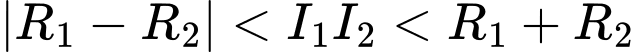 suy ra hai đường tròn cắt nhau.
suy ra hai đường tròn cắt nhau.Gọi điểm
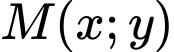 thuộc đường thẳng cần tìm
thuộc đường thẳng cần tìmTọa độ
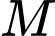 thỏa mãn hệ
thỏa mãn hệ 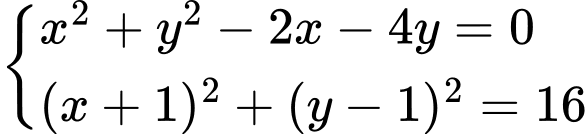
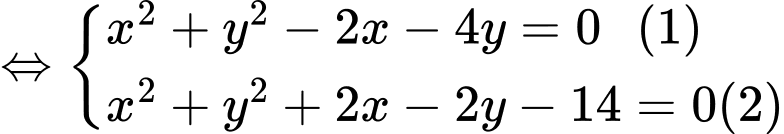
Lấy

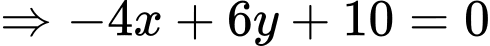
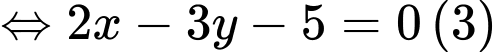
Nhận thấy
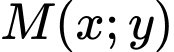 luôn thỏa mãn phương trình (3)
luôn thỏa mãn phương trình (3)Suy ra đường thẳng qua giao điểm của hai đường tròn là:
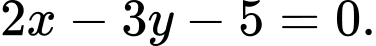
Dạng toán: Phương trình tiếp tuyến của đường tròn
Câu 10 [583009]: Trong mặt phẳng tọa độ 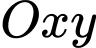 cho đường tròn
cho đường tròn 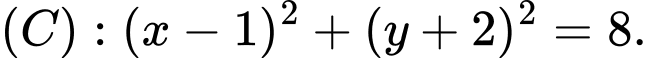
a) Viết phương trình tiếp tuyến của đường tròn tại điểm
tại điểm 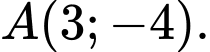
b) Viết phương trình tiếp tuyến của đường tròn qua điểm
qua điểm 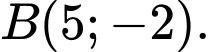
c) Viết phương trình tiếp tuyến của đường tròn biết tiếp tuyến vuông góc với
biết tiếp tuyến vuông góc với 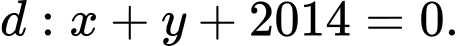
d) Viết phương trình tiếp tuyến của đường tròn biết tiếp tuyến tạo với trục tung một góc
biết tiếp tuyến tạo với trục tung một góc 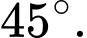
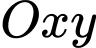 cho đường tròn
cho đường tròn 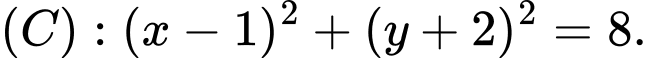
a) Viết phương trình tiếp tuyến của đường tròn
 tại điểm
tại điểm 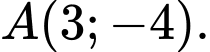
b) Viết phương trình tiếp tuyến của đường tròn
 qua điểm
qua điểm 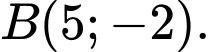
c) Viết phương trình tiếp tuyến của đường tròn
 biết tiếp tuyến vuông góc với
biết tiếp tuyến vuông góc với 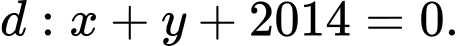
d) Viết phương trình tiếp tuyến của đường tròn
 biết tiếp tuyến tạo với trục tung một góc
biết tiếp tuyến tạo với trục tung một góc 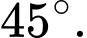
a) Đường tròn  có tâm
có tâm 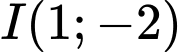 và bán kính
và bán kính 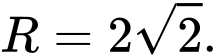
Do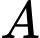 thuộc
thuộc  nên tiếp tuyến
nên tiếp tuyến  qua
qua 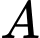 và nhận
và nhận 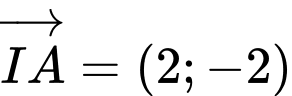 làm vectơ pháp tuyến
làm vectơ pháp tuyến
Vậy phương trình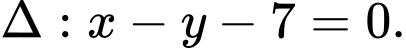
b) Gọi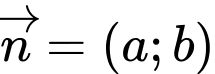 là vectơ pháp tuyến của
là vectơ pháp tuyến của 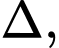 do đó
do đó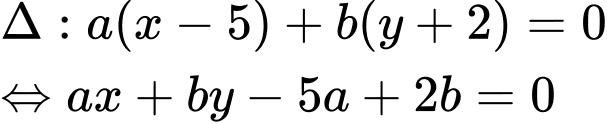
Do tiếp xúc với
tiếp xúc với  nên
nên
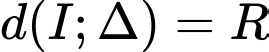
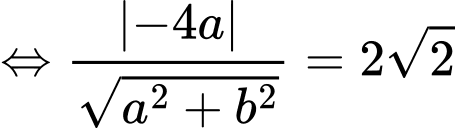
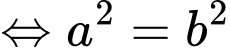
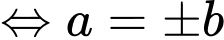
Với chọn
chọn 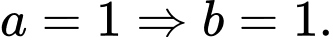 Phương trình tiếp tuyến
Phương trình tiếp tuyến  là
là 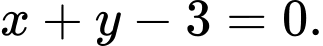
Với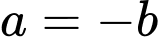 chọn
chọn 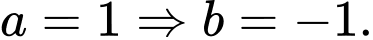 Phương trình tiếp tuyến
Phương trình tiếp tuyến  là
là 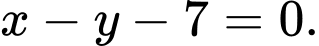
c) Tiếp tuyến vuông góc
vuông góc 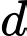 nên
nên  có dạng
có dạng 
Mà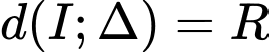
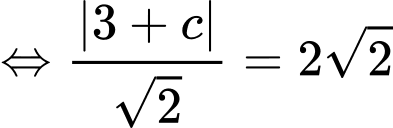
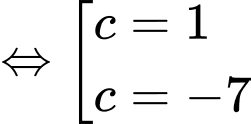
Vậy có 2 tiếp tuyến thỏa mãn: hoặc
hoặc 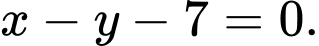
d) Gọi có dạng
có dạng 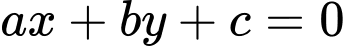
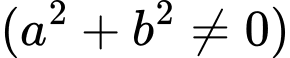
Theo câu ra ta có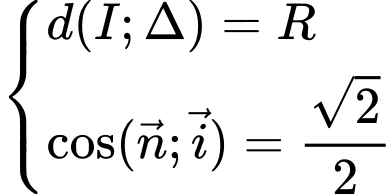
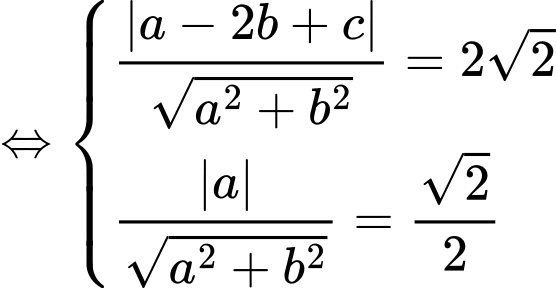
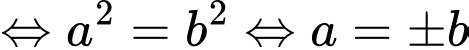
Với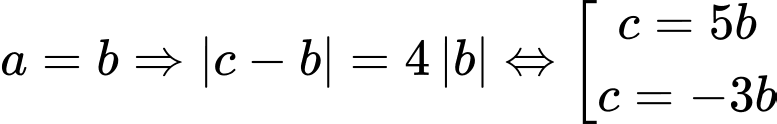
+ TH1: chọn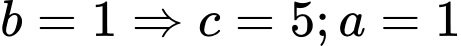 ta được
ta được 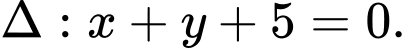
+ TH2: chọn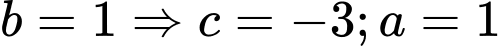 ta được
ta được 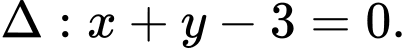
Với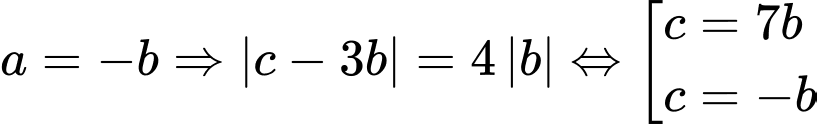
+ TH1: chọn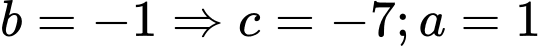 ta được
ta được 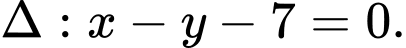
+ TH2: chọn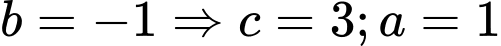 ta được
ta được 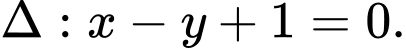
Vậy có 4 tiếp tuyến cần tìm là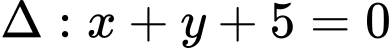 ;
; 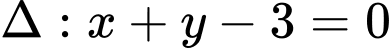 ;
; 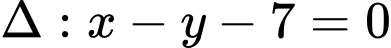 ;
; 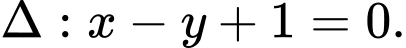
 có tâm
có tâm 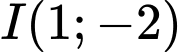 và bán kính
và bán kính 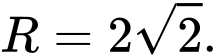
Do
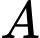 thuộc
thuộc  nên tiếp tuyến
nên tiếp tuyến  qua
qua 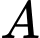 và nhận
và nhận 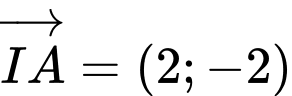 làm vectơ pháp tuyến
làm vectơ pháp tuyếnVậy phương trình
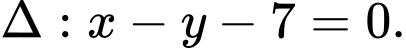
b) Gọi
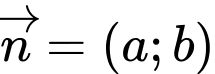 là vectơ pháp tuyến của
là vectơ pháp tuyến của 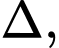 do đó
do đó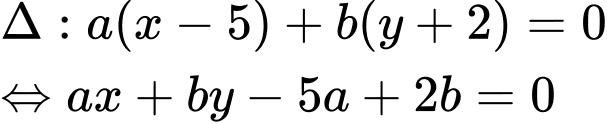
Do
 tiếp xúc với
tiếp xúc với  nên
nên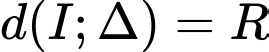
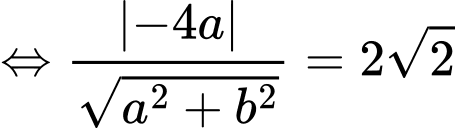
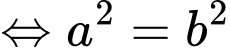
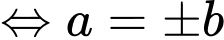
Với
 chọn
chọn 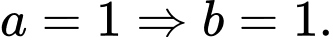 Phương trình tiếp tuyến
Phương trình tiếp tuyến  là
là 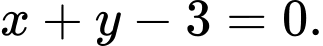
Với
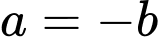 chọn
chọn 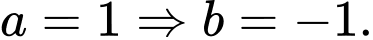 Phương trình tiếp tuyến
Phương trình tiếp tuyến  là
là 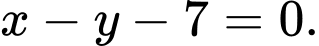
c) Tiếp tuyến
 vuông góc
vuông góc 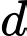 nên
nên  có dạng
có dạng 
Mà
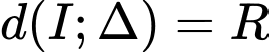
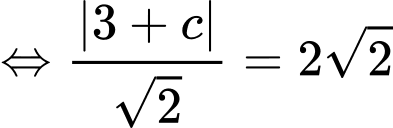
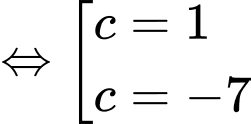
Vậy có 2 tiếp tuyến thỏa mãn:
 hoặc
hoặc 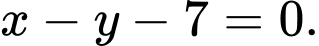
d) Gọi
 có dạng
có dạng 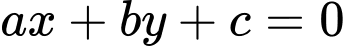
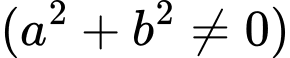
Theo câu ra ta có
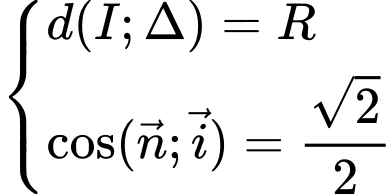
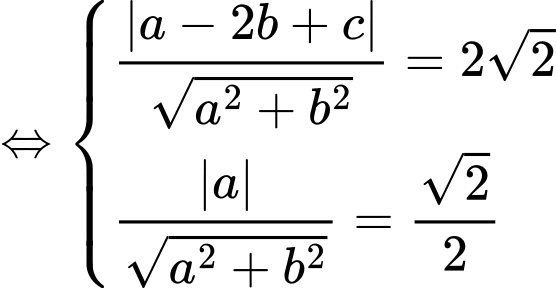
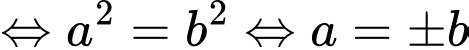
Với
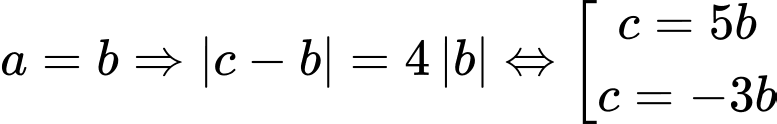
+ TH1: chọn
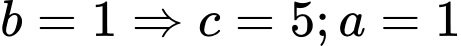 ta được
ta được 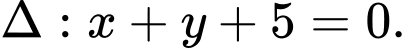
+ TH2: chọn
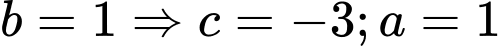 ta được
ta được 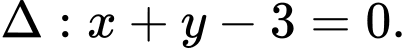
Với
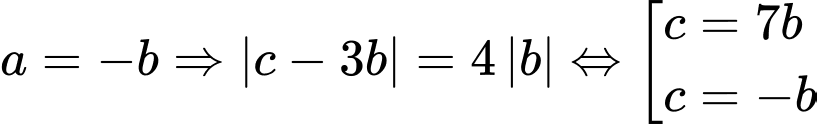
+ TH1: chọn
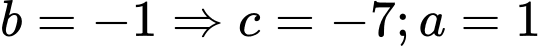 ta được
ta được 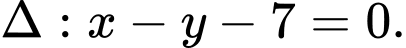
+ TH2: chọn
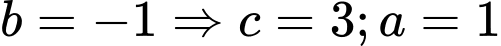 ta được
ta được 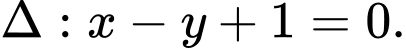
Vậy có 4 tiếp tuyến cần tìm là
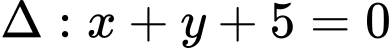 ;
; 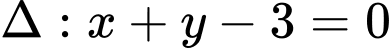 ;
; 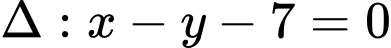 ;
; 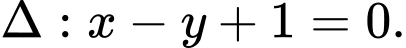
Câu 11 [583010]: Trong mặt phẳng tọa độ 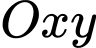 cho đường tròn
cho đường tròn 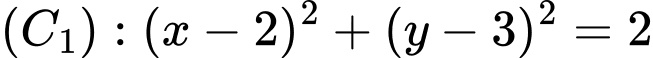 và
và 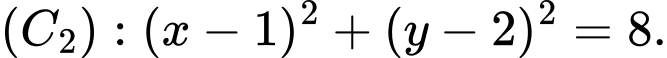 Viết phương trình tiếp tuyến chung của 2 đường tròn.
Viết phương trình tiếp tuyến chung của 2 đường tròn.
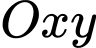 cho đường tròn
cho đường tròn 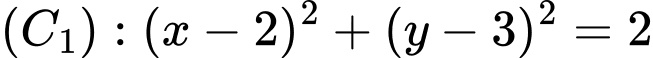 và
và 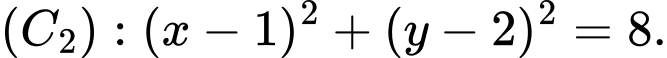 Viết phương trình tiếp tuyến chung của 2 đường tròn.
Viết phương trình tiếp tuyến chung của 2 đường tròn. 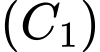 có tâm
có tâm 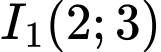 và bán kính
và bán kính 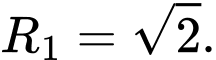
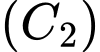 có tâm
có tâm 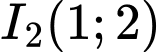 và bán kính
và bán kính 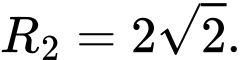
Ta có
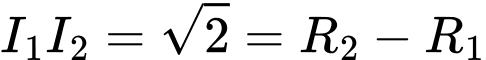 do đó 2 đường tròn tiếp xúc trong. Như vậy có 1 tiếp tuyến chung.
do đó 2 đường tròn tiếp xúc trong. Như vậy có 1 tiếp tuyến chung.
Tọa độ tiếp điểm của 2 đường tròn là nghiệm hệ
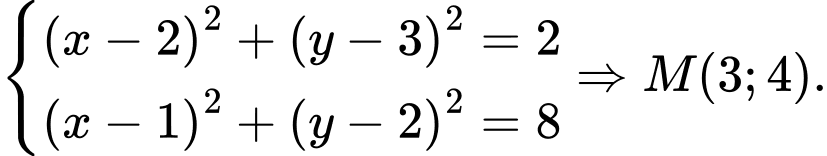
Tiếp tuyến chung
 là đường thẳng qua
là đường thẳng qua 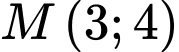 và nhận
và nhận 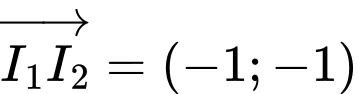 làm vectơ pháp tuyến nên có phương trình
làm vectơ pháp tuyến nên có phương trình 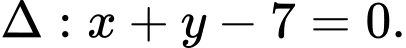
Câu 12 [583011]: Trong mặt phẳng 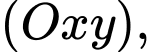 cho
cho 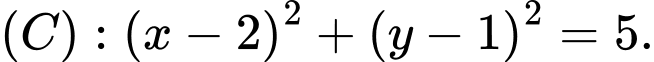 Viết phương trình tiếp tuyến của
Viết phương trình tiếp tuyến của  biết tiếp tuyến cắt
biết tiếp tuyến cắt 
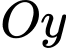 lần lượt tại
lần lượt tại 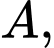
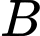 sao cho
sao cho 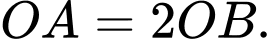
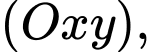 cho
cho 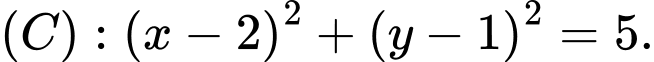 Viết phương trình tiếp tuyến của
Viết phương trình tiếp tuyến của  biết tiếp tuyến cắt
biết tiếp tuyến cắt 
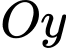 lần lượt tại
lần lượt tại 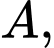
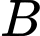 sao cho
sao cho 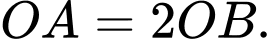
 có tâm
có tâm 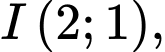 bán kính
bán kính 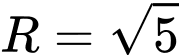
Tiếp tuyến cắt

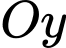 lần lượt tại
lần lượt tại 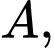
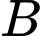 sao cho
sao cho 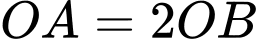
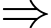 Tiếp tuyến có hệ số góc
Tiếp tuyến có hệ số góc 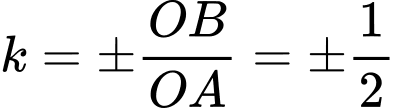 .
.Trường hợp 1: Với
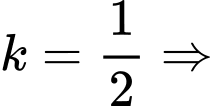 Phương trình tiếp tuyến có dạng
Phương trình tiếp tuyến có dạng 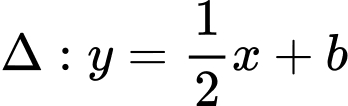
 là tiếp tuyến của
là tiếp tuyến của 
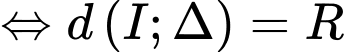
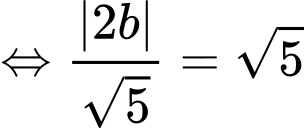
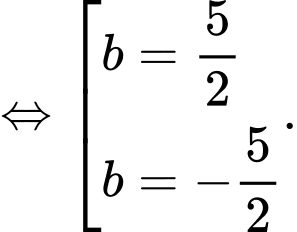
Suy ra phương trình tiếp tuyến cần tìm là
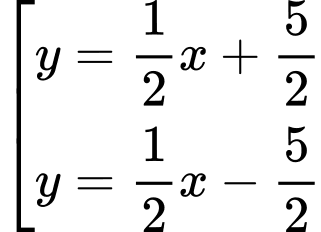
Trường hợp 2: Với
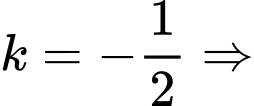 Phương trình tiếp tuyến có dạng
Phương trình tiếp tuyến có dạng 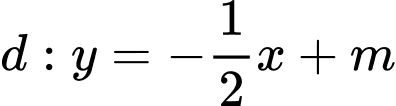
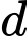 là tiếp tuyến của
là tiếp tuyến của 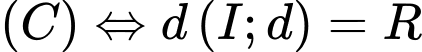
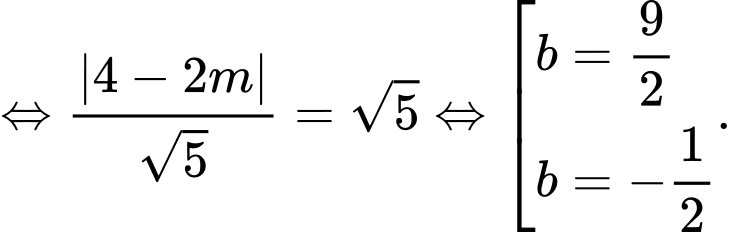
Suy ra phương trình tiếp tuyến cần tìm là
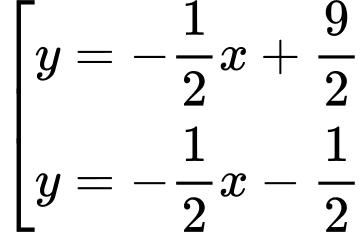
Vậy có 4 tiếp tuyến thỏa mãn điều kiện.
Dạng toán: Quỹ tích tâm đường tròn
Câu 13 [583012]: Trong mặt phẳng 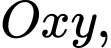 cho phương trình đường cong
cho phương trình đường cong  có phương trình:
có phương trình: 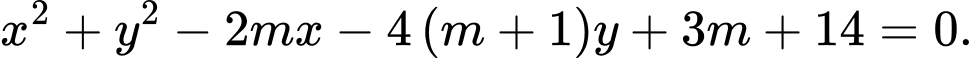
a) Tìm tham số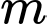 để
để  là đường tròn.
là đường tròn.
b) Tìm quỹ tích điểm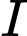 là tâm của đường tròn
là tâm của đường tròn 
 cho phương trình đường cong
cho phương trình đường cong  có phương trình:
có phương trình: 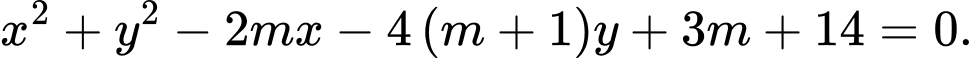
a) Tìm tham số
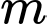 để
để  là đường tròn.
là đường tròn. b) Tìm quỹ tích điểm
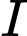 là tâm của đường tròn
là tâm của đường tròn 
a) Tìm tham số 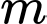 để
để  là đường tròn.
là đường tròn.
Điều kiện để là đường tròn :
là đường tròn : 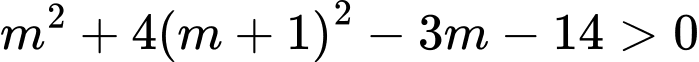
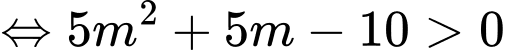
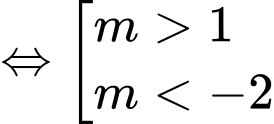 (1)
(1)
b) Tìm quỹ tích điểm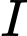 là tâm của đường tròn
là tâm của đường tròn 
Tâm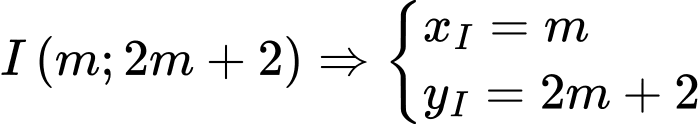
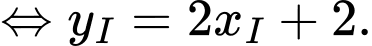
Theo điều kiện (1) (câu a), ta được quỹ tích tâm I của là một phần đường thẳng có phương trình :
là một phần đường thẳng có phương trình :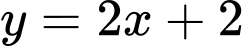 ứng với
ứng với 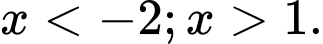
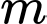 để
để  là đường tròn.
là đường tròn. Điều kiện để
 là đường tròn :
là đường tròn : 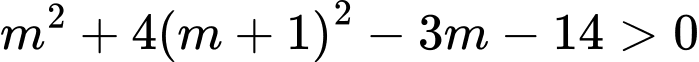
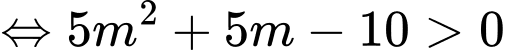
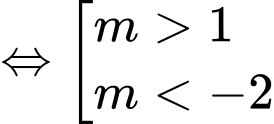 (1)
(1)b) Tìm quỹ tích điểm
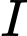 là tâm của đường tròn
là tâm của đường tròn 
Tâm
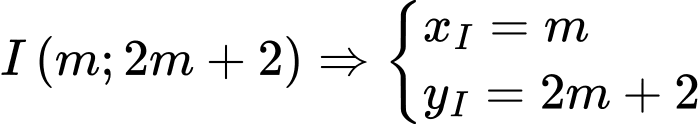
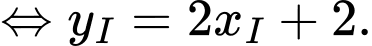
Theo điều kiện (1) (câu a), ta được quỹ tích tâm I của
 là một phần đường thẳng có phương trình :
là một phần đường thẳng có phương trình :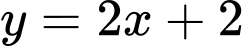 ứng với
ứng với 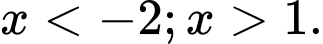
Câu 14 [583013]: Trong mặt phẳng 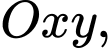 tìm quỹ tích điểm
tìm quỹ tích điểm 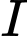 là tâm của đường tròn
là tâm của đường tròn  có bán kính
có bán kính 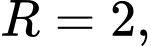 biết
biết  tiếp xúc tiếp xúc với đường tròn
tiếp xúc tiếp xúc với đường tròn 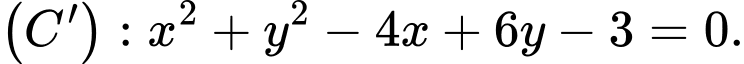
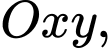 tìm quỹ tích điểm
tìm quỹ tích điểm 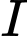 là tâm của đường tròn
là tâm của đường tròn  có bán kính
có bán kính 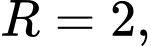 biết
biết  tiếp xúc tiếp xúc với đường tròn
tiếp xúc tiếp xúc với đường tròn 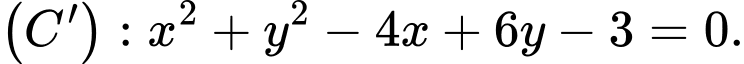
Gọi tâm 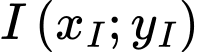 của đường tròn
của đường tròn 
 tiếp xúc với
tiếp xúc với 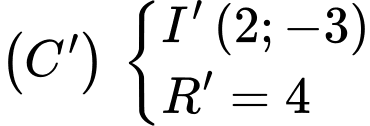 và có bán kính
và có bán kính 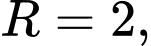 nên:
nên:
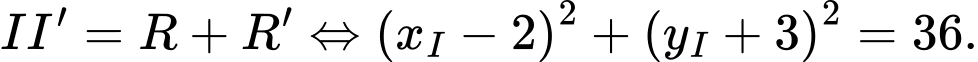
Vậy quỹ tích tâm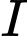 của đường tròn
của đường tròn  là đường tròn có phương trình:
là đường tròn có phương trình: 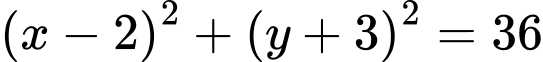
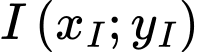 của đường tròn
của đường tròn 
 tiếp xúc với
tiếp xúc với 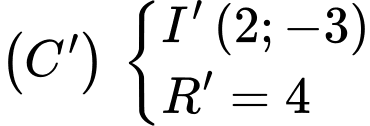 và có bán kính
và có bán kính 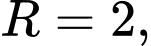 nên:
nên: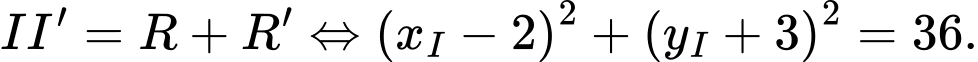
Vậy quỹ tích tâm
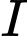 của đường tròn
của đường tròn  là đường tròn có phương trình:
là đường tròn có phương trình: 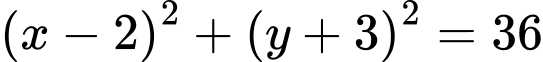
Câu 15 [583014]: Cho 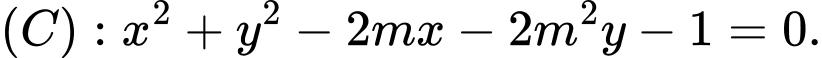 Tìm quỹ tích tâm
Tìm quỹ tích tâm 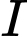 của đường tròn
của đường tròn 
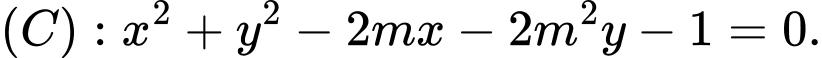 Tìm quỹ tích tâm
Tìm quỹ tích tâm 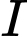 của đường tròn
của đường tròn 
 có dạng
có dạng 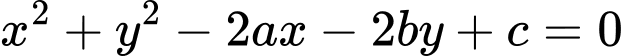 với
với 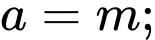
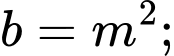
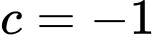 là phương trình đường tròn
là phương trình đường tròn 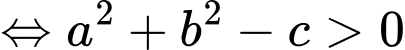
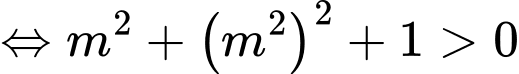
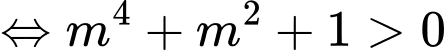 (Luôn đúng
(Luôn đúng 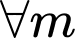 )
)Khi đó,
 có tâm
có tâm 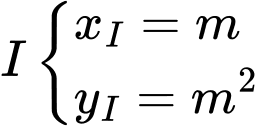
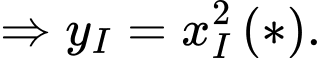 Tọa độ tâm
Tọa độ tâm 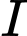 thỏa mãn
thỏa mãn 
Vậy
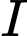 nằm trên Parabol có phương trình
nằm trên Parabol có phương trình