Dạng toán: Xác định một vectơ, phương, hướng của một vectơ
Câu 1 [582937]: Cho 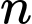 điểm phân biệt. Hãy xác định số vectơ khác vectơ
điểm phân biệt. Hãy xác định số vectơ khác vectơ  có điểm đầu và điểm cuối thuộc
có điểm đầu và điểm cuối thuộc 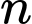 điểm trên?
điểm trên?
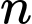 điểm phân biệt. Hãy xác định số vectơ khác vectơ
điểm phân biệt. Hãy xác định số vectơ khác vectơ  có điểm đầu và điểm cuối thuộc
có điểm đầu và điểm cuối thuộc 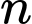 điểm trên?
điểm trên?
Khi có 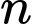 điểm, ta có
điểm, ta có 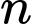 cách chọn điểm đầu và
cách chọn điểm đầu và 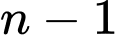 cách chọn điểm cuối. Nên ta sẽ có
cách chọn điểm cuối. Nên ta sẽ có 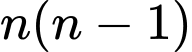 cách xác định số vectơ khác
cách xác định số vectơ khác  thuộc
thuộc 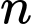 điểm trên.
điểm trên.
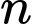 điểm, ta có
điểm, ta có 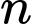 cách chọn điểm đầu và
cách chọn điểm đầu và 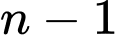 cách chọn điểm cuối. Nên ta sẽ có
cách chọn điểm cuối. Nên ta sẽ có 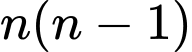 cách xác định số vectơ khác
cách xác định số vectơ khác  thuộc
thuộc 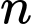 điểm trên.
điểm trên.
Câu 2 [582938]: Cho hình bình hành 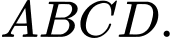 Tìm vectơ khác
Tìm vectơ khác 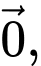 cùng phương với vectơ
cùng phương với vectơ 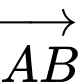 và có điểm đầu, điểm cuối là đỉnh của hình bình hành
và có điểm đầu, điểm cuối là đỉnh của hình bình hành 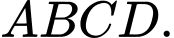
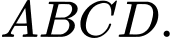 Tìm vectơ khác
Tìm vectơ khác 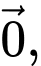 cùng phương với vectơ
cùng phương với vectơ 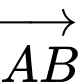 và có điểm đầu, điểm cuối là đỉnh của hình bình hành
và có điểm đầu, điểm cuối là đỉnh của hình bình hành 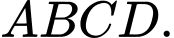
Các vectơ cùng phương với 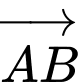 mà thỏa mãn điều kiện đầu câu là:
mà thỏa mãn điều kiện đầu câu là: 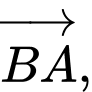
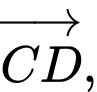
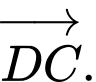
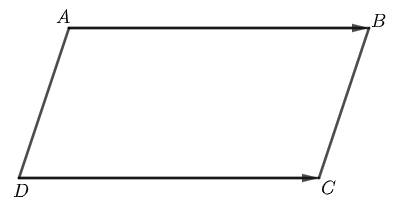
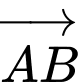 mà thỏa mãn điều kiện đầu câu là:
mà thỏa mãn điều kiện đầu câu là: 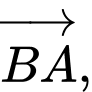
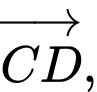
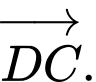

Câu 3 [582939]: Cho ba điểm 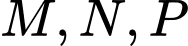 thẳng hàng, trong đó điểm
thẳng hàng, trong đó điểm 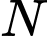 nằm giữa hai điểm
nằm giữa hai điểm 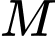 và
và 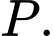 Khi đó các cặp vectơ nào sau đây cùng hướng?
Khi đó các cặp vectơ nào sau đây cùng hướng?
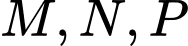 thẳng hàng, trong đó điểm
thẳng hàng, trong đó điểm 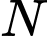 nằm giữa hai điểm
nằm giữa hai điểm 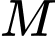 và
và 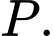 Khi đó các cặp vectơ nào sau đây cùng hướng?
Khi đó các cặp vectơ nào sau đây cùng hướng? A, 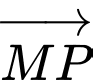 và
và 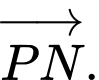
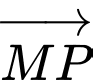 và
và 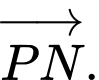
B, 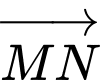 và
và 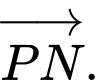
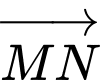 và
và 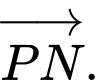
C,  và
và 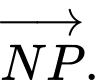
 và
và 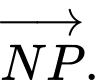
D, 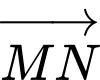 và
và 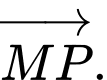
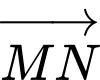 và
và 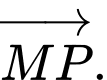

Cặp vectơ cùng hướng là
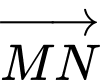 và
và 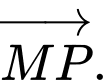 Đáp án: D
Đáp án: D Dạng toán: Chứng minh hai vectơ bằng nhau
Câu 4 [582940]: Cho hình vuông 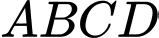 tâm
tâm  Hãy liệt kê tất cả các vectơ bằng nhau nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối.
Hãy liệt kê tất cả các vectơ bằng nhau nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối.
 tâm
tâm  Hãy liệt kê tất cả các vectơ bằng nhau nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối.
Hãy liệt kê tất cả các vectơ bằng nhau nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối. 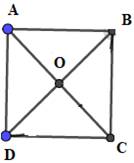
Các vectơ bằng nhau nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối là:
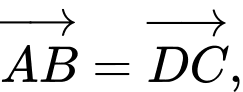
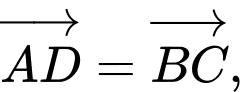
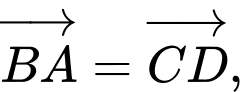
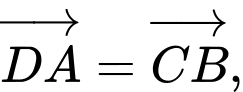
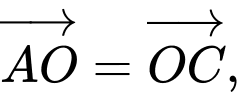
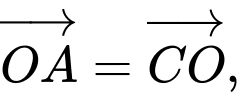
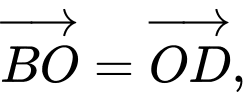
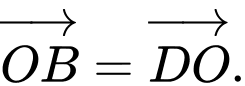
Câu 5 [582941]: Cho tam giác 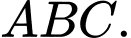 Gọi
Gọi 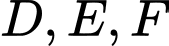 lần lượt là trung điểm các cạnh
lần lượt là trung điểm các cạnh 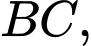
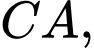
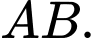 Chứng minh
Chứng minh 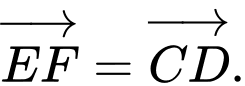
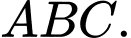 Gọi
Gọi 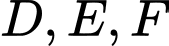 lần lượt là trung điểm các cạnh
lần lượt là trung điểm các cạnh 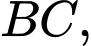
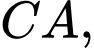
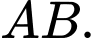 Chứng minh
Chứng minh 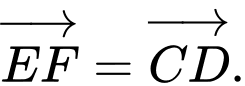
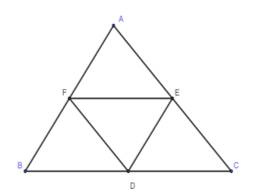
Cách 1: Vì
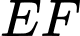 là đường trung bình của tam giác
là đường trung bình của tam giác 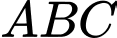 nên
nên 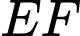 //
// 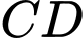 nên
nên 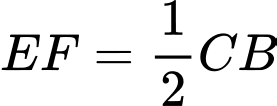
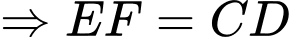
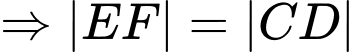 (1).
(1).Mặt khác:
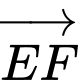 cùng hướng
cùng hướng 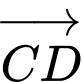 (2).
(2).Từ (1) và (2) ta có:
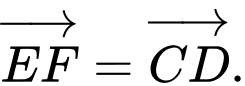
Cách 2: Chứng minh
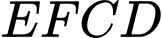 là hình bình hành
là hình bình hànhDễ chứng minh được
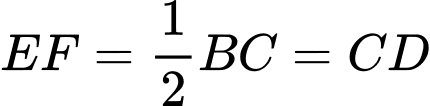 và
và 
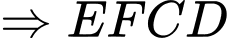 là hình bình hành
là hình bình hành 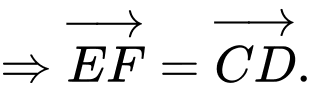
Câu 6 [582942]: Cho hình bình hành 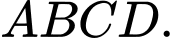 Gọi
Gọi 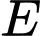 là điểm đối xứng
là điểm đối xứng  của qua
của qua  Chứng minh rằng
Chứng minh rằng 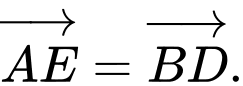
 Gọi
Gọi 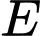 là điểm đối xứng
là điểm đối xứng  của qua
của qua  Chứng minh rằng
Chứng minh rằng 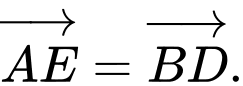
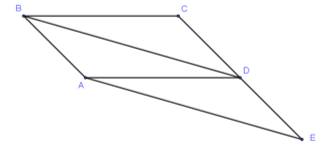
Vì
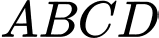 là hình bình hành nên ta có:
là hình bình hành nên ta có: 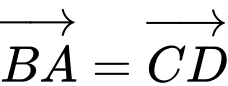 (1).
(1).Ta có:
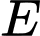 là điểm đối xứng
là điểm đối xứng  của qua
của qua 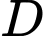 nên
nên 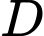 là trung điểm của
là trung điểm của 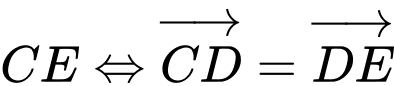 (2).
(2).Từ (1) và (2) ta có:
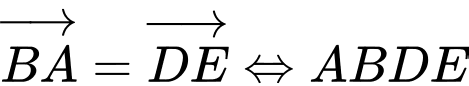 là hình bình hành nên
là hình bình hành nên 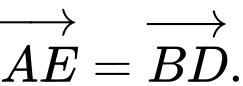
Dạng toán: Xác định điểm thoả đẳng thức vectơ
Câu 7 [582943]: Cho tam giác 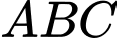 có trọng tâm
có trọng tâm  và
và 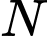 là điểm thỏa mãn
là điểm thỏa mãn 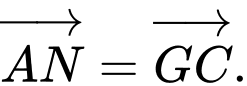 Hãy xác định vị trí điểm
Hãy xác định vị trí điểm 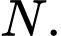
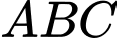 có trọng tâm
có trọng tâm  và
và 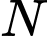 là điểm thỏa mãn
là điểm thỏa mãn 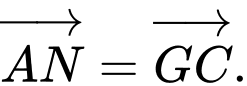 Hãy xác định vị trí điểm
Hãy xác định vị trí điểm 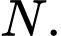
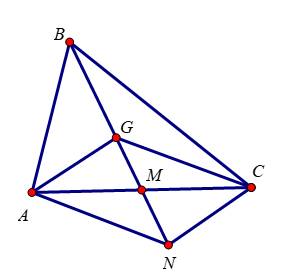
Do
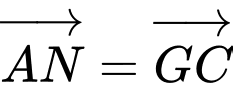 và
và 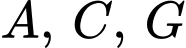 không thẳng hàng nên
không thẳng hàng nên 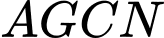 là hình bình hành.
là hình bình hành.
Vậy
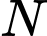 đối xứng với
đối xứng với  qua trung điểm
qua trung điểm 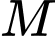 của
của 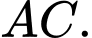
Câu 8 [582944]: Cho hình thang 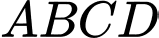 với đáy
với đáy 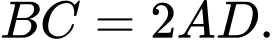 Gọi
Gọi 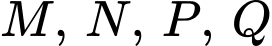 lần lượt là trung điểm của
lần lượt là trung điểm của 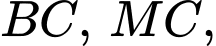
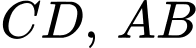 và
và 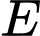 là điểm thỏa mãn
là điểm thỏa mãn 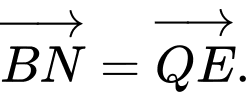 Xác định vị trí điểm
Xác định vị trí điểm 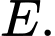
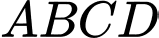 với đáy
với đáy 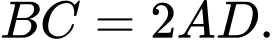 Gọi
Gọi 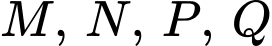 lần lượt là trung điểm của
lần lượt là trung điểm của 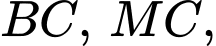
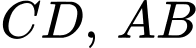 và
và 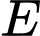 là điểm thỏa mãn
là điểm thỏa mãn 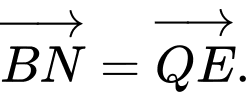 Xác định vị trí điểm
Xác định vị trí điểm 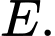
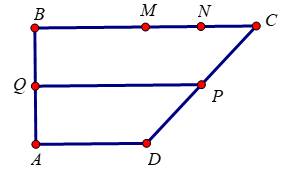
Ta có
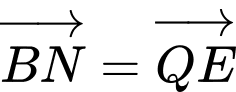 nên
nên 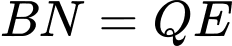 và
và 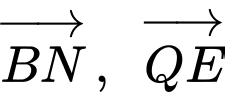 cùng hướng.
cùng hướng.
Mà
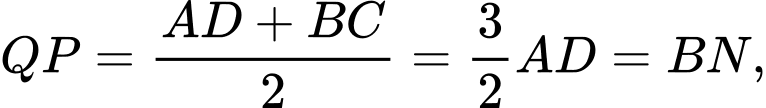 suy ra
suy ra 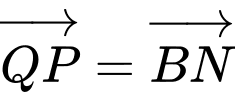 nên
nên 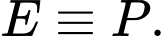
Câu 9 [582945]: Cho bốn điểm 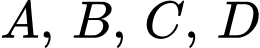 thỏa mãn
thỏa mãn 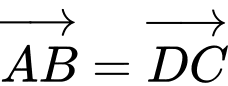 và các mệnh đề. Trong các mệnh đề sau có bao nhiêu mệnh đề đúng
và các mệnh đề. Trong các mệnh đề sau có bao nhiêu mệnh đề đúng
(I)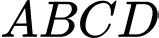 là hình bình hành.
là hình bình hành.
(II)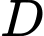 nằm giữa
nằm giữa 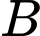 và
và 
(III) nằm trên đường thẳng đi qua điểm
nằm trên đường thẳng đi qua điểm 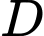 và song song hoặc trùng với đường thẳng
và song song hoặc trùng với đường thẳng 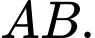
(IV) Bốn điểm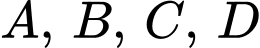 thẳng hàng.
thẳng hàng.
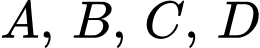 thỏa mãn
thỏa mãn 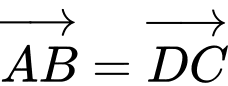 và các mệnh đề. Trong các mệnh đề sau có bao nhiêu mệnh đề đúng
và các mệnh đề. Trong các mệnh đề sau có bao nhiêu mệnh đề đúng(I)
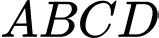 là hình bình hành.
là hình bình hành. (II)
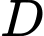 nằm giữa
nằm giữa 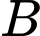 và
và 
(III)
 nằm trên đường thẳng đi qua điểm
nằm trên đường thẳng đi qua điểm 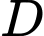 và song song hoặc trùng với đường thẳng
và song song hoặc trùng với đường thẳng 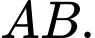
(IV) Bốn điểm
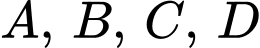 thẳng hàng.
thẳng hàng.
Ta có mệnh đề “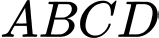 là hình bình hành” là sai khi ba điểm
là hình bình hành” là sai khi ba điểm 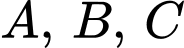 thẳng hàng.
thẳng hàng.
Mệnh đề “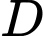 nằm giữa
nằm giữa 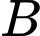 và
và  ” là sai khi ba điểm
” là sai khi ba điểm 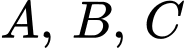 không thẳng hàng.
không thẳng hàng.
Mệnh đề “Bốn điểm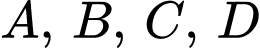 thẳng hàng” là sai khi ba điểm
thẳng hàng” là sai khi ba điểm 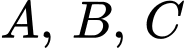 không thẳng hàng.
không thẳng hàng.
Mệnh đề “ nằm trên đường thẳng đi qua điểm
nằm trên đường thẳng đi qua điểm 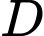 và song song hoặc trùng với đường thẳng
và song song hoặc trùng với đường thẳng  ” là đúng theo định nghĩa hai vectơ bằng nhau.
” là đúng theo định nghĩa hai vectơ bằng nhau.
Vậy số mệnh đề đúng là 1.
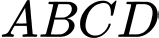 là hình bình hành” là sai khi ba điểm
là hình bình hành” là sai khi ba điểm 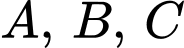 thẳng hàng.
thẳng hàng.Mệnh đề “
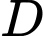 nằm giữa
nằm giữa 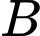 và
và  ” là sai khi ba điểm
” là sai khi ba điểm 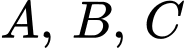 không thẳng hàng.
không thẳng hàng.Mệnh đề “Bốn điểm
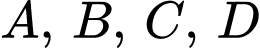 thẳng hàng” là sai khi ba điểm
thẳng hàng” là sai khi ba điểm 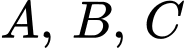 không thẳng hàng.
không thẳng hàng.Mệnh đề “
 nằm trên đường thẳng đi qua điểm
nằm trên đường thẳng đi qua điểm 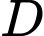 và song song hoặc trùng với đường thẳng
và song song hoặc trùng với đường thẳng  ” là đúng theo định nghĩa hai vectơ bằng nhau.
” là đúng theo định nghĩa hai vectơ bằng nhau.Vậy số mệnh đề đúng là 1.
Dạng toán: Tổng của các vectơ
Câu 10 [582946]: Cho 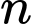 điểm
điểm 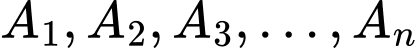 , xác định vectơ
, xác định vectơ
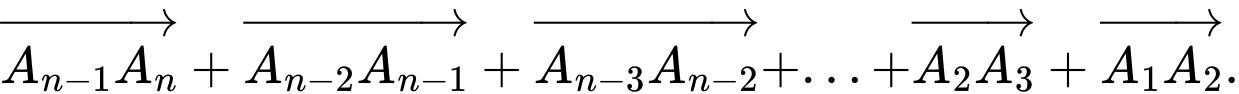
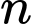 điểm
điểm 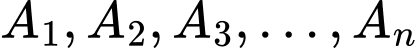 , xác định vectơ
, xác định vectơ 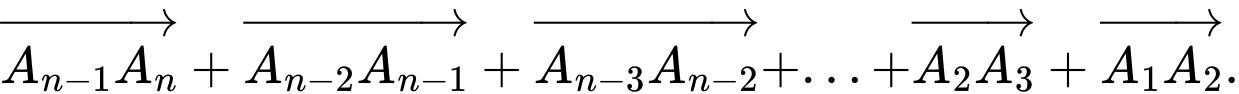
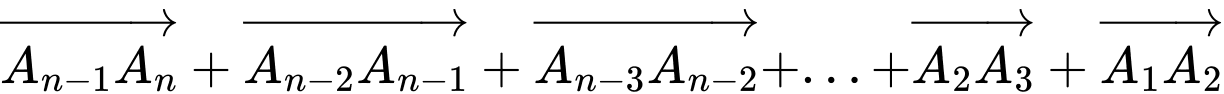
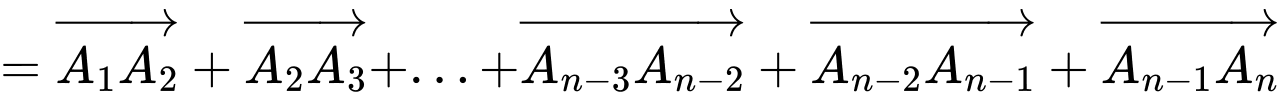
Do đó
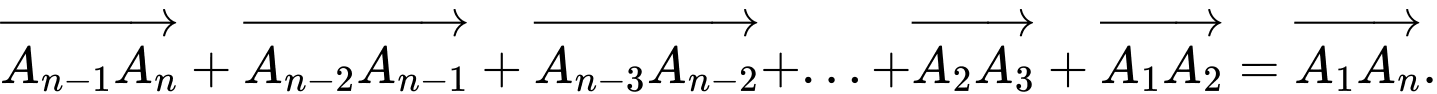
Câu 11 [582947]: Xét tam giác 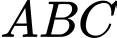 có trọng tâm
có trọng tâm  và tâm đường tròn ngoại tiếp
và tâm đường tròn ngoại tiếp  thỏa mãn
thỏa mãn 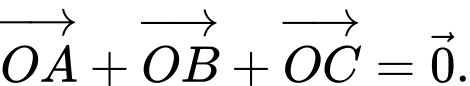 Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng?
Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng?
1)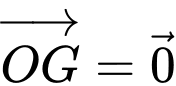 ;
;
2) Tam giác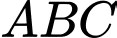 là tam giác vuông cân;
là tam giác vuông cân;
3) Tam giác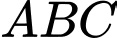 là tam giác đều;
là tam giác đều;
4) Tam giác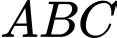 là tam giác cân
là tam giác cân
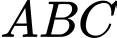 có trọng tâm
có trọng tâm  và tâm đường tròn ngoại tiếp
và tâm đường tròn ngoại tiếp  thỏa mãn
thỏa mãn 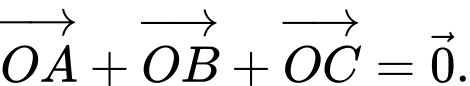 Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng?
Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng?1)
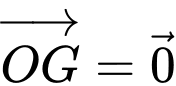 ;
;2) Tam giác
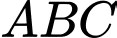 là tam giác vuông cân;
là tam giác vuông cân; 3) Tam giác
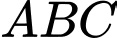 là tam giác đều;
là tam giác đều; 4) Tam giác
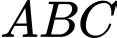 là tam giác cân
là tam giác cân 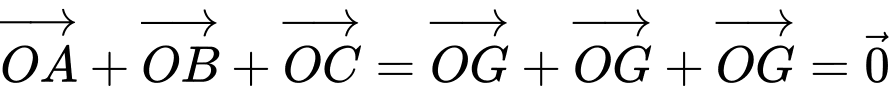

Do đó tam giác
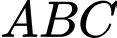 là tam giác đều.
là tam giác đều.
Câu 12 [582948]: Cho tam giác 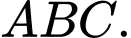 Bên ngoài của tam giác vẽ các hình bình hành
Bên ngoài của tam giác vẽ các hình bình hành 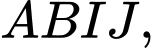
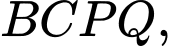
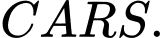 Chứng minh rằng
Chứng minh rằng 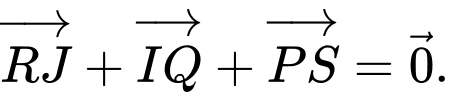
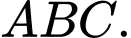 Bên ngoài của tam giác vẽ các hình bình hành
Bên ngoài của tam giác vẽ các hình bình hành 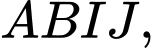
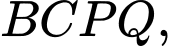
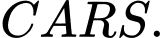 Chứng minh rằng
Chứng minh rằng 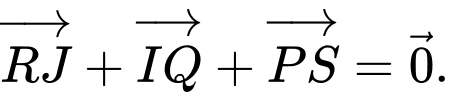
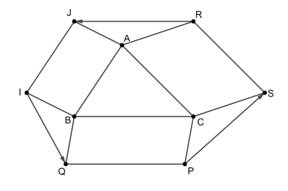
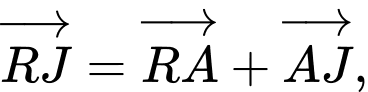
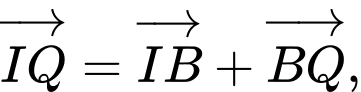
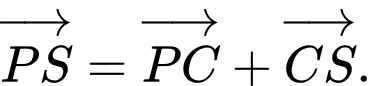
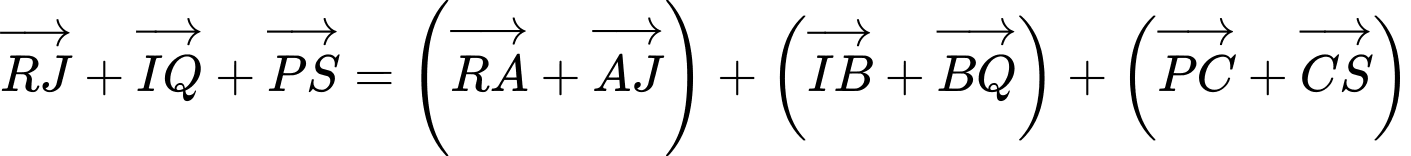
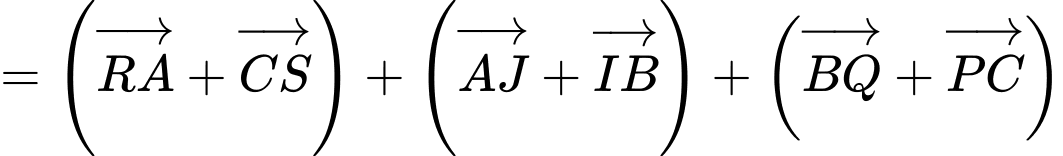
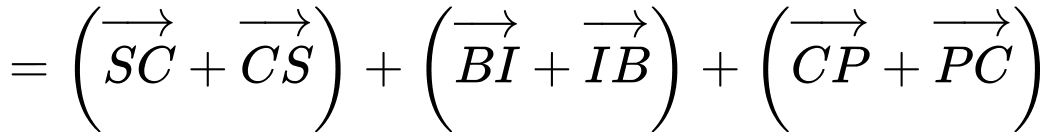
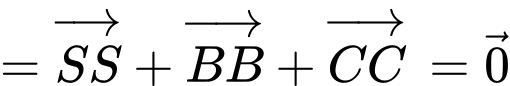
Vậy
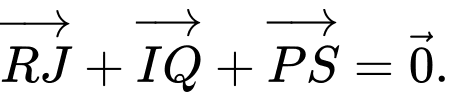
Dạng toán: Vectơ đối, hiệu của của hai vectơ
Câu 13 [582949]: Cho tam giác 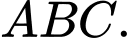 Các điểm
Các điểm 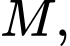
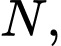
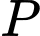 lần lượt là trung điểm của
lần lượt là trung điểm của 

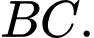
a) Tìm
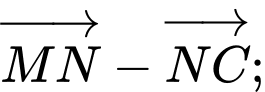
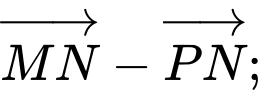
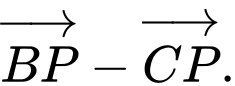
b) Phân tích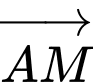 theo hai vectơ
theo hai vectơ 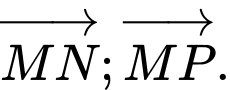
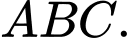 Các điểm
Các điểm 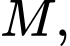
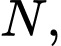
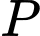 lần lượt là trung điểm của
lần lượt là trung điểm của 

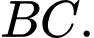
a) Tìm

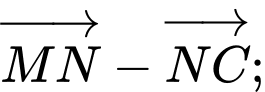
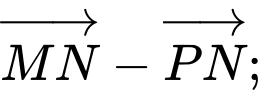
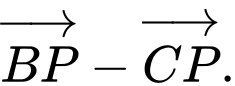
b) Phân tích
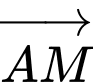 theo hai vectơ
theo hai vectơ 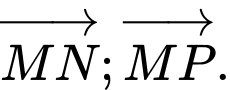
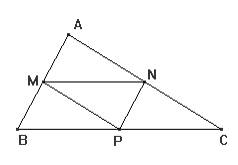
a)
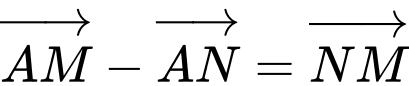
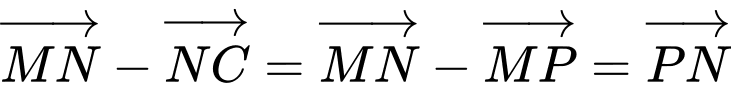 (Vì
(Vì 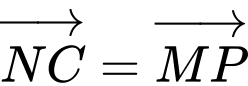 )
)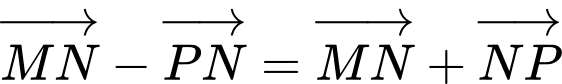 =
=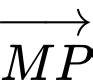
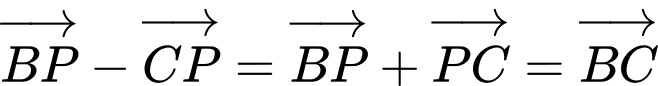
b)
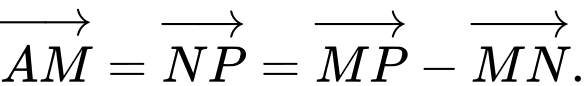
Câu 14 [582950]: Cho 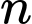 điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là
điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là 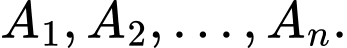 Bạn Bình kí hiệu chúng là
Bạn Bình kí hiệu chúng là 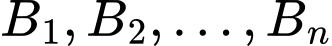 (
( 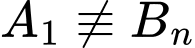 ). Chứng minh rằng:
). Chứng minh rằng: 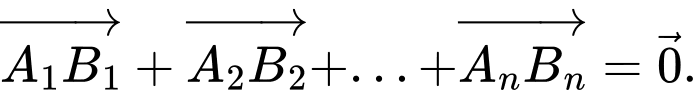
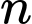 điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là
điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là 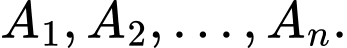 Bạn Bình kí hiệu chúng là
Bạn Bình kí hiệu chúng là 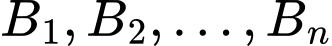 (
( 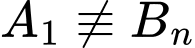 ). Chứng minh rằng:
). Chứng minh rằng: 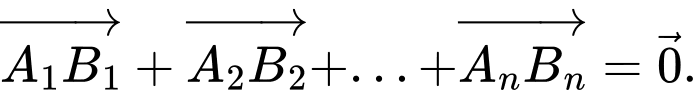
Lấy điểm  bất kì. Khi đó
bất kì. Khi đó
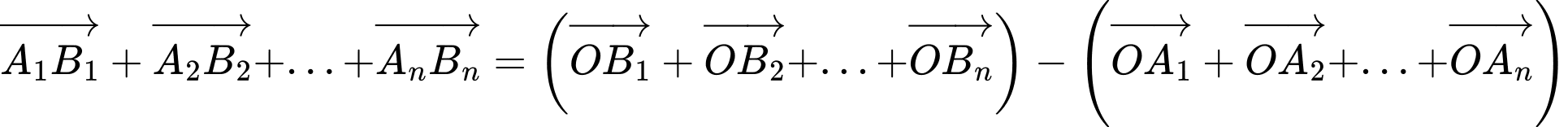
Vì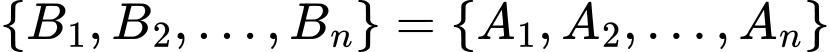 nên
nên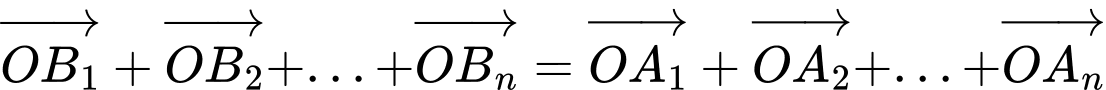
Do đó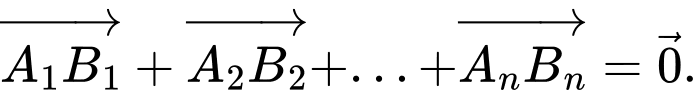
 bất kì. Khi đó
bất kì. Khi đó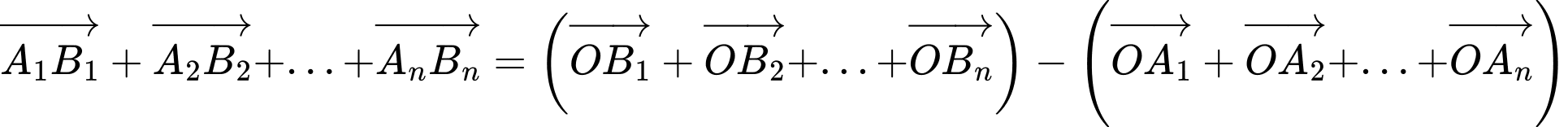
Vì
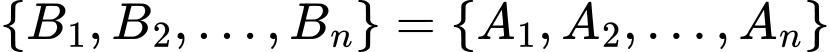 nên
nên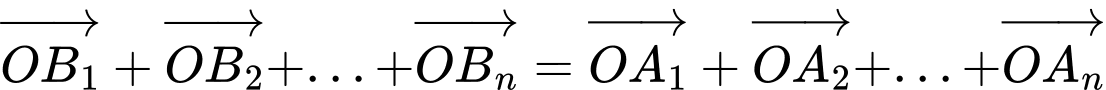
Do đó
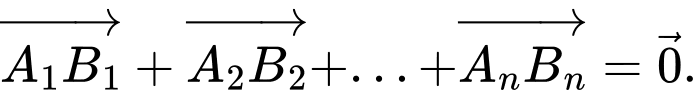
Câu 15 [582951]: Cho tam giác 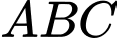 có
có 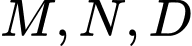 lần lượt là trung điểm của
lần lượt là trung điểm của 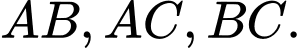 Khi đó, các vectơ đối của vectơ
Khi đó, các vectơ đối của vectơ  là:
là:
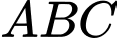 có
có 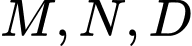 lần lượt là trung điểm của
lần lượt là trung điểm của 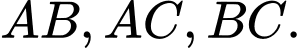 Khi đó, các vectơ đối của vectơ
Khi đó, các vectơ đối của vectơ  là:
là: A, 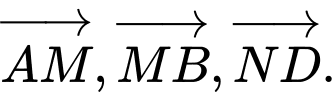
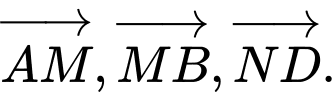
B, 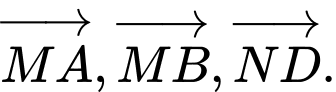
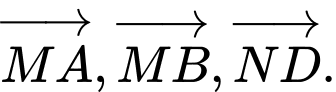
C, 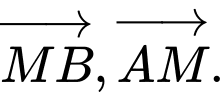
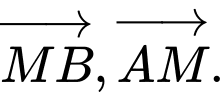
D, 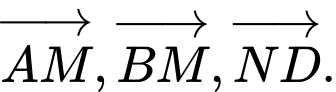
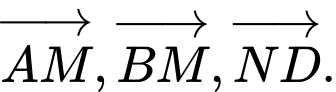
Chọn A
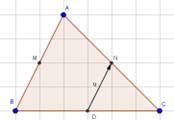
Nhìn hình ta thấy vectơ đối của vectơ là:
là: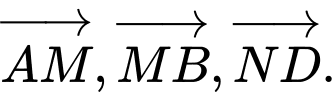 Đáp án: A
Đáp án: A

Nhìn hình ta thấy vectơ đối của vectơ
 là:
là: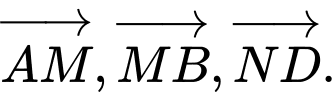 Đáp án: A
Đáp án: A
Câu 16 [582952]: Cho 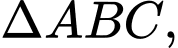 vẽ bên ngoài tam giác các hình bình hành
vẽ bên ngoài tam giác các hình bình hành 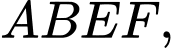
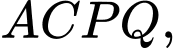
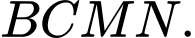 Xét các mệnh đề:
Xét các mệnh đề:
(I)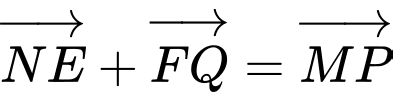
(II)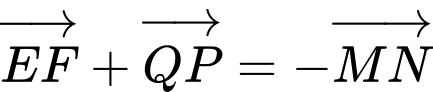
(III)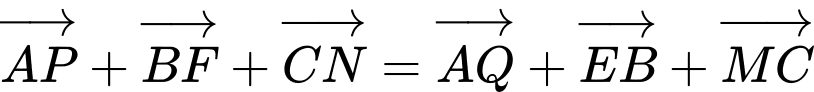
Mệnh đề đúng là :
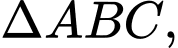 vẽ bên ngoài tam giác các hình bình hành
vẽ bên ngoài tam giác các hình bình hành 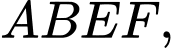
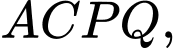
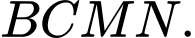 Xét các mệnh đề:
Xét các mệnh đề:(I)
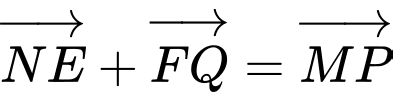
(II)
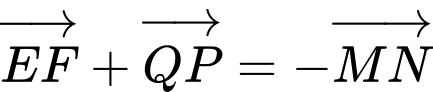
(III)
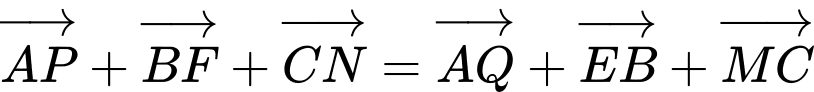
Mệnh đề đúng là :
A, Chỉ (I).
B, Chỉ (III).
C, (I) và (II).
D, Chỉ (II).
Chọn A
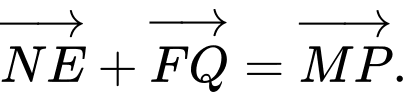 Đáp án: A
Đáp án: A
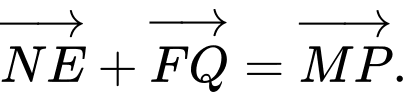 Đáp án: A
Đáp án: A Dạng toán: Tính dộ dài của vectơ
Câu 17 [582953]: Cho hình vuông 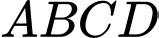 cạnh
cạnh 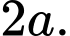 Tính
Tính 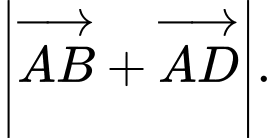
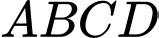 cạnh
cạnh 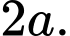 Tính
Tính 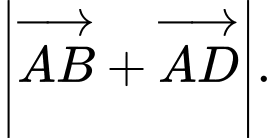
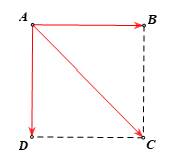
Ta có
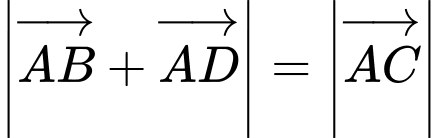

Câu 18 [582954]: Cho tam giác 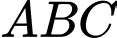 có
có  là trọng tâm,
là trọng tâm, 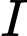 là trung điểm
là trung điểm 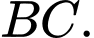 Tìm khẳng định sai.
Tìm khẳng định sai.
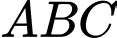 có
có  là trọng tâm,
là trọng tâm, 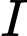 là trung điểm
là trung điểm 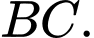 Tìm khẳng định sai.
Tìm khẳng định sai. A, 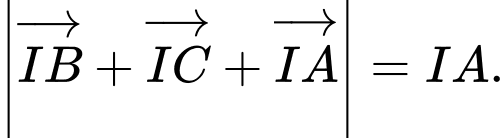
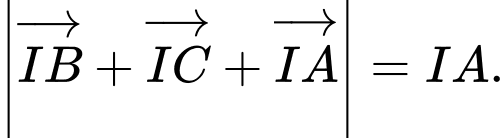
B, 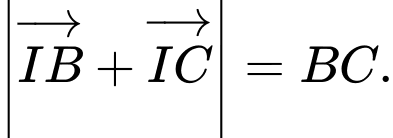
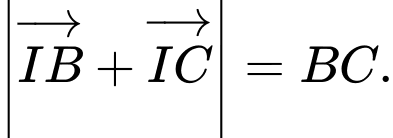
C, 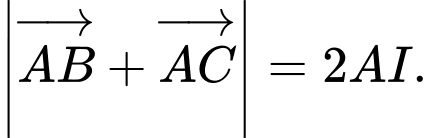
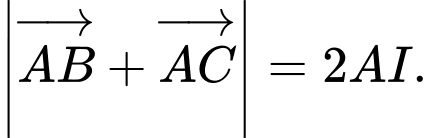
D, 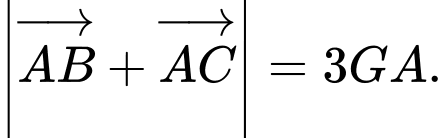
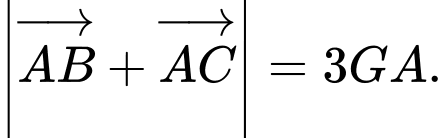
Chọn B
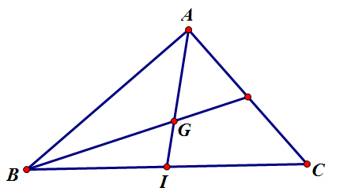
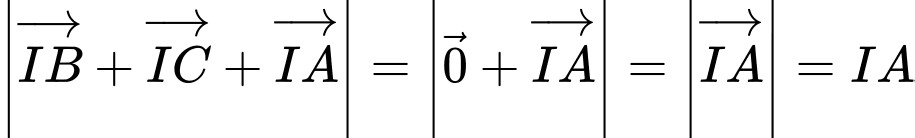 (Do
(Do 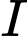 là trung điểm
là trung điểm 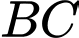 ) nên khẳng định ở A đúng.
) nên khẳng định ở A đúng.
 (Gọi
(Gọi 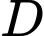 là điểm thỏa
là điểm thỏa 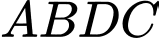 là hình bình hành,
là hình bình hành, 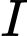 là trung điểm
là trung điểm 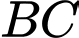 ) nên khẳng định ở C đúng.
) nên khẳng định ở C đúng.
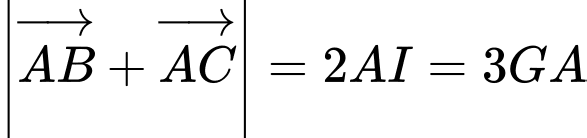 (Do
(Do  là trọng tâm tam giác
là trọng tâm tam giác 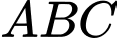 ) nên khẳng định ở D đúng.
) nên khẳng định ở D đúng.
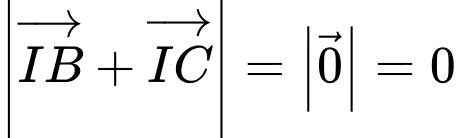 (Do
(Do 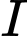 là trung điểm
là trung điểm 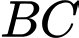 ) nên khẳng định ở B sai. Đáp án: B
) nên khẳng định ở B sai. Đáp án: B

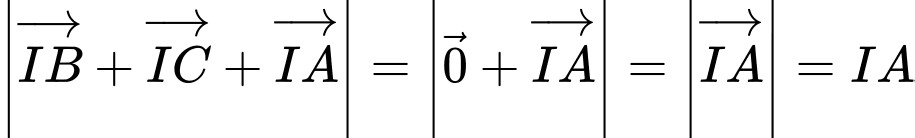 (Do
(Do 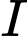 là trung điểm
là trung điểm 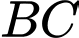 ) nên khẳng định ở A đúng.
) nên khẳng định ở A đúng. (Gọi
(Gọi 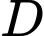 là điểm thỏa
là điểm thỏa 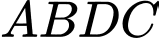 là hình bình hành,
là hình bình hành, 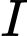 là trung điểm
là trung điểm 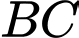 ) nên khẳng định ở C đúng.
) nên khẳng định ở C đúng.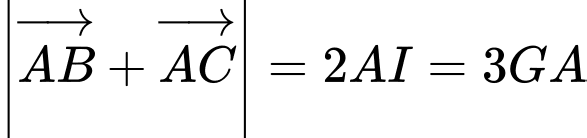 (Do
(Do  là trọng tâm tam giác
là trọng tâm tam giác 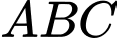 ) nên khẳng định ở D đúng.
) nên khẳng định ở D đúng.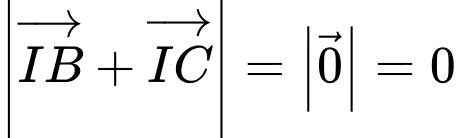 (Do
(Do 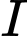 là trung điểm
là trung điểm 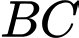 ) nên khẳng định ở B sai. Đáp án: B
) nên khẳng định ở B sai. Đáp án: B
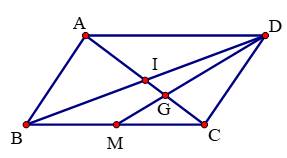
Câu 19 [582955]: Cho hình bình hành 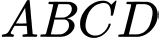 tâm
tâm 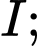
 là trọng tâm tam giác
là trọng tâm tam giác  Đẳng thức nào sau đây sai?
Đẳng thức nào sau đây sai?
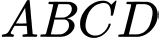 tâm
tâm 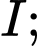
 là trọng tâm tam giác
là trọng tâm tam giác  Đẳng thức nào sau đây sai?
Đẳng thức nào sau đây sai? A, 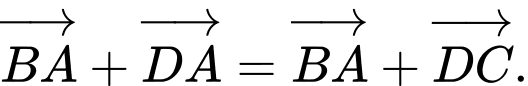
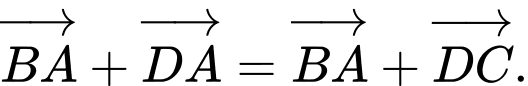
B, 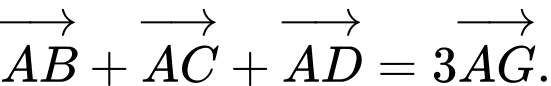
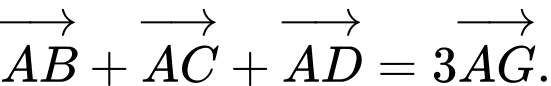
C, 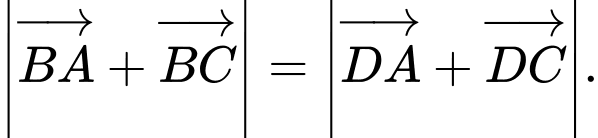
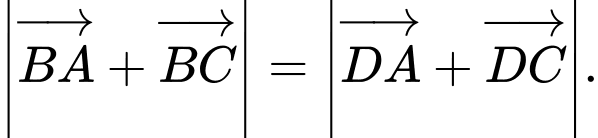
D, 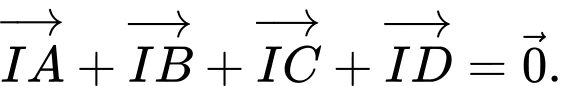
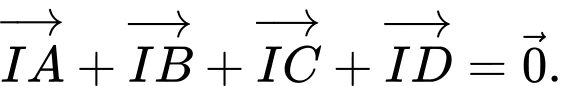
Chọn A
Ta có
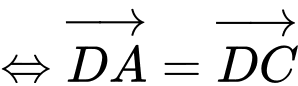 (vô lý)
(vô lý)  A sai.
A sai.
 là trọng tâm tam giác
là trọng tâm tam giác 
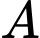 là một điểm nằm ngoài tam giác
là một điểm nằm ngoài tam giác 
 đẳng thức ở đáp án B đúng.
đẳng thức ở đáp án B đúng.
Ta có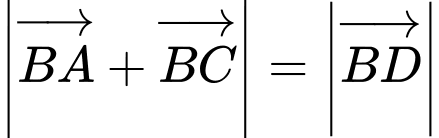 và
và 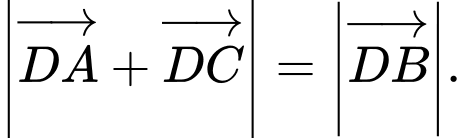 Mà
Mà 
 đáp án C đúng.
đáp án C đúng.
Ta có và
và  đối nhau, có độ dài bằng nhau
đối nhau, có độ dài bằng nhau 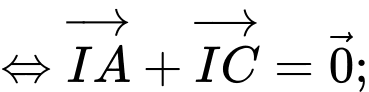 tương tự
tương tự 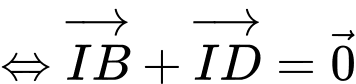 Đáp án: A
Đáp án: A

Ta có

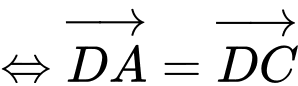 (vô lý)
(vô lý)  A sai.
A sai. là trọng tâm tam giác
là trọng tâm tam giác 
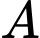 là một điểm nằm ngoài tam giác
là một điểm nằm ngoài tam giác 
 đẳng thức ở đáp án B đúng.
đẳng thức ở đáp án B đúng.Ta có
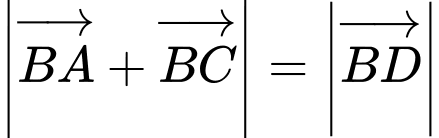 và
và 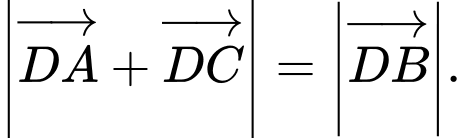 Mà
Mà 
 đáp án C đúng.
đáp án C đúng.Ta có
 và
và  đối nhau, có độ dài bằng nhau
đối nhau, có độ dài bằng nhau 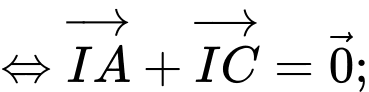 tương tự
tương tự 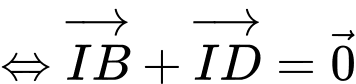 Đáp án: A
Đáp án: A