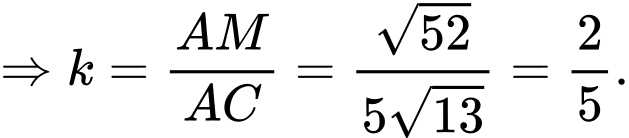Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
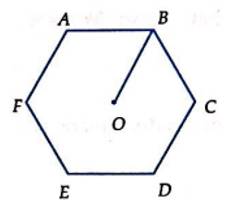
Câu 1 [582956]: Cho hình lục giác đều 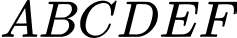 tâm
tâm  Số các vectơ khác vectơ không, cùng phương với vectơ
Số các vectơ khác vectơ không, cùng phương với vectơ 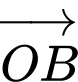 có điểm đầu và điểm cuối là các đỉnh của lục giác là
có điểm đầu và điểm cuối là các đỉnh của lục giác là
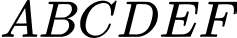 tâm
tâm  Số các vectơ khác vectơ không, cùng phương với vectơ
Số các vectơ khác vectơ không, cùng phương với vectơ 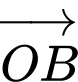 có điểm đầu và điểm cuối là các đỉnh của lục giác là
có điểm đầu và điểm cuối là các đỉnh của lục giác là A, 4.
B, 6.
C, 8.
D, 10.
Các vectơ cùng phương với vectơ
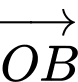 là:
là: 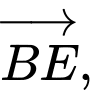
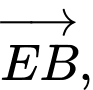
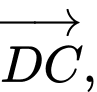
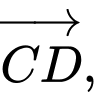

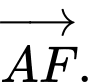 Đáp án: B
Đáp án: B
Câu 2 [582957]: Cho lục giác đều 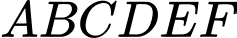 tâm
tâm  Số vectơ bằng vectơ
Số vectơ bằng vectơ 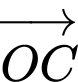 có điểm đầu và điểm cuối là các đỉnh của lục giác là
có điểm đầu và điểm cuối là các đỉnh của lục giác là
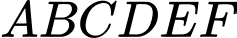 tâm
tâm  Số vectơ bằng vectơ
Số vectơ bằng vectơ 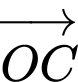 có điểm đầu và điểm cuối là các đỉnh của lục giác là
có điểm đầu và điểm cuối là các đỉnh của lục giác là A, 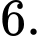
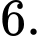
B, 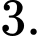
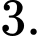
C, 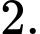
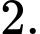
D, 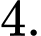
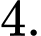
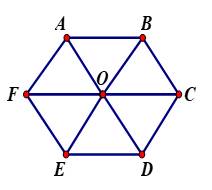
Các vectơ bằng vectơ
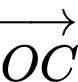 mà điểm đầu, điểm cuối là các đỉnh của lục giác là
mà điểm đầu, điểm cuối là các đỉnh của lục giác là 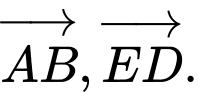 Đáp án: C
Đáp án: C
Câu 3 [582958]: Cho 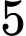 điểm phân biệt
điểm phân biệt 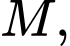
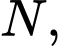
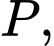

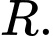 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
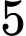 điểm phân biệt
điểm phân biệt 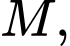
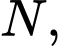
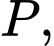

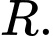 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng? A, 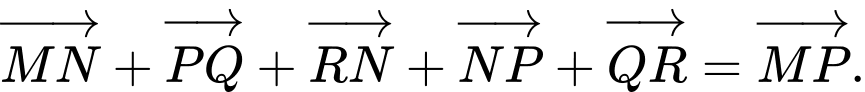
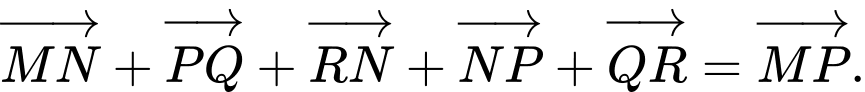
B, 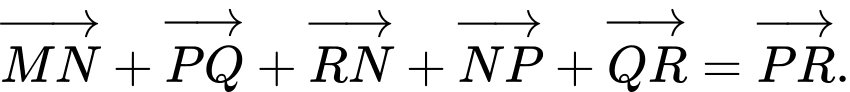
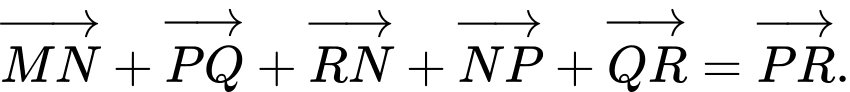
C, 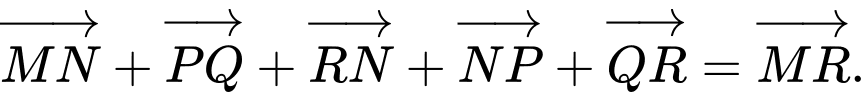
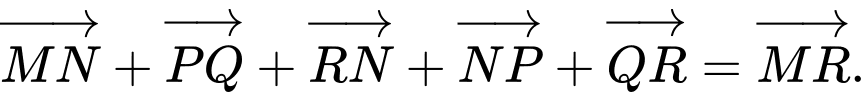
D, 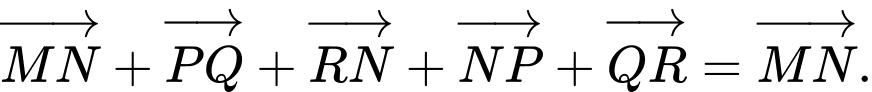
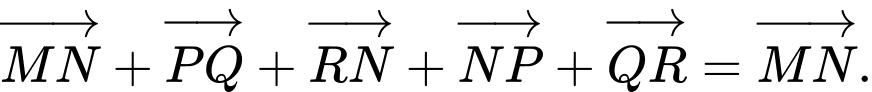
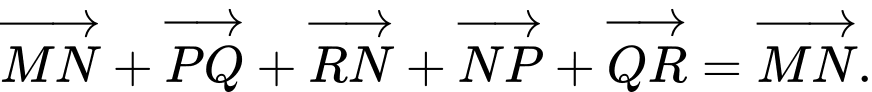 Đáp án: D
Đáp án: D
Câu 4 [582959]: Cho tam giác 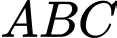 có trọng tâm
có trọng tâm  Gọi
Gọi 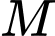 là trung điểm
là trung điểm 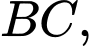
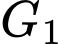 là điểm đối xứng của
là điểm đối xứng của  qua
qua 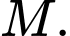 Vectơ tổng
Vectơ tổng 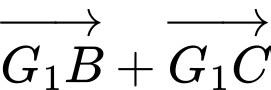 bằng
bằng
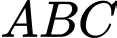 có trọng tâm
có trọng tâm  Gọi
Gọi 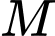 là trung điểm
là trung điểm 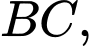
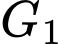 là điểm đối xứng của
là điểm đối xứng của  qua
qua 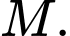 Vectơ tổng
Vectơ tổng 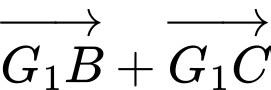 bằng
bằng A, 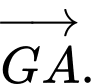
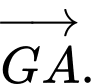
B, 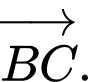
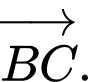
C, 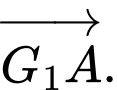
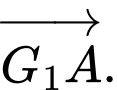
D, 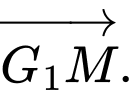
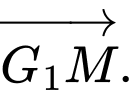
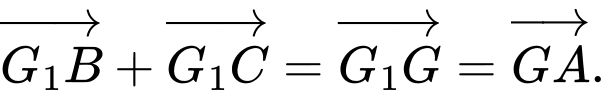 Đáp án: A
Đáp án: A
Câu 5 [582960]: Chỉ ra vectơ tổng 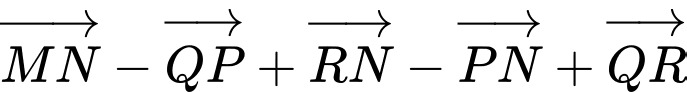 trong các vectơ sau.
trong các vectơ sau.
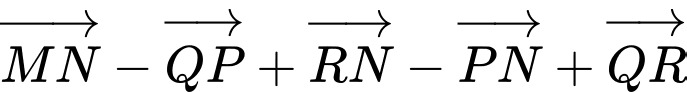 trong các vectơ sau.
trong các vectơ sau. A, 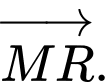
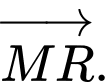
B, 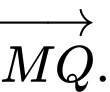
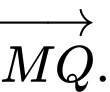
C, 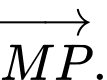
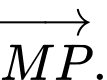
D, 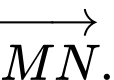
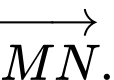
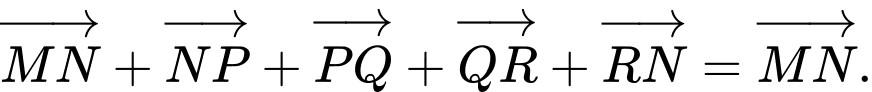 Đáp án: D
Đáp án: D
Câu 6 [582961]: Cho tam giác 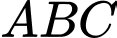 đều cạnh
đều cạnh 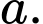 Tính
Tính 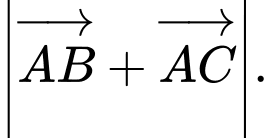
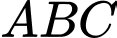 đều cạnh
đều cạnh 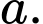 Tính
Tính 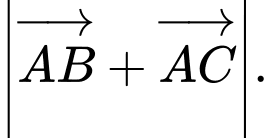
A, 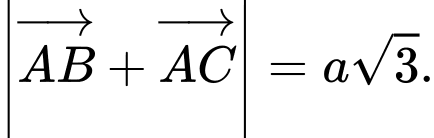
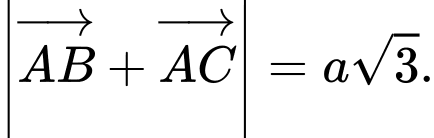
B, 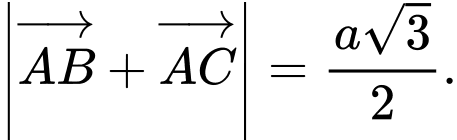
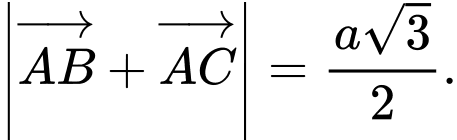
C, 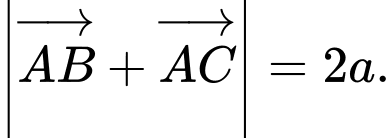
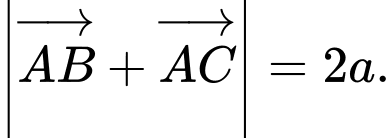
D, 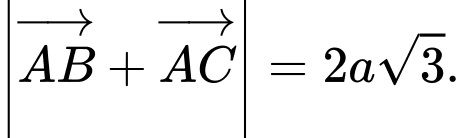
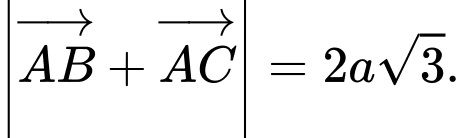
Gọi 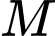 là điểm sao cho
là điểm sao cho 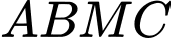 là hình bình hành. Ta có
là hình bình hành. Ta có 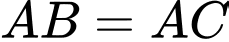 nên
nên 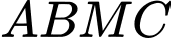 là hình thoi. Gọi
là hình thoi. Gọi  là tâm hình thoi
là tâm hình thoi 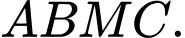
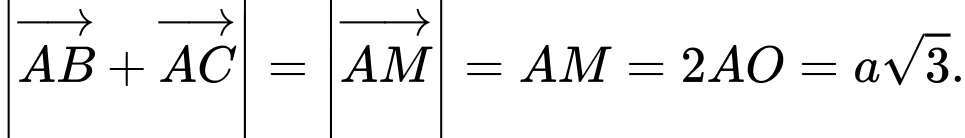 Đáp án: A
Đáp án: A
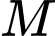 là điểm sao cho
là điểm sao cho 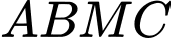 là hình bình hành. Ta có
là hình bình hành. Ta có 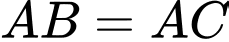 nên
nên 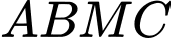 là hình thoi. Gọi
là hình thoi. Gọi  là tâm hình thoi
là tâm hình thoi 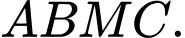
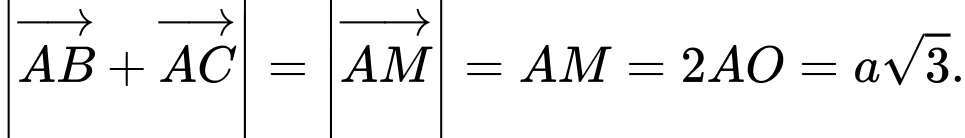 Đáp án: A
Đáp án: A
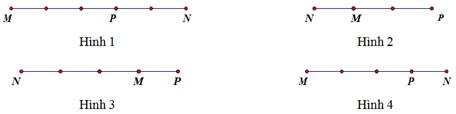
Câu 7 [582962]: Trên đường thẳng 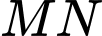 lấy điểm
lấy điểm 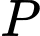 sao cho
sao cho 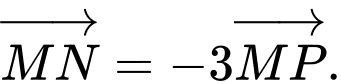 Điểm
Điểm 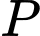 được xác định đúng trong hình vẽ nào sau đây:
được xác định đúng trong hình vẽ nào sau đây:
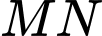 lấy điểm
lấy điểm 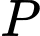 sao cho
sao cho 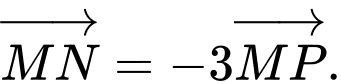 Điểm
Điểm 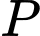 được xác định đúng trong hình vẽ nào sau đây:
được xác định đúng trong hình vẽ nào sau đây:
A, Hình 3.
B, Hình 4.
C, Hình 1.
D, Hình 2.
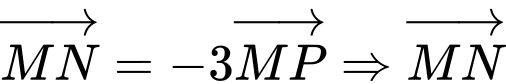 ngược hướng với
ngược hướng với 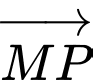 và
và 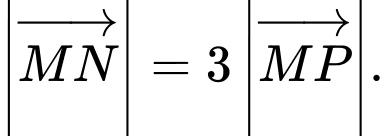 Đáp án: A
Đáp án: A
Câu 8 [582963]: Cho 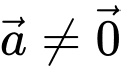 và điểm
và điểm  Gọi
Gọi 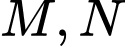 lần lượt là hai điểm thỏa mãn
lần lượt là hai điểm thỏa mãn 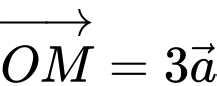 và
và 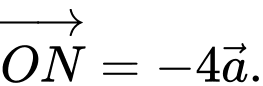 Khi đó:
Khi đó:
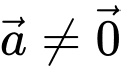 và điểm
và điểm  Gọi
Gọi 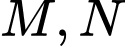 lần lượt là hai điểm thỏa mãn
lần lượt là hai điểm thỏa mãn 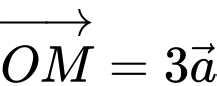 và
và 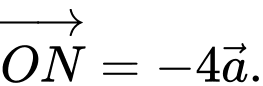 Khi đó:
Khi đó: A, 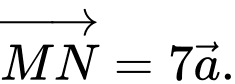
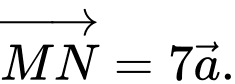
B, 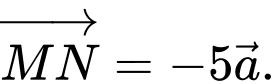
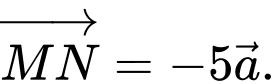
C, 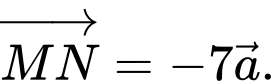
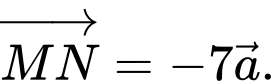
D, 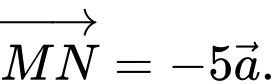
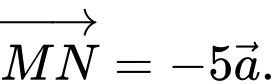
Ta có: 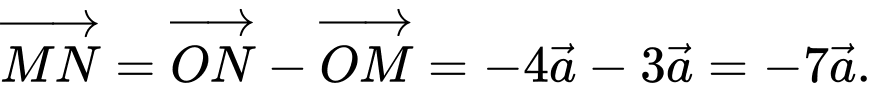 Đáp án: C
Đáp án: C
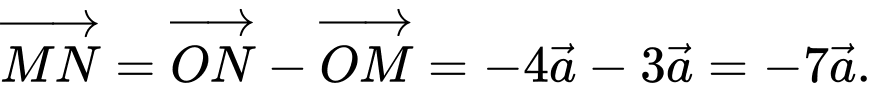 Đáp án: C
Đáp án: C
Câu 9 [582964]: Ba trung tuyến 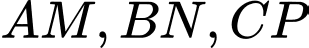 của tam giác
của tam giác 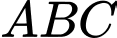 đồng quy tại
đồng quy tại  Hỏi vectơ
Hỏi vectơ 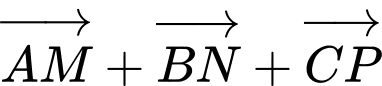 bằng vectơ nào?
bằng vectơ nào?
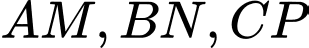 của tam giác
của tam giác 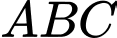 đồng quy tại
đồng quy tại  Hỏi vectơ
Hỏi vectơ 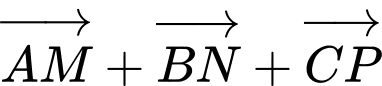 bằng vectơ nào?
bằng vectơ nào? A, 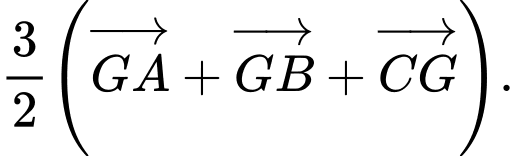
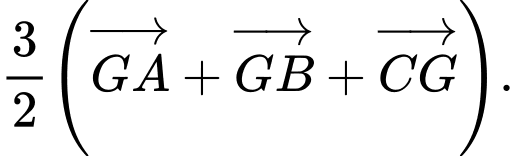
B, 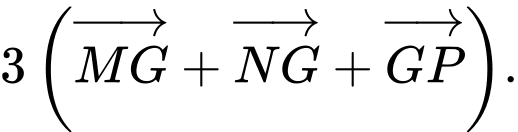
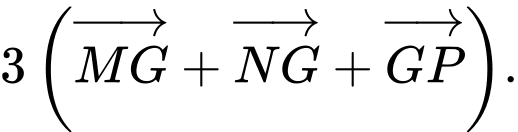
C, 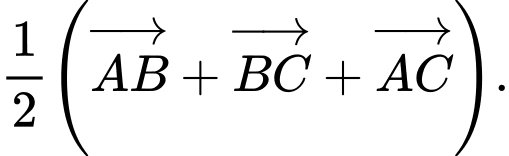
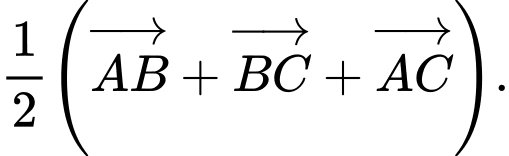
D, 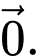
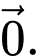
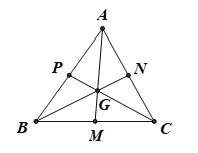
Ta có:
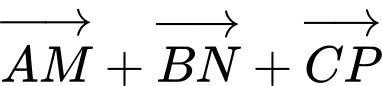
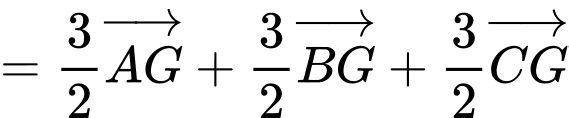
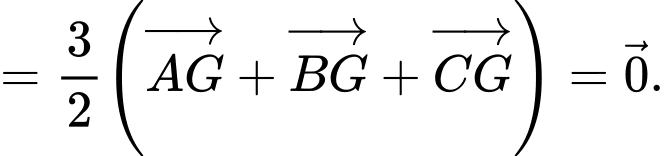 Đáp án: D
Đáp án: D
Câu 10 [582965]: Cho hình vuông 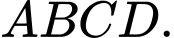 Tính
Tính 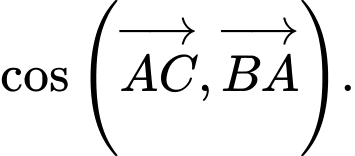
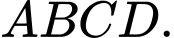 Tính
Tính 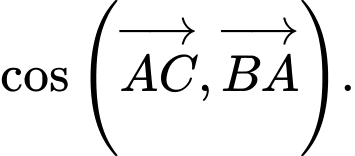
A, 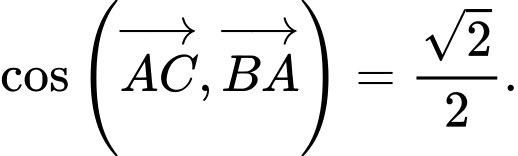
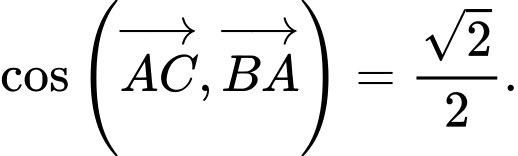
B, 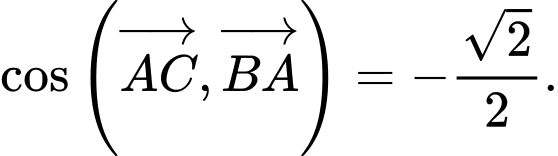
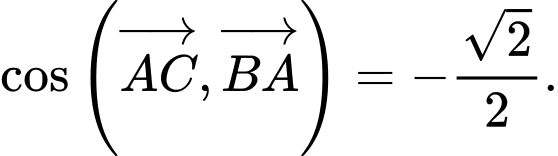
C, 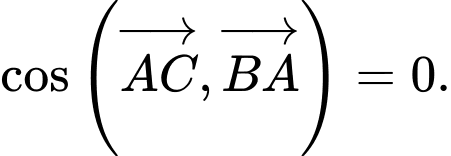
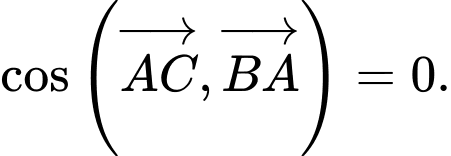
D, 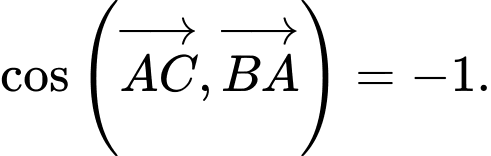
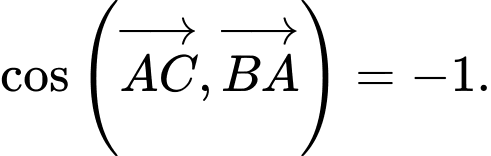
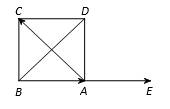
Vẽ
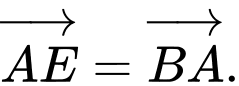
Khi đó
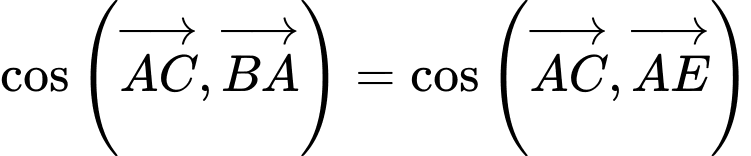
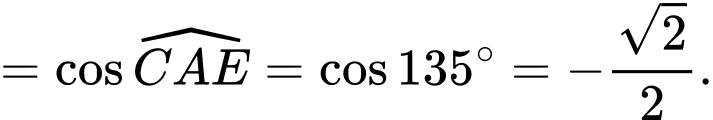 Đáp án: B
Đáp án: B
Câu 11 [582966]: Trong mặt phẳng tọa độ 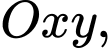 cho tam giác
cho tam giác 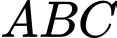 có
có 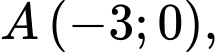
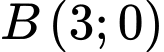 và
và 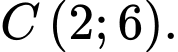 Gọi
Gọi  là tọa độ trực tâm của tam giác đã cho. Tính
là tọa độ trực tâm của tam giác đã cho. Tính 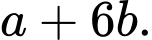
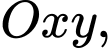 cho tam giác
cho tam giác 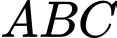 có
có 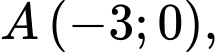
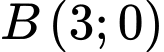 và
và 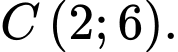 Gọi
Gọi  là tọa độ trực tâm của tam giác đã cho. Tính
là tọa độ trực tâm của tam giác đã cho. Tính 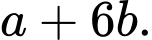
A, 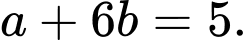
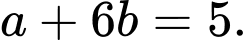
B, 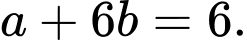
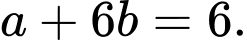
C, 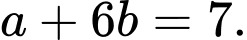
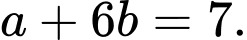
D, 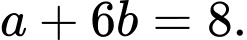
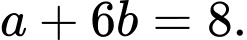
Gọi  là tọa độ trực tâm của tam giác đã cho khi đó ta có:
là tọa độ trực tâm của tam giác đã cho khi đó ta có:
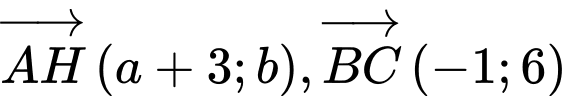
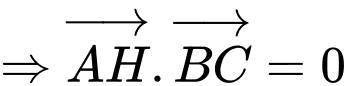
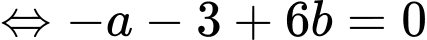
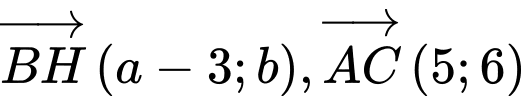
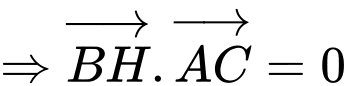
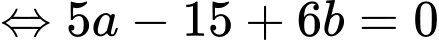
Từ đó ta có hệ phương trình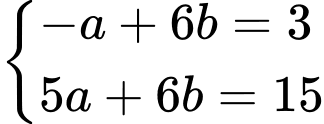
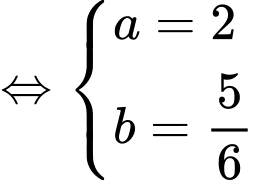
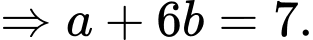 Đáp án: C
Đáp án: C
 là tọa độ trực tâm của tam giác đã cho khi đó ta có:
là tọa độ trực tâm của tam giác đã cho khi đó ta có: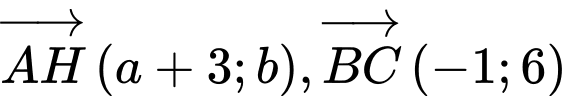
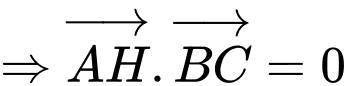
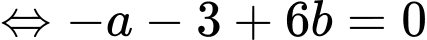
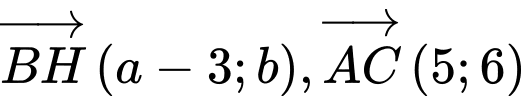
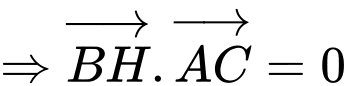
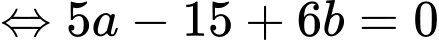
Từ đó ta có hệ phương trình
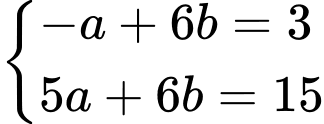
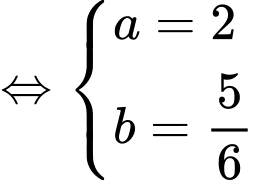
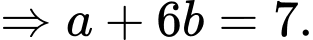 Đáp án: C
Đáp án: C
Câu 12 [582967]: Cho tam giác 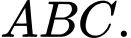 Tập hợp các điểm
Tập hợp các điểm 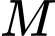 thỏa mãn
thỏa mãn 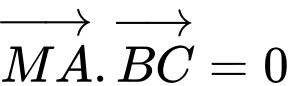 là:
là:
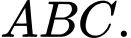 Tập hợp các điểm
Tập hợp các điểm 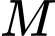 thỏa mãn
thỏa mãn 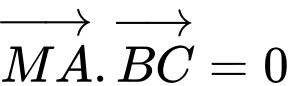 là:
là: A, một điểm.
B, đường thẳng.
C, đoạn thẳng.
D, đường tròn.
Ta có 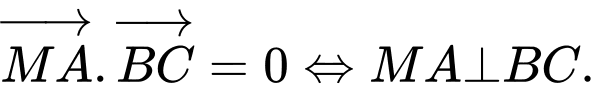
Vậy tập hợp các điểm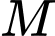 là đường thẳng đi qua
là đường thẳng đi qua 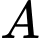 và vuông góc với
và vuông góc với 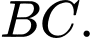 Đáp án: B
Đáp án: B
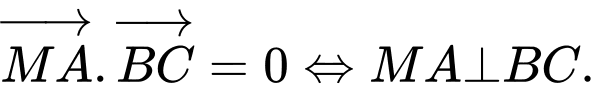
Vậy tập hợp các điểm
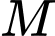 là đường thẳng đi qua
là đường thẳng đi qua 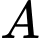 và vuông góc với
và vuông góc với 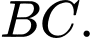 Đáp án: B
Đáp án: B
Câu 13 [582968]: Cho hai vectơ 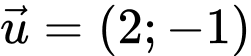 ,
,  Tích
Tích 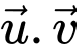 là
là
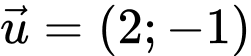 ,
,  Tích
Tích 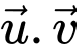 là
là A, 

B, 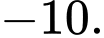
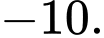
C, 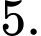
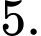
D, 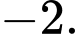
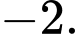
Với 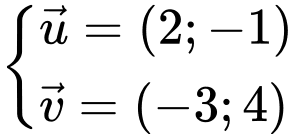
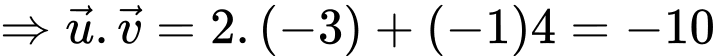 Đáp án: B
Đáp án: B
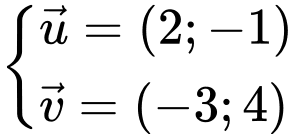
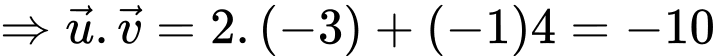 Đáp án: B
Đáp án: B
Câu 14 [582969]: Cho hình bình hành 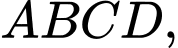 với
với 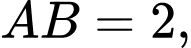
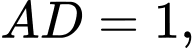
 Độ dài đường chéo
Độ dài đường chéo 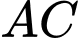 bằng
bằng
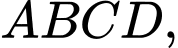 với
với 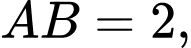
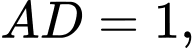
 Độ dài đường chéo
Độ dài đường chéo 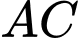 bằng
bằng A, 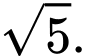
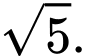
B, 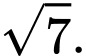
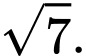
C, 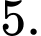
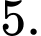
D, 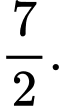
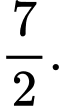
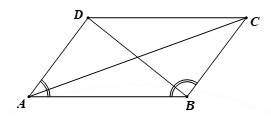
Ta có:
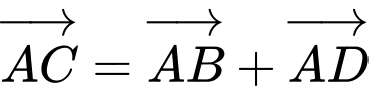
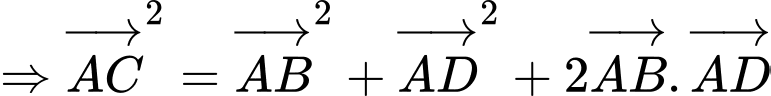
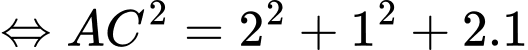
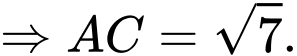 Đáp án: B
Đáp án: B
Câu 15 [582970]: Trong mặt phẳng 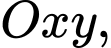 cho hai điểm
cho hai điểm 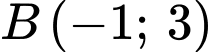 và
và 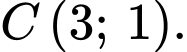 Tìm tọa độ điểm
Tìm tọa độ điểm 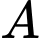 sao cho tam giác
sao cho tam giác 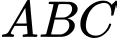 vuông cân tại
vuông cân tại 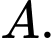
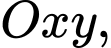 cho hai điểm
cho hai điểm 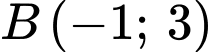 và
và 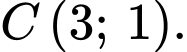 Tìm tọa độ điểm
Tìm tọa độ điểm 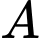 sao cho tam giác
sao cho tam giác 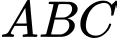 vuông cân tại
vuông cân tại 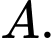
A, 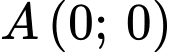 hoặc
hoặc 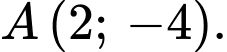
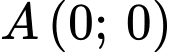 hoặc
hoặc 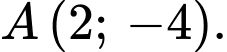
B, 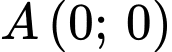 hoặc
hoặc 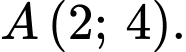
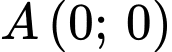 hoặc
hoặc 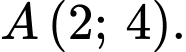
C, 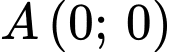 hoặc
hoặc 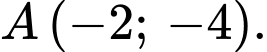
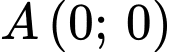 hoặc
hoặc 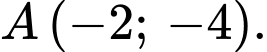
D, 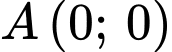 hoặc
hoặc 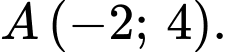
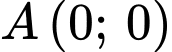 hoặc
hoặc 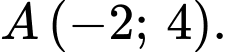
Tìm tọa độ điểm 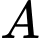 sao cho tam giác
sao cho tam giác 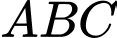 vuông cân tại
vuông cân tại 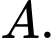
Gọi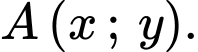 Tam giác
Tam giác 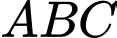 vuông cân tại
vuông cân tại 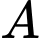
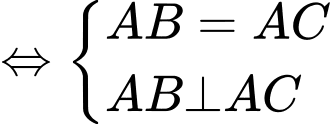
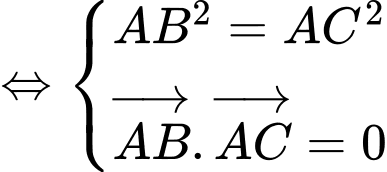
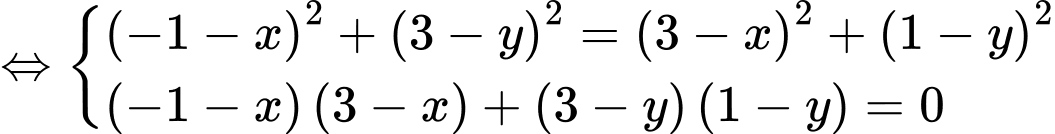
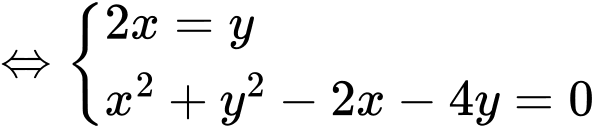
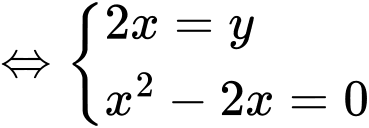
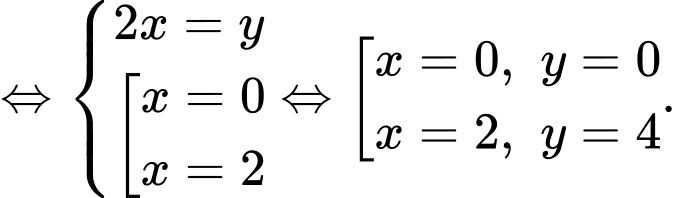
Vậy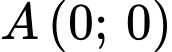 hoặc
hoặc 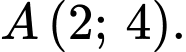
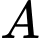 sao cho tam giác
sao cho tam giác 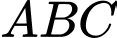 vuông cân tại
vuông cân tại 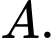
Gọi
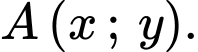 Tam giác
Tam giác 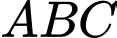 vuông cân tại
vuông cân tại 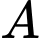
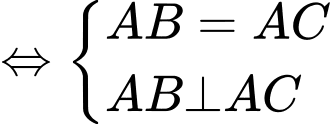
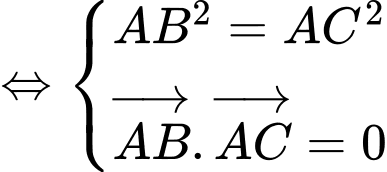
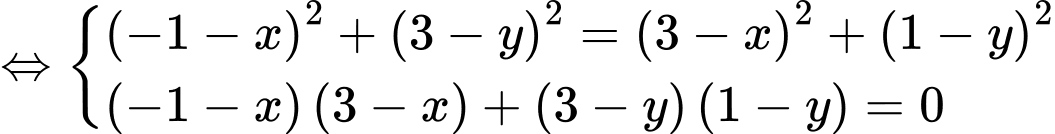
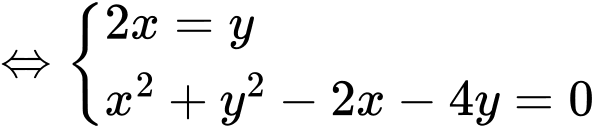
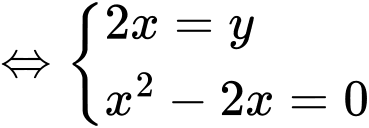
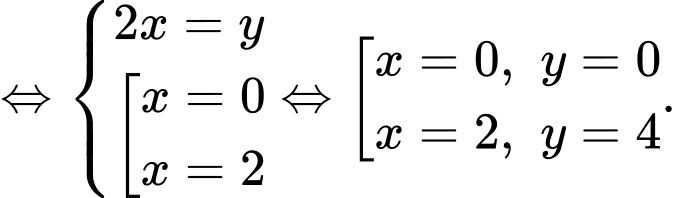
Vậy
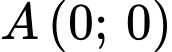 hoặc
hoặc 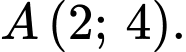
Dạng câu hỏi: Câu trắc nghiệm đúng sai.
(Thí sinh trả lời từ câu 16,17. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng
hoặc sai)
Câu 16 [582971]: Xét tam giác 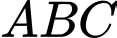 nội tiếp có
nội tiếp có  là tâm đường tròn ngoại tiếp,
là tâm đường tròn ngoại tiếp, 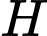 là trực tâm. Gọi
là trực tâm. Gọi 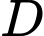 là điểm đối xứng của
là điểm đối xứng của 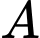 qua
qua 
a)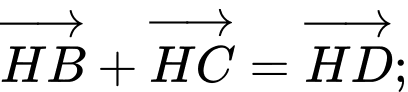
b)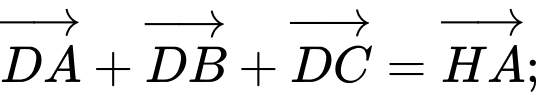
c)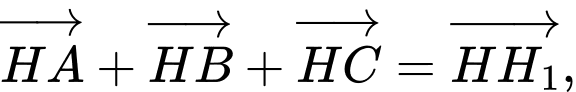 với
với 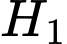 là điểm đối xứng của
là điểm đối xứng của 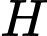 qua
qua 
d) Nếu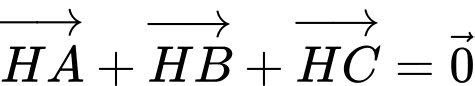 thì tam giác
thì tam giác 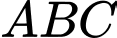 là tam giác đều.
là tam giác đều.
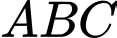 nội tiếp có
nội tiếp có  là tâm đường tròn ngoại tiếp,
là tâm đường tròn ngoại tiếp, 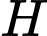 là trực tâm. Gọi
là trực tâm. Gọi 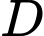 là điểm đối xứng của
là điểm đối xứng của 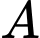 qua
qua 
a)
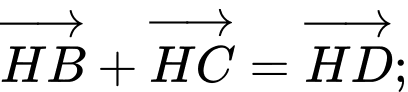
b)
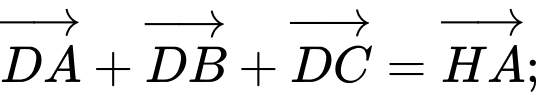
c)
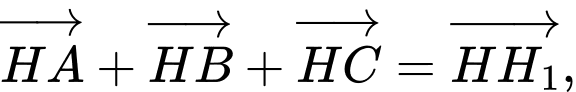 với
với 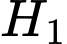 là điểm đối xứng của
là điểm đối xứng của 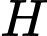 qua
qua 
d) Nếu
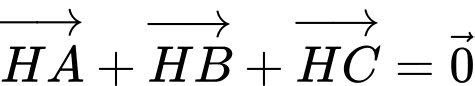 thì tam giác
thì tam giác 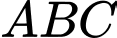 là tam giác đều.
là tam giác đều.
a) 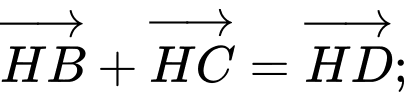 Đ
Đ
b)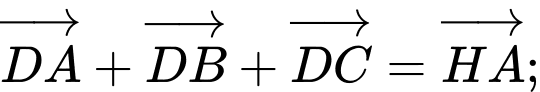 S
S
c)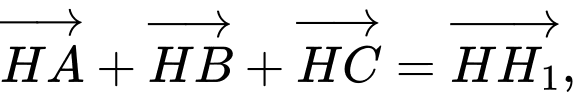 với
với 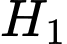 là điểm đối xứng của
là điểm đối xứng của 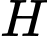 qua
qua  Đ
Đ
d) Nếu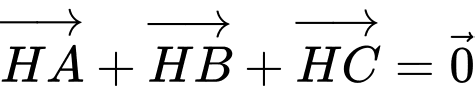 thì tam giác
thì tam giác 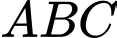 là tam giác đều. S
là tam giác đều. S
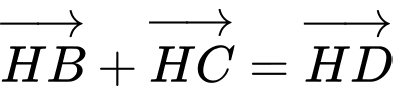
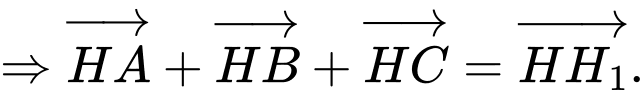
Nếu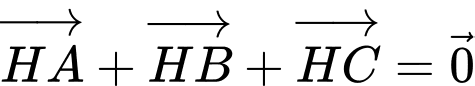 thì
thì 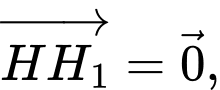 suy ra
suy ra 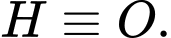
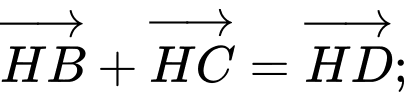 Đ
Đ b)
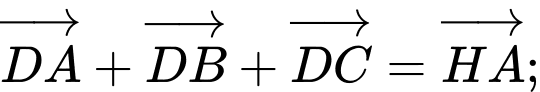 S
Sc)
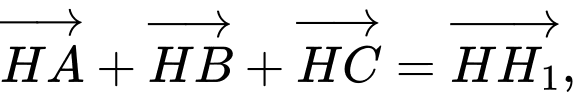 với
với 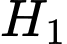 là điểm đối xứng của
là điểm đối xứng của 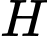 qua
qua  Đ
Đd) Nếu
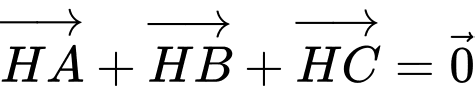 thì tam giác
thì tam giác 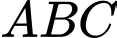 là tam giác đều. S
là tam giác đều. S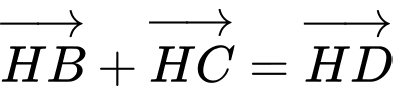
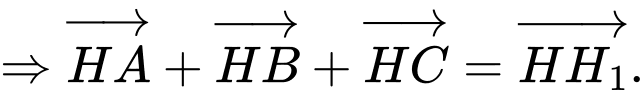
Nếu
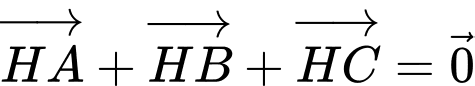 thì
thì 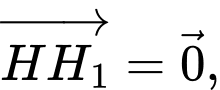 suy ra
suy ra 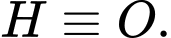
Câu 17 [582972]: Xét tam giác 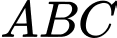 có trọng tâm
có trọng tâm 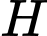 và tâm đường tròn ngoại tiếp
và tâm đường tròn ngoại tiếp  thỏa mãn
thỏa mãn 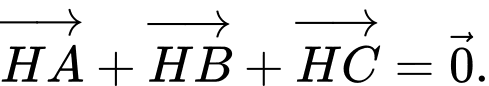 Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng?
Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng?
a)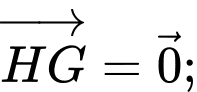
b) Tam giác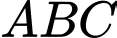 là tam giác vuông cân;
là tam giác vuông cân;
c)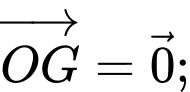
d) Tam giác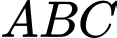 là tam giác cân.
là tam giác cân.
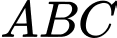 có trọng tâm
có trọng tâm 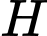 và tâm đường tròn ngoại tiếp
và tâm đường tròn ngoại tiếp  thỏa mãn
thỏa mãn 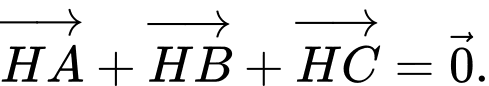 Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng?
Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng? a)
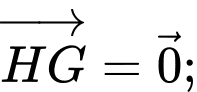
b) Tam giác
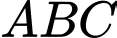 là tam giác vuông cân;
là tam giác vuông cân; c)
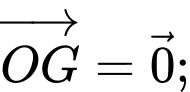
d) Tam giác
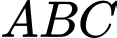 là tam giác cân.
là tam giác cân.
a) Đ
b) S
c) Đ
d) Đ
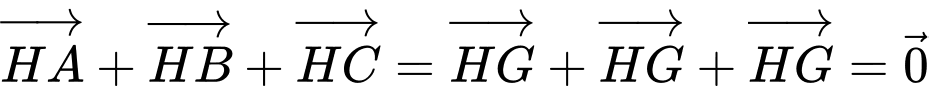
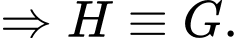 Do đó tam giác
Do đó tam giác 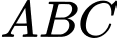 là tam giác đều.
là tam giác đều.
b) S
c) Đ
d) Đ
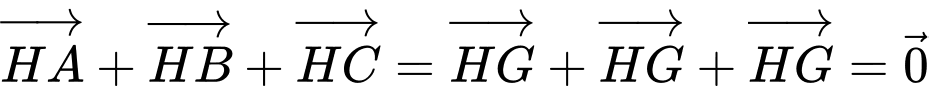
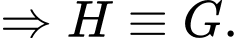 Do đó tam giác
Do đó tam giác 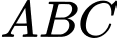 là tam giác đều.
là tam giác đều. Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 18 [582973]: Cho tam giác 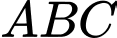 đều có cạnh
đều có cạnh 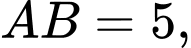
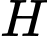 là trung điểm của
là trung điểm của 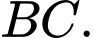 Tính
Tính 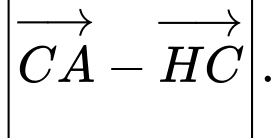
TRẢ LỜI: ……………………….
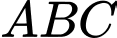 đều có cạnh
đều có cạnh 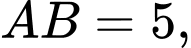
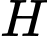 là trung điểm của
là trung điểm của 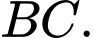 Tính
Tính 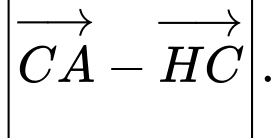
TRẢ LỜI: ……………………….
Gọi 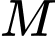 là điểm sao cho
là điểm sao cho 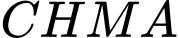 là hình bình hành.
là hình bình hành.
Ta có: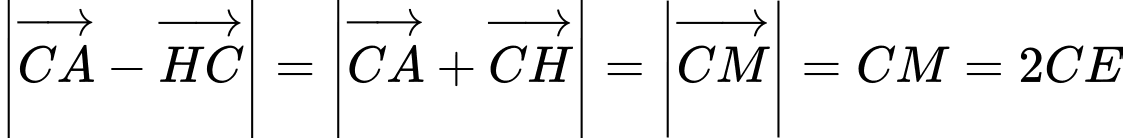 (
(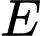 là tâm cúa hình bình hành
là tâm cúa hình bình hành 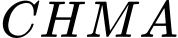 ).
).
Ta lại có: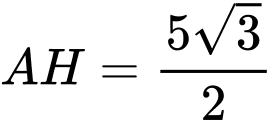 (
(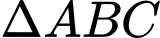 đều,
đều, 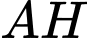 là đường cao).
là đường cao).
Trong tam giác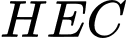 vuông tại
vuông tại 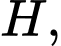 có:
có:
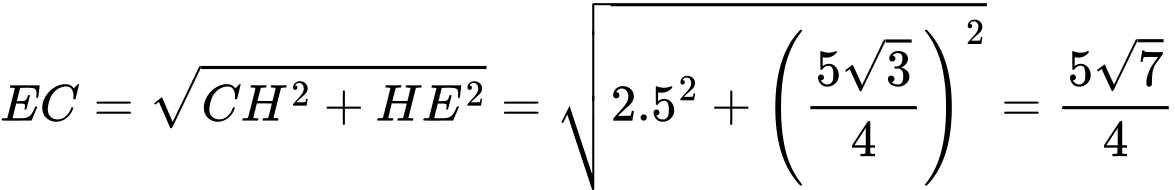
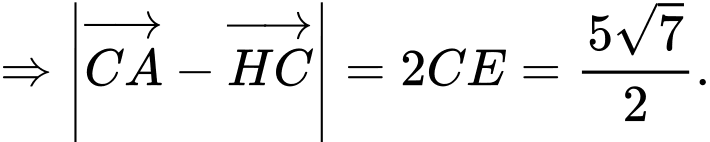
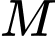 là điểm sao cho
là điểm sao cho 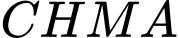 là hình bình hành.
là hình bình hành.Ta có:
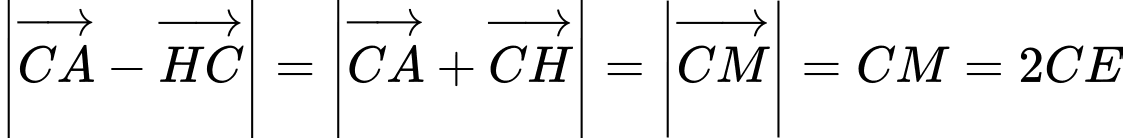 (
(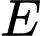 là tâm cúa hình bình hành
là tâm cúa hình bình hành 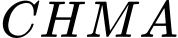 ).
).Ta lại có:
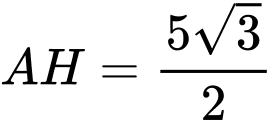 (
(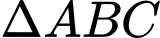 đều,
đều, 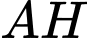 là đường cao).
là đường cao).
Trong tam giác
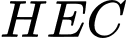 vuông tại
vuông tại 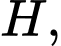 có:
có: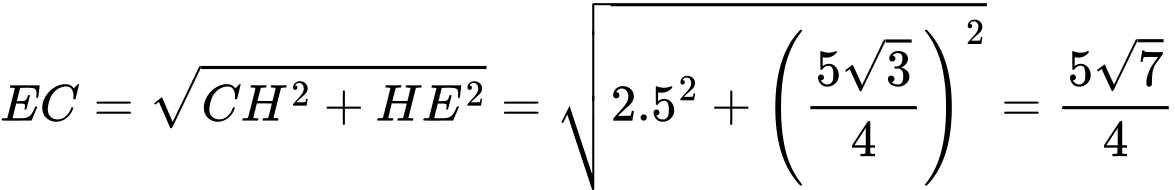
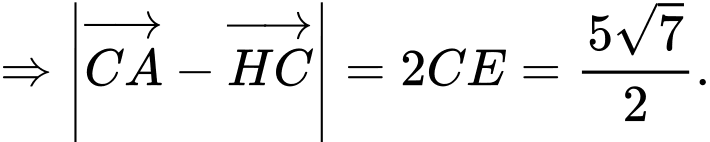
Câu 19 [582974]: Cho hai lực 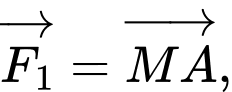
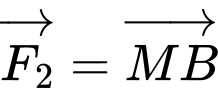 cùng tác động vào một vật tại điểm
cùng tác động vào một vật tại điểm 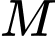 cường độ hai lực
cường độ hai lực 
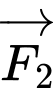 lần lượt là
lần lượt là 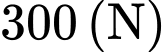 và
và 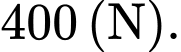
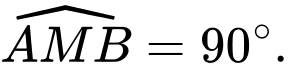 Tìm cường độ của lực tổng hợp tác động vào vật.
Tìm cường độ của lực tổng hợp tác động vào vật.
TRẢ LỜI: ……………………….
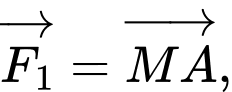
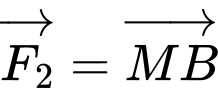 cùng tác động vào một vật tại điểm
cùng tác động vào một vật tại điểm 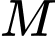 cường độ hai lực
cường độ hai lực 
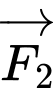 lần lượt là
lần lượt là 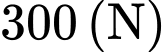 và
và 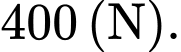
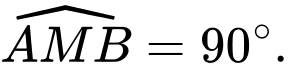 Tìm cường độ của lực tổng hợp tác động vào vật.
Tìm cường độ của lực tổng hợp tác động vào vật.TRẢ LỜI: ……………………….
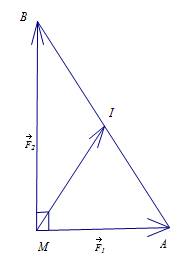
Cường độ lực tổng hợp của
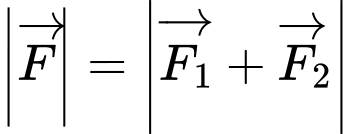
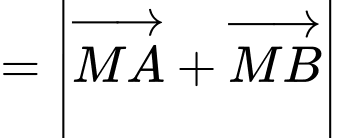
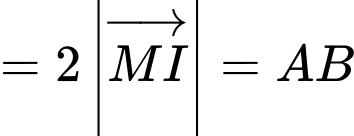 (
(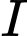 là trung điểm của
là trung điểm của  ).
). Ta có
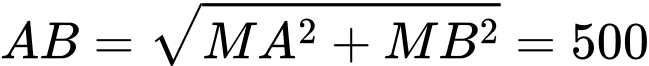 suy ra
suy ra 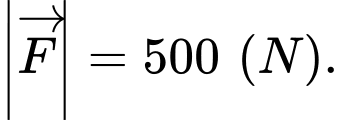
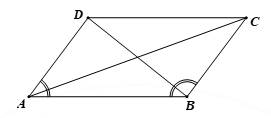
Câu 20 [582975]: Cho hình thang vuông 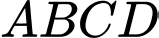 có đường cao
có đường cao 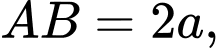 các cạnh đáy
các cạnh đáy 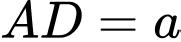 và
và 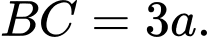 Gọi
Gọi 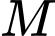 là điểm trên đoạn
là điểm trên đoạn 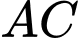 sao cho
sao cho 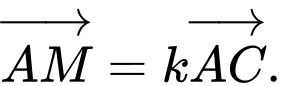 Tìm
Tìm 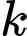 để
để 
TRẢ LỜI: ……………………….
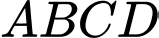 có đường cao
có đường cao 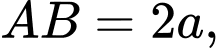 các cạnh đáy
các cạnh đáy 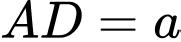 và
và 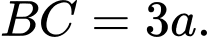 Gọi
Gọi 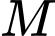 là điểm trên đoạn
là điểm trên đoạn 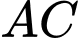 sao cho
sao cho 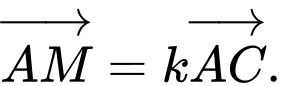 Tìm
Tìm 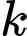 để
để 
TRẢ LỜI: ……………………….
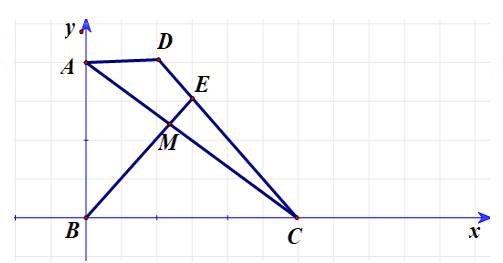
Chọn hệ trục tọa độ như hình vẽ sao cho gốc tọa độ trùng với điểm 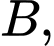 điểm
điểm 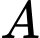 thuộc trục
thuộc trục 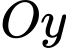 và điểm
và điểm  thuộc trục
thuộc trục 
Theo bài ra ta có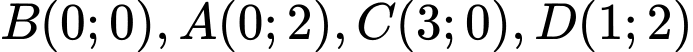
Khi đó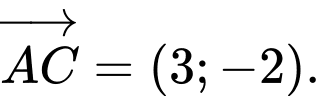 Phương trình tham số của đường thẳng
Phương trình tham số của đường thẳng 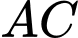 là
là 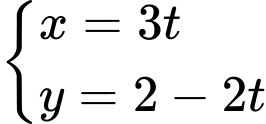
Gọi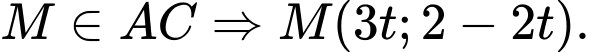 Ta có
Ta có 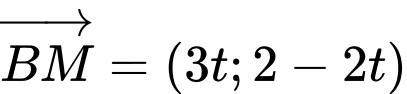 và
và 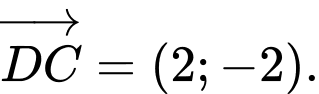
Để thì
thì 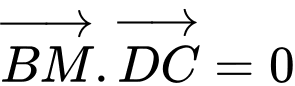
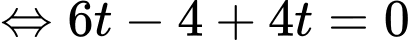
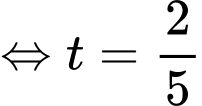
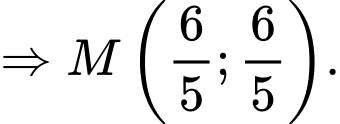
Khi đó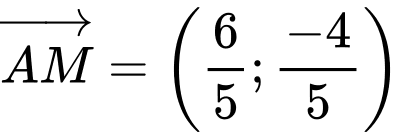
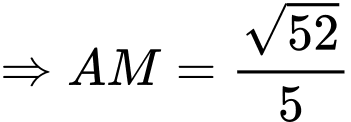 và
và 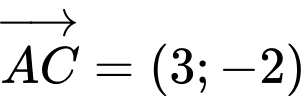
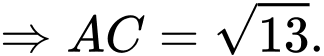
Vì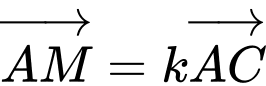 và
và 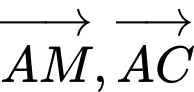 cùng chiều
cùng chiều 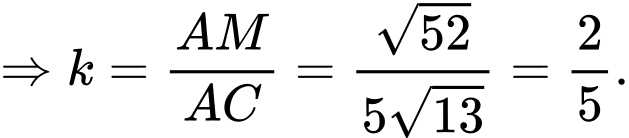
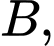 điểm
điểm 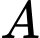 thuộc trục
thuộc trục 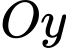 và điểm
và điểm  thuộc trục
thuộc trục 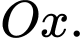

Theo bài ra ta có
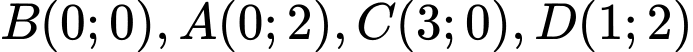
Khi đó
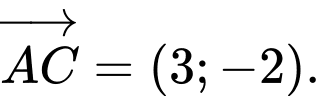 Phương trình tham số của đường thẳng
Phương trình tham số của đường thẳng 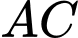 là
là 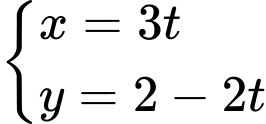
Gọi
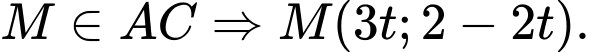 Ta có
Ta có 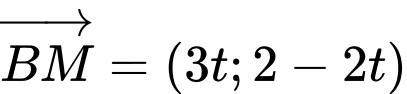 và
và 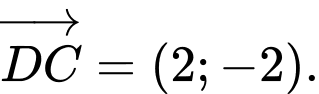
Để
 thì
thì 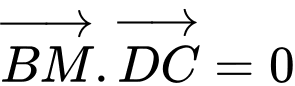
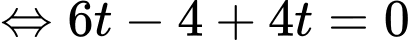
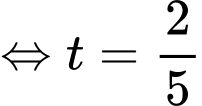
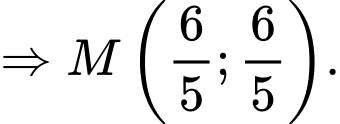
Khi đó
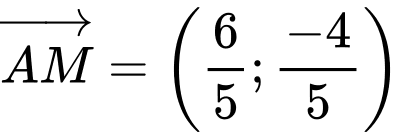
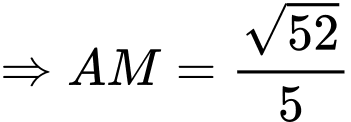 và
và 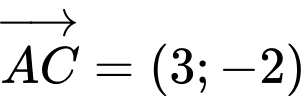
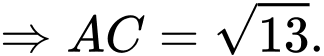
Vì
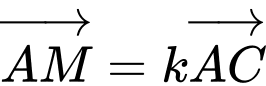 và
và 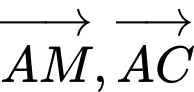 cùng chiều
cùng chiều