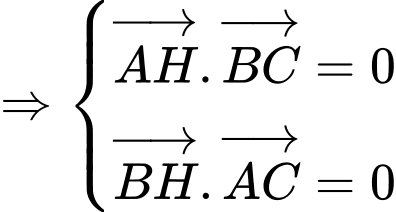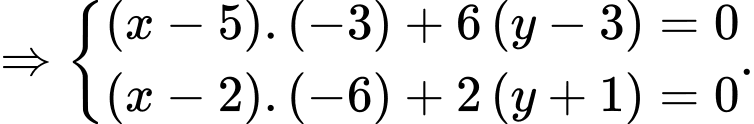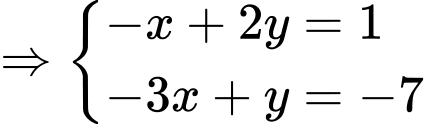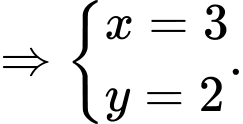Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
Câu 1 [582982]: Cho 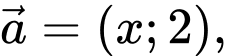
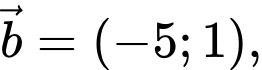
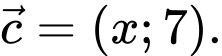 Vectơ
Vectơ 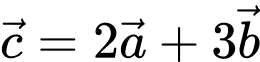 nếu:
nếu:
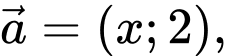
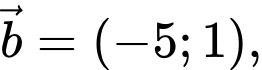
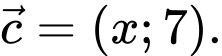 Vectơ
Vectơ 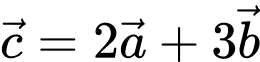 nếu:
nếu: A, 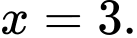
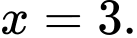
B, 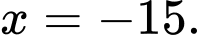
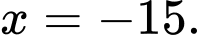
C, 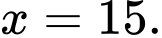
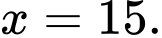
D, 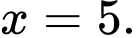
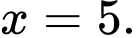
Chọn C
Ta có: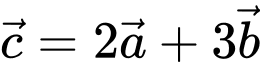
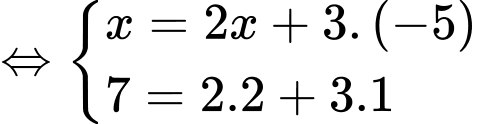
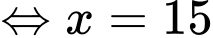 Đáp án: C
Đáp án: C
Ta có:
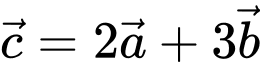
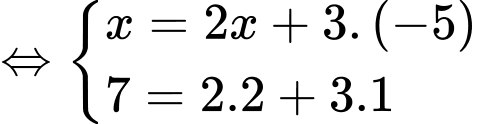
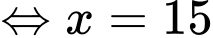 Đáp án: C
Đáp án: C
Câu 2 [582983]: Cho 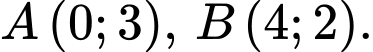 Điểm
Điểm 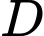 thỏa
thỏa 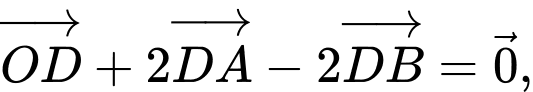 tọa độ
tọa độ 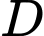 là:
là:
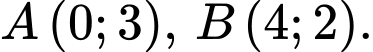 Điểm
Điểm 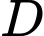 thỏa
thỏa 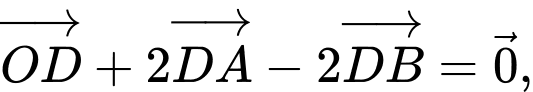 tọa độ
tọa độ 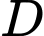 là:
là: A, 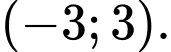
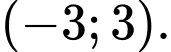
B, 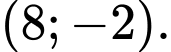
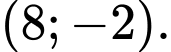
C, 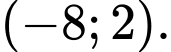
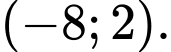
D, 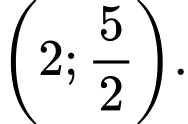
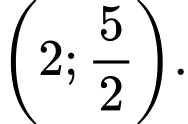
Chọn B
Ta có: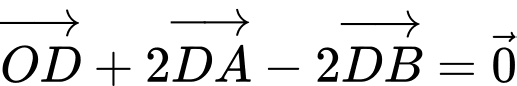
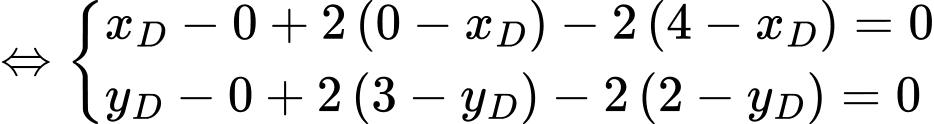
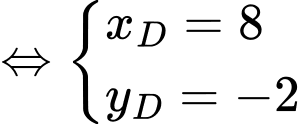 Đáp án: B
Đáp án: B
Ta có:
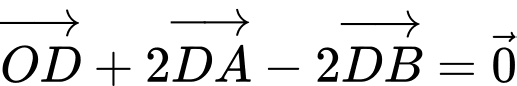
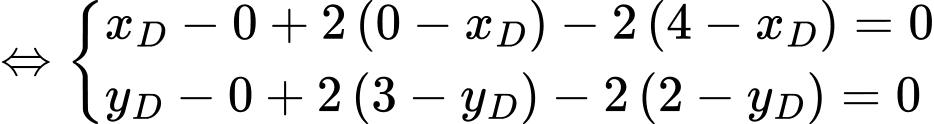
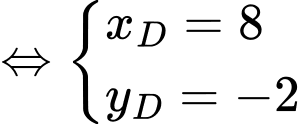 Đáp án: B
Đáp án: B
Câu 3 [582984]: Tam giác 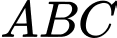 có
có 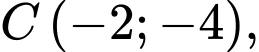 trọng tâm
trọng tâm 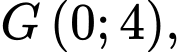 trung điểm cạnh
trung điểm cạnh 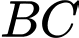 là
là 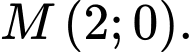 Tọa độ
Tọa độ 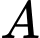 và
và 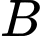 là:
là:
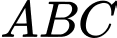 có
có 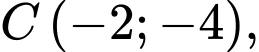 trọng tâm
trọng tâm 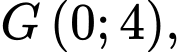 trung điểm cạnh
trung điểm cạnh 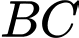 là
là 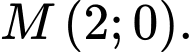 Tọa độ
Tọa độ 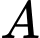 và
và 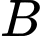 là:
là: A, 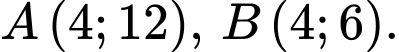
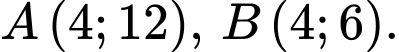
B, 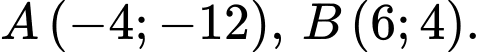
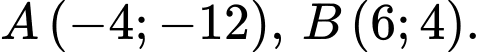
C, 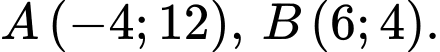
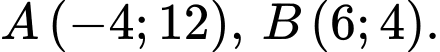
D, 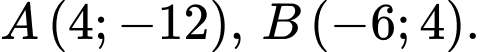
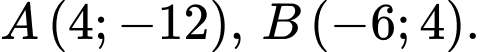
Chọn C
Ta có: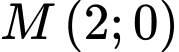 là trung điểm
là trung điểm 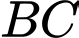 nên
nên 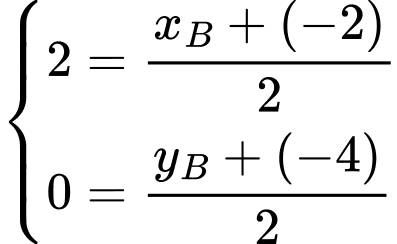
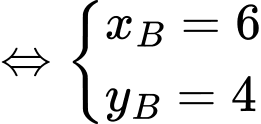
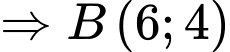
 là trọng tâm tam giác
là trọng tâm tam giác 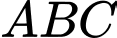 nên
nên 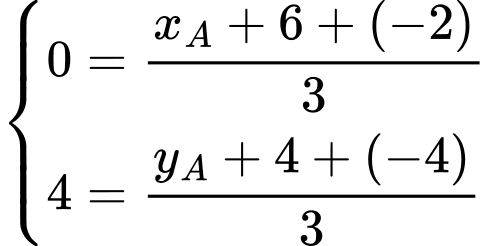
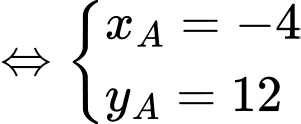
 Đáp án: C
Đáp án: C
Ta có:
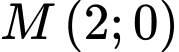 là trung điểm
là trung điểm 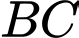 nên
nên 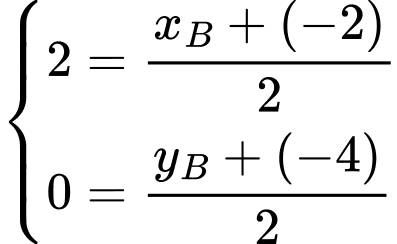
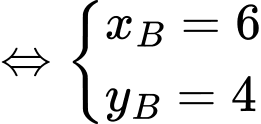
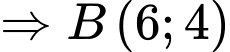
 là trọng tâm tam giác
là trọng tâm tam giác 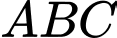 nên
nên 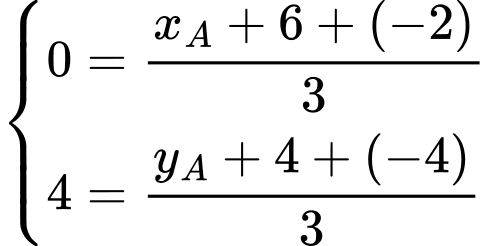
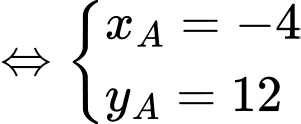
 Đáp án: C
Đáp án: C
Câu 4 [582985]: Cho 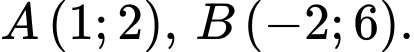 Điểm
Điểm 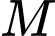 trên trục
trên trục 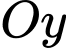 sao cho ba điểm
sao cho ba điểm 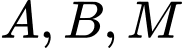 thẳng hàng thì tọa độ điểm
thẳng hàng thì tọa độ điểm 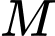 là:
là:
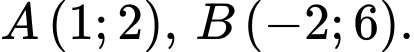 Điểm
Điểm 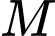 trên trục
trên trục 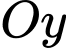 sao cho ba điểm
sao cho ba điểm 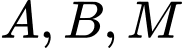 thẳng hàng thì tọa độ điểm
thẳng hàng thì tọa độ điểm 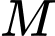 là:
là: A, 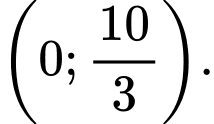
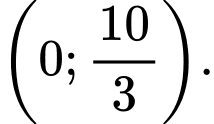
B, 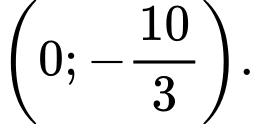
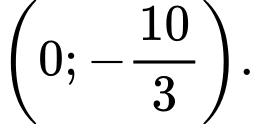
C, 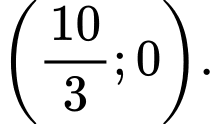
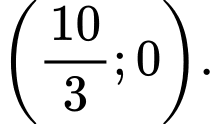
D, 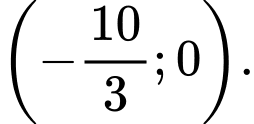
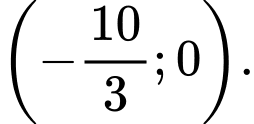
Chọn A
Ta có: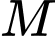 trên trục
trên trục 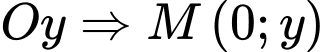
Ba điểm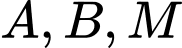 thẳng hàng khi
thẳng hàng khi 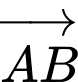 cùng phương với
cùng phương với 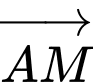
Ta có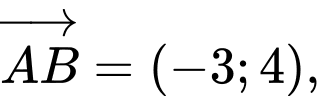
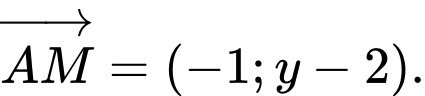 Do đó,
Do đó, 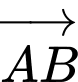 cùng phương với
cùng phương với 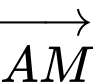
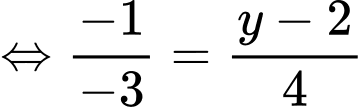
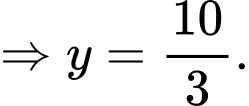
Vậy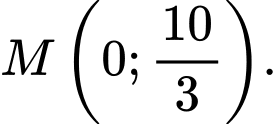 Đáp án: A
Đáp án: A
Ta có:
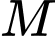 trên trục
trên trục 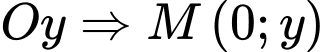
Ba điểm
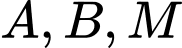 thẳng hàng khi
thẳng hàng khi 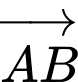 cùng phương với
cùng phương với 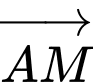
Ta có
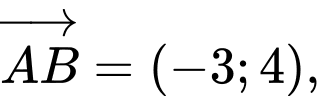
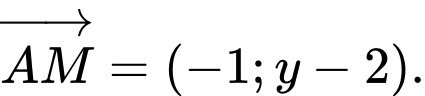 Do đó,
Do đó, 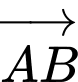 cùng phương với
cùng phương với 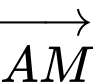
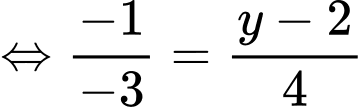
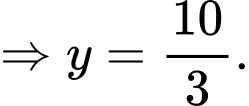
Vậy
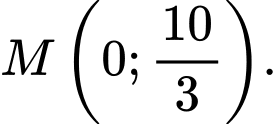 Đáp án: A
Đáp án: A
Câu 5 [582986]: Trong mặt phẳng 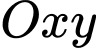 , cho
, cho 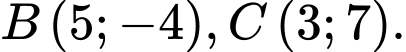 Tọa độ của điểm
Tọa độ của điểm 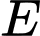 đối xứng với
đối xứng với  qua
qua 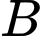 là
là
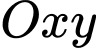 , cho
, cho 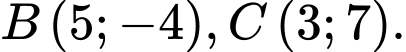 Tọa độ của điểm
Tọa độ của điểm 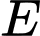 đối xứng với
đối xứng với  qua
qua 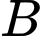 là
là A, 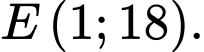
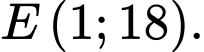
B, 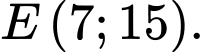
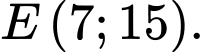
C, 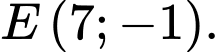
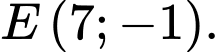
D, 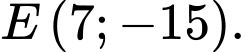
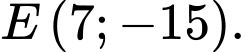
Chọn D
Ta có: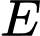 đối xứng với
đối xứng với  qua
qua 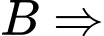
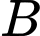 là trung điểm đoạn thẳng
là trung điểm đoạn thẳng 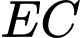
Do đó, ta có: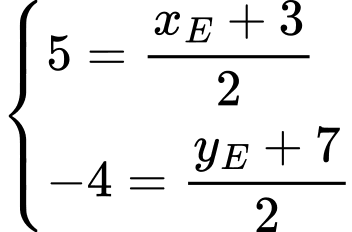
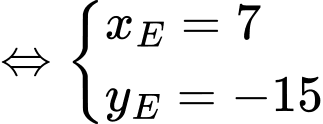
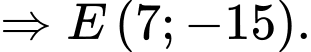 Đáp án: D
Đáp án: D
Ta có:
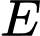 đối xứng với
đối xứng với  qua
qua 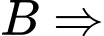
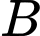 là trung điểm đoạn thẳng
là trung điểm đoạn thẳng 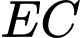
Do đó, ta có:
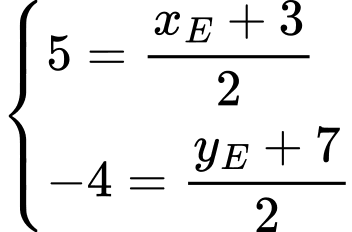
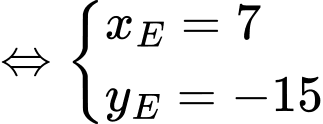
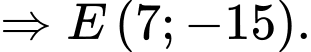 Đáp án: D
Đáp án: D
Câu 6 [582987]: Trong mặt phẳng tọa độ 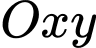 cho bốn điểm
cho bốn điểm 
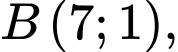
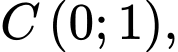
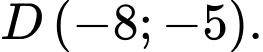 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
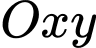 cho bốn điểm
cho bốn điểm 
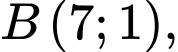
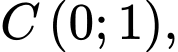
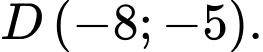 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng? A, 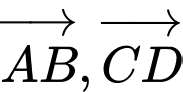 đối nhau.
đối nhau.
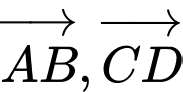 đối nhau.
đối nhau.B, 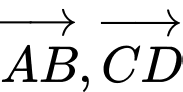 cùng phương nhưng ngược hướng.
cùng phương nhưng ngược hướng.
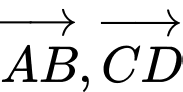 cùng phương nhưng ngược hướng.
cùng phương nhưng ngược hướng.C, 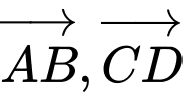 cùng phương cùng hướng.
cùng phương cùng hướng.
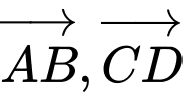 cùng phương cùng hướng.
cùng phương cùng hướng.D, 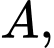
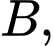
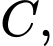
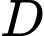 thẳng hàng.
thẳng hàng.
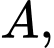
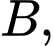
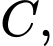
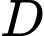 thẳng hàng.
thẳng hàng.
Chọn B
Ta có: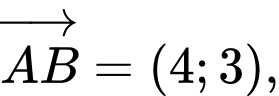
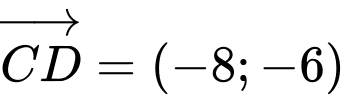
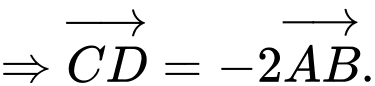 Đáp án: B
Đáp án: B
Ta có:
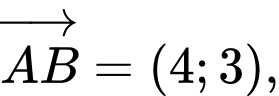
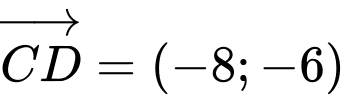
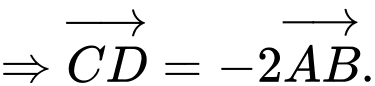 Đáp án: B
Đáp án: B
Câu 7 [582988]: Trong mặt phẳng 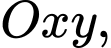 cho
cho 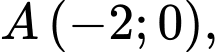
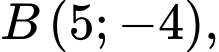
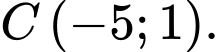 Tọa độ điểm
Tọa độ điểm 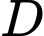 để tứ giác
để tứ giác 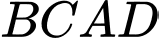 là hình bình hành là:
là hình bình hành là:
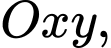 cho
cho 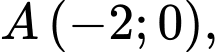
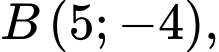
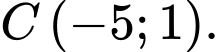 Tọa độ điểm
Tọa độ điểm 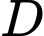 để tứ giác
để tứ giác 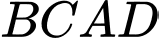 là hình bình hành là:
là hình bình hành là: A, 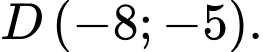
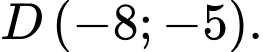
B, 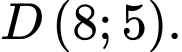
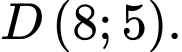
C, 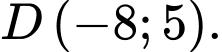
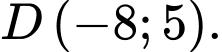
D, 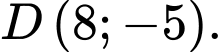
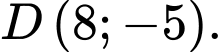
Chọn D
Ta có: tứ giác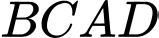 là hình bình hành khi
là hình bình hành khi 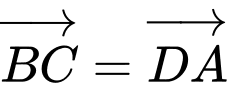
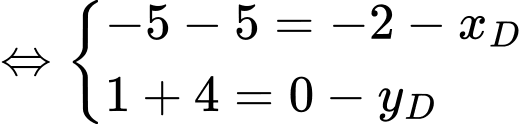
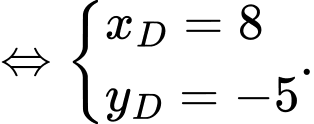 Đáp án: D
Đáp án: D
Ta có: tứ giác
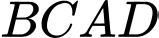 là hình bình hành khi
là hình bình hành khi 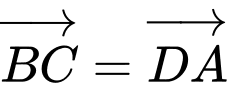
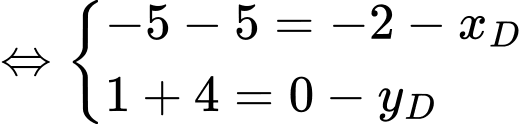
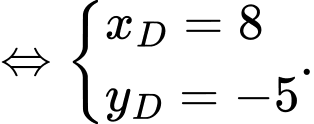 Đáp án: D
Đáp án: D
Câu 8 [582989]: Trong mặt phẳng 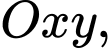 gọi
gọi 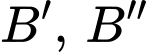 và
và 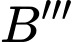 lần lượt là điểm đối xứng của
lần lượt là điểm đối xứng của 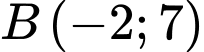 qua trục
qua trục 
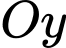 và qua gốc tọa độ
và qua gốc tọa độ  Tọa độ của các điểm
Tọa độ của các điểm 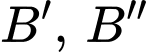 và
và 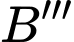 là:
là:
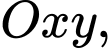 gọi
gọi 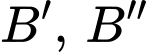 và
và 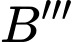 lần lượt là điểm đối xứng của
lần lượt là điểm đối xứng của 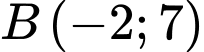 qua trục
qua trục 
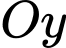 và qua gốc tọa độ
và qua gốc tọa độ  Tọa độ của các điểm
Tọa độ của các điểm 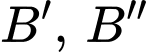 và
và 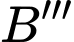 là:
là: A, 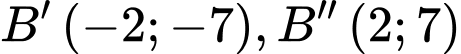 và
và 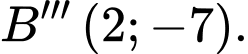
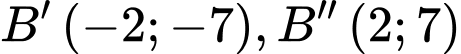 và
và 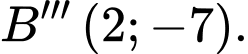
B, 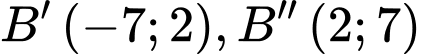 và
và 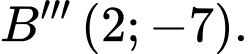
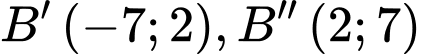 và
và 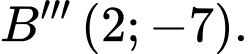
C, 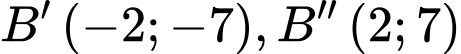 và
và 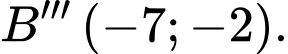
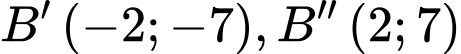 và
và 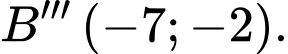
D, 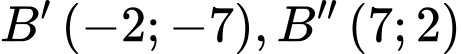 và
và 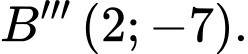
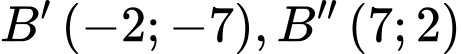 và
và 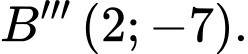
Chọn A
Ta có: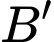 đối xứng với
đối xứng với 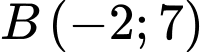 qua trục
qua trục 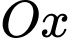

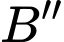 đối xứng với
đối xứng với 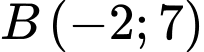 qua trục
qua trục 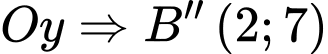
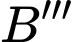 đối xứng với
đối xứng với 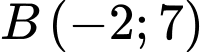 qua gốc tọa độ
qua gốc tọa độ 
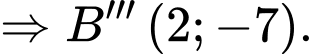 Đáp án: A
Đáp án: A
Ta có:
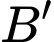 đối xứng với
đối xứng với 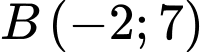 qua trục
qua trục 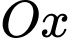

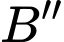 đối xứng với
đối xứng với 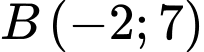 qua trục
qua trục 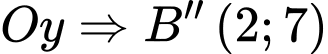
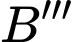 đối xứng với
đối xứng với 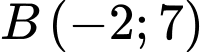 qua gốc tọa độ
qua gốc tọa độ 
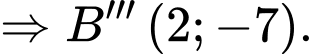 Đáp án: A
Đáp án: A
Câu 9 [582990]: Cho 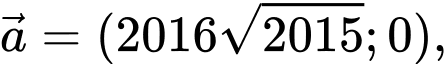
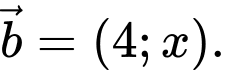 Hai vectơ
Hai vectơ 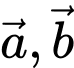 cùng phương nếu
cùng phương nếu
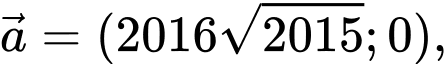
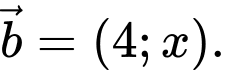 Hai vectơ
Hai vectơ 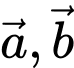 cùng phương nếu
cùng phương nếu A, 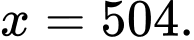
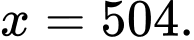
B, 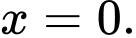
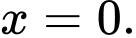
C, 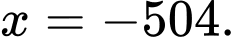
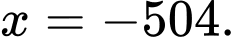
D, 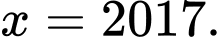
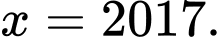
Chọn B
Ta có: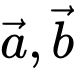 cùng phương
cùng phương 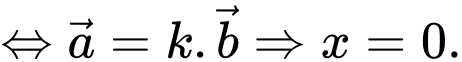 Đáp án: B
Đáp án: B
Ta có:
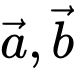 cùng phương
cùng phương 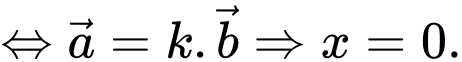 Đáp án: B
Đáp án: B
Câu 10 [582991]: Trong mặt phẳng tọa độ 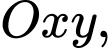 cho
cho 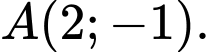 Điểm
Điểm 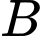 là điểm đối xứng của
là điểm đối xứng của 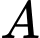 qua trục hoành. Tọa độ điểm
qua trục hoành. Tọa độ điểm 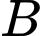 là:
là:
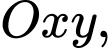 cho
cho 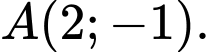 Điểm
Điểm 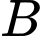 là điểm đối xứng của
là điểm đối xứng của 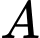 qua trục hoành. Tọa độ điểm
qua trục hoành. Tọa độ điểm 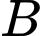 là:
là: A, 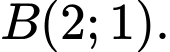
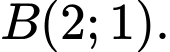
B, 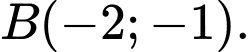
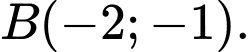
C, 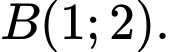
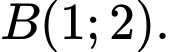
D, 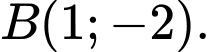
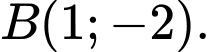
Chọn A
Ta có: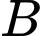 là điểm đối xứng của
là điểm đối xứng của 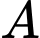 qua trục hoành
qua trục hoành 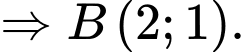 Đáp án: A
Đáp án: A
Ta có:
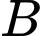 là điểm đối xứng của
là điểm đối xứng của 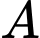 qua trục hoành
qua trục hoành 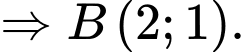 Đáp án: A
Đáp án: A
Câu 11 [582992]: Trong mặt phẳng 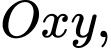 cho
cho 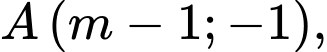
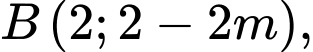
 Tìm giá trị
Tìm giá trị 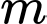 để
để 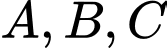 là ba điểm thẳng hàng?
là ba điểm thẳng hàng?
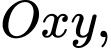 cho
cho 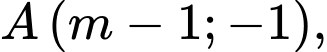
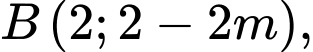
 Tìm giá trị
Tìm giá trị 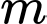 để
để 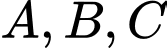 là ba điểm thẳng hàng?
là ba điểm thẳng hàng? A, 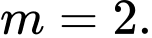
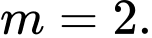
B, 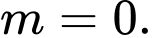
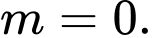
C, 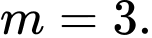
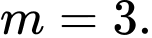
D, 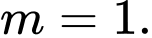
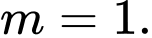
Chọn B
Ta có: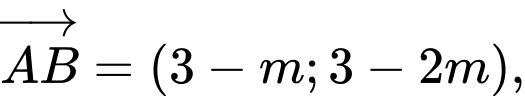
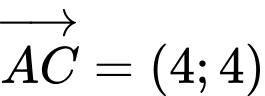
Ba điểm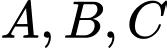 thẳng hàng khi và chỉ khi
thẳng hàng khi và chỉ khi 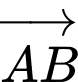 cùng phương với
cùng phương với 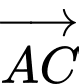
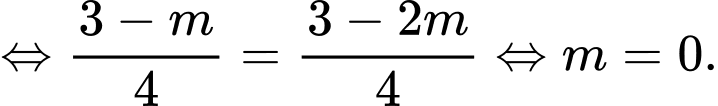 Đáp án: B
Đáp án: B
Ta có:
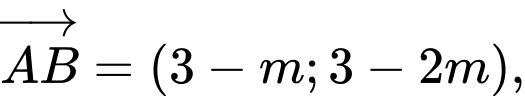
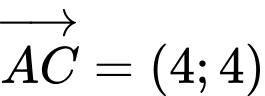
Ba điểm
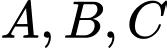 thẳng hàng khi và chỉ khi
thẳng hàng khi và chỉ khi 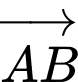 cùng phương với
cùng phương với 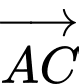
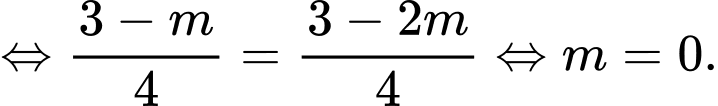 Đáp án: B
Đáp án: B
Câu 12 [582993]: Cho hai điểm 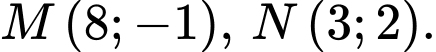 Nếu
Nếu 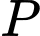 là điểm đối xứng với điểm
là điểm đối xứng với điểm 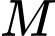 qua điểm
qua điểm 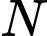 thì
thì 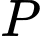 có tọa độ là:
có tọa độ là:
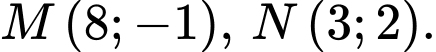 Nếu
Nếu 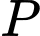 là điểm đối xứng với điểm
là điểm đối xứng với điểm 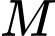 qua điểm
qua điểm 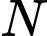 thì
thì 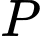 có tọa độ là:
có tọa độ là: A, 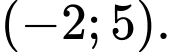
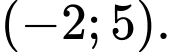
B, 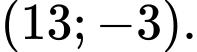
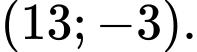
C, 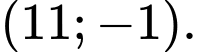
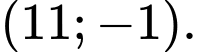
D, 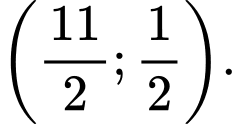
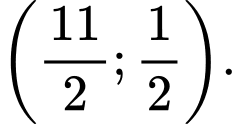
Chọn A
Ta có: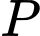 là điểm đối xứng với điểm
là điểm đối xứng với điểm 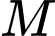 qua điểm
qua điểm 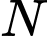 nên
nên 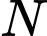 là trung điểm đoạn thẳng
là trung điểm đoạn thẳng 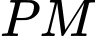
Do đó, ta có: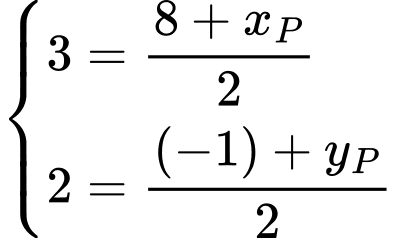
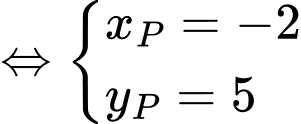
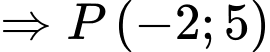 Đáp án: A
Đáp án: A
Ta có:
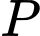 là điểm đối xứng với điểm
là điểm đối xứng với điểm 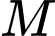 qua điểm
qua điểm 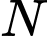 nên
nên 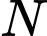 là trung điểm đoạn thẳng
là trung điểm đoạn thẳng 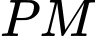
Do đó, ta có:
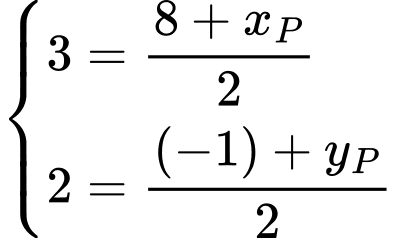
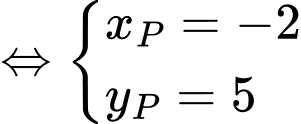
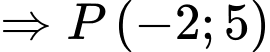 Đáp án: A
Đáp án: A
Câu 13 [582994]: Cho 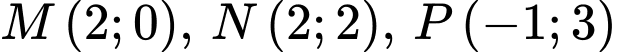 lần lượt là trung điểm các cạnh
lần lượt là trung điểm các cạnh 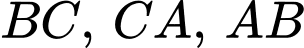 của
của 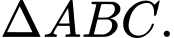 Tọa độ
Tọa độ 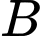 là:
là:
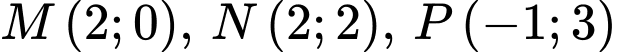 lần lượt là trung điểm các cạnh
lần lượt là trung điểm các cạnh 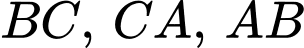 của
của 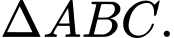 Tọa độ
Tọa độ 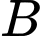 là:
là: A, 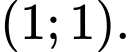
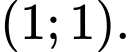
B, 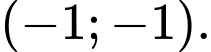
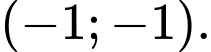
C, 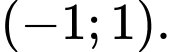
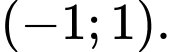
D, 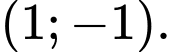
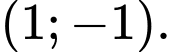
Chọn C
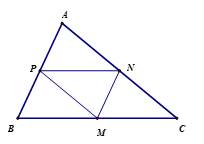
Ta có: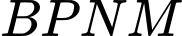 là hình bình hành nên
là hình bình hành nên
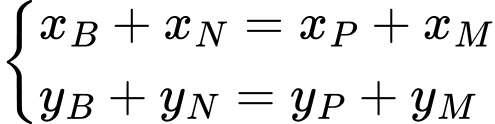
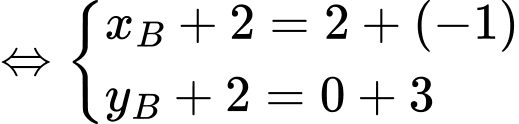
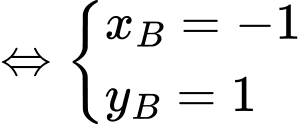 Đáp án: C
Đáp án: C

Ta có:
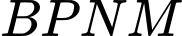 là hình bình hành nên
là hình bình hành nên 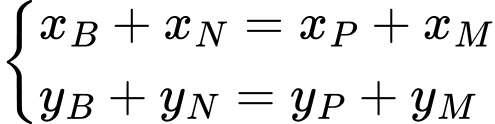
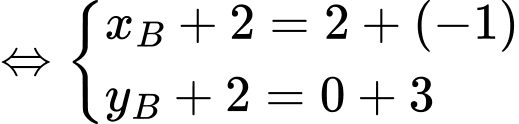
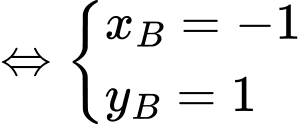 Đáp án: C
Đáp án: C
Câu 14 [582995]: Trong mặt phẳng tọa độ 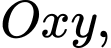 cho tam giác
cho tam giác 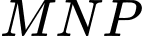 có
có 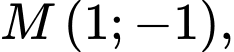
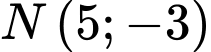 và
và 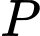 thuộc trục
thuộc trục 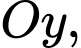 trọng tâm
trọng tâm  của tam giác nằm trên trục
của tam giác nằm trên trục 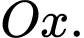 Toạ độ của điểm
Toạ độ của điểm 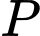 là
là
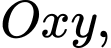 cho tam giác
cho tam giác 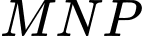 có
có 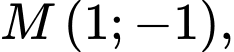
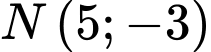 và
và 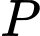 thuộc trục
thuộc trục 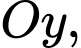 trọng tâm
trọng tâm  của tam giác nằm trên trục
của tam giác nằm trên trục 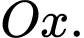 Toạ độ của điểm
Toạ độ của điểm 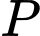 là
là A, 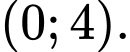
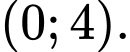
B, 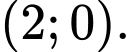
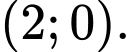
C, 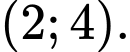
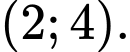
D, 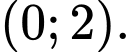
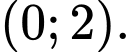
Chọn A
Ta có: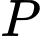 thuộc trục
thuộc trục 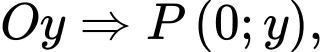
 nằm trên trục
nằm trên trục 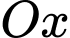
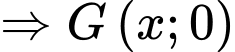
 là trọng tâm tam giác
là trọng tâm tam giác 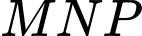 nên ta có:
nên ta có: 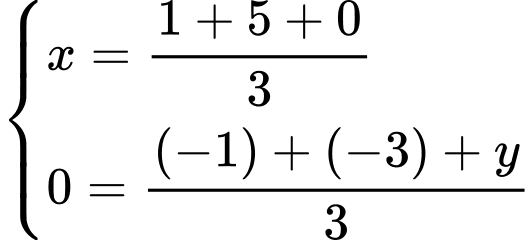
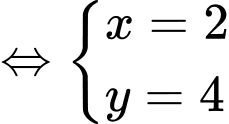
Vậy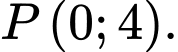 Đáp án: A
Đáp án: A
Ta có:
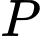 thuộc trục
thuộc trục 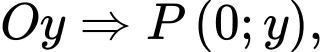
 nằm trên trục
nằm trên trục 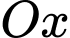
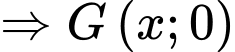
 là trọng tâm tam giác
là trọng tâm tam giác 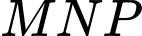 nên ta có:
nên ta có: 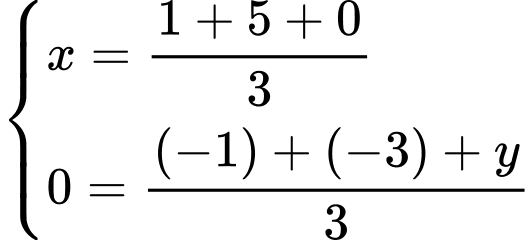
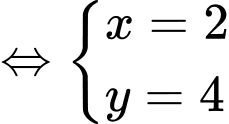
Vậy
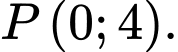 Đáp án: A
Đáp án: A
Câu 15 [582996]: Cho 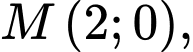
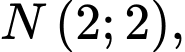
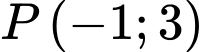 là trung điểm các cạnh
là trung điểm các cạnh 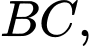
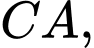
 của tam giác
của tam giác 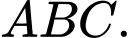 Tọa độ
Tọa độ 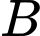 là:
là:
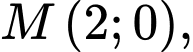
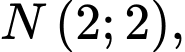
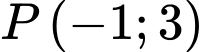 là trung điểm các cạnh
là trung điểm các cạnh 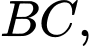
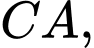
 của tam giác
của tam giác 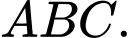 Tọa độ
Tọa độ 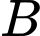 là:
là: A, 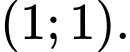
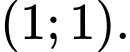
B, 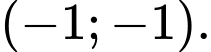
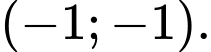
C, 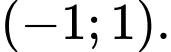
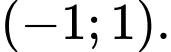
D, 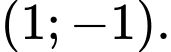
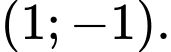
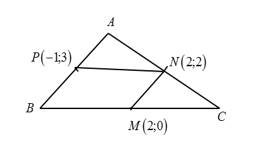
Chọn C.
Ta có
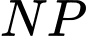 là đường trung bình của tam giác
là đường trung bình của tam giác 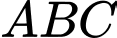
Nên
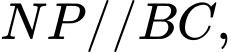
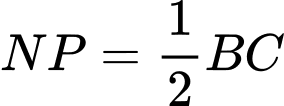 nên tứ giác
nên tứ giác 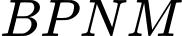 là hình bình hành. Do đó
là hình bình hành. Do đó 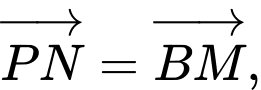 mà
mà 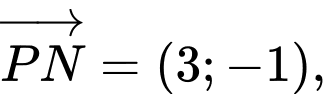 giả sử
giả sử 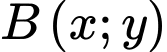 thì
thì 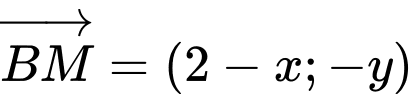
Khi đó
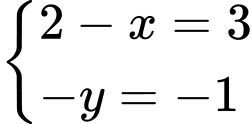

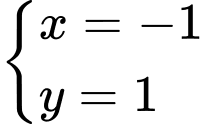
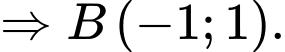
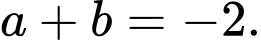 Đáp án: C
Đáp án: C Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 16 đến câu 18. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 16 [582997]: Trong mặt phẳng 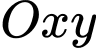 cho các điểm
cho các điểm 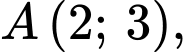
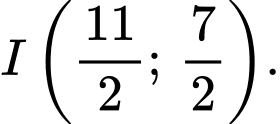
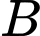 là điểm đối xứng với
là điểm đối xứng với 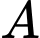 qua
qua 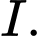 Giả sử
Giả sử  là điểm có tọa độ
là điểm có tọa độ 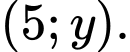 Giá trị của
Giá trị của 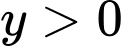 để tam giác
để tam giác 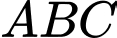 là tam giác vuông tại
là tam giác vuông tại  là
là
TRẢ LỜI: ……………………….
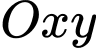 cho các điểm
cho các điểm 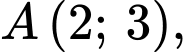
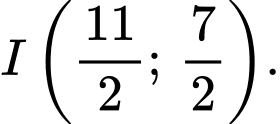
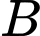 là điểm đối xứng với
là điểm đối xứng với 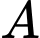 qua
qua 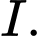 Giả sử
Giả sử  là điểm có tọa độ
là điểm có tọa độ 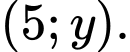 Giá trị của
Giá trị của 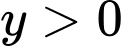 để tam giác
để tam giác 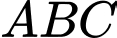 là tam giác vuông tại
là tam giác vuông tại  là
làTRẢ LỜI: ……………………….
TRẢ LỜI: 7
Cách 1:
Vì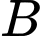 là điểm đối xứng với
là điểm đối xứng với 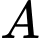 qua
qua 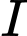 nên
nên 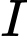 là trung điểm đoạn thẳng
là trung điểm đoạn thẳng 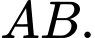 Khi đó, ta có
Khi đó, ta có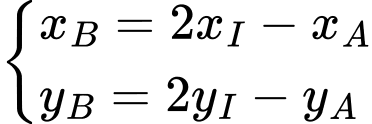
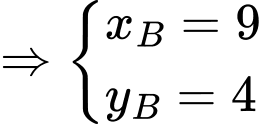
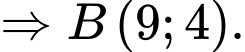
Tam giác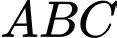 là tam giác vuông tại
là tam giác vuông tại  nên
nên 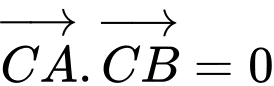
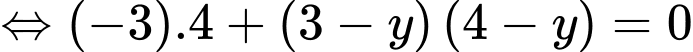
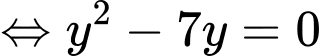
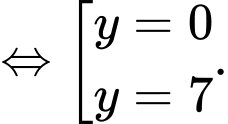
Cách 2:
Theo đề bài ta có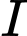 là trung điểm đoạn thẳng
là trung điểm đoạn thẳng  và tam giác
và tam giác 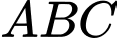 là tam giác vuông tại
là tam giác vuông tại  nên ta có
nên ta có 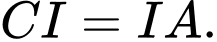 Ta có
Ta có 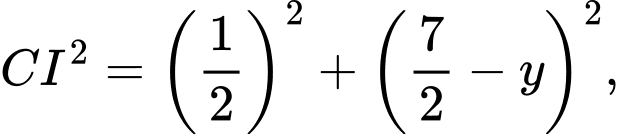
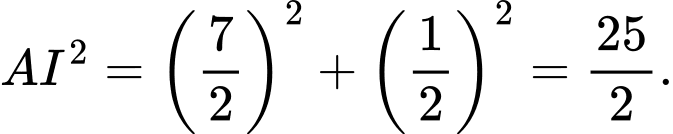
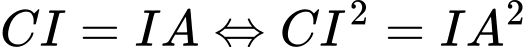
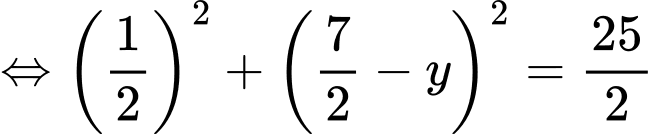
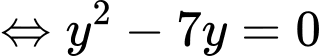
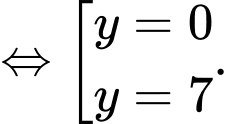
Cách 1:
Vì
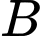 là điểm đối xứng với
là điểm đối xứng với 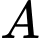 qua
qua 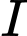 nên
nên 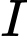 là trung điểm đoạn thẳng
là trung điểm đoạn thẳng 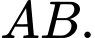 Khi đó, ta có
Khi đó, ta có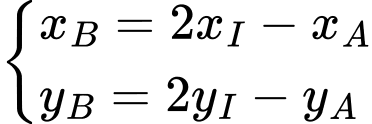
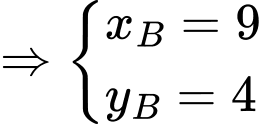
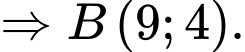
Tam giác
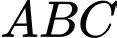 là tam giác vuông tại
là tam giác vuông tại  nên
nên 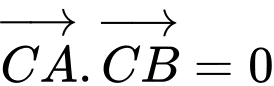
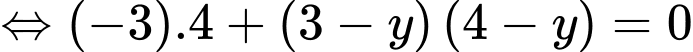
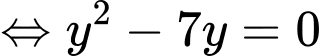
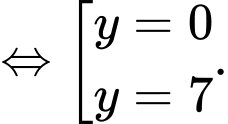
Cách 2:
Theo đề bài ta có
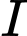 là trung điểm đoạn thẳng
là trung điểm đoạn thẳng  và tam giác
và tam giác 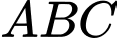 là tam giác vuông tại
là tam giác vuông tại  nên ta có
nên ta có 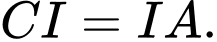 Ta có
Ta có 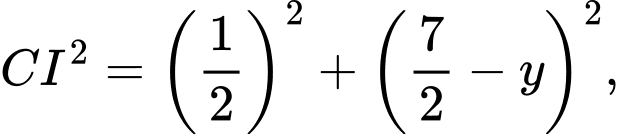
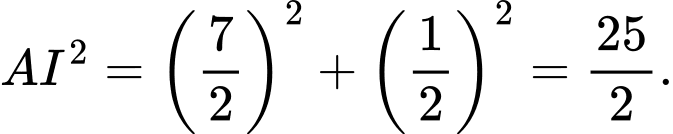
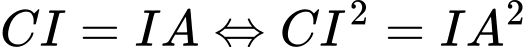
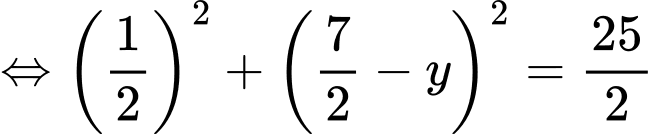
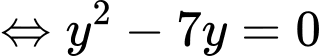
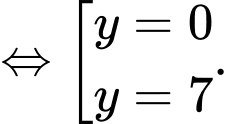
Câu 17 [582998]: Trong mặt phẳng 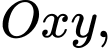 cho hình bình hành
cho hình bình hành 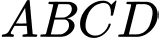 có
có 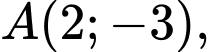
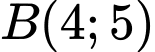 và
và 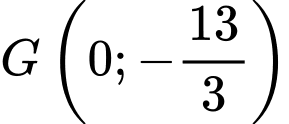 là trọng tâm tam giác
là trọng tâm tam giác 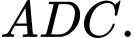 Gọi tọa độ đỉnh
Gọi tọa độ đỉnh 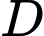 lần lượt là
lần lượt là 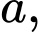
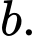 Tổng
Tổng 
TRẢ LỜI: ……………………….
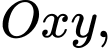 cho hình bình hành
cho hình bình hành 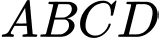 có
có 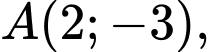
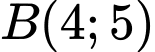 và
và 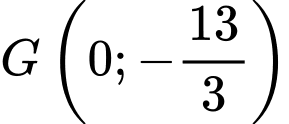 là trọng tâm tam giác
là trọng tâm tam giác 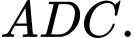 Gọi tọa độ đỉnh
Gọi tọa độ đỉnh 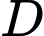 lần lượt là
lần lượt là 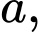
 Tổng
Tổng 
TRẢ LỜI: ……………………….
TRẢ LỜI: 85
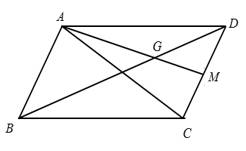
Chọn C.
Gọi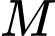 là trung điểm
là trung điểm 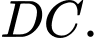
Do là trọng tâm nên
là trọng tâm nên
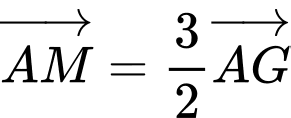
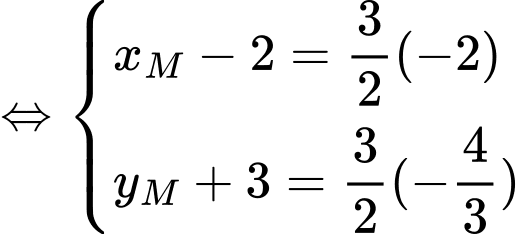
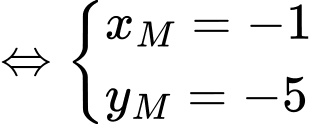

Mặt khác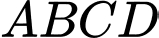 là hình bình hành nên
là hình bình hành nên 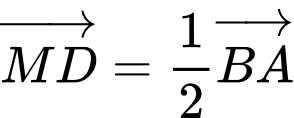
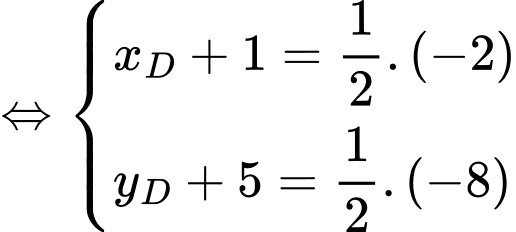
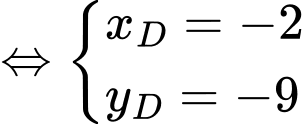
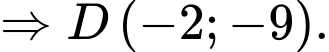
- Ngoài ra có thể sử dụng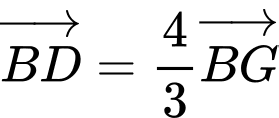 để tìm được điểm
để tìm được điểm 

Chọn C.
Gọi
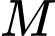 là trung điểm
là trung điểm 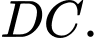
Do
 là trọng tâm nên
là trọng tâm nên 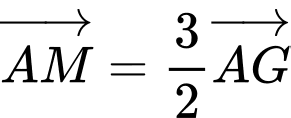
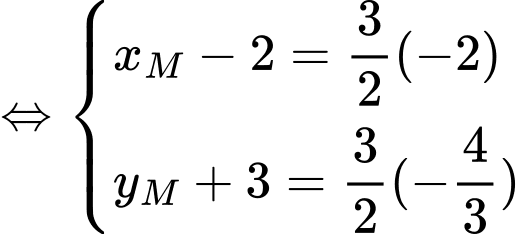
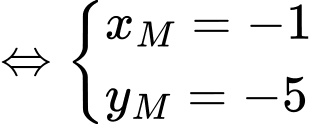

Mặt khác
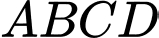 là hình bình hành nên
là hình bình hành nên 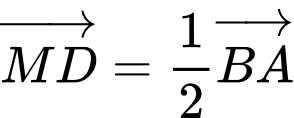
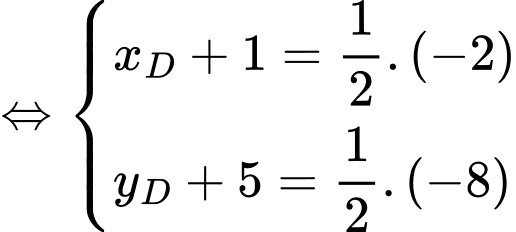
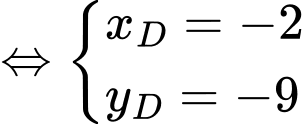
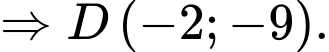
- Ngoài ra có thể sử dụng
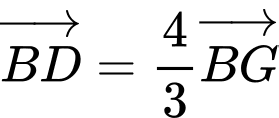 để tìm được điểm
để tìm được điểm 
Câu 18 [582999]: Trong mặt phẳng 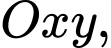 cho tam giác
cho tam giác 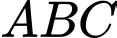 có
có 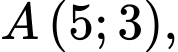
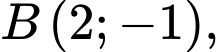
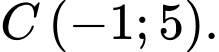 Tổng hoành độ và tung độ trực tâm
Tổng hoành độ và tung độ trực tâm 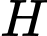 của tam giác.
của tam giác.
TRẢ LỜI: ……………………….
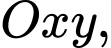 cho tam giác
cho tam giác 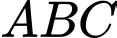 có
có 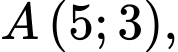
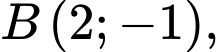
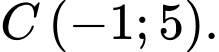 Tổng hoành độ và tung độ trực tâm
Tổng hoành độ và tung độ trực tâm 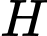 của tam giác.
của tam giác.TRẢ LỜI: ……………………….
TRẢ LỜI: 5
Do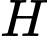 là trực tâm của tam giác
là trực tâm của tam giác 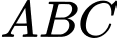 nên
nên  và
và 
Gọi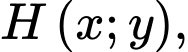 khi đó ta có
khi đó ta có
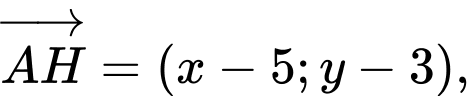
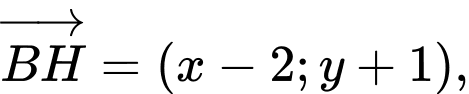
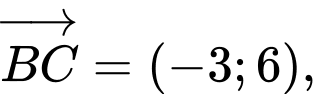
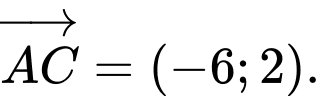
 và
và 
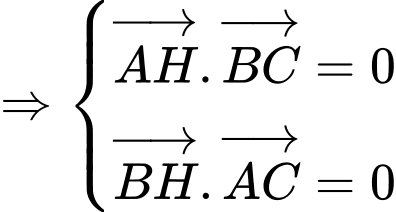
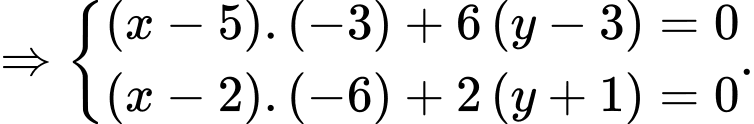
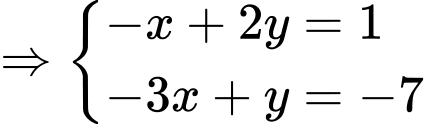
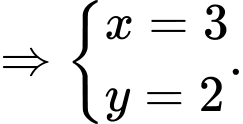
Do
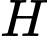 là trực tâm của tam giác
là trực tâm của tam giác 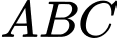 nên
nên  và
và 
Gọi
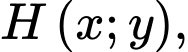 khi đó ta có
khi đó ta có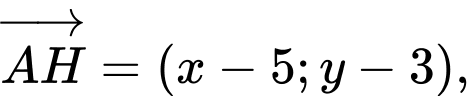
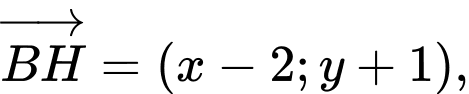
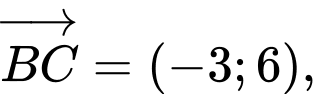
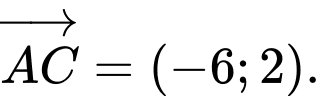
 và
và