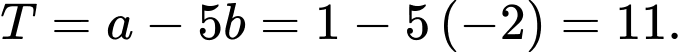Ví dụ
Câu 1 [583033]: Viết phương trình tham số của đường thẳng  biết
biết 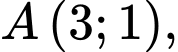
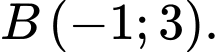
 biết
biết 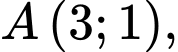
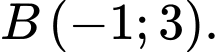
Ta có 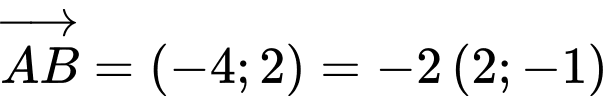
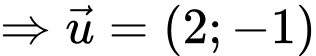 là một VTCP của đường thẳng
là một VTCP của đường thẳng 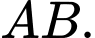
Vậy đi qua
đi qua 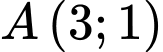 và có VTCP
và có VTCP 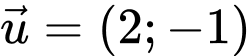 nên có PTTS
nên có PTTS 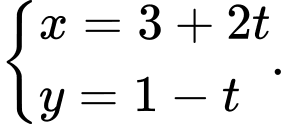
Lưu ý. Ta hoàn toàn có thể dùng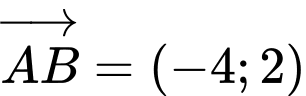 làm VTCP của đường thẳng
làm VTCP của đường thẳng 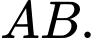
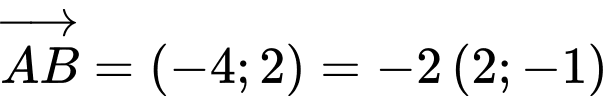
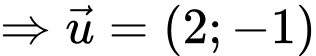 là một VTCP của đường thẳng
là một VTCP của đường thẳng 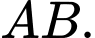
Vậy
 đi qua
đi qua 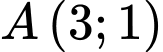 và có VTCP
và có VTCP 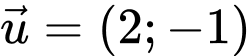 nên có PTTS
nên có PTTS 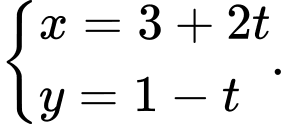
Lưu ý. Ta hoàn toàn có thể dùng
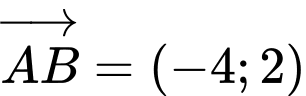 làm VTCP của đường thẳng
làm VTCP của đường thẳng 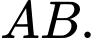
Câu 2 [583034]: Viết phương trình tổng quát của đường thẳng  đi qua
đi qua 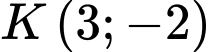 và song song với đường thẳng
và song song với đường thẳng 
 đi qua
đi qua 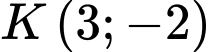 và song song với đường thẳng
và song song với đường thẳng 
Đường thẳng 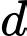 có một VTPT là
có một VTPT là 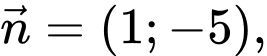 vì
vì 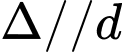 nên
nên  cũng nhận
cũng nhận 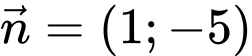 làm một VTPT vậy phương trình tham số của
làm một VTPT vậy phương trình tham số của  là
là 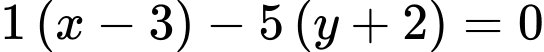
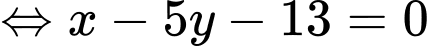
Lưu ý. Ta hoàn toàn có thể giải theo cách khác như sau.
Vì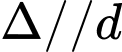 nên
nên 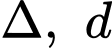 có cùng VTCP, phương trình tổng quát của
có cùng VTCP, phương trình tổng quát của  có dạng
có dạng 
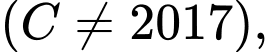 mà
mà  đi qua
đi qua 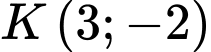 nên ta có
nên ta có 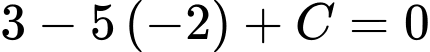
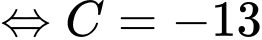
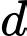 có một VTPT là
có một VTPT là 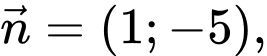 vì
vì 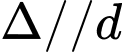 nên
nên  cũng nhận
cũng nhận 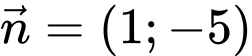 làm một VTPT vậy phương trình tham số của
làm một VTPT vậy phương trình tham số của  là
là 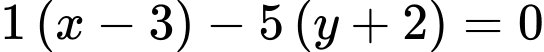
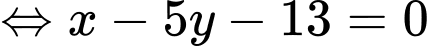
Lưu ý. Ta hoàn toàn có thể giải theo cách khác như sau.
Vì
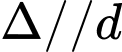 nên
nên 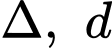 có cùng VTCP, phương trình tổng quát của
có cùng VTCP, phương trình tổng quát của  có dạng
có dạng 
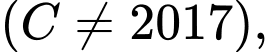 mà
mà  đi qua
đi qua 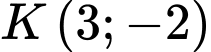 nên ta có
nên ta có 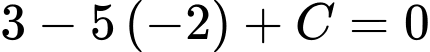
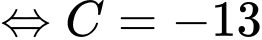
Câu 3 [583035]: Cho đường thẳng 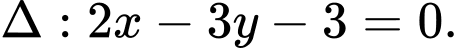 Viết phương trình tham số của đường thẳng.
Viết phương trình tham số của đường thẳng.
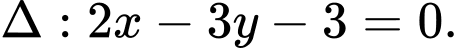 Viết phương trình tham số của đường thẳng.
Viết phương trình tham số của đường thẳng.
Cách 1.
Để tìm một điểm mà đường thẳng đi qua ta cho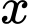 một giá trị bất kỳ tính
một giá trị bất kỳ tính 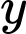 hoặc ngược lại.
hoặc ngược lại.
Cho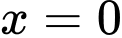 thế vào phương trình đường thẳng
thế vào phương trình đường thẳng  ta được
ta được 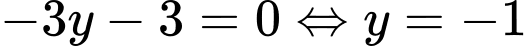
Vậy đường thẳng đi qua điểm
đi qua điểm 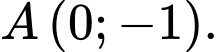 Và có VTPT
Và có VTPT 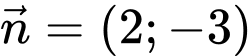 suy ra VTCP
suy ra VTCP 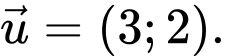
Vậy phương trình tham số của là
là 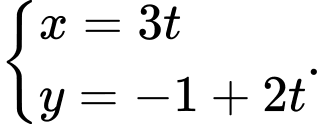
Cách 2.
Từ PTTQ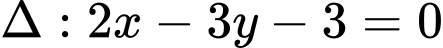
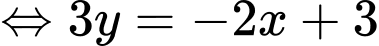
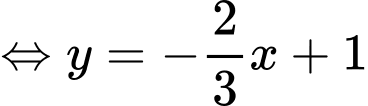
Đặt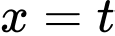 ta thu được phương trình tham số là
ta thu được phương trình tham số là 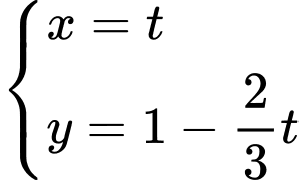
Để tìm một điểm mà đường thẳng đi qua ta cho
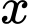 một giá trị bất kỳ tính
một giá trị bất kỳ tính 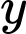 hoặc ngược lại.
hoặc ngược lại.Cho
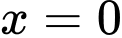 thế vào phương trình đường thẳng
thế vào phương trình đường thẳng  ta được
ta được 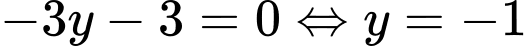
Vậy đường thẳng
 đi qua điểm
đi qua điểm 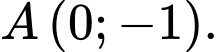 Và có VTPT
Và có VTPT 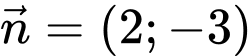 suy ra VTCP
suy ra VTCP 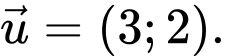
Vậy phương trình tham số của
 là
là 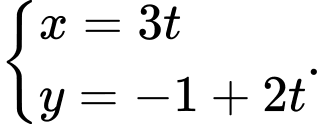
Cách 2.
Từ PTTQ
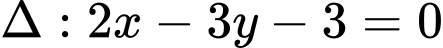
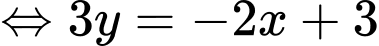
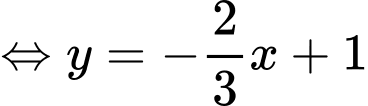
Đặt
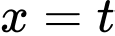 ta thu được phương trình tham số là
ta thu được phương trình tham số là 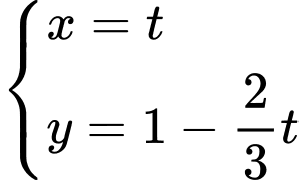
Câu 4 [583036]: Cho tam giác 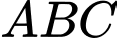 biết trực tâm
biết trực tâm 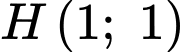 và phương trình cạnh
và phương trình cạnh 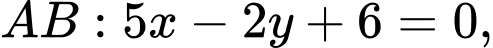 phương trình cạnh
phương trình cạnh 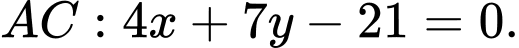 Phương trình cạnh
Phương trình cạnh 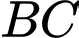 là
là
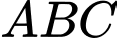 biết trực tâm
biết trực tâm 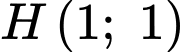 và phương trình cạnh
và phương trình cạnh 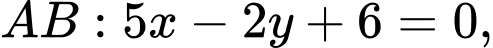 phương trình cạnh
phương trình cạnh 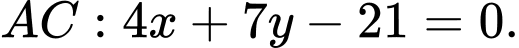 Phương trình cạnh
Phương trình cạnh 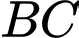 là
là 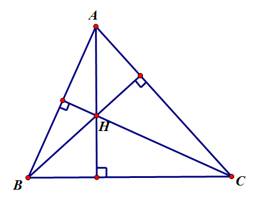
Phương trình
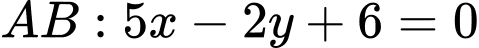
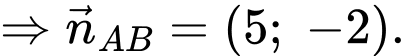
Phương trình
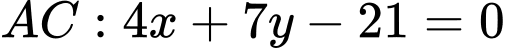
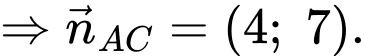
Ta có

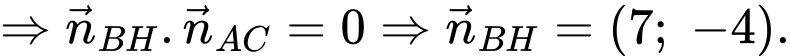
Suy ra phương trình đường thẳng
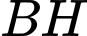 có
có 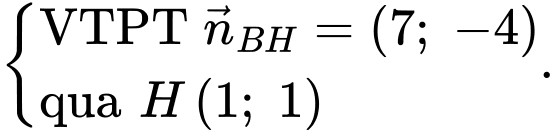
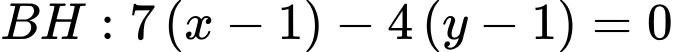
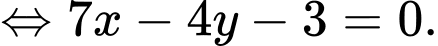
Ta có điểm
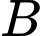 là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng  và
và 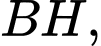 suy ra tọa độ điểm
suy ra tọa độ điểm 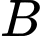 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình 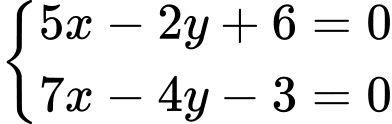
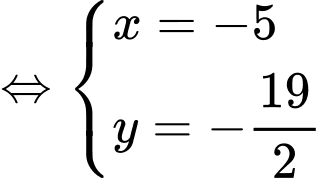
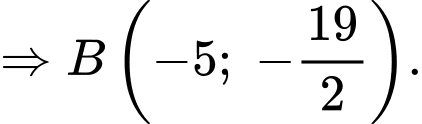
Ta lại có

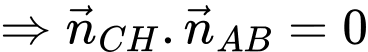
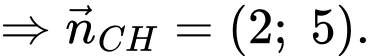
Suy ra phương trình đường thẳng
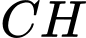 có
có 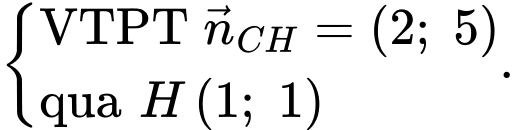
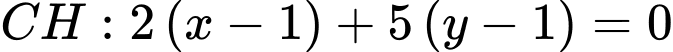
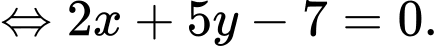
Ta có điểm
 là giao điểm của hai đường thẳng
là giao điểm của hai đường thẳng 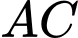 và
và 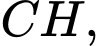 suy ra tọa độ điểm
suy ra tọa độ điểm  là nghiệm của hệ phương trình
là nghiệm của hệ phương trình 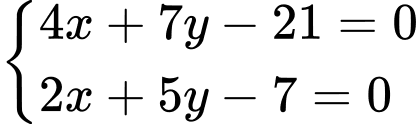
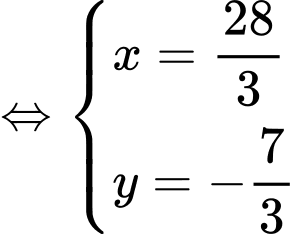
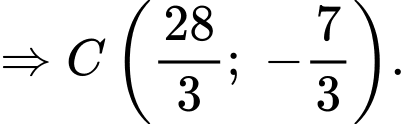
Ta có
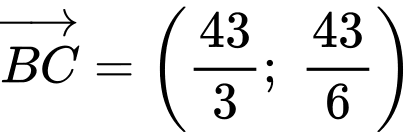
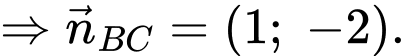
Phương trình cạnh
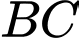 có
có 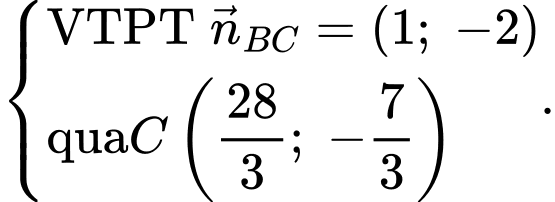
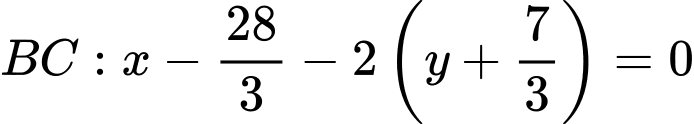
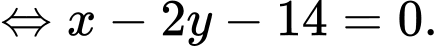
Vậy
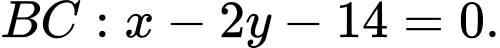
Câu 5 [583037]: Trong mặt phẳng tọa độ 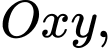 cho điểm
cho điểm 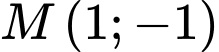 và hai đường thẳng có phương trình
và hai đường thẳng có phương trình 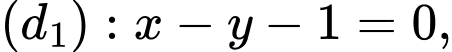
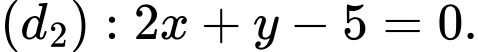 Gọi
Gọi 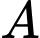 là giao điểm của hai đường thẳng trên. Biết rằng có hai đường thẳng
là giao điểm của hai đường thẳng trên. Biết rằng có hai đường thẳng  đi qua
đi qua 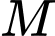 cắt hai đường thẳng trên lần lượt tại hai điểm
cắt hai đường thẳng trên lần lượt tại hai điểm 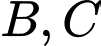 sao cho
sao cho 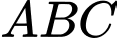 là tam giác có
là tam giác có 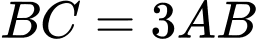 có dạng:
có dạng: 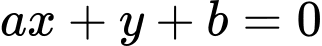 và
và  giá trị của
giá trị của 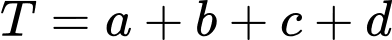 là
là
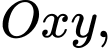 cho điểm
cho điểm 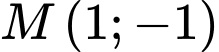 và hai đường thẳng có phương trình
và hai đường thẳng có phương trình 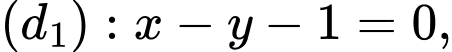
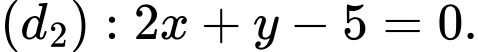 Gọi
Gọi 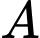 là giao điểm của hai đường thẳng trên. Biết rằng có hai đường thẳng
là giao điểm của hai đường thẳng trên. Biết rằng có hai đường thẳng  đi qua
đi qua 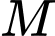 cắt hai đường thẳng trên lần lượt tại hai điểm
cắt hai đường thẳng trên lần lượt tại hai điểm 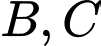 sao cho
sao cho 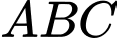 là tam giác có
là tam giác có 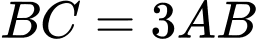 có dạng:
có dạng: 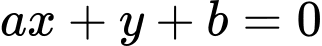 và
và  giá trị của
giá trị của 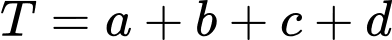 là
là 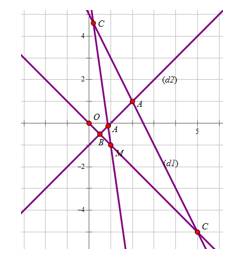
Tọa độ
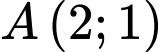
Gọi
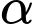 là góc giữa hai đường thẳng
là góc giữa hai đường thẳng 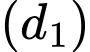 và
và 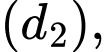
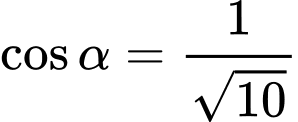
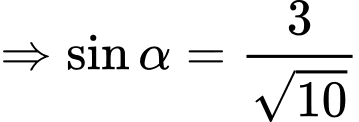
Xét tam giác
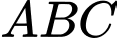 ta có:
ta có: 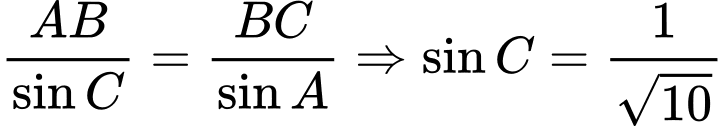
Gọi
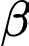 là góc giữa hai đường thẳng
là góc giữa hai đường thẳng  và
và 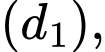 suy ra:
suy ra: 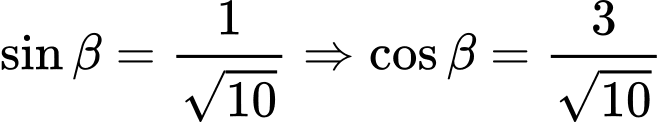

Giả sử
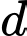 có vectơ pháp tuyến là
có vectơ pháp tuyến là 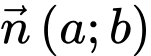
Từ
 ta có:
ta có: 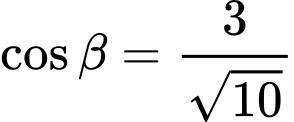
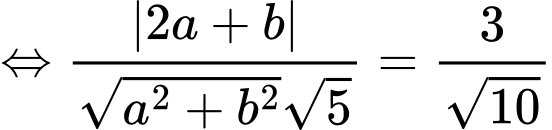
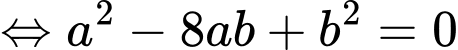
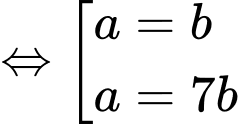
Với
 một vectơ pháp tuyến
một vectơ pháp tuyến 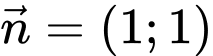
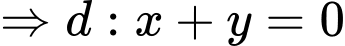
Với
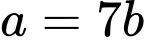 một vectơ pháp tuyến
một vectơ pháp tuyến 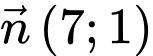

Vậy:

Câu 6 [583038]: Trong mặt phẳng 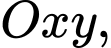 cho hai đường thẳng
cho hai đường thẳng  và
và 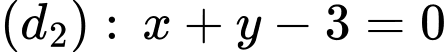 cắt nhau tại
cắt nhau tại 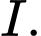 Phương trình đường thẳng đi qua
Phương trình đường thẳng đi qua 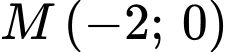 cắt
cắt 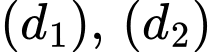 tại
tại 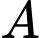 và
và 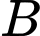 sao cho tam giác
sao cho tam giác 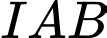 cân tại
cân tại 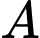 có phương trình dạng
có phương trình dạng 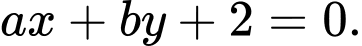 Tính
Tính 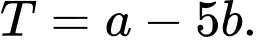
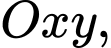 cho hai đường thẳng
cho hai đường thẳng  và
và 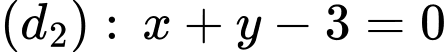 cắt nhau tại
cắt nhau tại 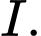 Phương trình đường thẳng đi qua
Phương trình đường thẳng đi qua 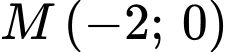 cắt
cắt 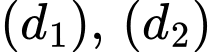 tại
tại 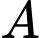 và
và 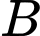 sao cho tam giác
sao cho tam giác 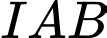 cân tại
cân tại 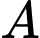 có phương trình dạng
có phương trình dạng 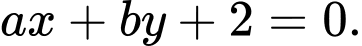 Tính
Tính 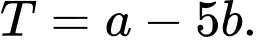
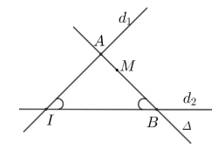
Đường thẳng
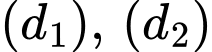 có vectơ pháp tuyến lần lượt là
có vectơ pháp tuyến lần lượt là 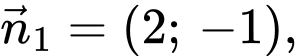
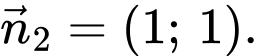
Gọi
 là đường thẳng cần tìm có vectơ pháp tuyến là
là đường thẳng cần tìm có vectơ pháp tuyến là 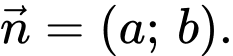
Góc giữa 2 đường thẳng
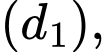
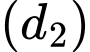 và
và 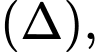
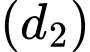 xác định bởi:
xác định bởi: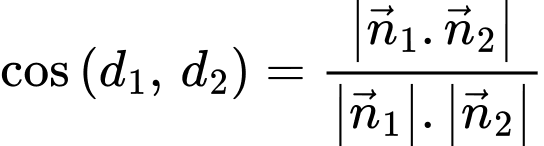
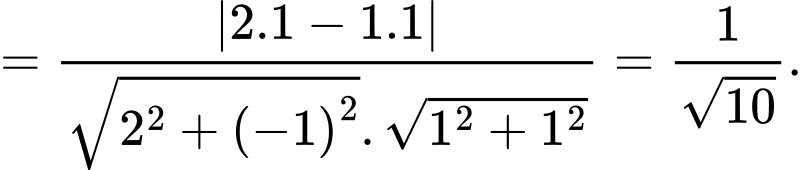
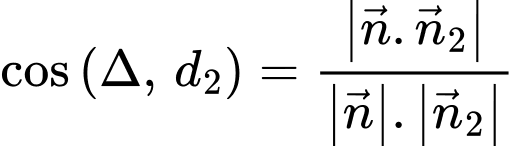
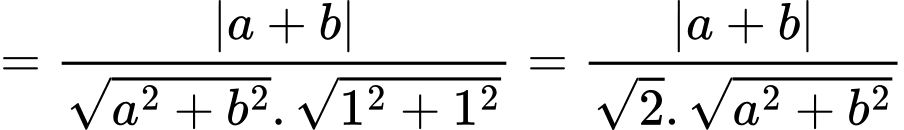
Vì
 cắt
cắt 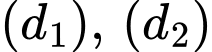 tại
tại 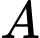 và
và 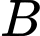 tạo thành tam giác
tạo thành tam giác 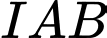 cân tại
cân tại 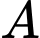 nên
nên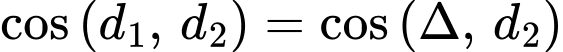
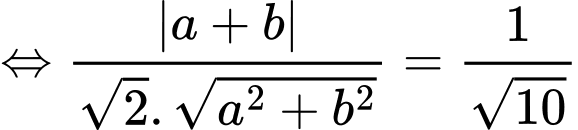
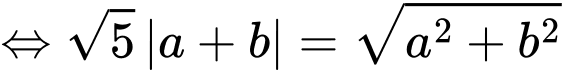
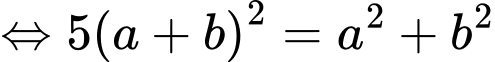
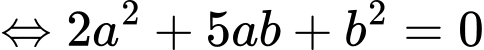
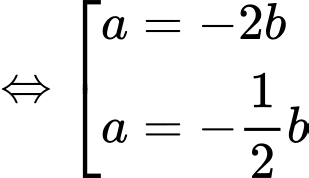
+
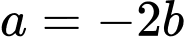 : chọn
: chọn 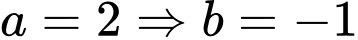 : phương trình đường thẳng là:
: phương trình đường thẳng là: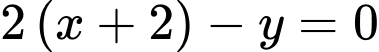
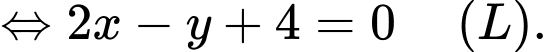
+
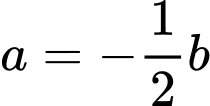 : chọn
: chọn 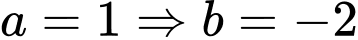 : phương trình đường thẳng là:
: phương trình đường thẳng là: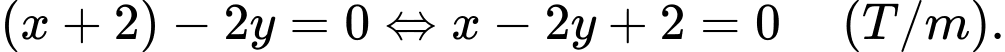
Do đó