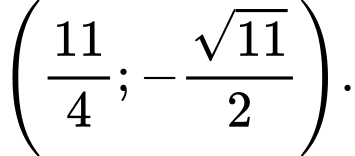Dạng 1: Các bài toán liên quan đến elip
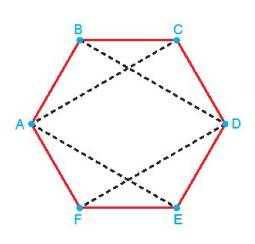
Câu 1 [583141]: Cho lục giác đều 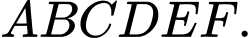 Chứng minh rằng bốn điểm
Chứng minh rằng bốn điểm 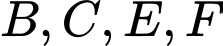 cùng thuộc một elip có hai tiêu điểm là
cùng thuộc một elip có hai tiêu điểm là 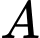 và
và 
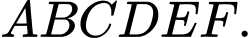 Chứng minh rằng bốn điểm
Chứng minh rằng bốn điểm 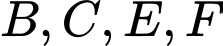 cùng thuộc một elip có hai tiêu điểm là
cùng thuộc một elip có hai tiêu điểm là 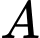 và
và 
Lục giác đều 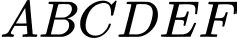 có các cạnh bằng nhau và các góc đều có số đo là
có các cạnh bằng nhau và các góc đều có số đo là 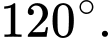 Do đó, các tam giác
Do đó, các tam giác 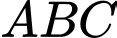 ,
, 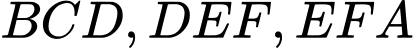 bằng nhau (c.g.c). Suy ra
bằng nhau (c.g.c). Suy ra 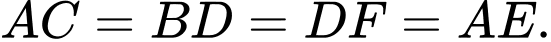 Từ đó, ta có
Từ đó, ta có 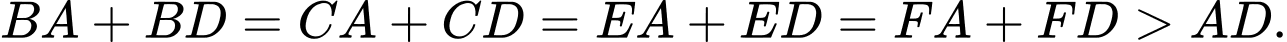 Vậy
Vậy 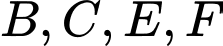 cùng thuộc một elip có hai tiêu điểm là
cùng thuộc một elip có hai tiêu điểm là 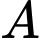 và
và 
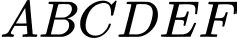 có các cạnh bằng nhau và các góc đều có số đo là
có các cạnh bằng nhau và các góc đều có số đo là 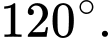 Do đó, các tam giác
Do đó, các tam giác 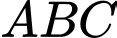 ,
, 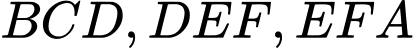 bằng nhau (c.g.c). Suy ra
bằng nhau (c.g.c). Suy ra 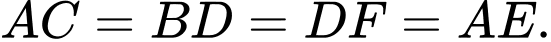 Từ đó, ta có
Từ đó, ta có 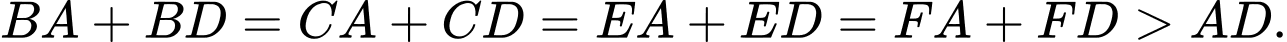 Vậy
Vậy 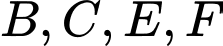 cùng thuộc một elip có hai tiêu điểm là
cùng thuộc một elip có hai tiêu điểm là 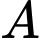 và
và 

Câu 2 [583142]: Cho elip có phương trình chính tắc 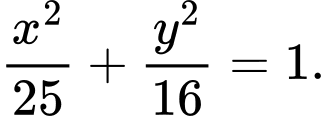 Tìm các tiêu điểm và tiêu cự của elip. Tính tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm.
Tìm các tiêu điểm và tiêu cự của elip. Tính tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm.
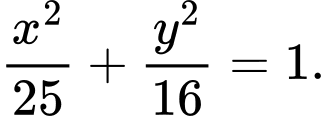 Tìm các tiêu điểm và tiêu cự của elip. Tính tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm.
Tìm các tiêu điểm và tiêu cự của elip. Tính tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm.
Ta có: 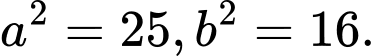 Do đó
Do đó 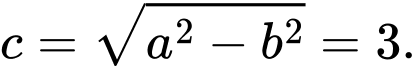
Vậy elip có hai tiêu điểm là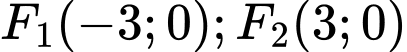 và tiêu cự là
và tiêu cự là 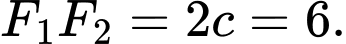
Ta có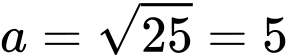 , nên tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng
, nên tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng 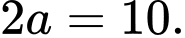
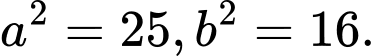 Do đó
Do đó 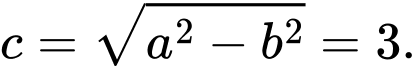
Vậy elip có hai tiêu điểm là
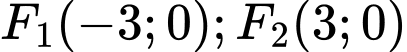 và tiêu cự là
và tiêu cự là 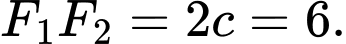
Ta có
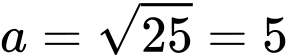 , nên tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng
, nên tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng 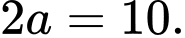
Dạng 2: Các bài toán liên quan đến hypebol
Câu 3 [583143]: Trên biển có hai đảo hình tròn với bán kính khác nhau. Tại vùng biển giữa hai đảo đó, người ta xác định một đường ranh giới cách đều hai đảo, tức là, đường mà khoảng cách từ mổi vị trí trên đó đến hai đảo là bằng nhau. Hỏi đường ranh giới đó có thuộc một nhánh của một hypebol hay không?
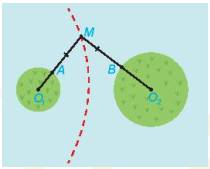
Chú ý. Khoảng cách từ một vị trí trên biển đến đảo hình tròn bằng hiệu của khoảng cách từ vị trí đó đến tâm đảo và bán kinh của đảo.

Chú ý. Khoảng cách từ một vị trí trên biển đến đảo hình tròn bằng hiệu của khoảng cách từ vị trí đó đến tâm đảo và bán kinh của đảo.
Giả sử đảo thứ nhất có tâm 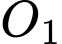 và bán kính
và bán kính 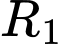 , đảo thứ hai có tâm
, đảo thứ hai có tâm 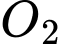 và bán kính
và bán kính 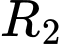 . Do hai đường tròn
. Do hai đường tròn 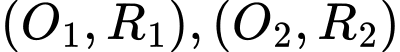 nằm ngoài nhau nên
nằm ngoài nhau nên  Gọi
Gọi 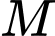 là một điểm bất kì thuộc đường ranh giới.
là một điểm bất kì thuộc đường ranh giới.
Vì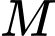 cách đều hai đảo nên
cách đều hai đảo nên

Vậy đường ranh giới thuộc một nhánh của hypebol với tiêu điểm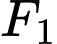 trùng
trùng 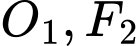 trùng
trùng 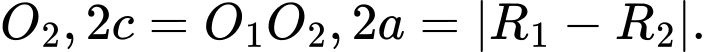
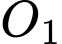 và bán kính
và bán kính 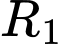 , đảo thứ hai có tâm
, đảo thứ hai có tâm 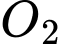 và bán kính
và bán kính 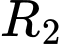 . Do hai đường tròn
. Do hai đường tròn 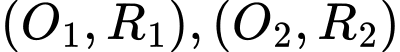 nằm ngoài nhau nên
nằm ngoài nhau nên  Gọi
Gọi 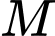 là một điểm bất kì thuộc đường ranh giới.
là một điểm bất kì thuộc đường ranh giới.Vì
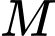 cách đều hai đảo nên
cách đều hai đảo nên
Vậy đường ranh giới thuộc một nhánh của hypebol với tiêu điểm
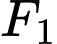 trùng
trùng 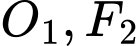 trùng
trùng 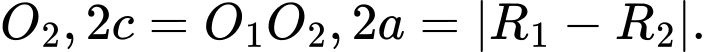
Câu 4 [583144]: Cho hypebol có phương trình chính tắc 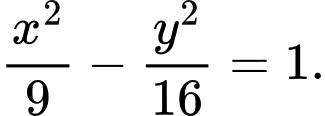 Tìm các tiêu điểm và tiêu cự của hypebol. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
Tìm các tiêu điểm và tiêu cự của hypebol. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
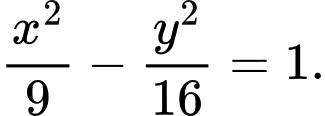 Tìm các tiêu điểm và tiêu cự của hypebol. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
Tìm các tiêu điểm và tiêu cự của hypebol. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
Ta có 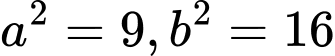 , nên
, nên 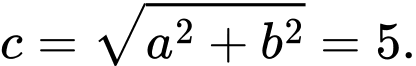
Vậy hypebol có hai tiêu điểm là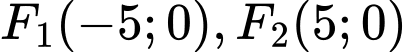 và có tiêu cự
và có tiêu cự 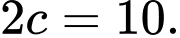
Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng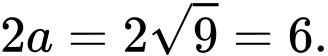
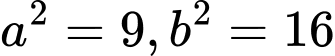 , nên
, nên 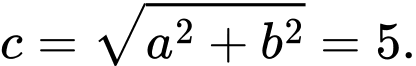
Vậy hypebol có hai tiêu điểm là
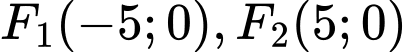 và có tiêu cự
và có tiêu cự 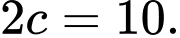
Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng
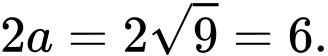
Dạng 3: Các bài toán liên quan đến parabol
Câu 5 [583145]: Cho parabol 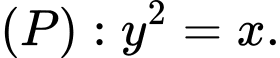
a) Tìm tiêu điểm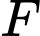 , đường chuẩn
, đường chuẩn  của
của 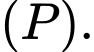
b) Tìm những điểm trên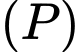 có khoảng cách tới
có khoảng cách tới 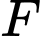 bằng 3.
bằng 3.
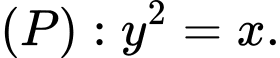
a) Tìm tiêu điểm
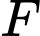 , đường chuẩn
, đường chuẩn  của
của 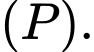
b) Tìm những điểm trên
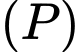 có khoảng cách tới
có khoảng cách tới 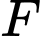 bằng 3.
bằng 3.
a) Ta có 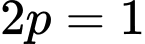 nên
nên 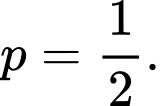
Parabol có tiêu điểm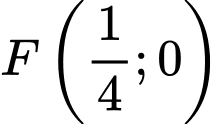 và đường chuẩn
và đường chuẩn 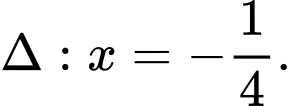
b) Điểm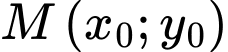 thuộc
thuộc 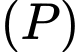 có khoảng cách tới
có khoảng cách tới 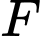 bằng 3 khi và chỉ khi
bằng 3 khi và chỉ khi 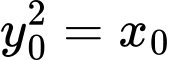 và
và 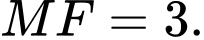
Do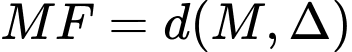 nên
nên 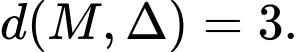
Mặt khác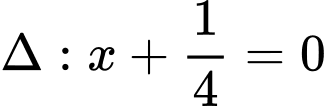 và
và 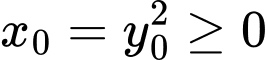 nên
nên 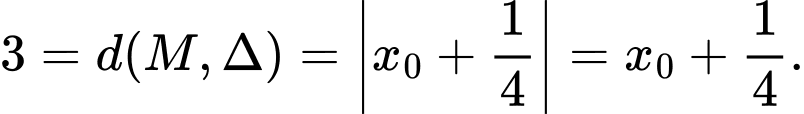
Vậy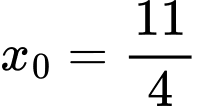 và
và 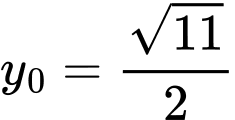 hoặc
hoặc 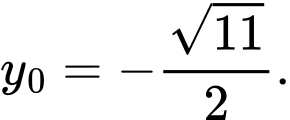
Vậy có hai điểm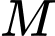 thoả mãn bài toán với toạ độ là
thoả mãn bài toán với toạ độ là 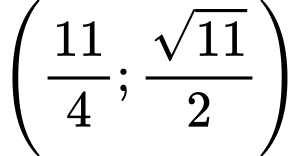 và
và 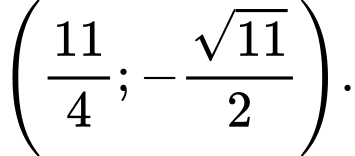
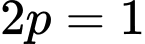 nên
nên 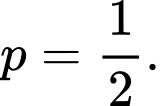
Parabol có tiêu điểm
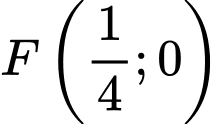 và đường chuẩn
và đường chuẩn 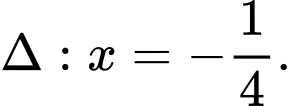
b) Điểm
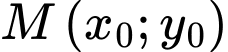 thuộc
thuộc 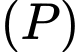 có khoảng cách tới
có khoảng cách tới 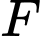 bằng 3 khi và chỉ khi
bằng 3 khi và chỉ khi 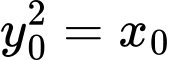 và
và 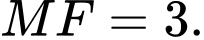
Do
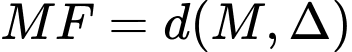 nên
nên 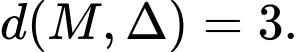
Mặt khác
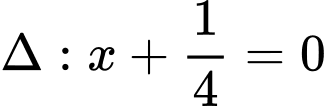 và
và 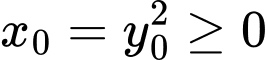 nên
nên 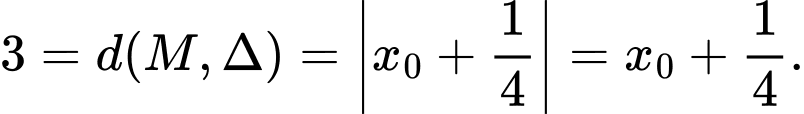
Vậy
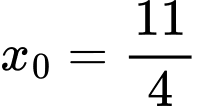 và
và 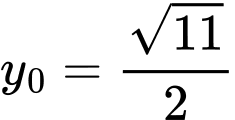 hoặc
hoặc 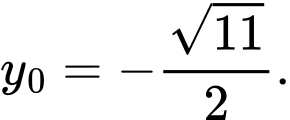
Vậy có hai điểm
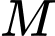 thoả mãn bài toán với toạ độ là
thoả mãn bài toán với toạ độ là 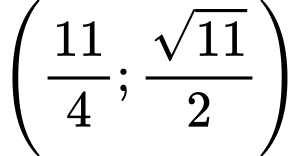 và
và