Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất)
Câu 1 [583146]: Đường Elip 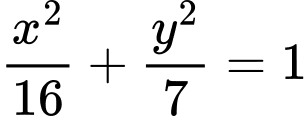 có tiêu cự bằng
có tiêu cự bằng
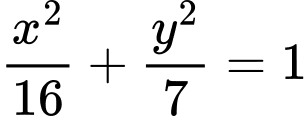 có tiêu cự bằng
có tiêu cự bằng A, 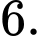
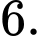
B, 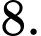
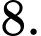
C, 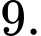
D, 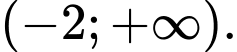
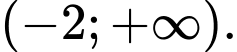
Elip 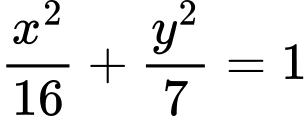 có
có 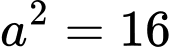 ,
, 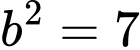
Suy ra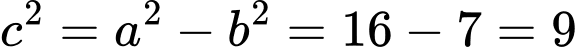
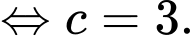
Vậy tiêu cự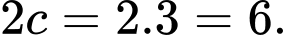 Đáp án: A
Đáp án: A
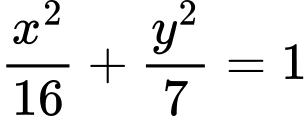 có
có 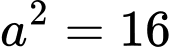 ,
, 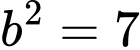
Suy ra
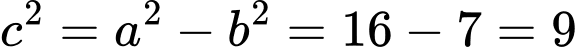
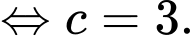
Vậy tiêu cự
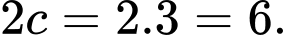 Đáp án: A
Đáp án: A
Câu 2 [583147]: Viết phương trình chính tắc của Parabol đi qua điểm 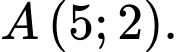
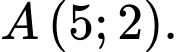
A, 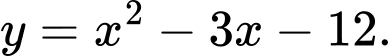
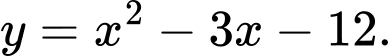
B, 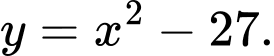
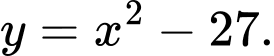
C, 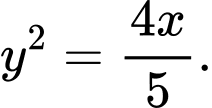
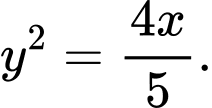
D, 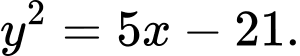
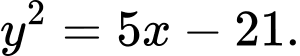
Phương trình chính tắc của parabol 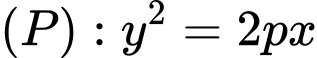
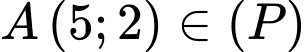
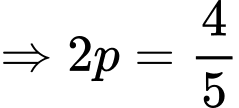
Vậy phương trình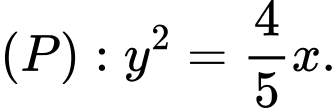 Đáp án: C
Đáp án: C
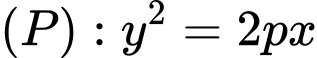
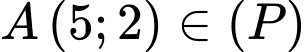
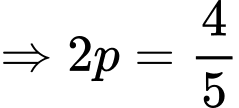
Vậy phương trình
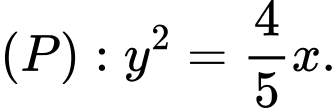 Đáp án: C
Đáp án: C
Câu 3 [583148]: Đường Hyperbol 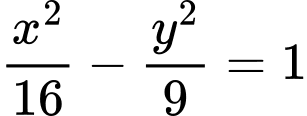 có một tiêu điểm là điểm nào dưới đây?
có một tiêu điểm là điểm nào dưới đây?
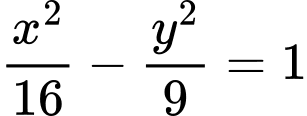 có một tiêu điểm là điểm nào dưới đây?
có một tiêu điểm là điểm nào dưới đây? A, 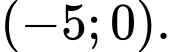
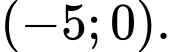
B, 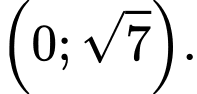
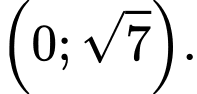
C, 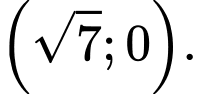
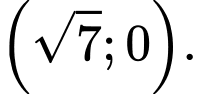
D, 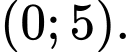
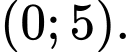
Ta có 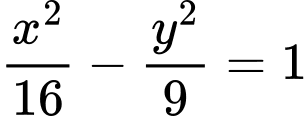 suy ra
suy ra
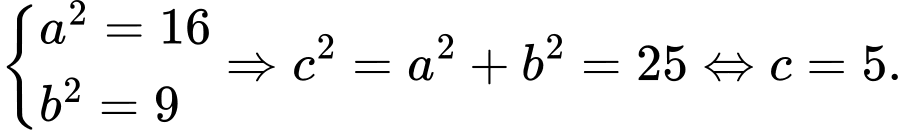
Tiêu điểm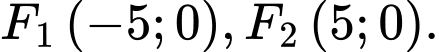 Đáp án: A
Đáp án: A
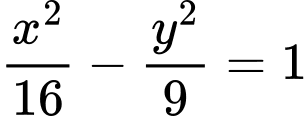 suy ra
suy ra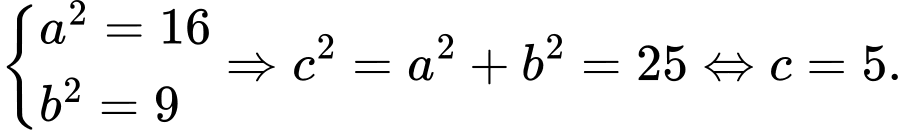
Tiêu điểm
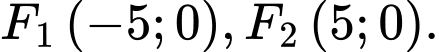 Đáp án: A
Đáp án: A
Câu 4 [583149]: Cho elip 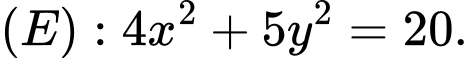 Diện tích hình chữ nhật cơ sở của
Diện tích hình chữ nhật cơ sở của  là
là
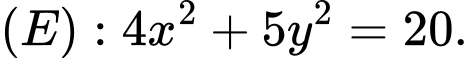 Diện tích hình chữ nhật cơ sở của
Diện tích hình chữ nhật cơ sở của  là
là A, 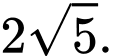
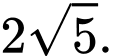
B, 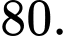
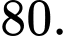
C, 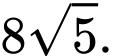
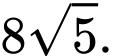
D, 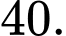
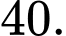
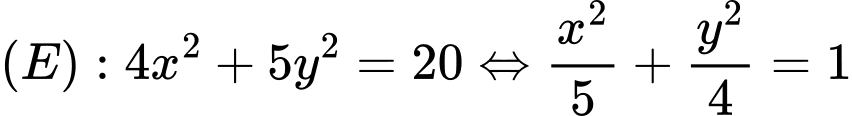
Độ dài trục lớn:
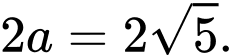
Độ dài trục bé:
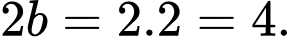
Diện tích hình chữ nhật cơ sở của
 là:
là: 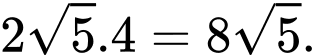 Đáp án: C
Đáp án: C
Câu 5 [583150]: Một điểm 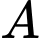 thuộc Parabol
thuộc Parabol 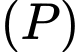 :
: 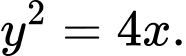 Nếu khoảng cách từ
Nếu khoảng cách từ 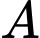 đến đường chuẩn bằng
đến đường chuẩn bằng 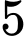 thì khoảng cách từ
thì khoảng cách từ 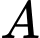 đến trục hoành bằng bao nhiêu?
đến trục hoành bằng bao nhiêu?
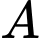 thuộc Parabol
thuộc Parabol 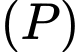 :
: 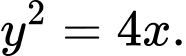 Nếu khoảng cách từ
Nếu khoảng cách từ 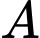 đến đường chuẩn bằng
đến đường chuẩn bằng 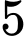 thì khoảng cách từ
thì khoảng cách từ 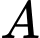 đến trục hoành bằng bao nhiêu?
đến trục hoành bằng bao nhiêu? A, 3.
B, 8.
C, 5.
D, 4.
Ta có: 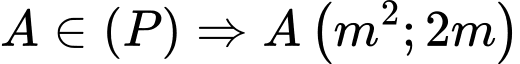 , đường chuẩn
, đường chuẩn 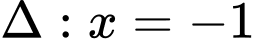
Khoảng cách từ A đến đường chuẩn
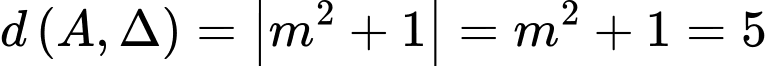
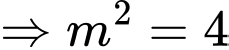
Vậy khoảng cách từ A đến trục hoành bằng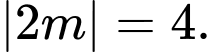 Đáp án: D
Đáp án: D
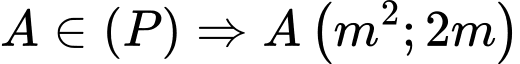 , đường chuẩn
, đường chuẩn 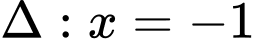
Khoảng cách từ A đến đường chuẩn
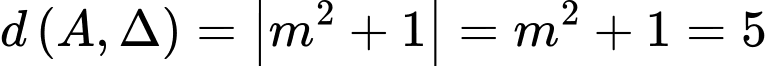
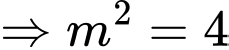
Vậy khoảng cách từ A đến trục hoành bằng
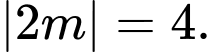 Đáp án: D
Đáp án: D
Câu 6 [583151]: Cho điểm 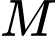 nằm trên hyperbol
nằm trên hyperbol 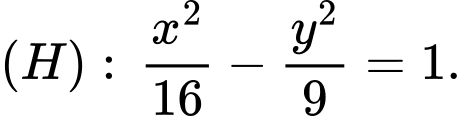 Nếu hoành độ điểm
Nếu hoành độ điểm 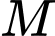 bằng
bằng 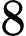 thì khoảng cách từ
thì khoảng cách từ 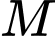 đến các tiêu điểm của
đến các tiêu điểm của  là bao nhiêu?
là bao nhiêu?
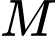 nằm trên hyperbol
nằm trên hyperbol 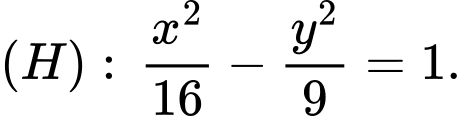 Nếu hoành độ điểm
Nếu hoành độ điểm 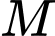 bằng
bằng 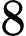 thì khoảng cách từ
thì khoảng cách từ 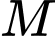 đến các tiêu điểm của
đến các tiêu điểm của  là bao nhiêu?
là bao nhiêu? A, 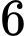 và
và 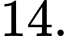
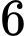 và
và 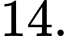
B, 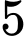 và
và 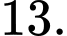
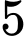 và
và 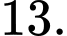
C, 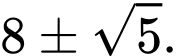
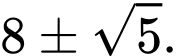
D, 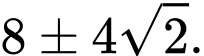
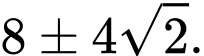
Ta có 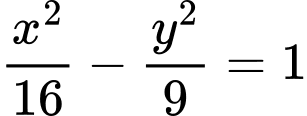 suy ra
suy ra
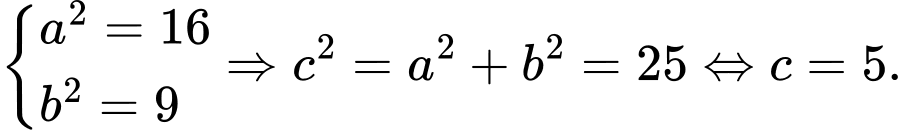
Suy ra tiêu điểm của hyperbol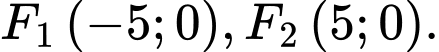
Do hoành độ của điểm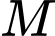 bằng
bằng 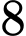 nên
nên 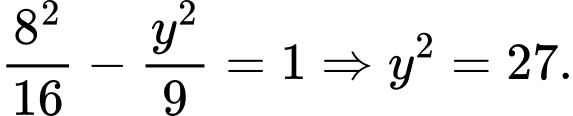
Suy ra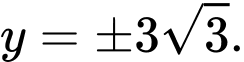
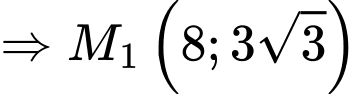 và
và 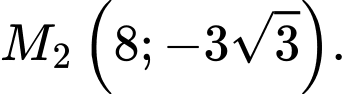
Vậy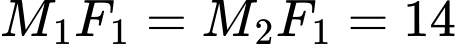 ;
; 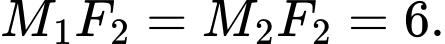 Đáp án: A
Đáp án: A
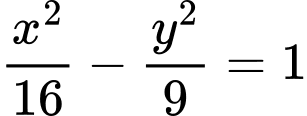 suy ra
suy ra 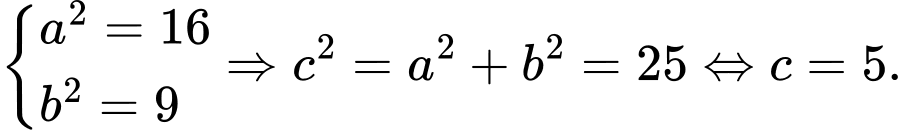
Suy ra tiêu điểm của hyperbol
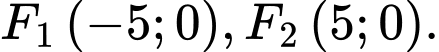
Do hoành độ của điểm
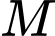 bằng
bằng 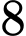 nên
nên 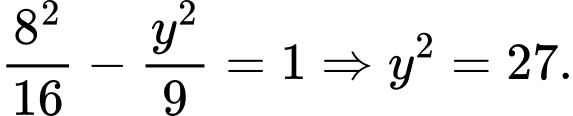
Suy ra
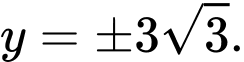
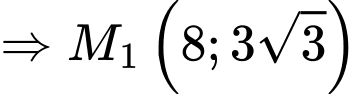 và
và 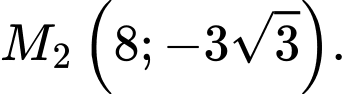
Vậy
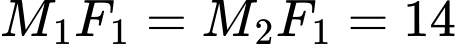 ;
; 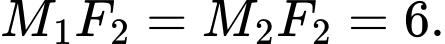 Đáp án: A
Đáp án: A
Câu 7 [583152]: Điểm nào trong 4 điểm 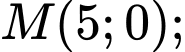
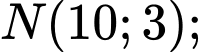
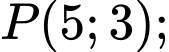
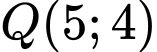 nằm trên một đường tiệm cận của hyperbol
nằm trên một đường tiệm cận của hyperbol 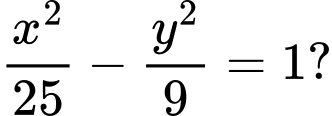
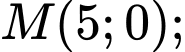
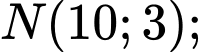
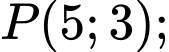
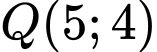 nằm trên một đường tiệm cận của hyperbol
nằm trên một đường tiệm cận của hyperbol 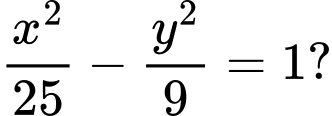
A, M.
B, N.
C, P.
D, Q.
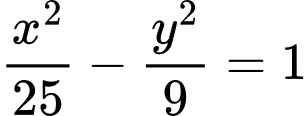
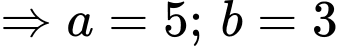
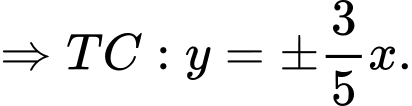
Vậy
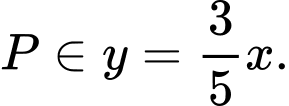 Đáp án: C
Đáp án: C
Câu 8 [583153]: Cho Parabol 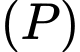 có phương trình chính tắc
có phương trình chính tắc 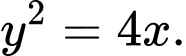 Một đường thẳng đi qua tiêu điểm
Một đường thẳng đi qua tiêu điểm 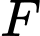 của
của 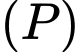 cắt
cắt 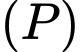 tại 2 điểm
tại 2 điểm 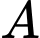 và
và 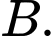 Nếu
Nếu 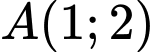 thì tọa độ của
thì tọa độ của 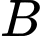 bằng bao nhiêu?
bằng bao nhiêu?
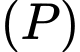 có phương trình chính tắc
có phương trình chính tắc 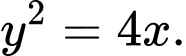 Một đường thẳng đi qua tiêu điểm
Một đường thẳng đi qua tiêu điểm 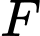 của
của 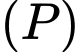 cắt
cắt 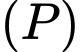 tại 2 điểm
tại 2 điểm 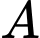 và
và 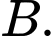 Nếu
Nếu 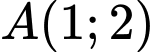 thì tọa độ của
thì tọa độ của 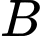 bằng bao nhiêu?
bằng bao nhiêu? A, 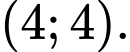
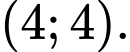
B, 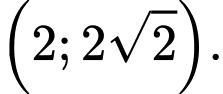
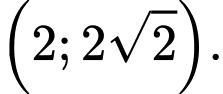
C, 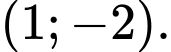
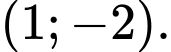
D, 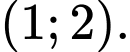
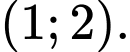
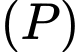 có tiêu điểm
có tiêu điểm 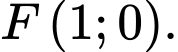
Đường thẳng
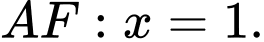
Đường thẳng
 cắt parabol tại
cắt parabol tại 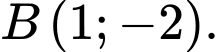
Vậy
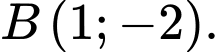 Đáp án: C
Đáp án: C
Câu 9 [583154]: Trong hệ trục 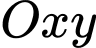 cho Elip
cho Elip  có các tiêu điểm
có các tiêu điểm 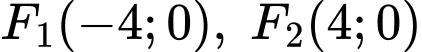 và một điểm
và một điểm 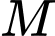 nằm trên
nằm trên 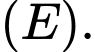 Biết rằng chu vi của tam giác
Biết rằng chu vi của tam giác 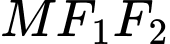 bằng 18. Xác định tâm sai e của
bằng 18. Xác định tâm sai e của 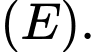
 cho Elip
cho Elip  có các tiêu điểm
có các tiêu điểm 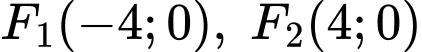 và một điểm
và một điểm 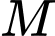 nằm trên
nằm trên 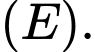 Biết rằng chu vi của tam giác
Biết rằng chu vi của tam giác 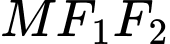 bằng 18. Xác định tâm sai e của
bằng 18. Xác định tâm sai e của 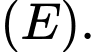
A, 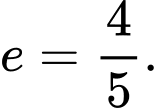
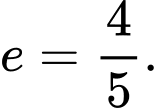
B, 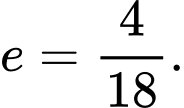
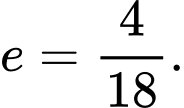
C, 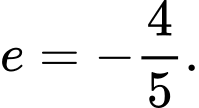
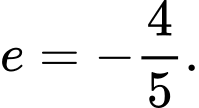
D, 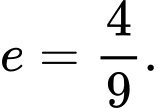
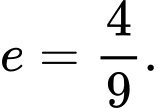
Ta có 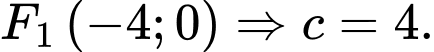
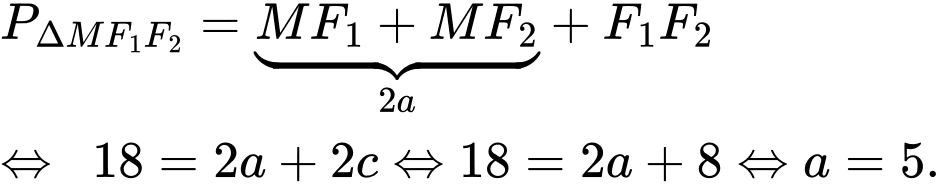
Tâm sai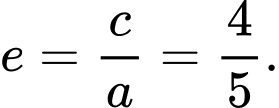 Đáp án: A
Đáp án: A
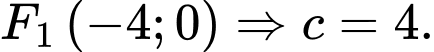
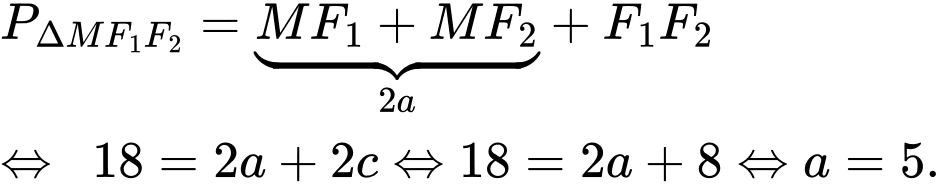
Tâm sai
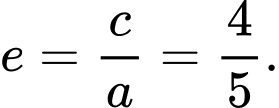 Đáp án: A
Đáp án: A
Câu 10 [583155]: Lập phương trình chính tắc của Elip đi qua điểm B(0;2) và có tâm sai 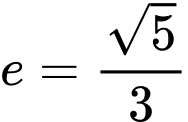
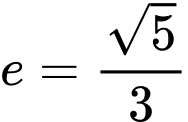
A, 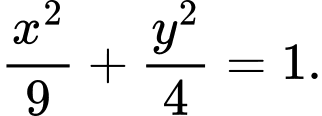
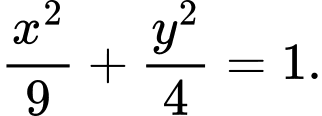
B, 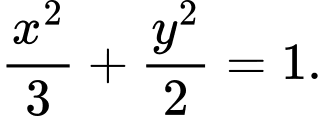
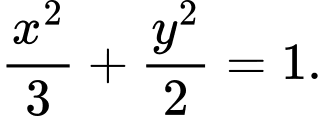
C, 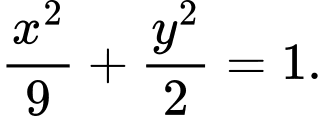
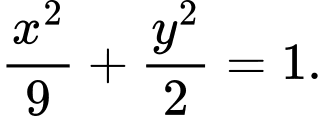
D, 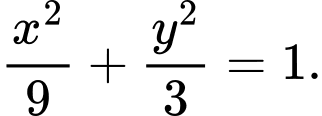
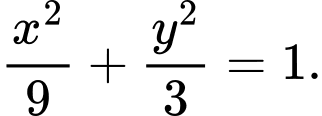
Phương trình chính tắc của Elip có dạng: 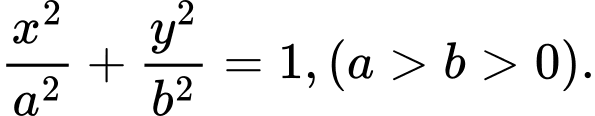
Elip đi qua điểm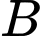 nên
nên 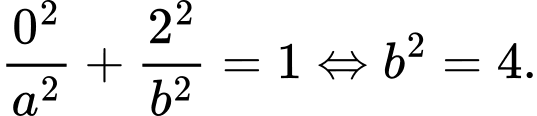
Tâm sai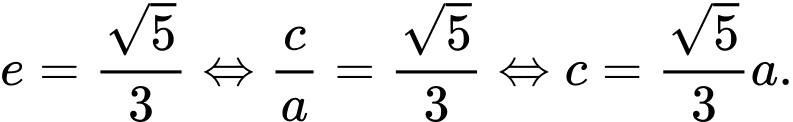
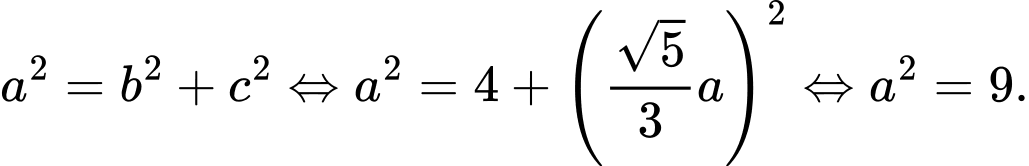
Vậy phương trình chính tắc của Elip cần tìm là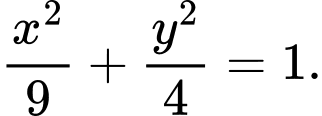 Đáp án: A
Đáp án: A
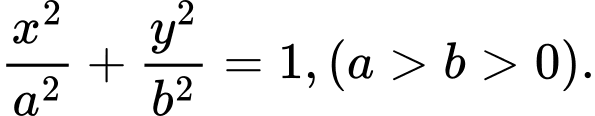
Elip đi qua điểm
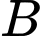 nên
nên 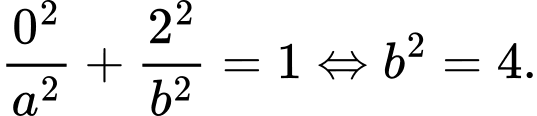
Tâm sai
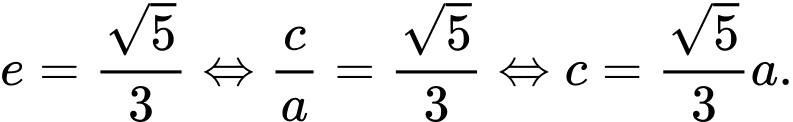
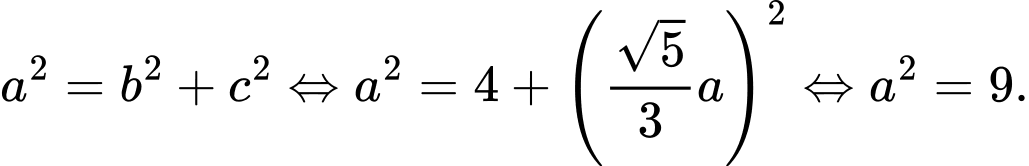
Vậy phương trình chính tắc của Elip cần tìm là
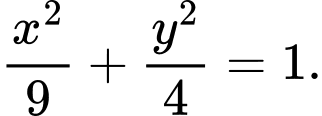 Đáp án: A
Đáp án: A
Câu 11 [583156]: Tìm phương trình chính tắc của Hypebol  biết nó tiêu điểm là
biết nó tiêu điểm là 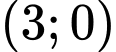 và một đường tiệm cận có phương trình là
và một đường tiệm cận có phương trình là 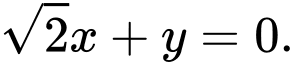
 biết nó tiêu điểm là
biết nó tiêu điểm là 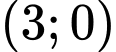 và một đường tiệm cận có phương trình là
và một đường tiệm cận có phương trình là 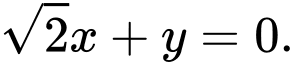
A, 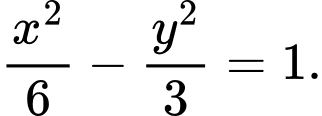
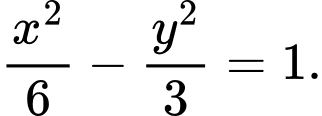
B, 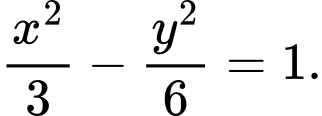
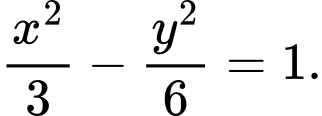
C, 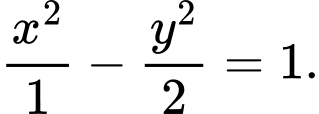
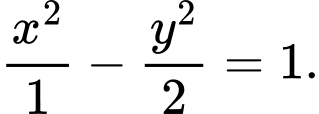
D, 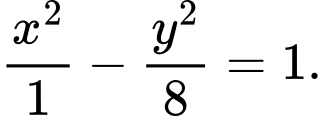
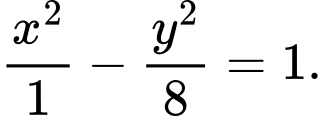
Xét hyperbol  có phương trình chính tắc là
có phương trình chính tắc là 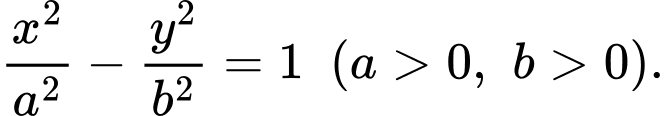
Do có một tiêu điểm là
có một tiêu điểm là 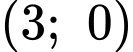 nên
nên 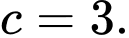
Đường tiệm cận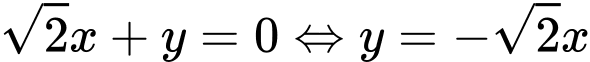
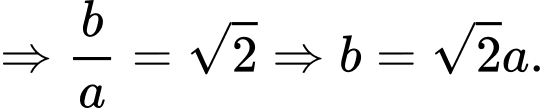
Vậy ta có
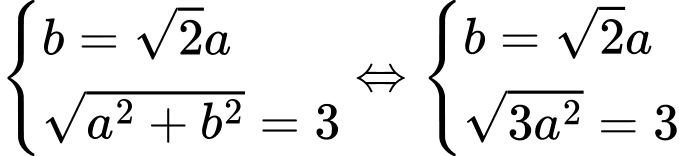
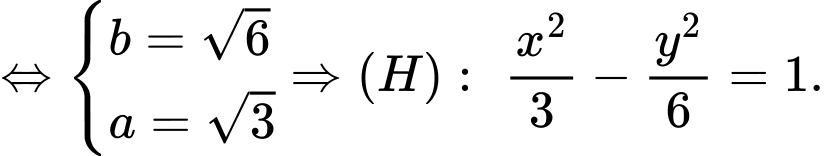
Suy ra phương án B đúng Đáp án: B
 có phương trình chính tắc là
có phương trình chính tắc là 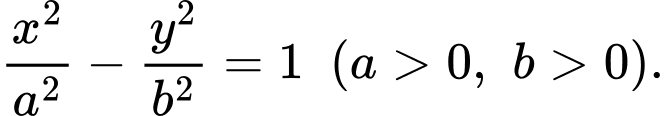
Do
 có một tiêu điểm là
có một tiêu điểm là 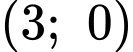 nên
nên 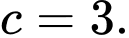
Đường tiệm cận
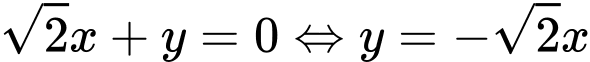
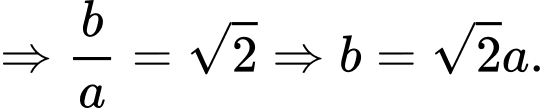
Vậy ta có
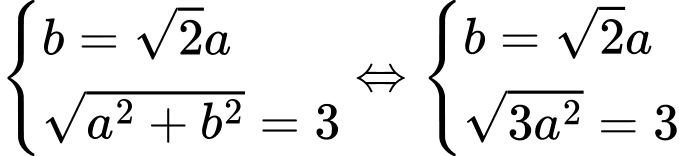
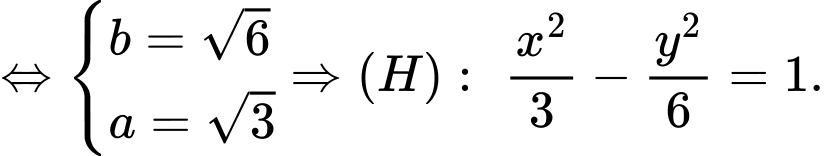
Suy ra phương án B đúng Đáp án: B
Câu 12 [583157]: Cho parabol 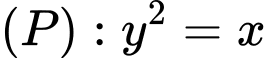 và đường thẳng
và đường thẳng 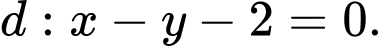 Gọi
Gọi 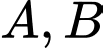 là giao điểm của
là giao điểm của 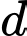 và
và 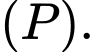 Tìm tung độ điểm
Tìm tung độ điểm  sao cho
sao cho 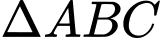 đều.
đều.
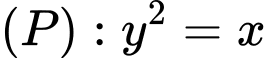 và đường thẳng
và đường thẳng 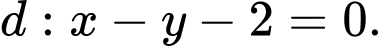 Gọi
Gọi 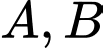 là giao điểm của
là giao điểm của 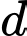 và
và 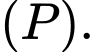 Tìm tung độ điểm
Tìm tung độ điểm  sao cho
sao cho 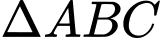 đều.
đều. A, 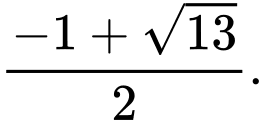
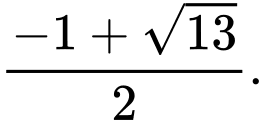
B, 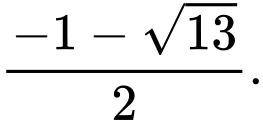
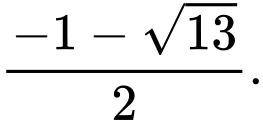
C, 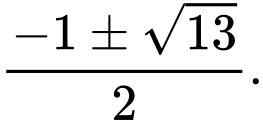
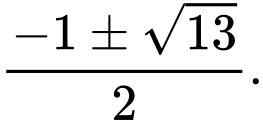
D, Không tồn tại điểm C.
Phương trình hoành độ giao điểm của 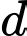 và
và 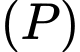 :
: 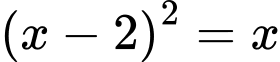

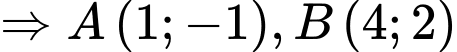
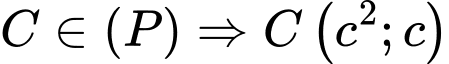
 ,
, 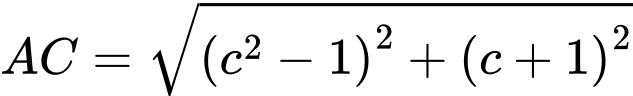 ,
, 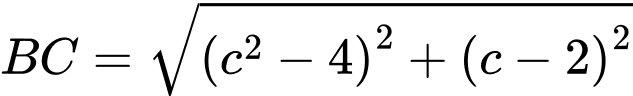
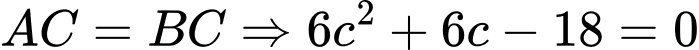
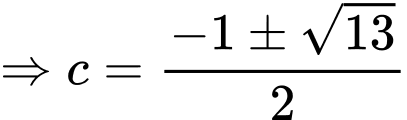
So với điều kiện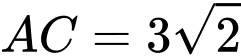 ta thấy không có giá trị
ta thấy không có giá trị  thoả.
thoả.
Vậy không tồn tại điểm C thoả đề. Đáp án: D
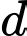 và
và 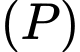 :
: 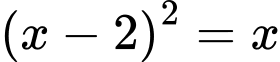

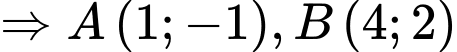
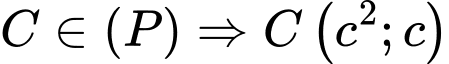
 ,
, 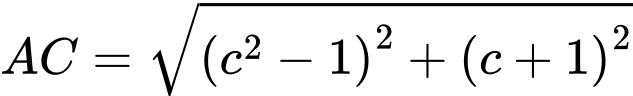 ,
, 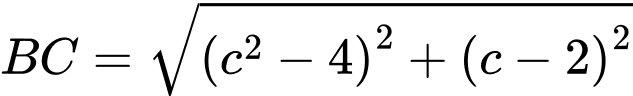
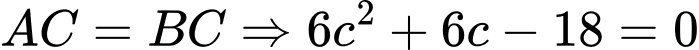
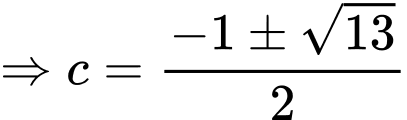
So với điều kiện
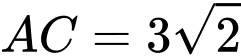 ta thấy không có giá trị
ta thấy không có giá trị  thoả.
thoả.Vậy không tồn tại điểm C thoả đề. Đáp án: D
Câu 13 [583158]: Ông Hoàng có một mảnh vườn hình Elip có chiều dài trục lớn và trục nhỏ lần lượt là 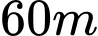 v
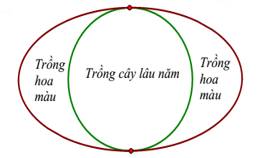
v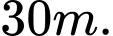 Ông chia mảnh vườn ra làm hai nửa bằng một đường tròn tiếp xúc trong với Elip để làm mục đích sử dụng khác nhau (xem hình vẽ). Nửa bên trong đường tròn ông trồng cây lâu năm, nửa bên ngoài đường tròn ông trồng hoa màu. Tính tỉ số diện tích T giữa phần trồng cây lâu năm so với diện tích trồng hoa màu. Biết diện tích hình Elip được tính theo công thức
Ông chia mảnh vườn ra làm hai nửa bằng một đường tròn tiếp xúc trong với Elip để làm mục đích sử dụng khác nhau (xem hình vẽ). Nửa bên trong đường tròn ông trồng cây lâu năm, nửa bên ngoài đường tròn ông trồng hoa màu. Tính tỉ số diện tích T giữa phần trồng cây lâu năm so với diện tích trồng hoa màu. Biết diện tích hình Elip được tính theo công thức 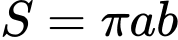 , với a, b lần lượt là nửa độ dài trục lớn và nửa độ dài trục nhỏ. Biết độ rộng của đường Elip là không đáng kể.
, với a, b lần lượt là nửa độ dài trục lớn và nửa độ dài trục nhỏ. Biết độ rộng của đường Elip là không đáng kể.
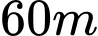 v
v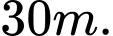 Ông chia mảnh vườn ra làm hai nửa bằng một đường tròn tiếp xúc trong với Elip để làm mục đích sử dụng khác nhau (xem hình vẽ). Nửa bên trong đường tròn ông trồng cây lâu năm, nửa bên ngoài đường tròn ông trồng hoa màu. Tính tỉ số diện tích T giữa phần trồng cây lâu năm so với diện tích trồng hoa màu. Biết diện tích hình Elip được tính theo công thức
Ông chia mảnh vườn ra làm hai nửa bằng một đường tròn tiếp xúc trong với Elip để làm mục đích sử dụng khác nhau (xem hình vẽ). Nửa bên trong đường tròn ông trồng cây lâu năm, nửa bên ngoài đường tròn ông trồng hoa màu. Tính tỉ số diện tích T giữa phần trồng cây lâu năm so với diện tích trồng hoa màu. Biết diện tích hình Elip được tính theo công thức 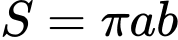 , với a, b lần lượt là nửa độ dài trục lớn và nửa độ dài trục nhỏ. Biết độ rộng của đường Elip là không đáng kể.
, với a, b lần lượt là nửa độ dài trục lớn và nửa độ dài trục nhỏ. Biết độ rộng của đường Elip là không đáng kể.
A, 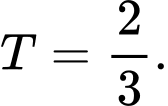
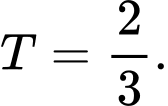
B, 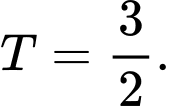
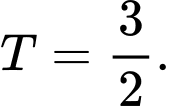
C, 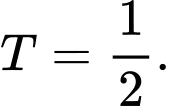
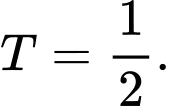
D, 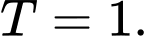
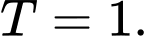
Theo đề ta có: Diện tích  là:
là: 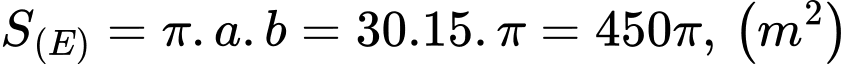
Vì đường tròn tiếp xúc trong, nên sẽ tiếp xúc tại đỉnh của trục nhỏ, suy ra bán kính đường tròn: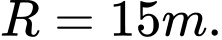
Diện tích hình tròn phần trồng cây lâu năm là:
phần trồng cây lâu năm là: 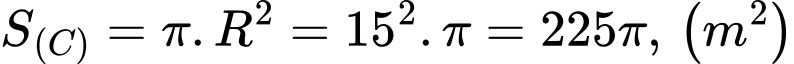
Suy ra diện tích phần trồng hoa màu là: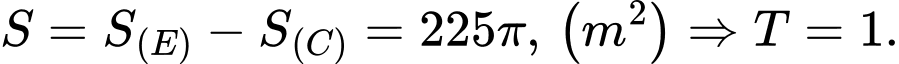 Đáp án: D
Đáp án: D
 là:
là: 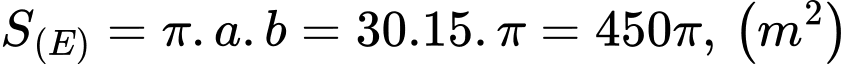
Vì đường tròn tiếp xúc trong, nên sẽ tiếp xúc tại đỉnh của trục nhỏ, suy ra bán kính đường tròn:
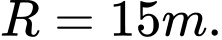
Diện tích hình tròn
 phần trồng cây lâu năm là:
phần trồng cây lâu năm là: 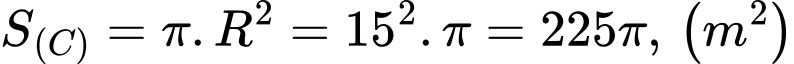
Suy ra diện tích phần trồng hoa màu là:
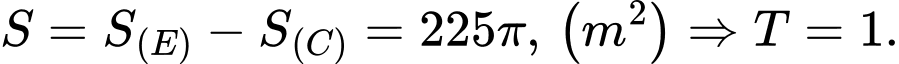 Đáp án: D
Đáp án: D
Câu 14 [583159]: Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc Oxy, cho điểm  và parabol
và parabol 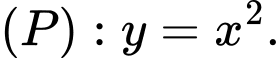 Xác định các điểm M trên (P) sao cho AM ngắn nhất.
Xác định các điểm M trên (P) sao cho AM ngắn nhất.
 và parabol
và parabol 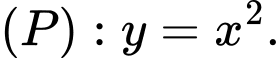 Xác định các điểm M trên (P) sao cho AM ngắn nhất.
Xác định các điểm M trên (P) sao cho AM ngắn nhất. A, 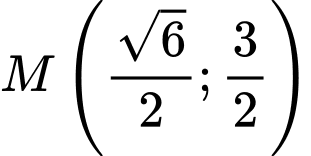 hoặc
hoặc 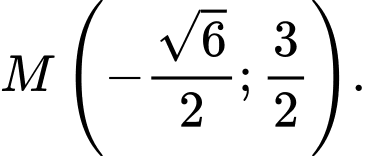
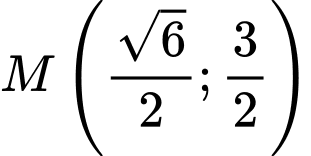 hoặc
hoặc 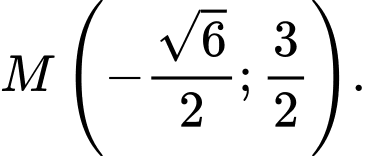
B, 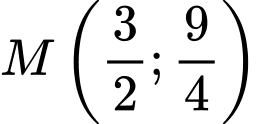 hoặc
hoặc 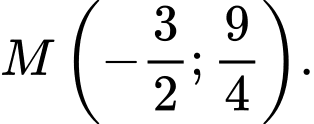
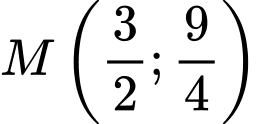 hoặc
hoặc 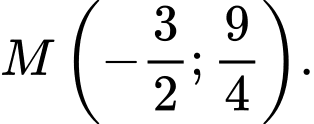
C, 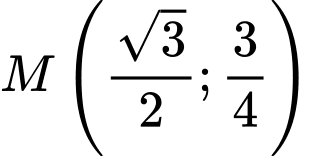 hoặc
hoặc 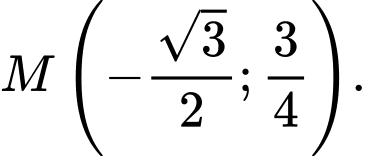
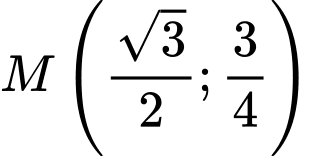 hoặc
hoặc 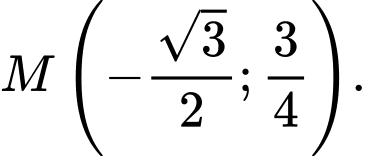
D, 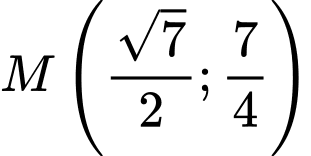 hoặc
hoặc 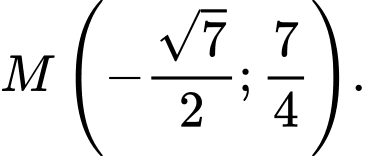
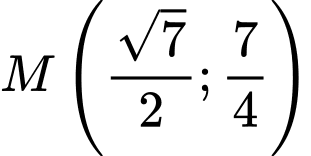 hoặc
hoặc 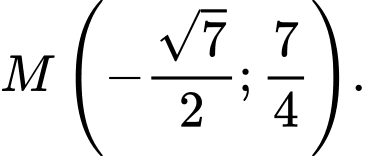
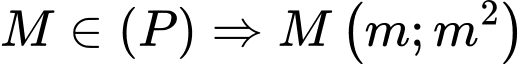
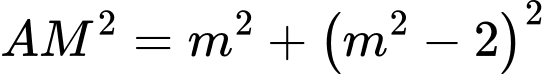
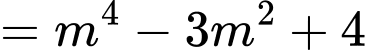
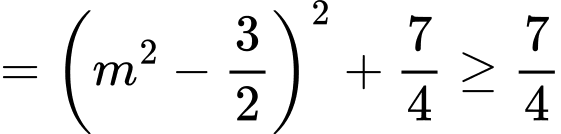
 ngắn nhất khi
ngắn nhất khi 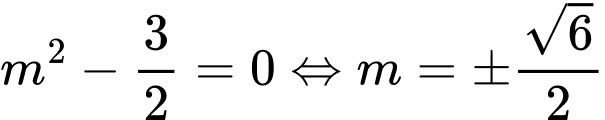
Vậy,
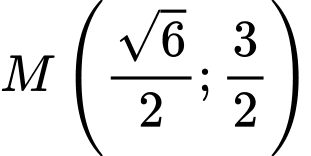 hoặc
hoặc 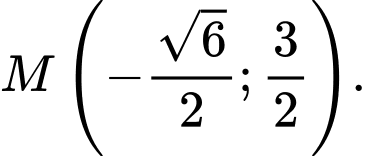 Đáp án: A
Đáp án: A
Câu 15 [583160]: Tìm góc giữa 2 đường tiệm cận của hyperbol 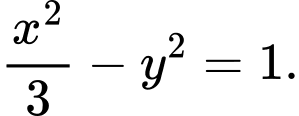
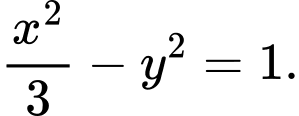
A, 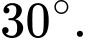
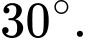
B, 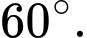
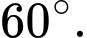
C, 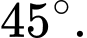
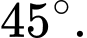
D, 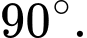
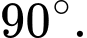
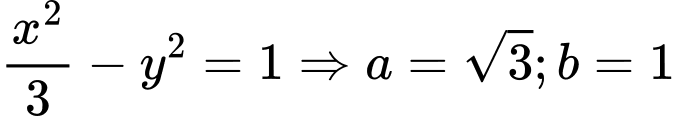
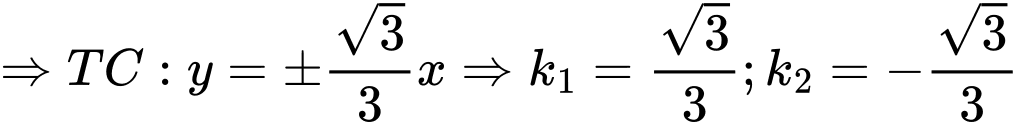
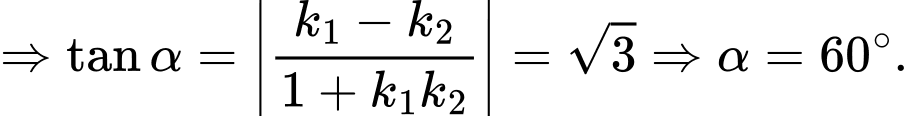 Đáp án: B
Đáp án: B Dạng câu hỏi: Câu trắc nghiệm đúng sai
(Thí sinh trả lời từ câu 16,17. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai)
Câu 16 [583161]: Cho hyperbol 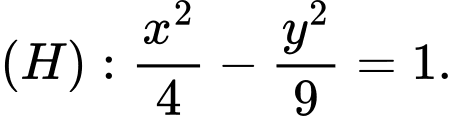 Gọi
Gọi  là đường thẳng đi qua gốc tọa độ
là đường thẳng đi qua gốc tọa độ  và có hệ số góc
và có hệ số góc 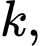
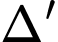 là đường thẳng đi qua
là đường thẳng đi qua  và vuông góc với
và vuông góc với 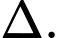
a) chỉ có 1 tiêu điểm duy nhất:
chỉ có 1 tiêu điểm duy nhất: 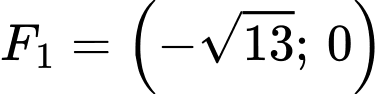
b) và
và 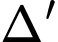 đều cắt
đều cắt  khi và chỉ khi
khi và chỉ khi 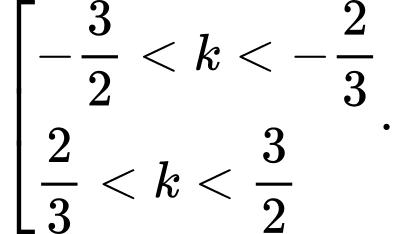
c) Tứ giác với bốn đỉnh là bốn giao điểm của và
và 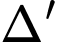 với
với  là hình vuông.
là hình vuông.
d) Tính diện tích tứ giác này theo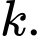
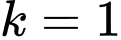 hoặc
hoặc 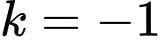 để diện tích tứ giác đó có giá trị nhỏ nhất.
để diện tích tứ giác đó có giá trị nhỏ nhất.
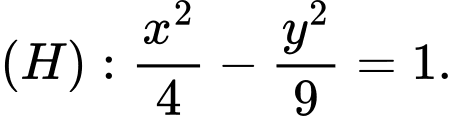 Gọi
Gọi  là đường thẳng đi qua gốc tọa độ
là đường thẳng đi qua gốc tọa độ  và có hệ số góc
và có hệ số góc 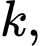
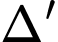 là đường thẳng đi qua
là đường thẳng đi qua  và vuông góc với
và vuông góc với 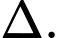
a)
 chỉ có 1 tiêu điểm duy nhất:
chỉ có 1 tiêu điểm duy nhất: 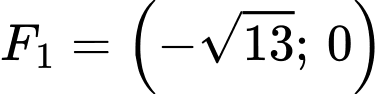
b)
 và
và 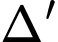 đều cắt
đều cắt  khi và chỉ khi
khi và chỉ khi 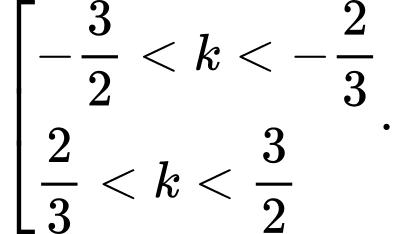
c) Tứ giác với bốn đỉnh là bốn giao điểm của
 và
và 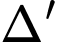 với
với  là hình vuông.
là hình vuông.d) Tính diện tích tứ giác này theo
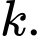
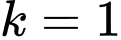 hoặc
hoặc 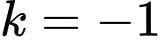 để diện tích tứ giác đó có giá trị nhỏ nhất.
để diện tích tứ giác đó có giá trị nhỏ nhất.
a) Ta có 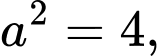
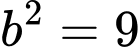
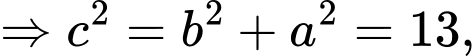 suy ra
suy ra 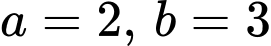 và
và 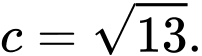
Vậy có các tiêu điểm
có các tiêu điểm 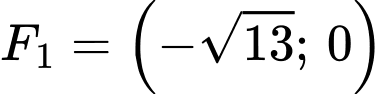 ,
,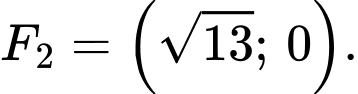
Suy ra ý a sai.
b)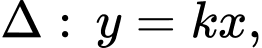
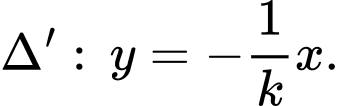
Hoành độ giao điểm của và
và  là nghiệm của phương trình
là nghiệm của phương trình
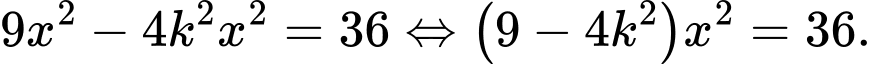
 cắt
cắt  khi
khi 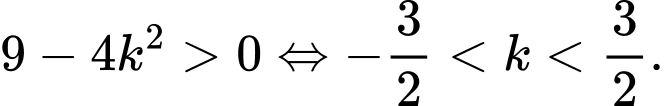
Tung độ giao điểm của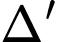 và
và  là nghiệm của phương trình
là nghiệm của phương trình
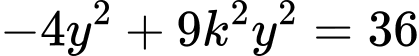
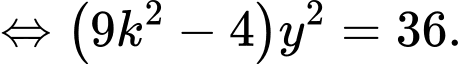
 cắt
cắt  khi
khi 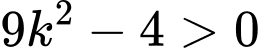
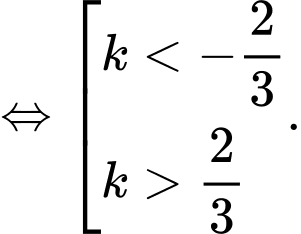
Vậy và
và 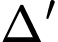 đều cắt
đều cắt  khi và chỉ khi
khi và chỉ khi
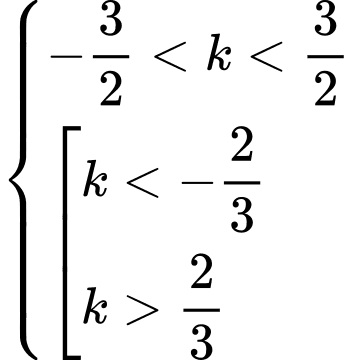
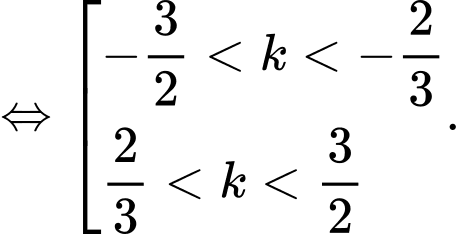
Suy ra ý b đúng.
c) Gọi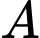 và
và  là các giao điểm của
là các giao điểm của  và
và 
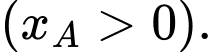
Gọi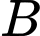 và
và 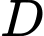 là các giao điểm của
là các giao điểm của 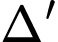 và
và 
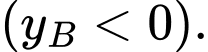
Do nhận
nhận  làm tâm đối xứng nên
làm tâm đối xứng nên 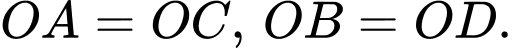
Suy ra tứ giác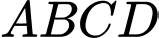 là hình bình hành.
là hình bình hành.
Mặt khác,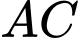 vuông góc với
vuông góc với 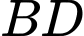 nên
nên 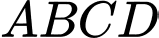 là hình thoi.
là hình thoi.
Suy ra ý c sai.
d) Giải hệ phương trình của và
và  :
: 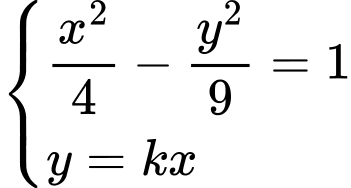 ta được
ta được
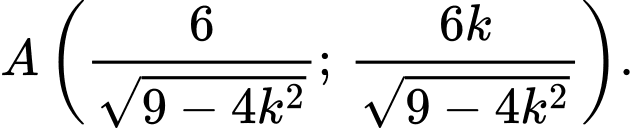
Giải hệ phương trình của và
và  :
: 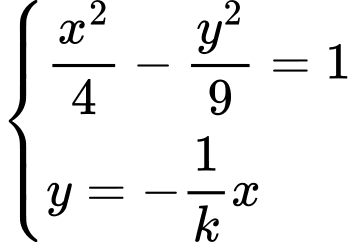 ta được
ta được
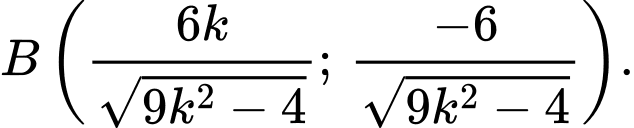
Ta có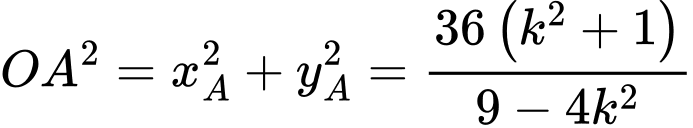
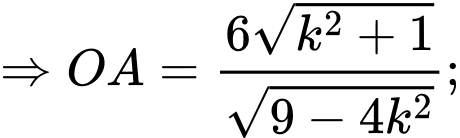
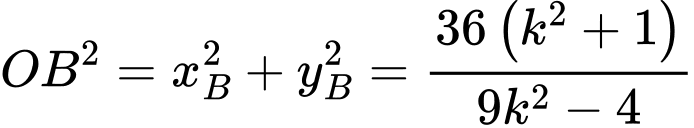
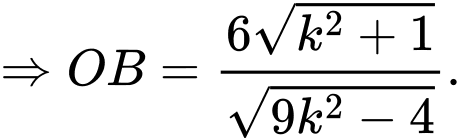
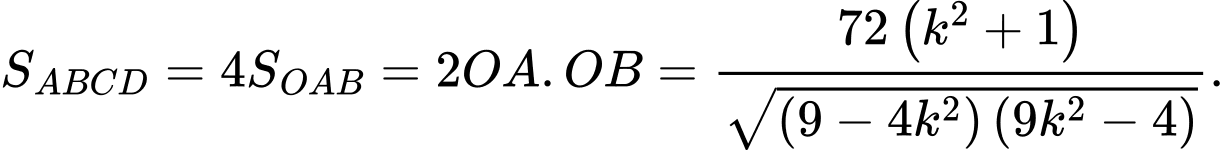
Áp dụng bất đẳng thức Cô-si ta có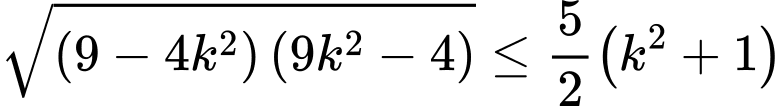 nên
nên 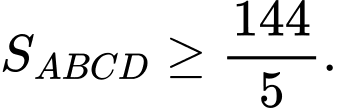
Vậy nhỏ nhất
nhỏ nhất 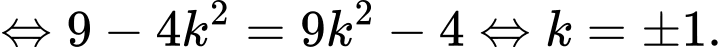
Suy ra ý d đúng.
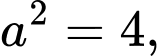
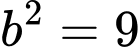
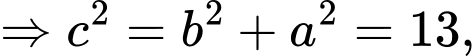 suy ra
suy ra 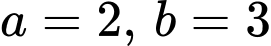 và
và 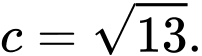
Vậy
 có các tiêu điểm
có các tiêu điểm 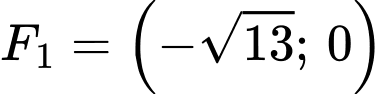 ,
,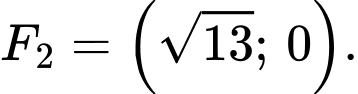
Suy ra ý a sai.
b)
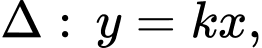
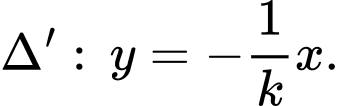
Hoành độ giao điểm của
 và
và  là nghiệm của phương trình
là nghiệm của phương trình 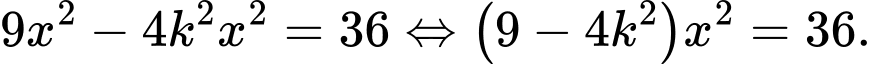
 cắt
cắt  khi
khi 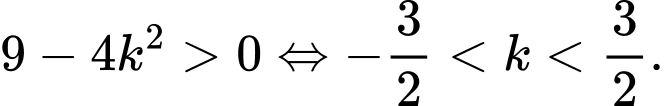
Tung độ giao điểm của
 và
và  là nghiệm của phương trình
là nghiệm của phương trình 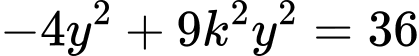
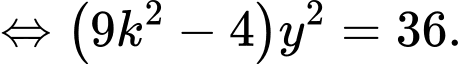
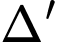 cắt
cắt  khi
khi 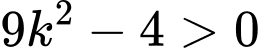
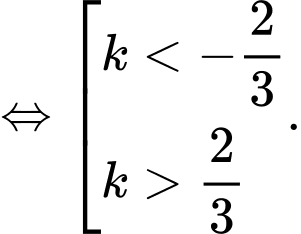
Vậy
 và
và 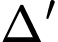 đều cắt
đều cắt  khi và chỉ khi
khi và chỉ khi 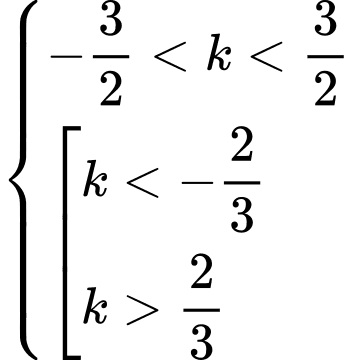
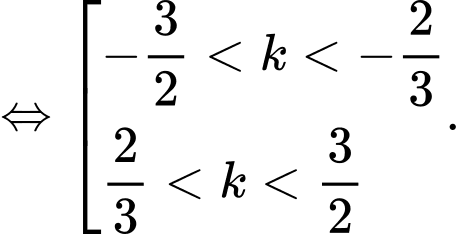
Suy ra ý b đúng.
c) Gọi
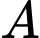 và
và  là các giao điểm của
là các giao điểm của  và
và 
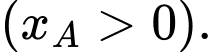
Gọi
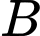 và
và 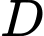 là các giao điểm của
là các giao điểm của 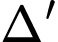 và
và 
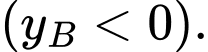
Do
 nhận
nhận  làm tâm đối xứng nên
làm tâm đối xứng nên 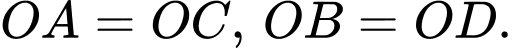
Suy ra tứ giác
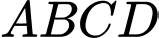 là hình bình hành.
là hình bình hành.Mặt khác,
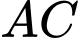 vuông góc với
vuông góc với 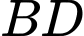 nên
nên 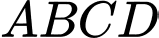 là hình thoi.
là hình thoi.Suy ra ý c sai.
d) Giải hệ phương trình của
 và
và  :
: 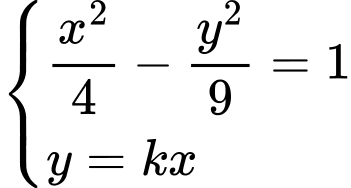 ta được
ta được 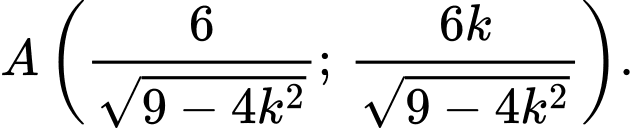
Giải hệ phương trình của
 và
và  :
: 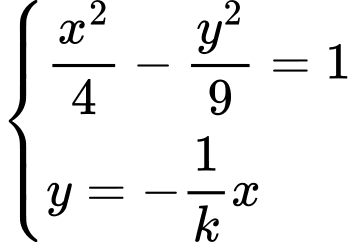 ta được
ta được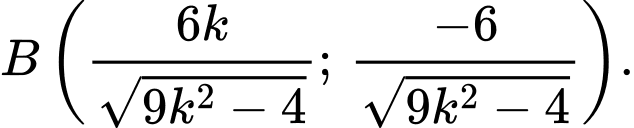
Ta có
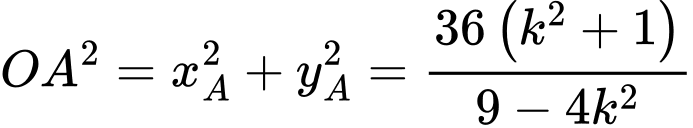
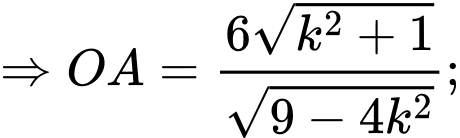
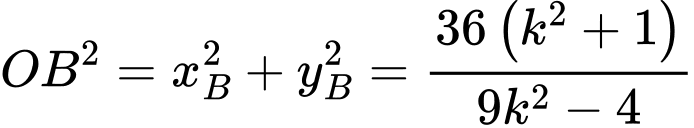
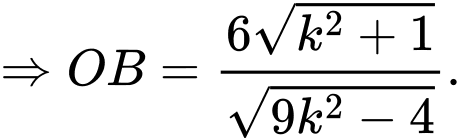
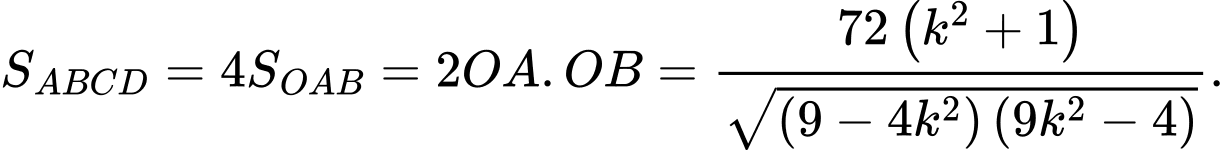
Áp dụng bất đẳng thức Cô-si ta có
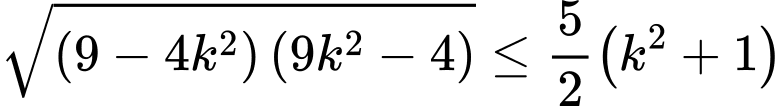 nên
nên 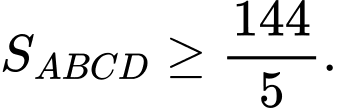
Vậy
 nhỏ nhất
nhỏ nhất 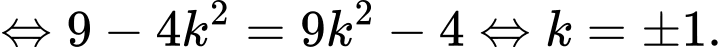
Suy ra ý d đúng.
Câu 17 [583162]: Cho hyperbol 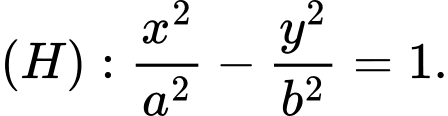 Gọi
Gọi 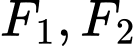 là các tiêu điểm,
là các tiêu điểm, 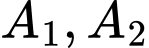 là các đỉnh của
là các đỉnh của
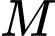 là điểm tùy ý trên
là điểm tùy ý trên  và
và 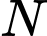 là hình chiếu của nó trên trục hoành. Chứng minh rằng
là hình chiếu của nó trên trục hoành. Chứng minh rằng
a)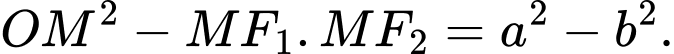
b)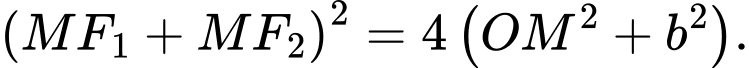
c)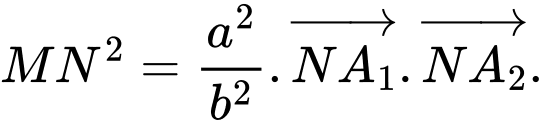
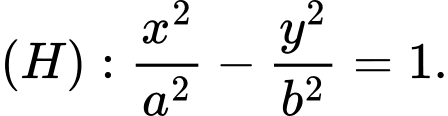 Gọi
Gọi 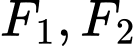 là các tiêu điểm,
là các tiêu điểm, 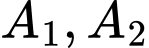 là các đỉnh của
là các đỉnh của
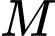 là điểm tùy ý trên
là điểm tùy ý trên  và
và 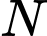 là hình chiếu của nó trên trục hoành. Chứng minh rằng
là hình chiếu của nó trên trục hoành. Chứng minh rằnga)
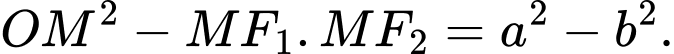
b)
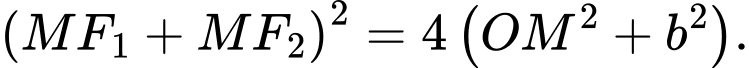
c)
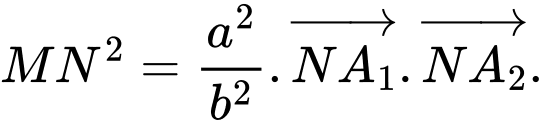
a) 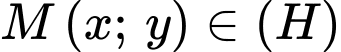
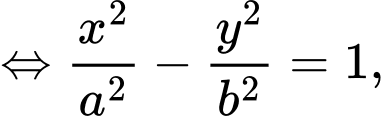
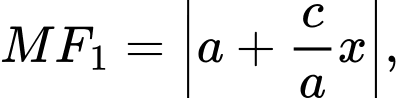
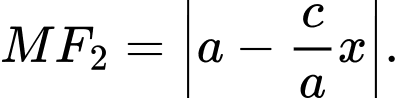
Khi đó: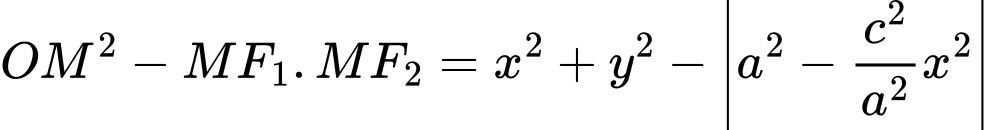
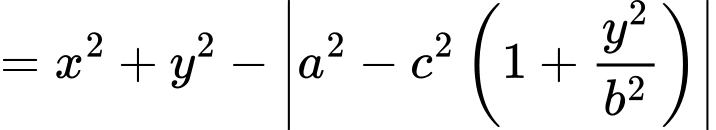
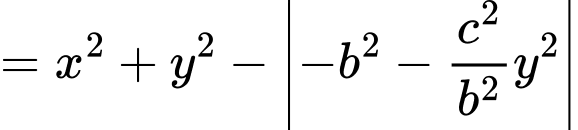
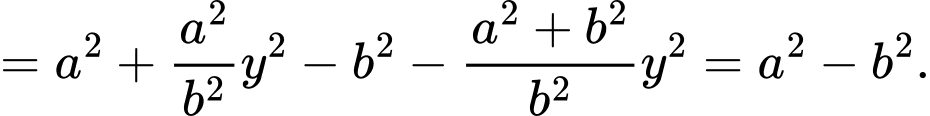
Suy ra ý a đúng.
b) Ta có
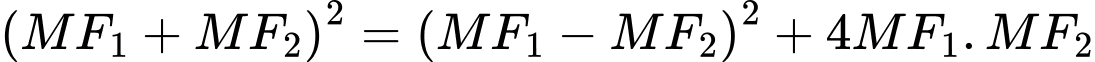
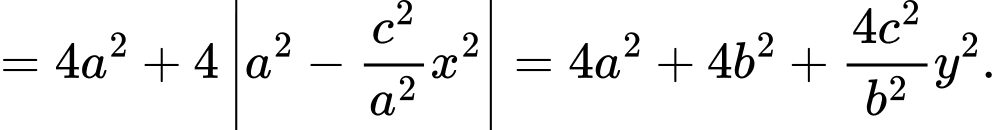
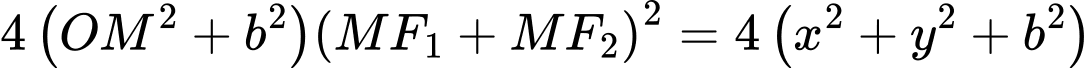
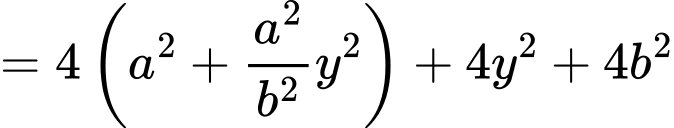
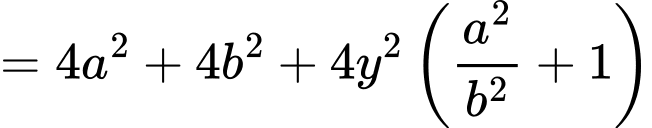
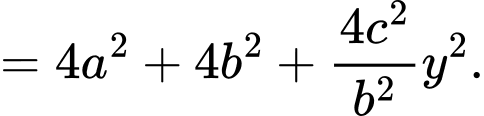
Vậy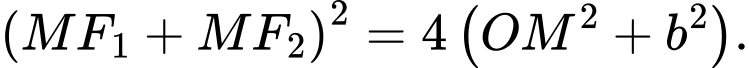
Suy ra ý b đúng.
c) Ta có
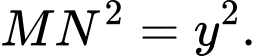
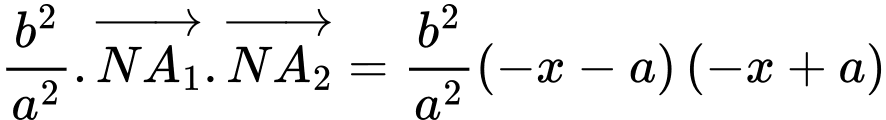
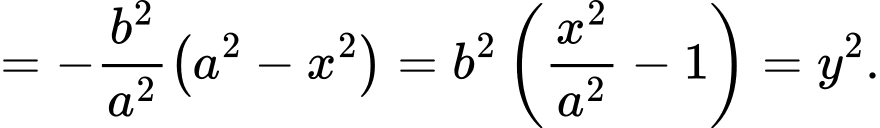
Vậy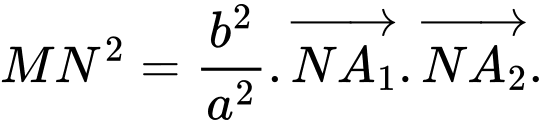
Suy ra ý c sai.
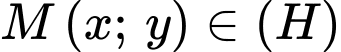
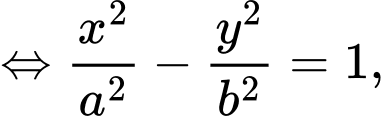
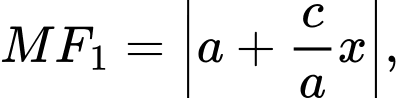
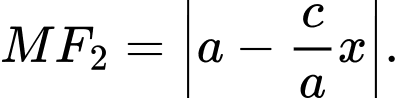
Khi đó:
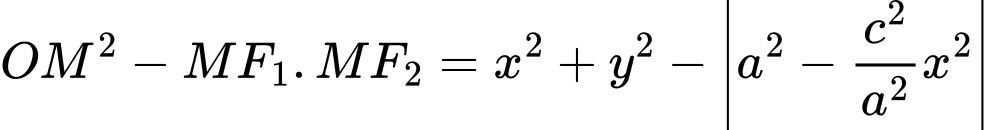
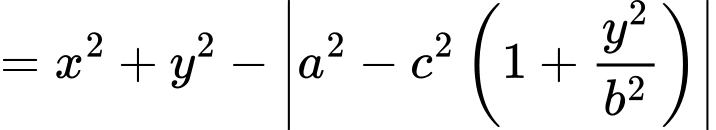
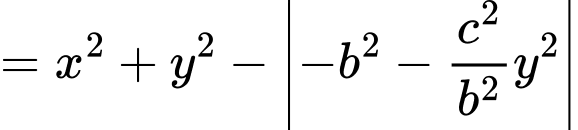
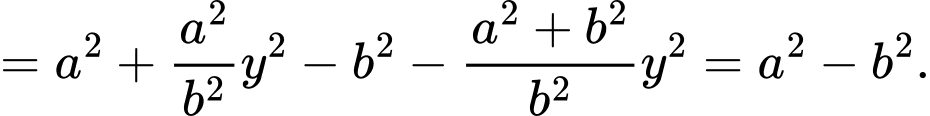
Suy ra ý a đúng.
b) Ta có
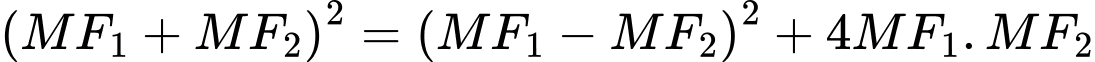
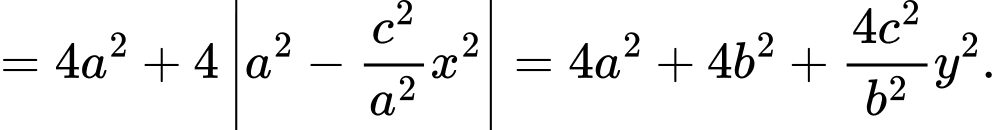
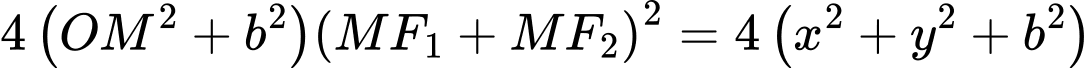
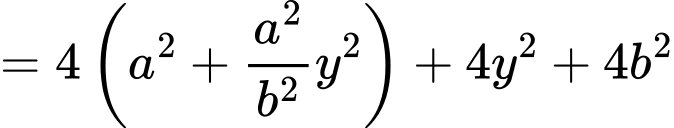
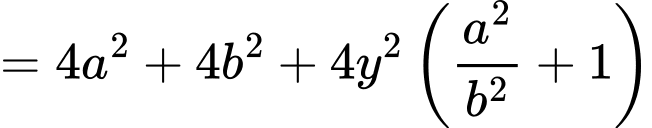
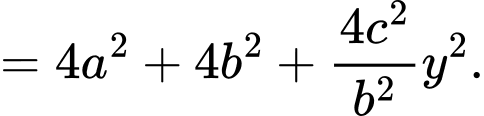
Vậy
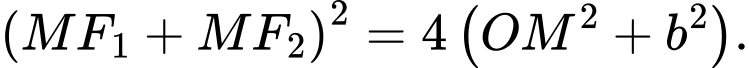
Suy ra ý b đúng.
c) Ta có
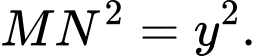
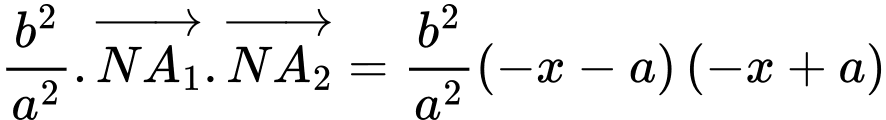
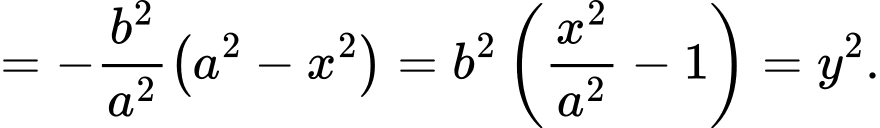
Vậy
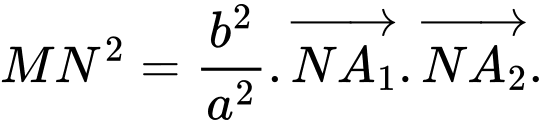
Suy ra ý c sai.
Dạng câu hỏi: Câu trả lời ngắn
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 18 [583163]: Trong mặt phẳng với hệ tọa độ 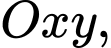 cho Elip
cho Elip 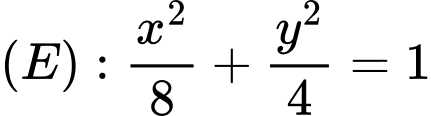 và đường thẳng
và đường thẳng 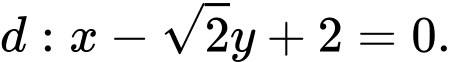 Đường thẳng
Đường thẳng 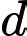 cắt
cắt  tại hai điểm
tại hai điểm 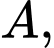
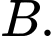 Biết điểm
Biết điểm  nằm trên
nằm trên  sao cho tam giác
sao cho tam giác 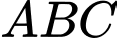 cân tại
cân tại  Có bao nhiêu điểm
Có bao nhiêu điểm  thỏa mãn đề bài?
thỏa mãn đề bài?
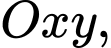 cho Elip
cho Elip 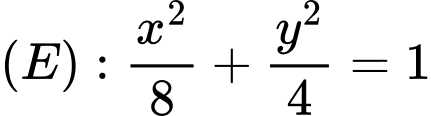 và đường thẳng
và đường thẳng 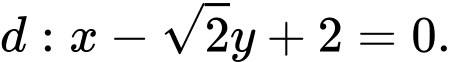 Đường thẳng
Đường thẳng 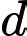 cắt
cắt  tại hai điểm
tại hai điểm 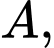
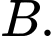 Biết điểm
Biết điểm  nằm trên
nằm trên  sao cho tam giác
sao cho tam giác 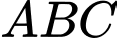 cân tại
cân tại  Có bao nhiêu điểm
Có bao nhiêu điểm  thỏa mãn đề bài?
thỏa mãn đề bài? 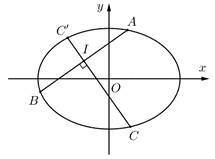
Đường thẳng
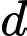 cắt
cắt  tại
tại 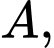
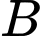 nên tọa độ
nên tọa độ 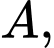
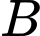 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình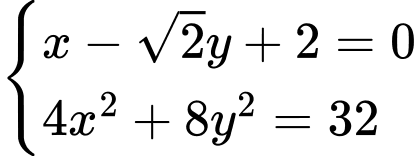
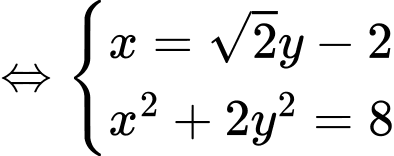
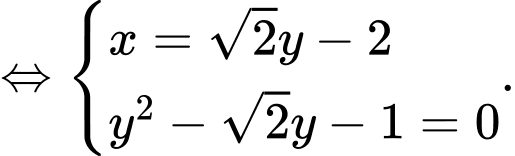
Gọi
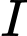 là trung điểm của
là trung điểm của 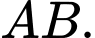
Suy ra
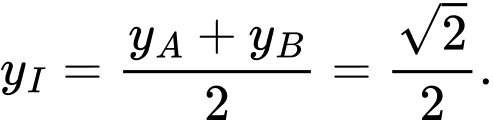
Thay vào
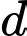 , ta được
, ta được 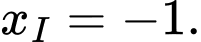
Do đó
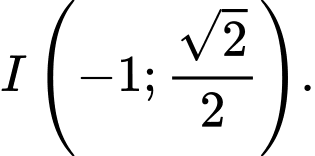
Gọi
 là đường thẳng đi qua
là đường thẳng đi qua 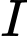 và vuông góc với
và vuông góc với 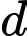 nên
nên 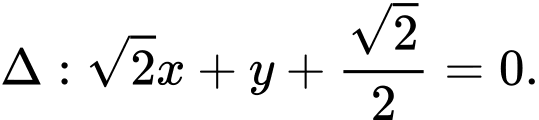
Theo giả thiết tam giác
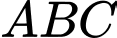 cân tại
cân tại  nên
nên 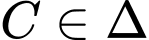 , đồng thời
, đồng thời 
Suy ra tọa độ điểm
 thỏa mãn hệ
thỏa mãn hệ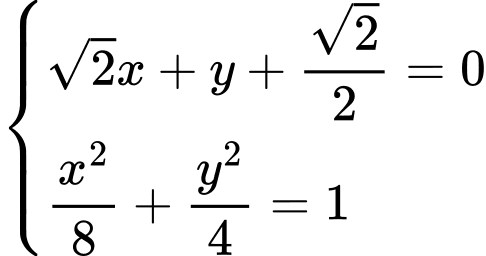
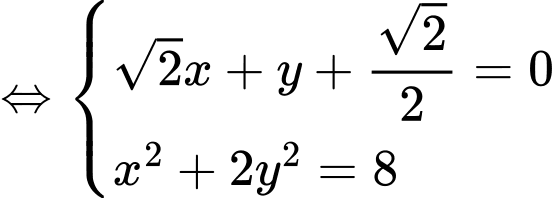
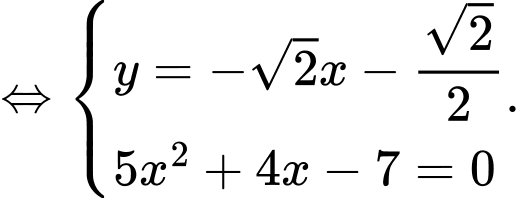
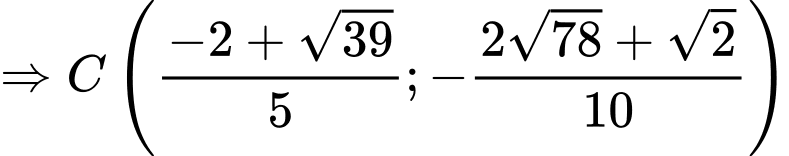 hoặc
hoặc 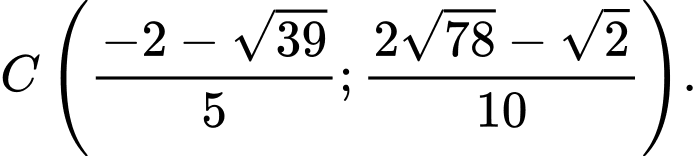
Vậy có 2 điểm C thỏa mãn
Câu 19 [583164]: Cho hai parabol 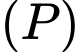 và
và 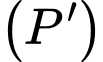 lần lượt có phương trình
lần lượt có phương trình 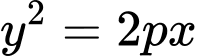 và
và 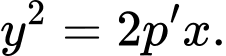 Qua
Qua  vẽ đường thẳng thay đổi cắt
vẽ đường thẳng thay đổi cắt 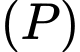 và
và 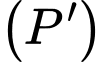 tại hai điểm phân biệt
tại hai điểm phân biệt 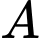 và
và 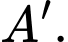 Biết tỉ số
Biết tỉ số 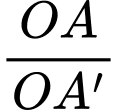 không thay đổi. Tính
không thay đổi. Tính 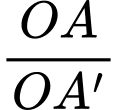 theo p và p’.
theo p và p’.
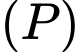 và
và 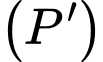 lần lượt có phương trình
lần lượt có phương trình 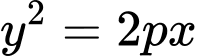 và
và 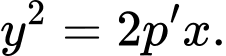 Qua
Qua  vẽ đường thẳng thay đổi cắt
vẽ đường thẳng thay đổi cắt 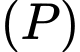 và
và 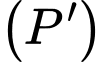 tại hai điểm phân biệt
tại hai điểm phân biệt 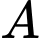 và
và 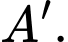 Biết tỉ số
Biết tỉ số 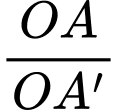 không thay đổi. Tính
không thay đổi. Tính 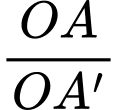 theo p và p’.
theo p và p’.
Đường thẳng đi qua  cắt hai parabol
cắt hai parabol 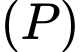 và
và 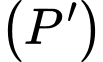 lần lượt tại hai điểm phân biệt
lần lượt tại hai điểm phân biệt 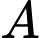 và
và 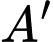 có dạng
có dạng 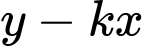 với
với 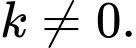
Giả sử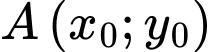 là nghiệm khác 0 của hệ phương trình:
là nghiệm khác 0 của hệ phương trình: 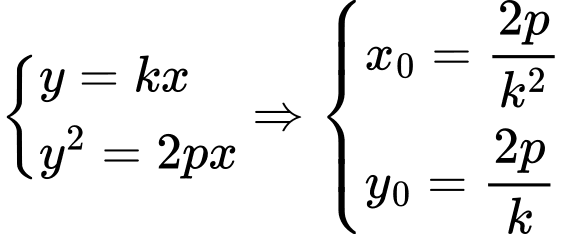 .
.
Do đó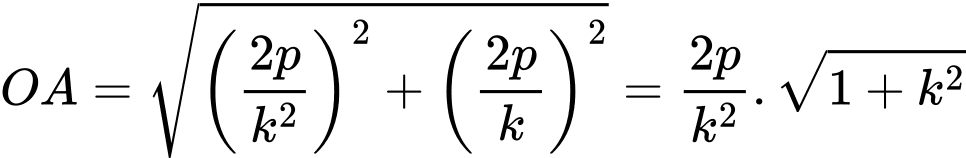
Tương tự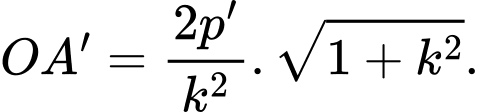
Vậy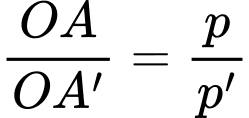
 cắt hai parabol
cắt hai parabol 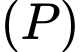 và
và 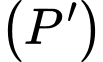 lần lượt tại hai điểm phân biệt
lần lượt tại hai điểm phân biệt 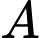 và
và 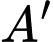 có dạng
có dạng 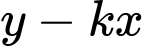 với
với 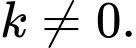
Giả sử
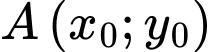 là nghiệm khác 0 của hệ phương trình:
là nghiệm khác 0 của hệ phương trình: 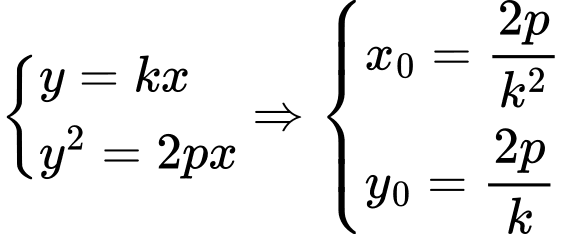 .
.Do đó
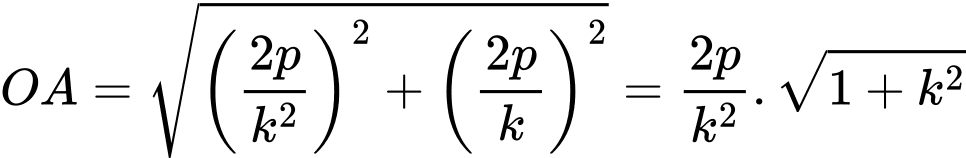
Tương tự
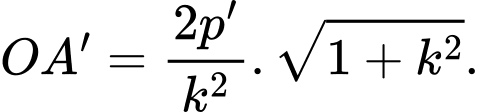
Vậy
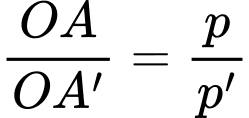
Câu 20 [583165]: Cho hypebol 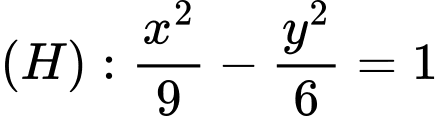 có tiêu điểm
có tiêu điểm 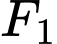 và
và 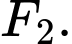 Có bao nhiêu điểm
Có bao nhiêu điểm 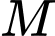 trên
trên  thỏa mãn điều kiện tổng khoảng cách từ
thỏa mãn điều kiện tổng khoảng cách từ 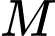 đến hai đường tiệm cận bằng
đến hai đường tiệm cận bằng 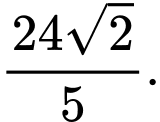
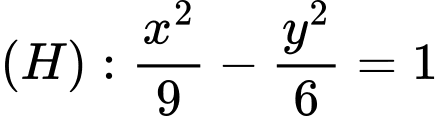 có tiêu điểm
có tiêu điểm 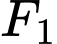 và
và 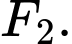 Có bao nhiêu điểm
Có bao nhiêu điểm 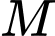 trên
trên  thỏa mãn điều kiện tổng khoảng cách từ
thỏa mãn điều kiện tổng khoảng cách từ 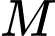 đến hai đường tiệm cận bằng
đến hai đường tiệm cận bằng 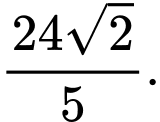
Phương trình hai tiệm cận là 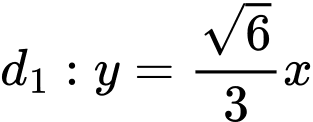 ,
, 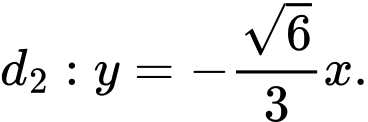
Tổng khoảng cách từ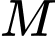 đến hai đường tiệm cận bằng
đến hai đường tiệm cận bằng 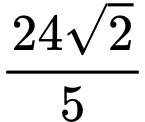 nên
nên
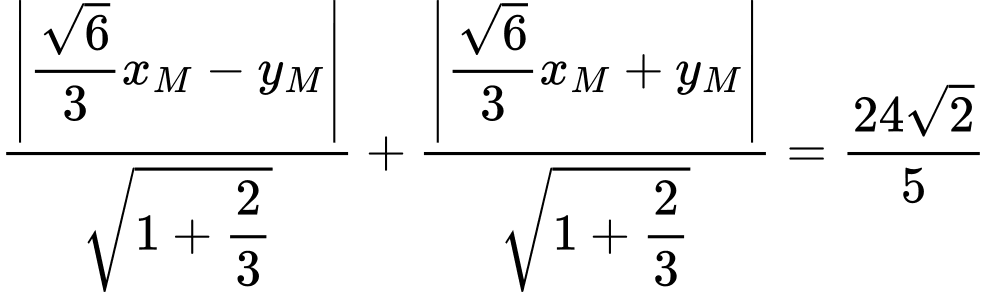
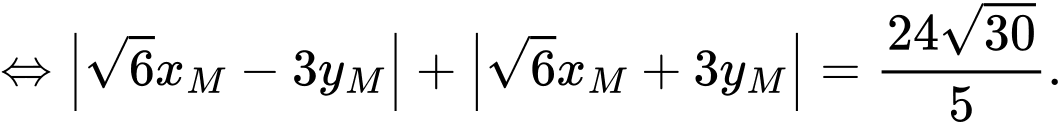
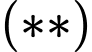
Mặt khác nên ta có
nên ta có
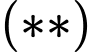
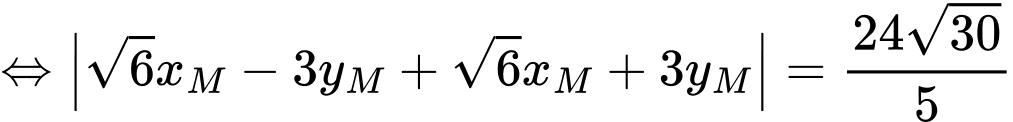
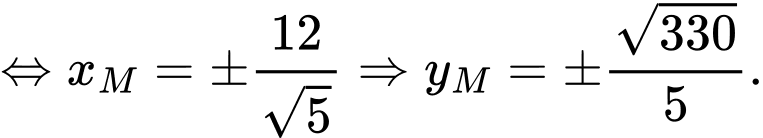
Vậy có 4 điểm M cần tìm là:
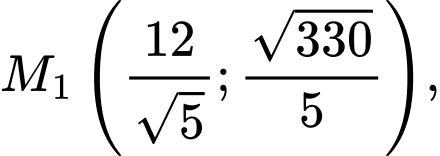
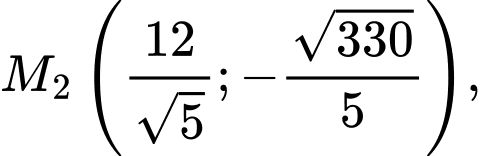
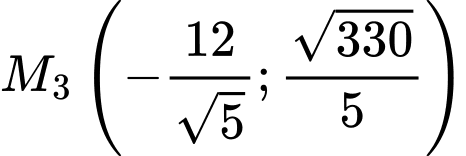 và
và 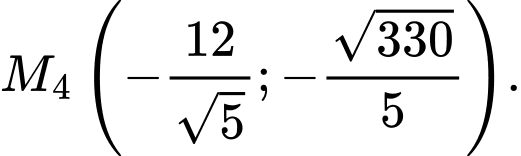
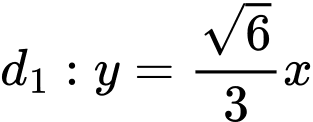 ,
, 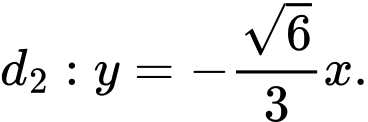
Tổng khoảng cách từ
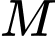 đến hai đường tiệm cận bằng
đến hai đường tiệm cận bằng 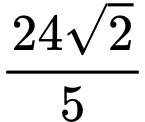 nên
nên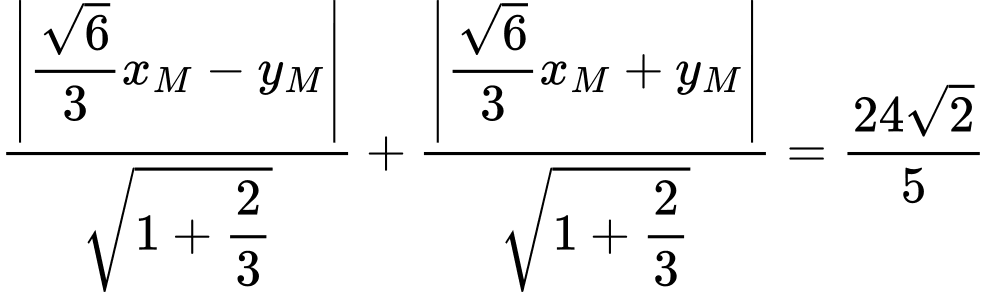
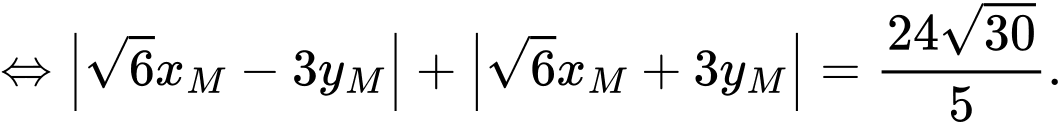
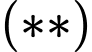
Mặt khác
 nên ta có
nên ta có
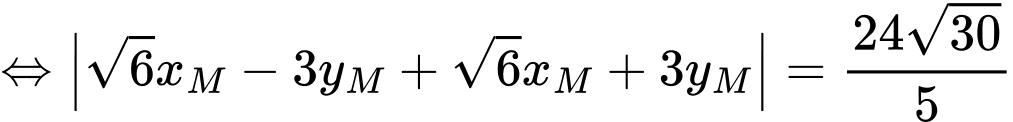
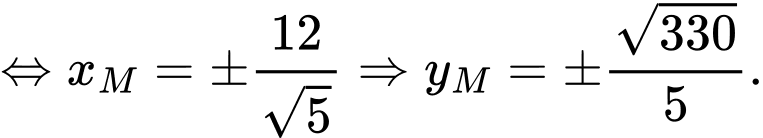
Vậy có 4 điểm M cần tìm là:
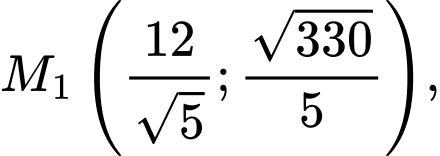
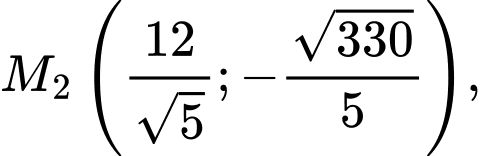
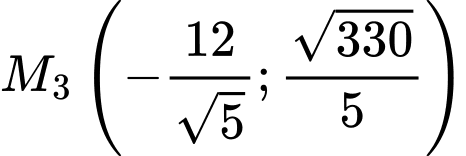 và
và 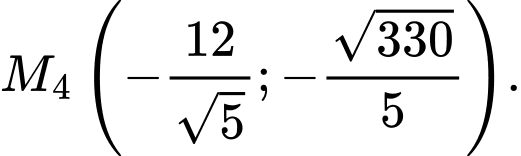
Dạng câu hỏi: Câu hỏi kéo thả
Câu 21 [583166]: Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
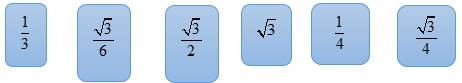
Trên mặt phẳng tọa độ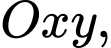 cho elip có phương trình
cho elip có phương trình 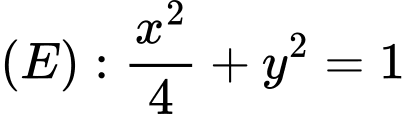 và điểm
và điểm 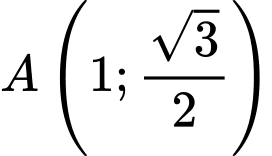 thuộc
thuộc 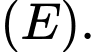
Tiếp tuyến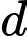 của
của  tại
tại 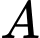 có hệ số góc là _______.
có hệ số góc là _______.
Diện tích hình phẳng giới hạn bởi ba đường: elip, đường thẳng
giới hạn bởi ba đường: elip, đường thẳng 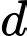 và trục
và trục 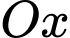 bằng _______ - _______π.
bằng _______ - _______π.
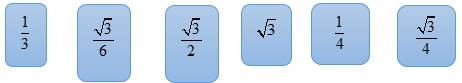
Trên mặt phẳng tọa độ
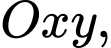 cho elip có phương trình
cho elip có phương trình 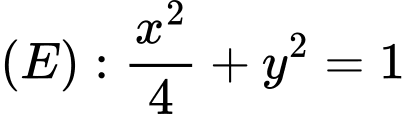 và điểm
và điểm 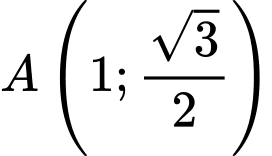 thuộc
thuộc 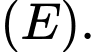
Tiếp tuyến
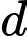 của
của  tại
tại 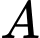 có hệ số góc là _______.
có hệ số góc là _______.Diện tích hình phẳng
 giới hạn bởi ba đường: elip, đường thẳng
giới hạn bởi ba đường: elip, đường thẳng 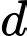 và trục
và trục 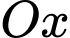 bằng _______ - _______π.
bằng _______ - _______π.
Đáp án
Trên mặt phẳng tọa độ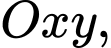 cho elip có phương trình
cho elip có phương trình 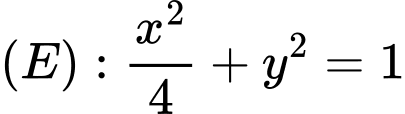 và điểm
và điểm 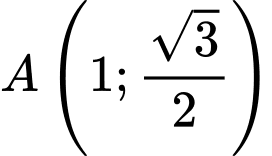 thuộc
thuộc 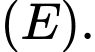
Tiếp tuyến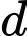 của
của  tại
tại 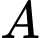 có hệ số góc là
có hệ số góc là 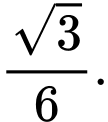
Diện tích hình phẳng giới hạn bởi ba đường: elip, đường thẳng
giới hạn bởi ba đường: elip, đường thẳng 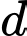 và trục
và trục 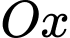 bằng
bằng 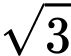 -
- 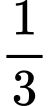 π.
π.
Giải thích
Phương trình nửa trên của elip là
là 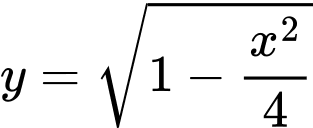 suy ra
suy ra 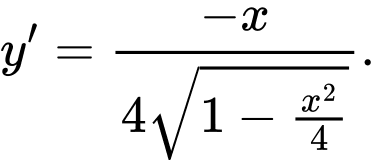
Phương trình tiếp tuyến với tại
tại 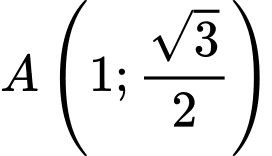 là
là
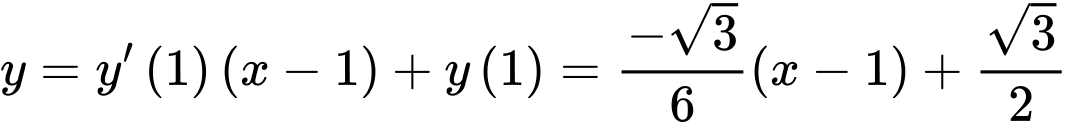 hay
hay 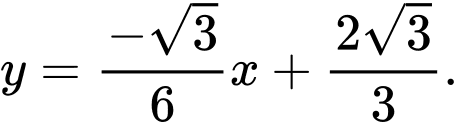
Đường thẳng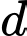 cắt trục hoành tại
cắt trục hoành tại 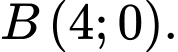 Hình phẳng
Hình phẳng  có ba đỉnh
có ba đỉnh 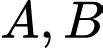 và
và 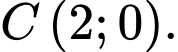
Kẻ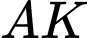 vuông góc với trục hoành, khi đó diện tích của hình
vuông góc với trục hoành, khi đó diện tích của hình  là
là  (
(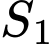 là diện tích giới hạn bởi
là diện tích giới hạn bởi 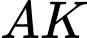 , trục
, trục 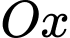 và
và  ).
).
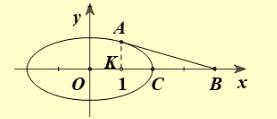
Ta có: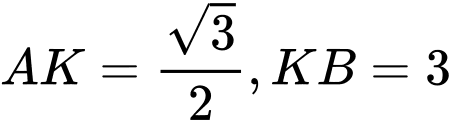 nên
nên 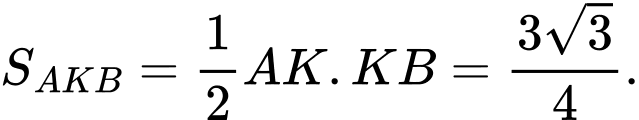
Những điểm thuộc hình có tung độ
có tung độ  nên từ phương trình
nên từ phương trình  suy ra
suy ra 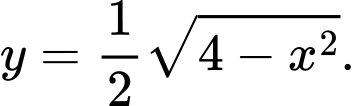 Do đó
Do đó 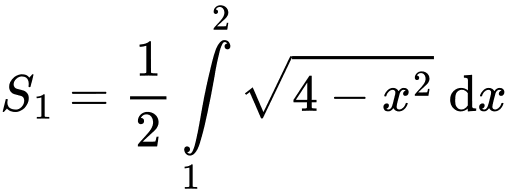
Đặt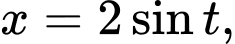 ta tính được
ta tính được 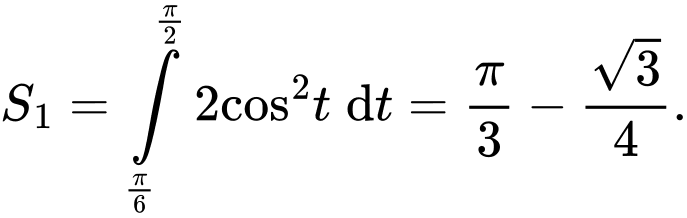
Vậy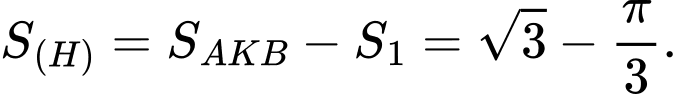
Trên mặt phẳng tọa độ
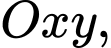 cho elip có phương trình
cho elip có phương trình 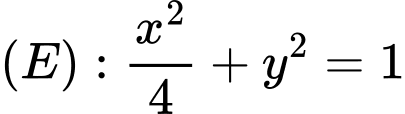 và điểm
và điểm 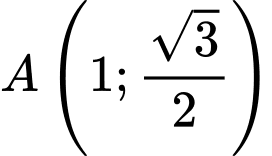 thuộc
thuộc 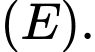
Tiếp tuyến
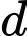 của
của  tại
tại 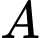 có hệ số góc là
có hệ số góc là 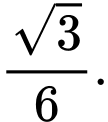
Diện tích hình phẳng
 giới hạn bởi ba đường: elip, đường thẳng
giới hạn bởi ba đường: elip, đường thẳng 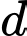 và trục
và trục 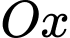 bằng
bằng 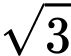 -
- 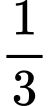 π.
π.Giải thích
Phương trình nửa trên của elip
 là
là 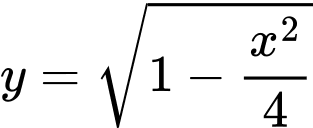 suy ra
suy ra 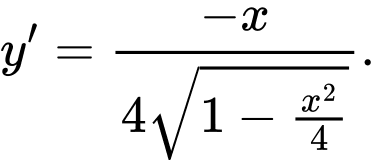
Phương trình tiếp tuyến với
 tại
tại 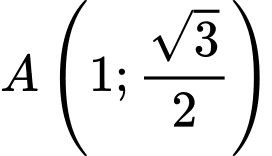 là
là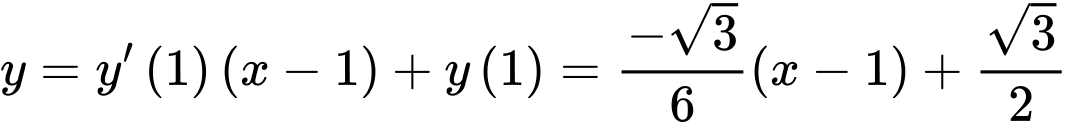 hay
hay 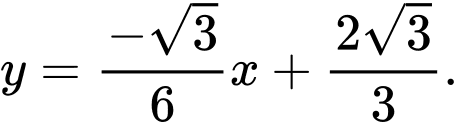
Đường thẳng
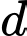 cắt trục hoành tại
cắt trục hoành tại 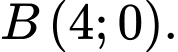 Hình phẳng
Hình phẳng  có ba đỉnh
có ba đỉnh 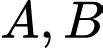 và
và 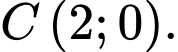
Kẻ
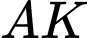 vuông góc với trục hoành, khi đó diện tích của hình
vuông góc với trục hoành, khi đó diện tích của hình  là
là  (
(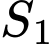 là diện tích giới hạn bởi
là diện tích giới hạn bởi 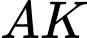 , trục
, trục 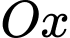 và
và  ).
).
Ta có:
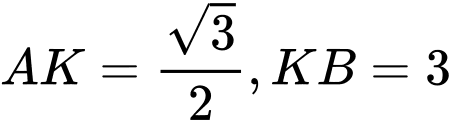 nên
nên 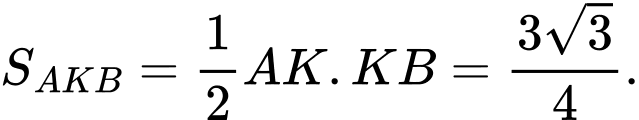
Những điểm thuộc hình
 có tung độ
có tung độ  nên từ phương trình
nên từ phương trình  suy ra
suy ra 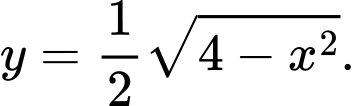 Do đó
Do đó 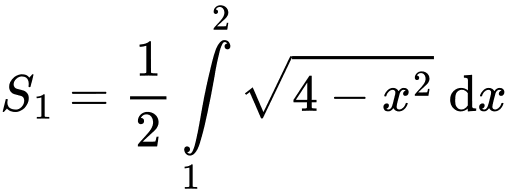
Đặt
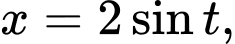 ta tính được
ta tính được 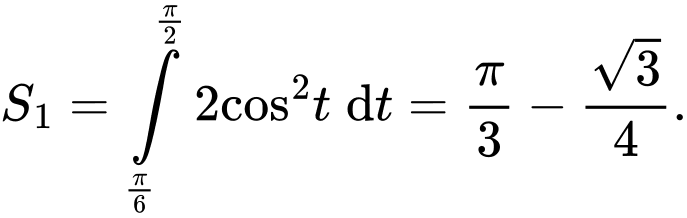
Vậy