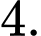Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
Câu 1 [582558]: Tập hợp nào sau đây có đúng một tập hợp con?
A, 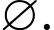
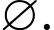
B, 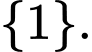
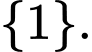
C, 

D, 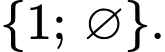
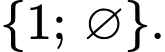
Đáp án A duy nhất một tập con là 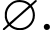
Đáp án B còn một tập con nữa là tập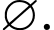
Đáp án C có hai tập con là và
và 
Đáp án D có ba tập con ,
, 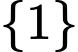 và
và 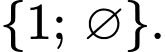 Đáp án: A
Đáp án: A
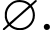
Đáp án B còn một tập con nữa là tập
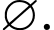
Đáp án C có hai tập con là
 và
và 
Đáp án D có ba tập con
 ,
, 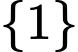 và
và 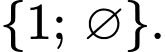 Đáp án: A
Đáp án: A
Câu 2 [582559]: Hai tập hợp nào dưới đây không bằng nhau?
A, 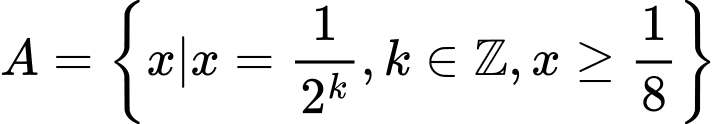 và
và 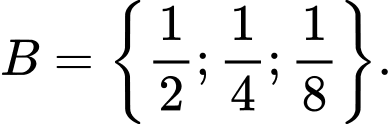
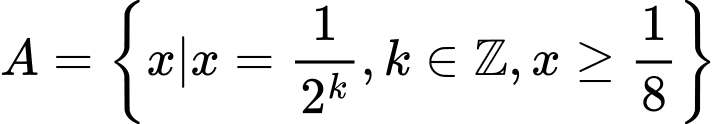 và
và 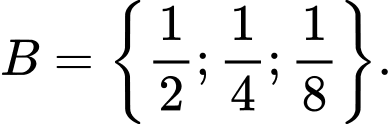
B, 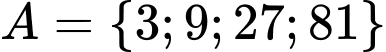 và
và 
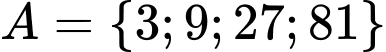 và
và 
C, 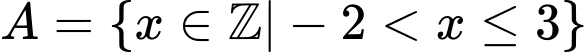 và
và 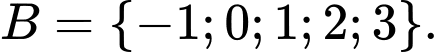
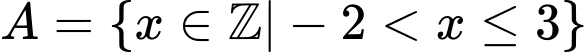 và
và 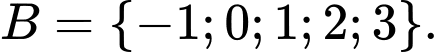
D, 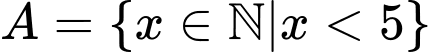 và
và 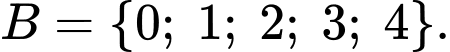
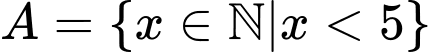 và
và 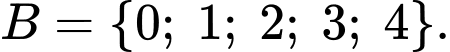
Xét tập hợp 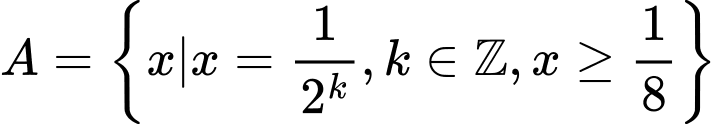 ta có:
ta có: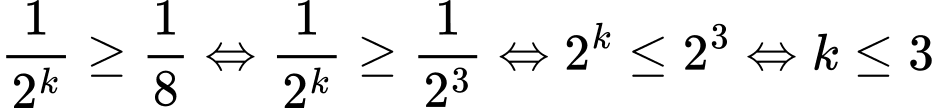 , suy ra:
, suy ra:
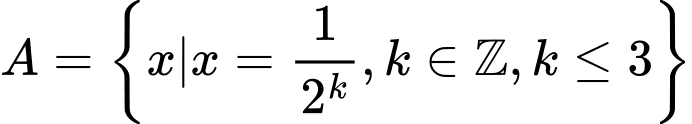
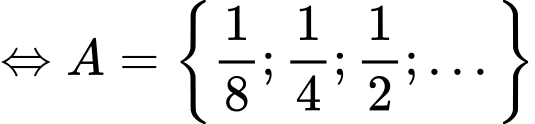 nên:
nên: 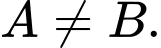 Đáp án: A
Đáp án: A
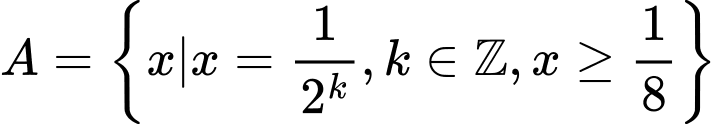 ta có:
ta có: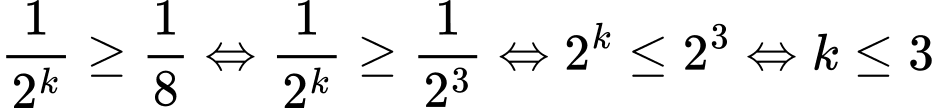 , suy ra:
, suy ra: 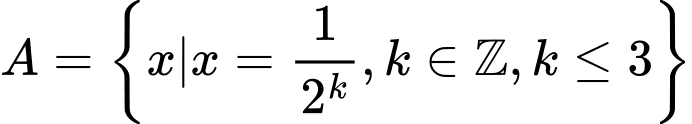
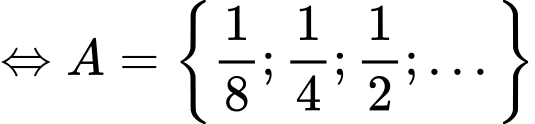 nên:
nên:  Đáp án: A
Đáp án: A
Câu 3 [582560]: Cho 2 tập hợp 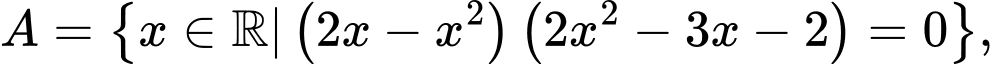
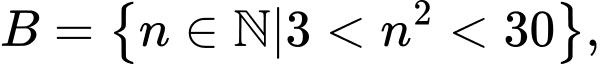 chọn mệnh đề đúng?
chọn mệnh đề đúng?
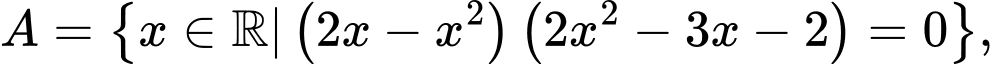
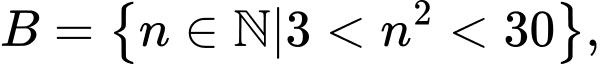 chọn mệnh đề đúng?
chọn mệnh đề đúng? A, 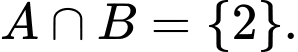
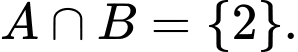
B, 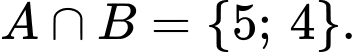
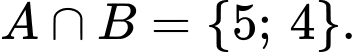
C, 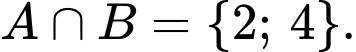
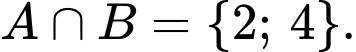
D, 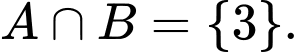
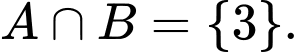
Xét tập hợp 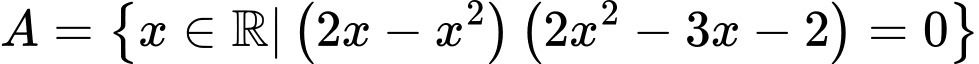 ta có:
ta có: 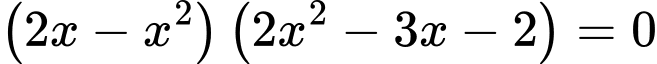
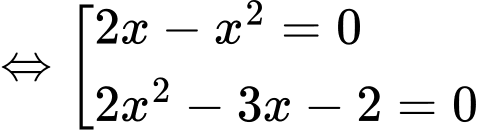
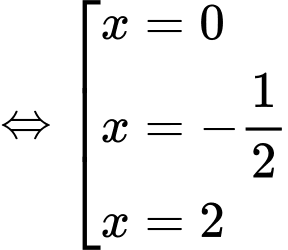
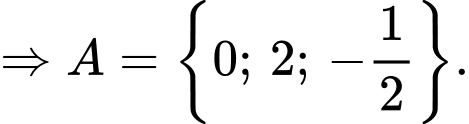
Xét tập hợp
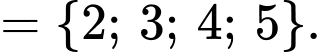
Vậy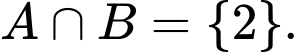 Đáp án: A
Đáp án: A
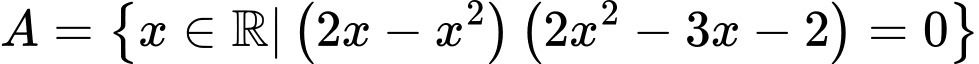 ta có:
ta có: 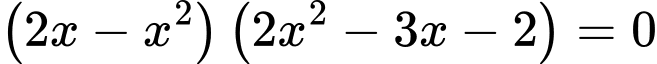
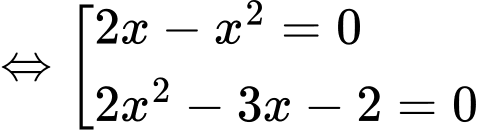
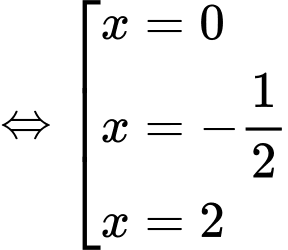
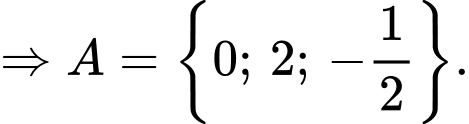
Xét tập hợp

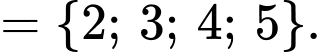
Vậy
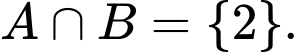 Đáp án: A
Đáp án: A
Câu 4 [582561]: Cho hai đa thức 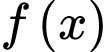 và
và 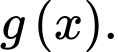 Xét các tập hợp
Xét các tập hợp 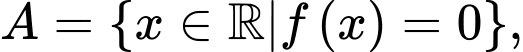
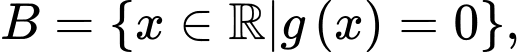
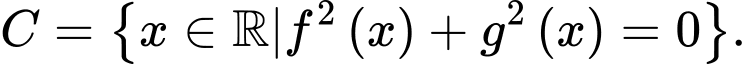 Trong các mệnh đề sau, mệnh đề nào đúng?
Trong các mệnh đề sau, mệnh đề nào đúng?
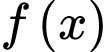 và
và 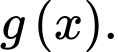 Xét các tập hợp
Xét các tập hợp 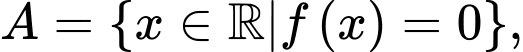
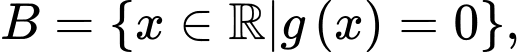
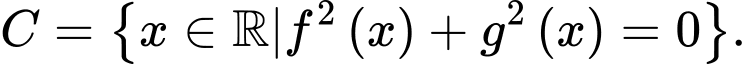 Trong các mệnh đề sau, mệnh đề nào đúng?
Trong các mệnh đề sau, mệnh đề nào đúng? A, 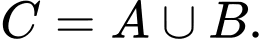
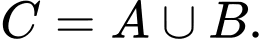
B, 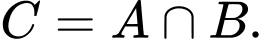
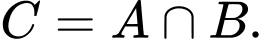
C, 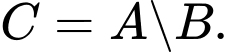
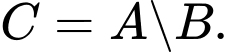
D, 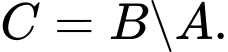
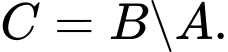
Ta có 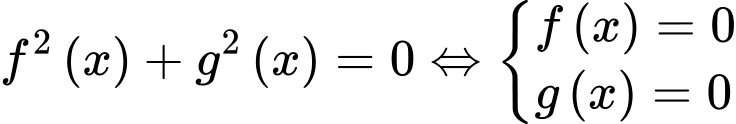 nên
nên 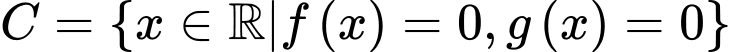 nên
nên 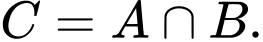 Đáp án: B
Đáp án: B
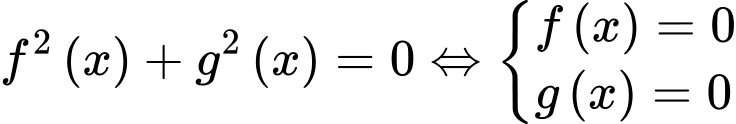 nên
nên 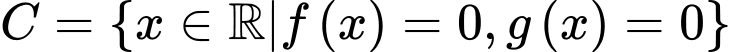 nên
nên 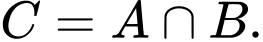 Đáp án: B
Đáp án: B
Câu 5 [582562]: Cho 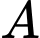 là tập hợp các hình thoi,
là tập hợp các hình thoi, 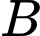 là tập hợp các hình chữ nhật và
là tập hợp các hình chữ nhật và  là tập hợp các hình vuông. Khi đó
là tập hợp các hình vuông. Khi đó
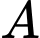 là tập hợp các hình thoi,
là tập hợp các hình thoi, 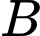 là tập hợp các hình chữ nhật và
là tập hợp các hình chữ nhật và  là tập hợp các hình vuông. Khi đó
là tập hợp các hình vuông. Khi đó A, 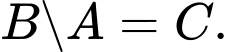
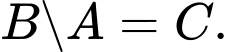
B, 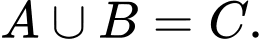
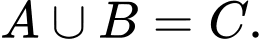
C, 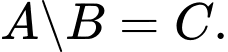
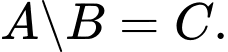
D, 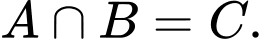
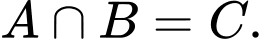
Theo tính chất của hình thoi, hình chữ nhật và hình vuông, ta có:
 và
và 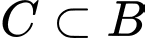 nên
nên 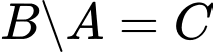 ,
, 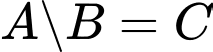 là các mệnh đề sai.
là các mệnh đề sai.
Vì hình vuông vừa là hình thoi và cũng là hình chữ nhật nên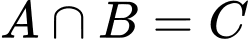 là mệnh đề đúng và
là mệnh đề đúng và 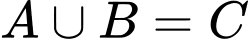 là mệnh đề sai.
Đáp án: D
là mệnh đề sai.
Đáp án: D
 và
và 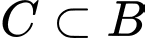 nên
nên 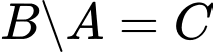 ,
, 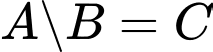 là các mệnh đề sai.
là các mệnh đề sai.
Vì hình vuông vừa là hình thoi và cũng là hình chữ nhật nên
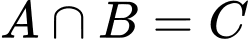 là mệnh đề đúng và
là mệnh đề đúng và 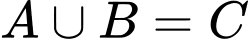 là mệnh đề sai.
Đáp án: D
là mệnh đề sai.
Đáp án: D
Câu 6 [582563]: Cho các tập hợp  và
và 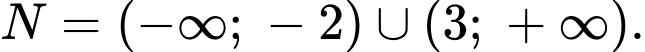 Khi đó
Khi đó  là
là
 và
và 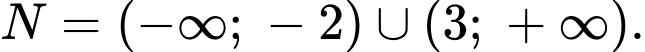 Khi đó
Khi đó  là
là A, 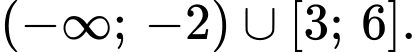
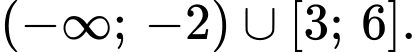
B, 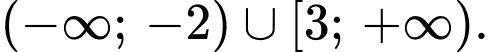
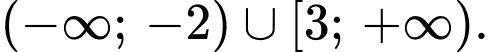
C, 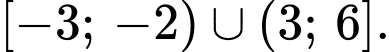
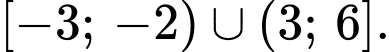
D, 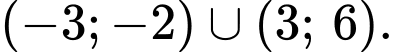
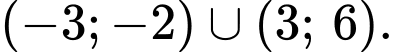
Biểu diễn trục số:
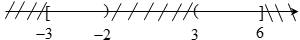
 và
và 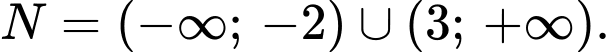
Khi đó: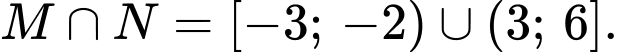 Đáp án: C
Đáp án: C
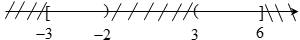
 và
và 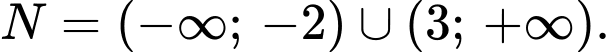
Khi đó:
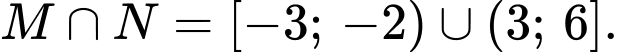 Đáp án: C
Đáp án: C
Câu 7 [582564]: Cho các tập hợp khác rỗng 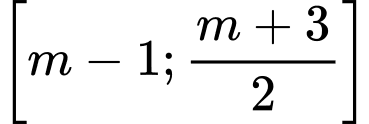 và
và 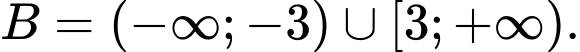 Tập hợp các giá trị thực của
Tập hợp các giá trị thực của 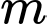 để
để 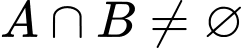 là
là
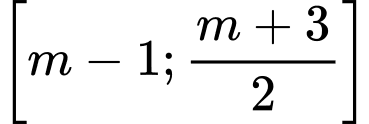 và
và 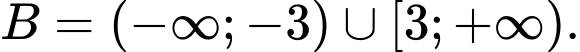 Tập hợp các giá trị thực của
Tập hợp các giá trị thực của 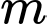 để
để  là
là A, 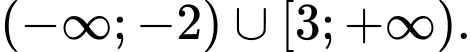
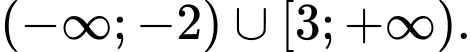
B, 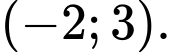
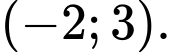
C, 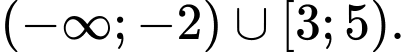
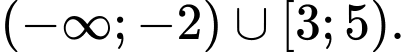
D, 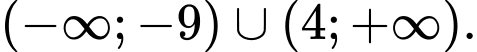
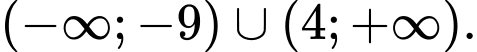
Để 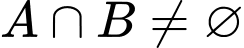 thì điều kiện là
thì điều kiện là 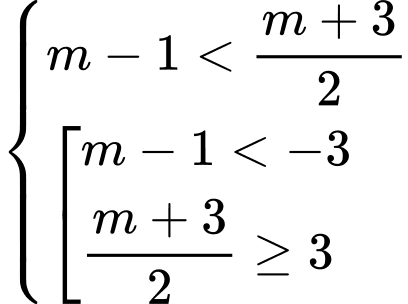
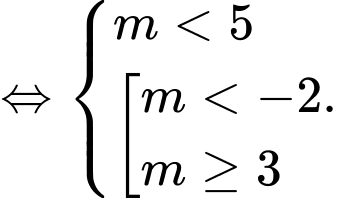
Vậy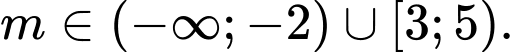 Đáp án: C
Đáp án: C
 thì điều kiện là
thì điều kiện là 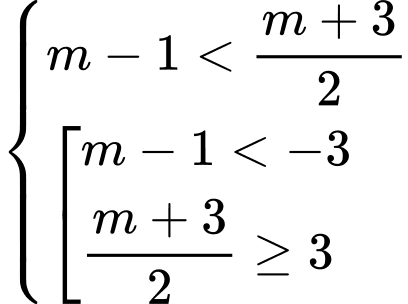
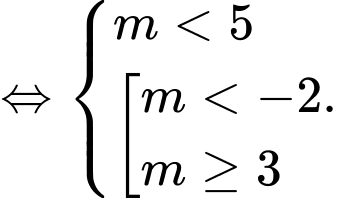
Vậy
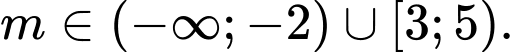 Đáp án: C
Đáp án: C
Câu 8 [582565]: Cho hai tập hợp 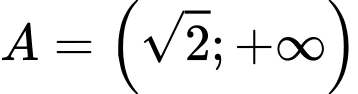 và
và 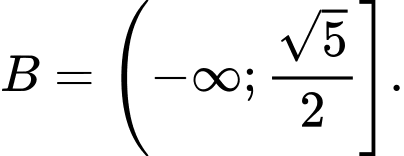 Khi đó
Khi đó 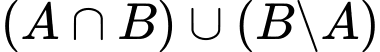 là
là
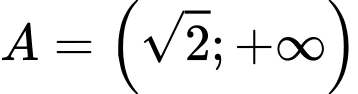 và
và 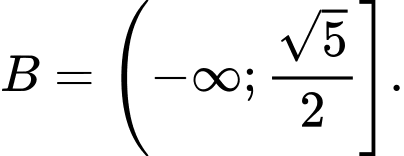 Khi đó
Khi đó 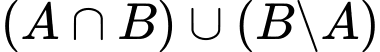 là
là A, 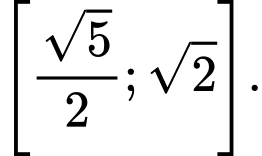
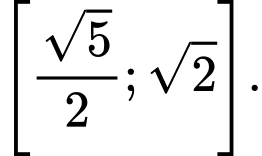
B, 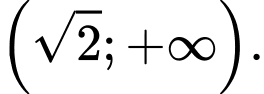
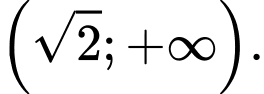
C, 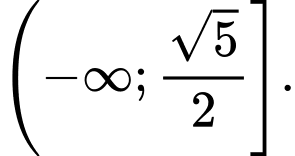
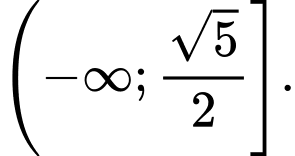
D, 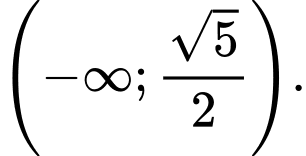
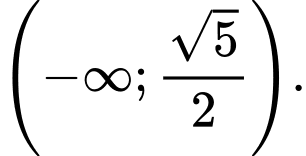
Ta có 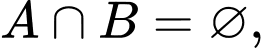
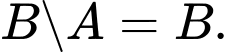
Do đó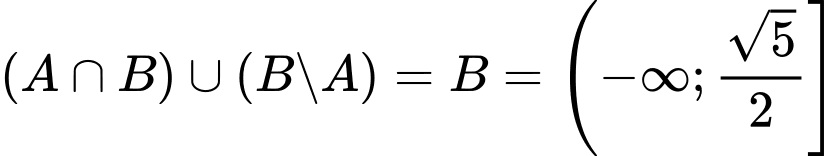
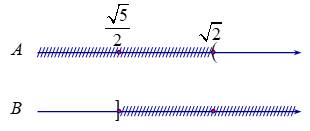 Đáp án: C
Đáp án: C
Do đó
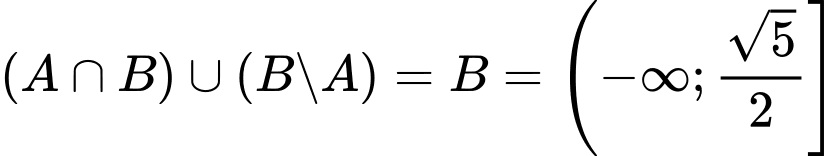
 Đáp án: C
Đáp án: C
Câu 9 [582566]: Cho 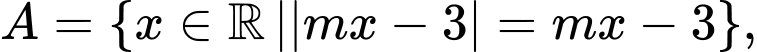
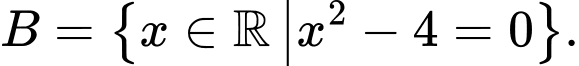 Tìm
Tìm 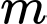 để
để 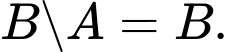
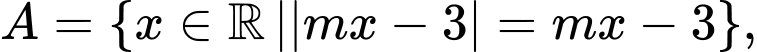
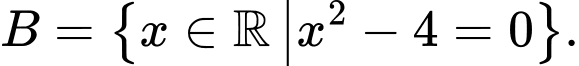 Tìm
Tìm 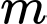 để
để 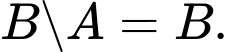
A, 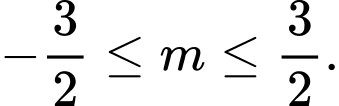
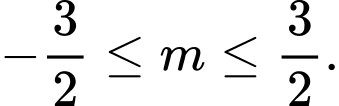
B, 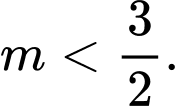
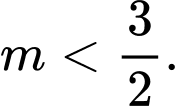
C, 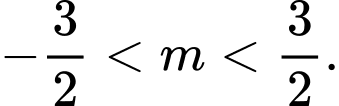
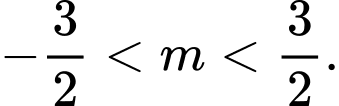
D, 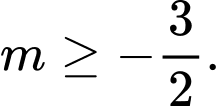
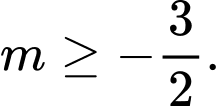
Ta có: 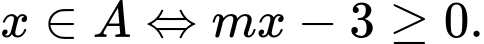

Ta có: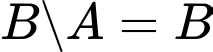
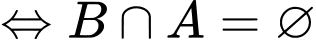
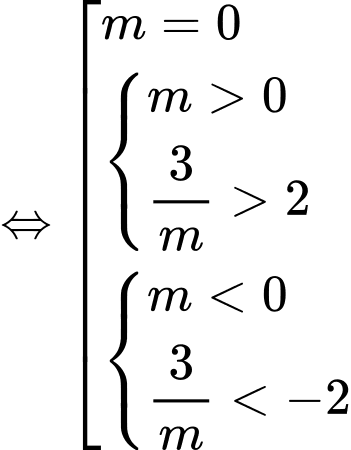
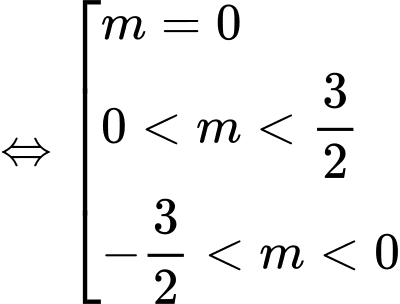
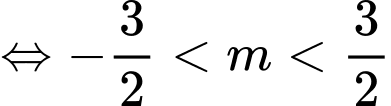 Đáp án: C
Đáp án: C
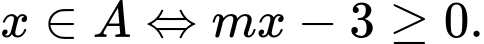

Ta có:
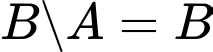
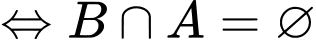
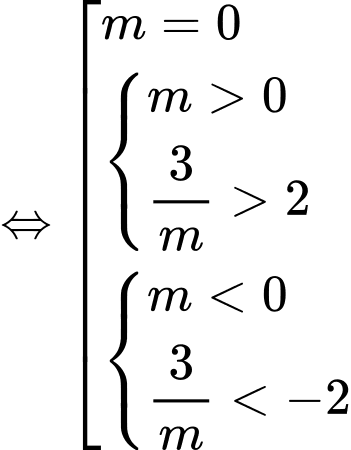
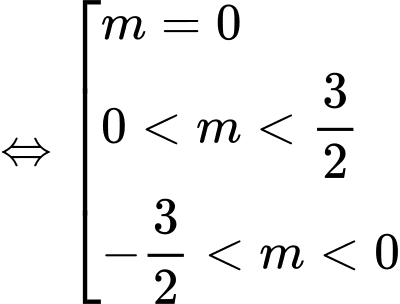
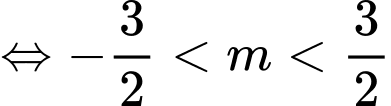 Đáp án: C
Đáp án: C
Câu 10 [582567]: Cho tập hợp 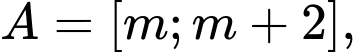
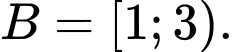 Điều kiện để
Điều kiện để 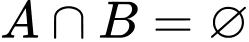 là:
là:
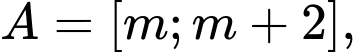
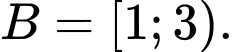 Điều kiện để
Điều kiện để 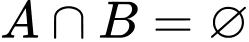 là:
là: A,  hoặc
hoặc 
 hoặc
hoặc 
B,  hoặc
hoặc 
 hoặc
hoặc 
C,  hoặc
hoặc 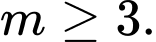
 hoặc
hoặc 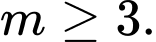
D,  hoặc
hoặc 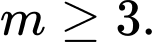
 hoặc
hoặc 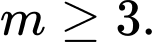
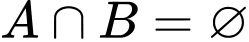
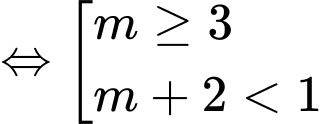
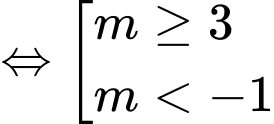 Đáp án: C
Đáp án: C
Câu 11 [582568]: Có bao nhiêu số nguyên là tổng của ba phần tử phân biệt của tập hợp 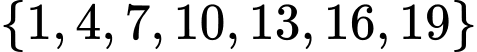 ?
?
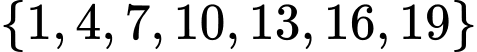 ?
? A, 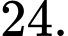
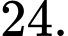
B, 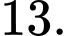
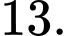
C, 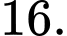
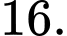
D, 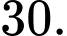
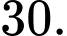
Các phần tử trong tập hợp đều chia hết cho 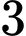 dư
dư 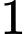 nên tổng của
nên tổng của 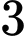 phần tử phân biệt của tập hợp sẽ chia hết cho
phần tử phân biệt của tập hợp sẽ chia hết cho 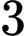 . Dễ kiểm tra được các bội của
. Dễ kiểm tra được các bội của 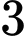 từ
từ 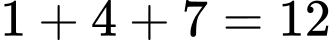 đến
đến  đều có thể tổng của
đều có thể tổng của 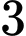 phần tử trong tập hợp. Mà từ
phần tử trong tập hợp. Mà từ  đến
đến 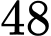 có
có  số là bội của
số là bội của 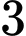 . Đáp án: B
. Đáp án: B
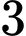 dư
dư 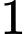 nên tổng của
nên tổng của 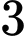 phần tử phân biệt của tập hợp sẽ chia hết cho
phần tử phân biệt của tập hợp sẽ chia hết cho 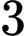 . Dễ kiểm tra được các bội của
. Dễ kiểm tra được các bội của 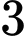 từ
từ 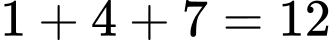 đến
đến  đều có thể tổng của
đều có thể tổng của 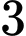 phần tử trong tập hợp. Mà từ
phần tử trong tập hợp. Mà từ  đến
đến 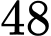 có
có  số là bội của
số là bội của 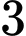 . Đáp án: B
. Đáp án: B
Câu 12 [582569]: Cho 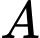 là tập hợp tất cả các nghiệm của phương trình
là tập hợp tất cả các nghiệm của phương trình 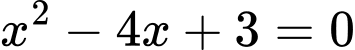 ;
; 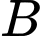 là tập hợp các số nguyên có giá trị tuyệt đối nhỏ hơn 4. Xác định tập hợp
là tập hợp các số nguyên có giá trị tuyệt đối nhỏ hơn 4. Xác định tập hợp 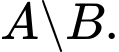
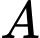 là tập hợp tất cả các nghiệm của phương trình
là tập hợp tất cả các nghiệm của phương trình 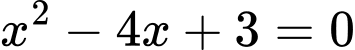 ;
; 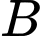 là tập hợp các số nguyên có giá trị tuyệt đối nhỏ hơn 4. Xác định tập hợp
là tập hợp các số nguyên có giá trị tuyệt đối nhỏ hơn 4. Xác định tập hợp 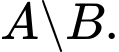
A, 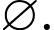
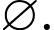
B, 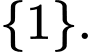
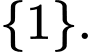
C, 

D, 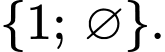
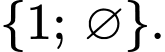
Ta có 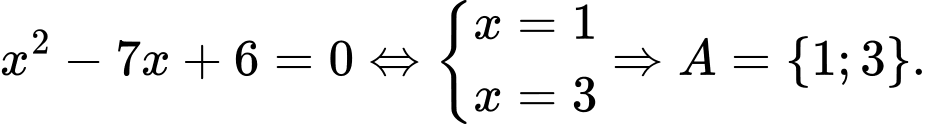
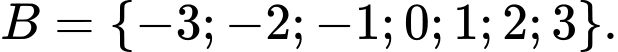 Do đó
Do đó 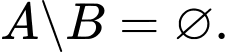 Đáp án: A
Đáp án: A
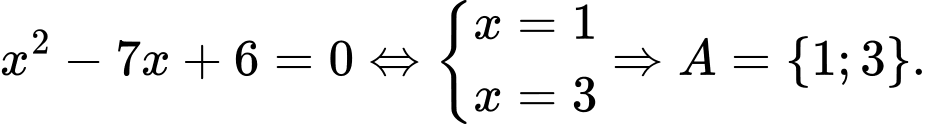
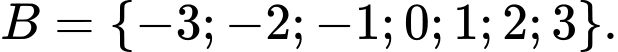 Do đó
Do đó 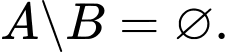 Đáp án: A
Đáp án: A
Câu 13 [582570]: Cho các tập hợp 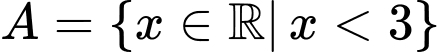 ,
, 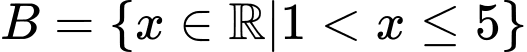 ,
, 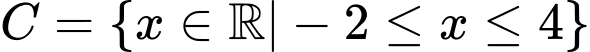 . Khi đó
. Khi đó 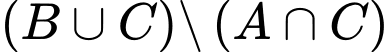 bằng
bằng
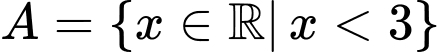 ,
, 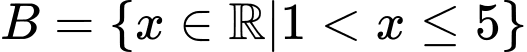 ,
, 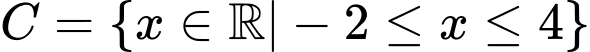 . Khi đó
. Khi đó 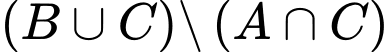 bằng
bằng A, 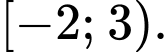
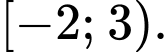
B, 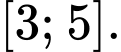
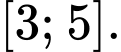
C, 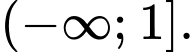
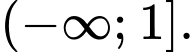
D, 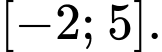
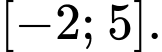
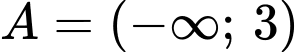 ,
, 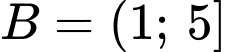 ,
, 
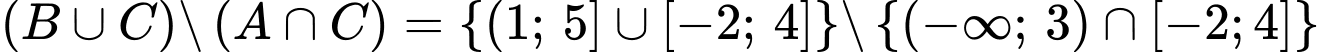
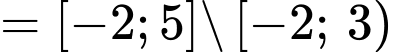
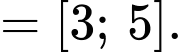 Đáp án: B
Đáp án: B
Câu 14 [582571]: Cho các tập hợp 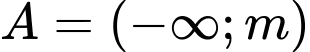 và
và 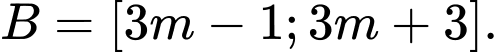 Tìm giá trị nhỏ nhất của
Tìm giá trị nhỏ nhất của 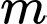 để
để 
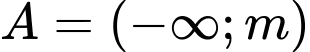 và
và 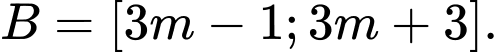 Tìm giá trị nhỏ nhất của
Tìm giá trị nhỏ nhất của 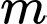 để
để 
A, 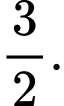
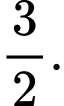
B, 
C, 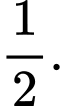
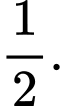
D, 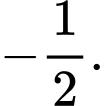
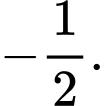
Ta có: 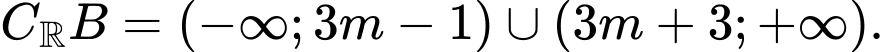
Vì vậy: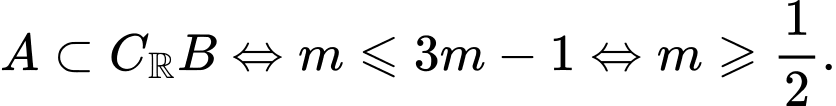
Suy ra giá trị nhỏ nhất của m là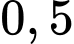 Đáp án: C
Đáp án: C
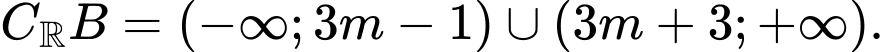
Vì vậy:
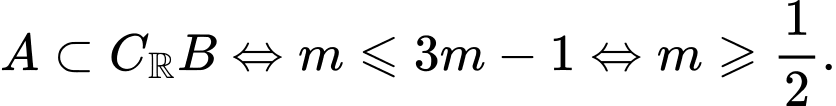
Suy ra giá trị nhỏ nhất của m là
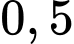 Đáp án: C
Đáp án: C
Câu 15 [582572]: Cho hai tập hợp 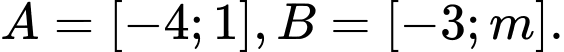 Có bao nhiêu giá trị nguyên của
Có bao nhiêu giá trị nguyên của 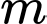 để
để 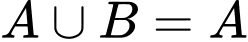 ?
?
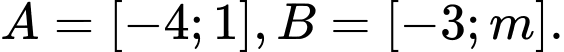 Có bao nhiêu giá trị nguyên của
Có bao nhiêu giá trị nguyên của 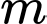 để
để 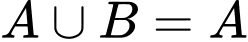 ?
? A, 4.
B, 5.
C, 2.
D, 3.
Điều kiện: 
Ta có: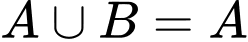 khi và chỉ khi
khi và chỉ khi  tức là
tức là 
Đối chiếu điều kiện, ta được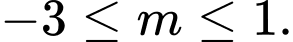 Suy ra
Suy ra 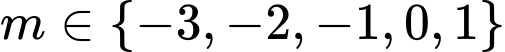 Đáp án: B
Đáp án: B

Ta có:
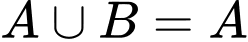 khi và chỉ khi
khi và chỉ khi  tức là
tức là 
Đối chiếu điều kiện, ta được
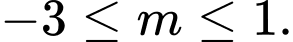 Suy ra
Suy ra 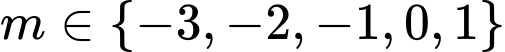 Đáp án: B
Đáp án: B Dạng câu hỏi: Câu trả lời đúng sai
(Thí sinh trả lời từ câu 16, 17. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai)
Câu 16 [582573]: Cho 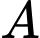 là tập hợp các học sinh lớp 10 đang học ở trường em và
là tập hợp các học sinh lớp 10 đang học ở trường em và 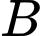 là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Vậy:
là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Vậy:
a) là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường em.
là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường em.
b)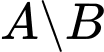 là tập hợp những học sinh lớp 10 nhưng không học Tiếng Anh ở trường em.
là tập hợp những học sinh lớp 10 nhưng không học Tiếng Anh ở trường em.
c) là tập hợp các học sinh lớp 10 hoặc học sinh học môn Tiếng Anh ở trường em.
là tập hợp các học sinh lớp 10 hoặc học sinh học môn Tiếng Anh ở trường em.
d)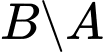 là tập hợp các học sinh học môn Tiếng Anh nhưng không học lớp 10 ở trường em.
là tập hợp các học sinh học môn Tiếng Anh nhưng không học lớp 10 ở trường em.
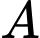 là tập hợp các học sinh lớp 10 đang học ở trường em và
là tập hợp các học sinh lớp 10 đang học ở trường em và 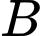 là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Vậy:
là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Vậy: a)
 là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường em.
là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường em. b)
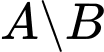 là tập hợp những học sinh lớp 10 nhưng không học Tiếng Anh ở trường em.
là tập hợp những học sinh lớp 10 nhưng không học Tiếng Anh ở trường em. c)
 là tập hợp các học sinh lớp 10 hoặc học sinh học môn Tiếng Anh ở trường em.
là tập hợp các học sinh lớp 10 hoặc học sinh học môn Tiếng Anh ở trường em. d)
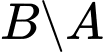 là tập hợp các học sinh học môn Tiếng Anh nhưng không học lớp 10 ở trường em.
là tập hợp các học sinh học môn Tiếng Anh nhưng không học lớp 10 ở trường em.
a) Đúng b) Đúng c) Đúng d) Đúng
a) là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường em.
là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường em.
b)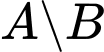 là tập hợp những học sinh lớp 10 nhưng không học Tiếng Anh ở trường em.
là tập hợp những học sinh lớp 10 nhưng không học Tiếng Anh ở trường em.
c) là tập hợp các học sinh lớp 10 hoặc học sinh học môn Tiếng Anh ở trường em.
là tập hợp các học sinh lớp 10 hoặc học sinh học môn Tiếng Anh ở trường em.
d)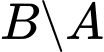 là tập hợp các học sinh học môn Tiếng Anh nhưng không học lớp 10 ở trường em.
là tập hợp các học sinh học môn Tiếng Anh nhưng không học lớp 10 ở trường em.
a)
 là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường em.
là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường em.
b)
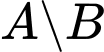 là tập hợp những học sinh lớp 10 nhưng không học Tiếng Anh ở trường em.
là tập hợp những học sinh lớp 10 nhưng không học Tiếng Anh ở trường em.
c)
 là tập hợp các học sinh lớp 10 hoặc học sinh học môn Tiếng Anh ở trường em.
là tập hợp các học sinh lớp 10 hoặc học sinh học môn Tiếng Anh ở trường em.
d)
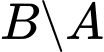 là tập hợp các học sinh học môn Tiếng Anh nhưng không học lớp 10 ở trường em.
là tập hợp các học sinh học môn Tiếng Anh nhưng không học lớp 10 ở trường em.
Câu 17 [582574]: Cho ba tập hợp 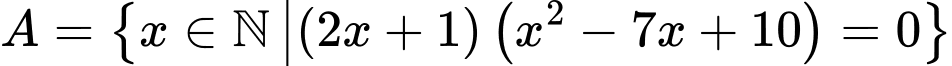 ,
, 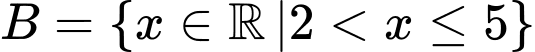 và
và 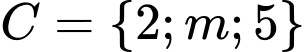
a) Tập hợp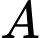 có hai tập hợp con khác rỗng.
có hai tập hợp con khác rỗng.
b)
c)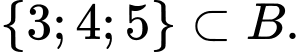
d) Không có giá trị nào của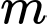 để
để 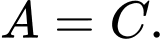
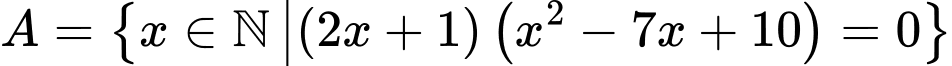 ,
, 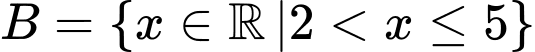 và
và 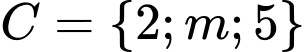
a) Tập hợp
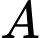 có hai tập hợp con khác rỗng.
có hai tập hợp con khác rỗng. b)

c)
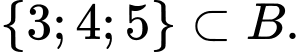
d) Không có giá trị nào của
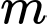 để
để 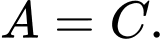
Ta có: 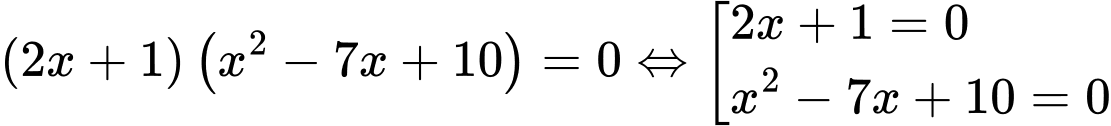
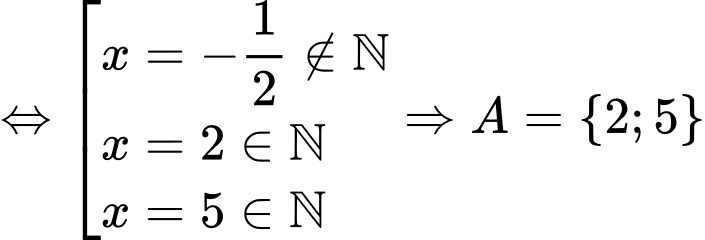
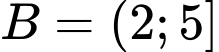
a) Sai vì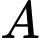 có 3 tập con khác rỗng là:
có 3 tập con khác rỗng là: 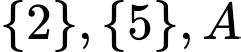
b) Sai vì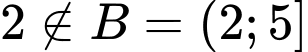
c) Đúng
d) Sai vì khi
khi 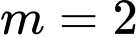 hoặc
hoặc 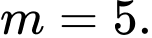
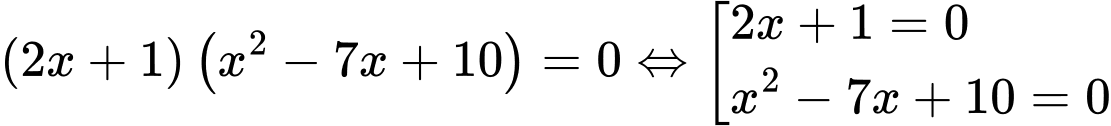
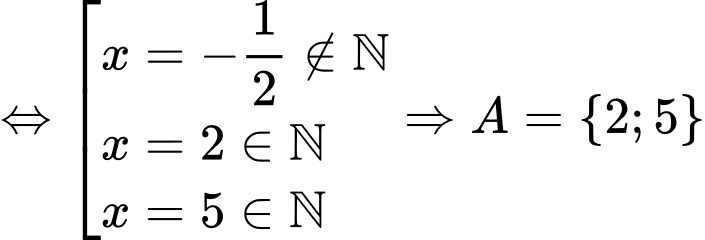
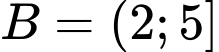
a) Sai vì
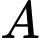 có 3 tập con khác rỗng là:
có 3 tập con khác rỗng là: 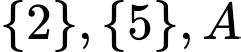
b) Sai vì
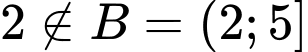
c) Đúng
d) Sai vì
 khi
khi 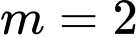 hoặc
hoặc 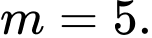
Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản (nếu có))
Câu 18 [582575]: Cho tập hợp 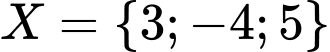 có hai tập con
có hai tập con 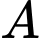 và
và 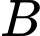 (số phần tử của tập
(số phần tử của tập 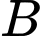 ít hơn số phần tử của tập
ít hơn số phần tử của tập  Có bao nhiêu cặp
Có bao nhiêu cặp 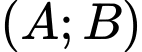 mà
mà 
Đáp án:……
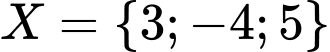 có hai tập con
có hai tập con 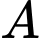 và
và 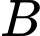 (số phần tử của tập
(số phần tử của tập 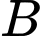 ít hơn số phần tử của tập
ít hơn số phần tử của tập  Có bao nhiêu cặp
Có bao nhiêu cặp 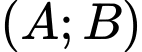 mà
mà 
Đáp án:……
Trả lời: 11
Lời giải
Do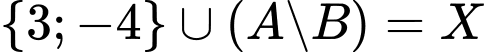 nên tập hợp
nên tập hợp 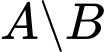 phải chứa phần tử 5. Từ đó suy ra:
phải chứa phần tử 5. Từ đó suy ra: 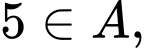
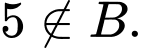
Các tập con của có phần tử 5 là:
có phần tử 5 là: 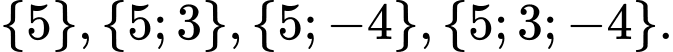
Do số phần tử của tập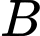 ít hơn số phần tử của tập
ít hơn số phần tử của tập 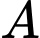 nên ta có các TH sau:
nên ta có các TH sau:
+ Nếu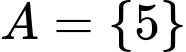 thì
thì 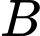 là tập con của
là tập con của 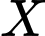 không chứa phần tử nào, tức là
không chứa phần tử nào, tức là 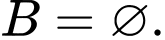
+ Nếu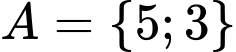 thì
thì 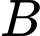 là tập con của
là tập con của 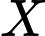 chứa ít hơn hai phần tử và không chứa phần tử 5, tức là
chứa ít hơn hai phần tử và không chứa phần tử 5, tức là 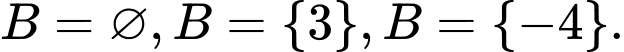
+ Nếu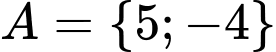 thì
thì 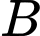 là tập con của
là tập con của 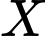 chứa ít hơn hai phần tử và không chứa phần tử 5, tức là
chứa ít hơn hai phần tử và không chứa phần tử 5, tức là 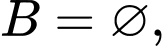
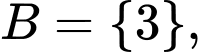
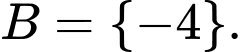
+ Nếu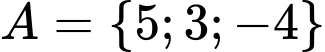 thì
thì 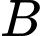 là tập con của
là tập con của 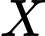 chứa ít hơn ba phần tử và không chứa phần tử 5, tức là
chứa ít hơn ba phần tử và không chứa phần tử 5, tức là 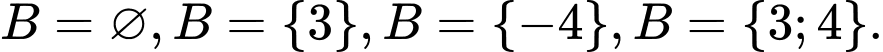
Vậy có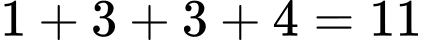 cặp
cặp 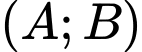 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
Lời giải
Do
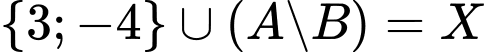 nên tập hợp
nên tập hợp 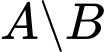 phải chứa phần tử 5. Từ đó suy ra:
phải chứa phần tử 5. Từ đó suy ra: 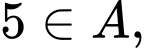
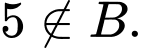
Các tập con của
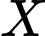 có phần tử 5 là:
có phần tử 5 là: 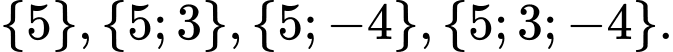
Do số phần tử của tập
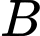 ít hơn số phần tử của tập
ít hơn số phần tử của tập 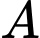 nên ta có các TH sau:
nên ta có các TH sau:+ Nếu
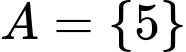 thì
thì 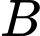 là tập con của
là tập con của 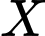 không chứa phần tử nào, tức là
không chứa phần tử nào, tức là 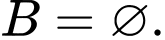
+ Nếu
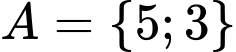 thì
thì 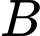 là tập con của
là tập con của 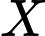 chứa ít hơn hai phần tử và không chứa phần tử 5, tức là
chứa ít hơn hai phần tử và không chứa phần tử 5, tức là 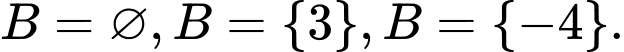
+ Nếu
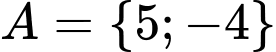 thì
thì 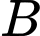 là tập con của
là tập con của 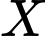 chứa ít hơn hai phần tử và không chứa phần tử 5, tức là
chứa ít hơn hai phần tử và không chứa phần tử 5, tức là 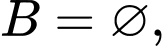
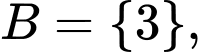
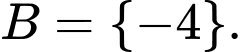
+ Nếu
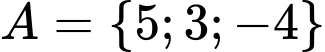 thì
thì 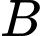 là tập con của
là tập con của 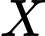 chứa ít hơn ba phần tử và không chứa phần tử 5, tức là
chứa ít hơn ba phần tử và không chứa phần tử 5, tức là 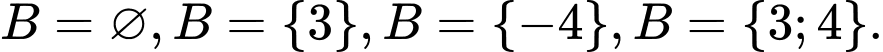
Vậy có
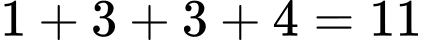 cặp
cặp 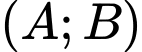 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
Câu 19 [582576]: Cho 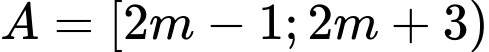 và
và 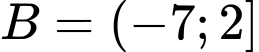 với
với 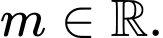 Tìm
Tìm 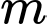 để tập hợp
để tập hợp  chứa đúng một phần tử.
chứa đúng một phần tử.
Đáp án:……
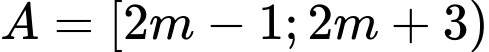 và
và 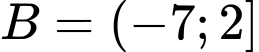 với
với 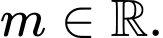 Tìm
Tìm 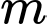 để tập hợp
để tập hợp  chứa đúng một phần tử.
chứa đúng một phần tử. Đáp án:……
Trả lời:
Lời giải
Để tập hợp chứa đúng một phần tử thì
chứa đúng một phần tử thì 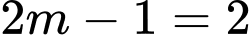 hay
hay 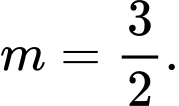
Lời giải
Để tập hợp
 chứa đúng một phần tử thì
chứa đúng một phần tử thì 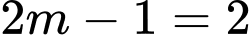 hay
hay 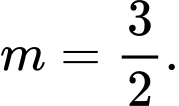
Câu 20 [582577]: Xác định số phần tử của tập hợp 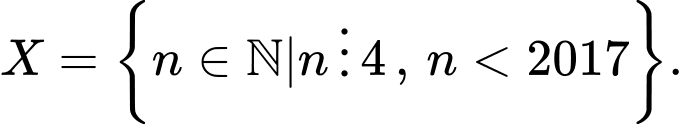
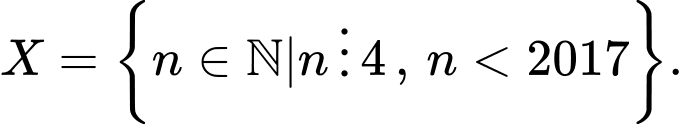
Trả lời: 505
Tập hợp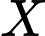 gồm các phần tử là những số tự nhiên nhỏ hơn
gồm các phần tử là những số tự nhiên nhỏ hơn  và chia hết cho
và chia hết cho 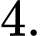
Từ đến
đến  có
có  số tự nhiên, ta thấy cứ
số tự nhiên, ta thấy cứ 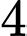 số tự nhiên liên tiếp sẽ có duy nhất một số chia hết cho
số tự nhiên liên tiếp sẽ có duy nhất một số chia hết cho 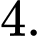 Suy ra có
Suy ra có 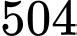 số tự nhiên chia hết cho
số tự nhiên chia hết cho 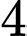 từ
từ  đến
đến 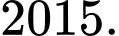 Hiển nhiên
Hiển nhiên 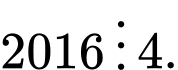
Vậy có tất cả số tự nhiên nhỏ hơn
số tự nhiên nhỏ hơn  và chia hết cho
và chia hết cho 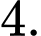
Tập hợp
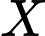 gồm các phần tử là những số tự nhiên nhỏ hơn
gồm các phần tử là những số tự nhiên nhỏ hơn  và chia hết cho
và chia hết cho 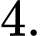
Từ
 đến
đến  có
có  số tự nhiên, ta thấy cứ
số tự nhiên, ta thấy cứ 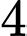 số tự nhiên liên tiếp sẽ có duy nhất một số chia hết cho
số tự nhiên liên tiếp sẽ có duy nhất một số chia hết cho 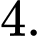 Suy ra có
Suy ra có 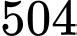 số tự nhiên chia hết cho
số tự nhiên chia hết cho 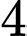 từ
từ  đến
đến 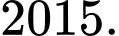 Hiển nhiên
Hiển nhiên 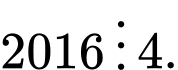
Vậy có tất cả
 số tự nhiên nhỏ hơn
số tự nhiên nhỏ hơn  và chia hết cho
và chia hết cho