Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
Câu 1 [582745]: Có bao nhiêu số tự nhiên nhỏ hơn 100 chia hết cho 2 và 3?
A, 12.
B, 16.
C, 17.
D, 20.
Số tự nhiên lớn nhất chia hết cho 2 và 3 là 96
Số tự nhiên nhỏ nhất chia hết cho 2 và 3 là 0
Ta thấy rằng từ 0 cần cộng thêm số bé nhất là bội của 6 và khác 0 để được 1 số tự nhiên tiếp theo chia hết cho 2 và 3, số bé nhất là bội của 6 khác 0 là 6
Suy ra số các số tự nhiên nhỏ hơn 100 chia hết cho 2 và 3 là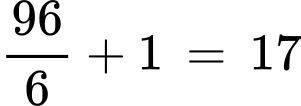 Đáp án: C
Đáp án: C
Số tự nhiên nhỏ nhất chia hết cho 2 và 3 là 0
Ta thấy rằng từ 0 cần cộng thêm số bé nhất là bội của 6 và khác 0 để được 1 số tự nhiên tiếp theo chia hết cho 2 và 3, số bé nhất là bội của 6 khác 0 là 6
Suy ra số các số tự nhiên nhỏ hơn 100 chia hết cho 2 và 3 là
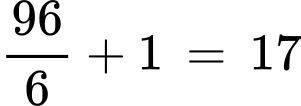 Đáp án: C
Đáp án: C
Câu 2 [582746]: Giả sử từ tỉnh 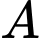 đến tỉnh
đến tỉnh 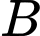 có thể đi bằng các phương tiện: ô tô, tàu hỏa, tàu thủy hoặc máy bay. Mỗi ngày có
có thể đi bằng các phương tiện: ô tô, tàu hỏa, tàu thủy hoặc máy bay. Mỗi ngày có  chuyến ô tô,
chuyến ô tô, 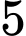 chuyến tàu hỏa,
chuyến tàu hỏa, 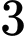 chuyến tàu thủy và
chuyến tàu thủy và 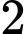 chuyến máy bay. Hỏi có bao nhiêu cách đi từ tỉnh
chuyến máy bay. Hỏi có bao nhiêu cách đi từ tỉnh 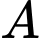 đến tỉnh
đến tỉnh 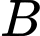 ?
?
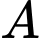 đến tỉnh
đến tỉnh 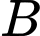 có thể đi bằng các phương tiện: ô tô, tàu hỏa, tàu thủy hoặc máy bay. Mỗi ngày có
có thể đi bằng các phương tiện: ô tô, tàu hỏa, tàu thủy hoặc máy bay. Mỗi ngày có  chuyến ô tô,
chuyến ô tô, 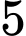 chuyến tàu hỏa,
chuyến tàu hỏa, 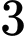 chuyến tàu thủy và
chuyến tàu thủy và 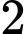 chuyến máy bay. Hỏi có bao nhiêu cách đi từ tỉnh
chuyến máy bay. Hỏi có bao nhiêu cách đi từ tỉnh 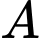 đến tỉnh
đến tỉnh 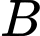 ?
? A, 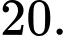
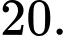
B, 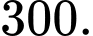
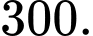
C, 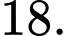
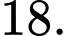
D, 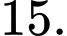
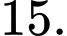
Áp dụng quy tắc cộng, số cách là 10+5+3+2=20 Đáp án: A
Câu 3 [582747]: Có bao nhiêu số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị?
A, 40.
B, 45.
C, 50.
D, 55.
Nếu chữ số hàng chục là thì n số có chữ số hàng đơn vị là thì n - 1 số các chữ số nhỏ hơn n nằm ở hàng đơn vị cũng bằng . Do chữ số hàng chục lớn hơn bằng 1 còn chữ số hàng đơn vị thì lớn hơn bằng 0
Vậy số các số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị là:
1+2+3+4+5+6+7+8+9=45
Cách 2: Từ 0 - 9 chọn 2 số khác nhau bất kì, do 2 số khác nhau nên luôn có cách sắp xếp sao cho chữ số hàng chục lớn hơn chữ số hàng đơn vị, vậy có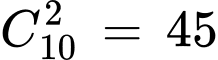 (số) Đáp án: B
(số) Đáp án: B
Vậy số các số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị là:
1+2+3+4+5+6+7+8+9=45
Cách 2: Từ 0 - 9 chọn 2 số khác nhau bất kì, do 2 số khác nhau nên luôn có cách sắp xếp sao cho chữ số hàng chục lớn hơn chữ số hàng đơn vị, vậy có
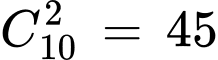 (số) Đáp án: B
(số) Đáp án: B
Câu 4 [582748]: Trong một giải thi đấu bóng đá có 20 đội tham gia với thể thức thi đấu vòng tròn. Cứ hai đội thì gặp nhau đúng một lần. Hỏi có tất cả bao nhiêu trận đấu xảy ra.
A, 190.
B, 182.
C, 280.
D, 194.
Ta thấy 1 đội sẽ phải thi đấu với 19 đội còn lại nên sẽ có 19.20 trận tuy nhiên như vậy một trận đấu đội A gặp B sẽ bị tính 2 lần do đó số trận thứ tế là 19.20:2=190 Đáp án: A
Câu 5 [582749]: Có 10 cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người phụ nữtrong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng:
A, 100.
B, 91.
C, 10.
D, 90.
Có cách 10 chọn 1 người đàn ông.
Có cách 10 chọn 1 người phụ nữ.
Tổng số cách chọn một người đàn ông và một người phụ nữ trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng: 10.10 -10 = 90 Đáp án: D
Có cách 10 chọn 1 người phụ nữ.
Tổng số cách chọn một người đàn ông và một người phụ nữ trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng: 10.10 -10 = 90 Đáp án: D
Câu 6 [582750]: Từ thành phố A đến thành phố B có 3 con đường, từ thành phố A đến thành phố C có 2 con
đường, từ thành phố B đến thành phố D có 2 con đường, từ thành phố C đến thành phố D có 3 con
đường, không có con đường nào nối từ thành phố C đến thành phố B. Hỏi có bao nhiêu con đường đi
từ thành phố A đến thành phố D.
A, 6.
B, 12.
C, 18.
D, 36.
Từ A đến B rồi đến D là 3.2=6
Từ A đến C rồi đến D là 3.2 =6
Nên có 6+6=12 cách Đáp án: B
Từ A đến C rồi đến D là 3.2 =6
Nên có 6+6=12 cách Đáp án: B
Câu 7 [582751]: Có bao nhiêu số tự nhiên có 3 chữ số được lập từ sáu chữ số 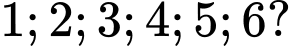
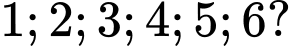
A, 120.
B, 216.
C, 256.
D, 20.
Mỗi chữ số trong số được lập có 6 cách chọn nên số các số tự nhiên là: 6.6.6=216 Đáp án: B
Câu 8 [582752]: Số các số tự nhiên chẵn, gồm bốn chữ số khác nhau đôi một và không tận cùng bằng 0 là:
A, 504.
B, 1792.
C, 953088.
D, 2296.
Chữ số cuối gồm các số 2, 4, 6, 8 nên có 4 cách chọn
Chữ số đầu từ 1 đến 9 và khác số cuối nên có 8 cách chọn
Chữ số thứ hai từ 0-9 khác số đầu và cuối nên có 8 cách chọn
Chữ số thứ ba từ 0-9 khác các chữ số còn lại nên có 7 cách chọn
Vậy số số là 4.8.8.7=1792 Đáp án: B
Chữ số đầu từ 1 đến 9 và khác số cuối nên có 8 cách chọn
Chữ số thứ hai từ 0-9 khác số đầu và cuối nên có 8 cách chọn
Chữ số thứ ba từ 0-9 khác các chữ số còn lại nên có 7 cách chọn
Vậy số số là 4.8.8.7=1792 Đáp án: B
Câu 9 [582753]: Trong một tuần bạn A dự định mỗi ngày đi thăm một người bạn trong 12 người bạn của mình. Hỏi bạn A có thể lập được bao nhiêu kế hoạch đi thăm bạn của mình?
A, 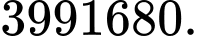
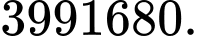
B, 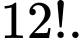
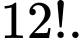
C, 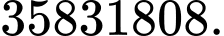
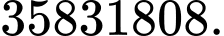
D, 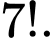
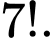
Thứ hai có 12 cách chọn
Các ngày sau mỗi ngày giảm dần 1 cách
Chủ nhật có 6 cách
Vậy có 12.11.10.9.8.7.6 = 3991680 kế hoạch Đáp án: A
Các ngày sau mỗi ngày giảm dần 1 cách
Chủ nhật có 6 cách
Vậy có 12.11.10.9.8.7.6 = 3991680 kế hoạch Đáp án: A
Câu 10 [582754]: Số 253125000 có bao nhiêu ước số tự nhiên?
A, 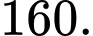
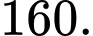
B, 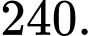
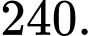
C, 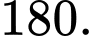
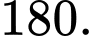
D, 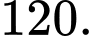
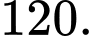
Ta có 253125000 =  nên mỗi ước số tự nhiên của số đó cho đều có dạng
nên mỗi ước số tự nhiên của số đó cho đều có dạng 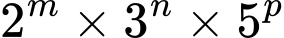 trong đó
trong đó 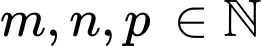 sao cho
sao cho 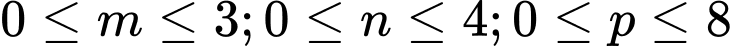
Có 4 cách chọn m
Có 5 cách chọn n
Có 9 cách chọn p
Vậy theo qui tắc nhân ta có 4.5.9=180 ước số tự nhiên. Đáp án: C
 nên mỗi ước số tự nhiên của số đó cho đều có dạng
nên mỗi ước số tự nhiên của số đó cho đều có dạng 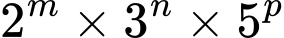 trong đó
trong đó 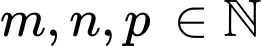 sao cho
sao cho 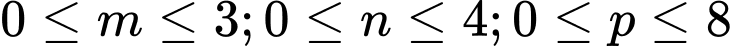
Có 4 cách chọn m
Có 5 cách chọn n
Có 9 cách chọn p
Vậy theo qui tắc nhân ta có 4.5.9=180 ước số tự nhiên. Đáp án: C
Câu 11 [582755]: Từ các chữ số 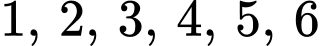 có thể lập được bao nhiêu số tự nhiên bé hơn
có thể lập được bao nhiêu số tự nhiên bé hơn 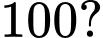
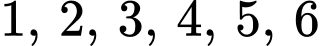 có thể lập được bao nhiêu số tự nhiên bé hơn
có thể lập được bao nhiêu số tự nhiên bé hơn 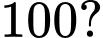
A, 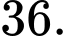
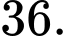
B, 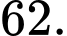
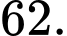
C, 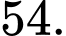
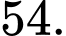
D, 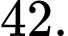
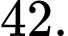
Số bé hơn 100 là số tự nhiên có 2 chữ số và 1 chữ số.
Với số có 2 chữ số, mỗi chữ số có 6 cách chọn, vậy có 6.6 = 36 (số).
Với số có 1 chữ số, có 6 số.
Tổng có 36 + 6 = 42 (số). Đáp án: D
Với số có 2 chữ số, mỗi chữ số có 6 cách chọn, vậy có 6.6 = 36 (số).
Với số có 1 chữ số, có 6 số.
Tổng có 36 + 6 = 42 (số). Đáp án: D
Câu 12 [582756]: Có bao nhiêu cách xếp 4 người A, B, C, D lên 3 toa tàu, biết mỗi toa có thể chứa 4 người?
A, 81.
B, 68.
C, 42.
D, 15.
Để xếp A ta có 3 cách lên một trong ba toa
Với mỗi cách xếp A ta có 3 cách xếp B lên toa tàu
Với mỗi cách xếp A, B ta có 3 cách xếp C lên toa tàu
Với mỗi cách xếp A, B, C ta có 3 cách xếp D lên toa tàu
Vậy có cách 3.3.3.3 = 81 xếp 4 người lên toa tàu.
Cách khác: 4 người A, B, C, D mỗi người có 3 cách chọn toa tàu. Vậy theo quy tắc nhân có 3.3.3.3 = 81 Đáp án: A
Với mỗi cách xếp A ta có 3 cách xếp B lên toa tàu
Với mỗi cách xếp A, B ta có 3 cách xếp C lên toa tàu
Với mỗi cách xếp A, B, C ta có 3 cách xếp D lên toa tàu
Vậy có cách 3.3.3.3 = 81 xếp 4 người lên toa tàu.
Cách khác: 4 người A, B, C, D mỗi người có 3 cách chọn toa tàu. Vậy theo quy tắc nhân có 3.3.3.3 = 81 Đáp án: A
Câu 13 [582757]: Tô màu các cạnh của hình vuông 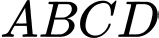 bởi
bởi 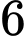 màu khác nhau sao cho mỗi cạnh được tô bởi một màu và hai cạnh kề nhau thì tô bởi hai màu khác nhau. Hỏi có bao nhiêu cách tô?
màu khác nhau sao cho mỗi cạnh được tô bởi một màu và hai cạnh kề nhau thì tô bởi hai màu khác nhau. Hỏi có bao nhiêu cách tô?
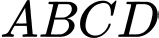 bởi
bởi 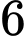 màu khác nhau sao cho mỗi cạnh được tô bởi một màu và hai cạnh kề nhau thì tô bởi hai màu khác nhau. Hỏi có bao nhiêu cách tô?
màu khác nhau sao cho mỗi cạnh được tô bởi một màu và hai cạnh kề nhau thì tô bởi hai màu khác nhau. Hỏi có bao nhiêu cách tô? A, 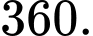
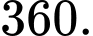
B, 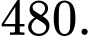
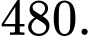
C, 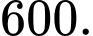
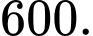
D, 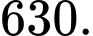
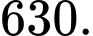
Th1: 1 cặp cạnh đối bất kì cùng màu giả sử là AB và CD
AB có 6 cách tô. BC có 5 cách, CD có 1 cách, AD có 4 cách
Tương tự cho AD và BC cùng màu.
Vậy có 5.4.6.2 = 240 cách
Th2: 2 cặp cạnh đối cùng màu
AB có 6 cách, CD có 1 cách, AD có 5 cách, BD có 1 cách
Vậy có 6.5 =30 cách
TH3: các cạnh đối khác màu
AB có 6 cách, BC có 5 cách, CD có 4 cách, AD có 3 cách
Vậy có 6.5.4.3= 360 cách
Tổng số cách là 360+240+30=630 Đáp án: D
AB có 6 cách tô. BC có 5 cách, CD có 1 cách, AD có 4 cách
Tương tự cho AD và BC cùng màu.
Vậy có 5.4.6.2 = 240 cách
Th2: 2 cặp cạnh đối cùng màu
AB có 6 cách, CD có 1 cách, AD có 5 cách, BD có 1 cách
Vậy có 6.5 =30 cách
TH3: các cạnh đối khác màu
AB có 6 cách, BC có 5 cách, CD có 4 cách, AD có 3 cách
Vậy có 6.5.4.3= 360 cách
Tổng số cách là 360+240+30=630 Đáp án: D
Câu 14 [582758]: Cho tập 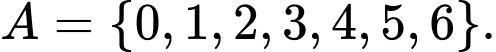 Từ tập A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau và chia hết cho 5.
Từ tập A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau và chia hết cho 5.
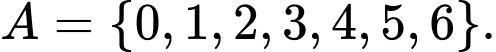 Từ tập A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau và chia hết cho 5.
Từ tập A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau và chia hết cho 5. A, 660.
B, 432.
C, 679.
D, 523.
Số cuối là số 0 các số sau có 6.5.4.3 cách chọn vậy có 360 số
Số cuối là số 5 các số sau có 5.5.4.3 cách chọn vậy có 300 số
Tổng là 660 số Đáp án: A
Số cuối là số 5 các số sau có 5.5.4.3 cách chọn vậy có 300 số
Tổng là 660 số Đáp án: A
Câu 15 [582759]: Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ?
A, 6.
B, 72.
C, 720.
D, 144.
Chọn vị trí 3 nam và 3 nữ: cách 2.1 chọn.
Xếp 3 nam có: cách 3.2.1 xếp.
Xếp 3 nữ có: cách 3.2.1 xếp.
Vậy có cách 6.6.2= 72 cách xếp Đáp án: B
Xếp 3 nam có: cách 3.2.1 xếp.
Xếp 3 nữ có: cách 3.2.1 xếp.
Vậy có cách 6.6.2= 72 cách xếp Đáp án: B
Dạng câu hỏi: Câu trắc nghiệm đúng sai.
(Thí sinh trả lời từ câu 16,17. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng
hoặc sai)
Câu 16 [582760]: Xếp 6 người A, B, C, D, E, F vào một ghế dài. Ta sẽ có số cách sắp xếp
a) A và F ngồi ở hai đầu ghế là 48 cách
b) A và F ngồi cạnh nhau là 120 cách
c) A và F không ngồi cạnh nhau là 240 cách
Trong các nhận định trên. Hãy xác định tính đúng sai?
a) A và F ngồi ở hai đầu ghế là 48 cách
b) A và F ngồi cạnh nhau là 120 cách
c) A và F không ngồi cạnh nhau là 240 cách
Trong các nhận định trên. Hãy xác định tính đúng sai?
a) Đúng
b) Sai
c) Sai
a) Xếp A có 2 cách, F có 1 cách, các vị trí còn lại có 4.3.2.1 cách vậy có 24.2=48 cách
b) Gộp A và F thành 1 ghế đôi và chỗ ngồi thành 5 chỗ
Xếp A và F có 2 cách, xếp ghế của A và F có 5 cách, các vị trí còn lại có 4.3.2.1 cách vậy có 240 cách
c) Số cách xếp 6 người là 6.5.4.3.2.1=720
Số cách xếp A và F không cạnh nhau là 720-240=480 Đáp án: B
b) Sai
c) Sai
a) Xếp A có 2 cách, F có 1 cách, các vị trí còn lại có 4.3.2.1 cách vậy có 24.2=48 cách
b) Gộp A và F thành 1 ghế đôi và chỗ ngồi thành 5 chỗ
Xếp A và F có 2 cách, xếp ghế của A và F có 5 cách, các vị trí còn lại có 4.3.2.1 cách vậy có 240 cách
c) Số cách xếp 6 người là 6.5.4.3.2.1=720
Số cách xếp A và F không cạnh nhau là 720-240=480 Đáp án: B
Câu 17 [582761]: Một bàn dài có 2 dãy ghế đối diện nhau, mỗi dãy gồm có 6 ghế. Người ta muốn xếp chỗ ngồi cho 6 học sinh trường A và 6 học sinh trường B vào bàn nói trên.
a) hai học sinh ngồi cạnh hoặc dối diện nhau thì khác trường có 146800 cách
b) hai học sinh ngối đối diện nhau thì khác trường nhau có 33177600 cách
a) hai học sinh ngồi cạnh hoặc dối diện nhau thì khác trường có 146800 cách
b) hai học sinh ngối đối diện nhau thì khác trường nhau có 33177600 cách
a)

Vậy có 1036800 cách
b)

Vậy có: cách 33177600 xếp.

Vậy có 1036800 cách
b)

Vậy có: cách 33177600 xếp.
Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 18 [582762]: Cho hai đường thẳng song song 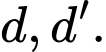 Trên
Trên 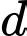 lấy
lấy  điểm phân biệt, trên
điểm phân biệt, trên 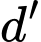 lấy
lấy  điểm phân biệt.
điểm phân biệt.
Hỏi có bao nhiêu tam giác mà đỉnh của nó được chọn từ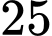 đỉnh nói trên?
đỉnh nói trên?
Đáp án:……
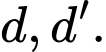 Trên
Trên 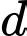 lấy
lấy  điểm phân biệt, trên
điểm phân biệt, trên 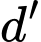 lấy
lấy  điểm phân biệt.
điểm phân biệt. Hỏi có bao nhiêu tam giác mà đỉnh của nó được chọn từ
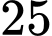 đỉnh nói trên?
đỉnh nói trên?Đáp án:……
TH1: có 2 đỉnh trên d và 1 đỉnh trên d’
2 đỉnh trên d có 10.9 cách chọn, đỉnh trên d’ có 15 cách
Vậy có 10.9.15= 1350 cách
TH2: có 2 đỉnh trên d’ và 1 đỉnh trên d
2 đỉnh trên d’ có 15.14 cách chọn, 1 đỉnh trên d có 10 cách
Vậy có 15.14.10=2100 cách
Tuy nhiên mỗi TH các tam giác sẽ bị lặp lại 1 lần nên ta phải chia hai
Vậy có 1725 tam giác.
2 đỉnh trên d có 10.9 cách chọn, đỉnh trên d’ có 15 cách
Vậy có 10.9.15= 1350 cách
TH2: có 2 đỉnh trên d’ và 1 đỉnh trên d
2 đỉnh trên d’ có 15.14 cách chọn, 1 đỉnh trên d có 10 cách
Vậy có 15.14.10=2100 cách
Tuy nhiên mỗi TH các tam giác sẽ bị lặp lại 1 lần nên ta phải chia hai
Vậy có 1725 tam giác.
Câu 19 [582763]: Cho tập 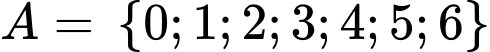 từ tập A có thể lập được bao nhiêu số tự nhiên có 5 chữ số và chia hết cho 2?
từ tập A có thể lập được bao nhiêu số tự nhiên có 5 chữ số và chia hết cho 2?
Đáp án:……
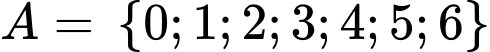 từ tập A có thể lập được bao nhiêu số tự nhiên có 5 chữ số và chia hết cho 2?
từ tập A có thể lập được bao nhiêu số tự nhiên có 5 chữ số và chia hết cho 2?Đáp án:……
Gọi số tự nhiên có 5 chữ số cần tìm là abcde
Do số cần tìm chia hết cho 2 nên e có 4 cách chọn {0; 2; 4; 6}
a có 6 cách chọn {1; 2; 3; 4; 5; 6}
b có 7 cách chọn {0; 1; 2; 3; 4; 5; 6}
c có 7 cách chọn {0; 1; 2; 3; 4; 5; 6}
d có 7 cách chọn {0; 1; 2; 3; 4; 5; 6}
Do đó ta có: 4.6.7.7.7 = 8232 cách chọn số có 5 chữ số chia hết cho 2
Do số cần tìm chia hết cho 2 nên e có 4 cách chọn {0; 2; 4; 6}
a có 6 cách chọn {1; 2; 3; 4; 5; 6}
b có 7 cách chọn {0; 1; 2; 3; 4; 5; 6}
c có 7 cách chọn {0; 1; 2; 3; 4; 5; 6}
d có 7 cách chọn {0; 1; 2; 3; 4; 5; 6}
Do đó ta có: 4.6.7.7.7 = 8232 cách chọn số có 5 chữ số chia hết cho 2
Câu 20 [582764]: Cho các chữ số 1, 2, 3,..., 9. Từ các số đó có thể lập được bao nhiêu số chẵn gồm 4 chữ số khác nhau và không vượt quá 2011.
Đáp án:……
Đáp án:……
Chữ số đầu tiên có 1 cách chọn là 1
Chữ số cuối có 4 cách là 2, 4, 6, 8
Chữ số thứ hai có 7 cách
Chữ số thứ ba có 6 cách
Vậy có 4.7.6=168 số.
Chữ số cuối có 4 cách là 2, 4, 6, 8
Chữ số thứ hai có 7 cách
Chữ số thứ ba có 6 cách
Vậy có 4.7.6=168 số.
Câu 21 [582765]: (Kéo thả hoặc click vào để điền)

Cho các số tự nhiên: 0, 1, 2, 3, 4.
a) Lập được số các số tự nhiên gồm cả năm chữ số trên là __________.
b) Lập được số các số tự nhiên gồm cả năm chữ số trên và chữ số 3 đứng ở chính giữa là __________.

Cho các số tự nhiên: 0, 1, 2, 3, 4.
a) Lập được số các số tự nhiên gồm cả năm chữ số trên là __________.
b) Lập được số các số tự nhiên gồm cả năm chữ số trên và chữ số 3 đứng ở chính giữa là __________.
Đáp án đúng:
Cho các số tự nhiên: 0, 1, 2, 3, 4.
a) Lập được số các số tự nhiên gồm cả năm chữ số trên là 96.
b) Lập được số các số tự nhiên gồm cả năm chữ số trên và chữ số 3 đứng ở chính giữa là 18.
Hướng dẫn giải:
Cách 1
a. Số tự nhiên cần lập có dạng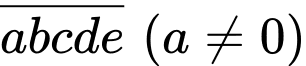
Trong đó chữ số a có 4 cách chọn.
Chữ số b có 4 cách chọn.
Chữ số c có 3 cách chọn.
Chữ số d có 2 cách chọn.
Chữ số e có 1 cách chọn.
Nên có tất cả 4.4.3.2.1 = 96 số thỏa mãn yêu cầu đề bài.
b. Số tự nhiên cần lập có dạng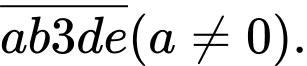
Chữ số a có 3 cách chọn.
Chữ số b có 3 cách chọn.
Chữ số d có 2 cách chọn.
Chữ sô e có 1 cách chọn.
Vậy thành lập được tất cả 3.3.2=18 số có 5 chữ số khác nhau mà số 3 đứng chính giữa từ các số trên.
Cách 2.
a. Mỗi số có 5 chữ số khác nhau được thành lập từ các số trên là một hoán vị của {0;1;2;3;4}.
Các số có dạng mà a;b;c;d khác nhau là một hoán vị của các số {1;2;3;4}.
mà a;b;c;d khác nhau là một hoán vị của các số {1;2;3;4}.
Nên 5 có tất cả 5! − 4! = 96 số có 5 chữ số khác nhau được thành lập từ các số trên.
b. Tương tự phần a; các số có dạng bằng với số hoán vị của 4 số {0;1;2;4}.
bằng với số hoán vị của 4 số {0;1;2;4}.
Các số có dạng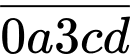 bằng số hoán vị của 3 số {1;2;4}.
bằng số hoán vị của 3 số {1;2;4}.
Nên có tất cả 4! - 3!=18 số có 5 chữ số khác nhau có số 3 đứng giữa được thành lập từ các số trên.
Cho các số tự nhiên: 0, 1, 2, 3, 4.
a) Lập được số các số tự nhiên gồm cả năm chữ số trên là 96.
b) Lập được số các số tự nhiên gồm cả năm chữ số trên và chữ số 3 đứng ở chính giữa là 18.
Hướng dẫn giải:
Cách 1
a. Số tự nhiên cần lập có dạng
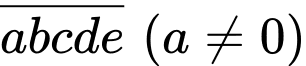
Trong đó chữ số a có 4 cách chọn.
Chữ số b có 4 cách chọn.
Chữ số c có 3 cách chọn.
Chữ số d có 2 cách chọn.
Chữ số e có 1 cách chọn.
Nên có tất cả 4.4.3.2.1 = 96 số thỏa mãn yêu cầu đề bài.
b. Số tự nhiên cần lập có dạng
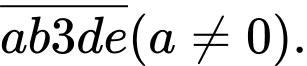
Chữ số a có 3 cách chọn.
Chữ số b có 3 cách chọn.
Chữ số d có 2 cách chọn.
Chữ sô e có 1 cách chọn.
Vậy thành lập được tất cả 3.3.2=18 số có 5 chữ số khác nhau mà số 3 đứng chính giữa từ các số trên.
Cách 2.
a. Mỗi số có 5 chữ số khác nhau được thành lập từ các số trên là một hoán vị của {0;1;2;3;4}.
Các số có dạng
 mà a;b;c;d khác nhau là một hoán vị của các số {1;2;3;4}.
mà a;b;c;d khác nhau là một hoán vị của các số {1;2;3;4}.Nên 5 có tất cả 5! − 4! = 96 số có 5 chữ số khác nhau được thành lập từ các số trên.
b. Tương tự phần a; các số có dạng
 bằng với số hoán vị của 4 số {0;1;2;4}.
bằng với số hoán vị của 4 số {0;1;2;4}.Các số có dạng
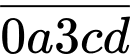 bằng số hoán vị của 3 số {1;2;4}.
bằng số hoán vị của 3 số {1;2;4}.Nên có tất cả 4! - 3!=18 số có 5 chữ số khác nhau có số 3 đứng giữa được thành lập từ các số trên.