Dạng 1 : Các bài toán chọn vật, chọn người
Câu 1 [582818]: Có 6 quả cầu xanh đánh số từ 1 đến 6, 5 quả cầu đỏ đánh số từ 1 đến 5, 4 quả cầu vàng đánh số từ 1 đến 4. Hỏi có bao nhiêu cách lấy ra 3 quả cầu vừa khác màu, vừa khác số?
Đáp án:……
Đáp án:……
+ Để lấy ra 3 quả cầu vừa khác màu vừa khác số, vậy ta phải chọn lấy lần lượt từ quả cầu có số lượngít nhất để tránh trùng lặp.
+ Chọn 1 quả cầu vàng có 4 cách
+ Chọn 1 quả cầu đỏ có 5 - 1 = 4 cách (do không chọn lại quả có cùng số với quả vàng)
+ Chọn 1 quả cầu xanh có 6 - 2 = 4 cách (do loại đi 1 quả cầu xanh trùng với số quả cầu vàng và 1 quả cầu xanh trùng với số quả cầu đỏ đã chọn trước đó)
Vậy có 4.4.4 = 64 cách chọn.
+ Chọn 1 quả cầu vàng có 4 cách
+ Chọn 1 quả cầu đỏ có 5 - 1 = 4 cách (do không chọn lại quả có cùng số với quả vàng)
+ Chọn 1 quả cầu xanh có 6 - 2 = 4 cách (do loại đi 1 quả cầu xanh trùng với số quả cầu vàng và 1 quả cầu xanh trùng với số quả cầu đỏ đã chọn trước đó)
Vậy có 4.4.4 = 64 cách chọn.
Câu 2 [582819]: Từ 20 câu hỏi trắc nghiệm gồm 9 câu dễ, 7 câu TB, 4 câu khó. Người ta chọn ra 10 câu để làm đề kiểm tra sao cho phải có đủ 3 loại dễ, TB, khó. Hỏi có thể lập được bao nhiêu đề kiểm tra?
A, 15600.
B, 14400.
C, 17651.
D, 18481.
Sử dụng phương pháp phần bù *
Bước 1: Chọn 10 câu tùy ý trong 20 câu có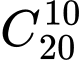 cách
cách
Bước 2: Chọn 10 câu không thỏa mãn yêu cầu, ta có các TH sau:
+ TH1: Chọn 10 câu dễ và TB trong 16 câu có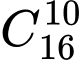 cách
cách
+ TH2: Chọn 10 câu dễ và khó trong 13 câu có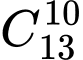 cách
cách
+ TH3: Chọn 10 câu TB và khó trong 11 câu có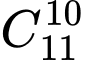 cách
cách
Kết luận: vậy có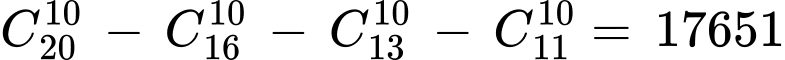 cách Đáp án: C
cách Đáp án: C
Bước 1: Chọn 10 câu tùy ý trong 20 câu có
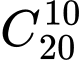 cách
cách Bước 2: Chọn 10 câu không thỏa mãn yêu cầu, ta có các TH sau:
+ TH1: Chọn 10 câu dễ và TB trong 16 câu có
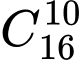 cách
cách + TH2: Chọn 10 câu dễ và khó trong 13 câu có
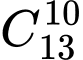 cách
cách + TH3: Chọn 10 câu TB và khó trong 11 câu có
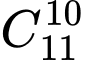 cách
cách Kết luận: vậy có
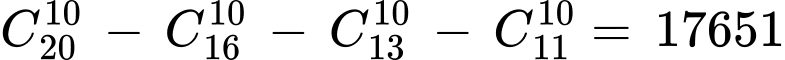 cách Đáp án: C
cách Đáp án: C Dạng toán: Các bài toán lập số - chọn số
Câu 3 [582820]: Có thể lập thành bao nhiêu số có 8 chữ số, trong đó chữ số 1 và chữ số 6 đều có mặt 2 lần, các chữ số 2, 3, 4, 5 đều có mặt đúng 1 lần?
A, 10080.
B, 9600.
C, 7460.
D, 15776.
Chọn vị trí để xếp chữ số 1 có mặt 2 lần có 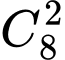 cách
cách
Chọn vị trí để xếp chữ số 6 có mặt 2 lần có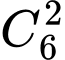 cách
cách
4 vị trí còn lại có 4! cách
Vậy có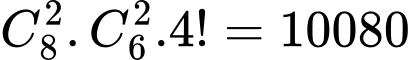 cách Đáp án: A
cách Đáp án: A
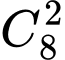 cách
cáchChọn vị trí để xếp chữ số 6 có mặt 2 lần có
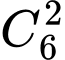 cách
cách4 vị trí còn lại có 4! cách
Vậy có
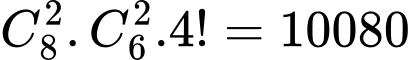 cách Đáp án: A
cách Đáp án: A
Câu 4 [582821]: Biển số xe là 1 dãy gồm 2 chữ cái đứng trước và 4 chữ số đứng sau: Các chữ cái được lấy từ 26 chữ cái A, B, C, …, Z. Các chữ số được chọn từ 10 chữ số 0, 1, 2, …, 9. Có bao nhiêu biển số xe có 2 chữ cái khác nhau, đồng thời có đúng 2 chữ số lẻ và 2 chữ số lẻ đó giống nhau?
Đáp án:……
Đáp án:……
+ Chọn 2 chữ cái khác nhau có 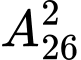 cách
cách
+ Chọn 2 số lẻ giống nhau co 5 cách (do chọn từ 1, 3, 5, 7, 9)
+ Chọn 2 trong 4 vị trí để đặt 2 chữ số lẻ giống nhau có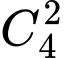 cách
cách
+ Sắp xếp 2 số chẵn từ 5 số (0, 2, 4, 6, 8) vào 2 vị trí còn lại có 5.5 cách
Vậy có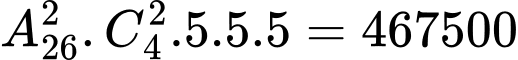 cách
cách
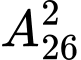 cách
cách + Chọn 2 số lẻ giống nhau co 5 cách (do chọn từ 1, 3, 5, 7, 9)
+ Chọn 2 trong 4 vị trí để đặt 2 chữ số lẻ giống nhau có
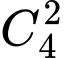 cách
cách + Sắp xếp 2 số chẵn từ 5 số (0, 2, 4, 6, 8) vào 2 vị trí còn lại có 5.5 cách
Vậy có
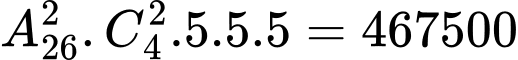 cách
cách Dạng toán: Các bài toán đếm trong hình học
Câu 5 [582822]: Tính số hình chữ nhật tạo thành từ 4 trong 20 đỉnh của đa giác đều có 20 cạnh nội tiếp đường tròn tâm O.
A, 20.
B, 25.
C, 40.
D, 45.
-Ta thấy hình chữ nhật nội tiếp đường tròn tâm O được tạo thành từ 2 đường chéo bất kỳ đi qua tâm O của đa giác đều 20 cạnh nói trên.
- Mà đa giác đều 20 cạnh nội tiếp đường tròn tâm O có 10 đường chéo đi qua tâm.
Vậy số hình chữ nhật cần tìm là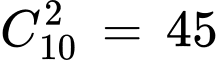 Đáp án: D
Đáp án: D
- Mà đa giác đều 20 cạnh nội tiếp đường tròn tâm O có 10 đường chéo đi qua tâm.
Vậy số hình chữ nhật cần tìm là
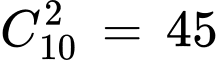 Đáp án: D
Đáp án: D
Câu 6 [582823]: Một đa giác đều có số đường chéo gấp đôi số cạnh. Hỏi đa giác đó có bao nhiêu cạnh?
Đa giác có 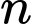 cạnh
cạnh 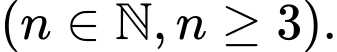
Khi đó số đường chéo trong đa giác là: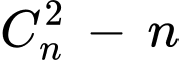
Ta có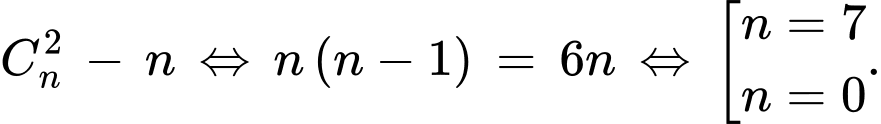
Vậy số cạnh của đa giác đó là 7.
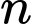 cạnh
cạnh 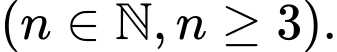
Khi đó số đường chéo trong đa giác là:
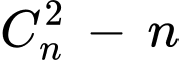
Ta có
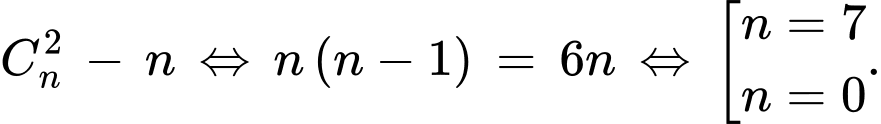
Vậy số cạnh của đa giác đó là 7.
Dạng toán: Các bài toán giải phương trình, bất phương trình
Câu 7 [582824]: Cho 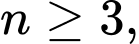
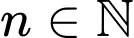 thỏa mãn :
thỏa mãn : 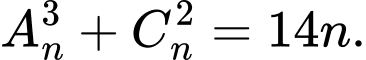 Xác định giá trị của
Xác định giá trị của 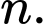
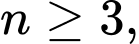
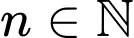 thỏa mãn :
thỏa mãn : 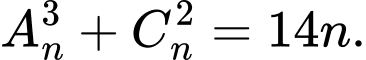 Xác định giá trị của
Xác định giá trị của 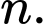
Sử dụng công thức: 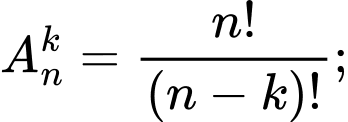
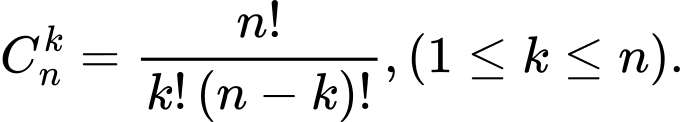
Ta có: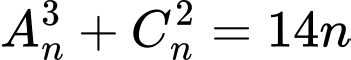
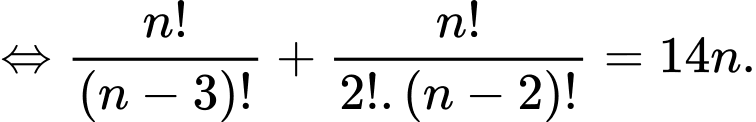
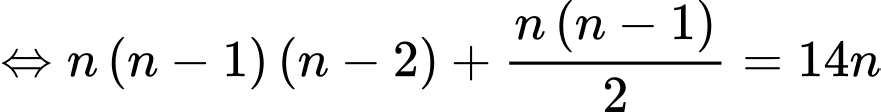
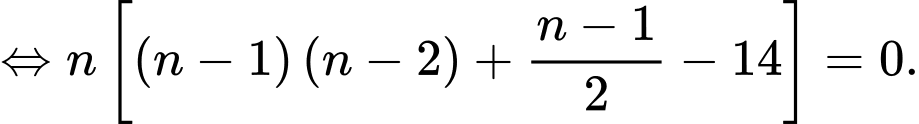

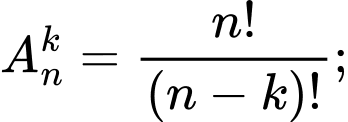
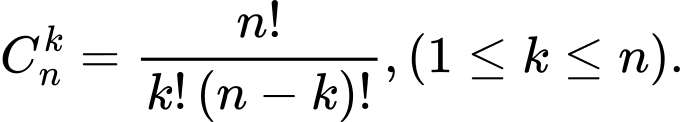
Ta có:
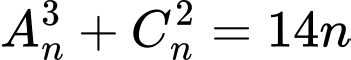
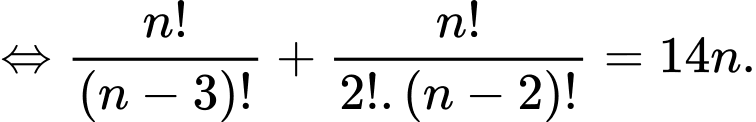
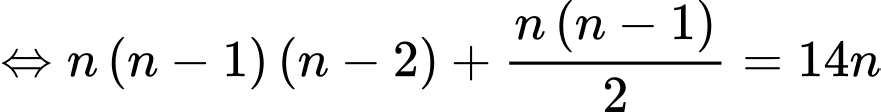
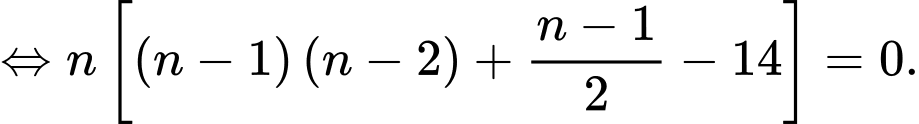

Câu 8 [582825]: Tính 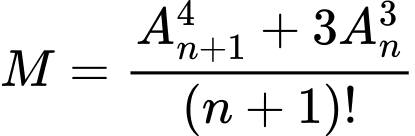 biết
biết 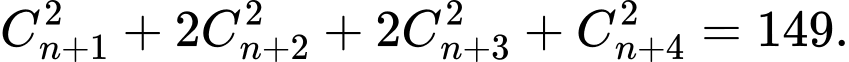
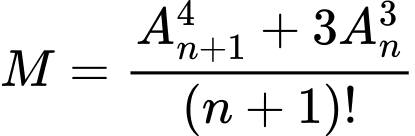 biết
biết 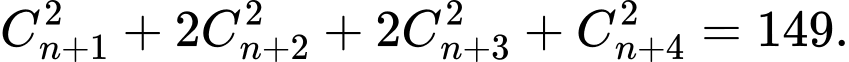
Ta có:
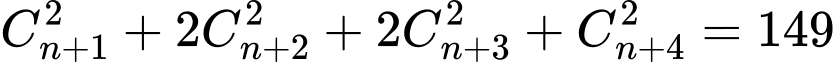
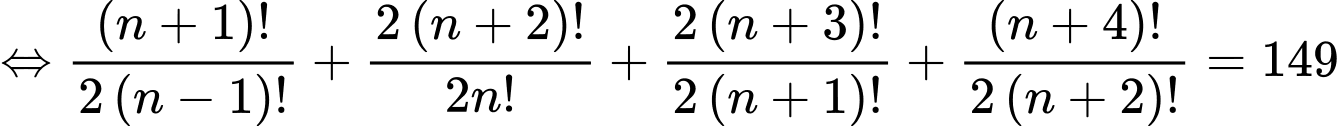
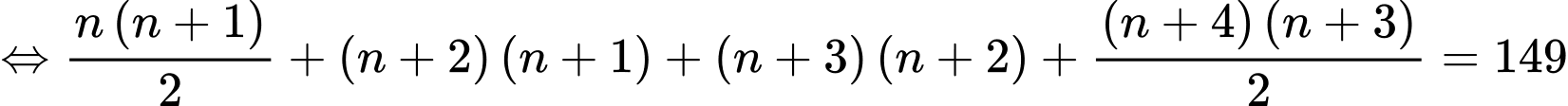
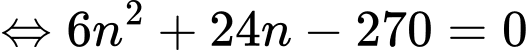

Thay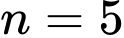 vào biểu thức
vào biểu thức 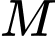 ta có:
ta có:
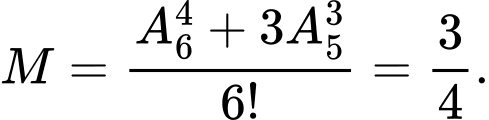
Vậy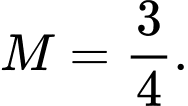
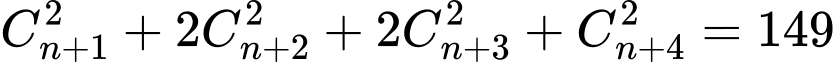
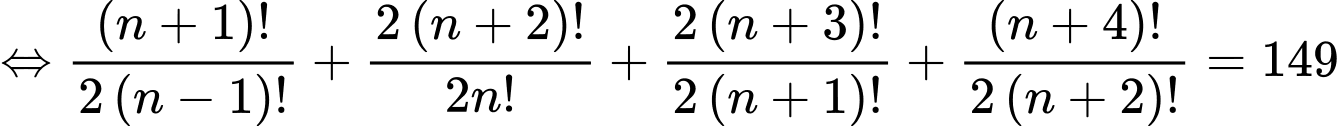
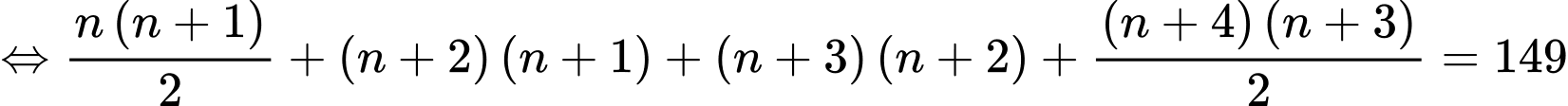
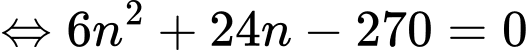

Thay
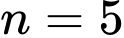 vào biểu thức
vào biểu thức 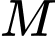 ta có:
ta có: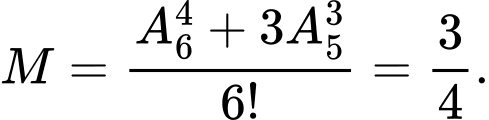
Vậy