Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
Câu 1 [582826]: Đội tuyển học sinh giỏi của một trường THPT có 8 học sinh nam và 4 học sinh nữ. Trong buổi lễ trao phần thưởng, các học sinh trên được xếp thành một hàng ngang. Hỏi có bao nhiêu cách xếp sao cho 2 học sinh nữ không đứng cạnh nhau?
A, 121927680.
B, 17569870.
C, 13607841.
D, 1008754.
Xếp 8 bạn nam vào 8 chỗ có 8! cách.
Khi đó 8 bạn nam tạo ra 9 khe trống, xếp 4 bạn nữ vào 9 khe trống đó có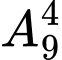 cách.
cách.
Vậy có 8!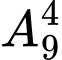 =121927680 cách Đáp án: A
=121927680 cách Đáp án: A
Khi đó 8 bạn nam tạo ra 9 khe trống, xếp 4 bạn nữ vào 9 khe trống đó có
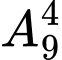 cách.
cách.Vậy có 8!
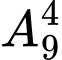 =121927680 cách Đáp án: A
=121927680 cách Đáp án: A
Câu 2 [582827]: Tổ 4 của lớp 12A3 có 4 học sinh nữ và 5 học sinh nam. Hỏi có bao nhiêu cách xếp các học sinh này vào một bàn tròn sao cho nhóm học sinh nữ ngồi với nhau; nhóm học sinh nam ngồi với nhau?
A, 1280.
B, 1360.
C, 2880.
D, 1860.
Ta coi 4 học sinh nữ là một nhóm X và 5 học sinh nam là nhóm Y.
+ Số cách xếp hai nhóm X và Y vào bàn tròn là (2-1)!= 1 cách.
+ Số cách xếp 4 học sinh nữ trong nhóm X là 4!.
+ Số cách xếp 5 học sinh nam trong nhóm Y là 5!.
⇒ Có: 1. 4!. 5!= 2880 cách xếp thỏa mãn đầu bài. Đáp án: C
+ Số cách xếp hai nhóm X và Y vào bàn tròn là (2-1)!= 1 cách.
+ Số cách xếp 4 học sinh nữ trong nhóm X là 4!.
+ Số cách xếp 5 học sinh nam trong nhóm Y là 5!.
⇒ Có: 1. 4!. 5!= 2880 cách xếp thỏa mãn đầu bài. Đáp án: C
Câu 3 [582828]: Đội thanh niên xung kích của trường THPT A gồm 9 Đoàn viên nam và 6 Đoàn viên nữ, trong đó có 2 Đoàn viên nam là ủy viên ban chấp hành. Đoàn trường cần chọn một nhóm 3 Đoàn viên đi kiểm tra việc thực hiện nội quy nhà trường trong sáng thứ hai. Hỏi có bao nhiêu cách chọn sao cho có cả nam, nữ, ủy viên ban chấp hành.
A, 120.
B, 240.
C, 114.
D, 86.
Có 3 trường hợp:
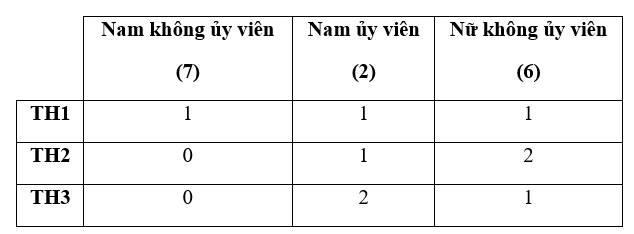
Vậy có tất cả cách chọn. Đáp án: A
cách chọn. Đáp án: A

Vậy có tất cả
 cách chọn. Đáp án: A
cách chọn. Đáp án: A
Câu 4 [582829]: Có 5 bưu thiếp khác nhau, 6 bì thư khác nhau. Chọn ra 3 bưu thiếp bỏ vào 3 bì thư, mỗi bì thư 1 bưu thiếp và gửi cho 3 người bạn, mỗi người bạn 1 bưu thiếp. Hỏi có mấy cách?
A, 4200.
B, 7200.
C, 3600.
D, 8400.
Chọn 3 bưu thiếp có: 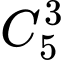 cách.
cách.
Chọn 3 bưu thiếp có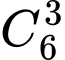 cách
cách
Có 3! Cách để nhét 3 bưu thiếp vào mỗi phong bì tương ứng.
Có 3! Cách để chia cho các bạn
Vậy có: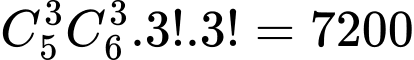 Đáp án: B
Đáp án: B
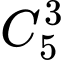 cách.
cách.Chọn 3 bưu thiếp có
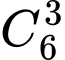 cách
cáchCó 3! Cách để nhét 3 bưu thiếp vào mỗi phong bì tương ứng.
Có 3! Cách để chia cho các bạn
Vậy có:
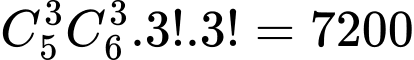 Đáp án: B
Đáp án: B
Câu 5 [582830]: Có bao nhiêu cách sắp xếp 15 viên bi vào 3 hộp đựng bi?
A, 15!.
B, 15.3.
C, 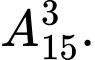
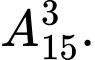
D, 315.
1 viên bi có 3 cách nên 15 viên bi có 315 Đáp án: D
Câu 6 [582831]: Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số khác nhau và tổng của các chữ số hàng chục, hàng trăm, hàng nghìn bằng 8?
A, 720.
B, 1440.
C, 2880.
D, 2440.
Gọi 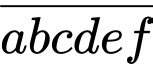 là số thỏa mãn yêu cầu thì
là số thỏa mãn yêu cầu thì 
Có 2 bộ ba số có tổng bằng 8 là {1,2,5} và {1,3,4}
Nếu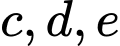 thuộc {1,2,5} thì có 3! cách chọn và
thuộc {1,2,5} thì có 3! cách chọn và 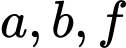 có
có 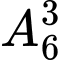 cách chọn suy ra có
cách chọn suy ra có 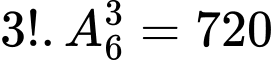
Bộ còn lại tương tự được 720 số
Vậy có 720.2=1440 số Đáp án: B
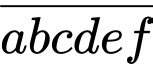 là số thỏa mãn yêu cầu thì
là số thỏa mãn yêu cầu thì 
Có 2 bộ ba số có tổng bằng 8 là {1,2,5} và {1,3,4}
Nếu
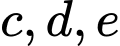 thuộc {1,2,5} thì có 3! cách chọn và
thuộc {1,2,5} thì có 3! cách chọn và 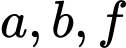 có
có 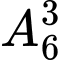 cách chọn suy ra có
cách chọn suy ra có 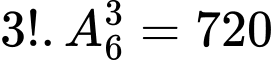
Bộ còn lại tương tự được 720 số
Vậy có 720.2=1440 số Đáp án: B
Câu 7 [582832]: Có bao nhiêu số tự nhiên có 7 chữ số, trong đó chữ số 2 có mặt đúng 2 lần, chữ số 3 có mặt đúng 3 lần, các chữ số còn lại có mặt không quá 1 lần?
A, 11340.
B, 9650.
C, 8820.
D, 2520.
Xét trường hợp có cả chữ số 0 đứng đầu.
Số cách chọn vị trí cho chữ số 2 là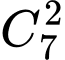
số cách chọn vị trí cho chữ số 3 là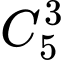
Số cách chọn 2 chữ số còn lại trong tập hợp {0; 1; 4; 5; 6; 7; 8; 9} để xếp vào hai vị trí cuối là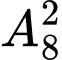
Do đó có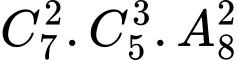 =11760 số.
=11760 số.
Xét trường hợp chữ số 0 đứng đầu.
Số cách chọn vị trí cho chữ số 2 là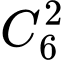
Số cách chọn vị trí cho chữ số 3 là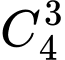
Số cách chọn chữ số cuối trong tập hợp {1; 4; 5; 6; 7; 8; 9} là 7 cách.
Do đó có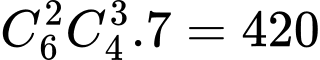 số.
số.
Vậy có 11760-420=11340 số Đáp án: A
Số cách chọn vị trí cho chữ số 2 là
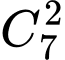
số cách chọn vị trí cho chữ số 3 là
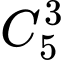
Số cách chọn 2 chữ số còn lại trong tập hợp {0; 1; 4; 5; 6; 7; 8; 9} để xếp vào hai vị trí cuối là
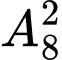
Do đó có
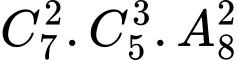 =11760 số.
=11760 số.Xét trường hợp chữ số 0 đứng đầu.
Số cách chọn vị trí cho chữ số 2 là
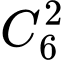
Số cách chọn vị trí cho chữ số 3 là
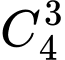
Số cách chọn chữ số cuối trong tập hợp {1; 4; 5; 6; 7; 8; 9} là 7 cách.
Do đó có
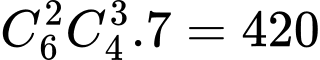 số.
số.Vậy có 11760-420=11340 số Đáp án: A
Câu 8 [582833]: Cho một đa giác đều 12 đỉnh 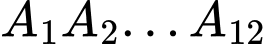 nội tiếp đường tròn
nội tiếp đường tròn  Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Hỏi có bao nhiêu hình chữ nhật mà bốn đỉnh của nó được chọn từ 12 vừa nói trên?
Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Hỏi có bao nhiêu hình chữ nhật mà bốn đỉnh của nó được chọn từ 12 vừa nói trên?
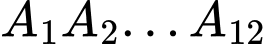 nội tiếp đường tròn
nội tiếp đường tròn  Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Hỏi có bao nhiêu hình chữ nhật mà bốn đỉnh của nó được chọn từ 12 vừa nói trên?
Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Hỏi có bao nhiêu hình chữ nhật mà bốn đỉnh của nó được chọn từ 12 vừa nói trên? A, 10.
B, 15.
C, 20.
D, 25.
Gọi đường chéo của đa giác đều 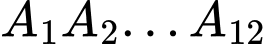 đi qua tâm đường tròn
đi qua tâm đường tròn  là đường chéo lớn thì đa giác đã cho có 6 đường chéo lớn. Mỗi hình chữ nhật có các đỉnh là 4 đỉnh trong 12 đỉnh
là đường chéo lớn thì đa giác đã cho có 6 đường chéo lớn. Mỗi hình chữ nhật có các đỉnh là 4 đỉnh trong 12 đỉnh 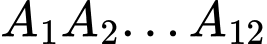 có các đường chéo là hai đường chéo lớn. Ngược lại, mỗi cặp đường chéo lớn có các đầu mút là 4 đỉnh của một hình chữ nhật. Do đó số hình chữ nhật được tạo thành là số cách chọn 2 đường chéo lớn trong 6 đường chéo lớn.
có các đường chéo là hai đường chéo lớn. Ngược lại, mỗi cặp đường chéo lớn có các đầu mút là 4 đỉnh của một hình chữ nhật. Do đó số hình chữ nhật được tạo thành là số cách chọn 2 đường chéo lớn trong 6 đường chéo lớn.
Suy ra số hình chữ nhật thỏa yêu cầu bài toán là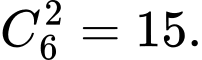 Đáp án: B
Đáp án: B
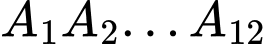 đi qua tâm đường tròn
đi qua tâm đường tròn  là đường chéo lớn thì đa giác đã cho có 6 đường chéo lớn. Mỗi hình chữ nhật có các đỉnh là 4 đỉnh trong 12 đỉnh
là đường chéo lớn thì đa giác đã cho có 6 đường chéo lớn. Mỗi hình chữ nhật có các đỉnh là 4 đỉnh trong 12 đỉnh 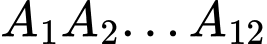 có các đường chéo là hai đường chéo lớn. Ngược lại, mỗi cặp đường chéo lớn có các đầu mút là 4 đỉnh của một hình chữ nhật. Do đó số hình chữ nhật được tạo thành là số cách chọn 2 đường chéo lớn trong 6 đường chéo lớn.
có các đường chéo là hai đường chéo lớn. Ngược lại, mỗi cặp đường chéo lớn có các đầu mút là 4 đỉnh của một hình chữ nhật. Do đó số hình chữ nhật được tạo thành là số cách chọn 2 đường chéo lớn trong 6 đường chéo lớn.Suy ra số hình chữ nhật thỏa yêu cầu bài toán là
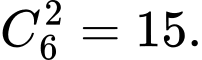 Đáp án: B
Đáp án: B
Câu 9 [582834]: Từ các chữ số 1; 2; 3; 4; 5; 6; 7; 8; 9 có thể lập được bao nhiêu số tự nhiên có 6 chữ số khác nhau sao cho luôn có đúng ba chữ số chẵn?
A, 28800.
B, 15600.
C, 4700.
D, 6541.
Chọn 3 chữ số chẵn trong 4 chữ số chẵn: có 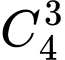 cách.
cách.
Chọn 3 chữ số lẻ trong 5 chữ số lẻ: có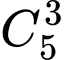 cách.
cách.
Xếp 6 chữ số trên vào 6 vị trí: có 6! cách.
Vậy có tất cả: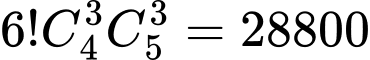 số cần tìm. Đáp án: A
số cần tìm. Đáp án: A
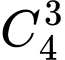 cách.
cách.Chọn 3 chữ số lẻ trong 5 chữ số lẻ: có
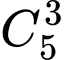 cách.
cách.Xếp 6 chữ số trên vào 6 vị trí: có 6! cách.
Vậy có tất cả:
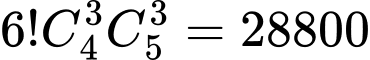 số cần tìm. Đáp án: A
số cần tìm. Đáp án: A
Câu 10 [582835]: Cho hai đường thẳng song song 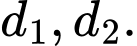 Trên đường thẳng
Trên đường thẳng 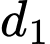 lấy 10 điểm phân biệt, trên
lấy 10 điểm phân biệt, trên 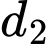 lấy 15 điểm phân biệt. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 25 vừa nói trên?
lấy 15 điểm phân biệt. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 25 vừa nói trên?
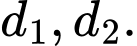 Trên đường thẳng
Trên đường thẳng 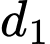 lấy 10 điểm phân biệt, trên
lấy 10 điểm phân biệt, trên 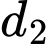 lấy 15 điểm phân biệt. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 25 vừa nói trên?
lấy 15 điểm phân biệt. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 25 vừa nói trên? A, 3460.
B, 675.
C, 1050.
D, 1725.
Số tam giác lập được thuộc vào một trong hai loại sau
Loại 1: Gồm hai đỉnh thuộc vào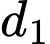 và một đỉnh thuộc vào
và một đỉnh thuộc vào 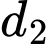
Số cách chọn bộ hai điềm trong 10 thuộc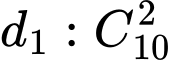
Số cách chọn một điềm trong 15 điềm thuộc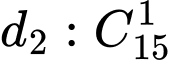
Loại này có: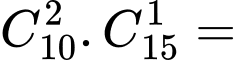 tam giác.
tam giác.
Loại 2: Gồm một đỉnh thuộc vào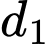 và hai đỉnh thuộc vào
và hai đỉnh thuộc vào 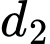
Số cách chọn một điềm trong 10 thuộc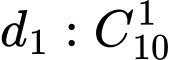
Số cách chọn bộ hai điềm trong 15 điểm thuộc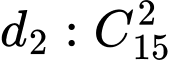
Loại này có: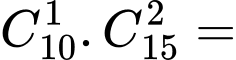 tam giác.
tam giác.
Vậy có tất cả: tam giác thỏa yêu cầu bài toán. Đáp án: D
tam giác thỏa yêu cầu bài toán. Đáp án: D
Loại 1: Gồm hai đỉnh thuộc vào
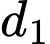 và một đỉnh thuộc vào
và một đỉnh thuộc vào 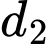
Số cách chọn bộ hai điềm trong 10 thuộc
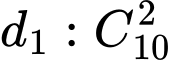
Số cách chọn một điềm trong 15 điềm thuộc
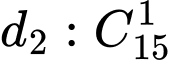
Loại này có:
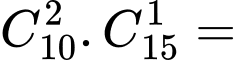 tam giác.
tam giác.Loại 2: Gồm một đỉnh thuộc vào
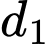 và hai đỉnh thuộc vào
và hai đỉnh thuộc vào 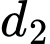
Số cách chọn một điềm trong 10 thuộc
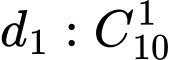
Số cách chọn bộ hai điềm trong 15 điểm thuộc
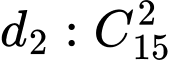
Loại này có:
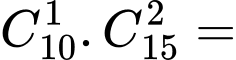 tam giác.
tam giác.Vậy có tất cả:
 tam giác thỏa yêu cầu bài toán. Đáp án: D
tam giác thỏa yêu cầu bài toán. Đáp án: D
Câu 11 [582836]: Cho một đa giác đều 10 cạnh nội tiếp đường tròn (O). Hỏi có bao nhiêu hình thang cân có bốn đỉnh là đỉnh của đa giác đều đó?
A, 70.
B, 50.
C, 56.
D, 68.
Gọi d là trục đối xứng của hình thang cân. Xét 2 trường hợp
+TH1: d đi qua 2 đỉnh của đa giác có 5 cách chọn d. Số hình thang cân là 5.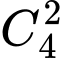
+TH2: d vuông góc với 2 cạnh đối có 5 cách chọn d. Số hình thang cân là 5.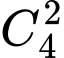 do mỗi hình chữ nhật được đếm 2 lần nên
do mỗi hình chữ nhật được đếm 2 lần nên
Số hình thang cân là 5.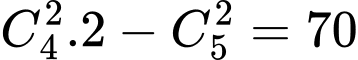 Đáp án: A
Đáp án: A
+TH1: d đi qua 2 đỉnh của đa giác có 5 cách chọn d. Số hình thang cân là 5.
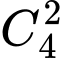
+TH2: d vuông góc với 2 cạnh đối có 5 cách chọn d. Số hình thang cân là 5.
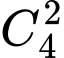 do mỗi hình chữ nhật được đếm 2 lần nên
do mỗi hình chữ nhật được đếm 2 lần nênSố hình thang cân là 5.
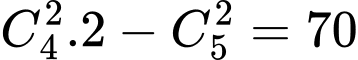 Đáp án: A
Đáp án: A
Câu 12 [582837]: Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên, mỗi số có 6 chữ số đồng thời thỏa mãn sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn tổng của 3 số sau một đơn vị?
A, 104.
B, 106.
C, 108.
D, 112.
Gọi 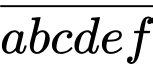 là số thỏa mãn yêu cầu
là số thỏa mãn yêu cầu
Ta có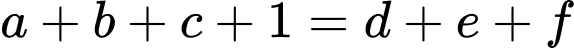
Lại có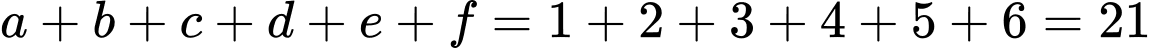
Nên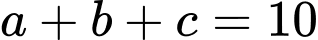
Có 3 bộ số là {1,3,6}, {2,3,5}, {1,4,5}
Với mỗi bộ có 3!.3!=36 số
Vậy có 3.36=108 số Đáp án: C
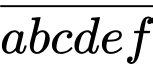 là số thỏa mãn yêu cầu
là số thỏa mãn yêu cầu Ta có
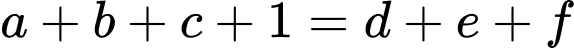
Lại có
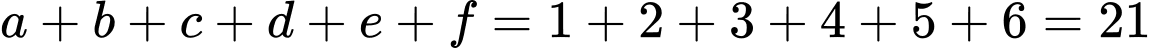
Nên
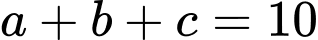
Có 3 bộ số là {1,3,6}, {2,3,5}, {1,4,5}
Với mỗi bộ có 3!.3!=36 số
Vậy có 3.36=108 số Đáp án: C
Câu 13 [582838]:  với
với 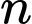 là số nguyên dương,
là số nguyên dương, 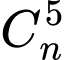 bằng bao nhiêu?
bằng bao nhiêu?
 với
với 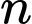 là số nguyên dương,
là số nguyên dương, 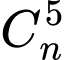 bằng bao nhiêu?
bằng bao nhiêu? A, 21.
B, 35.
C, 126.
D, 56.
Điều kiện: 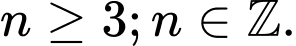
Ta có:
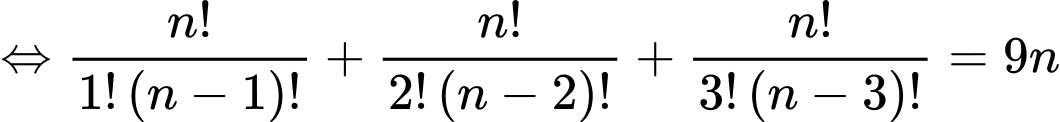
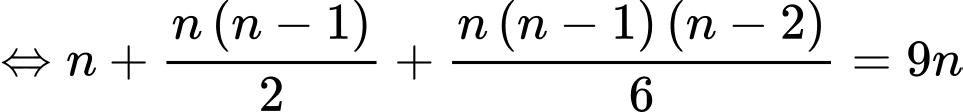
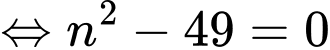
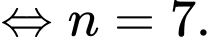
Vậy nghiệm của phương trình là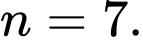 Đáp án: A
Đáp án: A
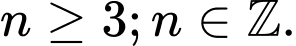
Ta có:

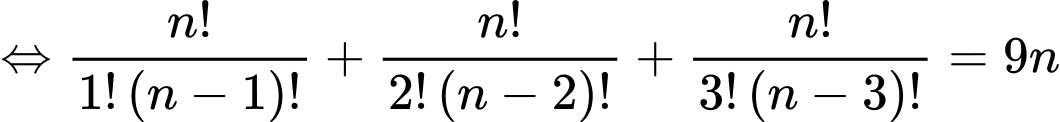
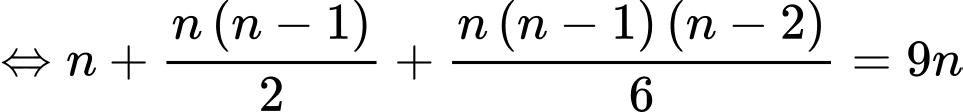
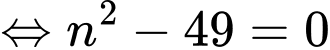
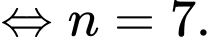
Vậy nghiệm của phương trình là
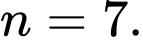 Đáp án: A
Đáp án: A
Câu 14 [582839]: Cho tứ giác ABCD trên cạnh AB lấy 3 điểm khác A, B; trên cạnh BC lấy 4 điểm khác B, C; trên cạnh CA lấy 5 điểm khác C, A.Trên cạnh DA lấy thêm 6 điểm phân biệt khác D, A. Gọi S là tổng số tam giác tạo thành khi lấy 3 điểm trong 18 điểm nói trên. Khi đó S bằng
A, 342.
B, 781.
C, 624.
D, 816.
Lấy ra 3 điểm từ 18 điểm có 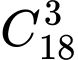 cách
cách
Lấy 3 điểm thẳng hàng bất kì có cách
cách
Tổng tam giác là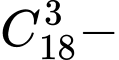 (
( )= 781 Đáp án: B
)= 781 Đáp án: B
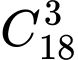 cách
cáchLấy 3 điểm thẳng hàng bất kì có
 cách
cáchTổng tam giác là
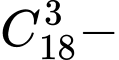 (
( )= 781 Đáp án: B
)= 781 Đáp án: B
Câu 15 [582840]: Có bao nhiêu cách chia hết 4 chiếc bánh khác nhau có 3 em nhỏ, mỗi em nhận được ít nhất một chiếc?
A, 32.
B, 40.
C, 36.
D, 54.
Chia 4 chiếc bánh khác nhau cho 3 em nhỏ, biết rằng mỗi em nhận được ít nhất 1 chiếc nên sẽ có một em nhận được 2 chiếc, hai em còn lại mỗi em nhận được 1 chiếc.
Chọn 2 trong 4 chiếc bánh chia cho 1 trong 3 em có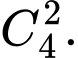 3 cách.
3 cách.
Lấy 2 chiếc bánh còn lại chia cho hai em còn lại có 2! cách.
Vậy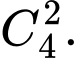 3.2! = 36 cách. Đáp án: C
3.2! = 36 cách. Đáp án: C
Chọn 2 trong 4 chiếc bánh chia cho 1 trong 3 em có
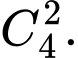 3 cách.
3 cách.Lấy 2 chiếc bánh còn lại chia cho hai em còn lại có 2! cách.
Vậy
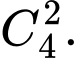 3.2! = 36 cách. Đáp án: C
3.2! = 36 cách. Đáp án: C Dạng câu hỏi: Câu trắc nghiệm đúng sai.
(Thí sinh trả lời từ câu 16,17. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng
hoặc sai)
hoặc sai)
Câu 16 [582841]: Huấn luyện viên một đội bóng muốn chọn 5 cầu thủ để đá quả luân lưu 11 mét
a) Có 462 cách chọn nếu 11 cầu thủ có khả năng như nhau
b) Có 120 cách chọn nếu có 3 cầu thủ chấn thương và cầu thủ A đá quả đầu, cầu thủ B đá quả thứ 4
a) Có 462 cách chọn nếu 11 cầu thủ có khả năng như nhau
b) Có 120 cách chọn nếu có 3 cầu thủ chấn thương và cầu thủ A đá quả đầu, cầu thủ B đá quả thứ 4
a) S
b) Đ
a) Chọn có thứ tự 5 cầu thủ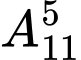 =55440
=55440
b) Còn lại 11-3=8 cầu thủ
Cầu thủ A đá quả 1 cầu thủ B quả 4 nên còn 3 vị trí, chọn có thứ tự 3 cầu thủ trong 6 cầu thủ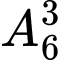
b) Đ
a) Chọn có thứ tự 5 cầu thủ
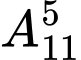 =55440
=55440b) Còn lại 11-3=8 cầu thủ
Cầu thủ A đá quả 1 cầu thủ B quả 4 nên còn 3 vị trí, chọn có thứ tự 3 cầu thủ trong 6 cầu thủ
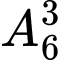
Câu 17 [582842]: Cho tập hợp A = {1, 2, 3, 4, 5, 6, 7}
a) Từ tập hợp A có thể lập được 3326400 số có 12 chữ số sao cho chữ số 5 có mặt 3 lần, chữ số 6 có mặt 4 lần, còn lại các chữ số khác có mặt 1 lần
b) Từ tập hợp A có thể lập được 22050 số có 7 chữ số sao cho có 1 chữ số lặp lại 4 lần, một chữ số khác lặp lại 2 lần và một chữ số khác với hai số trên
a) Từ tập hợp A có thể lập được 3326400 số có 12 chữ số sao cho chữ số 5 có mặt 3 lần, chữ số 6 có mặt 4 lần, còn lại các chữ số khác có mặt 1 lần
b) Từ tập hợp A có thể lập được 22050 số có 7 chữ số sao cho có 1 chữ số lặp lại 4 lần, một chữ số khác lặp lại 2 lần và một chữ số khác với hai số trên
a) Đ
b) Đ
a) Chữ số 5 có mặt 3 lần trong số có 12 chữ số nên có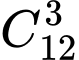 cách chọn vị trí cho chữ số 5.
cách chọn vị trí cho chữ số 5.
+ Chữ số 6 có mặt 4 lần trong 12−3=9 chữ số còn lại nên có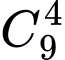 cách chọn vị trí cho chữ số
cách chọn vị trí cho chữ số 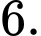
+ Còn 5 chữ số cuối cùng xếp vào 5 vị trí còn lại nên có 5! cách.
Vậy có tất cả số cách chọn số thỏa mãn đề bài là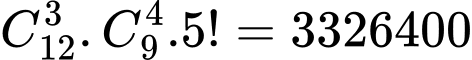 cách.
cách.
b) Có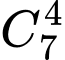 cách chọn vị trí cho chữ số lặp lại 4 lần. Tuy nhiên vì chữ số lặp lại 4 lần này ta chưa biết là số nào nên có 7 TH xảy ra, vậy có
cách chọn vị trí cho chữ số lặp lại 4 lần. Tuy nhiên vì chữ số lặp lại 4 lần này ta chưa biết là số nào nên có 7 TH xảy ra, vậy có 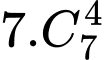 cách
cách
+ Có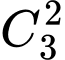 cách chọn vị trí cho chữ số lặp lại 2 lần. Tuy nhiên vì chữ số lặp lại 2 lần này ta chưa biết là số nào nên có 6 TH xảy ra, vậy có
cách chọn vị trí cho chữ số lặp lại 2 lần. Tuy nhiên vì chữ số lặp lại 2 lần này ta chưa biết là số nào nên có 6 TH xảy ra, vậy có  cách
cách
+ Còn 5 chữ số cuối cùng chỉ có thể xuất hiện 1 lần nên có 5 cách chọn.
Vậy có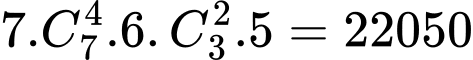 số.
số.
b) Đ
a) Chữ số 5 có mặt 3 lần trong số có 12 chữ số nên có
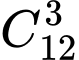 cách chọn vị trí cho chữ số 5.
cách chọn vị trí cho chữ số 5.+ Chữ số 6 có mặt 4 lần trong 12−3=9 chữ số còn lại nên có
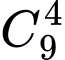 cách chọn vị trí cho chữ số
cách chọn vị trí cho chữ số 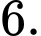
+ Còn 5 chữ số cuối cùng xếp vào 5 vị trí còn lại nên có 5! cách.
Vậy có tất cả số cách chọn số thỏa mãn đề bài là
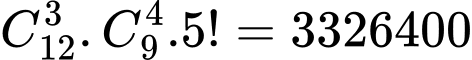 cách.
cách.b) Có
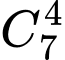 cách chọn vị trí cho chữ số lặp lại 4 lần. Tuy nhiên vì chữ số lặp lại 4 lần này ta chưa biết là số nào nên có 7 TH xảy ra, vậy có
cách chọn vị trí cho chữ số lặp lại 4 lần. Tuy nhiên vì chữ số lặp lại 4 lần này ta chưa biết là số nào nên có 7 TH xảy ra, vậy có 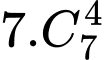 cách
cách+ Có
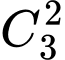 cách chọn vị trí cho chữ số lặp lại 2 lần. Tuy nhiên vì chữ số lặp lại 2 lần này ta chưa biết là số nào nên có 6 TH xảy ra, vậy có
cách chọn vị trí cho chữ số lặp lại 2 lần. Tuy nhiên vì chữ số lặp lại 2 lần này ta chưa biết là số nào nên có 6 TH xảy ra, vậy có  cách
cách + Còn 5 chữ số cuối cùng chỉ có thể xuất hiện 1 lần nên có 5 cách chọn.
Vậy có
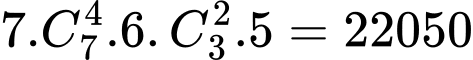 số.
số. Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 18 [582843]: Giải các phương trình sau:
a)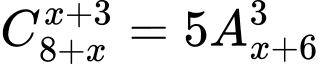
b)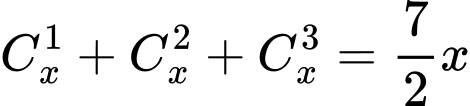
Đáp án:……
a)
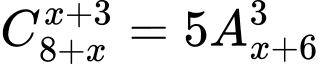
b)
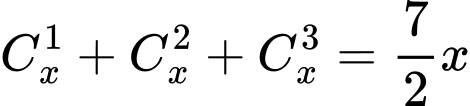
Đáp án:……
a) Điều kiện : 
Ta có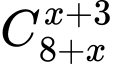 =5
=5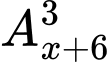

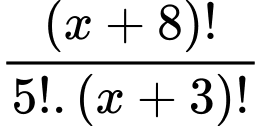 =5.
=5.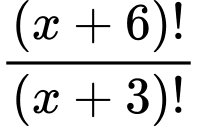

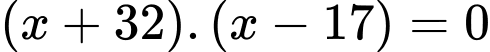
Vậy pt đã cho có 1 nghiệm là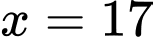
b) Điều kiện:
Ta có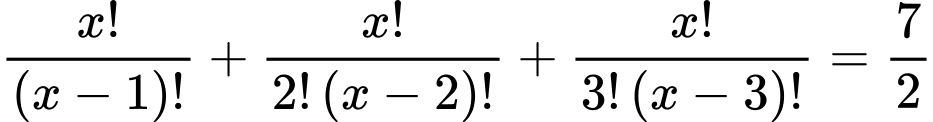

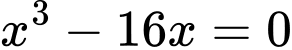
Vậy pt đã cho có 1 nghiệm

Ta có
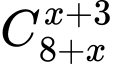 =5
=5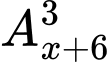

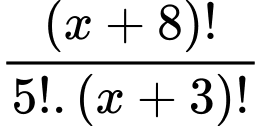 =5.
=5.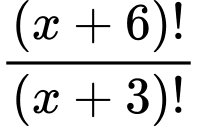

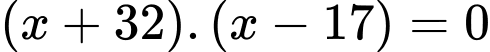
Vậy pt đã cho có 1 nghiệm là
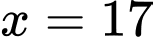
b) Điều kiện:

Ta có
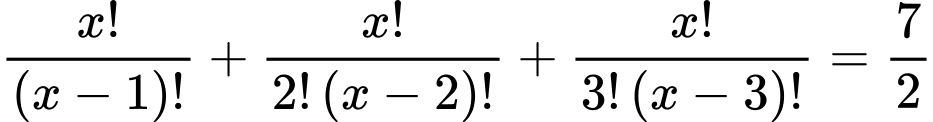

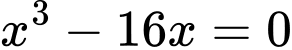
Vậy pt đã cho có 1 nghiệm

Câu 19 [582844]: Giải các bất phương trình sau: 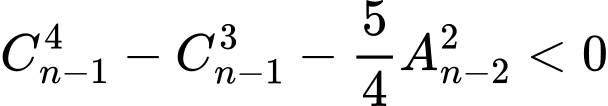
Đáp án:……
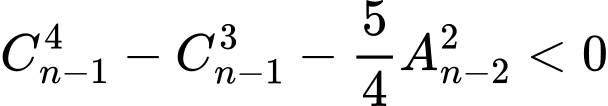
Đáp án:……
Đáp án: 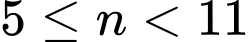
Điều kiện
Ta có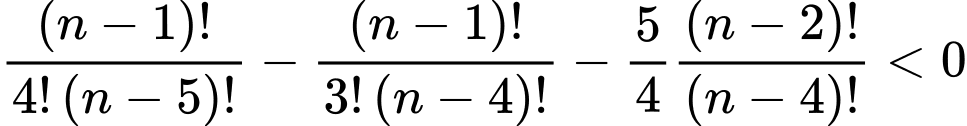
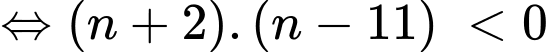
Kết hợp điều kiện, ta suy ra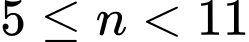 .
.
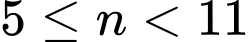
Điều kiện

Ta có
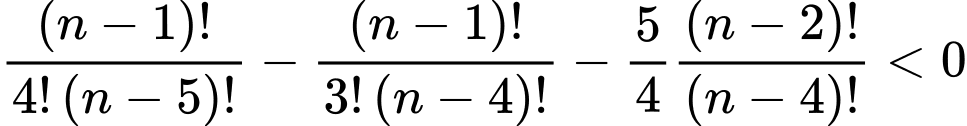
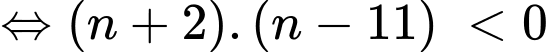
Kết hợp điều kiện, ta suy ra
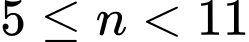 .
.
Câu 20 [582845]: Tìm tổng S của tất cả các số tự nhiên, mỗi số được tạo thành bởi hoán vị của 6 chữ số 1, 2, 3, 4, 5, 6.
Đáp án:……
Đáp án:……
Đáp án: 279999720
Nhận thấy: 1+6= 2+5= 3+4=7
S là tổng của 6! =720 số
Mỗi số trong tổng S tương ứng 1 và chỉ 1 số trong tổng đó sao cho tổng của chúng bằng 777777.
Vậy, các số trong tổng S tạo thành 720/60= 360 cặp và tổng mỗi cặp là 777777
⇨ S=60.777777=279999720
Nhận thấy: 1+6= 2+5= 3+4=7
S là tổng của 6! =720 số
Mỗi số trong tổng S tương ứng 1 và chỉ 1 số trong tổng đó sao cho tổng của chúng bằng 777777.
Vậy, các số trong tổng S tạo thành 720/60= 360 cặp và tổng mỗi cặp là 777777
⇨ S=60.777777=279999720
Dạng câu hỏi: Câu hỏi kéo thả.
Câu 21 [582846]: Kéo thả hoặc click vào để điền
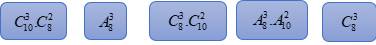
Từ một nhóm có 8 học sinh nam và 10 học sinh nữ, số cách chọn ra:
3 học sinh nam là: _______.
5 học sinh trong đó có 3 học sinh nam và 2 học sinh nữ là _______.
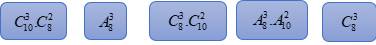
Từ một nhóm có 8 học sinh nam và 10 học sinh nữ, số cách chọn ra:
3 học sinh nam là: _______.
5 học sinh trong đó có 3 học sinh nam và 2 học sinh nữ là _______.
Đáp án đúng:
Từ một nhóm có 8 học sinh nam và 10 học sinh nữ, số cách chọn ra:
3 học sinh nam là: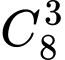 .
.
5 học sinh trong đó có 3 học sinh nam và 2 học sinh nữ là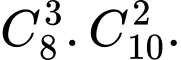
Hướng dẫn giải:
Số cách chọn ra 3 học sinh nam là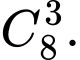
Số cách chọn ra 2 học sinh nữ từ 10 học sinh nữ là: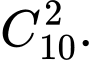
Vậy số cách chọn thỏa yêu cầu là: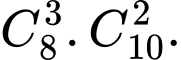
Từ một nhóm có 8 học sinh nam và 10 học sinh nữ, số cách chọn ra:
3 học sinh nam là:
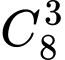 .
.
5 học sinh trong đó có 3 học sinh nam và 2 học sinh nữ là
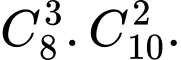
Hướng dẫn giải:
Số cách chọn ra 3 học sinh nam là
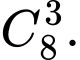
Số cách chọn ra 2 học sinh nữ từ 10 học sinh nữ là:
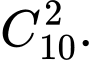
Vậy số cách chọn thỏa yêu cầu là: