Dạng toán: Xác suất về các bài toán số
Câu 1 [582705]: Chọn ngẫu nhiên một số có 2 chữ số từ các số 00 đến 99. Xác suất để có một con số tận cùng là 0 là:
A, 0,1.
B, 0,2.
C, 0,3.
D, 0,4.
Chọn A
Có 10 số trong 100 số trên có tận cùng là 0. Do đó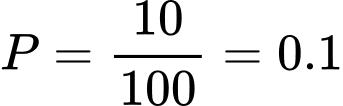
Đáp án: A
Có 10 số trong 100 số trên có tận cùng là 0. Do đó
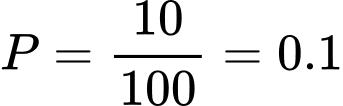Đáp án: A
Câu 2 [582706]: Lấy 3 số 1 cách ngẫu nhiên từ tập các số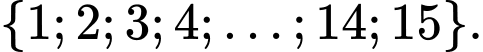 
Tính xác suất để tổng 3 số lấy ra bằng 11.
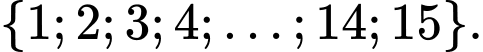Tính xác suất để tổng 3 số lấy ra bằng 11. A,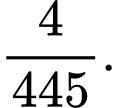 
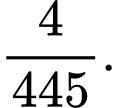
B,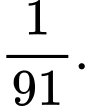 
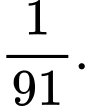
C,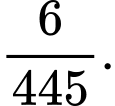 
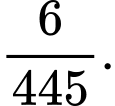
D,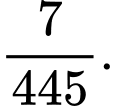 
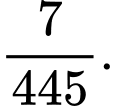
Chọn B
Số cách lấy 3 số từ tập 15 số là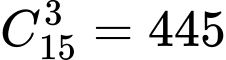
Các bộ 3 số có tổng bằng 11 lấy được từ tập trên là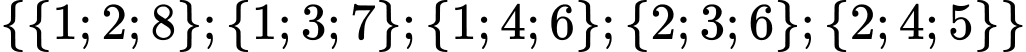
; có 5 bộ
Suy ra, xác suất cần tính bằng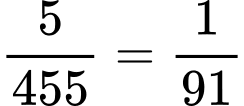
Đáp án: B
Số cách lấy 3 số từ tập 15 số là
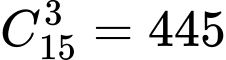
Các bộ 3 số có tổng bằng 11 lấy được từ tập trên là
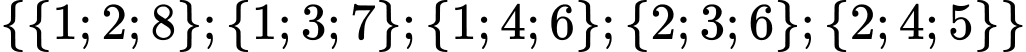; có 5 bộSuy ra, xác suất cần tính bằng
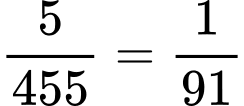Đáp án: B
Câu 3 [582707]: Từ các số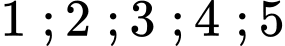 
ta lập các số có 5 chữ số, trong đó chữ số 3 có mặt 3 lần, các chữ số còn lại có mặt không quá 1 lần. Gọi 
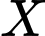là tập hợp các số đã lập nói trên, lấy ngẫu nhiên từ 
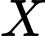1 số. Tính xác suất để lấy được số chia hết cho 3.
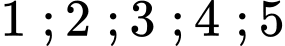ta lập các số có 5 chữ số, trong đó chữ số 3 có mặt 3 lần, các chữ số còn lại có mặt không quá 1 lần. Gọi 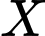là tập hợp các số đã lập nói trên, lấy ngẫu nhiên từ 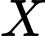1 số. Tính xác suất để lấy được số chia hết cho 3.
- Sắp số 3 vào 5 vị trí có :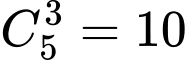 
cách
- Chọn 2 chữ số trong 4 số và xếp vào 2 vị trí còn lại có 12 cách
Vậy không gian mẫu có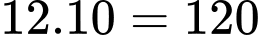
phần tử
Gọi A là biến cố: “Chọn được số chia hết cho 3” khi đó 2 số khác số 3 đã chọn ở bước 2 phải có tổng chia hết cho 3
+ Chọn được 2 số 1 và 2 có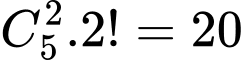
+ Chọn được 2 số 1 và 5 có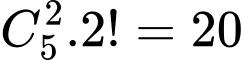
+ Chọn được 2 số 2 và 4 có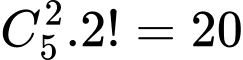
+ Chọn được 2 số 4 và 5 có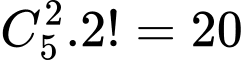
Do vậy biến cố A có 40 phần tử: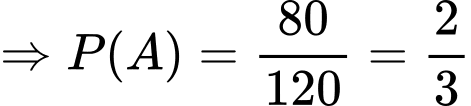
.
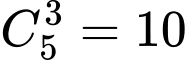cách- Chọn 2 chữ số trong 4 số và xếp vào 2 vị trí còn lại có 12 cách
Vậy không gian mẫu có
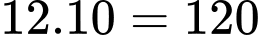phần tửGọi A là biến cố: “Chọn được số chia hết cho 3” khi đó 2 số khác số 3 đã chọn ở bước 2 phải có tổng chia hết cho 3
+ Chọn được 2 số 1 và 2 có
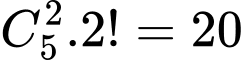
+ Chọn được 2 số 1 và 5 có
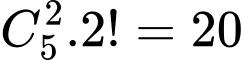
+ Chọn được 2 số 2 và 4 có
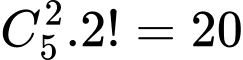
+ Chọn được 2 số 4 và 5 có
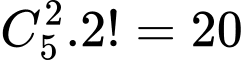
Do vậy biến cố A có 40 phần tử:
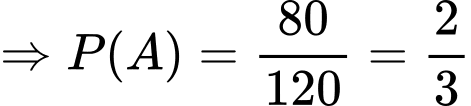. Dạng toán: Xác suất về các bài toán chọn và sắp xếp
Câu 4 [582708]: Tính ngẫu nhiên ba người đàn ông, hai người đàn bà và một đứa bé vào ngồi 6 cái ghế xếp thành hang ngang. Tính xác suất sao cho đứa bé ngồi giữa hai người đàn bà.
A,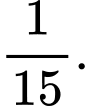 
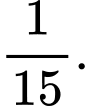
B,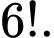 
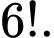
C,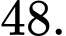 
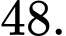
D,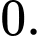 
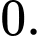
Chọn A
Xếp 6 người vào 6 cái ghế nên số cách xếp là một hoán vị của 6.Do đó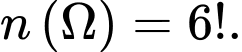
Gọi biến cố A “Đứa bé được xếp giữa hai người đàn bà” Ta xếp như sau:
+ Xếp đứa bé ngồi vào ghế thứ 2 đến ghế thứ 5 nên có 4 cách xếp.
+ Ứng với mỗi cách xếp đứa bé thì có 2 cách xếp hai người đàn bà ngồi hai bên.
+ Còn ba chỗ còn lại xếp ba người đàn ông thì có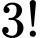
Cách xếp
Theo quy tắc nhân ta có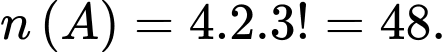
Vậy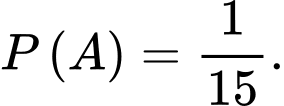
Đáp án: A
Xếp 6 người vào 6 cái ghế nên số cách xếp là một hoán vị của 6.Do đó
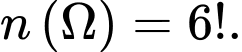
Gọi biến cố A “Đứa bé được xếp giữa hai người đàn bà” Ta xếp như sau:
+ Xếp đứa bé ngồi vào ghế thứ 2 đến ghế thứ 5 nên có 4 cách xếp.
+ Ứng với mỗi cách xếp đứa bé thì có 2 cách xếp hai người đàn bà ngồi hai bên.
+ Còn ba chỗ còn lại xếp ba người đàn ông thì có
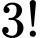Cách xếpTheo quy tắc nhân ta có
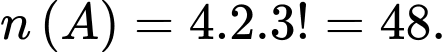Vậy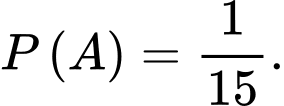 Đáp án: A
Câu 5 [582709]: Hai bạn nam và hai bạn nữ được xếp ngồi ngẫu nhiên vào bốn ghế xếp thành hai dãy đối diện nhau. Tính xác suất sao cho nữ ngồi đối diện nhau.
Đánh số ghế như hình vẽ
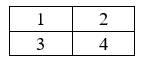
Không gian mẫu: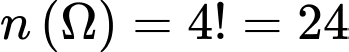
phần tử.
Biến cố B “Nữ ngồi đối diện nhau”.
Ta chọn chỗ ngồi cho bạn nữ đầu tiên: Có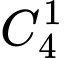
cách chọn.
Vì bạn nữ thứ hai ngồi đối diện bạn nữ đầu tiên nên ta có đúng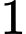
cách chọn.
Sau đó, ta xếp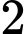
bạn nam vào 
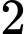chỗ ngồi còn lại, vì 
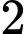bạn nam có thể đổi chỗ cho nhau nên ta có: 
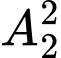cách chọn.
Khi đó: số cách chọn để B xảy ra là là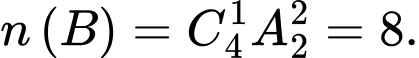
Vậy xác suất của B là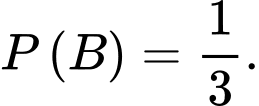
Không gian mẫu:
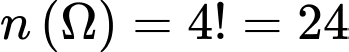phần tử.Biến cố B “Nữ ngồi đối diện nhau”.
Ta chọn chỗ ngồi cho bạn nữ đầu tiên: Có
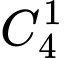cách chọn.
Vì bạn nữ thứ hai ngồi đối diện bạn nữ đầu tiên nên ta có đúng
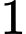cách chọn.
Sau đó, ta xếp
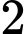bạn nam vào 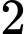chỗ ngồi còn lại, vì 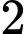bạn nam có thể đổi chỗ cho nhau nên ta có: 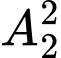cách chọn.
Khi đó: số cách chọn để B xảy ra là là
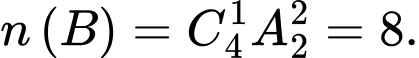
Vậy xác suất của B là
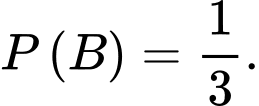
Câu 6 [582710]: Có 5 nam và 3 nữ xếp ngồi ngẫu nhiên quanh bàn tròn. Tính xác suất sao cho không có 2 bạn nữ nào ngồi cạnh nhau.
Xếp ngẫu nhiên 7 người vào 7 ghế đặt quanh một bàn tròn sẽ có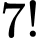 
cách xếp. Khi đó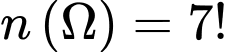 
Gọi biến cố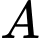
“không có 2 bạn nữ nào ngồi cạnh nhau.”
+) Xếp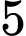
nam vào bàn tròn trước sẽ có 
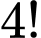cách
+) Giữa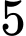
nam có 
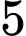khoảng trống. Xếp 
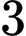nữ vào 
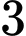trong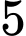 
khoảng trống đó sẽ có 
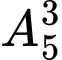cách
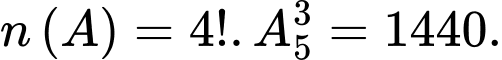Do vậy
Vậy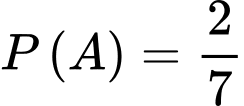 
.
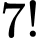cách xếp. Khi đó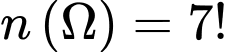 Gọi biến cố
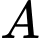“không có 2 bạn nữ nào ngồi cạnh nhau.”+) Xếp
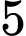nam vào bàn tròn trước sẽ có 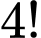cách+) Giữa
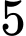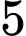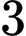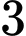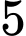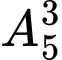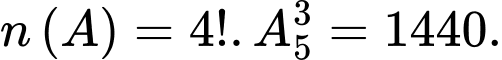nam có khoảng trống. Xếp nữ vào trong khoảng trống đó sẽ có cáchDo vậy
Vậy 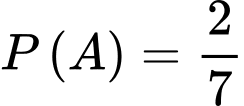. Dạng toán: Tính xác suất bằng kỹ thuật tạo vách ngăn
Câu 7 [582711]: Một nhóm có 4 học sinh nam và 3 học sinh nữ. Nhóm muốn xếp theo hàng ngang để chụp ảnh kỉ niệm. Tính xác suất để không có bạn nam nào đứng kề nhau.
Xếp thứ tự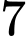 
bạn theo hàng ngang có 
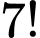cách 
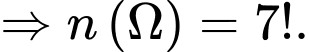
Gọi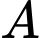
là biến cố xếp 
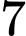bạn theo hàng ngang sao cho không có bạn nam nào đứng cạnh nhau.
Xếp thứ tự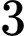
bạn nữ có 
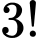cách.
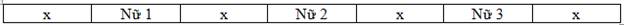
Khi đó các bạn nam đứng ở các vị trí x.
Xếp thứ tự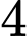
bạn nam vào 
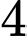vị trí x có 
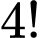cách.
Suy ra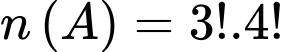
.
Vậy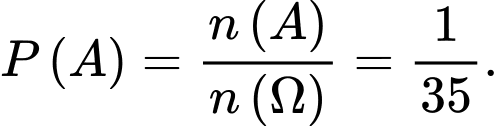
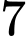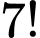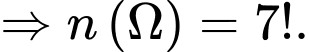
bạn theo hàng ngang có cách Gọi
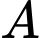là biến cố xếp 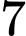bạn theo hàng ngang sao cho không có bạn nam nào đứng cạnh nhau.Xếp thứ tự
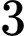bạn nữ có 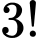cách.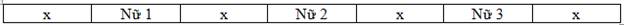Khi đó các bạn nam đứng ở các vị trí x.
Xếp thứ tự
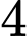bạn nam vào 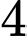vị trí x có 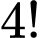cách.Suy ra
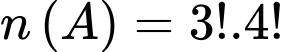.Vậy
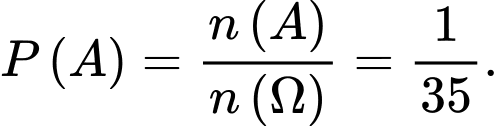
Câu 8 [582712]: Có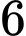 
học sinh lớp 11 và 
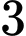học sinh lớp 12 được xếp ngẫu nhiên vào 
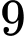ghế thành một dãy. Tính xác suất để xếp được 
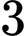học sinh lớp 12 xen kẽ giữa 
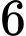học sinh lớp 11.
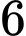học sinh lớp 11 và 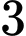học sinh lớp 12 được xếp ngẫu nhiên vào 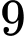ghế thành một dãy. Tính xác suất để xếp được 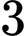học sinh lớp 12 xen kẽ giữa 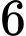học sinh lớp 11.
Không gian mẫu là số cách sắp xếp tất cả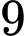 
học sinh vào một ghế dài.
Suy ra số phần tử của không gian mẫu là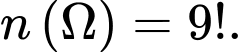
Gọi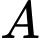
là biến cố "Xếp 
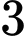học sinh lớp 
xen kẽ giữa 
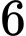học sinh lớp 
". Ta mô tả khả năng thuận lợi của biến cố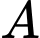 
như sau:
● Đầu tiên xếp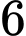
học sinh lớp 
thành một dãy, có 
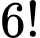cách.
● Sau đó xem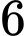
học sinh này như 
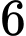vách ngăn nên có 
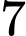vị trí để xếp 
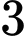học sinh lớp 
(gồm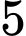 
vị trí giữa 
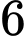học sinh và 
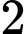vị trí hai đầu). Do đó có 
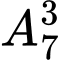cách xếp 
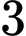học sinh lớp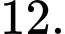 
Suy ra số phần tử của biến cố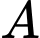
là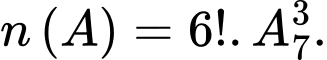 
Vậy xác suất cần tính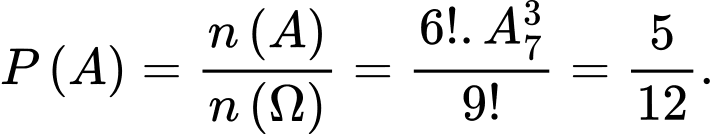
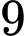học sinh vào một ghế dài.Suy ra số phần tử của không gian mẫu là
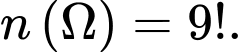
Gọi
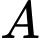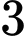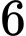là biến cố "Xếp học sinh lớp xen kẽ giữa học sinh lớp ". Ta mô tả khả năng thuận lợi của biến cố 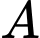như sau:● Đầu tiên xếp
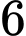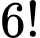học sinh lớp thành một dãy, có cách.● Sau đó xem
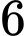học sinh này như 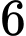vách ngăn nên có 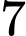vị trí để xếp 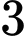học sinh lớp (gồm 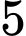vị trí giữa 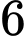học sinh và 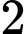vị trí hai đầu). Do đó có 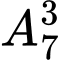cách xếp 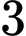học sinh lớp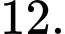 Suy ra số phần tử của biến cố
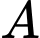là 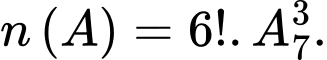Vậy xác suất cần tính
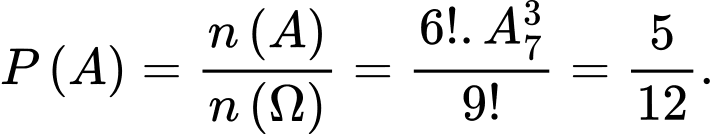
Câu 9 [582713]: Tính lập một số tự nhiên có 5 chữ số. Tính xác suất để số đó có chữ số đứng trước không nhỏ hơn chữ số đứng sau.
Ta có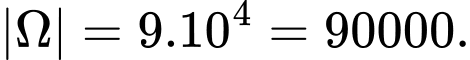 
Gọi A là biến cố: “Chọn được số có chữ số đứng trước không nhỏ hơn chữ số đứng sau”
Gọi số có 5 chữ số là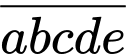
thỏa mãn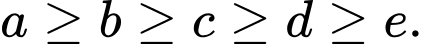 
Ta có
Có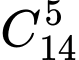
cách chọn ra bộ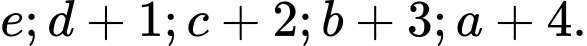 
Suy ra có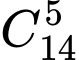
cách chọn ra bộ 
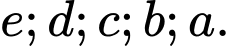Trong số 
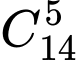cách chọn đó, bỏ bộ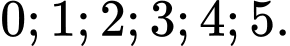 
Vậy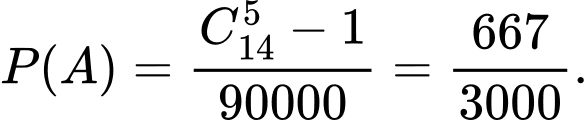
Cách 2:
Ta có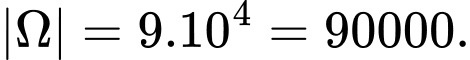
Gọi A là biến cố: “Chọn được số có chữ số đứng trước không nhỏ hơn chữ số đứng sau”
Gọi số có 5 chữ số là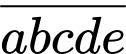
thỏa mãn 
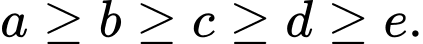Có các trường hợp sau:
Trường hợp 1: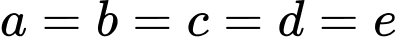
có 9 số.
Trường hợp 2: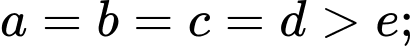
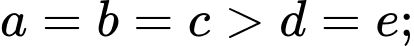
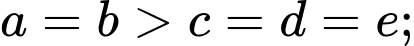
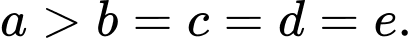
Mỗi trường hợp có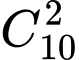
số.
Trường hợp 3: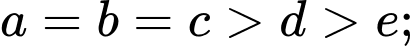
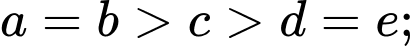
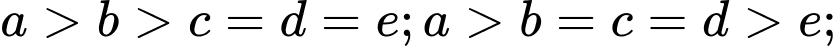
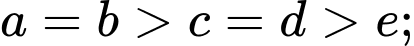
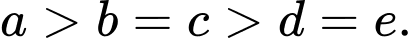
Mỗi trường hợp c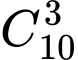ó
số.
Trường hợp 4: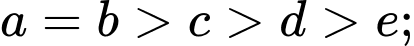
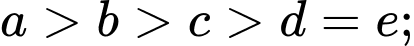
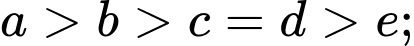
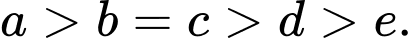
Mỗi trường hợp c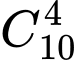ó
số.
Trường hợp 5: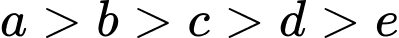
có 
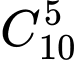số.
Suy ra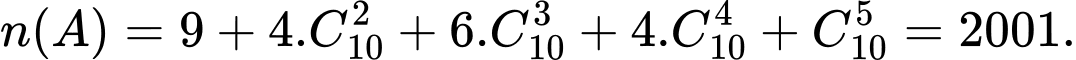
Vậy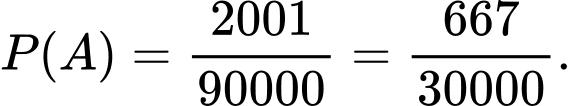
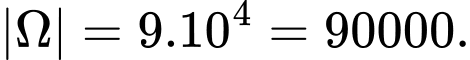
Gọi A là biến cố: “Chọn được số có chữ số đứng trước không nhỏ hơn chữ số đứng sau”
Gọi số có 5 chữ số là
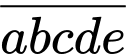thỏa mãn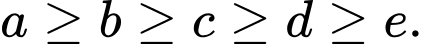 Ta có
Có
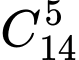cách chọn ra bộ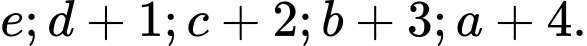 Suy ra có
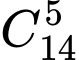cách chọn ra bộ 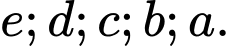Trong số 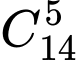cách chọn đó, bỏ bộ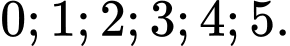 Vậy
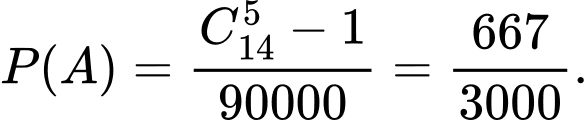
Cách 2:
Ta có
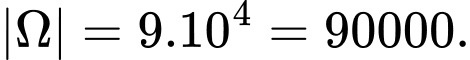
Gọi A là biến cố: “Chọn được số có chữ số đứng trước không nhỏ hơn chữ số đứng sau”
Gọi số có 5 chữ số là
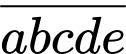thỏa mãn 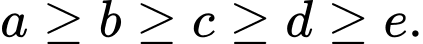Có các trường hợp sau:Trường hợp 1:
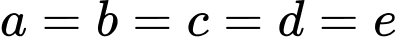có 9 số.Trường hợp 2:
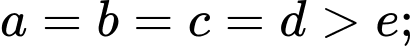
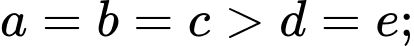
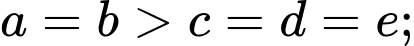
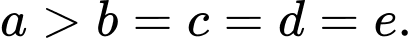
Mỗi trường hợp có
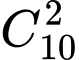số.Trường hợp 3:
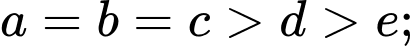
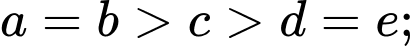
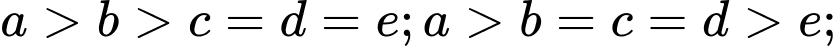
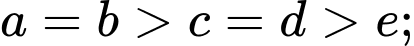
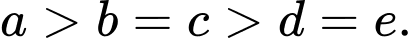
Mỗi trường hợp có
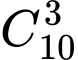số.Trường hợp 4:
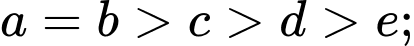
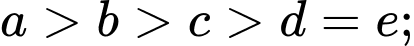
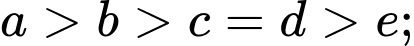
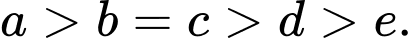
Mỗi trường hợp có
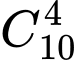số.Trường hợp 5:
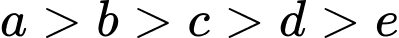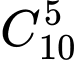có số.Suy ra
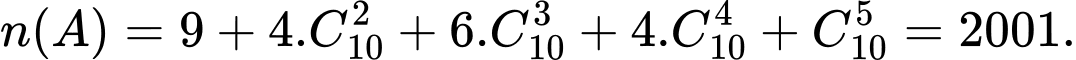
Vậy
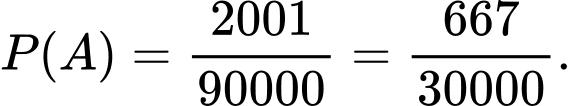
Dạng toán: Xác suất bằng công thức cộng
Câu 10 [582714]: Một lớp học có 30 học sinh, trong đó có 8 học sinh giỏi, 15 học sinh khá và 7 học sinh trung bình. Gọi ngẫu nhiên 3 học sinh lên bảng giải bài tập. Tính xác suất để có ít nhất 1 học sinh giỏi.
Số cách chọn ngẫu nhiên 3 học sinh từ 30 học sinh lên bảng là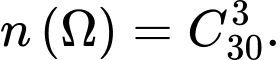 
Số học sinh trung bình và khá là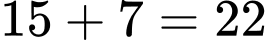
học sinh.
Gọi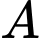
là biến cố: “3 học sinh được chọn đều không giỏi”.
Suy ra
là biến cố: “3 học sinh được chọn có ít nhất 1 học sinh giỏi”.
Ta có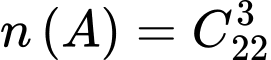
; 
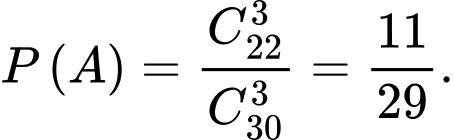
Vậy xác suất cần tính là :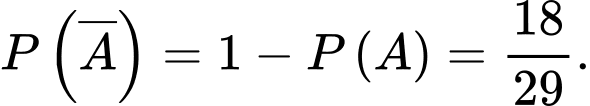
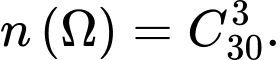
Số học sinh trung bình và khá là
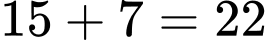học sinh.Gọi
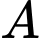là biến cố: “3 học sinh được chọn đều không giỏi”.Suy ra
là biến cố: “3 học sinh được chọn có ít nhất 1 học sinh giỏi”.Ta có
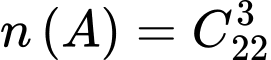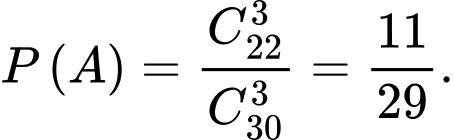
; Vậy xác suất cần tính là :
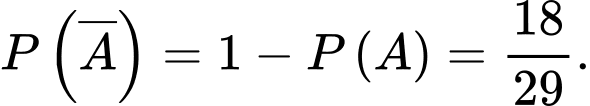
Câu 11 [582715]: Một hộp có 
quả cầu xanh, 
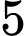quả cầu đỏ. Lấy ngẫu nhiên 
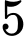quả từ hộp đó. Tính xác suất để được 
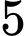quả có đủ hai màu.
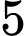quả cầu xanh, quả cầu đỏ. Lấy ngẫu nhiên 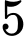quả từ hộp đó. Tính xác suất để được 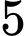quả có đủ hai màu.
Số phần tử của không gian mẫu: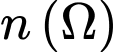 
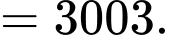
Gọi biến cố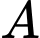
: “
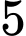quả lấy ra có đủ hai màu”. Suy ra biến cố 
: “
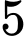quả lấy ra chỉ có 
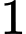màu”.
TH1: Lấy ra từ hộp 5 quả cầu xanh, có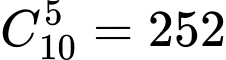
cách.
TH2: Lấy ra từ hộp 5 quả cầu đỏ, có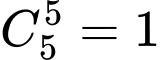
cách.
Suy ra: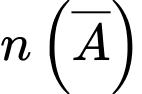
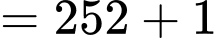
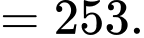
Xác suất để được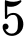
quả có đủ hai màu là: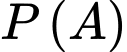 
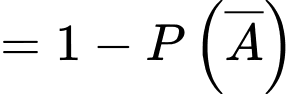
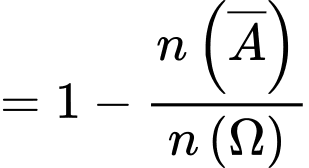
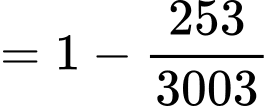
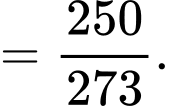
Vậy xác suất cần tìm là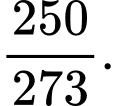
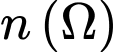
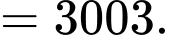
Gọi biến cố
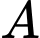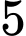: “ quả lấy ra có đủ hai màu”. Suy ra biến cố : “ 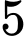quả lấy ra chỉ có 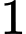màu”.TH1: Lấy ra từ hộp 5 quả cầu xanh, có
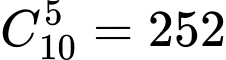cách.TH2: Lấy ra từ hộp 5 quả cầu đỏ, có
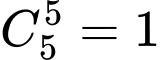cách.Suy ra:
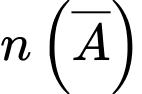
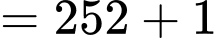
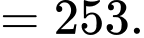
Xác suất để được
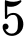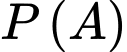
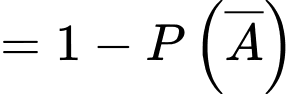
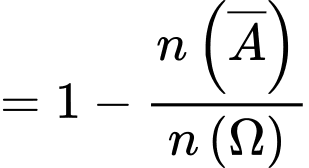
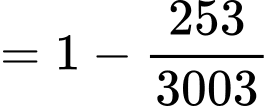
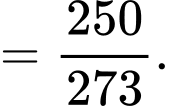
quả có đủ hai màu là: Vậy xác suất cần tìm là
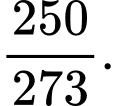
Câu 12 [582716]: Trong kho đèn trang trí có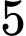 
bóng đèn loại I và 
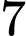bóng đèn loại II, các bóng đèn khác nhau về màu sắc và hình dáng. Lấy ra 
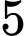bóng đèn bất kì. Tính xác suất để 
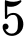bóng đèn lấy ra có đủ hai loại và số bóng đèn loại I nhiều hơn số bóng đèn loại II.
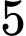bóng đèn loại I và 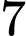bóng đèn loại II, các bóng đèn khác nhau về màu sắc và hình dáng. Lấy ra 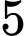bóng đèn bất kì. Tính xác suất để 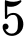bóng đèn lấy ra có đủ hai loại và số bóng đèn loại I nhiều hơn số bóng đèn loại II.
Số phần tử của không gian mẫu là: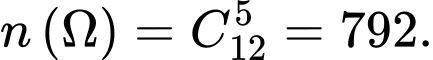 
Gọi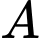
là biến cố: “
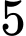bóng đèn lấy ra có đủ hai loại và số bóng đèn loại I nhiều hơn số bóng đèn loại II”.
Xảy ra các trường hợp:
Trường hợp 1: Lấy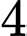
bóng đèn loại I và 
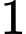bóng đèn loại II, có 
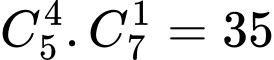cách.
Trường hợp 2: Lấy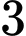
bóng đèn loại I và 
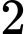bóng đèn loại II, có 
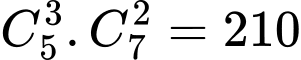cách.
Ta có
Vậy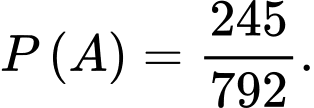
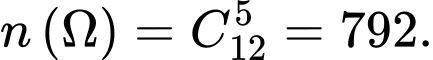
Gọi
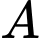là biến cố: “ 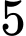bóng đèn lấy ra có đủ hai loại và số bóng đèn loại I nhiều hơn số bóng đèn loại II”.Xảy ra các trường hợp:
Trường hợp 1: Lấy
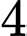bóng đèn loại I và 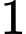bóng đèn loại II, có 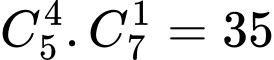cách.Trường hợp 2: Lấy
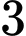bóng đèn loại I và 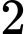bóng đèn loại II, có 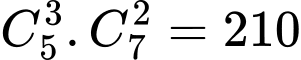cách.Ta có
Vậy
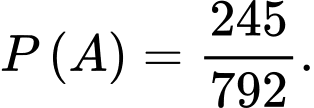
Dạng toán: Xác suất bằng công thức nhân
Câu 13 [582717]: Gieo hai con xúc xắc I và II cân đối, đồng chất một cách độc lập. Ta có biến cố A: “Có ít nhất một con xúc xắc xuất hiện mặt 6 chấm”. Tính xác suất biến cố A.
Gọi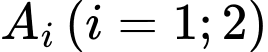 
là biến cố : “Con xúc xắc thứ 
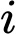ra mặt 6 chấm”
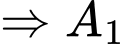và 
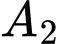là hai biến cố độc lập và ta có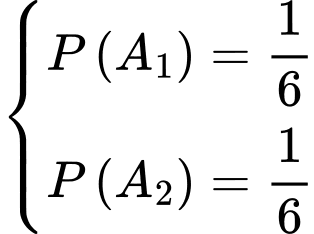 
Thay vì tính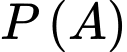
ta đi tính 
Ta có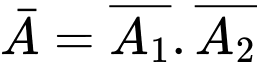 
.
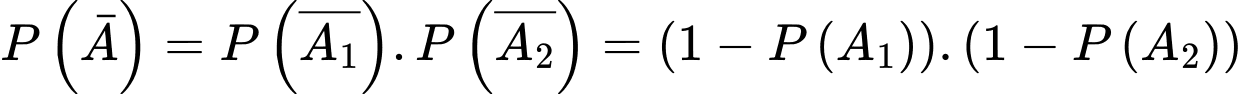
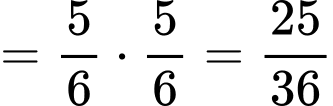
Vậy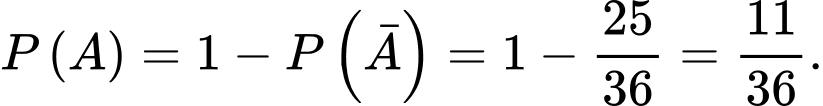
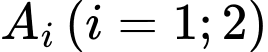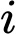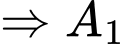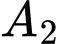là biến cố : “Con xúc xắc thứ ra mặt 6 chấm” và là hai biến cố độc lập và ta có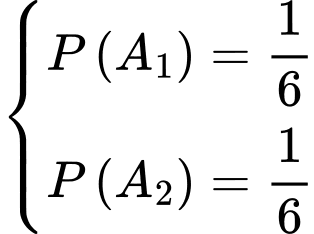 Thay vì tính
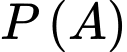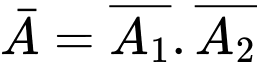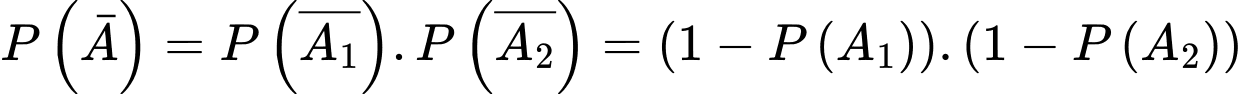
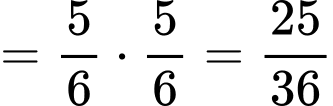
ta đi tính Ta có .Vậy
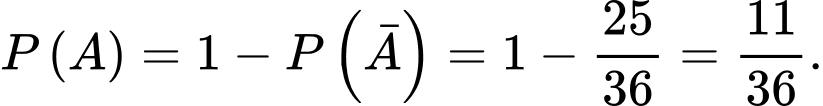
Câu 14 [582718]: Xác suất để người xạ thủ bắn trúng bia là 0,2. Tính xác suất để trong 3 lần bắn người xạ thủ bắn trúng bia một lần.
Gọi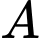 
là biến cố người xạ thủ bắn trúng bia.
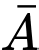là biến cố người xạ thủ không bắn trúng bia.
Ta có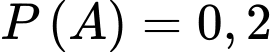
và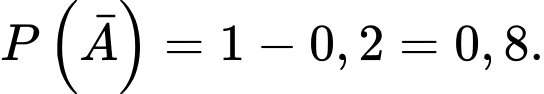 
Xác suất để người xạ thủ bắn trúng bia lần 1 và không trúng hai lần sau là:
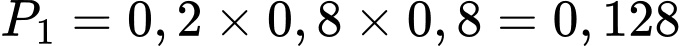
Tương tự xạ thủ bắn trúng lần 2, lần 1 và lần 3 không trúng là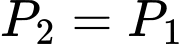
.
Tương tự xạ thủ bắn trúng lần 3, lần 1 và lần 2 không trúng là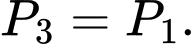
Vậy xác suất để trong 3 lần bắn người xạ thủ bắn trúng một lần là: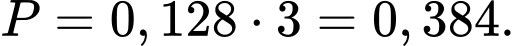
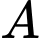là biến cố người xạ thủ bắn trúng bia. 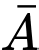là biến cố người xạ thủ không bắn trúng bia.Ta có
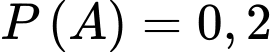và 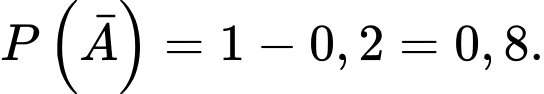Xác suất để người xạ thủ bắn trúng bia lần 1 và không trúng hai lần sau là:
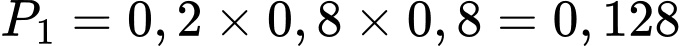
Tương tự xạ thủ bắn trúng lần 2, lần 1 và lần 3 không trúng là
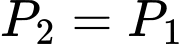.Tương tự xạ thủ bắn trúng lần 3, lần 1 và lần 2 không trúng là
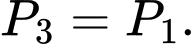
Vậy xác suất để trong 3 lần bắn người xạ thủ bắn trúng một lần là:
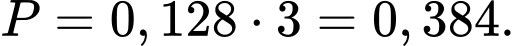
Câu 15 [582719]: Một chiếc hộp đựng 
quả bóng trong đó có 
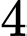quả màu đỏ và 
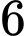quả màu xanh. Bốc liên tiếp hai quả bóng trong hộp ra. Tính xác suất để lần một bốc được quả màu đỏ và lần hai bốc được quả màu xanh.
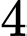quả bóng trong đó có quả màu đỏ và 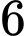quả màu xanh. Bốc liên tiếp hai quả bóng trong hộp ra. Tính xác suất để lần một bốc được quả màu đỏ và lần hai bốc được quả màu xanh.
Gọi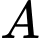 
là biến cố “ Lần một bốc được quả màu đỏ ’’.
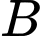là biến cố “ Lần hai bốc được quả màu xanh ’’.
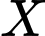là biến cố “ Lần một bốc được quả màu đỏ và lần hai bốc được quả màu xanh ’’.
Ta có: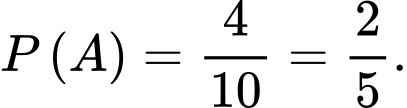
Mà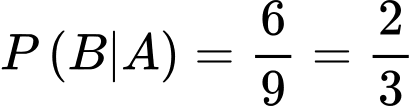
và 
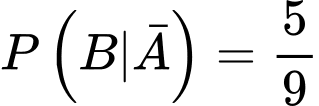nên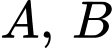 
là hai biến cố không độc lập.
Vậy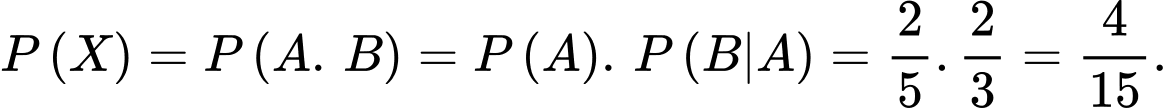
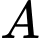là biến cố “ Lần một bốc được quả màu đỏ ’’. 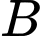là biến cố “ Lần hai bốc được quả màu xanh ’’. 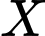là biến cố “ Lần một bốc được quả màu đỏ và lần hai bốc được quả màu xanh ’’.Ta có:
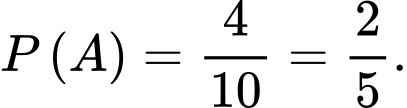
Mà
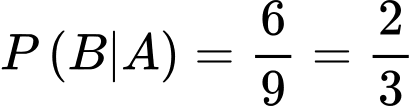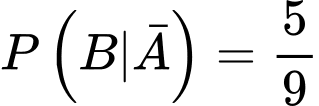và nên 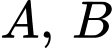là hai biến cố không độc lập.Vậy