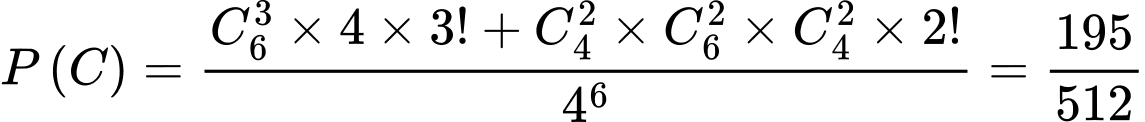Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất)
Câu 1 [582724]: Gieo một đồng xu cân đối đồng chất liên tiếp cho đến khi lần đầu tiên xuất hiện mặt ngửa hoặc cả 6 lần xuất hiện mặt sấp thì dừng lại. Xác suất để số lần gieo là 6:
A, 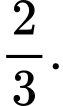
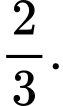
B, 7.
C, 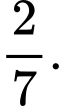
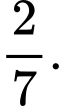
D, 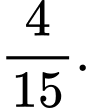
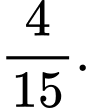
Ở bài toán này, ta phải hiểu mỗi phần tử trong không gian mẫu không phải đại diện cho một kết quả gieo đồng xu, mà đại diện cho một chuỗi hành động gieo đồng xu liên tiếp.
Không gian mẫu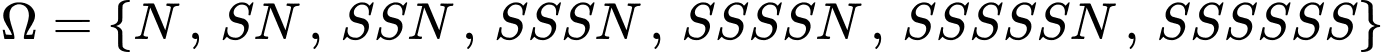

Biến cố

Xác suất của biến cố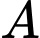 là
là 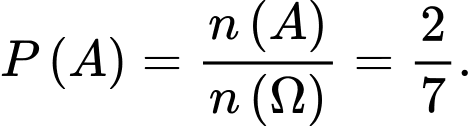 Đáp án: C
Đáp án: C
Không gian mẫu
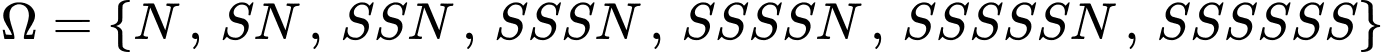

Biến cố


Xác suất của biến cố
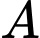 là
là 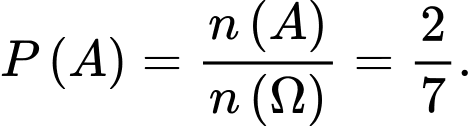 Đáp án: C
Đáp án: C
Câu 2 [582725]: Có 30 tấm thẻ đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Tính xác suất để có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong đó chỉ có 1 tấm thẻ chia hết cho 10.
A, 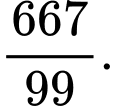
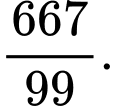
B, 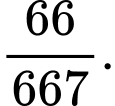
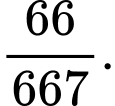
C, 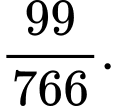
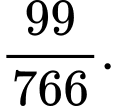
D, 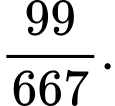
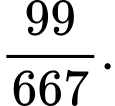
Chọn 10 tấm thẻ bất kì trong 30 tấm thẻ ta được 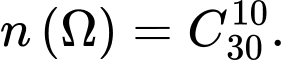
Gọi là biến cố “lấy được 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong đó chỉ có 1 tấm thẻ chia hết cho 10”
là biến cố “lấy được 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong đó chỉ có 1 tấm thẻ chia hết cho 10”
Từ 1 đến 30 có 15 thẻ mang số lẻ, 15 thẻ mang số chẵn trong đó có 3 thẻ chia hết cho 10 là nên số phần tử của biến cố
nên số phần tử của biến cố  là:
là: 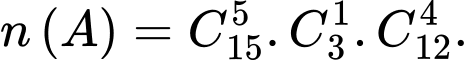
Vậy xác suất cần tìm là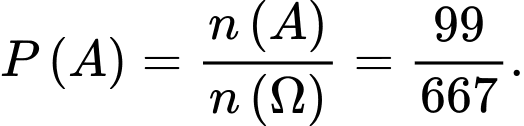 Đáp án: D
Đáp án: D
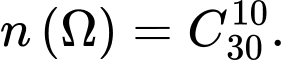
Gọi
 là biến cố “lấy được 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong đó chỉ có 1 tấm thẻ chia hết cho 10”
là biến cố “lấy được 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong đó chỉ có 1 tấm thẻ chia hết cho 10”Từ 1 đến 30 có 15 thẻ mang số lẻ, 15 thẻ mang số chẵn trong đó có 3 thẻ chia hết cho 10 là
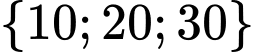 nên số phần tử của biến cố
nên số phần tử của biến cố  là:
là: 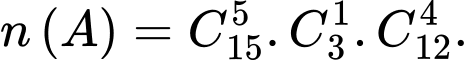
Vậy xác suất cần tìm là
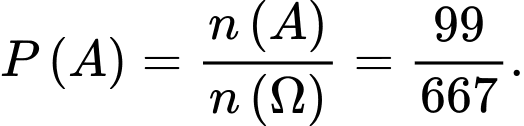 Đáp án: D
Đáp án: D
Câu 3 [582726]: Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng 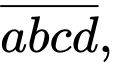 trong đó
trong đó 
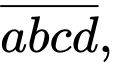 trong đó
trong đó 
A, 0,1.
B, 0,055.
C, 0,65.
D, 0.45.
Số phần tử của không gian mẫu là 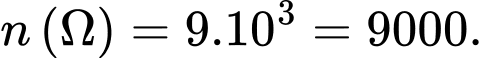
Từ giả thiết
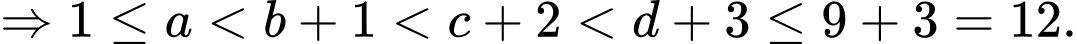
Số cách chọn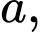
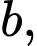
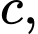
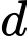 và sắp xếp chúng theo một thứ tự duy nhất là
và sắp xếp chúng theo một thứ tự duy nhất là 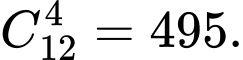
Vậy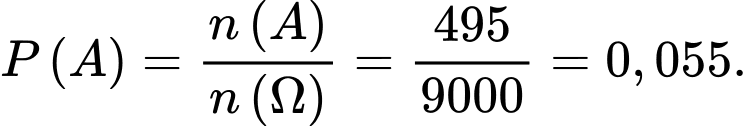 Đáp án: B
Đáp án: B
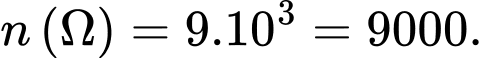
Từ giả thiết

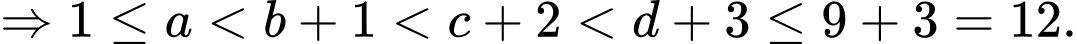
Số cách chọn
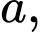
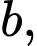
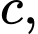
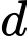 và sắp xếp chúng theo một thứ tự duy nhất là
và sắp xếp chúng theo một thứ tự duy nhất là 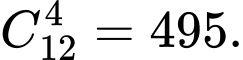
Vậy
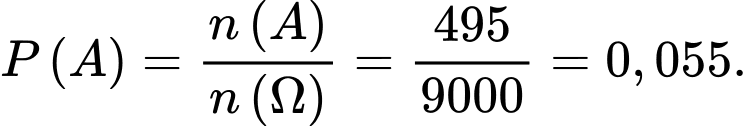 Đáp án: B
Đáp án: B
Câu 4 [582727]: Trong kỳ thi thử trung học phổ thông quốc gia một trường THPT đã dùng 7 cuốn toán, 6 cuốn lý, 5 cuốn hóa (các sách cùng thể loại giống nhau) để làm giải thưởng cho 9 học sinh có kết quả cao nhất, mỗi học sinh được 2 cuỗn sách khác loại. Trong số 9 học sinh có A và B, tính xác suất để khi phát phần thưởng, học sinh A và B có phần thưởng giống nhau.
A, 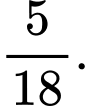
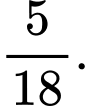
B, 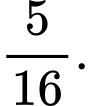
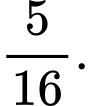
C, 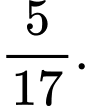
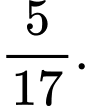
D, 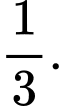
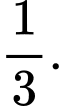
Giả sử các phần thưởng được xếp thành 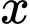 bộ toán – lý,
bộ toán – lý, 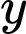 bộ toán – hóa,
bộ toán – hóa, 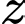 bộ hóa – lý.
bộ hóa – lý.
Ta có hệ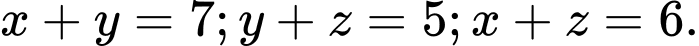 Giải hệ ta được
Giải hệ ta được 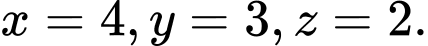
Số cách chọn phần thưởng cho A và B là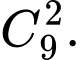
TH1: A, B cùng nhận được cặp toán – lý. Số cách chọn là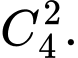
TH2: A, B cùng nhận được cặp toán – hóa. Số cách chọn là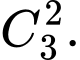
TH3: A, B cùng nhận được cặp hóa – lý. Số cách phát sách là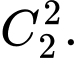
Xác suất cần tính là: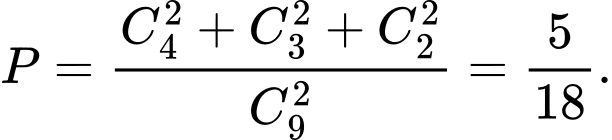 Đáp án: A
Đáp án: A
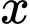 bộ toán – lý,
bộ toán – lý, 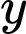 bộ toán – hóa,
bộ toán – hóa, 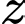 bộ hóa – lý.
bộ hóa – lý.Ta có hệ
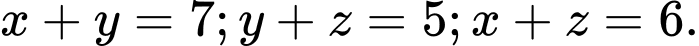 Giải hệ ta được
Giải hệ ta được 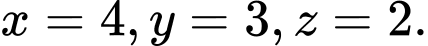
Số cách chọn phần thưởng cho A và B là
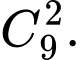
TH1: A, B cùng nhận được cặp toán – lý. Số cách chọn là
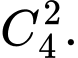
TH2: A, B cùng nhận được cặp toán – hóa. Số cách chọn là
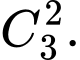
TH3: A, B cùng nhận được cặp hóa – lý. Số cách phát sách là
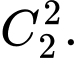
Xác suất cần tính là:
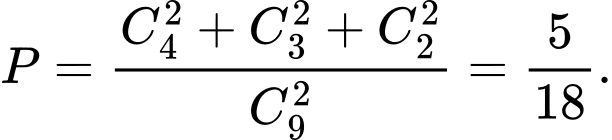 Đáp án: A
Đáp án: A
Câu 5 [582728]: Một lớp học có 30 học sinh, trong đó có 8 học sinh giỏi, 15 học sinh khá và 7 học sinh trung bình. Gọi ngẫu nhiên 3 học sinh lên bảng giải bài tập. Tính xác suất để có ít nhất 1 học sinh giỏi.
A, 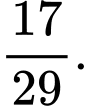
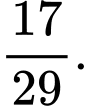
B, 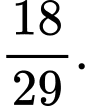
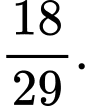
C, 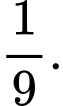
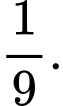
D, 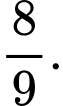
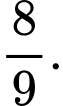
Số cách chọn ngẫu nhiên 3 học sinh từ 30 học sinh lên bảng là 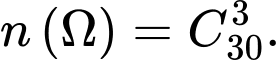
Số học sinh trung bình và khá là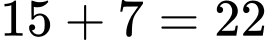 học sinh.
học sinh.
Gọi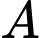 là biến cố: “3 học sinh được chọn đều không giỏi”.
là biến cố: “3 học sinh được chọn đều không giỏi”.
Suy ra là biến cố: “3 học sinh được chọn có ít nhất 1 học sinh giỏi”.
là biến cố: “3 học sinh được chọn có ít nhất 1 học sinh giỏi”.
Ta có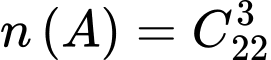 ;
; 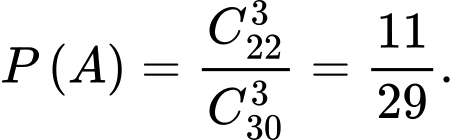
Vậy xác suất cần tính là :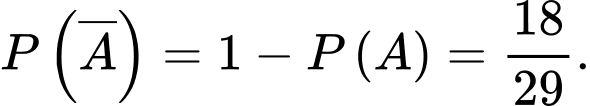 Đáp án: B
Đáp án: B
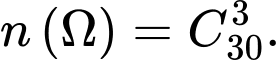
Số học sinh trung bình và khá là
 học sinh.
học sinh.Gọi
 là biến cố: “3 học sinh được chọn đều không giỏi”.
là biến cố: “3 học sinh được chọn đều không giỏi”.Suy ra
 là biến cố: “3 học sinh được chọn có ít nhất 1 học sinh giỏi”.
là biến cố: “3 học sinh được chọn có ít nhất 1 học sinh giỏi”.Ta có
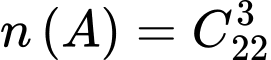 ;
; 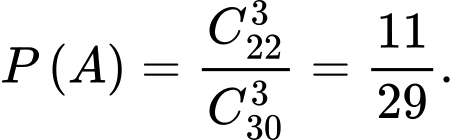
Vậy xác suất cần tính là :
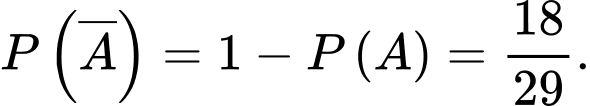 Đáp án: B
Đáp án: B
Câu 6 [582729]: Có bao nhiêu cách chia 30 cái kẹo không thể phân biệt cho 7 em bé sao cho mỗi em có ít nhất một cái. (Hai cách chia được coi là khác nhau nếu có ít nhất một em có số kẹo nhận được thay đổi).
A, 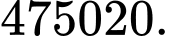
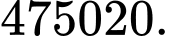
B, 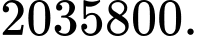
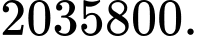
C, 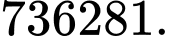
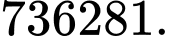
D, 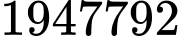
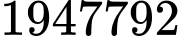
Bài toán này còn có tên là bài toán chia kẹo Euler.
Xếp 30 cái kẹo thành 1 hàng ngang. Có 29 vị trí xen giữa các chiếc kẹo. Để chia kẹo cho 7 em bé ta dùng 6 chiếc đũa đặt vào 6 trong 29 vị trí nói trên. Khi đó kẹo sẽ được chia làm 7 phần: gồm 5 nằm giữa các chiếc đũa và 2 phần nằm trước chiếc đũa đầu tiên và sau chiếc đũa cuối cùng.
Đáp án bài toán là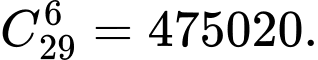 Đáp án: A
Đáp án: A
Xếp 30 cái kẹo thành 1 hàng ngang. Có 29 vị trí xen giữa các chiếc kẹo. Để chia kẹo cho 7 em bé ta dùng 6 chiếc đũa đặt vào 6 trong 29 vị trí nói trên. Khi đó kẹo sẽ được chia làm 7 phần: gồm 5 nằm giữa các chiếc đũa và 2 phần nằm trước chiếc đũa đầu tiên và sau chiếc đũa cuối cùng.
Đáp án bài toán là
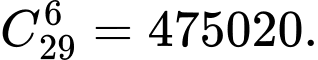 Đáp án: A
Đáp án: A
Câu 7 [582730]: Có 12 người, trong đó có 3 cặp vợ chồng. Xác suất để chọn ra 5 người sao cho trong đó không có cặp vợ chồng nào
A, 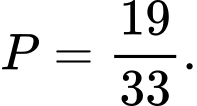
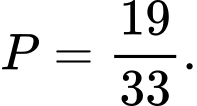
B, 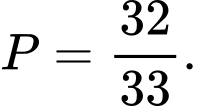
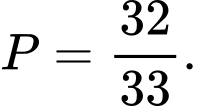
C, 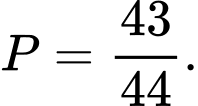
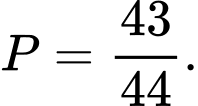
D, 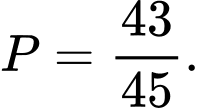
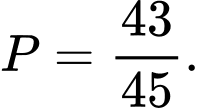
Chọn A
Ta có không gian mẫu là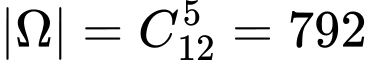
Gọi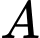 là biến cố «chọn ra
là biến cố «chọn ra 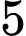 người sao cho không có cặp vợ chồng nào»
người sao cho không có cặp vợ chồng nào»
Ta sẽ tìm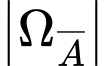
- Chọn ra 5 người trong đó có 2 cặp là vợ chồng là: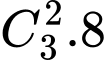
- Chọn ra 5 người trong đó có đúng 1 cặp là vợ chồng là: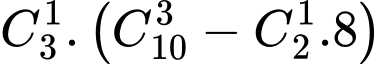
Suy ra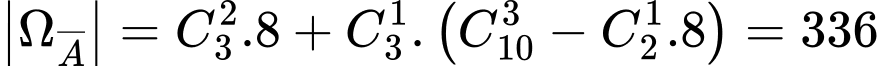
Suy ra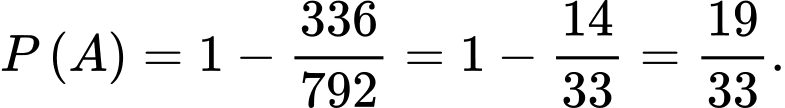 Đáp án: A
Đáp án: A
Ta có không gian mẫu là
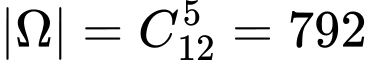
Gọi
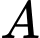 là biến cố «chọn ra
là biến cố «chọn ra 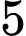 người sao cho không có cặp vợ chồng nào»
người sao cho không có cặp vợ chồng nào»Ta sẽ tìm
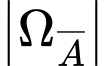
- Chọn ra 5 người trong đó có 2 cặp là vợ chồng là:
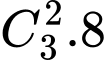
- Chọn ra 5 người trong đó có đúng 1 cặp là vợ chồng là:
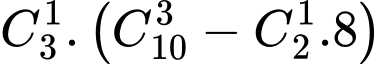
Suy ra
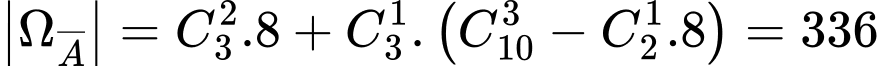
Suy ra
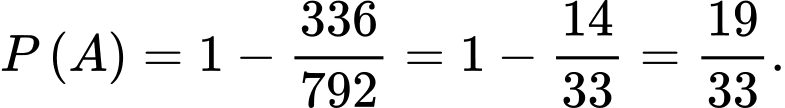 Đáp án: A
Đáp án: A
Câu 8 [582731]: Có hai xạ thủ loại 1 và 8 xạ thủ loại 2. Xác suất bắn trúng đích của các xạ thủ lần lượt là 0,4 và 0,6. Lấy ra ngẫu nhiên 1 xạ thủ bắn 2 viên đạn. Tìm xác suất để có ít nhất 1 viên đạn bắn trúng đích.
A, 0,296.
B, 0,8.
C, 0,196.
D, 0,3.
Trường hợp 1: Xác suất chọn trúng xạ thủ loại 1 là 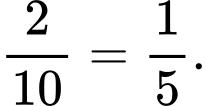
Xác suất bắn cả hai lần đều hụt của xạ thủ loại 1 là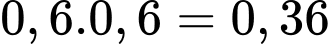
 Xác suất bắn trúng của ít nhất 1 lần của xạ thủ loại 1 là
Xác suất bắn trúng của ít nhất 1 lần của xạ thủ loại 1 là 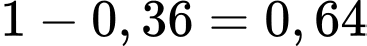
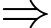 Xác suất viên đạn trúng đích ít nhất 1 lần là
Xác suất viên đạn trúng đích ít nhất 1 lần là 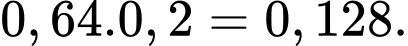
Trường hợp 2: Xác suất chọn trúng xạ thủ loại 2 là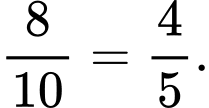
Xác suất bắn cả hai lần đều hụt của xạ thủ loại 2 là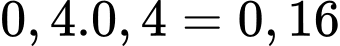
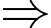 Xác suất bắn trúng ít nhất 1 viên của xạ thủ loại 2 là
Xác suất bắn trúng ít nhất 1 viên của xạ thủ loại 2 là 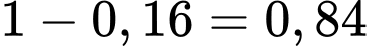
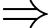 Xác suất viên đạn trúng đích là
Xác suất viên đạn trúng đích là 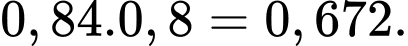
Vậy xác suất viên đạn bắn trúng đích là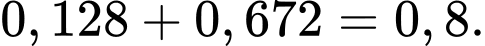 Đáp án: B
Đáp án: B
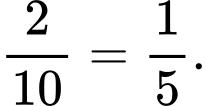
Xác suất bắn cả hai lần đều hụt của xạ thủ loại 1 là
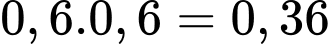
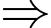 Xác suất bắn trúng của ít nhất 1 lần của xạ thủ loại 1 là
Xác suất bắn trúng của ít nhất 1 lần của xạ thủ loại 1 là 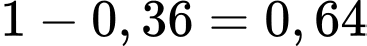
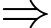 Xác suất viên đạn trúng đích ít nhất 1 lần là
Xác suất viên đạn trúng đích ít nhất 1 lần là 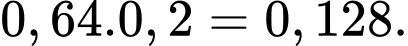
Trường hợp 2: Xác suất chọn trúng xạ thủ loại 2 là
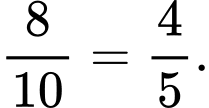
Xác suất bắn cả hai lần đều hụt của xạ thủ loại 2 là
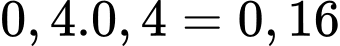
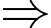 Xác suất bắn trúng ít nhất 1 viên của xạ thủ loại 2 là
Xác suất bắn trúng ít nhất 1 viên của xạ thủ loại 2 là 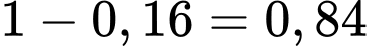
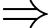 Xác suất viên đạn trúng đích là
Xác suất viên đạn trúng đích là 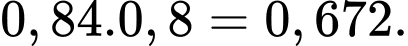
Vậy xác suất viên đạn bắn trúng đích là
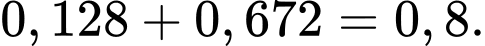 Đáp án: B
Đáp án: B
Câu 9 [582732]: Từ các chữ số 1, 2, 3, 4, 5, 6 lập các số có 5 chữ số. Tính xác suất trong các số vừa lập ở trên lấy được một số mà trong đó chữ số 1 có mặt 3 lần, các chữ số còn lại có mặt không quá 1 lần.
A, 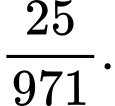
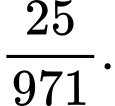
B, 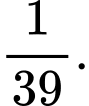
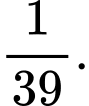
C, 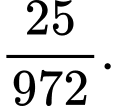
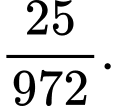
D, 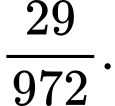
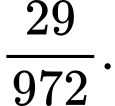
Gọi A là biến cố lấy được số có 5 chữ số mà trong đó chữ số 1 có mặt 3 lần, các chữ số còn lại có mặt không quá 1 lần.
Ta có: Từ các chữ số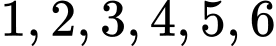 lập được số các số có 5 chữ số là:
lập được số các số có 5 chữ số là: 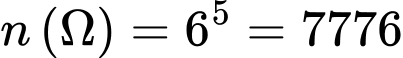 (số).
(số).
Xếp chữ số 1 vào 3 vị trí trong 5 vị trí có: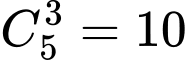 (cách).
(cách).
Lấy 2 trong 5 chữ số còn lại xếp vào 2 vị trí trống có: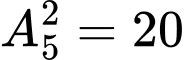 (cách).
(cách).
Số các số có 5 chữ số mà trong đó chữ số 1 có mặt 3 lần, các chữ số còn lại có mặt không quá 1 lần là: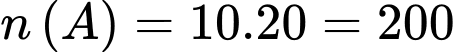 (số).
(số).
Vậy xác suất trong các số vừa lập ở trên lấy được một số mà trong đó chữ số 1 có mặt 3 lần, các chữ số còn lại có mặt không quá 1 lần là:
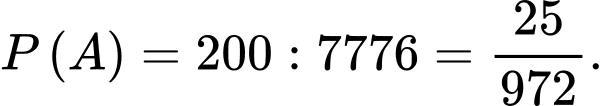 Đáp án: C
Đáp án: C
Ta có: Từ các chữ số
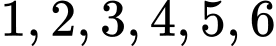 lập được số các số có 5 chữ số là:
lập được số các số có 5 chữ số là: 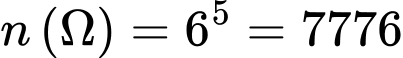 (số).
(số).Xếp chữ số 1 vào 3 vị trí trong 5 vị trí có:
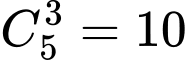 (cách).
(cách).Lấy 2 trong 5 chữ số còn lại xếp vào 2 vị trí trống có:
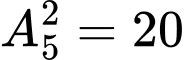 (cách).
(cách).Số các số có 5 chữ số mà trong đó chữ số 1 có mặt 3 lần, các chữ số còn lại có mặt không quá 1 lần là:
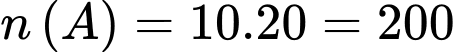 (số).
(số).Vậy xác suất trong các số vừa lập ở trên lấy được một số mà trong đó chữ số 1 có mặt 3 lần, các chữ số còn lại có mặt không quá 1 lần là:
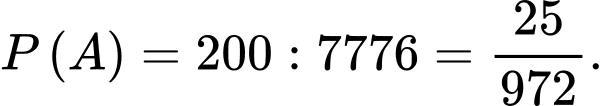 Đáp án: C
Đáp án: C
Câu 10 [582733]: Một đoàn tình nguyện đến một trường tiểu học miền núi để trao tặng 20 suất quà cho 10 em học sinh nghèo học giỏi. Trong 20 suất quà đó gồm 7 chiếc áo mùa đông, 9 thùng sữa tươi và 4 chiếc cặp sách. Tất cả các suất quà đều có giá trị tương đương nhau. Biết rằng mỗi em được nhận 2 suất quà khác loại (ví dụ : 1 chiếc áo và 1 thùng sữa tươi). Trong số các em được nhận quà có hai em Việt và Nam. Tính xác suất để hai em Việt và Nam đó nhận được suất quà giống nhau.
A, 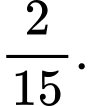
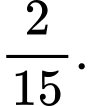
B, 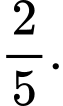
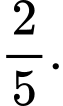
C, 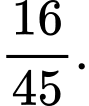
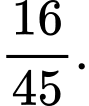
D, 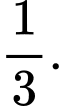
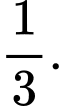
Ta chia các suất quà như sau : 6 áo và 6 thùng sữa, 3 thùng sữa và 3 cặp, 1 cặp và 1 áo. Số phần tử của không gian mẫu: 
Trường hợp 1: Nam và Việt nhận một thùng sữa và một chiếc áo: Có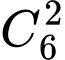 cách.
cách.
Trường hợp 2: Nam và Việt nhận một thùng sữa và một chiếc cặp: Có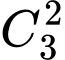 cách.
cách.
Gọi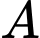 là biến cố "Hai em Việt và Nam đó nhận được suất quà giống nhau".
là biến cố "Hai em Việt và Nam đó nhận được suất quà giống nhau".
Ta có: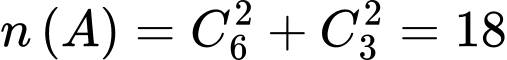
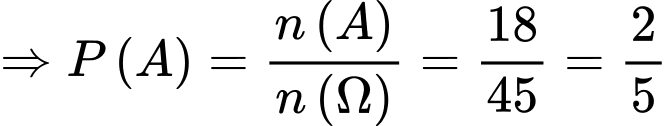
Vậy xác suất đề hai em Việt và Nam nhận được suất quà giống nhau là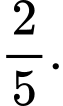 Đáp án: B
Đáp án: B

Trường hợp 1: Nam và Việt nhận một thùng sữa và một chiếc áo: Có
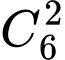 cách.
cách.Trường hợp 2: Nam và Việt nhận một thùng sữa và một chiếc cặp: Có
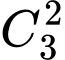 cách.
cách.Gọi
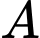 là biến cố "Hai em Việt và Nam đó nhận được suất quà giống nhau".
là biến cố "Hai em Việt và Nam đó nhận được suất quà giống nhau".Ta có:
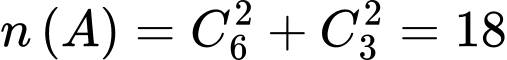
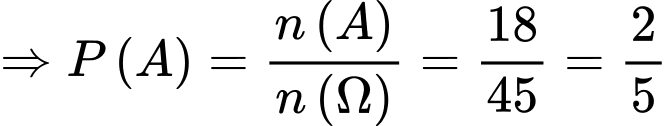
Vậy xác suất đề hai em Việt và Nam nhận được suất quà giống nhau là
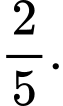 Đáp án: B
Đáp án: B
Câu 11 [582734]: Có hai lô hàng. Người ta lấy ngẫu nhiên từ mỗi lô hàng một sản phẩm. Xác suất để lấy được sản phẩm chất lượng tốt ở từng lô hàng lầm lượt là 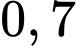 và
và 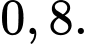 Tính xác suất để trong hai sản phẩm được lấy ra có đúng một sản phẩm có chất lượng tốt.
Tính xác suất để trong hai sản phẩm được lấy ra có đúng một sản phẩm có chất lượng tốt.
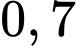 và
và 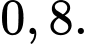 Tính xác suất để trong hai sản phẩm được lấy ra có đúng một sản phẩm có chất lượng tốt.
Tính xác suất để trong hai sản phẩm được lấy ra có đúng một sản phẩm có chất lượng tốt. A, 0,38.
B, 0,48.
C, 0,39.
D, 0,4.
Gọi  là biến cố “ Lấy được sản phẩm tốt từ lô hàng thứ nhất ’’.
là biến cố “ Lấy được sản phẩm tốt từ lô hàng thứ nhất ’’.
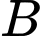 là biến cố “ Lấy được sản phẩm tốt từ lô hàng thứ hai ’’.
là biến cố “ Lấy được sản phẩm tốt từ lô hàng thứ hai ’’.
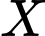 là biến cố “ trong hai sản phẩm lấy ra có đúng một sản phẩm có chất lượng tốt ’’.
là biến cố “ trong hai sản phẩm lấy ra có đúng một sản phẩm có chất lượng tốt ’’.
Ta có :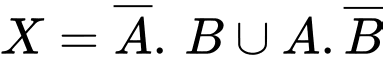
Do và
và  xung khắc đồng thời các cặp biến cố
xung khắc đồng thời các cặp biến cố 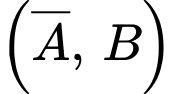 và
và 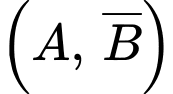 độc lập
độc lập
Nên ta có:
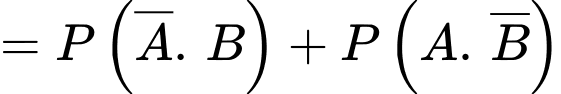
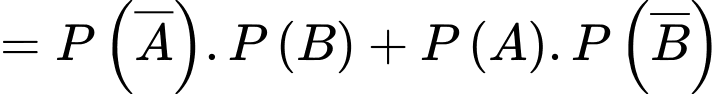
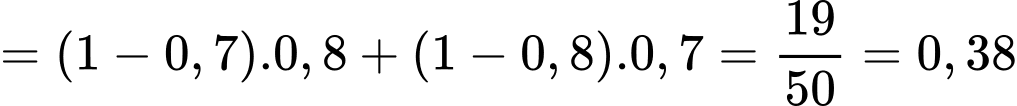 Đáp án: A
Đáp án: A
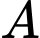 là biến cố “ Lấy được sản phẩm tốt từ lô hàng thứ nhất ’’.
là biến cố “ Lấy được sản phẩm tốt từ lô hàng thứ nhất ’’.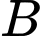 là biến cố “ Lấy được sản phẩm tốt từ lô hàng thứ hai ’’.
là biến cố “ Lấy được sản phẩm tốt từ lô hàng thứ hai ’’.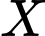 là biến cố “ trong hai sản phẩm lấy ra có đúng một sản phẩm có chất lượng tốt ’’.
là biến cố “ trong hai sản phẩm lấy ra có đúng một sản phẩm có chất lượng tốt ’’.Ta có :
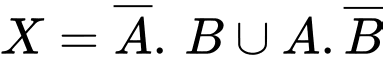
Do
 và
và  xung khắc đồng thời các cặp biến cố
xung khắc đồng thời các cặp biến cố 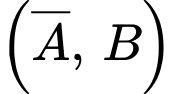 và
và 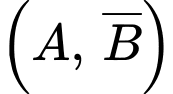 độc lập
độc lậpNên ta có:

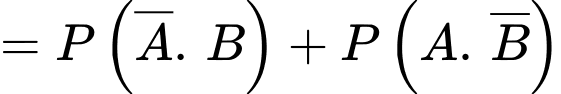
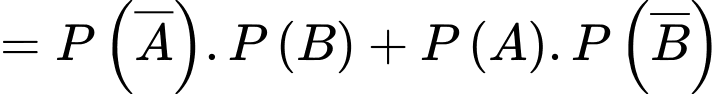
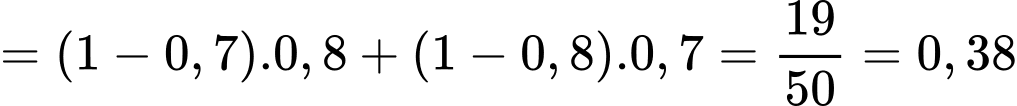 Đáp án: A
Đáp án: A
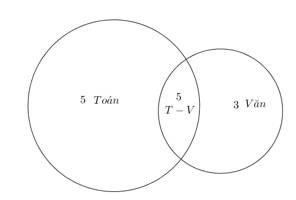
Câu 12 [582735]: Một lớp có 45 học sinh trong đó có 10 học sinh giỏi toán, 8 học sinh giỏi Văn trong đó có 5 học sinh giỏi Toán lẫn Văn. Chọn ngẫu nhiên 2 học sinh. Tính xác suất để 2 học sinh được chọn chỉ giỏi Toán hoặc Văn.
A, 28.
B, 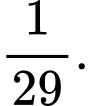
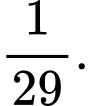
C, 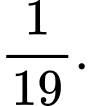
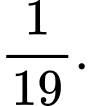
D, 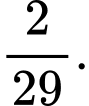
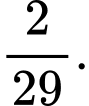
Chọn B
Số phần tử không gian mẫu là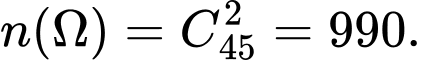
Gọi biến cố “Hai học sinh được chọn chỉ giỏi Toán hoặc Văn”.
“Hai học sinh được chọn chỉ giỏi Toán hoặc Văn”.
Sử dụng biểu đồ Venn để xác định số học sinh giỏi: Toán; Văn; Toán-Văn.
Hai học sinh được chọn chỉ giỏi Toán có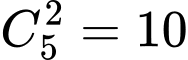 (cách).
(cách).
Hai học sinh được chọn chỉ giỏi Văn có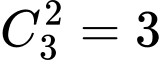 (cách).
(cách).
Hai học sinh được chọn có một chỉ giỏi Toán và một chỉ giỏi Văn có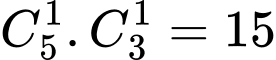 (cách).
(cách).
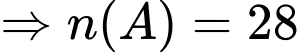
Vậy xác suất của biến cố là
là 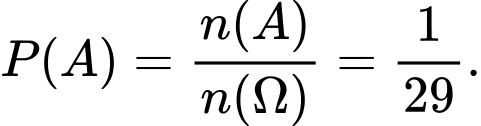
Hoặc: Có 5 học sinh giỏi toán, 3 học sinh giỏi Văn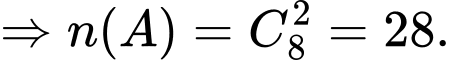 Đáp án: B
Đáp án: B
Số phần tử không gian mẫu là
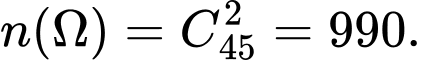
Gọi biến cố
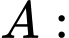 “Hai học sinh được chọn chỉ giỏi Toán hoặc Văn”.
“Hai học sinh được chọn chỉ giỏi Toán hoặc Văn”.Sử dụng biểu đồ Venn để xác định số học sinh giỏi: Toán; Văn; Toán-Văn.

Hai học sinh được chọn chỉ giỏi Toán có
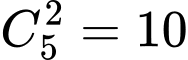 (cách).
(cách).Hai học sinh được chọn chỉ giỏi Văn có
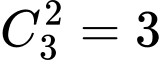 (cách).
(cách).Hai học sinh được chọn có một chỉ giỏi Toán và một chỉ giỏi Văn có
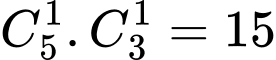 (cách).
(cách).
Vậy xác suất của biến cố
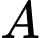 là
là 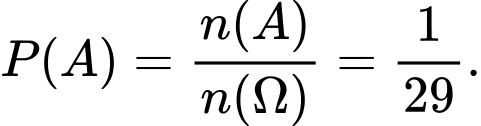
Hoặc: Có 5 học sinh giỏi toán, 3 học sinh giỏi Văn
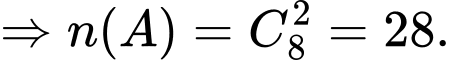 Đáp án: B
Đáp án: B
Câu 13 [582736]: Bạn Đăng có một bảng gồm  điểm, các điểm cách nhau 1 đơn vị. Lấy ra ba đỉnh bất kì trong 20 đỉnh trên, tính xác suất để ba đỉnh đó tạo được thành tam giác?
điểm, các điểm cách nhau 1 đơn vị. Lấy ra ba đỉnh bất kì trong 20 đỉnh trên, tính xác suất để ba đỉnh đó tạo được thành tam giác?
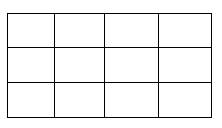
 điểm, các điểm cách nhau 1 đơn vị. Lấy ra ba đỉnh bất kì trong 20 đỉnh trên, tính xác suất để ba đỉnh đó tạo được thành tam giác?
điểm, các điểm cách nhau 1 đơn vị. Lấy ra ba đỉnh bất kì trong 20 đỉnh trên, tính xác suất để ba đỉnh đó tạo được thành tam giác?
A, 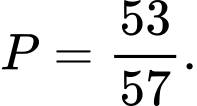
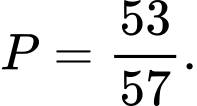
B, 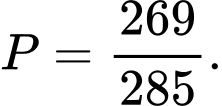
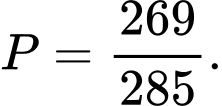
C, 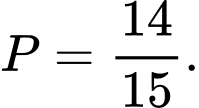
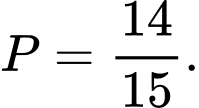
D, 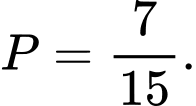
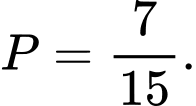
Không gian mẫu 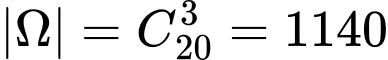
Gọi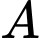 là biến cố “để ba đỉnh đó tạo được thành tam giác”
là biến cố “để ba đỉnh đó tạo được thành tam giác”
Xảy ra các trường hợp vi phạm sau:
- Ba điểm được chọn nằm trên hàng dọc ( có 5 hàng dọc) suy ra có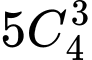
- Ba điểm được chọn nằm trên hàng ngang ( có 4 hàng ngang) suy ra có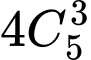
- Ba điểm được chọn nằm trên đường chéo có 3 điểm ( có 4 đường chéo như thế) suy ra có
- Ba điểm được chọn nằm trên đường chéo có 4 điểm ( có 4 đường chéo như thế) suy ra có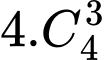
Suy ra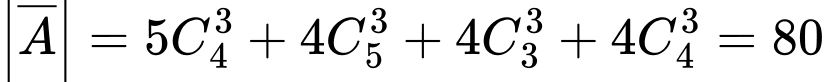
Suy ra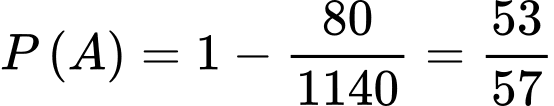 Đáp án: A
Đáp án: A
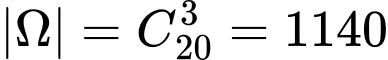
Gọi
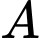 là biến cố “để ba đỉnh đó tạo được thành tam giác”
là biến cố “để ba đỉnh đó tạo được thành tam giác”Xảy ra các trường hợp vi phạm sau:
- Ba điểm được chọn nằm trên hàng dọc ( có 5 hàng dọc) suy ra có
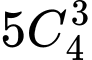
- Ba điểm được chọn nằm trên hàng ngang ( có 4 hàng ngang) suy ra có
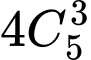
- Ba điểm được chọn nằm trên đường chéo có 3 điểm ( có 4 đường chéo như thế) suy ra có

- Ba điểm được chọn nằm trên đường chéo có 4 điểm ( có 4 đường chéo như thế) suy ra có
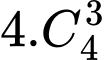
Suy ra
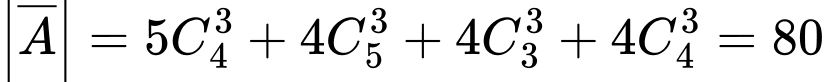
Suy ra
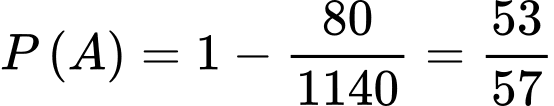 Đáp án: A
Đáp án: A
Câu 14 [582737]: Trong không gian 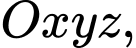 gọi
gọi 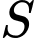 là tập hợp các điểm có tọa độ
là tập hợp các điểm có tọa độ 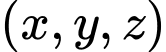 nguyên thỏa mãn
nguyên thỏa mãn 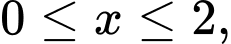
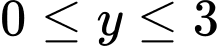 và
và 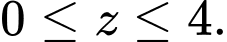 Chọn ngẫu nhiên 2 điểm phân biệt trong
Chọn ngẫu nhiên 2 điểm phân biệt trong 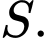 Xác suất để trung điểm của đoạn thẳng đó cũng thuộc
Xác suất để trung điểm của đoạn thẳng đó cũng thuộc 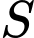 là:
là:
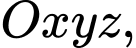 gọi
gọi 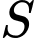 là tập hợp các điểm có tọa độ
là tập hợp các điểm có tọa độ 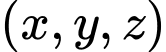 nguyên thỏa mãn
nguyên thỏa mãn 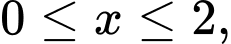
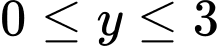 và
và 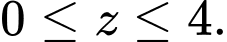 Chọn ngẫu nhiên 2 điểm phân biệt trong
Chọn ngẫu nhiên 2 điểm phân biệt trong 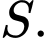 Xác suất để trung điểm của đoạn thẳng đó cũng thuộc
Xác suất để trung điểm của đoạn thẳng đó cũng thuộc 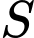 là:
là: A, 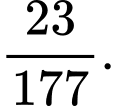
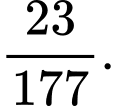
B, 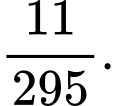
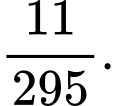
C, 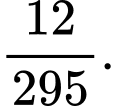
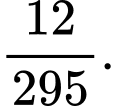
D, 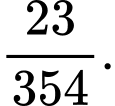
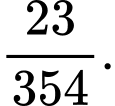
Không gian mẫu  là tập hợp tất cả các cách chọn ngẫu nhiên
là tập hợp tất cả các cách chọn ngẫu nhiên điểm trong
điểm trong  điểm của tập
điểm của tập  Ta được
Ta được 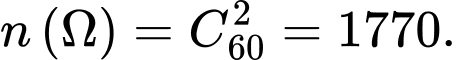
Gọi là biến cố :” Trung điểm của đoạn thẳng đó cũng thuộc
là biến cố :” Trung điểm của đoạn thẳng đó cũng thuộc  ”
”
Gọi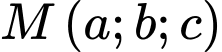 và
và 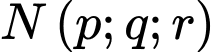 là hai điểm được chọn.
là hai điểm được chọn.
Ta thấy mỗi cặp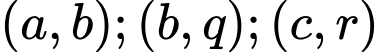 phải cùng tính chẵn lẻ.
phải cùng tính chẵn lẻ.
Suy ra số cách chọn các điểm như thế là
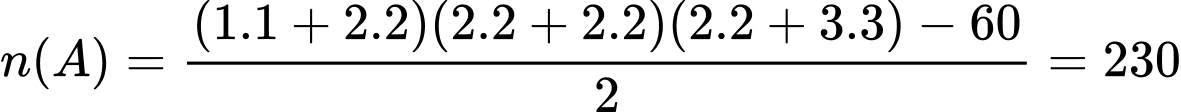
Vậy xác suất cần tính là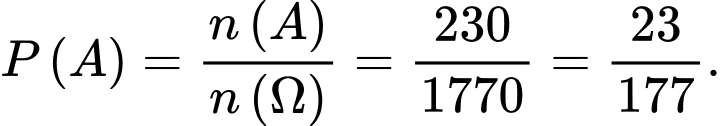 Đáp án: A
Đáp án: A
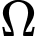 là tập hợp tất cả các cách chọn ngẫu nhiên
là tập hợp tất cả các cách chọn ngẫu nhiên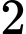 điểm trong
điểm trong 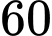 điểm của tập
điểm của tập  Ta được
Ta được 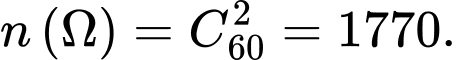
Gọi
 là biến cố :” Trung điểm của đoạn thẳng đó cũng thuộc
là biến cố :” Trung điểm của đoạn thẳng đó cũng thuộc  ”
”
Gọi
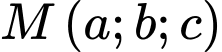 và
và 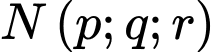 là hai điểm được chọn.
là hai điểm được chọn.
Ta thấy mỗi cặp
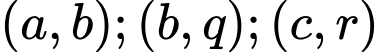 phải cùng tính chẵn lẻ.
phải cùng tính chẵn lẻ.
Suy ra số cách chọn các điểm như thế là
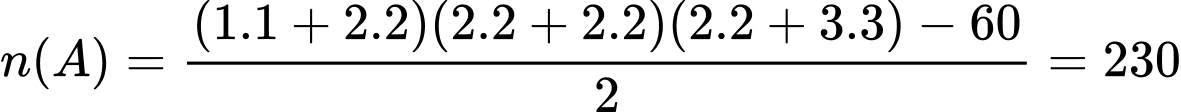
Vậy xác suất cần tính là
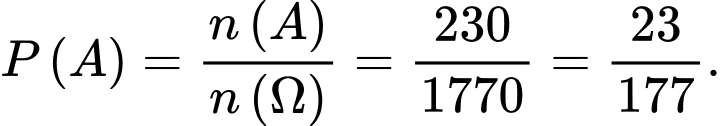 Đáp án: A
Đáp án: A
Câu 15 [582738]: Một vận động viên bắn súng, bắn ba viên đạn. Xác suất để trúng ba viên vòng 10 là 0,008, xác suất để 1 viên trúng vòng 8 là 0,15 và xác suất để 1 viên trúng dưới vòng 8 là 0,4. Biết rằng các lần bắn là độc lập với nhau. Tìm xác suất để vận động viên đạt ít nhất 28 điểm.
A, 1.
B, 0,0936.
C, 0,0835.
D, 0,0935.
Gọi 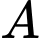 là biến cố “ 1 viên trúng vòng 10”. Khi đó từ giả thiết ta có :
là biến cố “ 1 viên trúng vòng 10”. Khi đó từ giả thiết ta có :
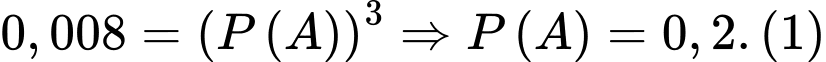
Gọi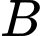 là biến cố “ 1 viên trúng vòng 9”.
là biến cố “ 1 viên trúng vòng 9”.  là biến cố “ 1 viên trúng vòng 8”,
là biến cố “ 1 viên trúng vòng 8”, 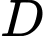 là biến cố “ 1 viên trúng dưới vòng 8”. Theo giả thiết ta có :
là biến cố “ 1 viên trúng dưới vòng 8”. Theo giả thiết ta có :
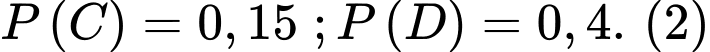
Rõ ràng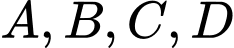 là các biến cố đôi một xung khắc với nhau nên ta có :
là các biến cố đôi một xung khắc với nhau nên ta có :
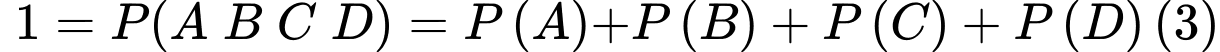
Từ suy ra
suy ra 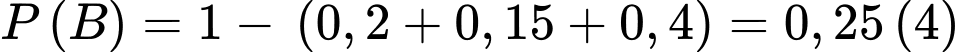
Gọi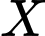 là biến cố “vận động viên đạt ít nhất 28 điểm”.
là biến cố “vận động viên đạt ít nhất 28 điểm”.
Để đạt được ít nhất 28 điểm thì:
- Hoặc là 2 viên trúng vòng 10, một viên vòng 8. Theo quy tắc cộng và nhân xác suất điều này xảy ra với xác suất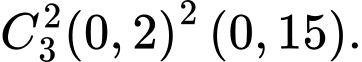
- Hoặc 2 viên trúng vòng 9 một viên trúng vòng 10. Theo quy tắc cộng và nhân xác suất điều này xảy ra với xác suất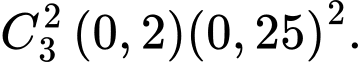
- Hoặc 2 viên trúng vòng 10, một viên trúng vòng 9. Điều này xảy ra với xác suất: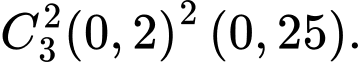
- Hoặc cả ba viên điều trúng vòng 10 với xác suất theo giả thiết là 0,008. Theo quy tắc cộng và nhân xác suất của các biến cố xung khắc, ta có:
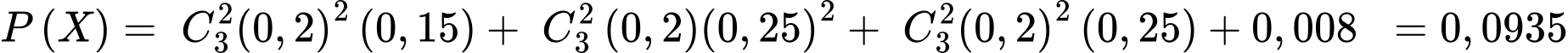
Vậy vận động viên bắn súng đạt ít nhất 28 điểm với xác suất là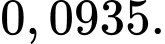 Đáp án: D
Đáp án: D
 là biến cố “ 1 viên trúng vòng 10”. Khi đó từ giả thiết ta có :
là biến cố “ 1 viên trúng vòng 10”. Khi đó từ giả thiết ta có :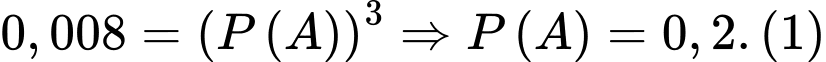
Gọi
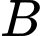 là biến cố “ 1 viên trúng vòng 9”.
là biến cố “ 1 viên trúng vòng 9”.  là biến cố “ 1 viên trúng vòng 8”,
là biến cố “ 1 viên trúng vòng 8”, 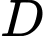 là biến cố “ 1 viên trúng dưới vòng 8”. Theo giả thiết ta có :
là biến cố “ 1 viên trúng dưới vòng 8”. Theo giả thiết ta có : 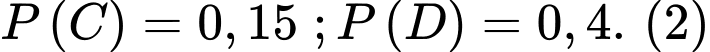
Rõ ràng
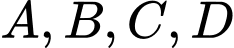 là các biến cố đôi một xung khắc với nhau nên ta có :
là các biến cố đôi một xung khắc với nhau nên ta có :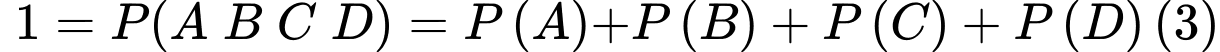
Từ
 suy ra
suy ra 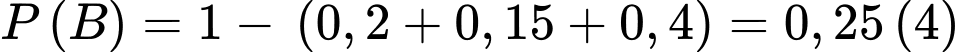
Gọi
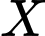 là biến cố “vận động viên đạt ít nhất 28 điểm”.
là biến cố “vận động viên đạt ít nhất 28 điểm”.Để đạt được ít nhất 28 điểm thì:
- Hoặc là 2 viên trúng vòng 10, một viên vòng 8. Theo quy tắc cộng và nhân xác suất điều này xảy ra với xác suất
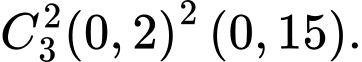
- Hoặc 2 viên trúng vòng 9 một viên trúng vòng 10. Theo quy tắc cộng và nhân xác suất điều này xảy ra với xác suất
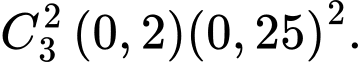
- Hoặc 2 viên trúng vòng 10, một viên trúng vòng 9. Điều này xảy ra với xác suất:
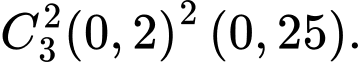
- Hoặc cả ba viên điều trúng vòng 10 với xác suất theo giả thiết là 0,008. Theo quy tắc cộng và nhân xác suất của các biến cố xung khắc, ta có:
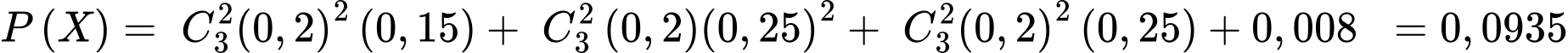
Vậy vận động viên bắn súng đạt ít nhất 28 điểm với xác suất là
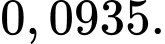 Đáp án: D
Đáp án: D Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 16 đến câu 18. Đáp án là số nguyên hoặc phân số tối giản (nếu có))
Câu 16 [582741]: Cho đa giác đều  đỉnh. Gọi
đỉnh. Gọi 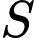 là tập hợp các tam giác có đỉnh là đỉnh của đa giác. Chọn ngẫu nhiên một tam giác trong tập
là tập hợp các tam giác có đỉnh là đỉnh của đa giác. Chọn ngẫu nhiên một tam giác trong tập 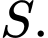 Tính xác suất để chọn được tam giác có một góc lớn hơn
Tính xác suất để chọn được tam giác có một góc lớn hơn 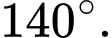
Đáp án:……
 đỉnh. Gọi
đỉnh. Gọi 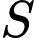 là tập hợp các tam giác có đỉnh là đỉnh của đa giác. Chọn ngẫu nhiên một tam giác trong tập
là tập hợp các tam giác có đỉnh là đỉnh của đa giác. Chọn ngẫu nhiên một tam giác trong tập 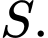 Tính xác suất để chọn được tam giác có một góc lớn hơn
Tính xác suất để chọn được tam giác có một góc lớn hơn 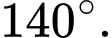
Đáp án:……
Đáp án: 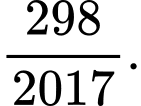
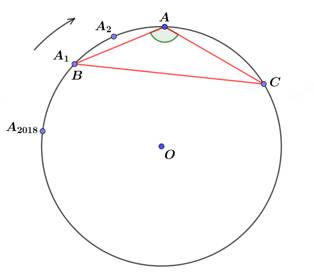
Số đo góc ở tâm chắn mỗi cạnh của đa giác bằng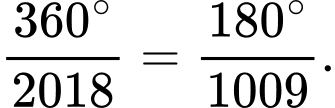
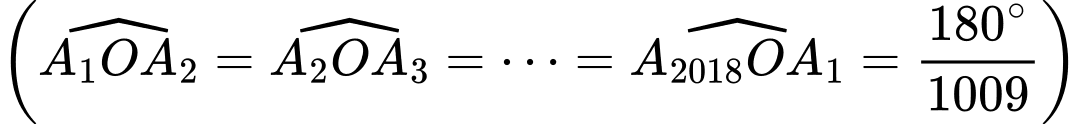
Tam giác có đỉnh là đỉnh của đa giác nên các góc của tam giác là các góc nội tiếp Để tạo một tam giác có
Để tạo một tam giác có 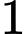 góc lớn hơn
góc lớn hơn 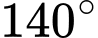 ta làm như sau:
ta làm như sau:
• Chọn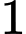 đỉnh làm đỉnh có góc lớn hơn
đỉnh làm đỉnh có góc lớn hơn 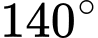 , có
, có 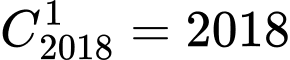 , giả sử là đỉnh
, giả sử là đỉnh 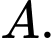
• Với 2 đỉnh còn lại giả sử là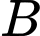 ,
,  có số đo góc
có số đo góc 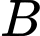 ,
,  lần lượt là
lần lượt là 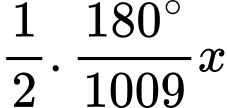 ,
, 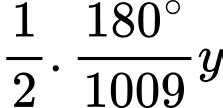 (Giải thích: số đo góc
(Giải thích: số đo góc 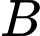 ,
,  bằng bội nguyên dương là số đo của góc nội tiếp chắn một cạnh của đa giác).
bằng bội nguyên dương là số đo của góc nội tiếp chắn một cạnh của đa giác).
Số đo góc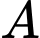 là
là
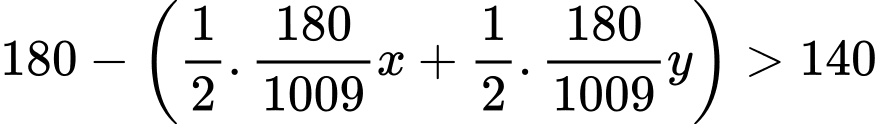 (độ)
(độ)
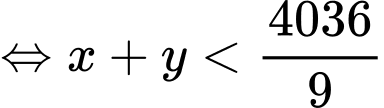
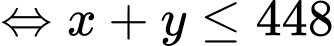
• Số cách chọn hai đỉnh ,
,  bằng số nghiệm nguyên dương của phương trình
bằng số nghiệm nguyên dương của phương trình  và bằng
và bằng 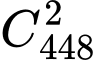 (theo bài toán chia kẹo euler). Suy ra số tam giác thỏa yêu cầu bài toán là
(theo bài toán chia kẹo euler). Suy ra số tam giác thỏa yêu cầu bài toán là 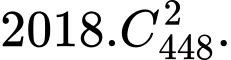
Vậy xác suất cần tìm là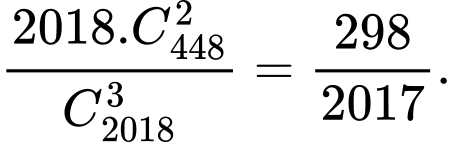
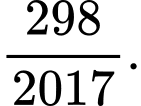

Số đo góc ở tâm chắn mỗi cạnh của đa giác bằng
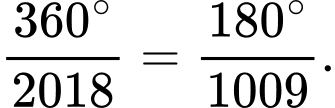
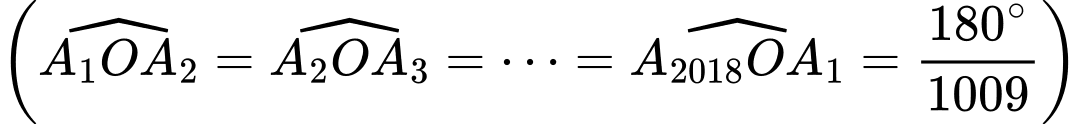
Tam giác có đỉnh là đỉnh của đa giác nên các góc của tam giác là các góc nội tiếp
 Để tạo một tam giác có
Để tạo một tam giác có 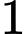 góc lớn hơn
góc lớn hơn 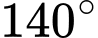 ta làm như sau:
ta làm như sau:• Chọn
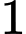 đỉnh làm đỉnh có góc lớn hơn
đỉnh làm đỉnh có góc lớn hơn 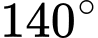 , có
, có 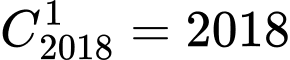 , giả sử là đỉnh
, giả sử là đỉnh 
• Với 2 đỉnh còn lại giả sử là
 ,
,  có số đo góc
có số đo góc 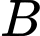 ,
,  lần lượt là
lần lượt là 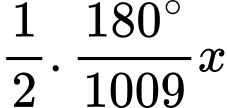 ,
, 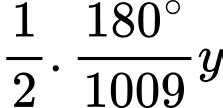 (Giải thích: số đo góc
(Giải thích: số đo góc 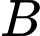 ,
,  bằng bội nguyên dương là số đo của góc nội tiếp chắn một cạnh của đa giác).
bằng bội nguyên dương là số đo của góc nội tiếp chắn một cạnh của đa giác).Số đo góc
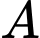 là
là (độ)
(độ)
• Số cách chọn hai đỉnh
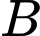 ,
,  bằng số nghiệm nguyên dương của phương trình
bằng số nghiệm nguyên dương của phương trình  và bằng
và bằng 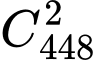 (theo bài toán chia kẹo euler). Suy ra số tam giác thỏa yêu cầu bài toán là
(theo bài toán chia kẹo euler). Suy ra số tam giác thỏa yêu cầu bài toán là 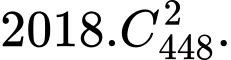
Vậy xác suất cần tìm là
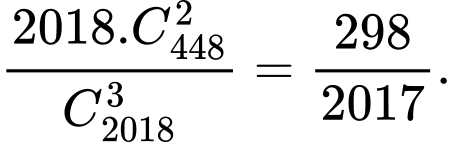
Câu 17 [582742]: Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp 12A, 3 học sinh lớp 12B và 5 học sinh lớp 12C thành một hàng ngang. Tính xác suất để trong 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau.
Đáp án:……
Đáp án:……
Đáp án: 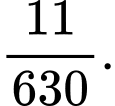
Số phần tử không gian mẫu chính là số cách xếp 10 học sinh vào 10 vị trí. Suy ra số phần tử của không gian mẫu là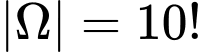
Gọi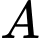 là biến cố: “ Xếp 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau ”. Sắp xếp 5 học sinh lớp 12C vào 5 vị trí, có 5! cách. Ứng mỗi cách xếp 5 học sinh lớp 12C sẽ có 6 khoảng trống gồm 4 vị trí ở giữa và hai vị trí hai đầu để xếp các học sinh còn lại.
là biến cố: “ Xếp 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau ”. Sắp xếp 5 học sinh lớp 12C vào 5 vị trí, có 5! cách. Ứng mỗi cách xếp 5 học sinh lớp 12C sẽ có 6 khoảng trống gồm 4 vị trí ở giữa và hai vị trí hai đầu để xếp các học sinh còn lại.

* TH1: Xếp 3 học sinh lớp 12B vào 4 vị trí trống ở giữa (không xếp vào hai đầu), có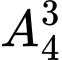 cách.
cách.
Ứng với mỗi cách xếp đó, chọn lấy 1 trong 2 học sinh lớp 12A xếp vào vị trí trống thứ 4
(để hai học sinh lớp 12C không được ngồi cạnh nhau), có 2 cách.
Ứng với mỗi cách xếp được 9 học sinh trên sẽ tạo ra 10 vị trí trống, bỏ đi 2 vị trí trống hai bên học sinh lớp 12A, thì còn 8 vị trí trống để xếp 1 học sinh lớp 12A còn lại.
Theo quy tắc nhân ta có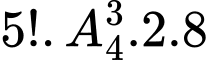 cách.
cách.
*TH2: Xếp 2 trong 3 học sinh lớp 12B vào 4 vị trí trống ở giữa và học sinh còn lại xếp vào hai đầu có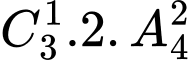 cách .
cách .
Ứng với mỗi cách xếp đó sẽ còn 2 vị trí trống ở giữa, xếp 2 học sinh lớp 12A vào vị trí đó có 2 cách .
Theo quy tắc nhân ta có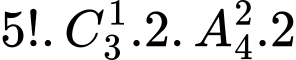 cách.
cách.
Do đó số cách sắp xếp không có học sinh cùng lớp nào ngồi cạnh nhau là:
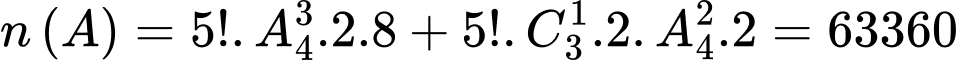
Vậy xác suất của biến cố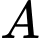 là :
là : 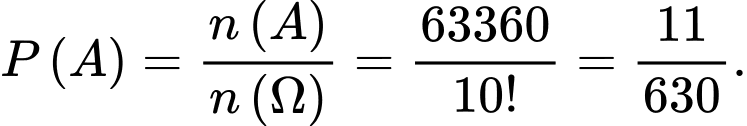
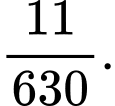
Số phần tử không gian mẫu chính là số cách xếp 10 học sinh vào 10 vị trí. Suy ra số phần tử của không gian mẫu là
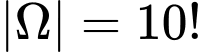
Gọi
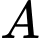 là biến cố: “ Xếp 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau ”. Sắp xếp 5 học sinh lớp 12C vào 5 vị trí, có 5! cách. Ứng mỗi cách xếp 5 học sinh lớp 12C sẽ có 6 khoảng trống gồm 4 vị trí ở giữa và hai vị trí hai đầu để xếp các học sinh còn lại.
là biến cố: “ Xếp 10 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau ”. Sắp xếp 5 học sinh lớp 12C vào 5 vị trí, có 5! cách. Ứng mỗi cách xếp 5 học sinh lớp 12C sẽ có 6 khoảng trống gồm 4 vị trí ở giữa và hai vị trí hai đầu để xếp các học sinh còn lại.
* TH1: Xếp 3 học sinh lớp 12B vào 4 vị trí trống ở giữa (không xếp vào hai đầu), có
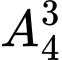 cách.
cách.Ứng với mỗi cách xếp đó, chọn lấy 1 trong 2 học sinh lớp 12A xếp vào vị trí trống thứ 4
(để hai học sinh lớp 12C không được ngồi cạnh nhau), có 2 cách.
Ứng với mỗi cách xếp được 9 học sinh trên sẽ tạo ra 10 vị trí trống, bỏ đi 2 vị trí trống hai bên học sinh lớp 12A, thì còn 8 vị trí trống để xếp 1 học sinh lớp 12A còn lại.
Theo quy tắc nhân ta có
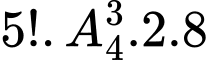 cách.
cách. *TH2: Xếp 2 trong 3 học sinh lớp 12B vào 4 vị trí trống ở giữa và học sinh còn lại xếp vào hai đầu có
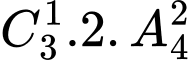 cách .
cách .Ứng với mỗi cách xếp đó sẽ còn 2 vị trí trống ở giữa, xếp 2 học sinh lớp 12A vào vị trí đó có 2 cách .
Theo quy tắc nhân ta có
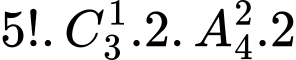 cách.
cách.Do đó số cách sắp xếp không có học sinh cùng lớp nào ngồi cạnh nhau là:
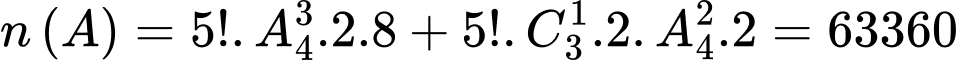
Vậy xác suất của biến cố
 là :
là : 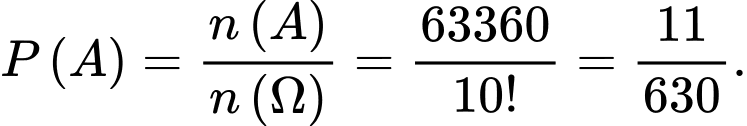
Câu 18 [582743]: Ba cầu thủ sút phạt đền 11m, mỗi người đá một lần với xác suất làm bàn tương ướng là 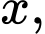
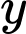 và 0,6 (với
và 0,6 (với 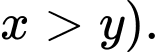 Biết xác suất để ít nhất một trong ba cầu thủ ghi bàn là 0,976 và xác suất để cả 3 cầu thủ đều ghi bàn là 0,336. Tính xác suất để có đúng hai cầu thủ ghi bàn
Biết xác suất để ít nhất một trong ba cầu thủ ghi bàn là 0,976 và xác suất để cả 3 cầu thủ đều ghi bàn là 0,336. Tính xác suất để có đúng hai cầu thủ ghi bàn
Đáp án:……
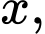
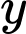 và 0,6 (với
và 0,6 (với 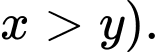 Biết xác suất để ít nhất một trong ba cầu thủ ghi bàn là 0,976 và xác suất để cả 3 cầu thủ đều ghi bàn là 0,336. Tính xác suất để có đúng hai cầu thủ ghi bàn
Biết xác suất để ít nhất một trong ba cầu thủ ghi bàn là 0,976 và xác suất để cả 3 cầu thủ đều ghi bàn là 0,336. Tính xác suất để có đúng hai cầu thủ ghi bànĐáp án:……
Gọi 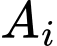 là biến cố “người thứ
là biến cố “người thứ 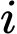 ghi bàn” với
ghi bàn” với 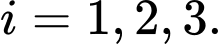
Ta có các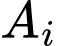 độc lập với nhau và
độc lập với nhau và 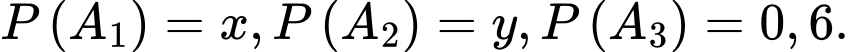
Gọi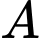 là biến cố: “ Có ít nhất một trong ba cầu thủ ghi bàn”
là biến cố: “ Có ít nhất một trong ba cầu thủ ghi bàn”
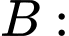 “Cả ba cầu thủ đều ghi bàn”
“Cả ba cầu thủ đều ghi bàn”
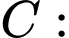 “Có đúng hai cầu thủ ghi bàn”
“Có đúng hai cầu thủ ghi bàn”
Ta có: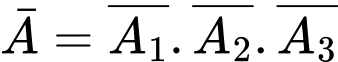
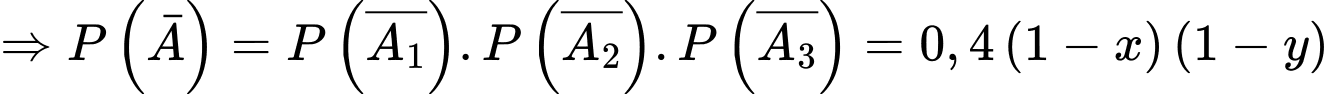
Nên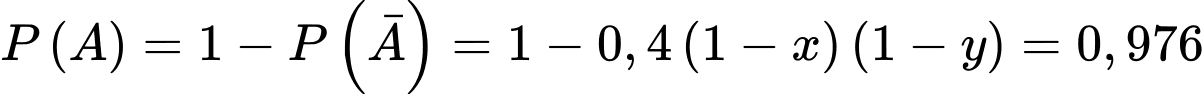
Suy ra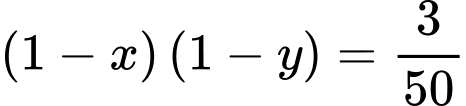
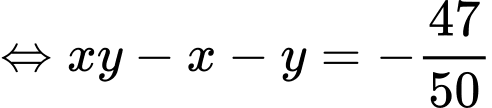 (1).
(1).
Tương tự: suy ra:
suy ra:
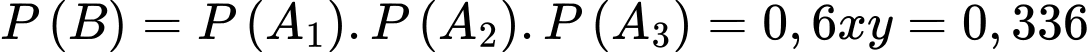 hay là
hay là 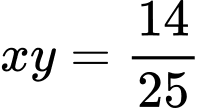
Từ (1) và (2) ta có hệ: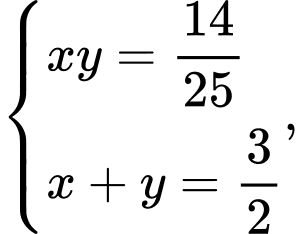 giải hệ này kết hợp với
giải hệ này kết hợp với  ta tìm được
ta tìm được 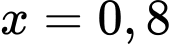 và
và 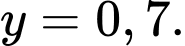
Ta có: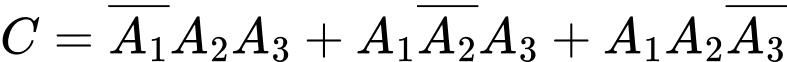
Nên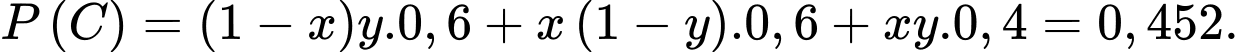
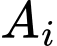 là biến cố “người thứ
là biến cố “người thứ 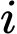 ghi bàn” với
ghi bàn” với 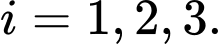
Ta có các
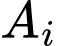 độc lập với nhau và
độc lập với nhau và 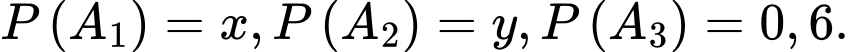
Gọi
 là biến cố: “ Có ít nhất một trong ba cầu thủ ghi bàn”
là biến cố: “ Có ít nhất một trong ba cầu thủ ghi bàn” “Cả ba cầu thủ đều ghi bàn”
“Cả ba cầu thủ đều ghi bàn” “Có đúng hai cầu thủ ghi bàn”
“Có đúng hai cầu thủ ghi bàn”Ta có:
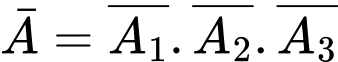
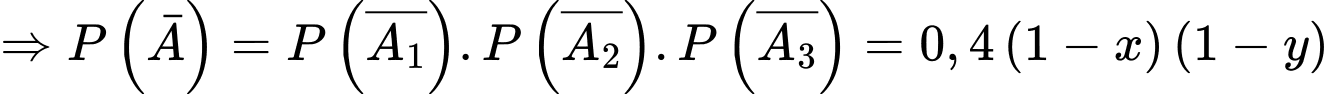
Nên
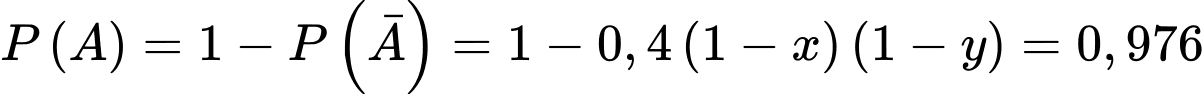
Suy ra
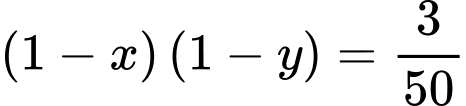
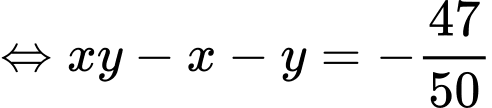 (1).
(1).Tương tự:
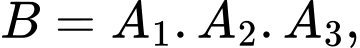 suy ra:
suy ra: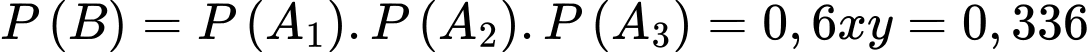 hay là
hay là 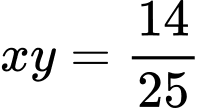
Từ (1) và (2) ta có hệ:
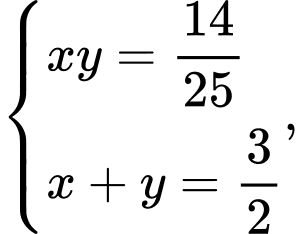 giải hệ này kết hợp với
giải hệ này kết hợp với  ta tìm được
ta tìm được 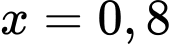 và
và 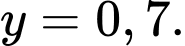
Ta có:
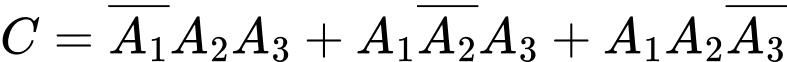
Nên
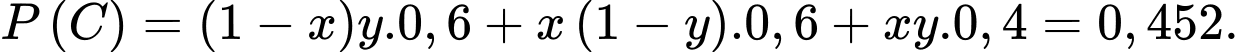
Dạng câu hỏi: Câu hỏi kéo thả.
Câu 19 [582744]: Kéo số ở các ô vuông thả vào vị trí thích hợp?

Một đoàn tàu có 4 toa được đánh số I, II, III, IV đỗ ở sân ga. Có 6 hành khách từ sân ga lên tàu. Mỗi người độc lập với nhau chọn ngẫu nhiên một toa. Xác suất để:
+) Toa I có 3 người, toa II có 2 người và toa III có 1 người là: ……….
+) Một toa có 3 người, một toa 2 người, một toa có 1 người là: ………
+) Mỗi toa có ít nhất một người là:..........

Một đoàn tàu có 4 toa được đánh số I, II, III, IV đỗ ở sân ga. Có 6 hành khách từ sân ga lên tàu. Mỗi người độc lập với nhau chọn ngẫu nhiên một toa. Xác suất để:
+) Toa I có 3 người, toa II có 2 người và toa III có 1 người là: ……….
+) Một toa có 3 người, một toa 2 người, một toa có 1 người là: ………
+) Mỗi toa có ít nhất một người là:..........
+) Lần lượt chọn 3 người xếp vào toa đầu, 2 người xếp vào toa II và 1 người xếp vào toa III, ta có 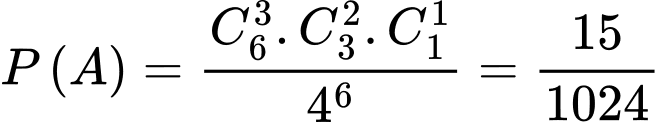
+) Chọn 3 người xếp vào 1 toa, rồi chọn 2 người xếp vào một toa khác, cuối cùng cho người còn lại vào 1 toa. Ta có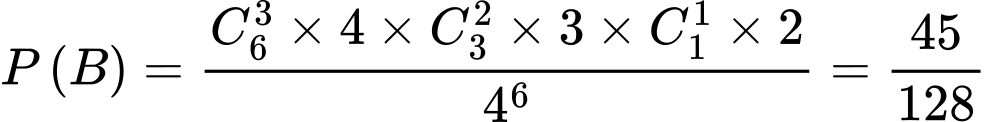
+) Mỗi toa ít nhất 1 người thì có 2 khả năng: 1 là 1 toa 3 người, 3 toa 1 người; 2 là 2 toa 2 người, 2 toa 1 người. Ta có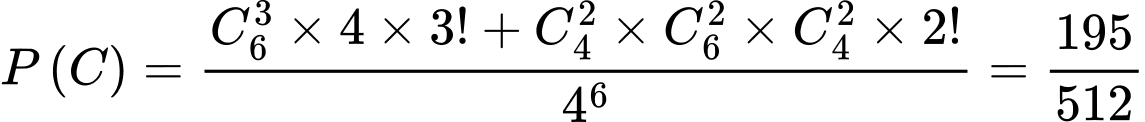
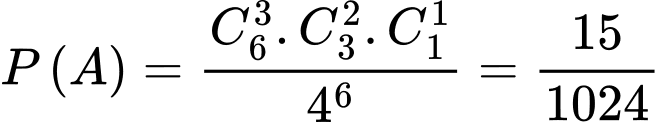
+) Chọn 3 người xếp vào 1 toa, rồi chọn 2 người xếp vào một toa khác, cuối cùng cho người còn lại vào 1 toa. Ta có
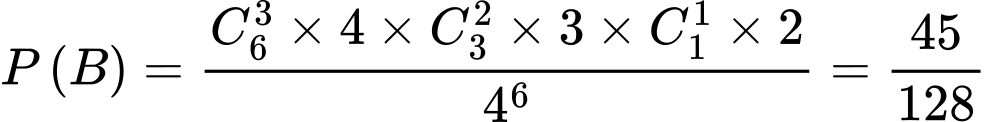
+) Mỗi toa ít nhất 1 người thì có 2 khả năng: 1 là 1 toa 3 người, 3 toa 1 người; 2 là 2 toa 2 người, 2 toa 1 người. Ta có