1. Dạng toán: Tìm tập xác định của hàm số
Câu 1 [582785]: Tồn tại bao nhiêu giá trị nguyên dương của 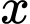 để hàm số
để hàm số  xác định
xác định
Đáp án:……
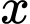 để hàm số
để hàm số  xác định
xác định Đáp án:……
Hàm số  xác định
xác định 
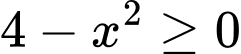
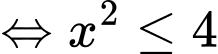

Mà và
và 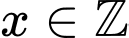 nên
nên 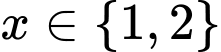
Vậy tồn tại 2 giá trị nguyên dương của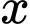 để hàm số
để hàm số  xác định.
xác định.
 xác định
xác định 
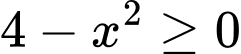
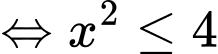

Mà
 và
và 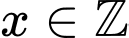 nên
nên 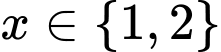
Vậy tồn tại 2 giá trị nguyên dương của
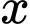 để hàm số
để hàm số  xác định.
xác định.
Câu 2 [582786]: Tìm tập xác định của hàm số sau: 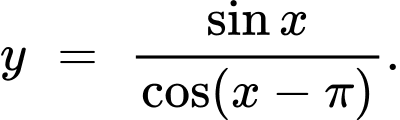
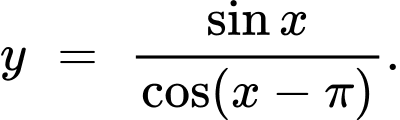
A, 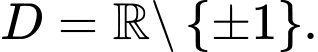
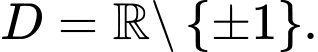
B, 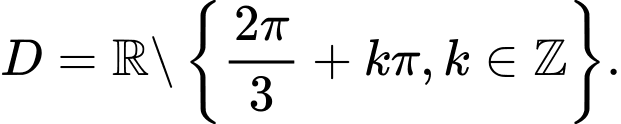
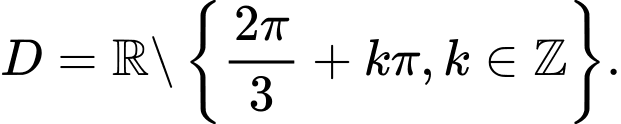
C, 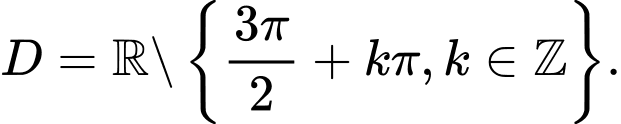
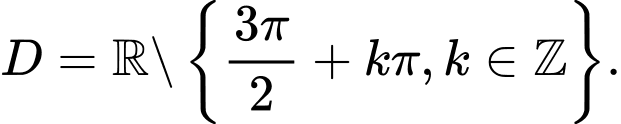
D, 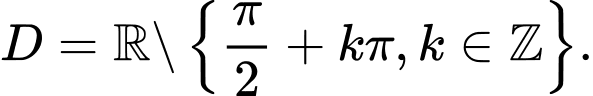
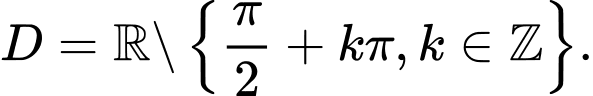
Hàm số 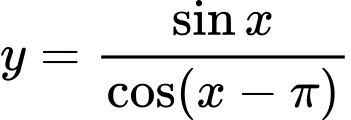 xác định
xác định 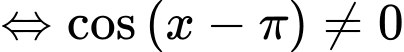
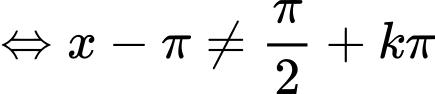
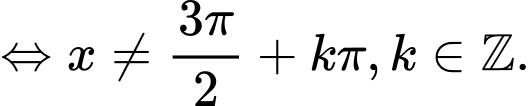
Vậy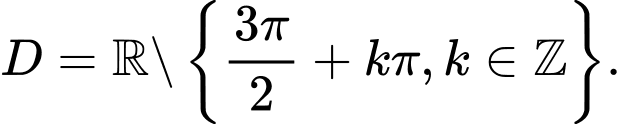
=> Chọn C Đáp án: C
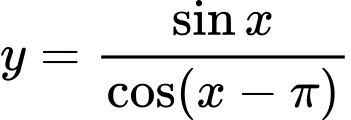 xác định
xác định 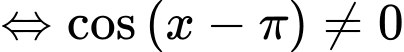
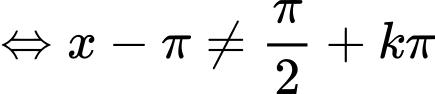
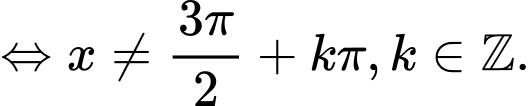
Vậy
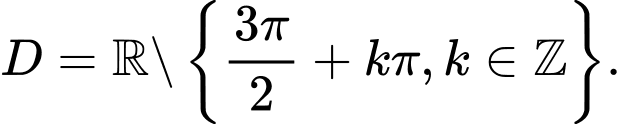
=> Chọn C Đáp án: C
Câu 3 [582787]: Tìm m để hàm số sau đây xác định trên 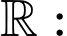
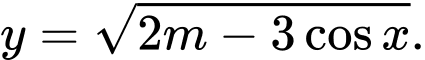
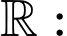
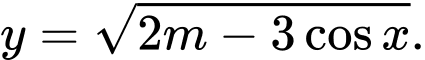
A, 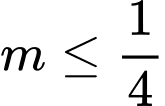 .
.
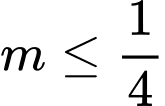 .
.B, 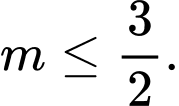
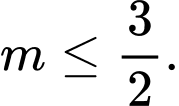
C, 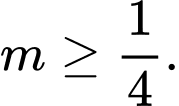
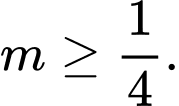
D, 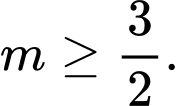
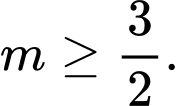
Hàm số đã cho xác định trên 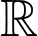 khi và chỉ khi
khi và chỉ khi 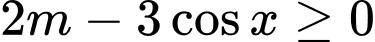
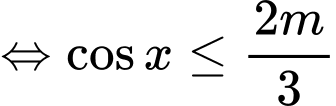
Bất đẳng thức trên đúng với mọi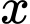 khi
khi 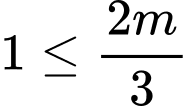
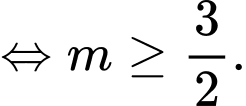
=>Chọn D Đáp án: D
 khi và chỉ khi
khi và chỉ khi 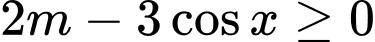
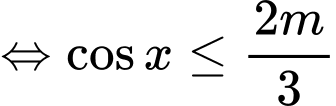
Bất đẳng thức trên đúng với mọi
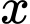 khi
khi 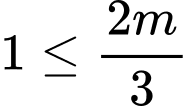
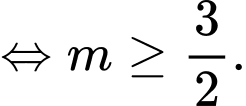
=>Chọn D Đáp án: D
2. Dạng toán: Xét tính chẵn lẻ của hàm số
Câu 4 [582788]: Trong các hàm số sau hàm số nào là hàm số chẵn?
A, 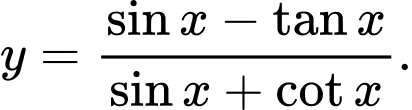
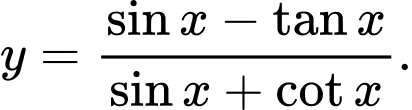
B, 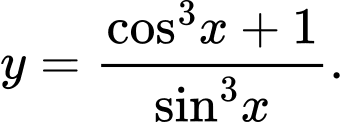
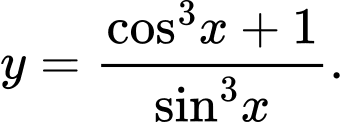
C, 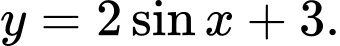
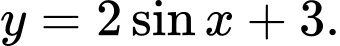
D, 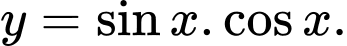
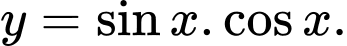
- Hàm số 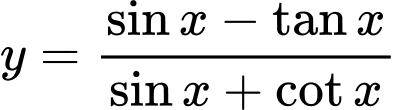 xác định khi
xác định khi
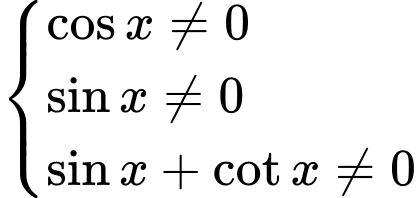
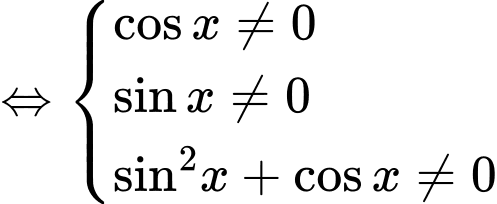
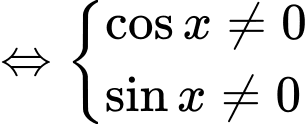
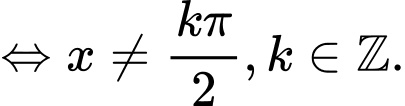
TXĐ: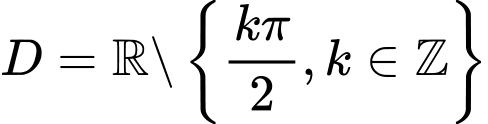 Suy ra
Suy ra 
Ta có: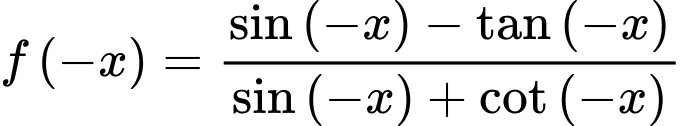
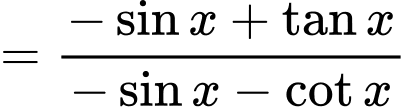
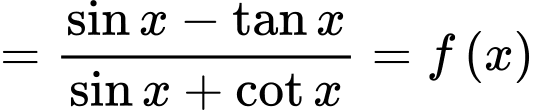
Do đó hàm số đã cho là hàm số chẵn.
-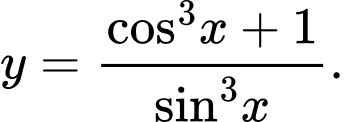
TXĐ: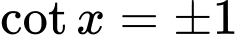
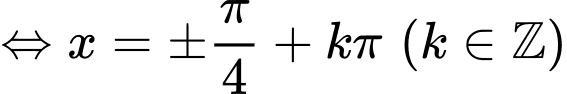 Suy ra
Suy ra 
Ta có: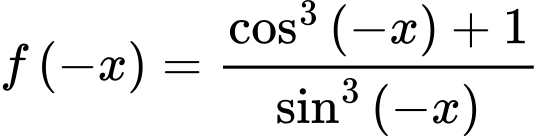
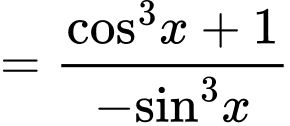
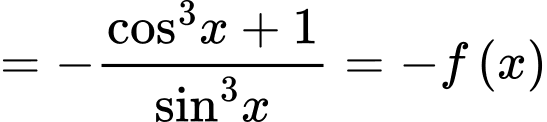
Do đó hàm số đã cho là hàm số lẻ.
-
TXĐ: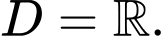 Suy ra
Suy ra 
Ta có:
 ;
; 
Nhận thấy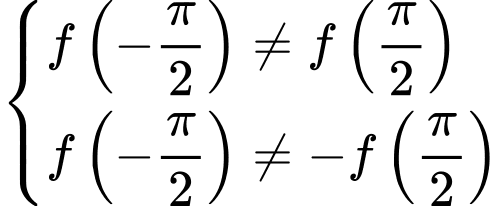
Do đó hàm số không chẵn không lẻ.
–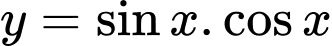
TXĐ: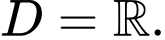 Suy ra
Suy ra 
Ta có: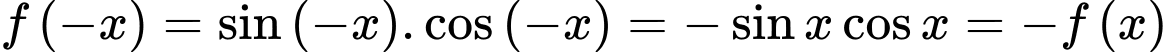
Do đó hàm số đã cho là hàm số lẻ.
=> Chọn A. Đáp án: A
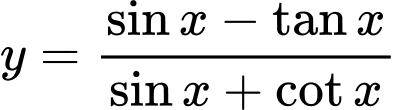 xác định khi
xác định khi 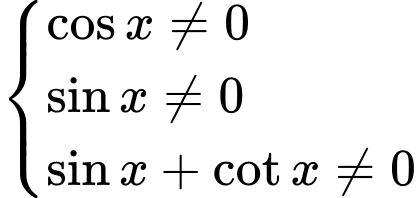
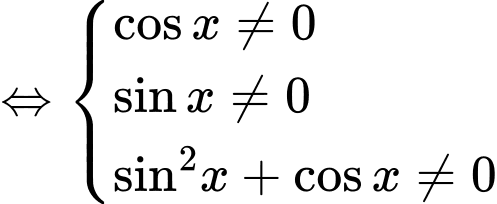
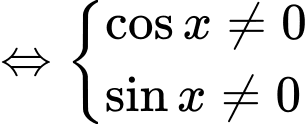
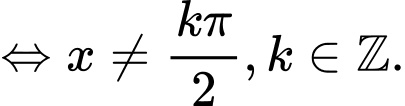
TXĐ:
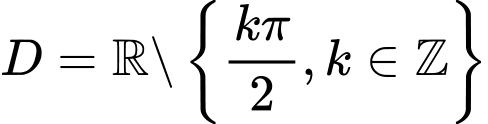 Suy ra
Suy ra 
Ta có:
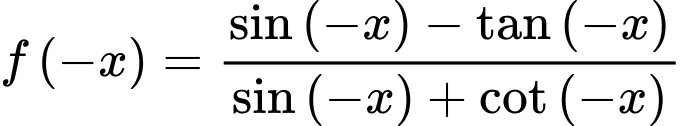
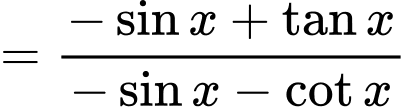
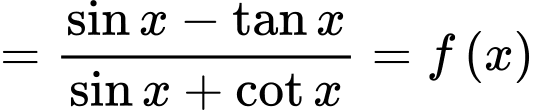
Do đó hàm số đã cho là hàm số chẵn.
-
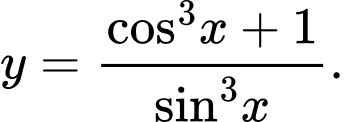
TXĐ:
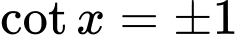
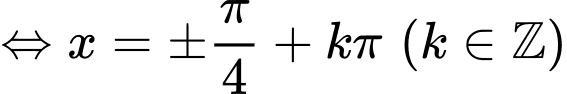 Suy ra
Suy ra 
Ta có:
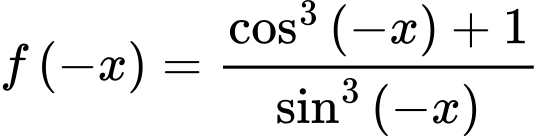
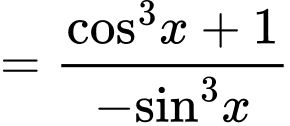
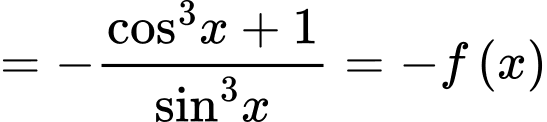
Do đó hàm số đã cho là hàm số lẻ.
-

TXĐ:
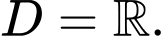 Suy ra
Suy ra 
Ta có:
 ;
; 
Nhận thấy
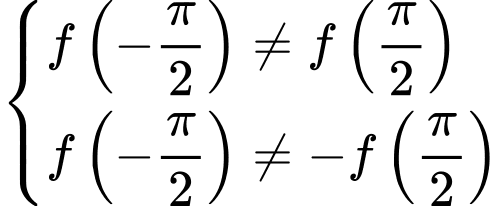
Do đó hàm số không chẵn không lẻ.
–
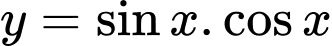
TXĐ:
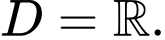 Suy ra
Suy ra 
Ta có:
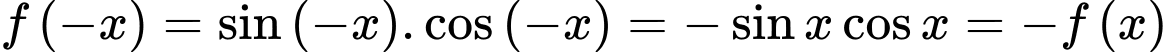
Do đó hàm số đã cho là hàm số lẻ.
=> Chọn A. Đáp án: A
Câu 5 [582789]: Xác định tham số 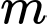 để hàm số sau:
để hàm số sau: 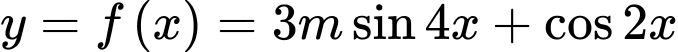 là hàm số chẵn.
là hàm số chẵn.
Đáp án:……
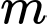 để hàm số sau:
để hàm số sau: 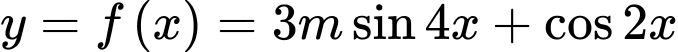 là hàm số chẵn.
là hàm số chẵn. Đáp án:……
TXĐ: 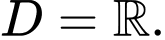 Suy ra
Suy ra 
Ta có: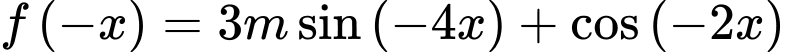
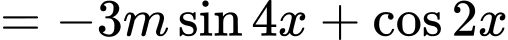
Để hàm số đã cho là hàm số chẵn thì:
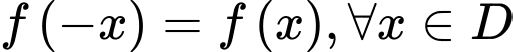
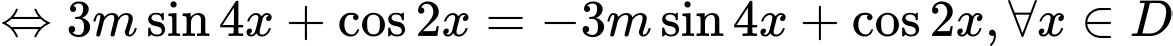

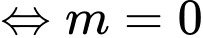
=> Điền: 0
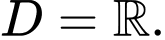 Suy ra
Suy ra 
Ta có:
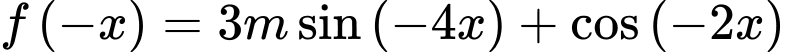
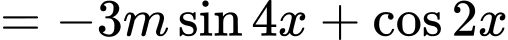
Để hàm số đã cho là hàm số chẵn thì:
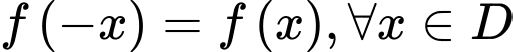
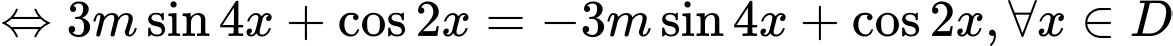

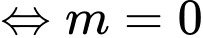
=> Điền: 0
3. Dạng toán: Tìm GTLN và GTNN của hàm số lượng giác
Câu 6 [582790]: Tìm GTLN của hàm số 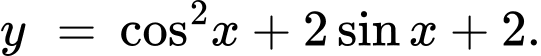
Đáp án:……
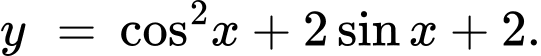
Đáp án:……
Ta có:
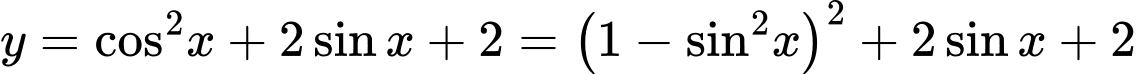
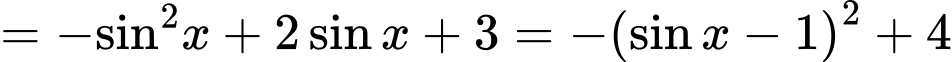
Vì
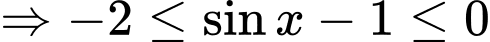
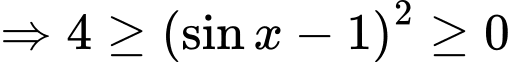
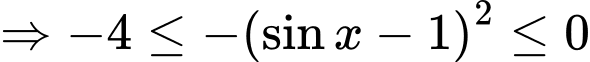
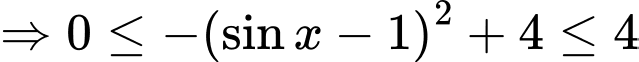
Hay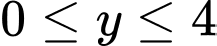
Do đó:
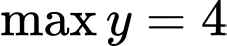 khi
khi 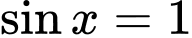
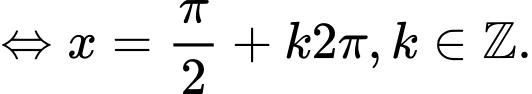
=> Điền: 4
* Lưu ý:
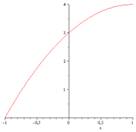
Nếu đặt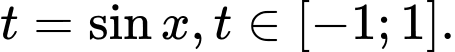 Ta có (P):
Ta có (P): 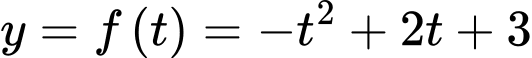 xác định với mọi
xác định với mọi  (P) có hoành độ đỉnh
(P) có hoành độ đỉnh 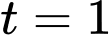 và trên đoạn
và trên đoạn 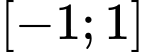 hàm số đồng biến nên hàm số đạt giá trị nhỏ nhất tại
hàm số đồng biến nên hàm số đạt giá trị nhỏ nhất tại 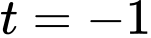 hay
hay 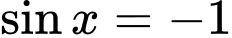 và đạt giá trị lớn nhất khi
và đạt giá trị lớn nhất khi 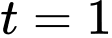 hay
hay 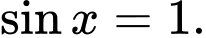
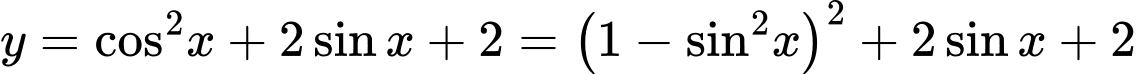
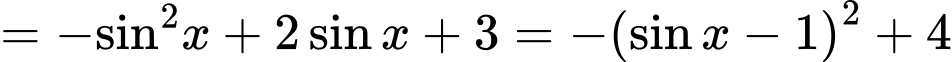
Vì

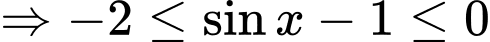
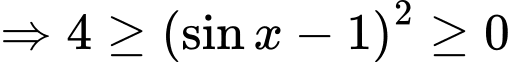
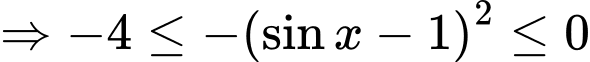
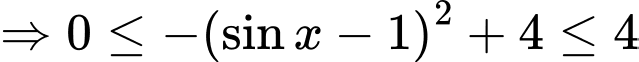
Hay
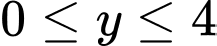
Do đó:
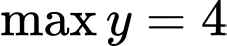 khi
khi 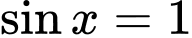
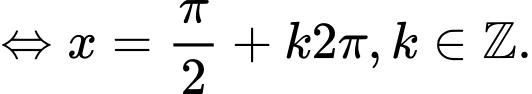
=> Điền: 4
* Lưu ý:

Nếu đặt
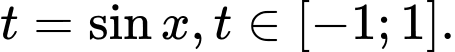 Ta có (P):
Ta có (P): 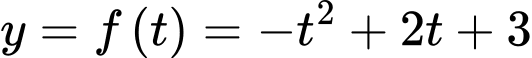 xác định với mọi
xác định với mọi  (P) có hoành độ đỉnh
(P) có hoành độ đỉnh 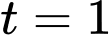 và trên đoạn
và trên đoạn 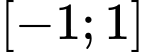 hàm số đồng biến nên hàm số đạt giá trị nhỏ nhất tại
hàm số đồng biến nên hàm số đạt giá trị nhỏ nhất tại 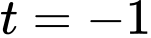 hay
hay 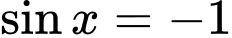 và đạt giá trị lớn nhất khi
và đạt giá trị lớn nhất khi 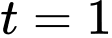 hay
hay 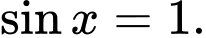
Câu 7 [582791]: Giả sử 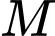 và
và 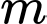 lần lượt là GTLN và GTNN của hàm số
lần lượt là GTLN và GTNN của hàm số 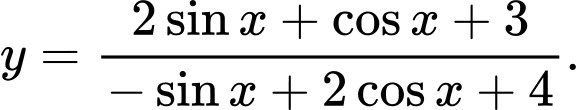 Tính giá trị của
Tính giá trị của 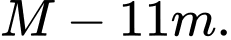
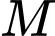 và
và 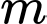 lần lượt là GTLN và GTNN của hàm số
lần lượt là GTLN và GTNN của hàm số 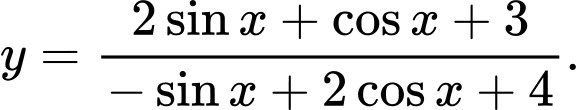 Tính giá trị của
Tính giá trị của 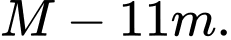
A, 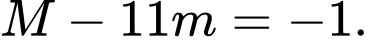
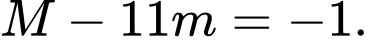
B, 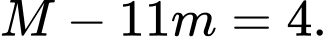
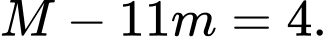
C, 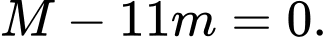
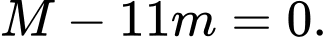
D, 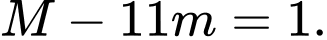
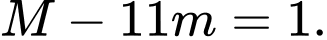
Tự luận: Do 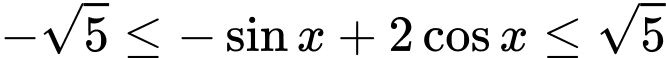 nên
nên 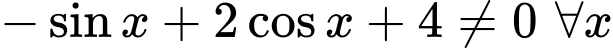
Ta có: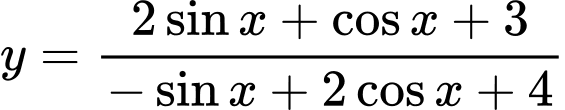
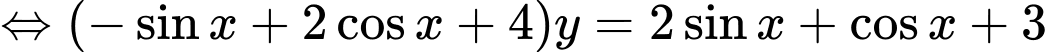
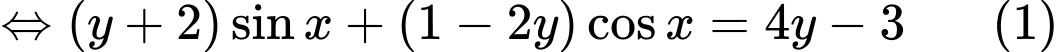
Hàm số có GTLN và GTNN nên ta suy ra phương trình (1) có nghiệm
Điều này tương đương với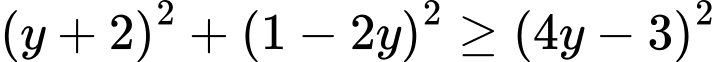
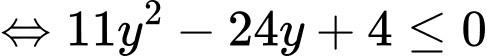
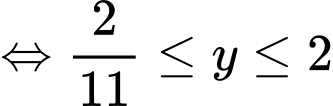
Thay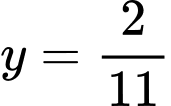 vào (1) ta được:
vào (1) ta được: 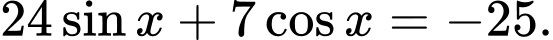
Thay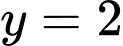 vào (1) ta được:
vào (1) ta được: 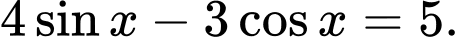
Cả hai phương trình trên đều có nghiệm. Do đó ta kết luận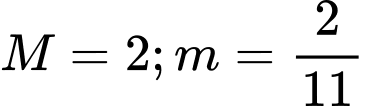 và
và 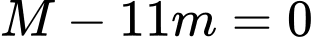
Trắc nghiệm: (Sử dụng MTCT )
+ Chuyển đơn vị đo từ độ (chữ D) sang radian (chữ R)
+ Vào chức năng TABLE ( MODE 7): Bấm hàm số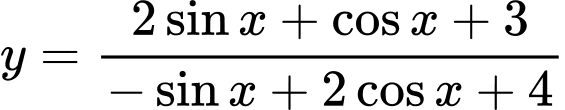
START: 0 END: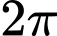 STEP:
STEP: 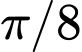 , ta được bảng các giá trị của hàm số trên
, ta được bảng các giá trị của hàm số trên 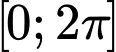 như sau:
như sau:
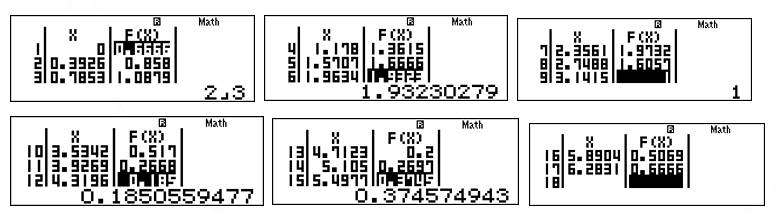
Dựa vào bảng trên, ta nhận xét rằng:
 Đáp án: C
Đáp án: C
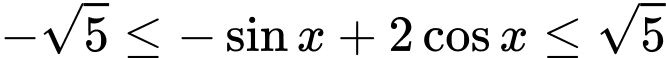 nên
nên 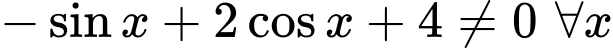
Ta có:
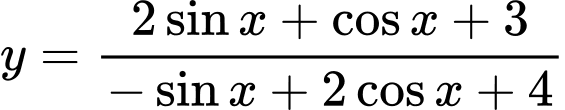
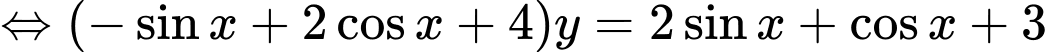
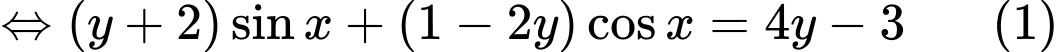
Hàm số có GTLN và GTNN nên ta suy ra phương trình (1) có nghiệm
Điều này tương đương với
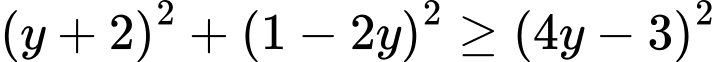
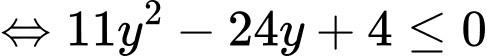
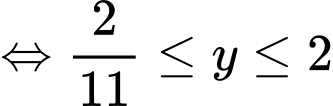
Thay
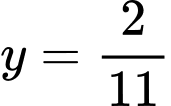 vào (1) ta được:
vào (1) ta được: 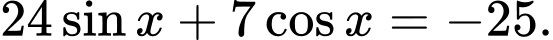
Thay
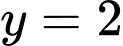 vào (1) ta được:
vào (1) ta được: 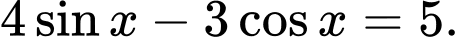
Cả hai phương trình trên đều có nghiệm. Do đó ta kết luận
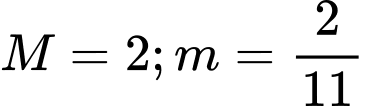 và
và 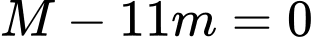
Trắc nghiệm: (Sử dụng MTCT )
+ Chuyển đơn vị đo từ độ (chữ D) sang radian (chữ R)
+ Vào chức năng TABLE ( MODE 7): Bấm hàm số
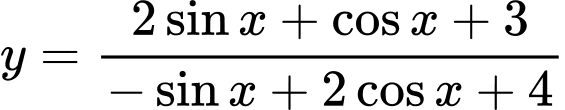
START: 0 END:
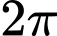 STEP:
STEP: 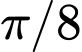 , ta được bảng các giá trị của hàm số trên
, ta được bảng các giá trị của hàm số trên 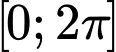 như sau:
như sau:
Dựa vào bảng trên, ta nhận xét rằng:
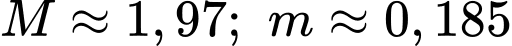
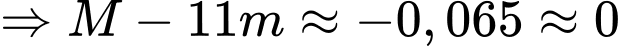 Đáp án: C
Đáp án: C
Câu 8 [582792]: Tìm GTLN và GTNN của hàm số 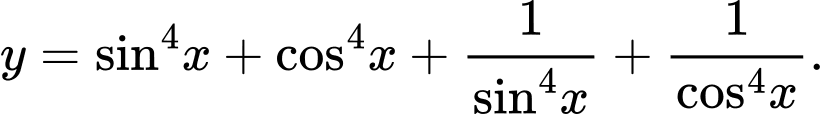
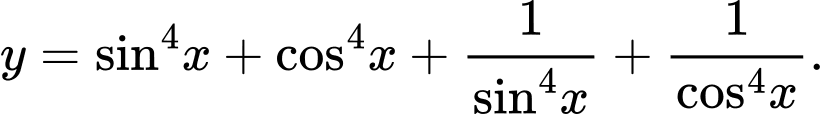
A, 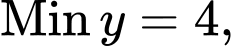
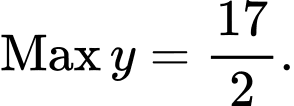
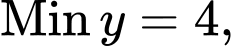
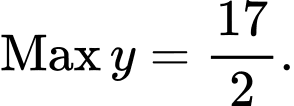
B, 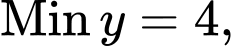
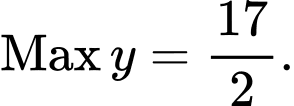
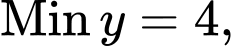
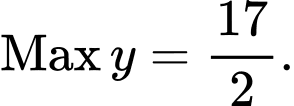
C, 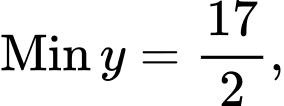
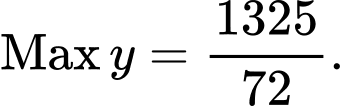
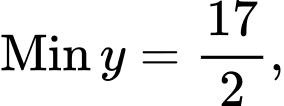
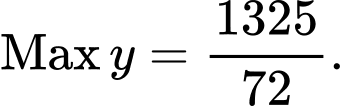
D, 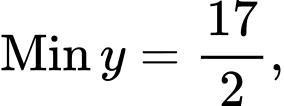 không tồn tại GTLN.
không tồn tại GTLN.
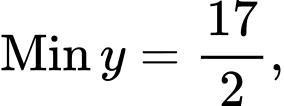 không tồn tại GTLN.
không tồn tại GTLN.
Giải tự luận:
Hàm số xác định khi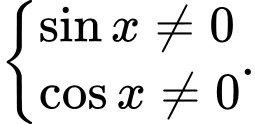
Chú ý rằng khi rất nhỏ (
rất nhỏ (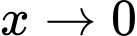 ) thi
) thi 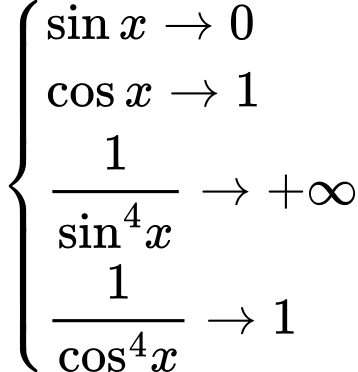 , do đó hàm số không có GTLN.
, do đó hàm số không có GTLN.
Để tìm ta cố gắng biến đổi về hàm chỉ chứa 1 HSLG ( Với hi vọng dựa vào tập giá trị để đánh giá)
ta cố gắng biến đổi về hàm chỉ chứa 1 HSLG ( Với hi vọng dựa vào tập giá trị để đánh giá)
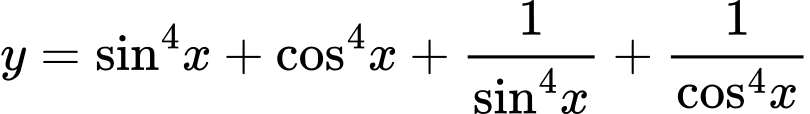
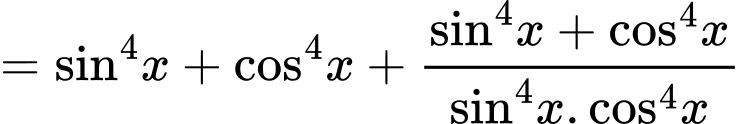
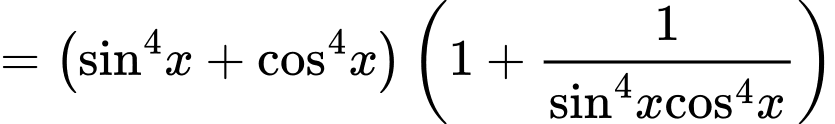
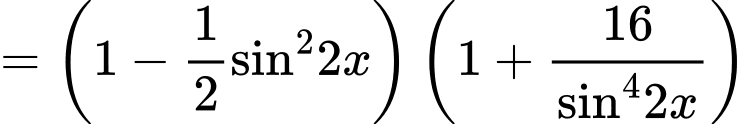
Ta có: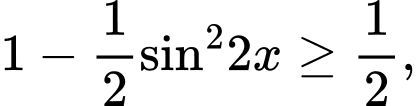 đẳng thức xảy ra khi
đẳng thức xảy ra khi 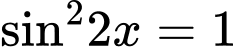 hay
hay 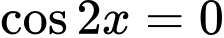
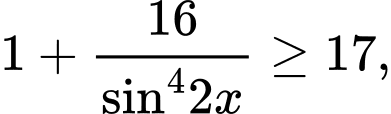 đẳng thức xảy ra khi
đẳng thức xảy ra khi 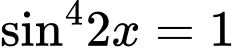 hay
hay 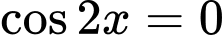
Suy ra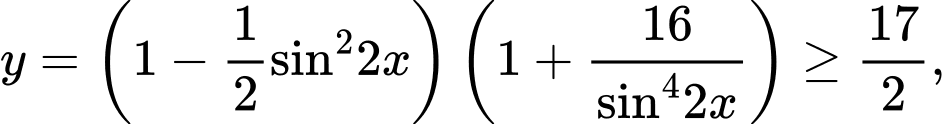 đẳng thức xảy ra khi
đẳng thức xảy ra khi 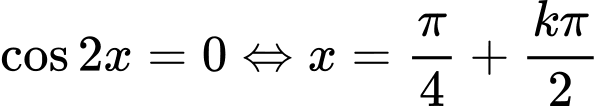
Vậy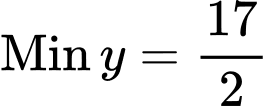
Chú ý: Một số bạn biến đổi như sau:
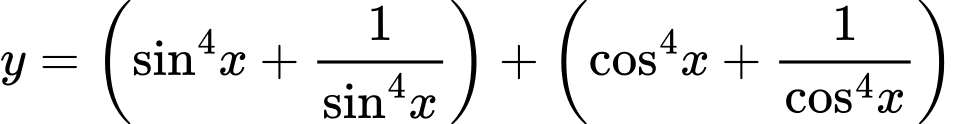
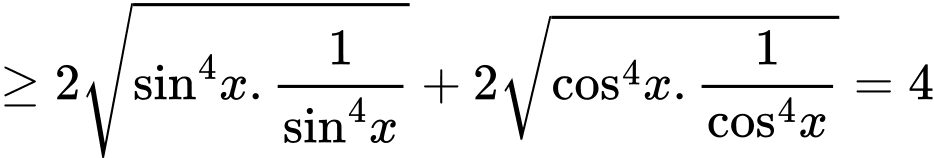
Và kết luận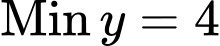 là hoàn toàn sai lầm, vì hai bất đẳng thức Cô si ở trên không thể đồng thời xảy ra dấu bằng.
là hoàn toàn sai lầm, vì hai bất đẳng thức Cô si ở trên không thể đồng thời xảy ra dấu bằng.
Giải trắc nghiệm: (Sử dụng MTCT )
Sử dụng TABLE như ví dụ 2, ta có bảng sau:
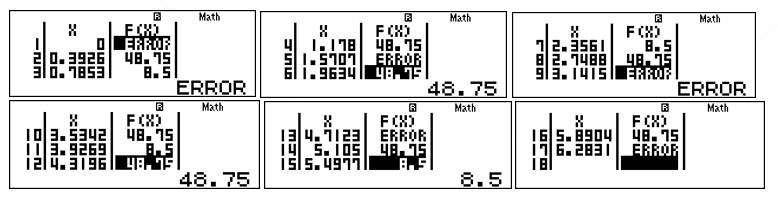
Dựa vào bảng trên, ta thấy GTNN của hàm số là 8,5 và GTLN là 48,75(!!!). Cần chú ý rằng tại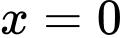 hàm số không xác định (ERROR) và bảng trên chưa liệt kê các giá trị
hàm số không xác định (ERROR) và bảng trên chưa liệt kê các giá trị 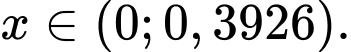 Để kiểm tra kĩ hơn, ta có thể chọn lại như sau: START :0 END: 0,3926 STEP: 0,05
Để kiểm tra kĩ hơn, ta có thể chọn lại như sau: START :0 END: 0,3926 STEP: 0,05
Kết quả như sau: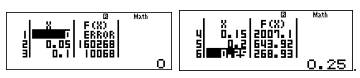
Nhìn vào bảng, ta thấy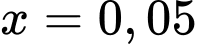 thì giá trị của hàm số rất lớn. Do đó hàm số không có GTLN.
thì giá trị của hàm số rất lớn. Do đó hàm số không có GTLN.
( Đây cũng là một hạn chế khi sử dụng CASIO để tìm Min và Max) Đáp án: A
Hàm số xác định khi
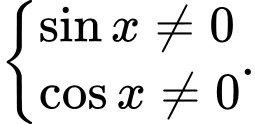
Chú ý rằng khi
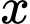 rất nhỏ (
rất nhỏ (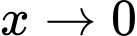 ) thi
) thi 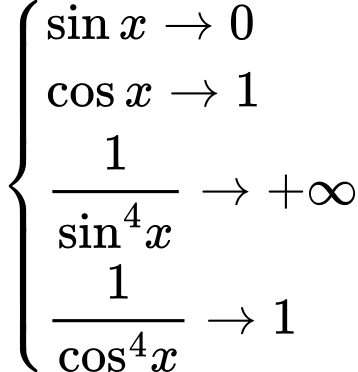 , do đó hàm số không có GTLN.
, do đó hàm số không có GTLN.Để tìm
 ta cố gắng biến đổi về hàm chỉ chứa 1 HSLG ( Với hi vọng dựa vào tập giá trị để đánh giá)
ta cố gắng biến đổi về hàm chỉ chứa 1 HSLG ( Với hi vọng dựa vào tập giá trị để đánh giá)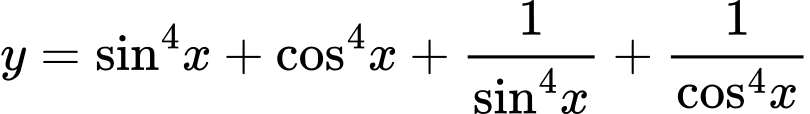
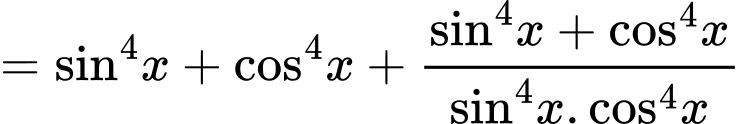
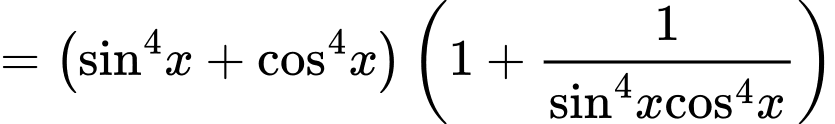
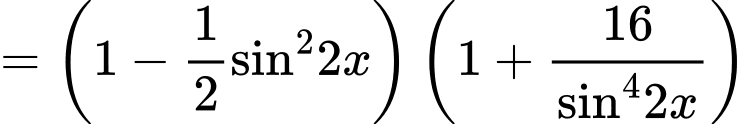
Ta có:
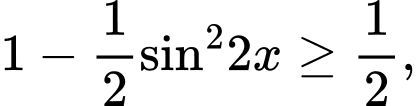 đẳng thức xảy ra khi
đẳng thức xảy ra khi 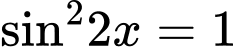 hay
hay 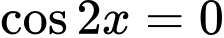
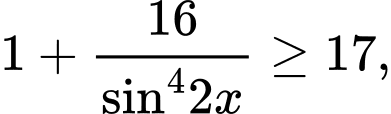 đẳng thức xảy ra khi
đẳng thức xảy ra khi 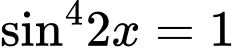 hay
hay 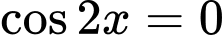
Suy ra
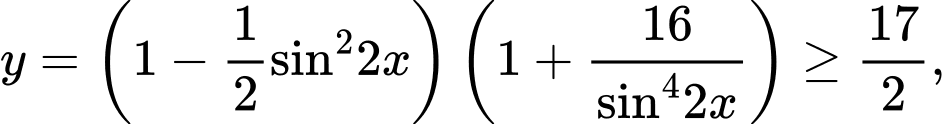 đẳng thức xảy ra khi
đẳng thức xảy ra khi 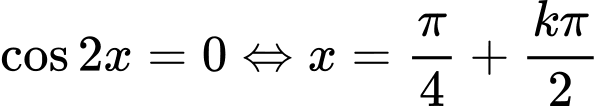
Vậy
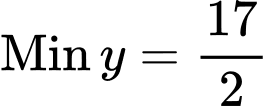
Chú ý: Một số bạn biến đổi như sau:
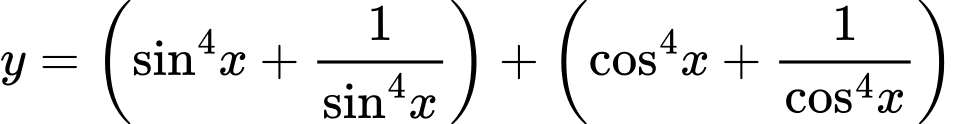
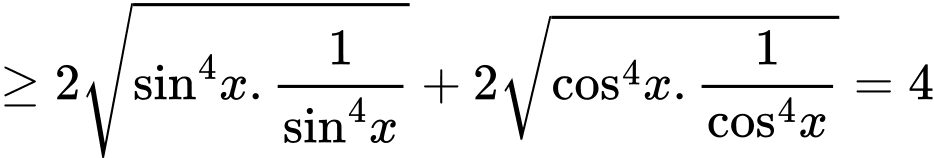
Và kết luận
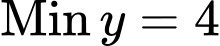 là hoàn toàn sai lầm, vì hai bất đẳng thức Cô si ở trên không thể đồng thời xảy ra dấu bằng.
là hoàn toàn sai lầm, vì hai bất đẳng thức Cô si ở trên không thể đồng thời xảy ra dấu bằng.Giải trắc nghiệm: (Sử dụng MTCT )
Sử dụng TABLE như ví dụ 2, ta có bảng sau:

Dựa vào bảng trên, ta thấy GTNN của hàm số là 8,5 và GTLN là 48,75(!!!). Cần chú ý rằng tại
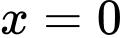 hàm số không xác định (ERROR) và bảng trên chưa liệt kê các giá trị
hàm số không xác định (ERROR) và bảng trên chưa liệt kê các giá trị 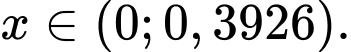 Để kiểm tra kĩ hơn, ta có thể chọn lại như sau: START :0 END: 0,3926 STEP: 0,05
Để kiểm tra kĩ hơn, ta có thể chọn lại như sau: START :0 END: 0,3926 STEP: 0,05 Kết quả như sau:

Nhìn vào bảng, ta thấy
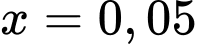 thì giá trị của hàm số rất lớn. Do đó hàm số không có GTLN.
thì giá trị của hàm số rất lớn. Do đó hàm số không có GTLN.( Đây cũng là một hạn chế khi sử dụng CASIO để tìm Min và Max) Đáp án: A
4. Dạng toán: Chứng minh hàm số tuần hoàn và xác định chu kỳ của nó
Câu 9 [582793]: Tìm giá trị của 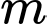 để hàm số
để hàm số 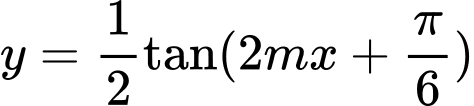 có chu kì
có chu kì 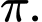
Đáp án:............
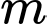 để hàm số
để hàm số 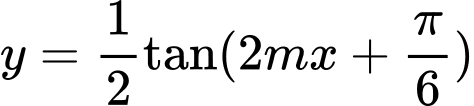 có chu kì
có chu kì 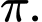
Đáp án:............
Ta có: hàm số 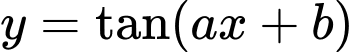 có chu kỳ là
có chu kỳ là 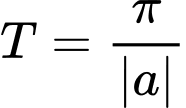
Áp dụng: hàm số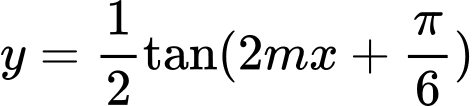 có chu kỳ
có chu kỳ 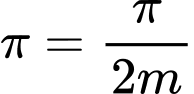
Vậy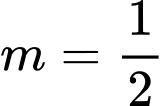
=> Điền: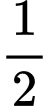
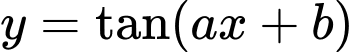 có chu kỳ là
có chu kỳ là 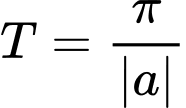
Áp dụng: hàm số
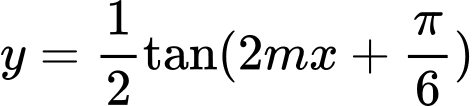 có chu kỳ
có chu kỳ 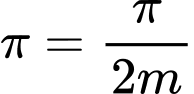
Vậy
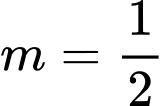
=> Điền:
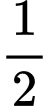
Câu 10 [582794]: Số hàm số không tuần hoàn trong các hàm số sau:
a)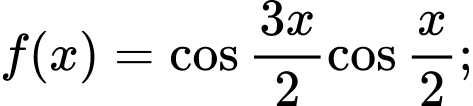
b)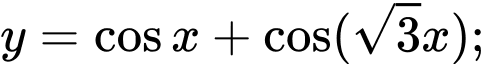
c)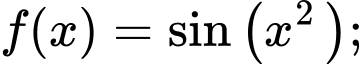
d)
a)
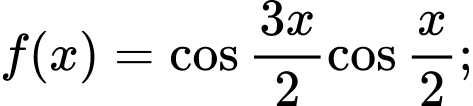
b)
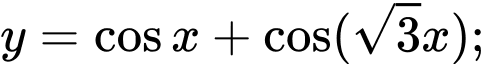
c)
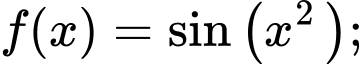
d)

A, 4.
B, 3.
C, 2.
D, 1.
- Hàm số 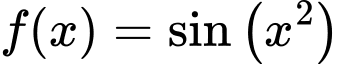 không tuần hoàn vì khoảng cách giữa các nghiệm (không điểm) liên tiếp của nó dần tới 0
không tuần hoàn vì khoảng cách giữa các nghiệm (không điểm) liên tiếp của nó dần tới 0
-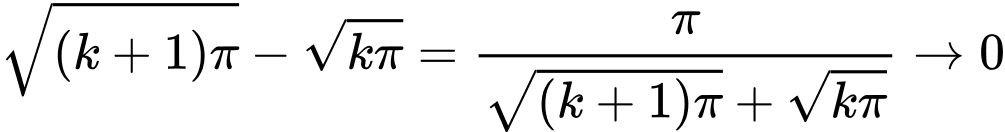 khi
khi 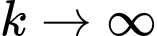
- Hàm số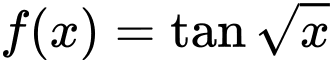 không tuần hoàn vì khoảng cách giữa các nghiệm (không điểm) liên tiếp của nó dần tới
không tuần hoàn vì khoảng cách giữa các nghiệm (không điểm) liên tiếp của nó dần tới 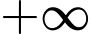
-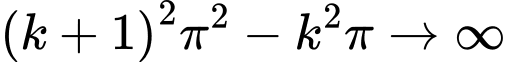 khi
khi 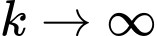
=> Chọn C Đáp án: C
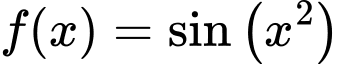 không tuần hoàn vì khoảng cách giữa các nghiệm (không điểm) liên tiếp của nó dần tới 0
không tuần hoàn vì khoảng cách giữa các nghiệm (không điểm) liên tiếp của nó dần tới 0-
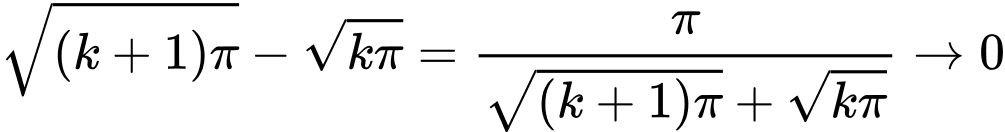 khi
khi 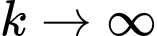
- Hàm số
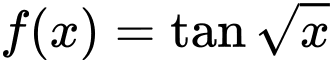 không tuần hoàn vì khoảng cách giữa các nghiệm (không điểm) liên tiếp của nó dần tới
không tuần hoàn vì khoảng cách giữa các nghiệm (không điểm) liên tiếp của nó dần tới 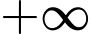
-
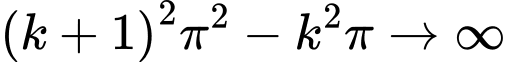 khi
khi 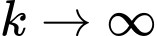
=> Chọn C Đáp án: C
5. Dạng toán: Đồ thị của hàm số lượng giác
Câu 11 [582795]: Từ đồ thị của hàm số 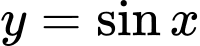
 ta được đồ thị hàm số
ta được đồ thị hàm số 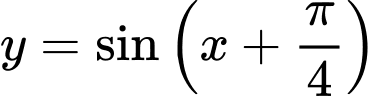 bằng cách nào sau đây?
bằng cách nào sau đây?
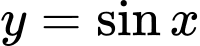
 ta được đồ thị hàm số
ta được đồ thị hàm số 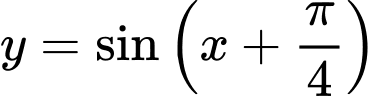 bằng cách nào sau đây?
bằng cách nào sau đây? A, Tịnh tiến (C) sang trái một đoạn là 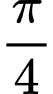 đơn vị.
đơn vị.
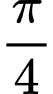 đơn vị.
đơn vị.B, Tịnh tiến (C) sang phải một đoạn là 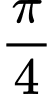 đơn vị.
đơn vị.
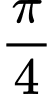 đơn vị.
đơn vị.C, Tịnh tiến (C) lên trên trục hoành một đoạn là 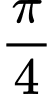 đơn vị.
đơn vị.
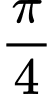 đơn vị.
đơn vị.D, Tịnh tiến (C) xuống dưới trục hoành một đoạn là 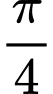 đơn vị.
đơn vị.
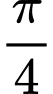 đơn vị.
đơn vị.
Ta có đồ thị của hàm số 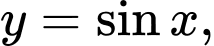 (C) như sau:
(C) như sau:
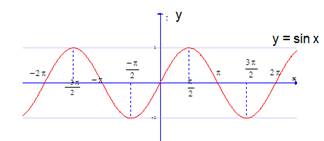
Từ đồ thị (C), ta có đồ thị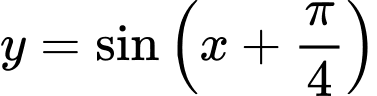 bằng cách tịnh tiến (C) sang trái một đoạn là
bằng cách tịnh tiến (C) sang trái một đoạn là 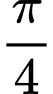 đơn vị, ta được đồ thị hàm số
đơn vị, ta được đồ thị hàm số 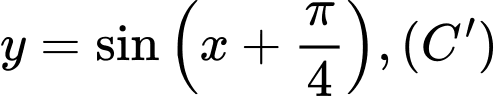 như sau:
như sau:
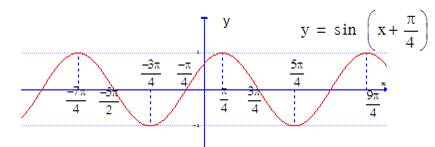
=> Chọn A Đáp án: A
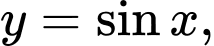 (C) như sau:
(C) như sau:
Từ đồ thị (C), ta có đồ thị
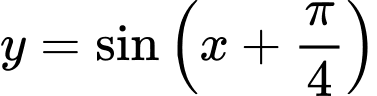 bằng cách tịnh tiến (C) sang trái một đoạn là
bằng cách tịnh tiến (C) sang trái một đoạn là 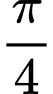 đơn vị, ta được đồ thị hàm số
đơn vị, ta được đồ thị hàm số 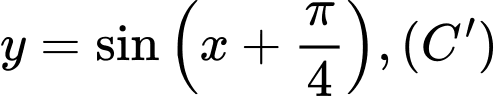 như sau:
như sau:
=> Chọn A Đáp án: A
Câu 12 [582796]: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D. Hỏi hàm số đó là hàm số nào?
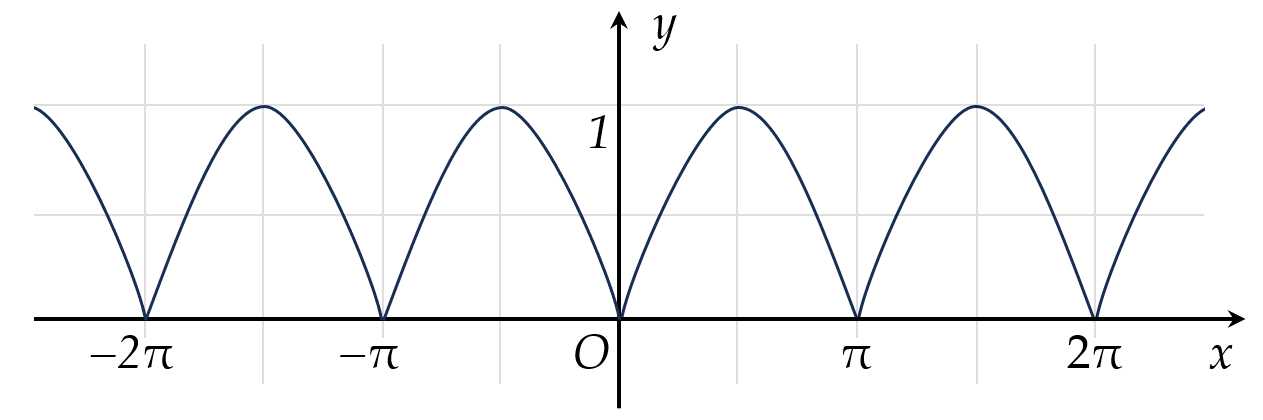

A, 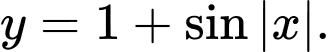
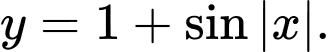
B, 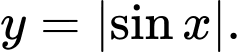
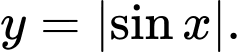
C, 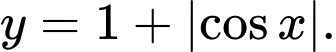
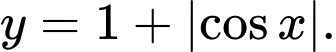
D, 

Ta có 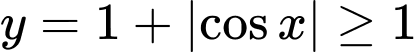 và
và 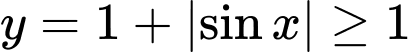 nên loại C và D
nên loại C và D
Ta thấy tại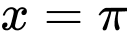 thì
thì 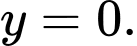 Thay vào hai đáp án A và B thì chỉ có B thỏa.
Thay vào hai đáp án A và B thì chỉ có B thỏa.
=> Chọn B Đáp án: B
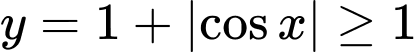 và
và 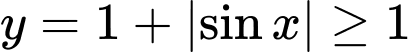 nên loại C và D
nên loại C và DTa thấy tại
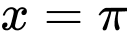 thì
thì 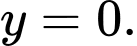 Thay vào hai đáp án A và B thì chỉ có B thỏa.
Thay vào hai đáp án A và B thì chỉ có B thỏa.=> Chọn B Đáp án: B