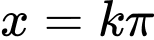Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
Câu 1 [582797]: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A, 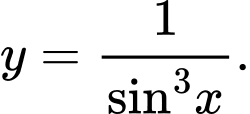
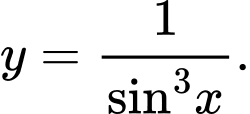
B, 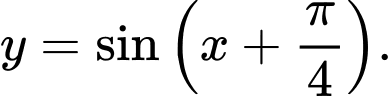
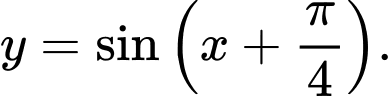
C, 

D, 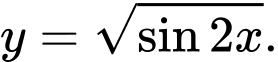
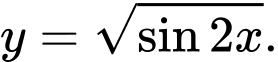
Viết lại đáp án B là 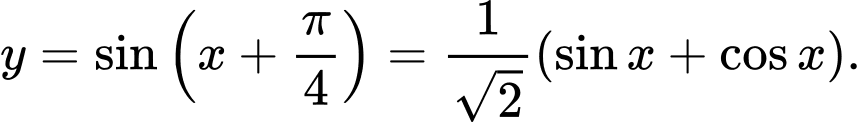
Viết lại đáp án C là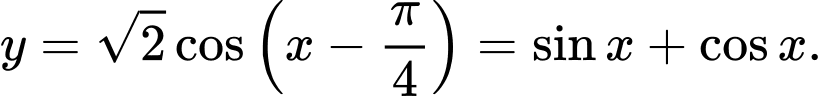
Kiểm tra được đáp án A là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ.
Ta kiểm tra được đáp án B và C là các hàm số không chẵn, không lẻ.
Xét đáp án D.
Hàm số xác định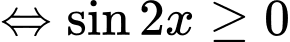
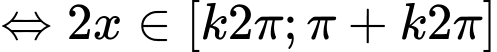
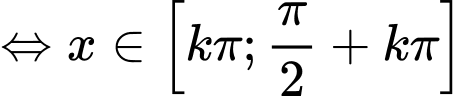
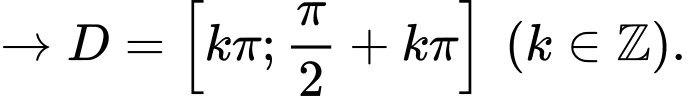
Chọn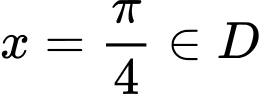 nhưng
nhưng 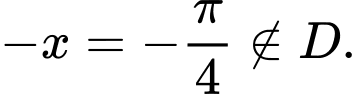
Vậy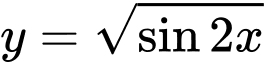 không chẵn, không lẻ. Đáp án: A
không chẵn, không lẻ. Đáp án: A
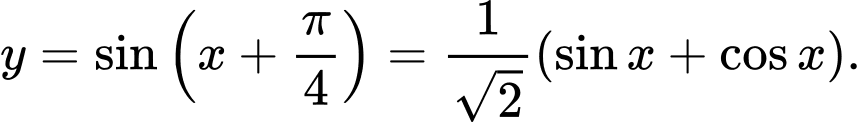
Viết lại đáp án C là
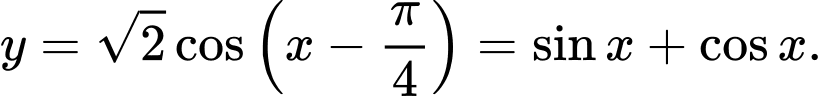
Kiểm tra được đáp án A là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ.
Ta kiểm tra được đáp án B và C là các hàm số không chẵn, không lẻ.
Xét đáp án D.
Hàm số xác định
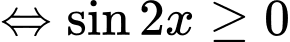
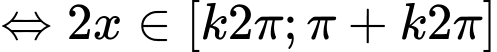
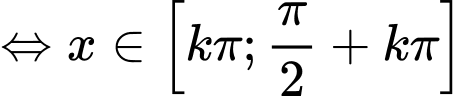
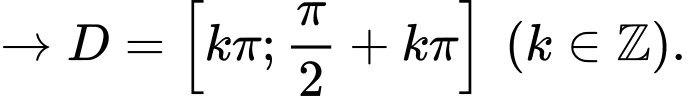
Chọn
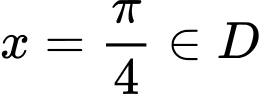 nhưng
nhưng 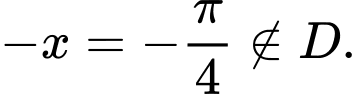
Vậy
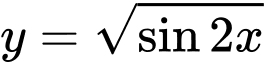 không chẵn, không lẻ. Đáp án: A
không chẵn, không lẻ. Đáp án: A
Câu 2 [582798]: Tìm tập giá trị 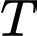 của hàm số
của hàm số 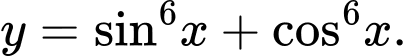
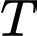 của hàm số
của hàm số 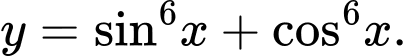
A, 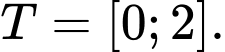
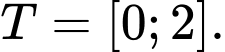
B, 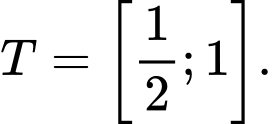
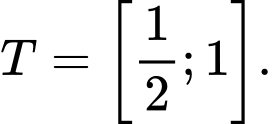
C, 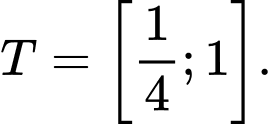
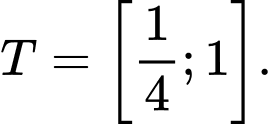
D, 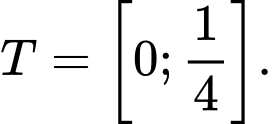
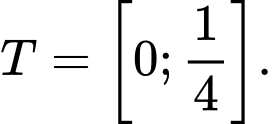
Ta có 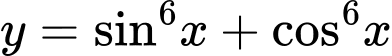
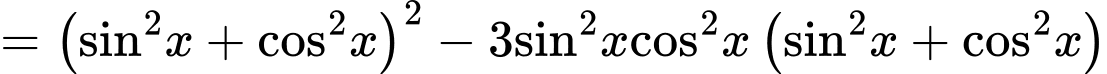
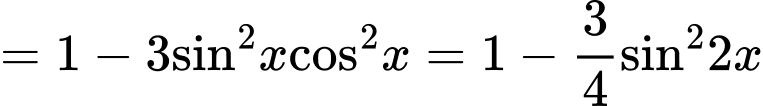
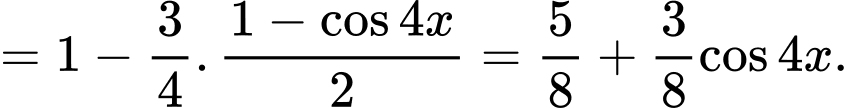
Mà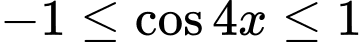
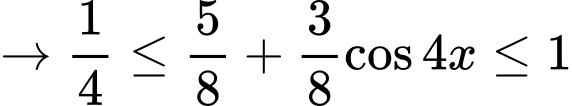
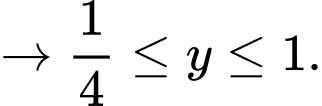 Đáp án: C
Đáp án: C
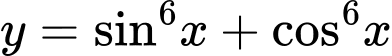
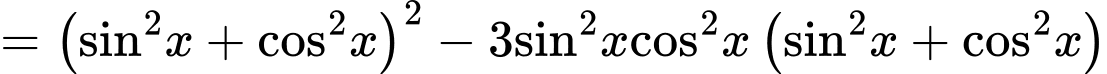
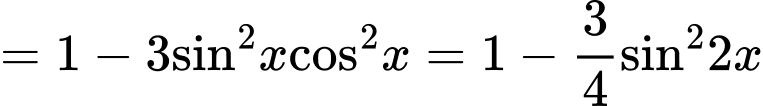
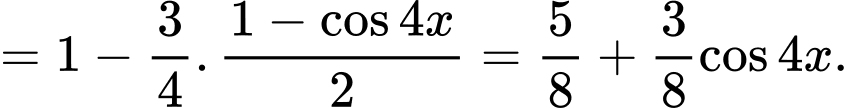
Mà
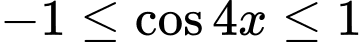
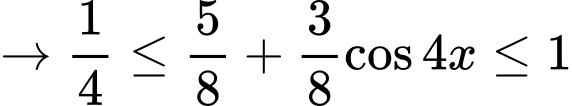
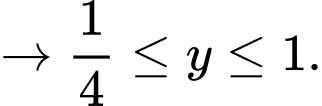 Đáp án: C
Đáp án: C
Câu 3 [582799]: Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ  của năm
của năm  được cho bởi một hàm số
được cho bởi một hàm số 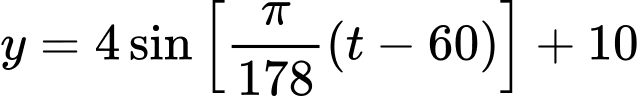 với
với 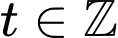 và
và  Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
 của năm
của năm  được cho bởi một hàm số
được cho bởi một hàm số 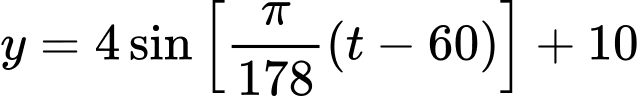 với
với 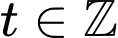 và
và  Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất? A, 28 tháng 5.
B, 29 tháng 5.
C, 30 tháng 5.
D, 31 tháng 5.
Vì 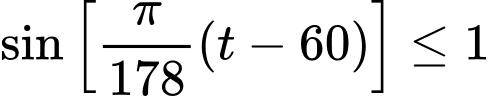
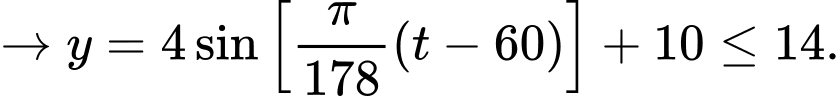
Ngày có ánh sáng mặt trời nhiều nhất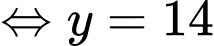
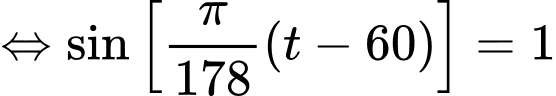
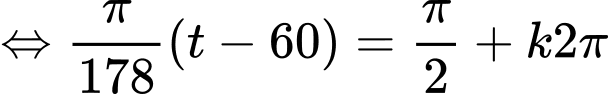
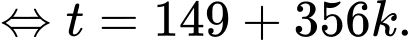
Do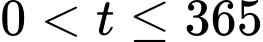

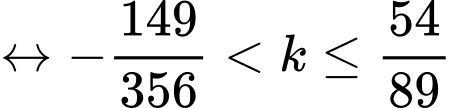
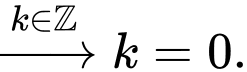
Với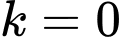
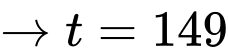 rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày, tháng 4 có 30 ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có 28 ngày hoặc dựa vào dữ kiện
rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày, tháng 4 có 30 ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có 28 ngày hoặc dựa vào dữ kiện 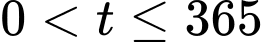 thì ta biết năm này tháng 2 chỉ có 28 ngày). Đáp án: B
thì ta biết năm này tháng 2 chỉ có 28 ngày). Đáp án: B
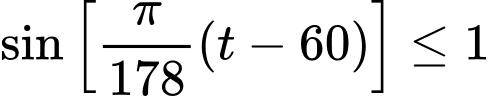
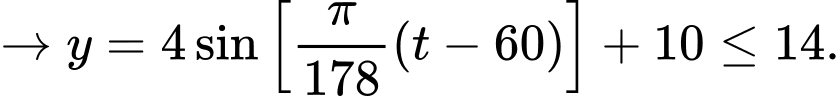
Ngày có ánh sáng mặt trời nhiều nhất
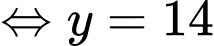
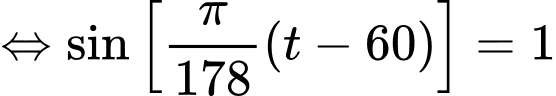
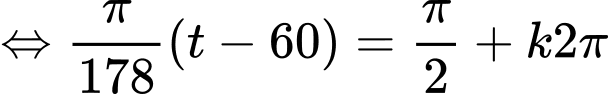
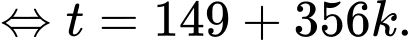
Do
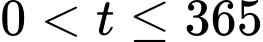

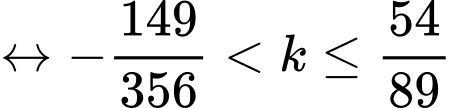
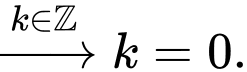
Với
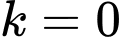
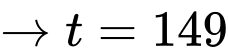 rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày, tháng 4 có 30 ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có 28 ngày hoặc dựa vào dữ kiện
rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày, tháng 4 có 30 ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có 28 ngày hoặc dựa vào dữ kiện 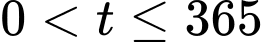 thì ta biết năm này tháng 2 chỉ có 28 ngày). Đáp án: B
thì ta biết năm này tháng 2 chỉ có 28 ngày). Đáp án: B
Câu 4 [582800]: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D
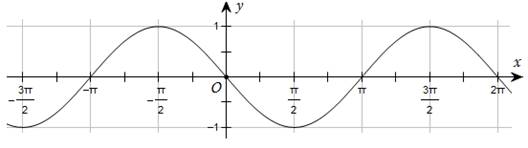
Hỏi hàm số đó là hàm số nào?

Hỏi hàm số đó là hàm số nào?
A, 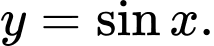
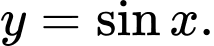
B, 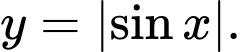
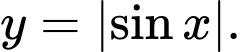
C, 

D, 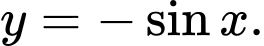
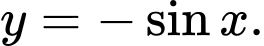
Ta thấy tại 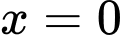 thì
thì 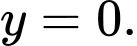 Cả 4 đáp án đều thỏa.
Cả 4 đáp án đều thỏa.
Tại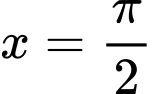 thì
thì 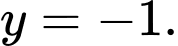 Do đó chỉ có đáp án D thỏa mãn. Đáp án: D
Do đó chỉ có đáp án D thỏa mãn. Đáp án: D
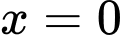 thì
thì 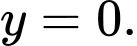 Cả 4 đáp án đều thỏa.
Cả 4 đáp án đều thỏa.Tại
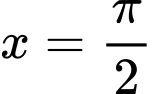 thì
thì 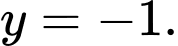 Do đó chỉ có đáp án D thỏa mãn. Đáp án: D
Do đó chỉ có đáp án D thỏa mãn. Đáp án: D
Câu 5 [582801]: Tìm chu kì  của hàm số
của hàm số 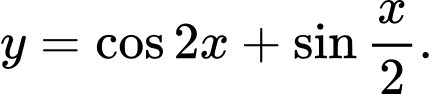
 của hàm số
của hàm số 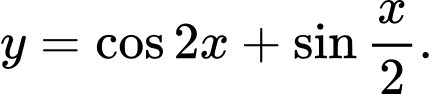
A, 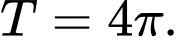
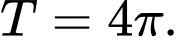
B, 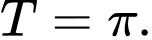
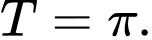
C, 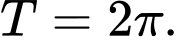
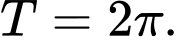
D, 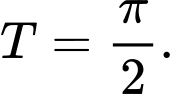
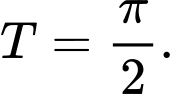
Hàm số 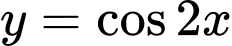 tuần hoàn với chu kì
tuần hoàn với chu kì 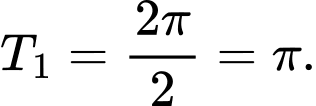
Hàm số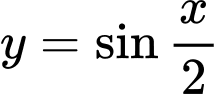 tuần hoàn với chu kì
tuần hoàn với chu kì 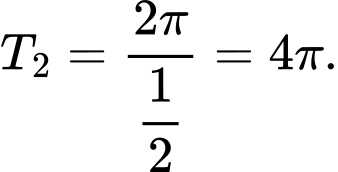
Suy ra hàm số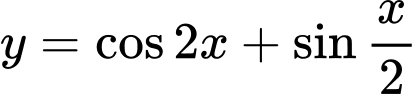 tuần hoàn với chu kì
tuần hoàn với chu kì 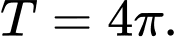
Nhận xét: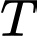 là bội chung nhỏ nhất của
là bội chung nhỏ nhất của 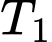 và
và 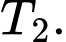 Đáp án: A
Đáp án: A
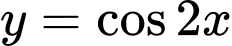 tuần hoàn với chu kì
tuần hoàn với chu kì 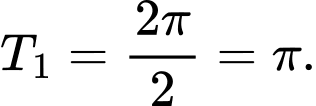
Hàm số
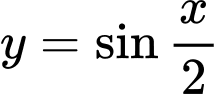 tuần hoàn với chu kì
tuần hoàn với chu kì 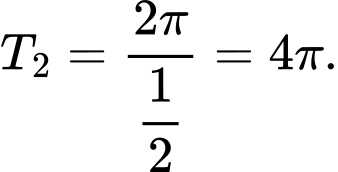
Suy ra hàm số
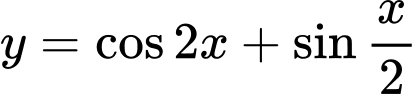 tuần hoàn với chu kì
tuần hoàn với chu kì 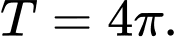
Nhận xét:
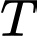 là bội chung nhỏ nhất của
là bội chung nhỏ nhất của 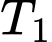 và
và 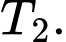 Đáp án: A
Đáp án: A
Câu 6 [582802]: Đồ thị hàm số 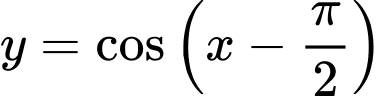 được suy ra từ đồ thị
được suy ra từ đồ thị  của hàm số
của hàm số  bằng cách:
bằng cách:
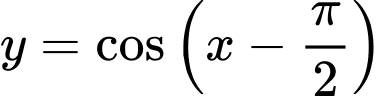 được suy ra từ đồ thị
được suy ra từ đồ thị  của hàm số
của hàm số  bằng cách:
bằng cách:
A, Tịnh tiến  qua trái một đoạn có độ dài là
qua trái một đoạn có độ dài là 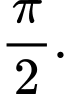
 qua trái một đoạn có độ dài là
qua trái một đoạn có độ dài là 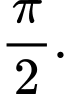
B, Tịnh tiến  qua phải một đoạn có độ dài là
qua phải một đoạn có độ dài là 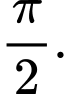
 qua phải một đoạn có độ dài là
qua phải một đoạn có độ dài là 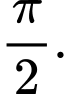
C, Tịnh tiến  lên trên một đoạn có độ dài là
lên trên một đoạn có độ dài là 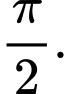
 lên trên một đoạn có độ dài là
lên trên một đoạn có độ dài là 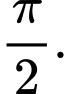
D, Tịnh tiến  xuống dưới một đoạn có độ dài là
xuống dưới một đoạn có độ dài là 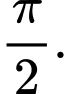
 xuống dưới một đoạn có độ dài là
xuống dưới một đoạn có độ dài là 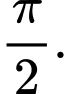
Đồ thị hàm số 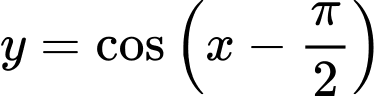 được suy ra từ đồ thị
được suy ra từ đồ thị  của hàm số
của hàm số  bằng cách tịnh tiến sang phải 1 đoạn có độ dài là
bằng cách tịnh tiến sang phải 1 đoạn có độ dài là 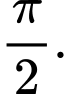
Lưu ý: Nhắc lại kiến thức
Cho hàm số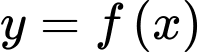 có đồ thị là
có đồ thị là  Với
Với  ta có:
ta có:
+) Tịnh tiến lên trên
lên trên  đơn vị thì đồ thị hàm số
đơn vị thì đồ thị hàm số 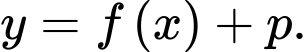
+) Tịnh tiến xuống dưới
xuống dưới 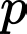 đơn vị thì đồ thị hàm số
đơn vị thì đồ thị hàm số 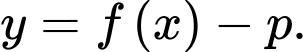
+) Tịnh tiến sang trái
sang trái 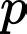 đơn vị thì đồ thị hàm số
đơn vị thì đồ thị hàm số 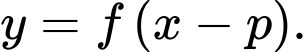
+) Tịnh tiến sang phải
sang phải 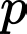 đơn vị thì đồ thị hàm số
đơn vị thì đồ thị hàm số 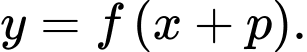 Đáp án: B
Đáp án: B
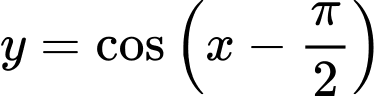 được suy ra từ đồ thị
được suy ra từ đồ thị  của hàm số
của hàm số  bằng cách tịnh tiến sang phải 1 đoạn có độ dài là
bằng cách tịnh tiến sang phải 1 đoạn có độ dài là 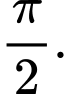
Lưu ý: Nhắc lại kiến thức
Cho hàm số
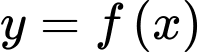 có đồ thị là
có đồ thị là  Với
Với  ta có:
ta có:
+) Tịnh tiến
 lên trên
lên trên 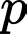 đơn vị thì đồ thị hàm số
đơn vị thì đồ thị hàm số 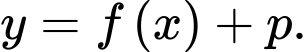
+) Tịnh tiến
 xuống dưới
xuống dưới 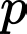 đơn vị thì đồ thị hàm số
đơn vị thì đồ thị hàm số 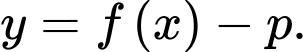
+) Tịnh tiến
 sang trái
sang trái 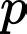 đơn vị thì đồ thị hàm số
đơn vị thì đồ thị hàm số 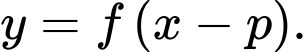
+) Tịnh tiến
 sang phải
sang phải 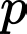 đơn vị thì đồ thị hàm số
đơn vị thì đồ thị hàm số 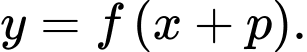 Đáp án: B
Đáp án: B
Câu 7 [582803]: Hình vẽ nào dưới đây biểu diễn đồ thị hàm số 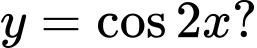
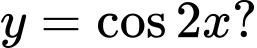
A, 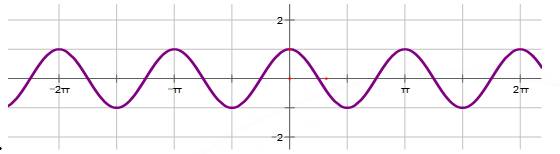

B, 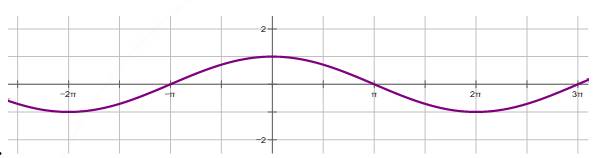

C, 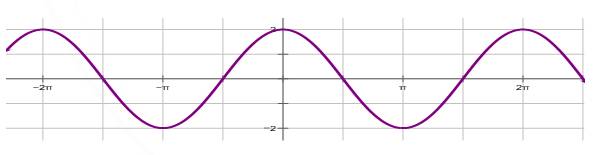

D, 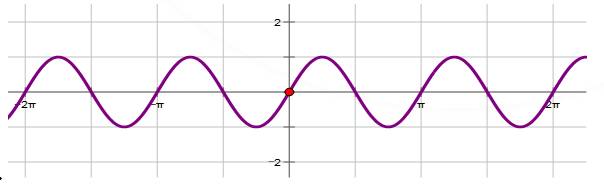

Ta thấy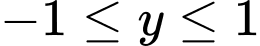 nên ta loại C.
nên ta loại C.
Tiếp theo ta có hàm số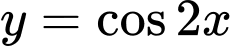 có chu kì tuần hoàn là
có chu kì tuần hoàn là 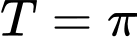 nên loại B.
nên loại B.
Ta thấy với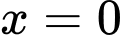 thì
thì  nên ta loại D. Đáp án: A
nên ta loại D. Đáp án: A
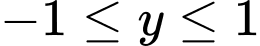 nên ta loại C.
nên ta loại C.Tiếp theo ta có hàm số
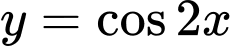 có chu kì tuần hoàn là
có chu kì tuần hoàn là 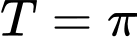 nên loại B.
nên loại B.Ta thấy với
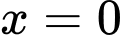 thì
thì  nên ta loại D. Đáp án: A
nên ta loại D. Đáp án: A
Câu 8 [582804]: Trong mặt phẳng tọa độ 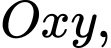 điểm nào sau đây thuộc đồ thị hàm số
điểm nào sau đây thuộc đồ thị hàm số 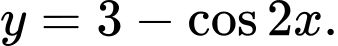
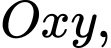 điểm nào sau đây thuộc đồ thị hàm số
điểm nào sau đây thuộc đồ thị hàm số 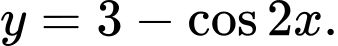
A, 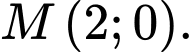
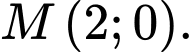
B, 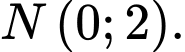
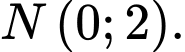
C, 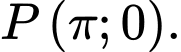
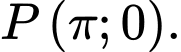
D, 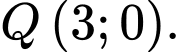
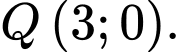
Thay 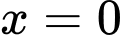 vào hàm số
vào hàm số  ta được
ta được 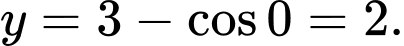 Do đó đồ thị hàm số đi qua
Do đó đồ thị hàm số đi qua 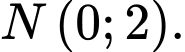 Đáp án: B
Đáp án: B
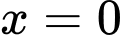 vào hàm số
vào hàm số  ta được
ta được 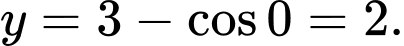 Do đó đồ thị hàm số đi qua
Do đó đồ thị hàm số đi qua 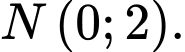 Đáp án: B
Đáp án: B
Câu 9 [582805]: Tìm tập xác định 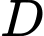 của hàm số
của hàm số 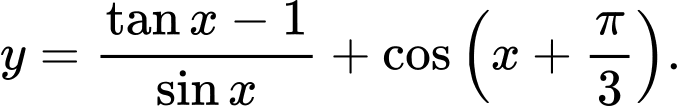
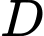 của hàm số
của hàm số 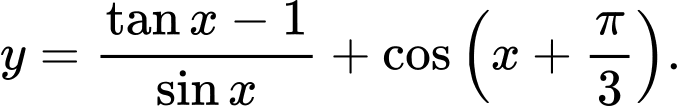
A, 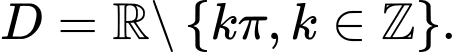
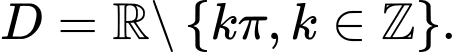
B, 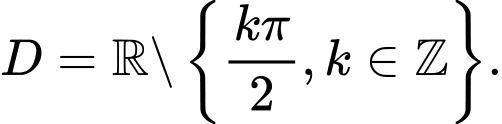
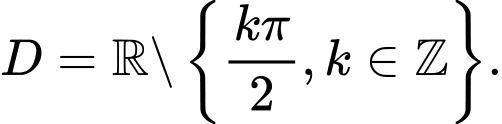
C, 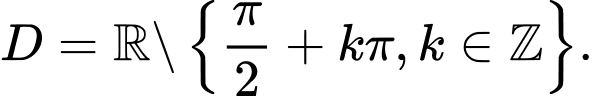
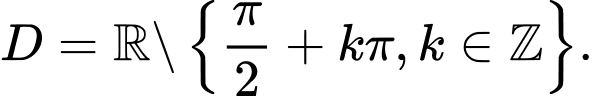
D, 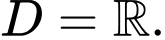
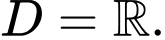
Hàm số 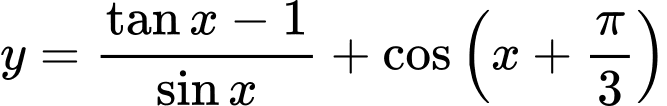 xác định khi:
xác định khi:
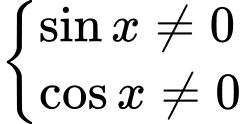
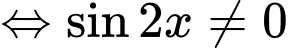
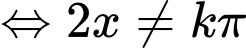
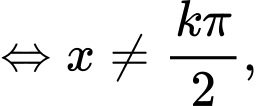
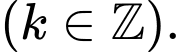 Đáp án: B
Đáp án: B
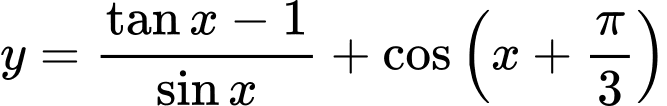 xác định khi:
xác định khi: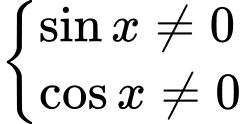
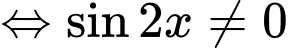
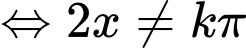
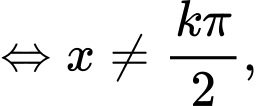
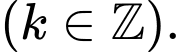 Đáp án: B
Đáp án: B
Câu 10 [582806]: Chu kỳ của hàm số 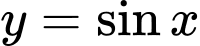 là:
là:
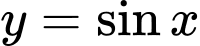 là:
là: A, 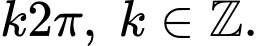
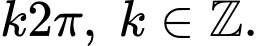
B, 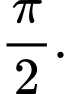
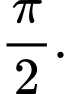
C, 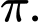
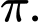
D, 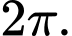
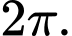
Tập xác định của hàm số: 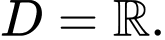
Với mọi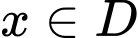 ,
, 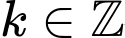 ta có
ta có 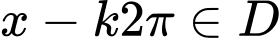 và
và 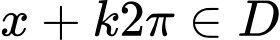 ,
, 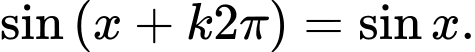
Vậy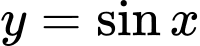 là hàm số tuần hoàn với chu kì
là hàm số tuần hoàn với chu kì 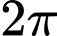 là số dương nhỏ nhất thỏa
là số dương nhỏ nhất thỏa 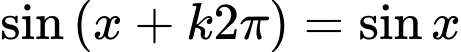 Đáp án: D
Đáp án: D
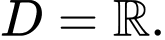
Với mọi
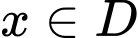 ,
, 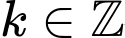 ta có
ta có 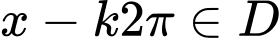 và
và 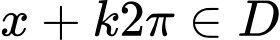 ,
, 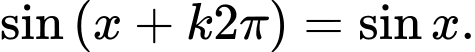
Vậy
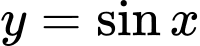 là hàm số tuần hoàn với chu kì
là hàm số tuần hoàn với chu kì 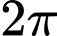 là số dương nhỏ nhất thỏa
là số dương nhỏ nhất thỏa 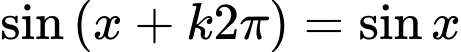 Đáp án: D
Đáp án: D
Câu 11 [582807]: Tìm giá trị lớn nhất của hàm số 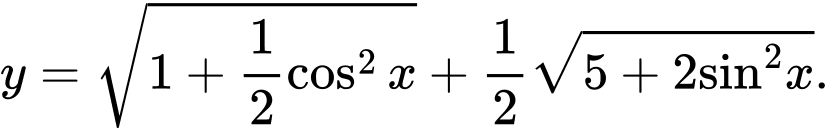
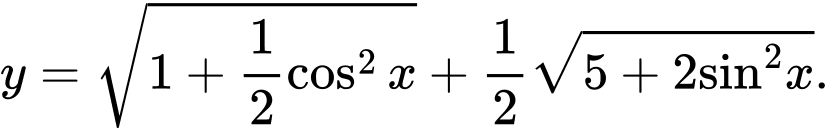
A, 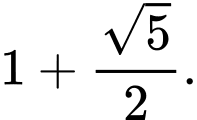
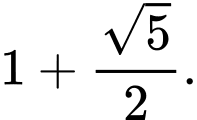
B, 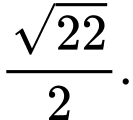
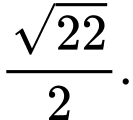
C, 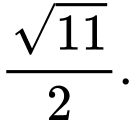
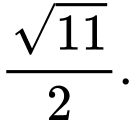
D, 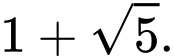
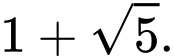
Ta có 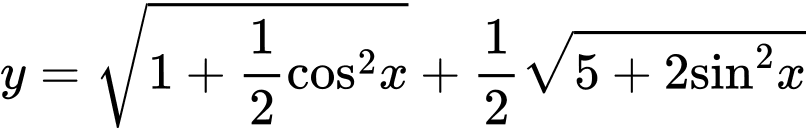
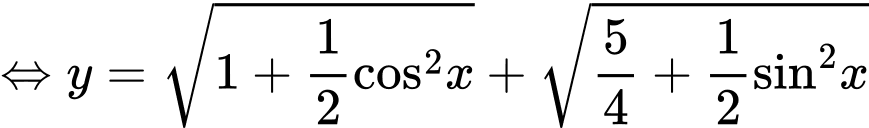
Áp dụng bất đẳng thức Bunyakopvsky cho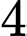 số: 1; 1;
số: 1; 1; 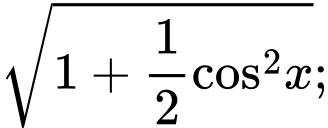
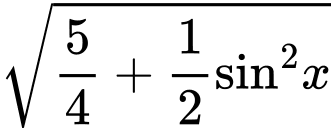 ta có:
ta có:
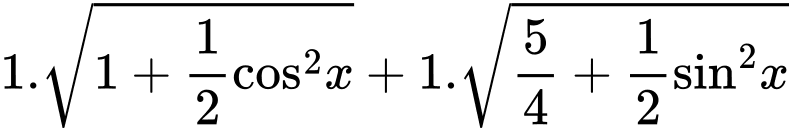
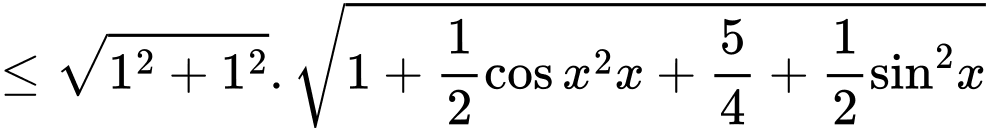
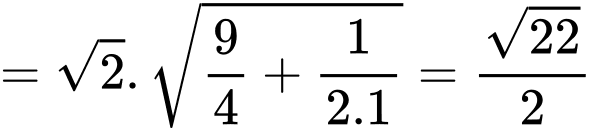
Hay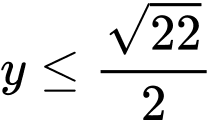
Dấu bằng xảy ra khi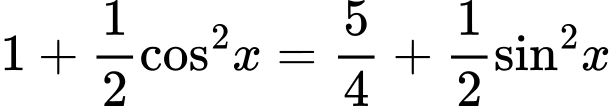
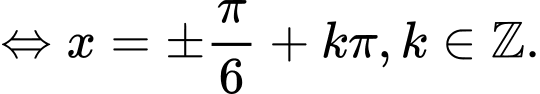 Đáp án: B
Đáp án: B
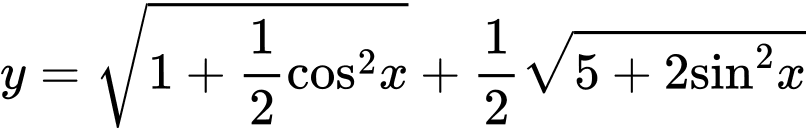
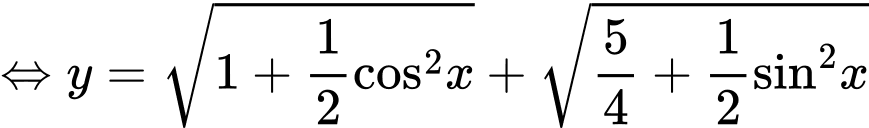
Áp dụng bất đẳng thức Bunyakopvsky cho
 số: 1; 1;
số: 1; 1; 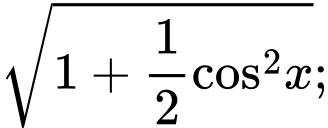
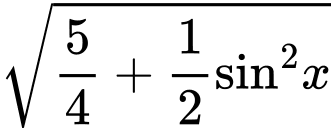 ta có:
ta có: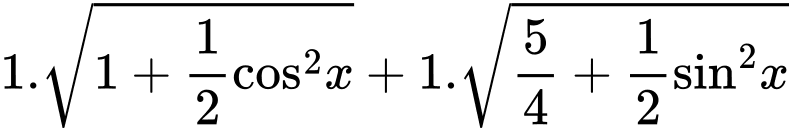
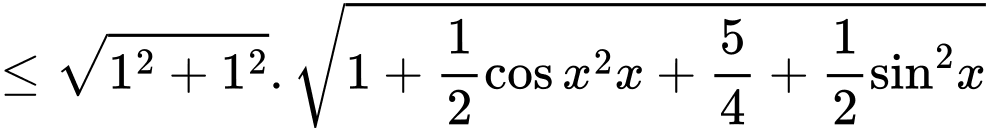
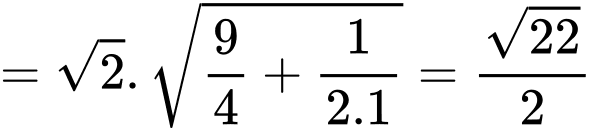
Hay
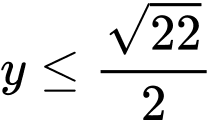
Dấu bằng xảy ra khi
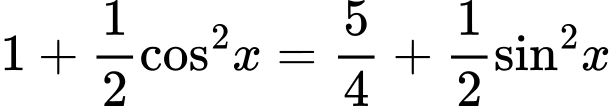
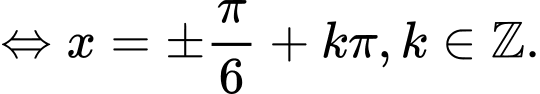 Đáp án: B
Đáp án: B
Câu 12 [582808]: Hàm số 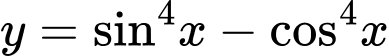 đạt giá trị nhỏ nhất tại
đạt giá trị nhỏ nhất tại 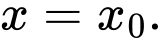 Mệnh đề nào sau đây là đúng?
Mệnh đề nào sau đây là đúng?
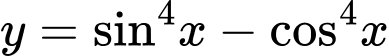 đạt giá trị nhỏ nhất tại
đạt giá trị nhỏ nhất tại 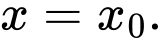 Mệnh đề nào sau đây là đúng?
Mệnh đề nào sau đây là đúng? A, 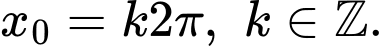
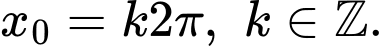
B, 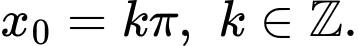
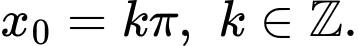
C, 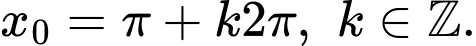
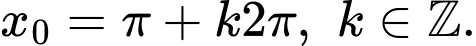
D, 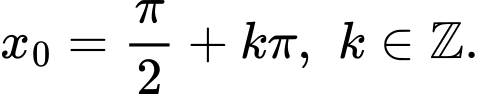
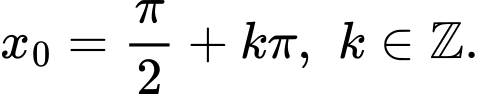
Ta có 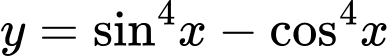
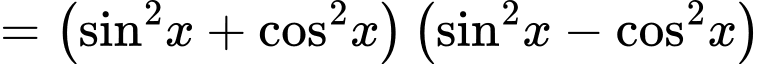
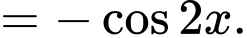
Mà
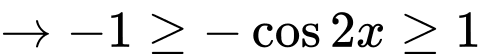
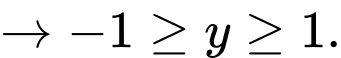
Do đó giá trị nhỏ nhất của hàm số là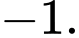
Đẳng thức xảy ra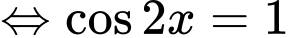
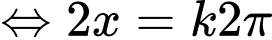
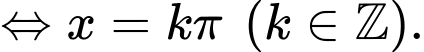 Đáp án: B
Đáp án: B
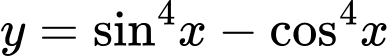
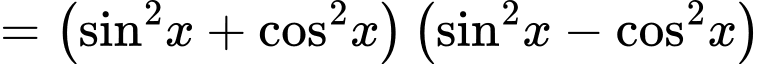
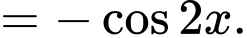
Mà

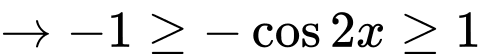
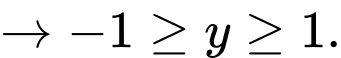
Do đó giá trị nhỏ nhất của hàm số là
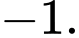
Đẳng thức xảy ra
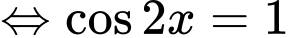
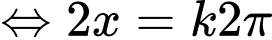
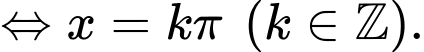 Đáp án: B
Đáp án: B
Câu 13 [582809]: Với giá trị nào của 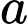 thì hàm số
thì hàm số 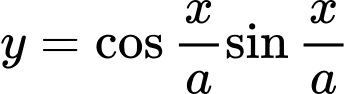 có chu kì
có chu kì 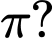
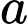 thì hàm số
thì hàm số 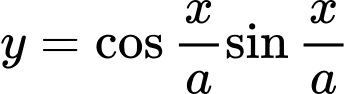 có chu kì
có chu kì 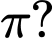
A, 1.
B, 2.
C, 3.
D, 0.
Ta có: 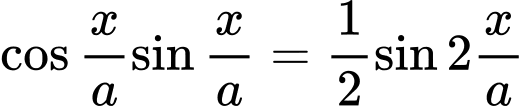
Hàm số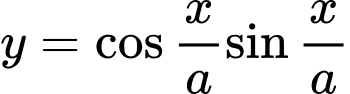 tuần hoàn với chu kì
tuần hoàn với chu kì 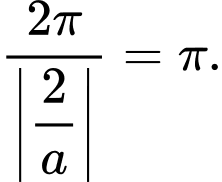 Vậy
Vậy 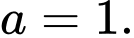 Đáp án: A
Đáp án: A
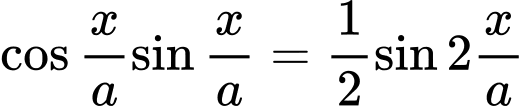
Hàm số
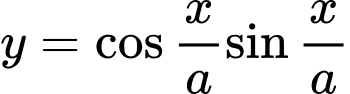 tuần hoàn với chu kì
tuần hoàn với chu kì 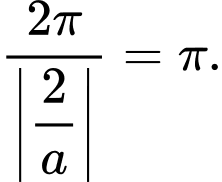 Vậy
Vậy 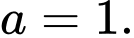 Đáp án: A
Đáp án: A
Câu 14 [582810]: Xét sự biến thiên của hàm số 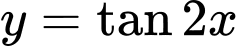 trên một chu kì tuần hoàn. Trong các kết luận sau, kết luận nào đúng?
trên một chu kì tuần hoàn. Trong các kết luận sau, kết luận nào đúng?
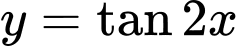 trên một chu kì tuần hoàn. Trong các kết luận sau, kết luận nào đúng?
trên một chu kì tuần hoàn. Trong các kết luận sau, kết luận nào đúng? A, Hàm số đã cho đồng biến trên khoảng 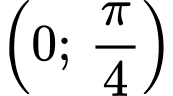 và
và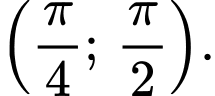
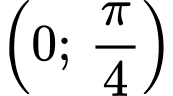 và
và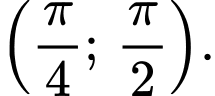
B, Hàm số đã cho đồng biến trên khoảng 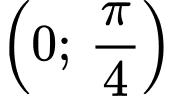 và nghịch biến trên khoảng
và nghịch biến trên khoảng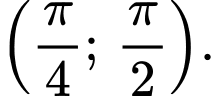
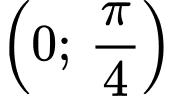 và nghịch biến trên khoảng
và nghịch biến trên khoảng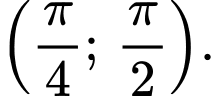
C, Hàm số đã cho luôn đồng biến trên khoảng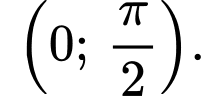
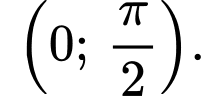
D, Hàm số đã cho nghịch biến trên khoảng 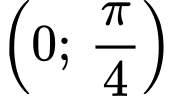 và đồng biến trên khoảng
và đồng biến trên khoảng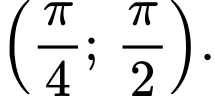
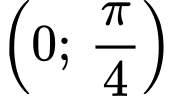 và đồng biến trên khoảng
và đồng biến trên khoảng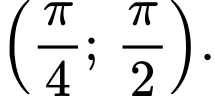
Tập xác định của hàm số đã cho là 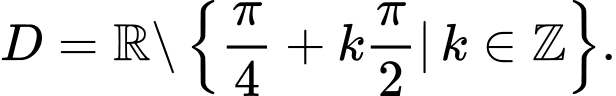
Hàm số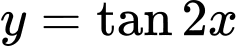 tuần hoàn với chu kì
tuần hoàn với chu kì 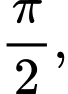 dựa vào các phương án A; B; C; D thì ta sẽ xét tính đơn điệu của hàm số trên
dựa vào các phương án A; B; C; D thì ta sẽ xét tính đơn điệu của hàm số trên 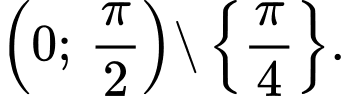
Dựa theo kết quả khảo sát sự biến thiên của hàm số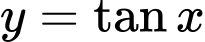 ở phần lý thuyết ta có thể suy ra với hàm số
ở phần lý thuyết ta có thể suy ra với hàm số 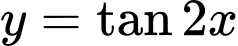 đồng biến trên khoảng
đồng biến trên khoảng 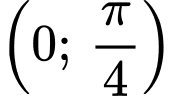 và
và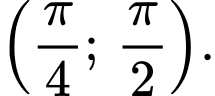 Đáp án: A
Đáp án: A
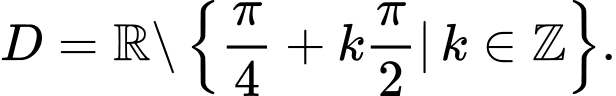
Hàm số
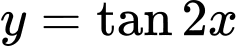 tuần hoàn với chu kì
tuần hoàn với chu kì 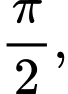 dựa vào các phương án A; B; C; D thì ta sẽ xét tính đơn điệu của hàm số trên
dựa vào các phương án A; B; C; D thì ta sẽ xét tính đơn điệu của hàm số trên 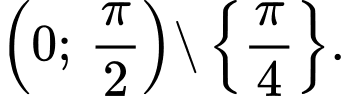
Dựa theo kết quả khảo sát sự biến thiên của hàm số
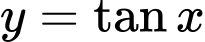 ở phần lý thuyết ta có thể suy ra với hàm số
ở phần lý thuyết ta có thể suy ra với hàm số 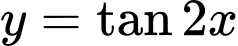 đồng biến trên khoảng
đồng biến trên khoảng 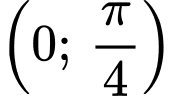 và
và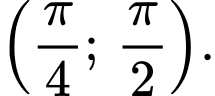 Đáp án: A
Đáp án: A
Câu 15 [582811]: Chu kì của hàm số 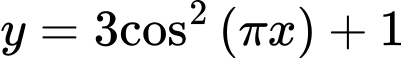 là:
là:
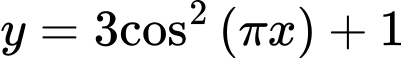 là:
là: A, 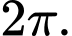
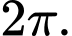
B, 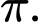
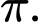
C, 1.
D, 2.
TXĐ 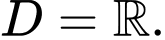 Ta có
Ta có 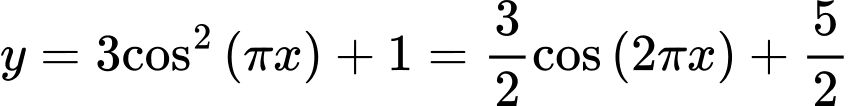
Giả sử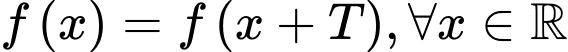
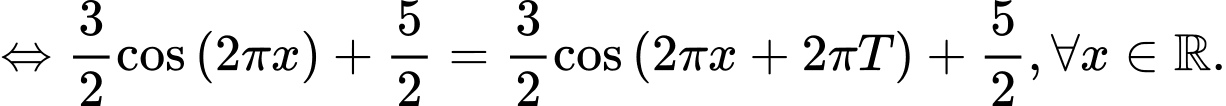
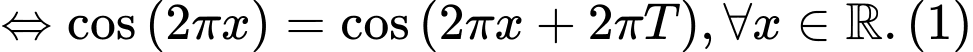
Với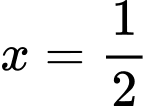 thì
thì  cũng phải đúng, tức là
cũng phải đúng, tức là

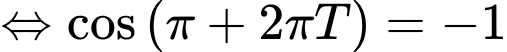
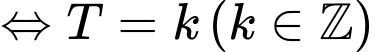
Ngược lại,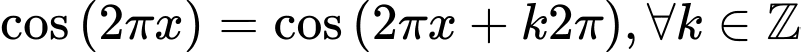 ,
, 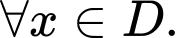
Vậy khi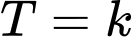 ,
,  thì ta có
thì ta có 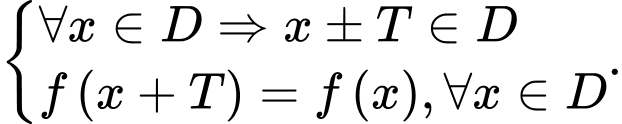
Tức là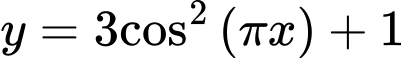 làm hàm số tuần hoàn.
làm hàm số tuần hoàn.
Mặt khác trong các số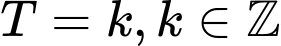 thì số dương nhỏ nhất là
thì số dương nhỏ nhất là 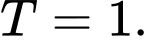
Do đó hàm số đã cho là hàm số tuần hoàn có chu kỳ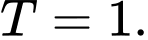 Đáp án: C
Đáp án: C
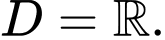 Ta có
Ta có 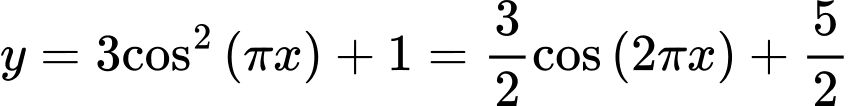
Giả sử
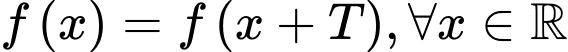
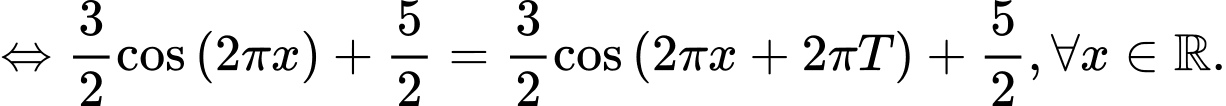
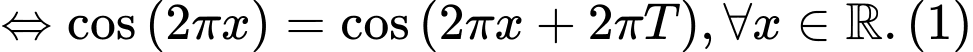
Với
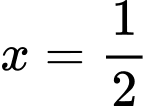 thì
thì  cũng phải đúng, tức là
cũng phải đúng, tức là
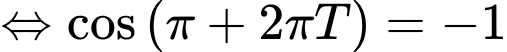
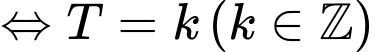
Ngược lại,
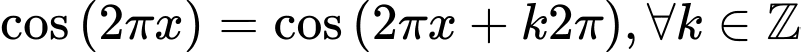 ,
, 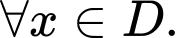
Vậy khi
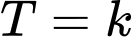 ,
,  thì ta có
thì ta có 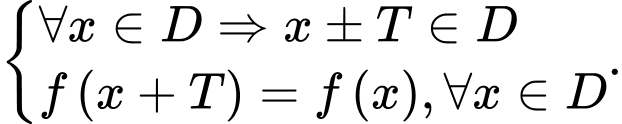
Tức là
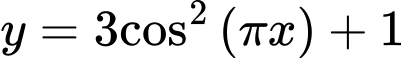 làm hàm số tuần hoàn.
làm hàm số tuần hoàn.Mặt khác trong các số
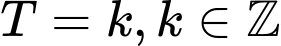 thì số dương nhỏ nhất là
thì số dương nhỏ nhất là 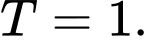
Do đó hàm số đã cho là hàm số tuần hoàn có chu kỳ
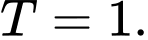 Đáp án: C
Đáp án: C Dạng câu hỏi: Câu trắc nghiệm đúng sai.
(Thí sinh trả lời từ câu 16,17. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng
hoặc sai)
Câu 16 [582812]: Cho hai hàm số 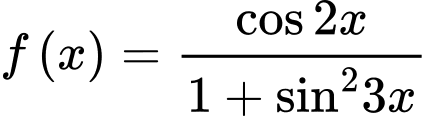 và
và 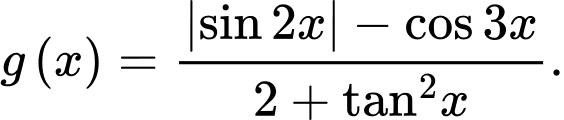
a)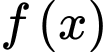 và
và 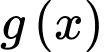 lẻ.
lẻ.
b) Tập xác định của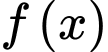 là:
là: 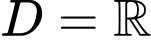
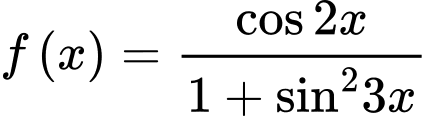 và
và 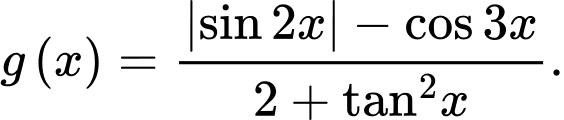
a)
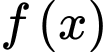 và
và 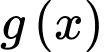 lẻ.
lẻ.b) Tập xác định của
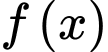 là:
là: 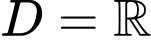
Mệnh đề a) sai vì
Xét hàm số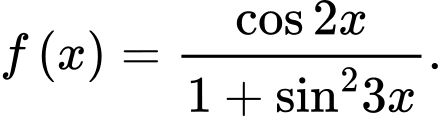
TXĐ: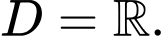 Do đó
Do đó 
Ta có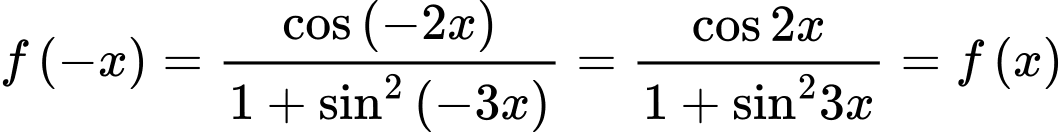
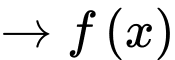 là hàm số chẵn.
là hàm số chẵn.
Xét hàm số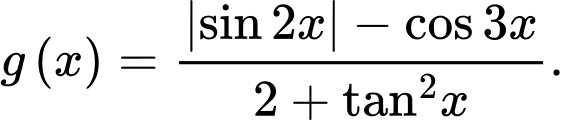
TXĐ: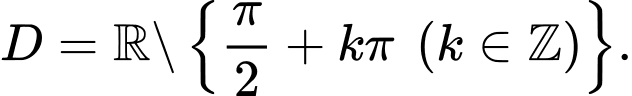 Do đó
Do đó 
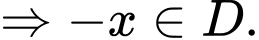
Ta có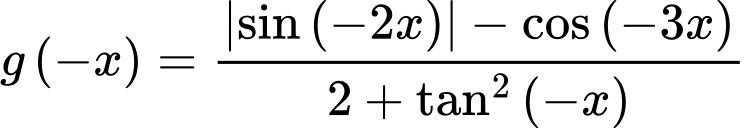
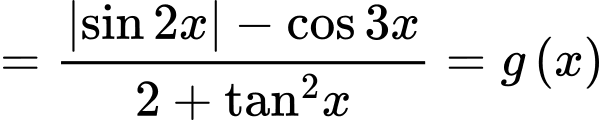
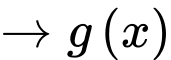 là hàm số chẵn.
là hàm số chẵn.
Vậy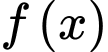 và
và 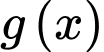 chẵn.
chẵn.
Xét hàm số
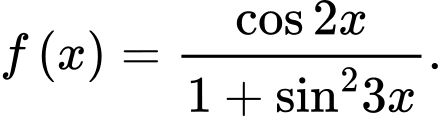
TXĐ:
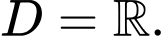 Do đó
Do đó 
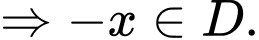
Ta có
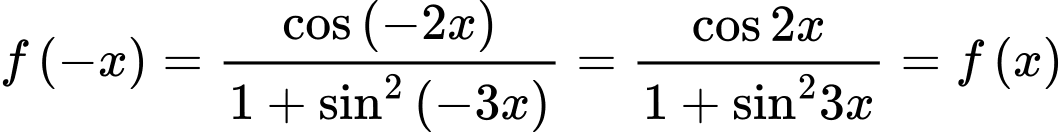
 là hàm số chẵn.
là hàm số chẵn.Xét hàm số
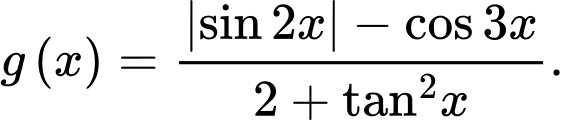
TXĐ:
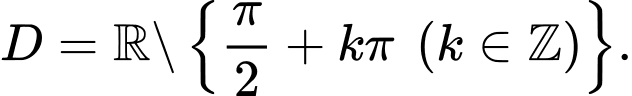 Do đó
Do đó 
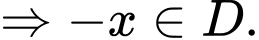
Ta có
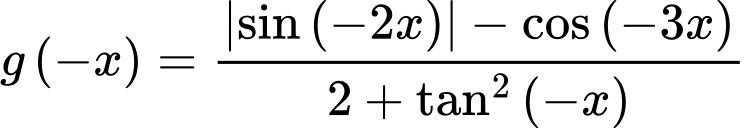
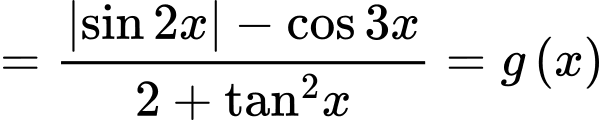
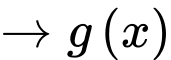 là hàm số chẵn.
là hàm số chẵn.Vậy
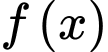 và
và 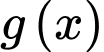 chẵn.
chẵn.
Câu 17 [582813]: Cho đồ thị của hàm số sau.
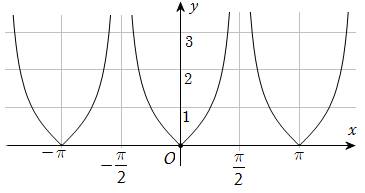
Xác định khẳng định đúng sai trong các khẳng định sau:
a) Hàm số của đồ thị hàm số trên là hàm chẵn.
b) Hàm số có GTNN bằng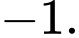

Xác định khẳng định đúng sai trong các khẳng định sau:
a) Hàm số của đồ thị hàm số trên là hàm chẵn.
b) Hàm số có GTNN bằng
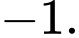
Mệnh đề b) sai vì hàm số có GTNN bằng 0.
Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 18 [582814]: Với giá trị nào của 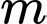 thì hàm số
thì hàm số 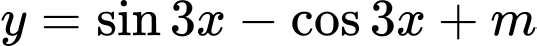 có giá trị lớn nhất bằng
có giá trị lớn nhất bằng 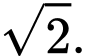
TRẢ LỜI: ……………………….
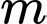 thì hàm số
thì hàm số 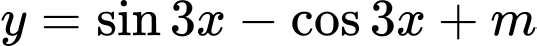 có giá trị lớn nhất bằng
có giá trị lớn nhất bằng 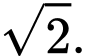
TRẢ LỜI: ……………………….
Ta có 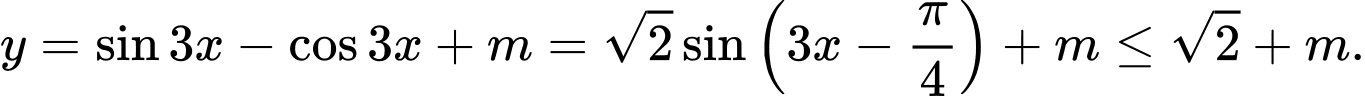 Để hàm số có giá trị lớn nhất bằng
Để hàm số có giá trị lớn nhất bằng 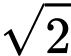 thì
thì 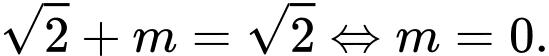
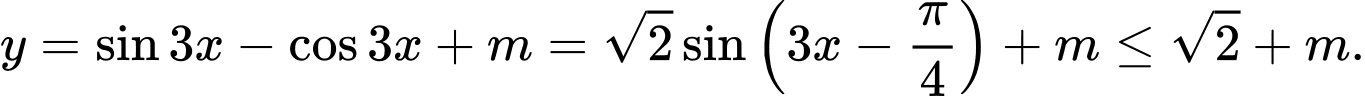 Để hàm số có giá trị lớn nhất bằng
Để hàm số có giá trị lớn nhất bằng 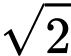 thì
thì 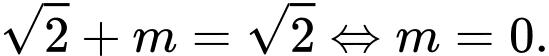
Câu 19 [582815]: Có bao nhiêu giá trị nguyên của m để hàm số 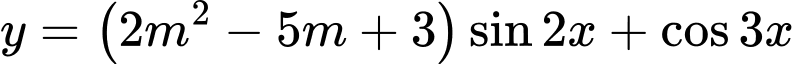 là hàm số chẵn?
là hàm số chẵn?
TRẢ LỜI: ……………………….
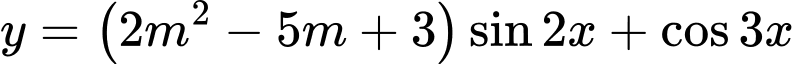 là hàm số chẵn?
là hàm số chẵn? TRẢ LỜI: ……………………….
TXĐ 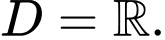 Ta có
Ta có 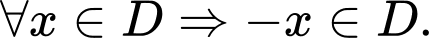
Để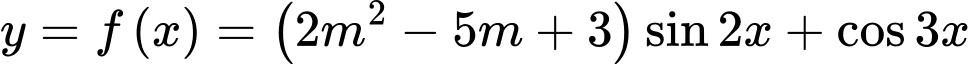 là hàm số chẵn
là hàm số chẵn
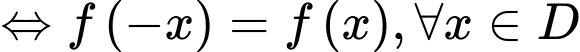
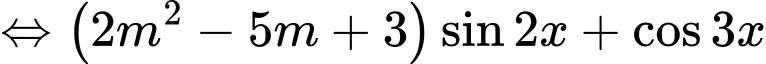
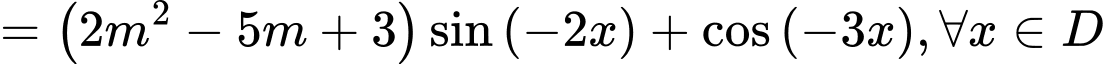
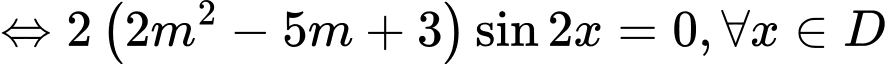
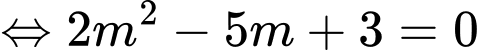
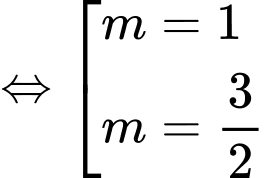
Vì nên
nên 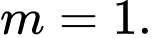
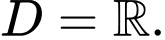 Ta có
Ta có 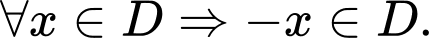
Để
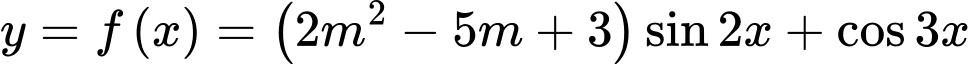 là hàm số chẵn
là hàm số chẵn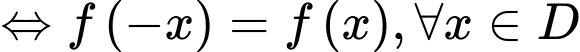
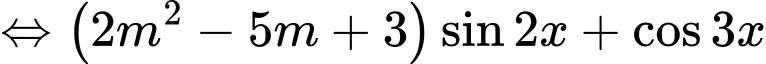
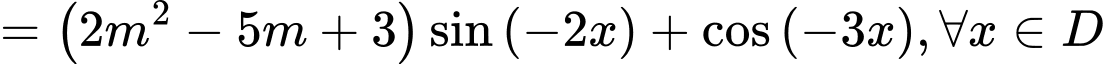
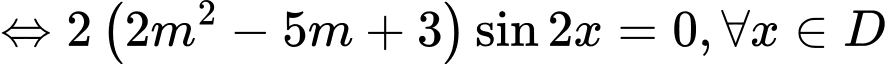
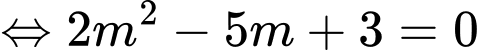
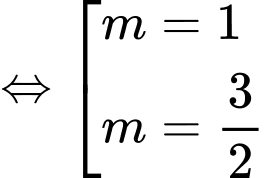
Vì
 nên
nên 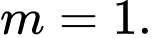
Câu 20 [582816]: Tìm GTLN của hàm số 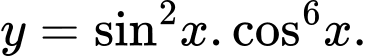
TRẢ LỜI: ……………………….
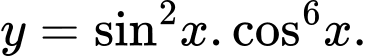
TRẢ LỜI: ……………………….
Do số mũ lớn và phải tìm Max nên ta nghĩ đến việc sử dụng BĐT Cô si theo chiều:
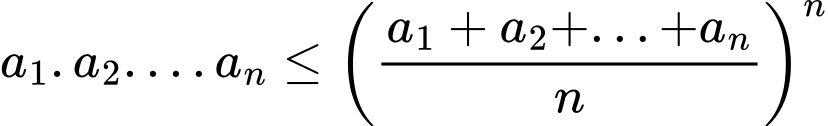
Dễ thấy rằng, nếu áp dụng trực tiếp như sau: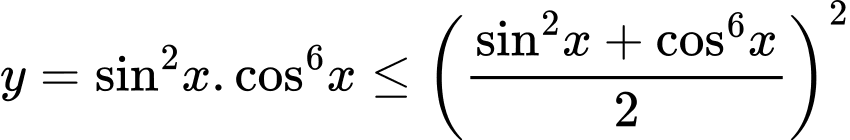 thì việc đánh giá biểu thức ở vế phải vẫn gặp khó khăn.
thì việc đánh giá biểu thức ở vế phải vẫn gặp khó khăn.
Chú ý rằng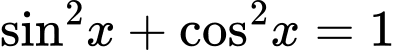 nên để sau bước đánh giá, biểu thức ở vế phải đơn giản hơn, ta tiến hành tách như sau:
nên để sau bước đánh giá, biểu thức ở vế phải đơn giản hơn, ta tiến hành tách như sau:
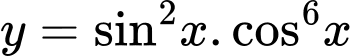
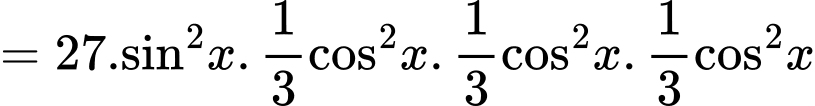
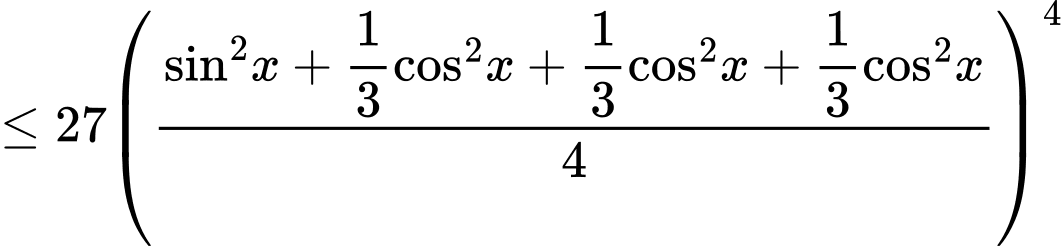
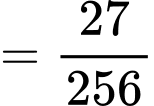
Đẳng thức xảy ra khi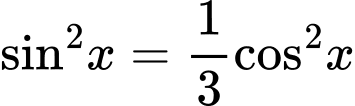
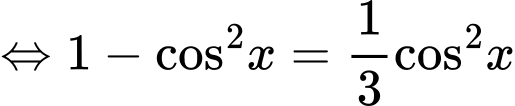
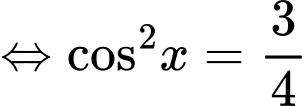
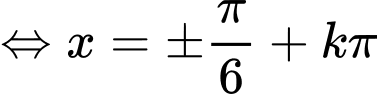
Vậy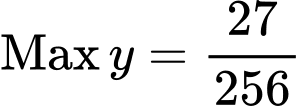 tại
tại 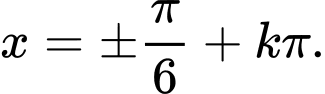
Giải trắc nghiệm: (Sử dụng MTCT)
+ Chuyển đơn vị đo từ độ (chữ D) sang radian (chữ R)
+ Vào chức năng TABLE ( MODE 7): Bấm hàm số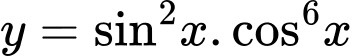
START: 0 END: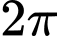 STEP:
STEP: 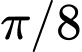 , ta được bảng các giá trị của hàm số trên
, ta được bảng các giá trị của hàm số trên 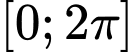 như sau:
như sau:
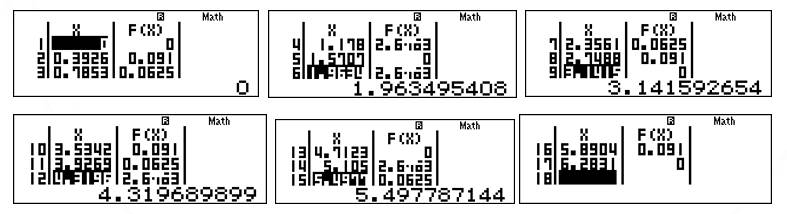
Dựa vào bảng trên, ta thấy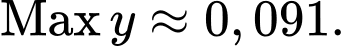 Đối chiếu với 4 đáp án, ta thấy chỉ có đáp án B với
Đối chiếu với 4 đáp án, ta thấy chỉ có đáp án B với 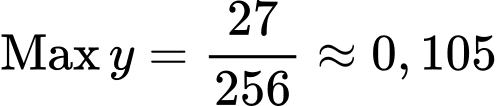 là gần nhất (Nếu không thể kết luận được thì nên chọn lại STEP là
là gần nhất (Nếu không thể kết luận được thì nên chọn lại STEP là 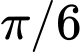 )
)
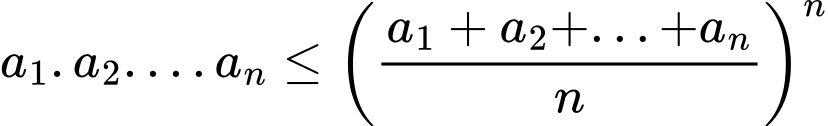
Dễ thấy rằng, nếu áp dụng trực tiếp như sau:
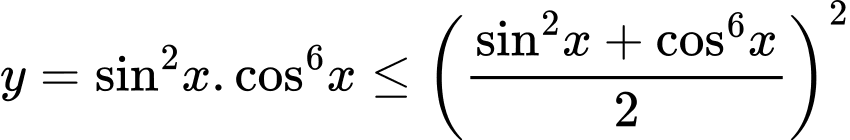 thì việc đánh giá biểu thức ở vế phải vẫn gặp khó khăn.
thì việc đánh giá biểu thức ở vế phải vẫn gặp khó khăn.Chú ý rằng
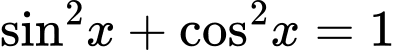 nên để sau bước đánh giá, biểu thức ở vế phải đơn giản hơn, ta tiến hành tách như sau:
nên để sau bước đánh giá, biểu thức ở vế phải đơn giản hơn, ta tiến hành tách như sau: 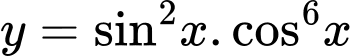
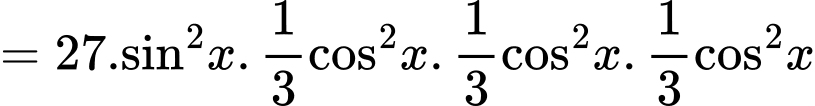
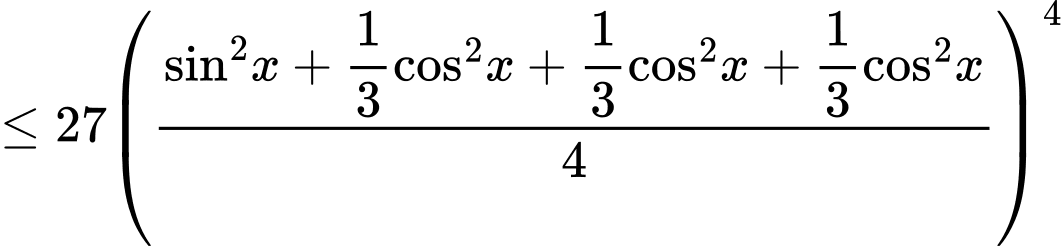
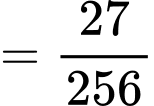
Đẳng thức xảy ra khi
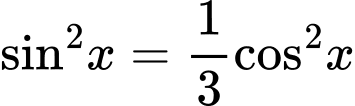
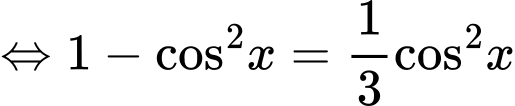
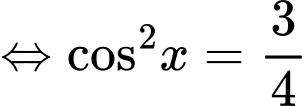
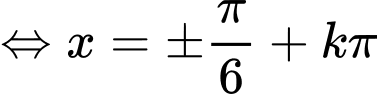
Vậy
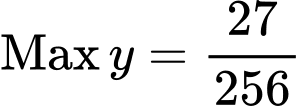 tại
tại 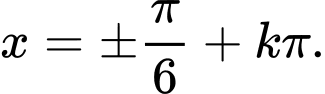
Giải trắc nghiệm: (Sử dụng MTCT)
+ Chuyển đơn vị đo từ độ (chữ D) sang radian (chữ R)
+ Vào chức năng TABLE ( MODE 7): Bấm hàm số
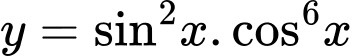
START: 0 END:
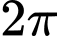 STEP:
STEP: 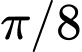 , ta được bảng các giá trị của hàm số trên
, ta được bảng các giá trị của hàm số trên 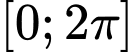 như sau:
như sau:
Dựa vào bảng trên, ta thấy
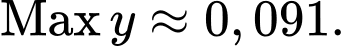 Đối chiếu với 4 đáp án, ta thấy chỉ có đáp án B với
Đối chiếu với 4 đáp án, ta thấy chỉ có đáp án B với 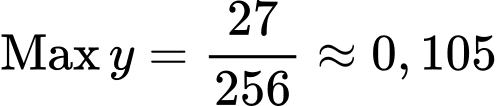 là gần nhất (Nếu không thể kết luận được thì nên chọn lại STEP là
là gần nhất (Nếu không thể kết luận được thì nên chọn lại STEP là 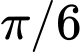 )
) Dạng câu hỏi: Câu hỏi kéo thả.
Câu 21 [582817]: Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Hàm số tuần hoàn với chu kì...
tuần hoàn với chu kì...
Hàm số không xác định với mọi x có dạng ... (
không xác định với mọi x có dạng ... (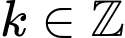 ).
).

Hàm số
 tuần hoàn với chu kì...
tuần hoàn với chu kì...Hàm số
 không xác định với mọi x có dạng ... (
không xác định với mọi x có dạng ... (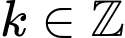 ).
).
Đáp án
Hàm số tuần hoàn với chu kì
tuần hoàn với chu kì 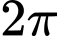
Hàm số không xác định với mọi
không xác định với mọi 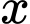 có dạng
có dạng 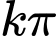 (
(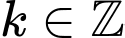 ).
).
Phương pháp giải
Hàm số tuần hoàn với chu kì
tuần hoàn với chu kì 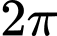
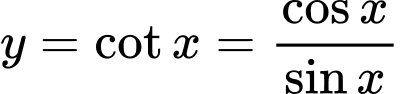 không xác định khi
không xác định khi 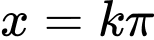
Hàm số
 tuần hoàn với chu kì
tuần hoàn với chu kì 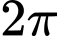
Hàm số
 không xác định với mọi
không xác định với mọi 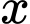 có dạng
có dạng 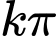 (
(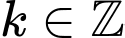 ).
).Phương pháp giải
Hàm số
 tuần hoàn với chu kì
tuần hoàn với chu kì 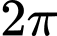
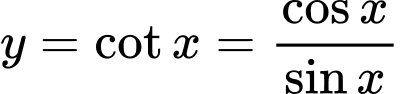 không xác định khi
không xác định khi