1. Dạng toán: Phương trình lượng giác cơ bản
Câu 1 [583168]: Tập nghiệm của phương trình 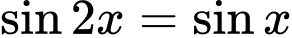 là
là
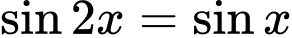 là
là A, 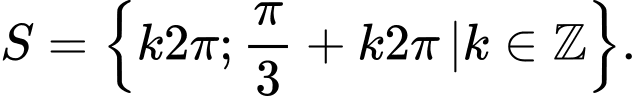
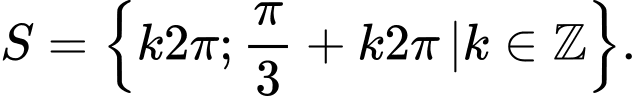
B, 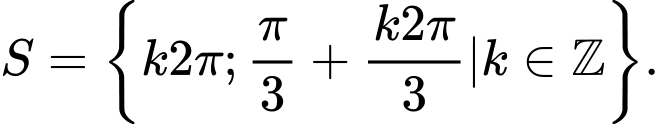
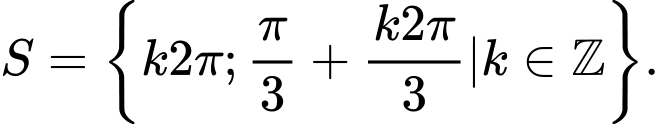
C, 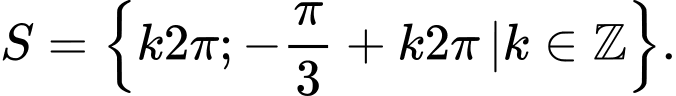
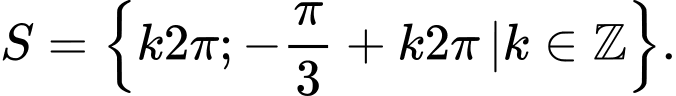
D, 

Ta có 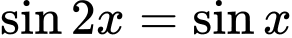
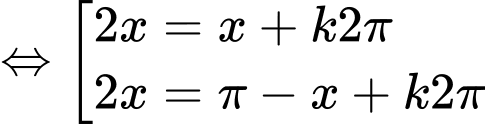
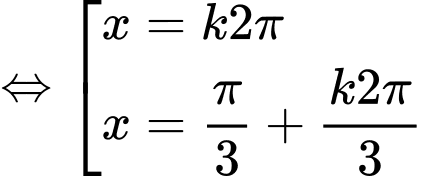
 .
.
=> Chọn B. Đáp án: B
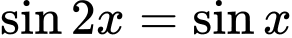
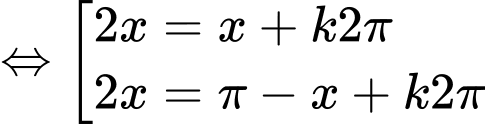
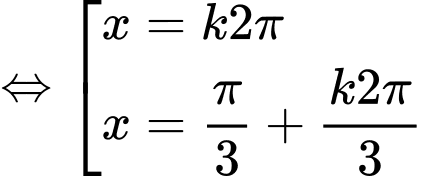
 .
. => Chọn B. Đáp án: B
Câu 2 [583169]: Biểu diễn họ nghiệm của phương trình 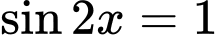 trên đường tròn đơn vị ta được bao nhiêu điểm?
trên đường tròn đơn vị ta được bao nhiêu điểm?
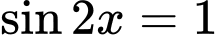 trên đường tròn đơn vị ta được bao nhiêu điểm?
trên đường tròn đơn vị ta được bao nhiêu điểm? A, 
B, 
C, 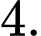
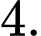
D, 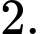
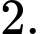
Ta có: 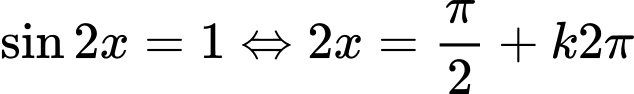
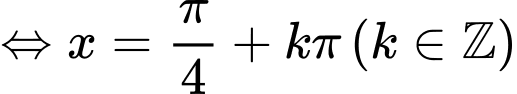
Do đó khi biểu diễn họ nghiệm của phương trình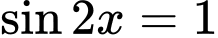 trên đường tròn đơn vị ta được
trên đường tròn đơn vị ta được 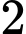 điểm.
điểm.
=> Chọn D. Đáp án: D
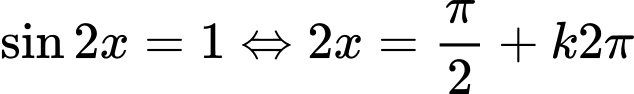
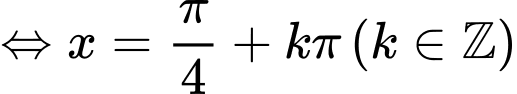
Do đó khi biểu diễn họ nghiệm của phương trình
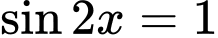 trên đường tròn đơn vị ta được
trên đường tròn đơn vị ta được 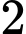 điểm.
điểm.
=> Chọn D. Đáp án: D
Câu 3 [583170]: Tổng tất cả các nghiệm của phương trình 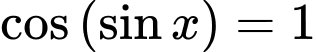 trên
trên 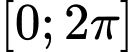 bằng:
bằng:
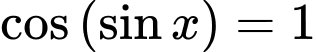 trên
trên 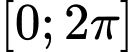 bằng:
bằng: A,  .
.
 .
.B, 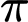 .
.
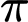 .
.C, 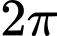 .
.
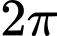 .
.D, 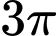 .
.
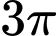 .
.
Ta có 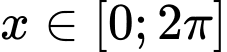
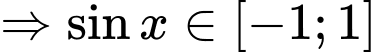
Khi đó: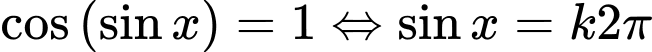
 với
với  .
.
Phương trình trở thành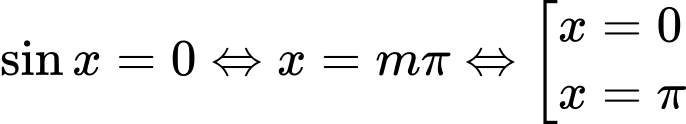
 .
.
Vậy tổng tất cả các nghiệm của phương trình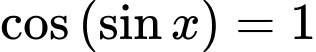 trên
trên 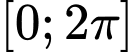 bằng
bằng 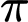 .
.
=> Chọn B. Đáp án: B
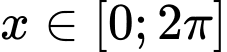
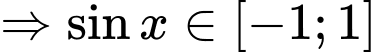
Khi đó:
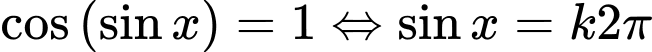
 với
với  .
.
Phương trình trở thành
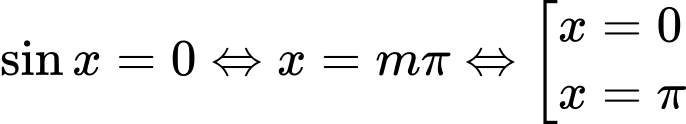
 .
.
Vậy tổng tất cả các nghiệm của phương trình
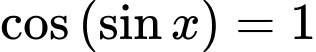 trên
trên 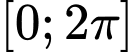 bằng
bằng 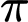 .
.
=> Chọn B. Đáp án: B
Câu 4 [583171]: Số giá trị nguyên của 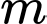 để phương trình
để phương trình 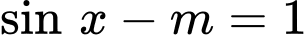 có nghiệm là:
có nghiệm là:
Đáp án:……
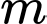 để phương trình
để phương trình 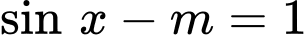 có nghiệm là:
có nghiệm là:Đáp án:……
Ta có 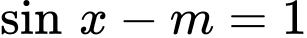
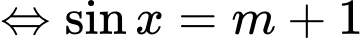
Vì
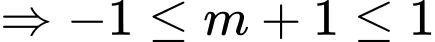
 .
.
Vậy tồn tại 3 giá trị của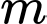 để phương trình bài ra có nghiệm. => Điền:…3….
để phương trình bài ra có nghiệm. => Điền:…3….
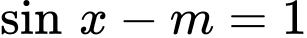
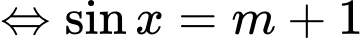
Vì

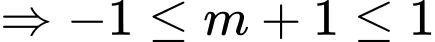
 .
.Vậy tồn tại 3 giá trị của
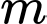 để phương trình bài ra có nghiệm. => Điền:…3….
để phương trình bài ra có nghiệm. => Điền:…3…. 2. Dạng toán: Phương trình bậc hai đối với hàm số lượng giác
Câu 5 [583172]: Số nghiệm của phương trình 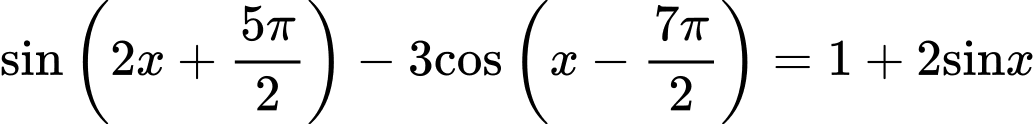 với
với 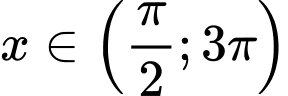 là:
là:
Đáp án:……
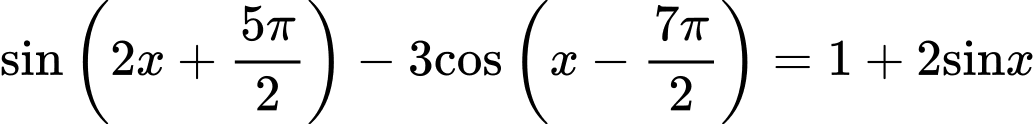 với
với 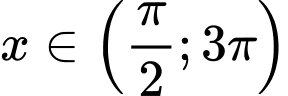 là:
là:Đáp án:……
Tự luận:
Phương trình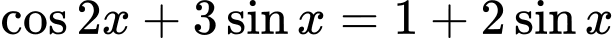

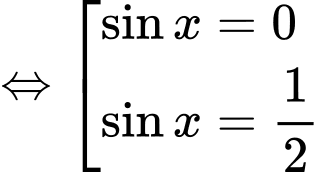
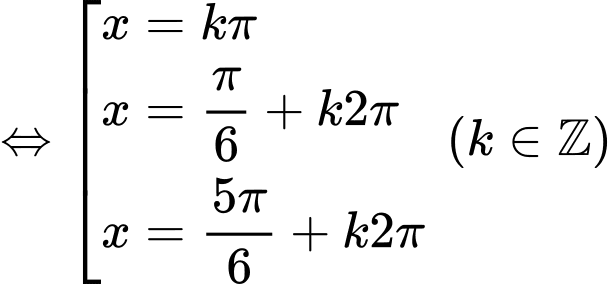
- Để
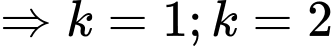
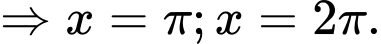
- Để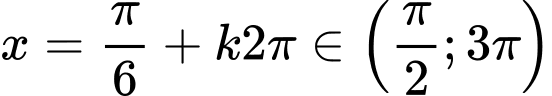
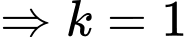
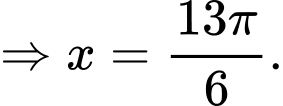
- Để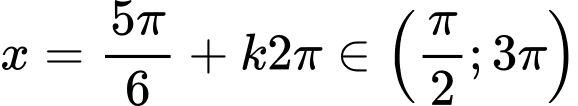
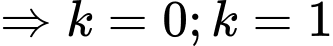
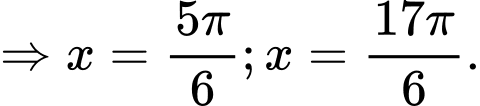
Vậy phương trình đã cho có 5 nghiệm.
Trắc nghiệm:
Từ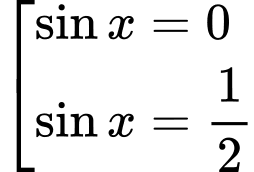 ta sử dụng đường tròn lượng giác để chỉ ra số nghiêm của phương trình thuộc khoảng
ta sử dụng đường tròn lượng giác để chỉ ra số nghiêm của phương trình thuộc khoảng 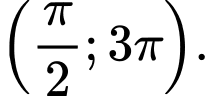
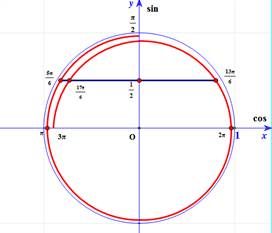
=> Điền:..5.…
Phương trình
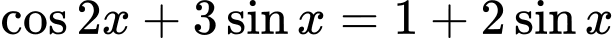

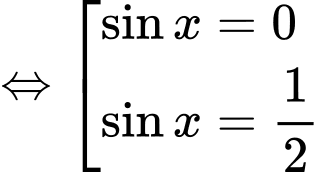
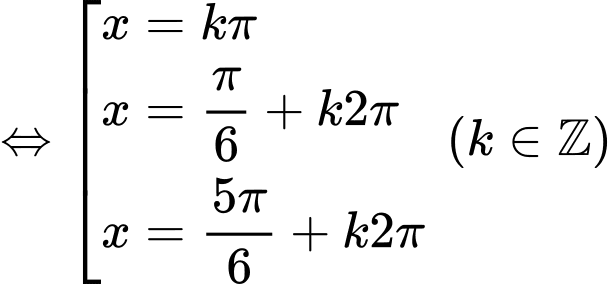
- Để

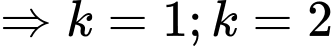
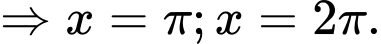
- Để
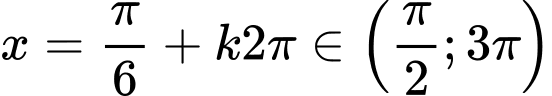
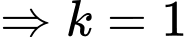
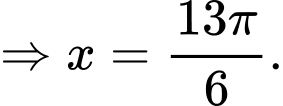
- Để
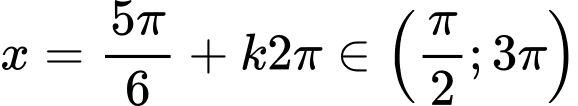
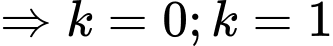
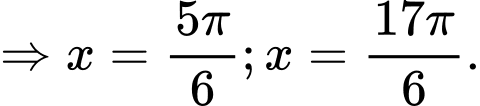
Vậy phương trình đã cho có 5 nghiệm.
Trắc nghiệm:
Từ
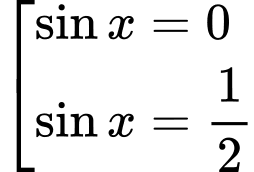 ta sử dụng đường tròn lượng giác để chỉ ra số nghiêm của phương trình thuộc khoảng
ta sử dụng đường tròn lượng giác để chỉ ra số nghiêm của phương trình thuộc khoảng 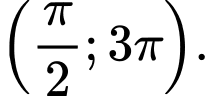

=> Điền:..5.…
Câu 6 [583173]: Giải phương trình lượng giác sau: 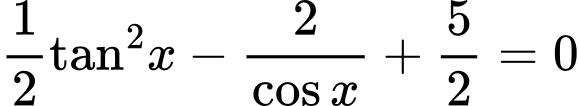
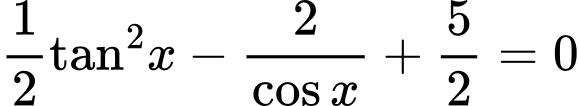
A, 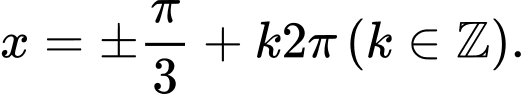
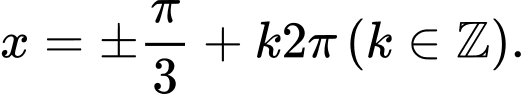
B, 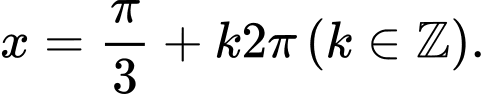
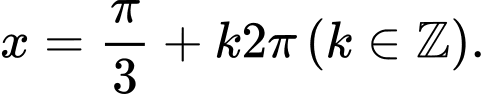
C, 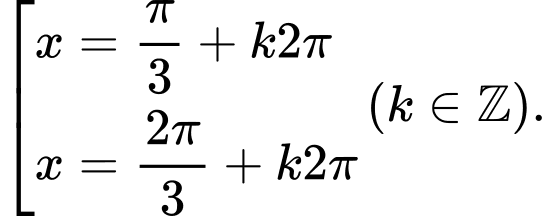
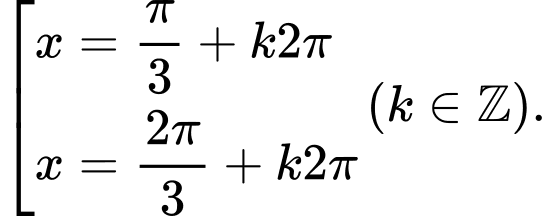
D, Phương trình vô nghiệm.
Giải tự luận:
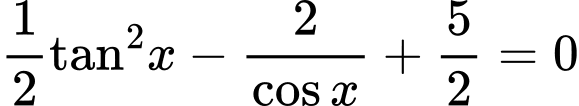
Điều kiện: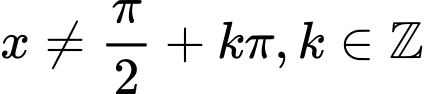
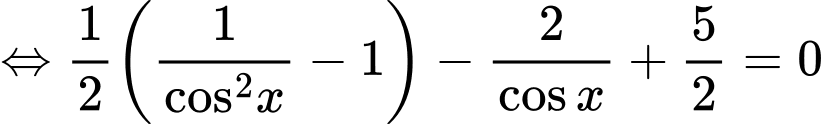
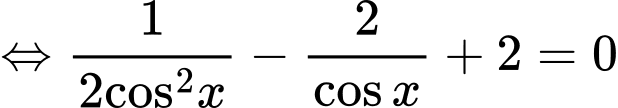
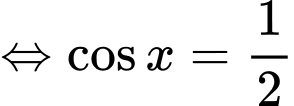
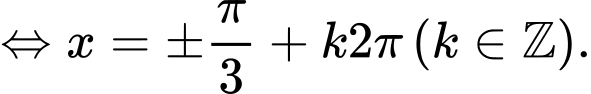
Giải trắc nghiệm: (Hướng dẫn sử dụng MTCT nếu được)
Nhập phương trình: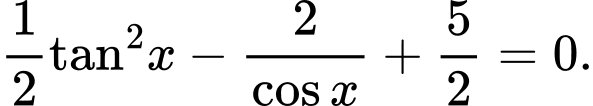
Nhập phương trình (Nhớ chuyển qua radian)
(Nhớ chuyển qua radian)
từng đáp án ta chọn đáp án A.
=> Chọn A Đáp án: A
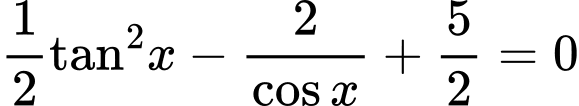
Điều kiện:
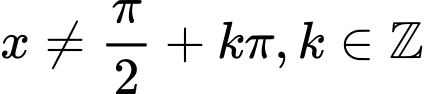
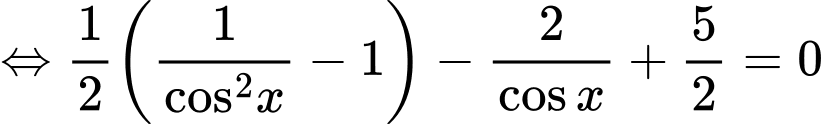
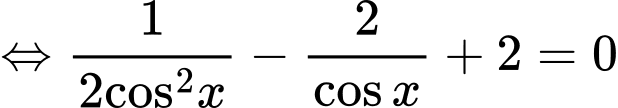
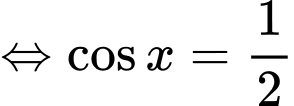
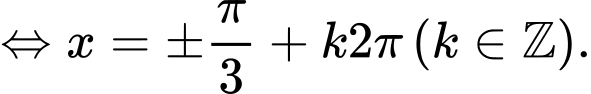
Giải trắc nghiệm: (Hướng dẫn sử dụng MTCT nếu được)
Nhập phương trình:
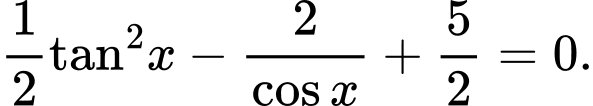
Nhập phương trình
 (Nhớ chuyển qua radian)
(Nhớ chuyển qua radian) từng đáp án ta chọn đáp án A.
=> Chọn A Đáp án: A
Câu 7 [583174]: Giải phương trình lượng giác sau: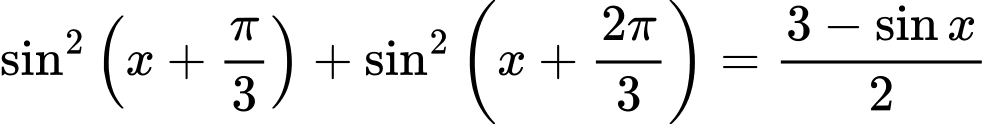
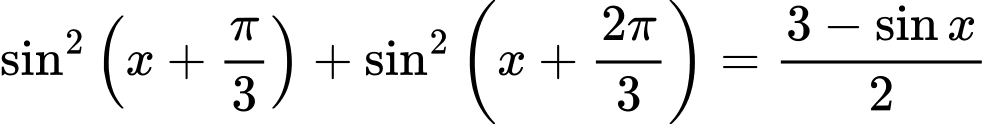
A, 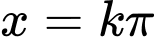
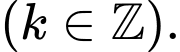
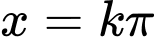
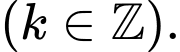
B, 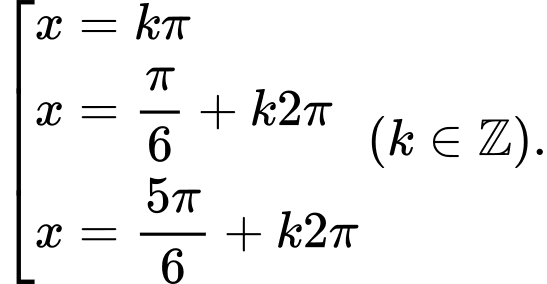
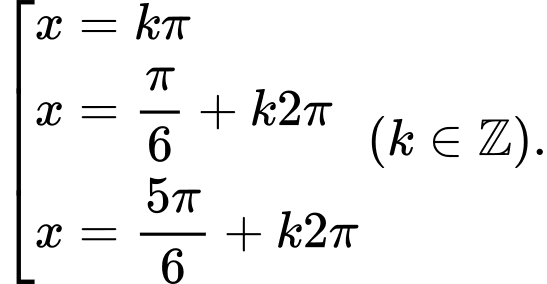
C, 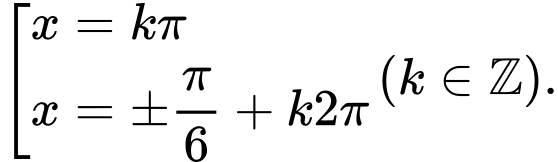
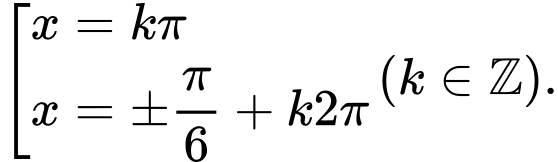
D, 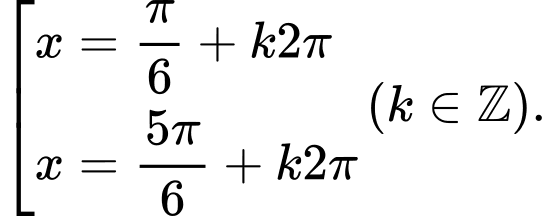
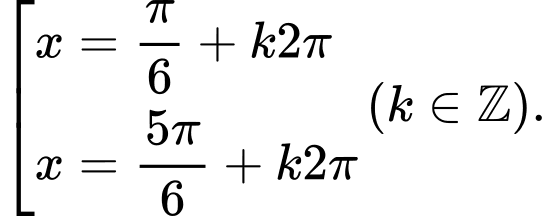
Giải tự luận: 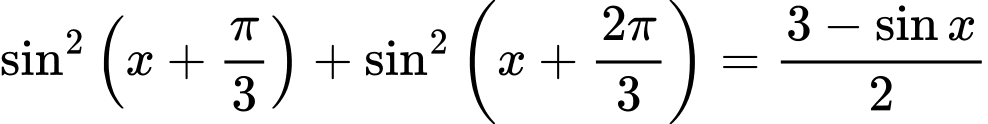
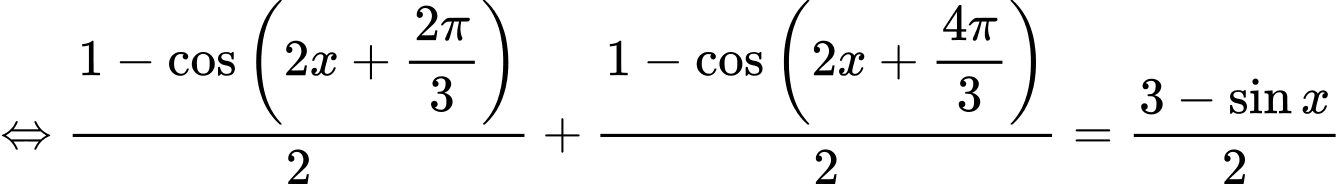
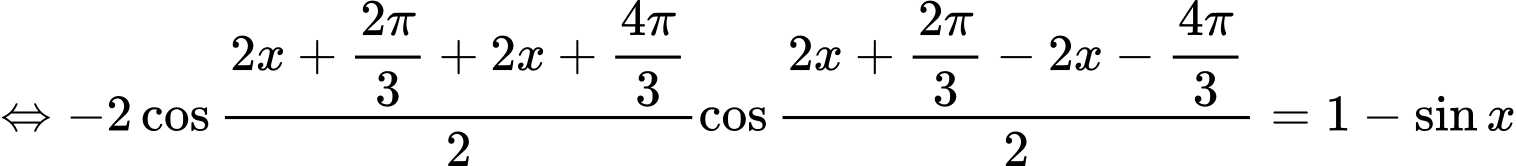
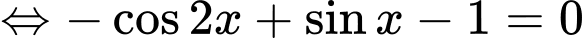


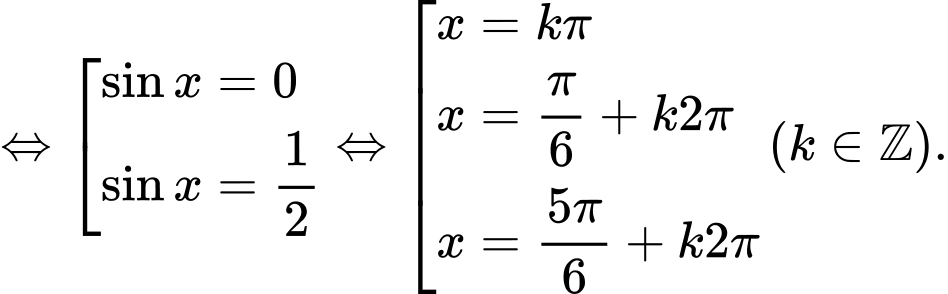
Giải trắc nghiệm: Nhập phương trình: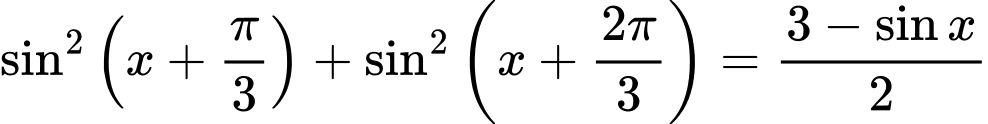
CALC từng đáp án ta chọn đáp án B.
=>Chọn B Đáp án: B
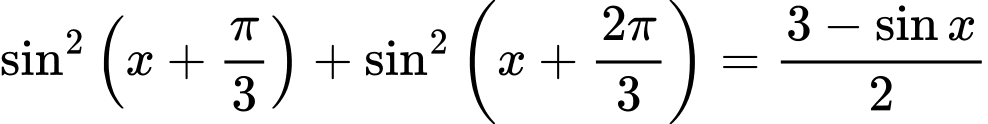
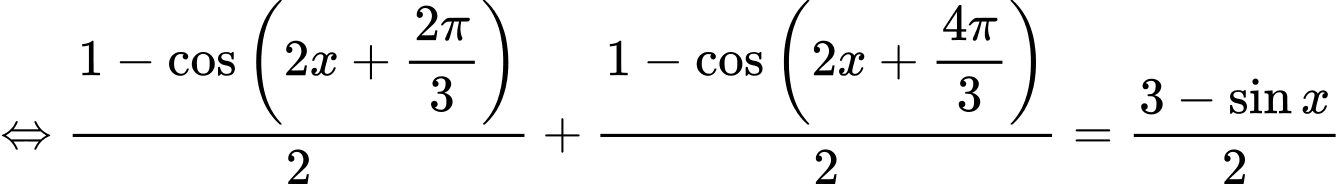
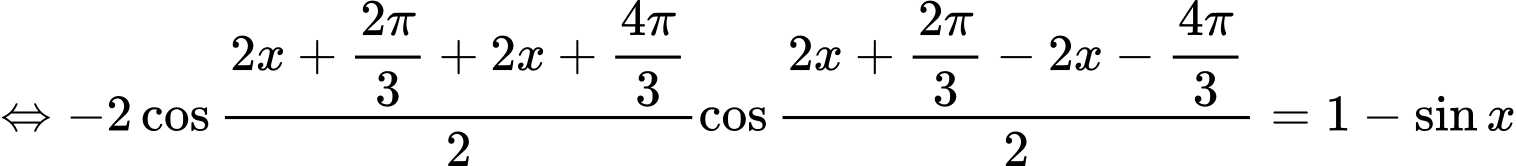
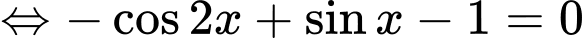


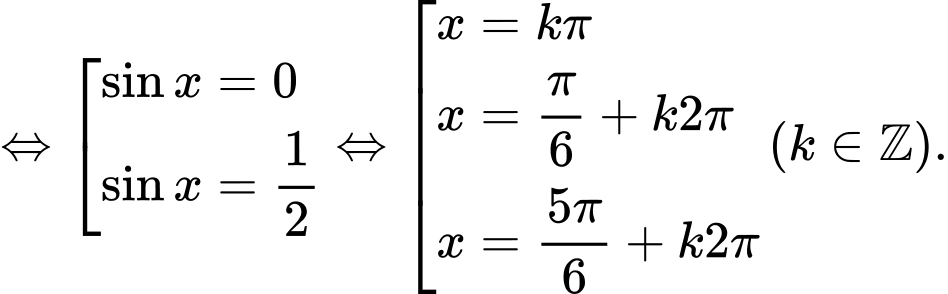
Giải trắc nghiệm: Nhập phương trình:
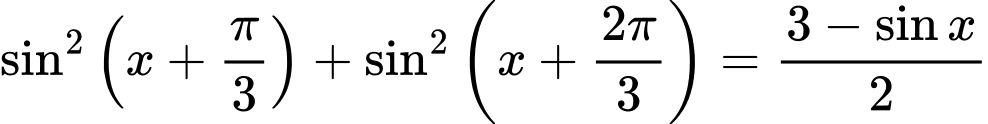
CALC từng đáp án ta chọn đáp án B.
=>Chọn B Đáp án: B
Câu 8 [583175]: Tìm 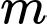 để phương trình
để phương trình 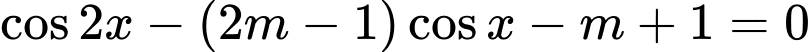 có đúng hai nghiệm phân biệt
có đúng hai nghiệm phân biệt 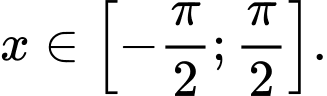
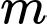 để phương trình
để phương trình 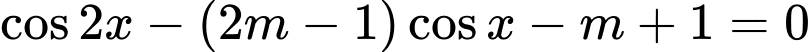 có đúng hai nghiệm phân biệt
có đúng hai nghiệm phân biệt 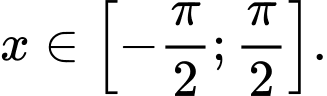
A, 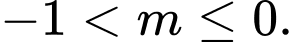
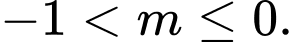
B, 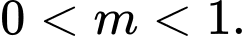
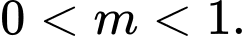
C, 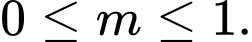
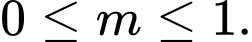
D, 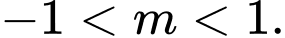
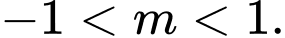
Ta có:
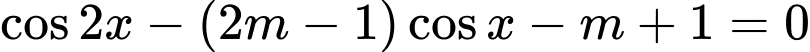
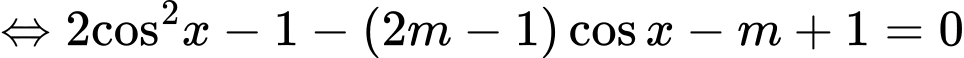
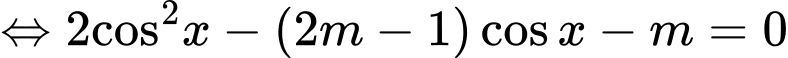
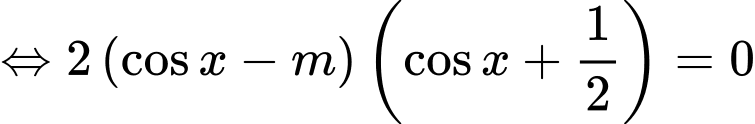
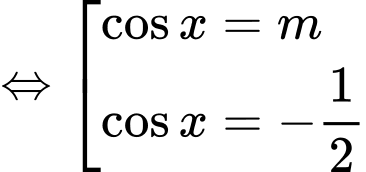
Do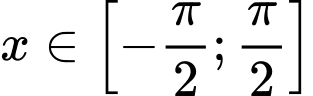
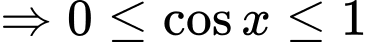
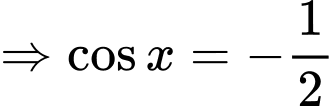 loại.
loại.
Vẽ đường tròn lượng giác kết hợp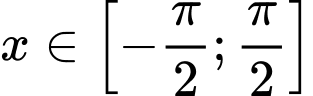 ta suy ra được
ta suy ra được 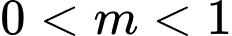 nên chọn đáp án B.
nên chọn đáp án B.
⇨ Chọn B Đáp án: B
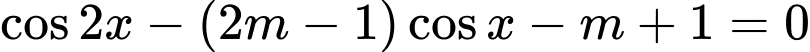
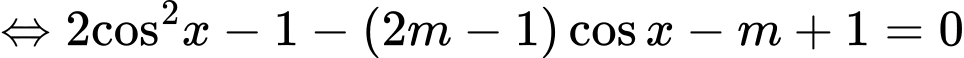
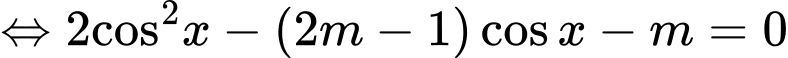
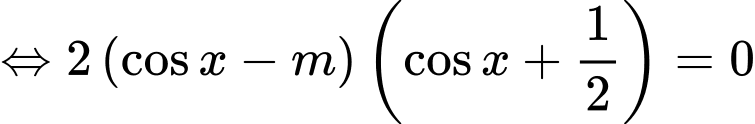
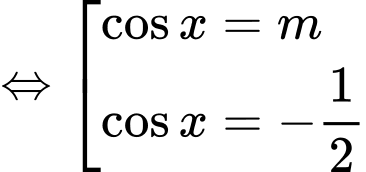
Do
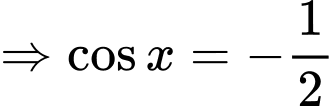 loại.
loại.Vẽ đường tròn lượng giác kết hợp
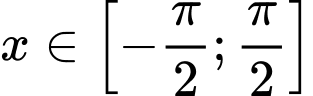 ta suy ra được
ta suy ra được 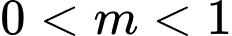 nên chọn đáp án B.
nên chọn đáp án B. ⇨ Chọn B Đáp án: B
3. Dạng toán: Phương trình bậc đối với sin và cos
Câu 9 [583176]: Giải phương trình 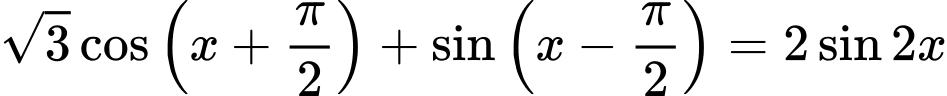
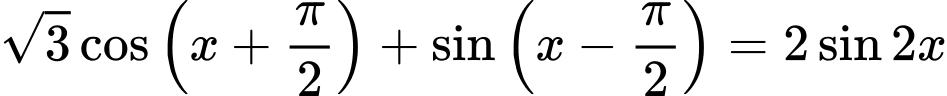
A, 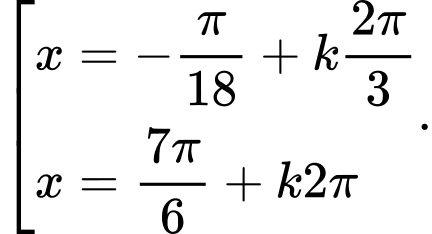
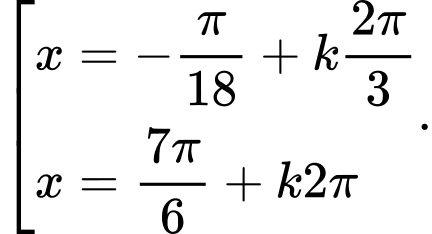
B,  .
.
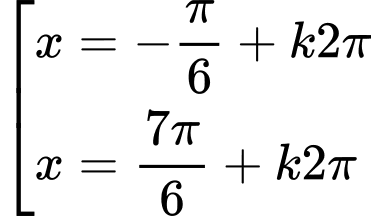 .
.C, 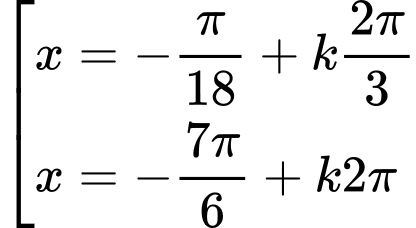 .
.
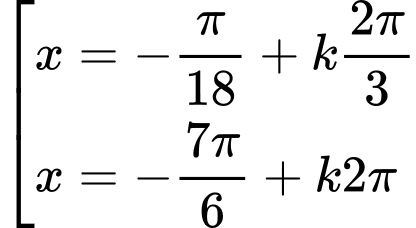 .
.D, 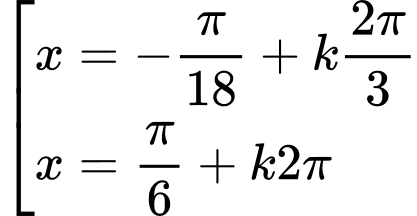 .
.
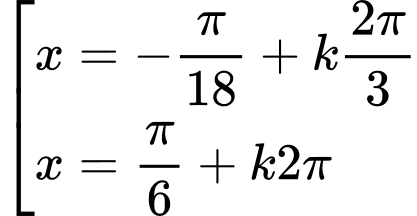 .
.
Phương trình 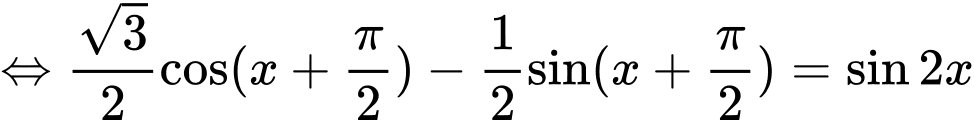
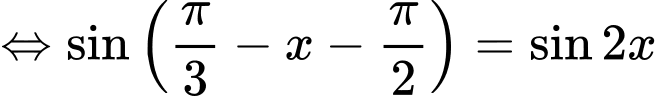
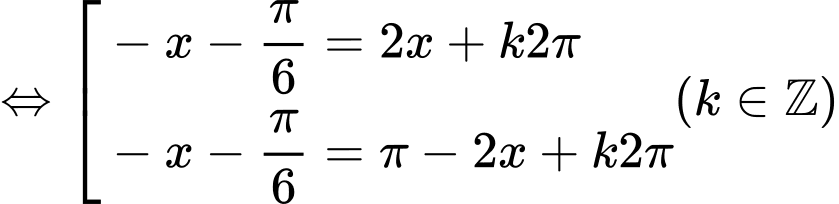
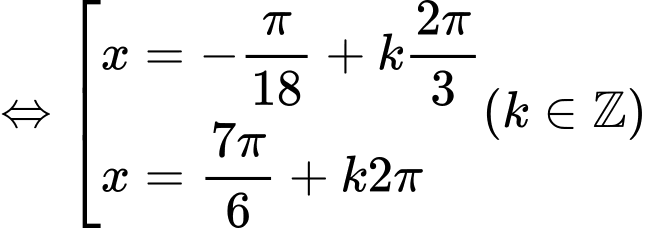
=>Chọn A. Đáp án: A
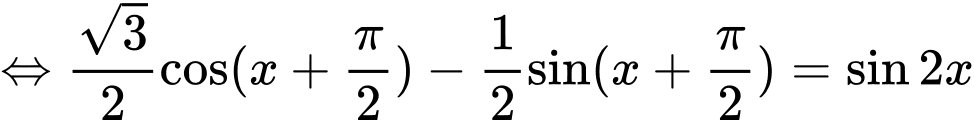
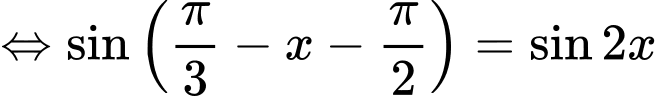
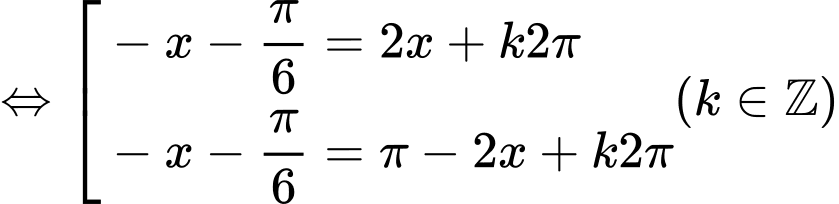
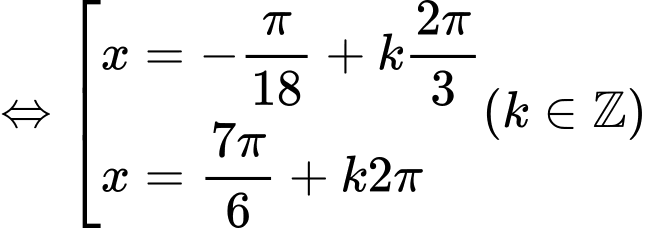
=>Chọn A. Đáp án: A
Câu 10 [583177]: Biểu diễn nghiệm của phương trình  trên đường tròn lượng giác. Số điểm biểu diễn là:
trên đường tròn lượng giác. Số điểm biểu diễn là:
Đáp án:……
 trên đường tròn lượng giác. Số điểm biểu diễn là:
trên đường tròn lượng giác. Số điểm biểu diễn là:Đáp án:……
Tự luận: Phương trình 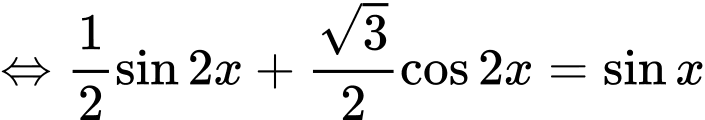
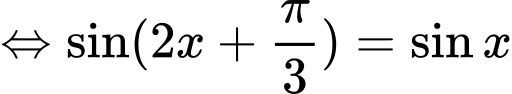
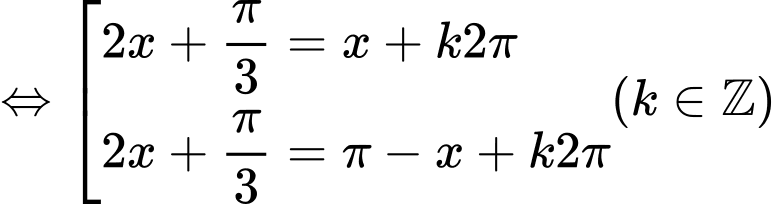
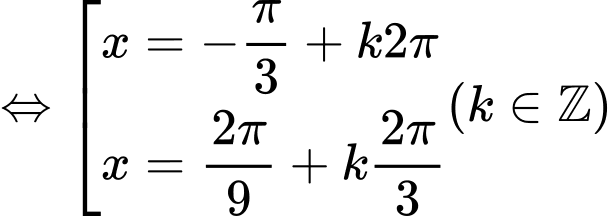
Hai họ nghiệm không có điểm biểu diễn trùng nhau. Suy ra số điểm biểu diễn là 4.
Trắc nghiệm: SHIFP MODE 3.
Lập bảng cho biểu thức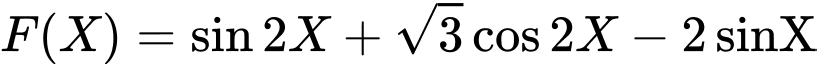 ,
, 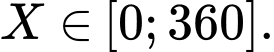
Với: Start ; End
; End 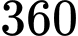 ; Step:
; Step:  .
.
Quan sát bảng thấy F(X) đổi dấu 4 lần. Tức phương trình có 4 nghiệm thuộc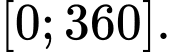
=> Điền: 4
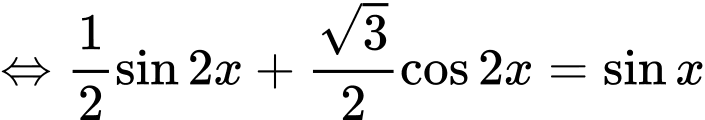
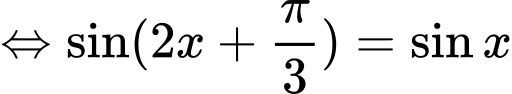
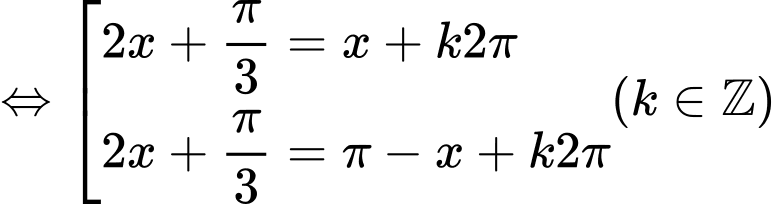
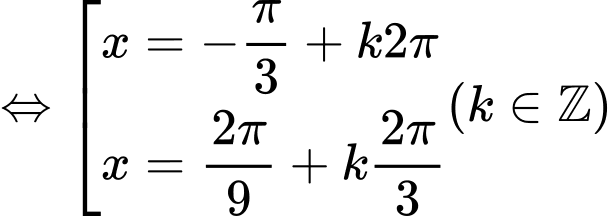
Hai họ nghiệm không có điểm biểu diễn trùng nhau. Suy ra số điểm biểu diễn là 4.
Trắc nghiệm: SHIFP MODE 3.
Lập bảng cho biểu thức
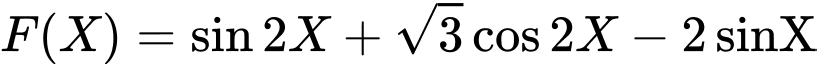 ,
, 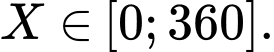
Với: Start
 ; End
; End 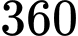 ; Step:
; Step:  .
.Quan sát bảng thấy F(X) đổi dấu 4 lần. Tức phương trình có 4 nghiệm thuộc
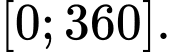
=> Điền: 4
Câu 11 [583178]: Khi biểu diễn nghiệm của phương trình 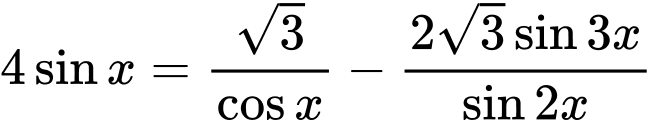 trên đường tròn lượng giác, ta được số điểm ngọn là:
trên đường tròn lượng giác, ta được số điểm ngọn là:
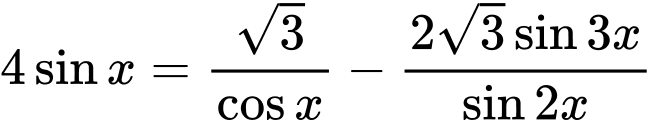 trên đường tròn lượng giác, ta được số điểm ngọn là:
trên đường tròn lượng giác, ta được số điểm ngọn là: A, 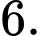
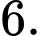
B, 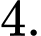
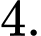
C, 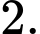
D, 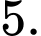
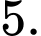
+/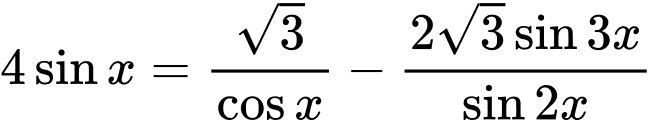
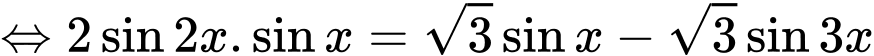
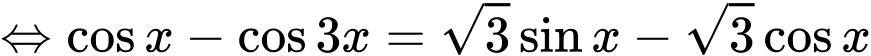

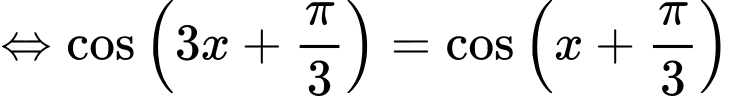
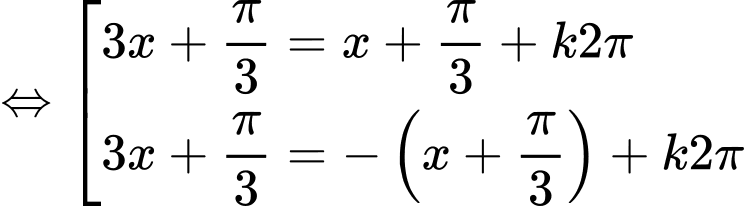
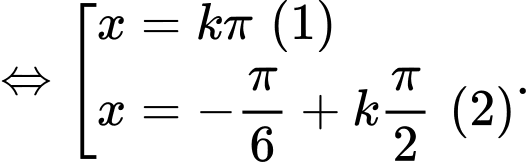
+/ Họ nghiệm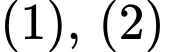 khi biểu diễn trên đường tròn lượng giác có số điểm ngọn lần lượt là 2 và 4 ( các điểm ngọn của hai họ nghiệm này không trùng nhau). Vậy số điểm ngọn cần tìm là 6.
khi biểu diễn trên đường tròn lượng giác có số điểm ngọn lần lượt là 2 và 4 ( các điểm ngọn của hai họ nghiệm này không trùng nhau). Vậy số điểm ngọn cần tìm là 6.
=> Chọn A
Chú ý cách biến đổi khác:
+/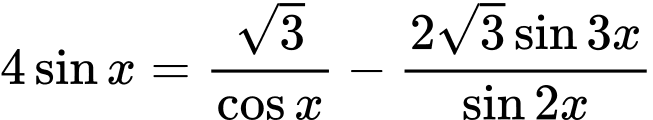
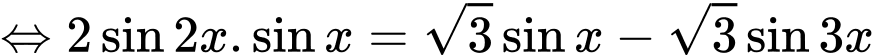
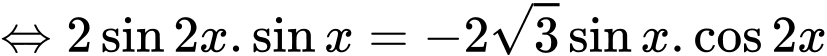
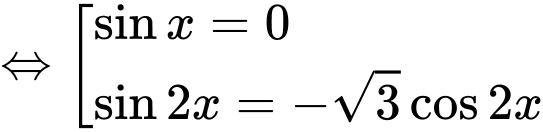
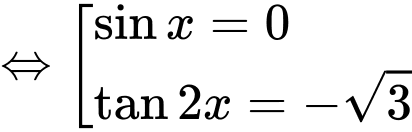
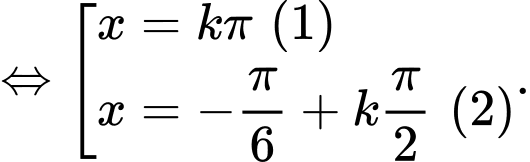 Đáp án: A
Đáp án: A
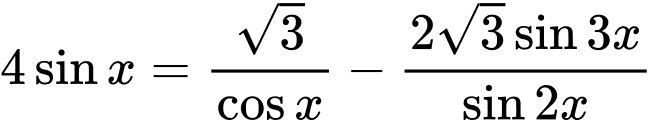
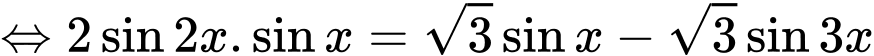
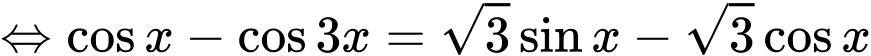

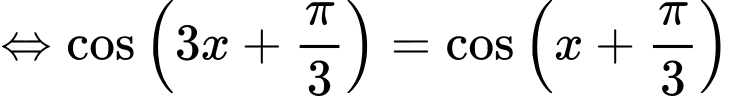
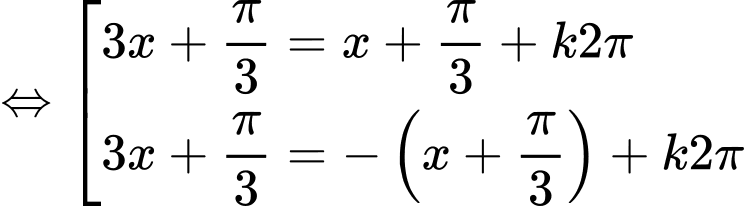
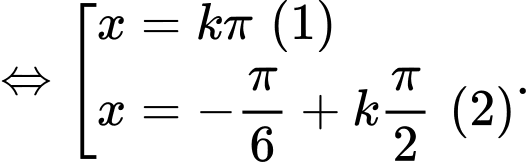
+/ Họ nghiệm
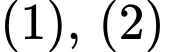 khi biểu diễn trên đường tròn lượng giác có số điểm ngọn lần lượt là 2 và 4 ( các điểm ngọn của hai họ nghiệm này không trùng nhau). Vậy số điểm ngọn cần tìm là 6.
khi biểu diễn trên đường tròn lượng giác có số điểm ngọn lần lượt là 2 và 4 ( các điểm ngọn của hai họ nghiệm này không trùng nhau). Vậy số điểm ngọn cần tìm là 6.=> Chọn A
Chú ý cách biến đổi khác:
+/
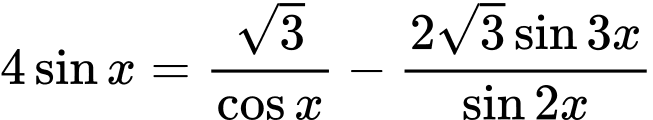
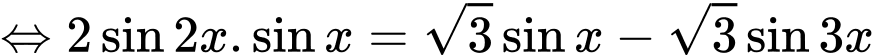
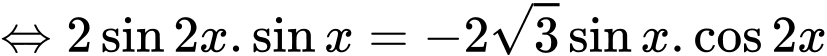
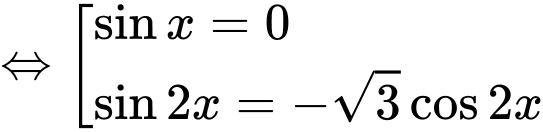
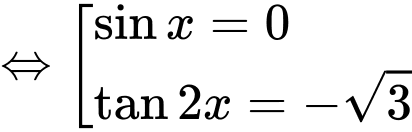
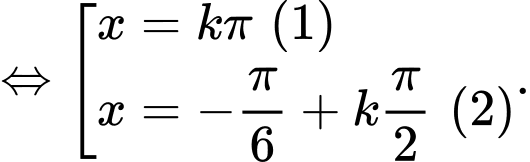 Đáp án: A
Đáp án: A
Câu 12 [583179]: Có bao nhiêu giá trị của 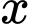 thuộc đoạn
thuộc đoạn 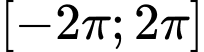 mà tại đó hàm số
mà tại đó hàm số 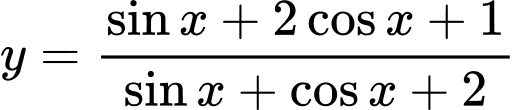 đạt giá trị lớn nhất:
đạt giá trị lớn nhất:
Đáp án:……
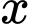 thuộc đoạn
thuộc đoạn 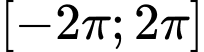 mà tại đó hàm số
mà tại đó hàm số 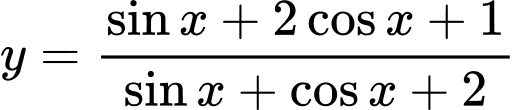 đạt giá trị lớn nhất:
đạt giá trị lớn nhất:Đáp án:……
Tự luận: Vì phương trình 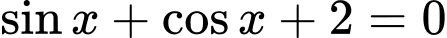 vô nghiệm nên :
vô nghiệm nên :
TXĐ: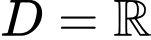
Biến đổi hàm số đã cho về dạng:
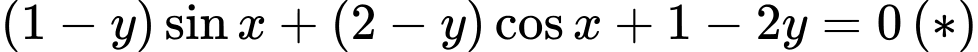
Phương trình (*) là phương trình bậc nhất đối với sin và cos, ta có:
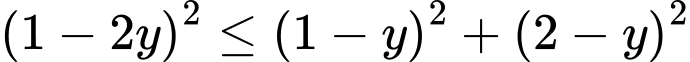
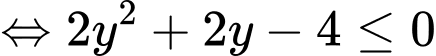
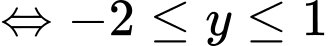
Ta thấy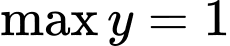 khi
khi 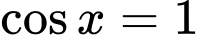
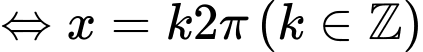
Trên đoạn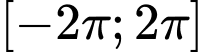 có các giá trị
có các giá trị 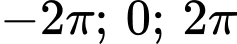 thỏa mãn.
thỏa mãn.
Trắc nghiệm:
Lập bảng cho biểu thức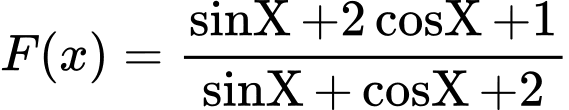 ,
, 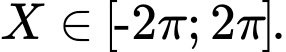
Với: Start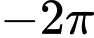 ; End
; End 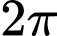 ; Step:
; Step: 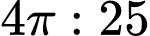 . Quan sát bảng thấy F(X) có 3 lần đạt giá trị gần bằng 1 (lớn nhất).
. Quan sát bảng thấy F(X) có 3 lần đạt giá trị gần bằng 1 (lớn nhất).
=> Điền:…3…..
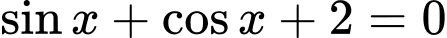 vô nghiệm nên :
vô nghiệm nên :TXĐ:
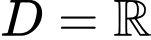
Biến đổi hàm số đã cho về dạng:
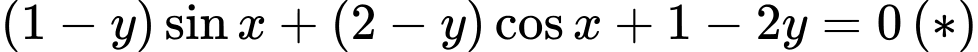
Phương trình (*) là phương trình bậc nhất đối với sin và cos, ta có:
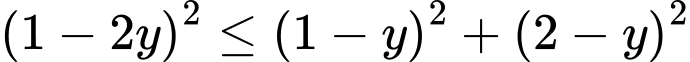
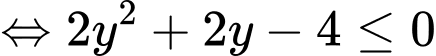
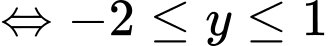
Ta thấy
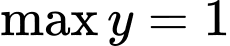 khi
khi 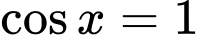
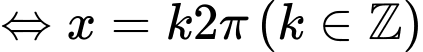
Trên đoạn
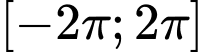 có các giá trị
có các giá trị 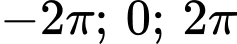 thỏa mãn.
thỏa mãn.Trắc nghiệm:
Lập bảng cho biểu thức
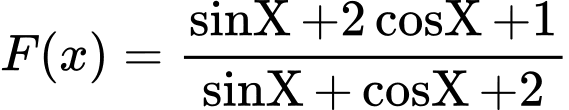 ,
, 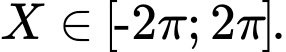
Với: Start
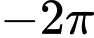 ; End
; End 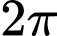 ; Step:
; Step: 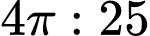 . Quan sát bảng thấy F(X) có 3 lần đạt giá trị gần bằng 1 (lớn nhất).
. Quan sát bảng thấy F(X) có 3 lần đạt giá trị gần bằng 1 (lớn nhất).=> Điền:…3…..
4. Dạng toán: Phương trình đẳng cấp đối với sin và cos
Câu 13 [583180]: Phương trình 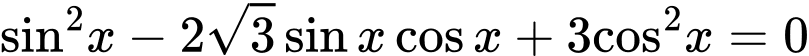 có nghiệm là:
có nghiệm là:
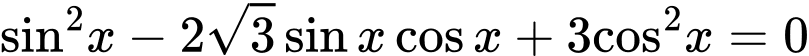 có nghiệm là:
có nghiệm là: A, 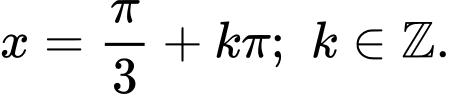
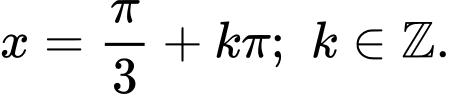
B, 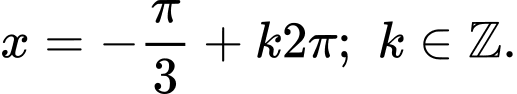
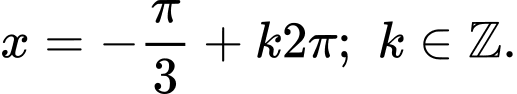
C, 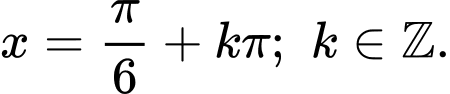
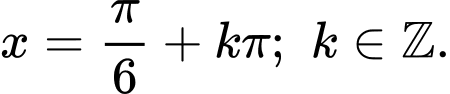
D, 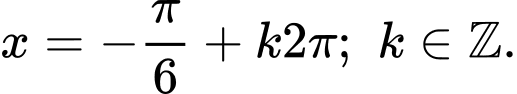
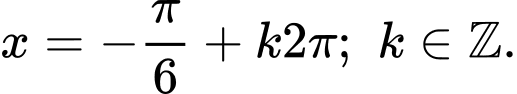
Giải tự luận: Ta có: 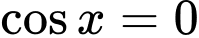 không là nghiệm của phương trình.
không là nghiệm của phương trình.
Phương trình đã cho tương đương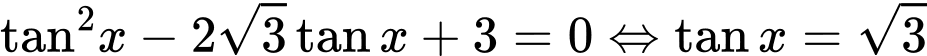
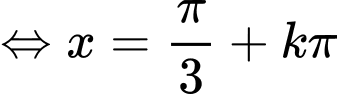 ;
; 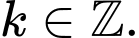
Giải trắc nghiệm: Nhập phương trình vào máy tính, thử nghiệm.
=> Chọn A. Đáp án: A
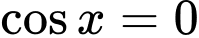 không là nghiệm của phương trình.
không là nghiệm của phương trình.Phương trình đã cho tương đương
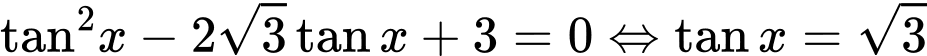
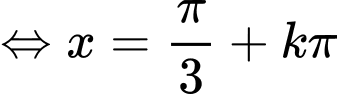 ;
; 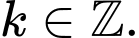
Giải trắc nghiệm: Nhập phương trình vào máy tính, thử nghiệm.
=> Chọn A. Đáp án: A
Câu 14 [583181]: Tìm tất cả các giá trị của tham số 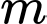 để phương trình
để phương trình 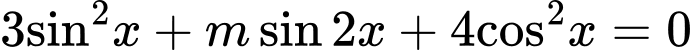 có nghiệm.
có nghiệm.
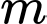 để phương trình
để phương trình 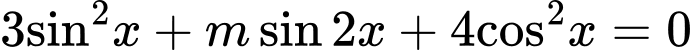 có nghiệm.
có nghiệm. A, 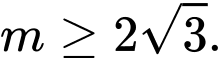
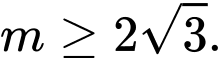
B, 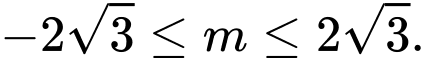
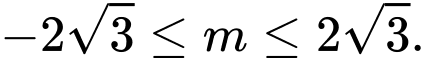
C, 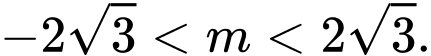
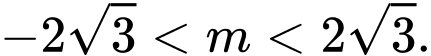
D, 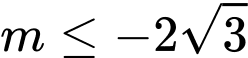
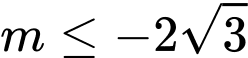
Xét 2 trường hợp:
Trường hợp 1: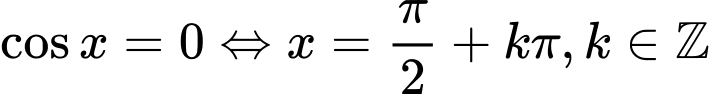
Thay vào phương trình ta được (vô lý)
(vô lý)
Vậy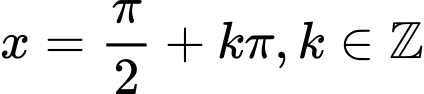 không phải là nghiệm của phương trình với mọi
không phải là nghiệm của phương trình với mọi 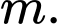
Trường hợp 2: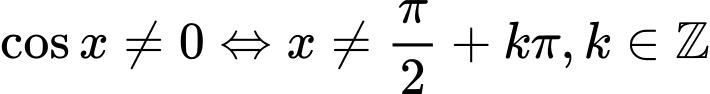 phương trình có dạng
phương trình có dạng 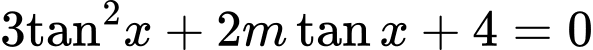
Đặt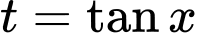 ta có
ta có 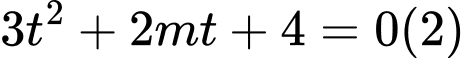
Vậy điều kiện để phương trình có nghiệm là
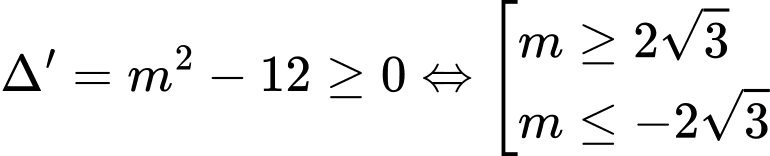
=> Chọn D. Đáp án: D
Trường hợp 1:
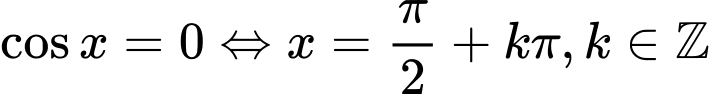
Thay vào phương trình ta được
 (vô lý)
(vô lý)Vậy
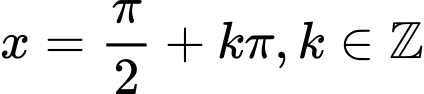 không phải là nghiệm của phương trình với mọi
không phải là nghiệm của phương trình với mọi 
Trường hợp 2:
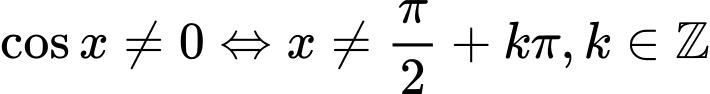 phương trình có dạng
phương trình có dạng 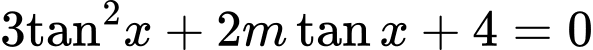
Đặt
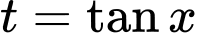 ta có
ta có 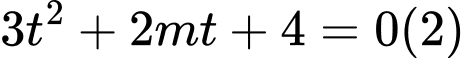
Vậy điều kiện để phương trình có nghiệm là
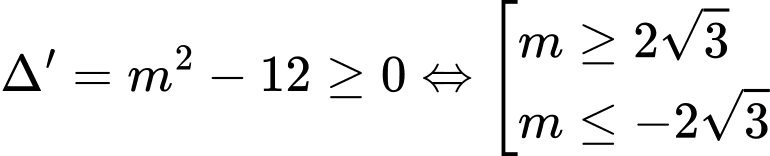
=> Chọn D. Đáp án: D
Câu 15 [583182]: Phương trình 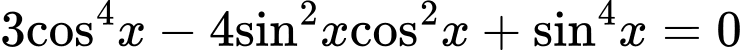 có bao nhiêu nghiệm thuộc
có bao nhiêu nghiệm thuộc 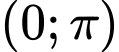 ?
?
Đáp án:……
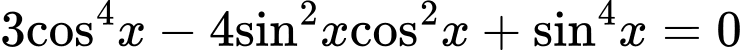 có bao nhiêu nghiệm thuộc
có bao nhiêu nghiệm thuộc 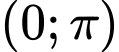 ?
?Đáp án:……
Ta có: 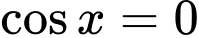 không là nghiệm của phương trình. Chia cả hai vế của phương trình cho
không là nghiệm của phương trình. Chia cả hai vế của phương trình cho 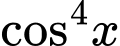
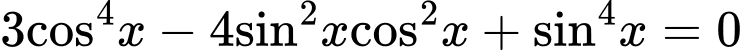
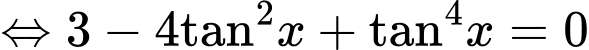
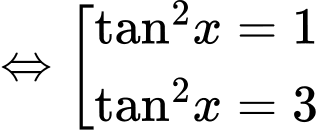
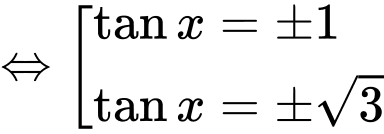
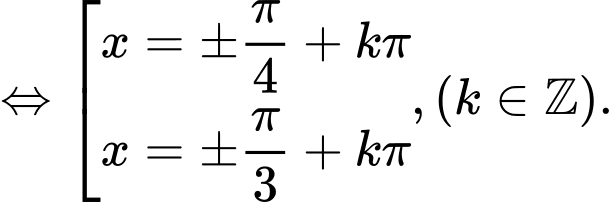
Nghiệm thuộc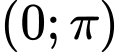
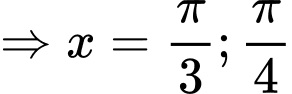 .
.
Vậy phương trình đã cho có 2 nghiệm thuộc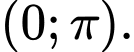
=> Điền:…2..
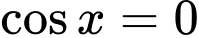 không là nghiệm của phương trình. Chia cả hai vế của phương trình cho
không là nghiệm của phương trình. Chia cả hai vế của phương trình cho 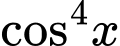
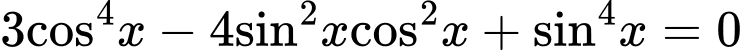
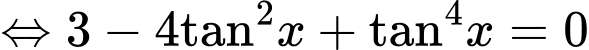
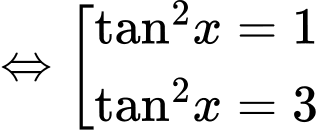
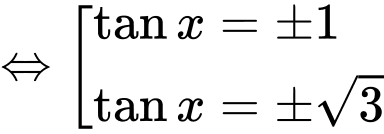
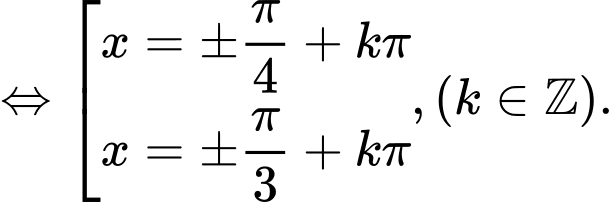
Nghiệm thuộc
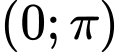
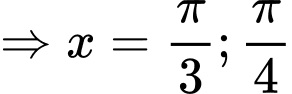 .
.Vậy phương trình đã cho có 2 nghiệm thuộc
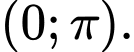
=> Điền:…2..
Câu 16 [583183]: Tổng tất cả các nghiệm thuộc 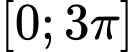 của phương trình
của phương trình
 là:
là:
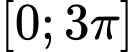 của phương trình
của phương trình là:
là: A, 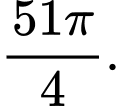
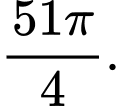
B, 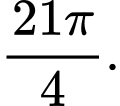
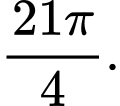
C, 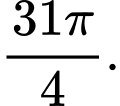
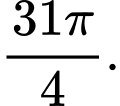
D, 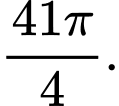
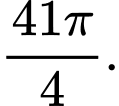
Ta có: 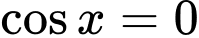 không là nghiệm của phương trình. Chia cả hai vế của phương trình cho
không là nghiệm của phương trình. Chia cả hai vế của phương trình cho 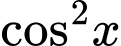

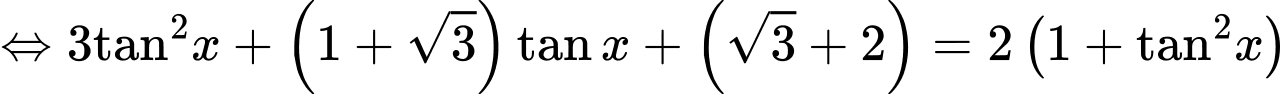
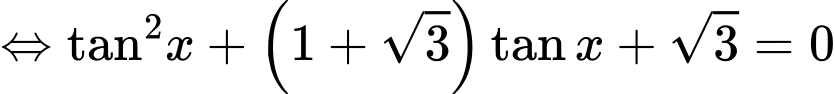
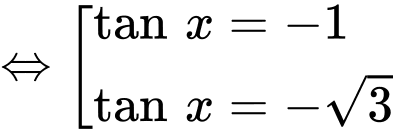
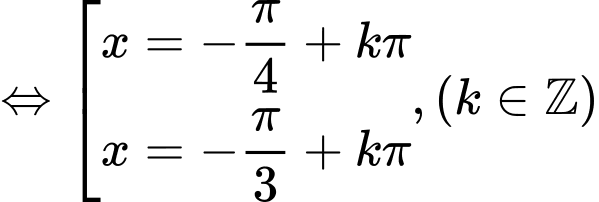
Vì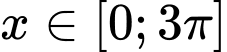
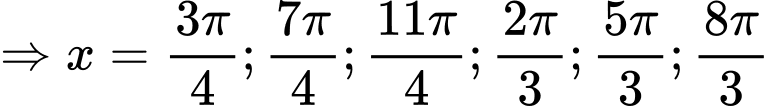
Tổng tất cả các nghiệm thuộc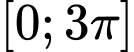 là:
là: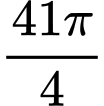
=> Chọn D. Đáp án: D
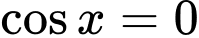 không là nghiệm của phương trình. Chia cả hai vế của phương trình cho
không là nghiệm của phương trình. Chia cả hai vế của phương trình cho 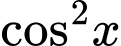

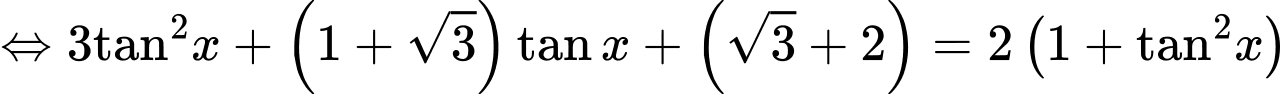
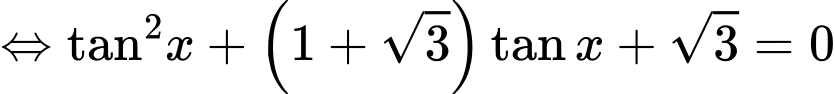
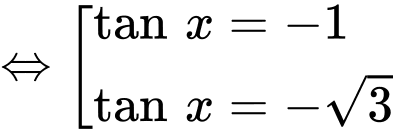
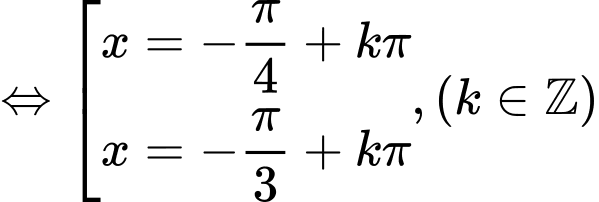
Vì
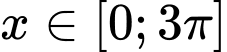
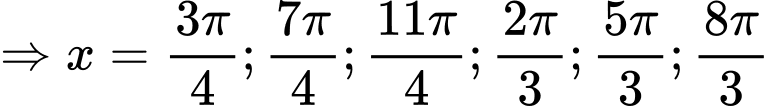
Tổng tất cả các nghiệm thuộc
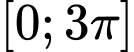 là:
là: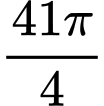
=> Chọn D. Đáp án: D
5. Dạng toán: Phương trình lượng giác chứa giá trị tuyệt đối
Câu 17 [583184]: Tập nghiệm của phương trình 

A, 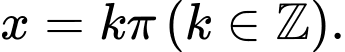
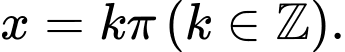
B, 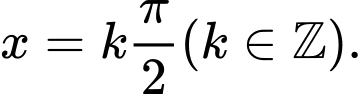
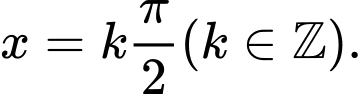
C, 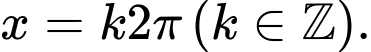
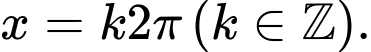
D, 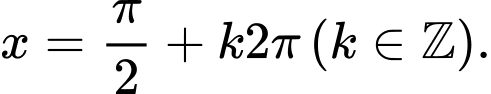
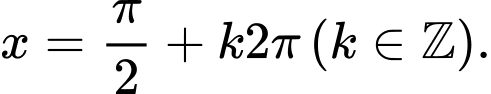
Giải tự luận:
+ Với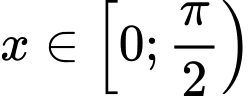
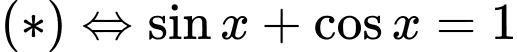
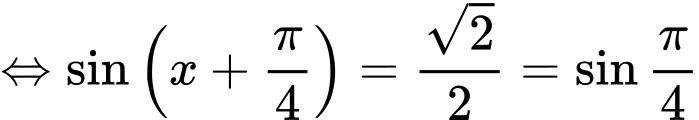
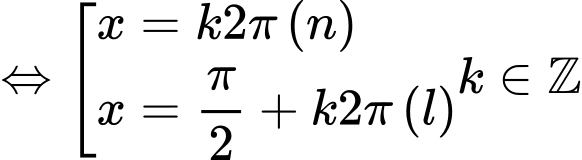
+ Với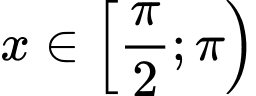
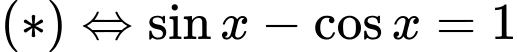
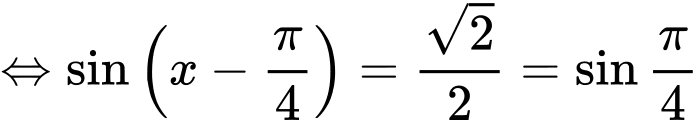
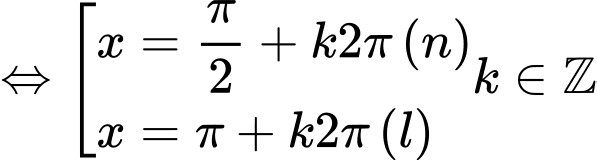
+ Với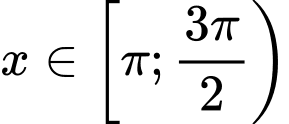
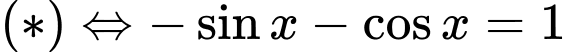
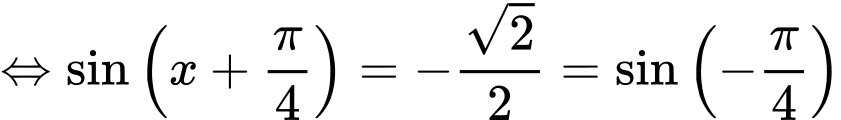
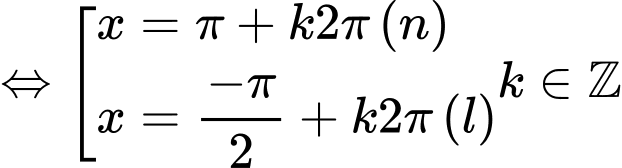
+ Với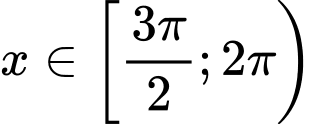
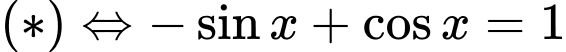
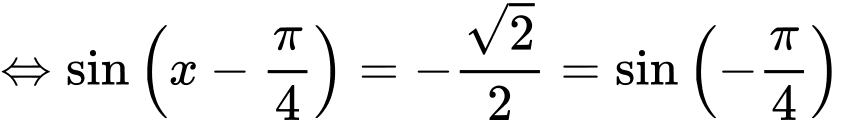
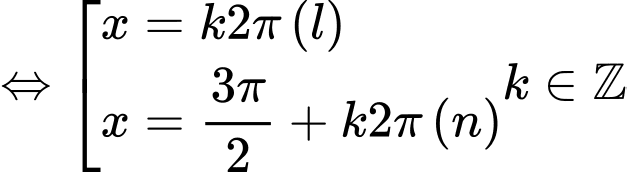
Vậy nghiệm của phương trình là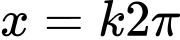 ;
; 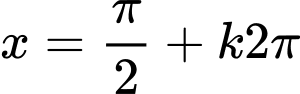 ;
;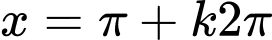 ;
;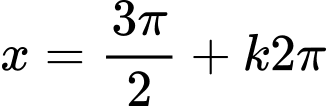
=>Chọn B
Giải trắc nghiệm: (Hướng dẫn sử dụng MTCT nếu được)
Dùng mode 7 để tìm khỏang nghiệm, sau khi tìm được khoảng nghiệm, ta sử dụng shift solve để tìm ra nghiệm chính xác. Rồi so với kết quả. Đáp án: B
+ Với
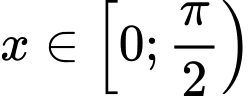
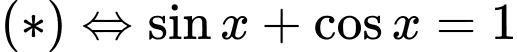
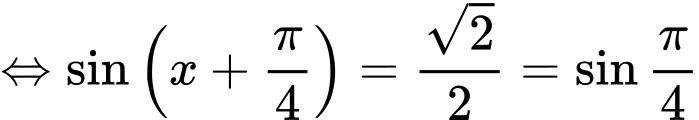
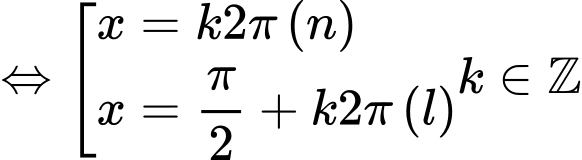
+ Với
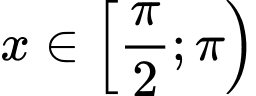
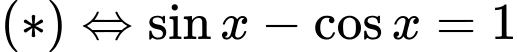
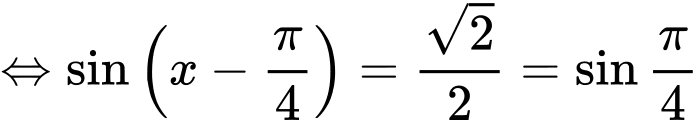
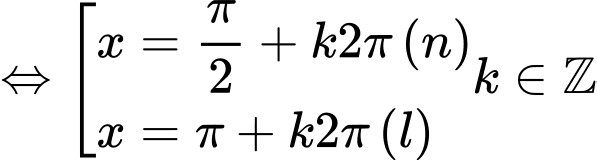
+ Với
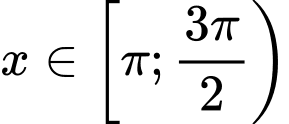
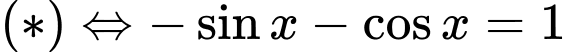
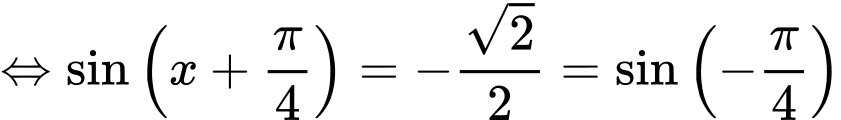
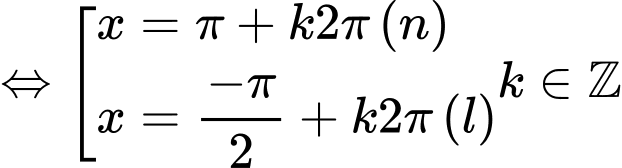
+ Với
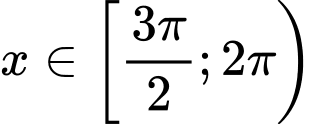
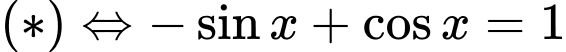
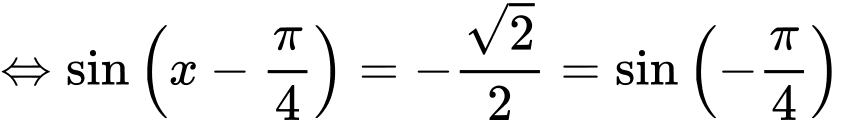
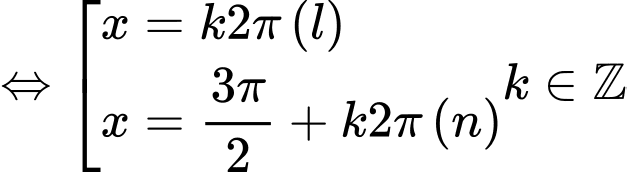
Vậy nghiệm của phương trình là
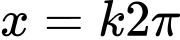 ;
; 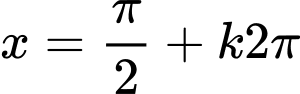 ;
;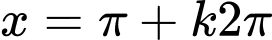 ;
;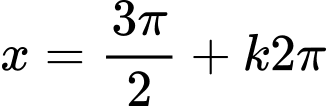
=>Chọn B
Giải trắc nghiệm: (Hướng dẫn sử dụng MTCT nếu được)
Dùng mode 7 để tìm khỏang nghiệm, sau khi tìm được khoảng nghiệm, ta sử dụng shift solve để tìm ra nghiệm chính xác. Rồi so với kết quả. Đáp án: B
Câu 18 [583185]: Số nghiệm của phương trình 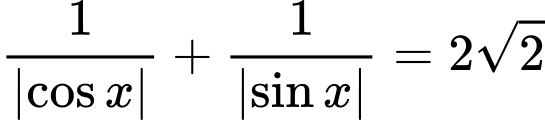 trên đoạn
trên đoạn 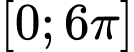 là:
là:
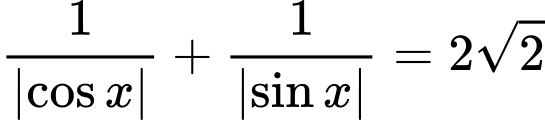 trên đoạn
trên đoạn 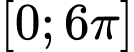 là:
là: A, 6 nghiệm.
B, 5 nghiệm.
C, 4 nghiệm.
D, 3 nghiệm.
Phương trình tương đương với 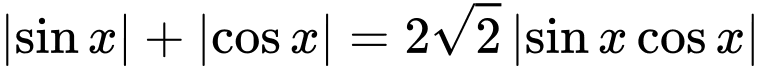 (1)
(1)
Đặt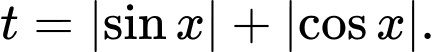 Khi đó
Khi đó 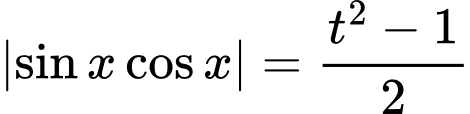
Vì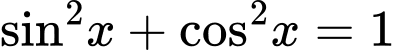 nên
nên 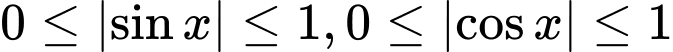
Do đó
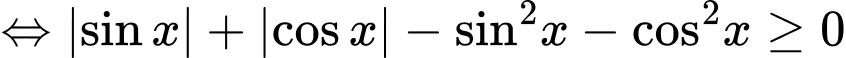
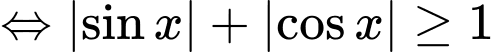
Nên điều kiện của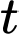 là
là 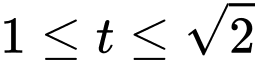
(1)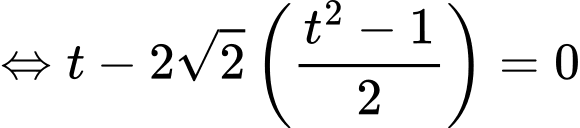
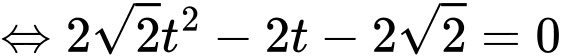
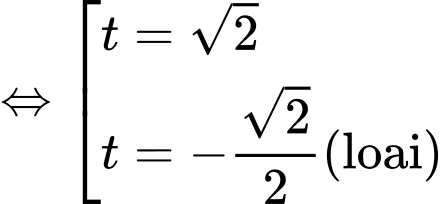
+ Với
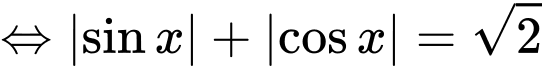
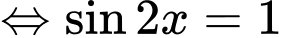
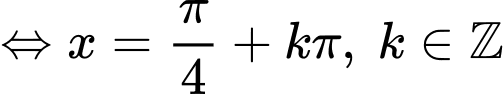
- Do đó trên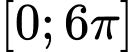 ta tìm được 6 nghiệm. =>Chọn A Đáp án: A
ta tìm được 6 nghiệm. =>Chọn A Đáp án: A
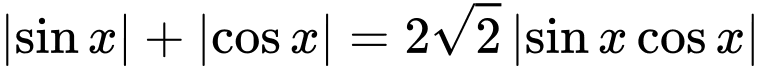 (1)
(1)Đặt
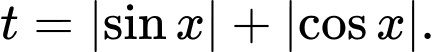 Khi đó
Khi đó 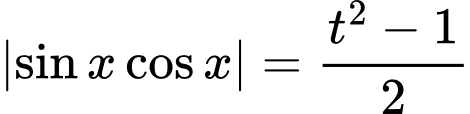
Vì
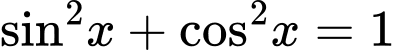 nên
nên 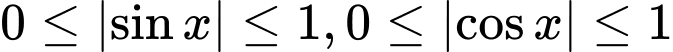
Do đó

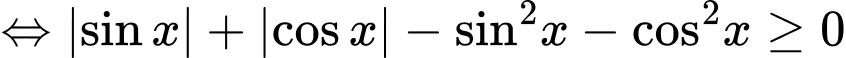
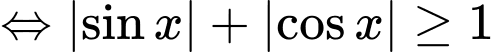
Nên điều kiện của
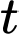 là
là 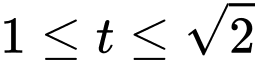
(1)
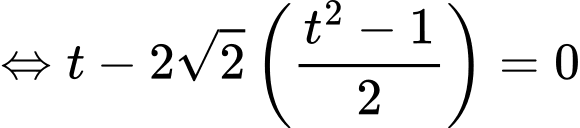
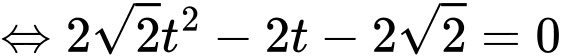
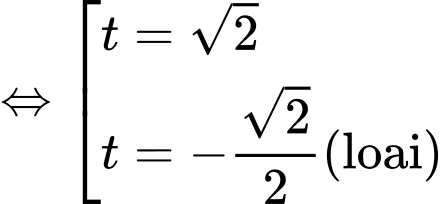
+ Với

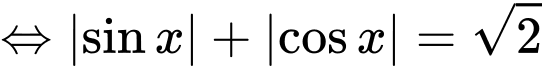
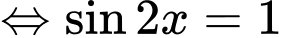
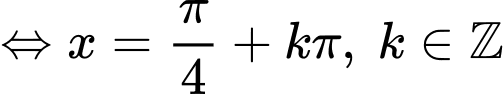
- Do đó trên
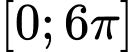 ta tìm được 6 nghiệm. =>Chọn A Đáp án: A
ta tìm được 6 nghiệm. =>Chọn A Đáp án: A
Câu 19 [583186]: Tìm 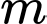 để phương trình có nghiệm
để phương trình có nghiệm 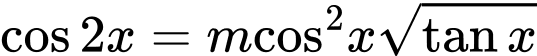 trên đoạn
trên đoạn 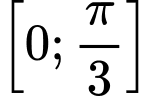
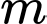 để phương trình có nghiệm
để phương trình có nghiệm 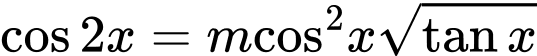 trên đoạn
trên đoạn 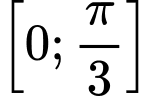
A, 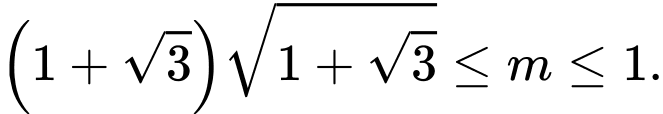
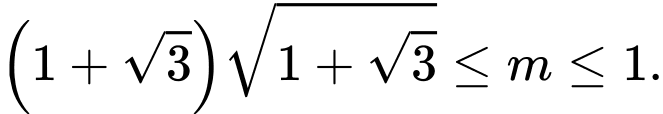
B, 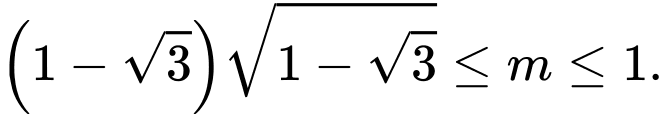
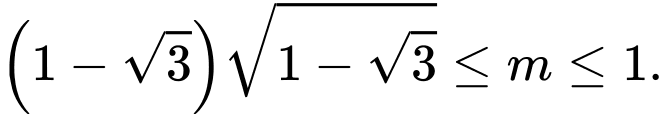
C, 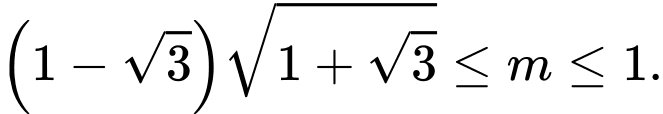
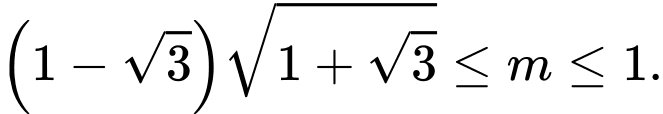
D, 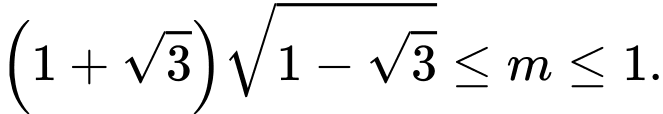
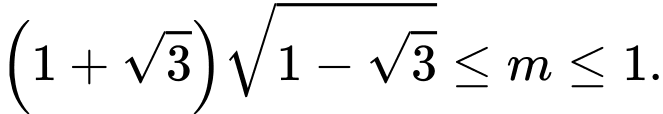
Đặt 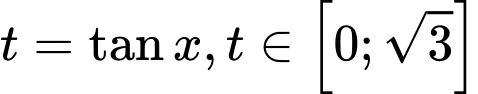
Phương trình trở thành: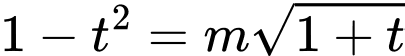 (đã chia hai vế cho
(đã chia hai vế cho  )
)
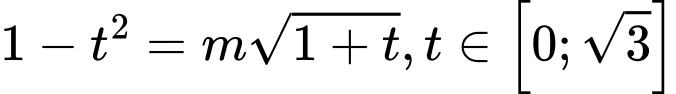
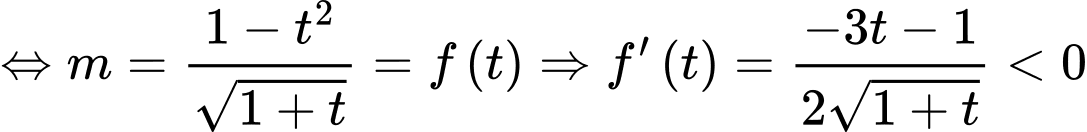
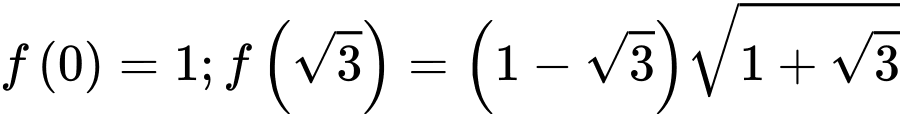
Vậy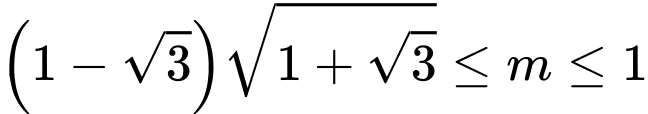
=> Chọn C Đáp án: C
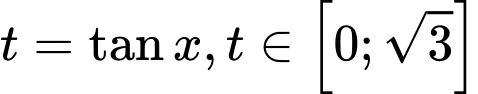
Phương trình trở thành:
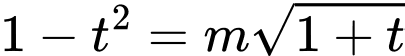 (đã chia hai vế cho
(đã chia hai vế cho  )
)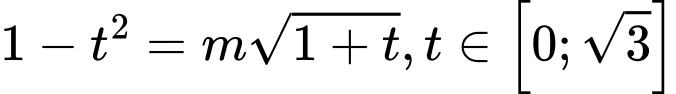
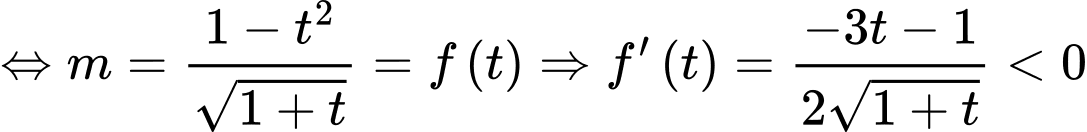
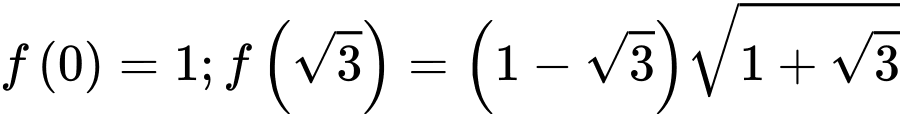
Vậy
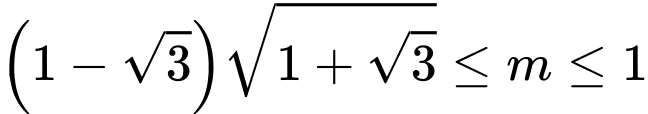
=> Chọn C Đáp án: C
6. Dạng toán: Phương trình lượng giác chứa căn thức
Câu 20 [583187]: Cho 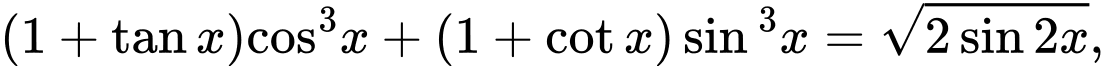 số nghiệm của phương trình trong khoảng
số nghiệm của phương trình trong khoảng 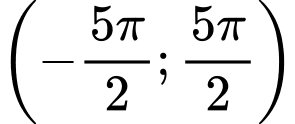 là:
là:
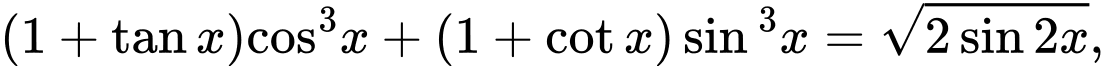 số nghiệm của phương trình trong khoảng
số nghiệm của phương trình trong khoảng 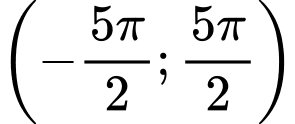 là:
là: A, 3.
B, 2.
C, 4.
D, 5.
Điều kiện 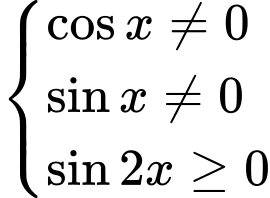
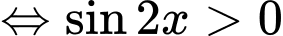 (*)
(*)
(3)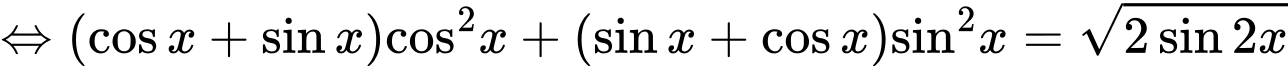
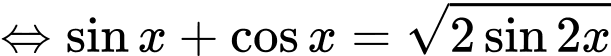
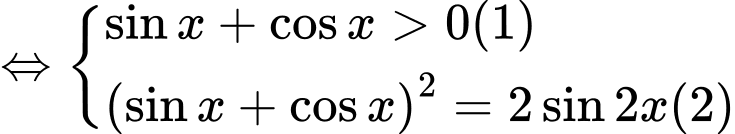
Giải (2) ta được:
Kiểm tra điều kiện (1):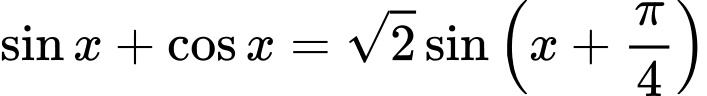
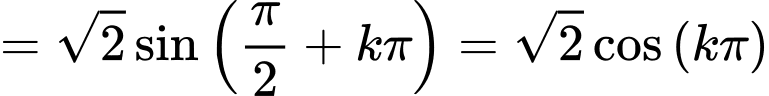
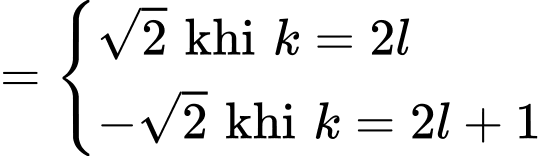 , từ đó nghiệm của phương trình là
, từ đó nghiệm của phương trình là 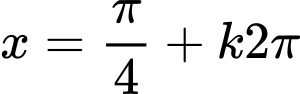
- Xét trên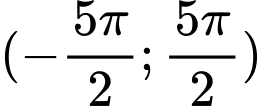 ta có 3 nghiệm là:
ta có 3 nghiệm là: 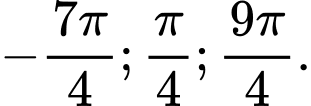
=> Chọn A. Đáp án: A
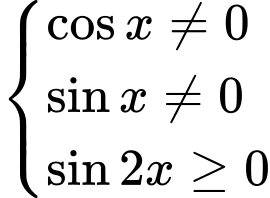
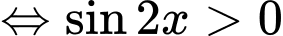 (*)
(*)(3)
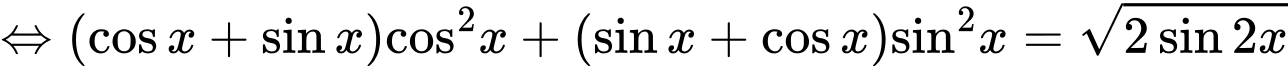
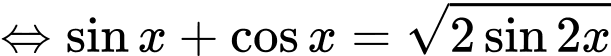
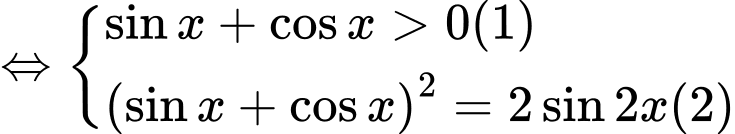
Giải (2) ta được:
Kiểm tra điều kiện (1):
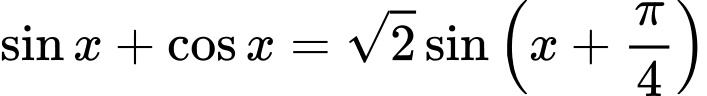
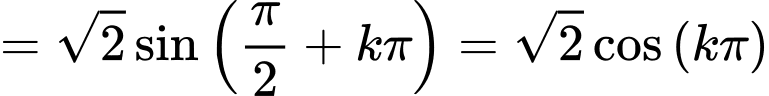
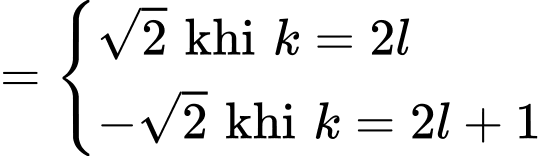 , từ đó nghiệm của phương trình là
, từ đó nghiệm của phương trình là 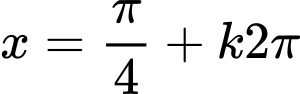
- Xét trên
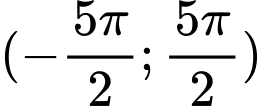 ta có 3 nghiệm là:
ta có 3 nghiệm là: 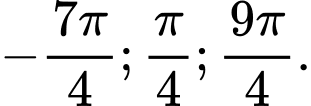
=> Chọn A. Đáp án: A
Câu 21 [583188]: Cho phương trình 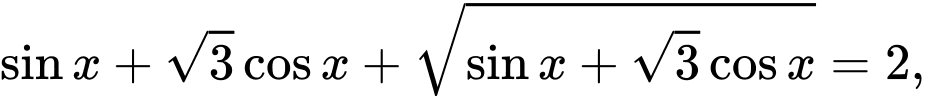 xét trên đoạn
xét trên đoạn 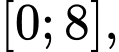 hiệu của nghiệm lớn nhất và bé nhất là:
hiệu của nghiệm lớn nhất và bé nhất là:
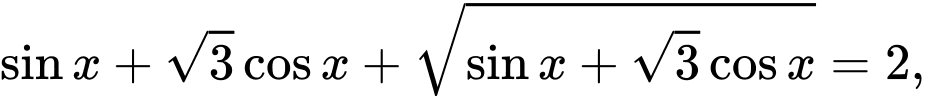 xét trên đoạn
xét trên đoạn 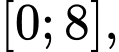 hiệu của nghiệm lớn nhất và bé nhất là:
hiệu của nghiệm lớn nhất và bé nhất là: A, 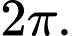
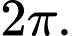
B, 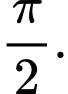
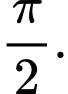
C, 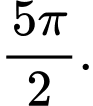
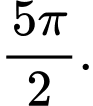
D, 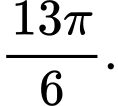
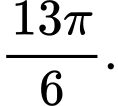
- Đặt 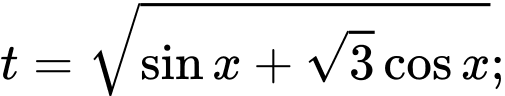
Ta có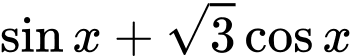
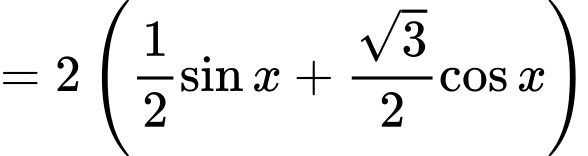
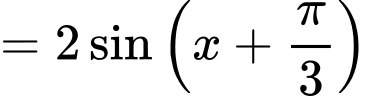
Suy ra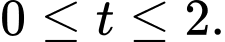 Phương trình trở thành:
Phương trình trở thành: 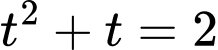
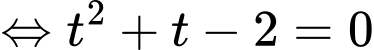
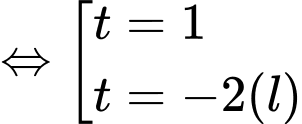
+ Với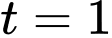
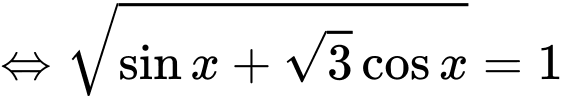
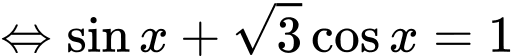
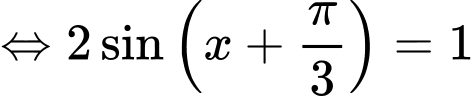
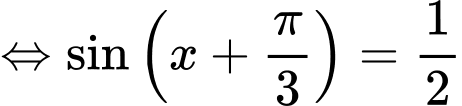
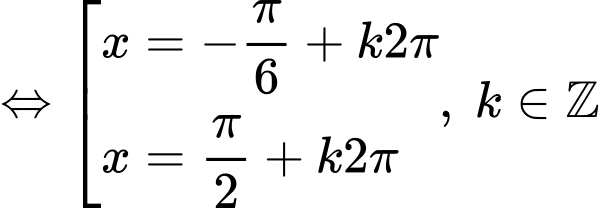
- Từ đó ta tìm được nghiệm lớn nhất và bé nhất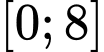 là:
là: 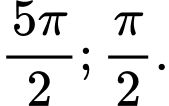
⇨ Chọn A Đáp án: A
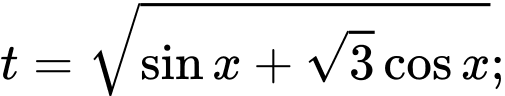
Ta có
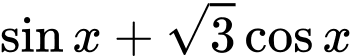
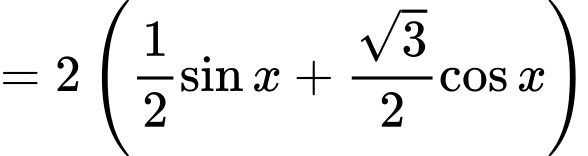
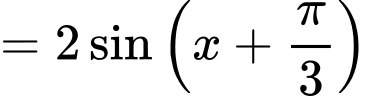
Suy ra
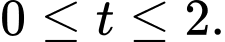 Phương trình trở thành:
Phương trình trở thành: 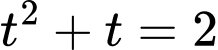
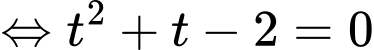
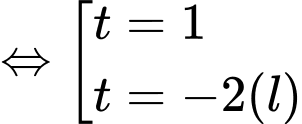
+ Với
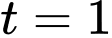
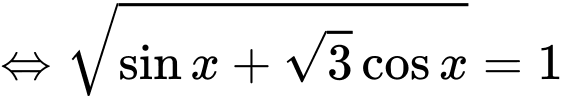
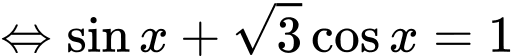
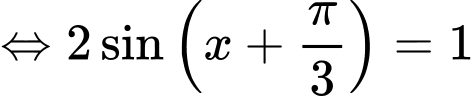
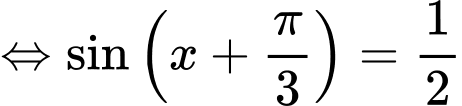
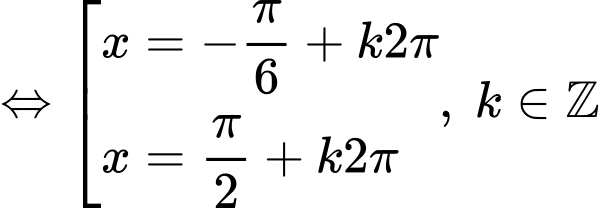
- Từ đó ta tìm được nghiệm lớn nhất và bé nhất
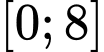 là:
là: 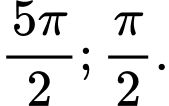
⇨ Chọn A Đáp án: A
7. Dạng toán: Sử dụng công thức biến đổi
7.1. Giải phương trình lượng giác biến đổi tích thành tổng
Câu 22 [583189]: Phương trình 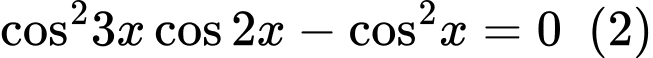 có số họ nghiệm là
có số họ nghiệm là
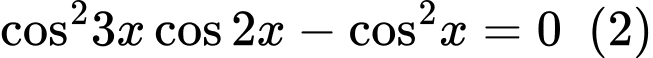 có số họ nghiệm là
có số họ nghiệm là A, 0.
B, 1.
C, 2.
D, 3.
TXĐ: 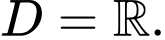

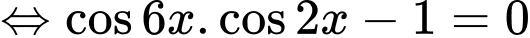
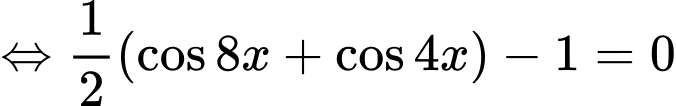
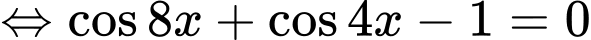
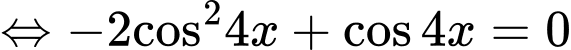
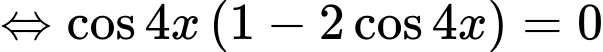
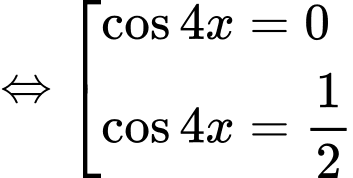
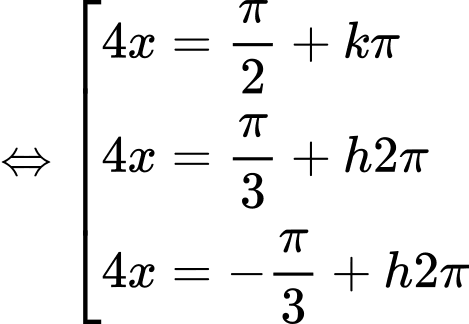
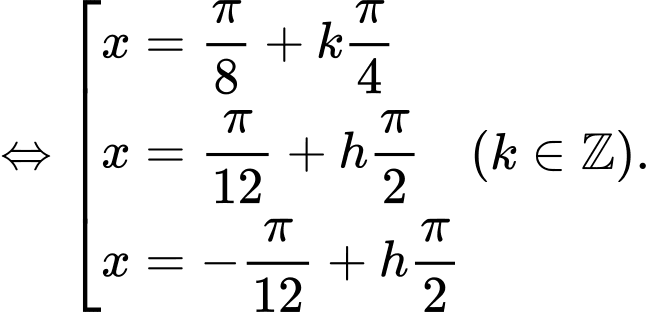
=>Chọn D. Đáp án: D
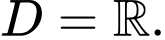

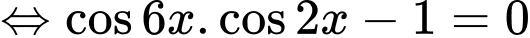
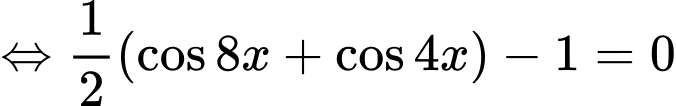
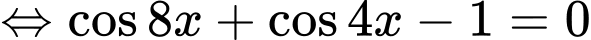
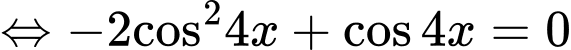
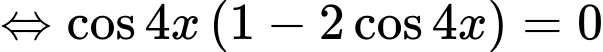
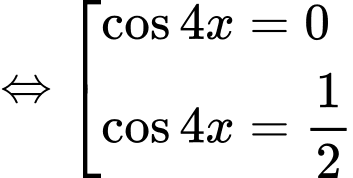
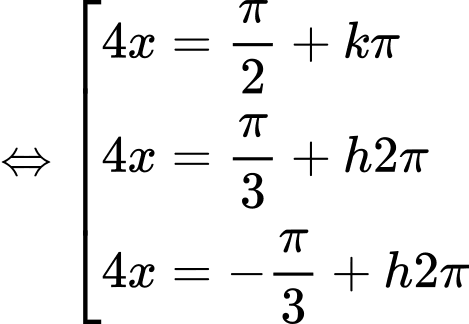
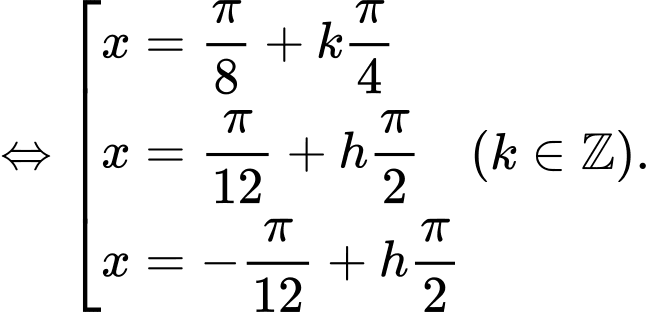
=>Chọn D. Đáp án: D
Câu 23 [583190]: Phương trình 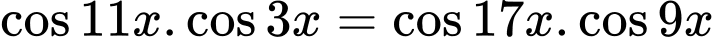 có nghiệm là
có nghiệm là
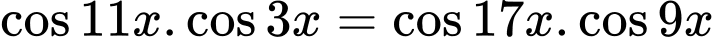 có nghiệm là
có nghiệm là A, 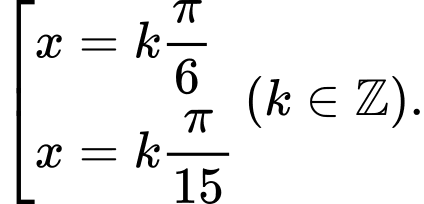
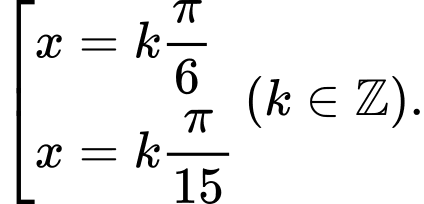
B, 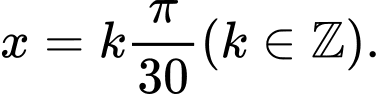
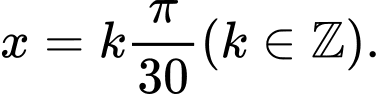
C, 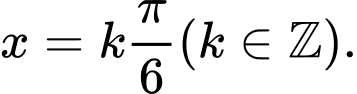
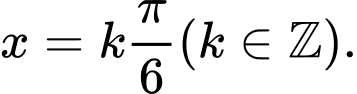
D, 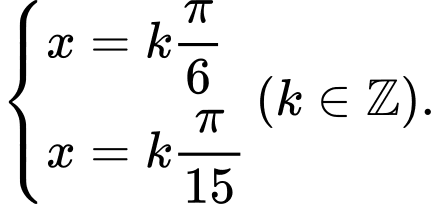
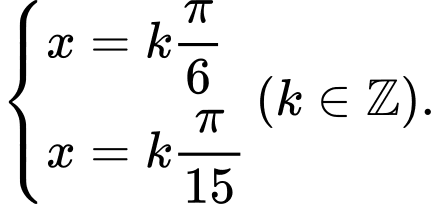
TXĐ: 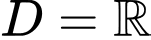
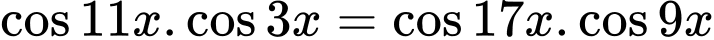
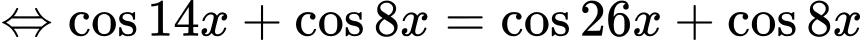
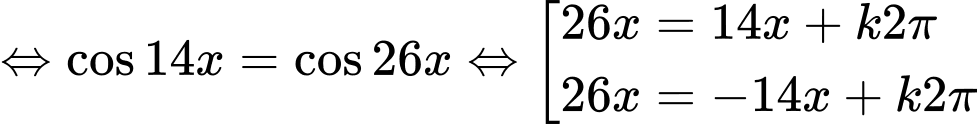
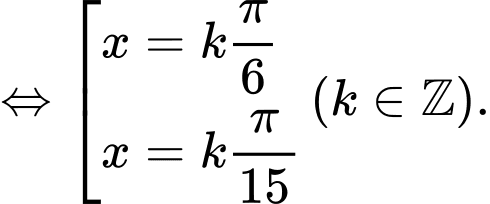
=> Chọn A. Đáp án: A
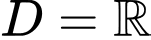
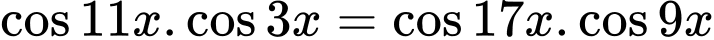
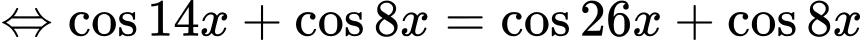
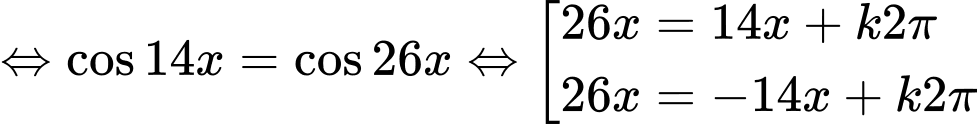
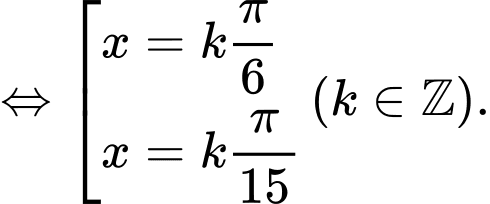
=> Chọn A. Đáp án: A
7.2. Giải phương trình lượng giác biến đổi tổng thành tích
Câu 24 [583191]: Phương trình 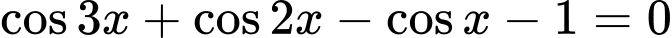 có các họ nghiệm là
có các họ nghiệm là
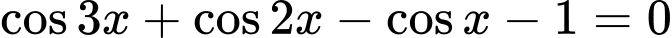 có các họ nghiệm là
có các họ nghiệm là A, 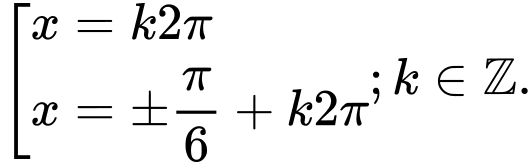
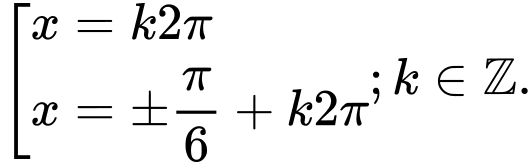
B, 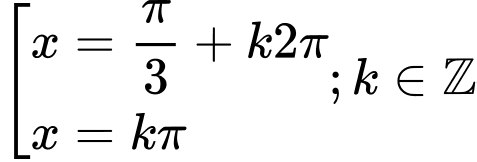 .
.
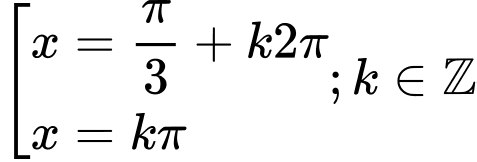 .
.C, 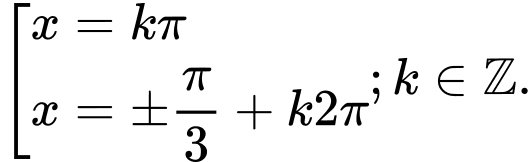
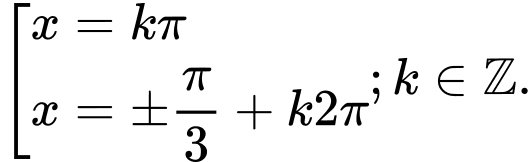
D, 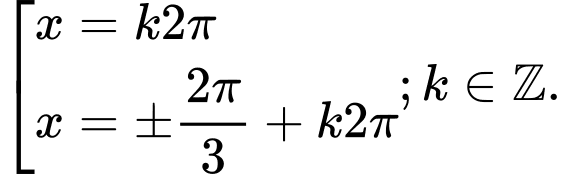
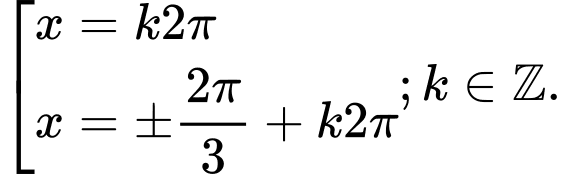
Ta có 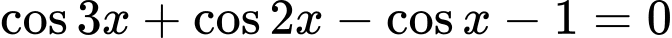
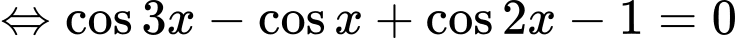
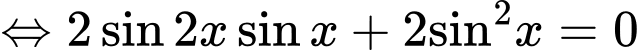
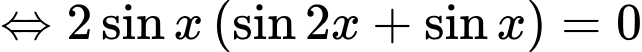
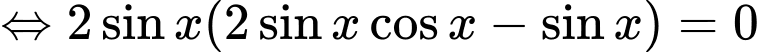
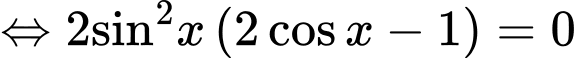
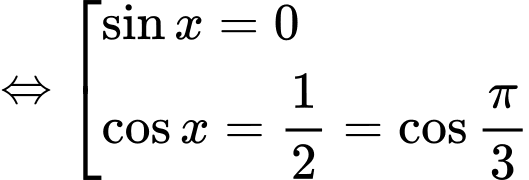
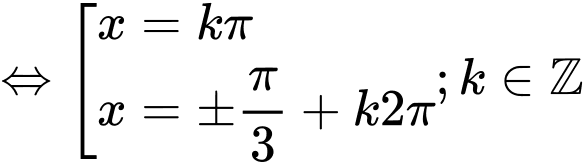
=> Chọn C Đáp án: C
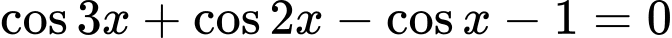
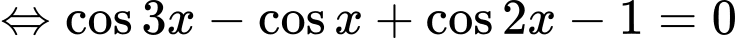
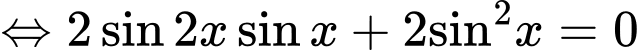
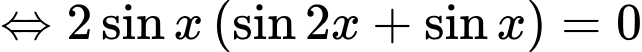
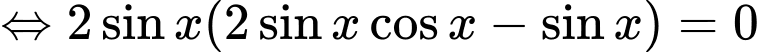
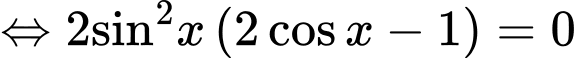
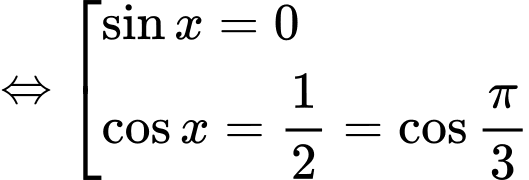
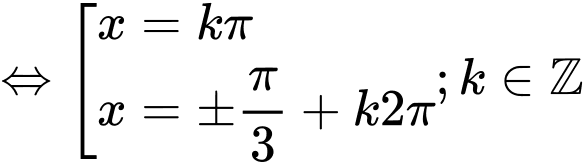
=> Chọn C Đáp án: C
Câu 25 [583192]: Khi biểu diễn các nghiệm của 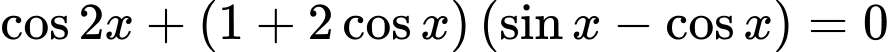 trên đường tròn lượng giác ta được bao nhiêu điểm biểu diễn.
trên đường tròn lượng giác ta được bao nhiêu điểm biểu diễn.
Đáp án:..........
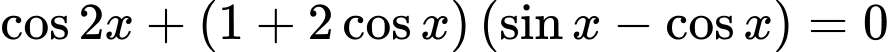 trên đường tròn lượng giác ta được bao nhiêu điểm biểu diễn.
trên đường tròn lượng giác ta được bao nhiêu điểm biểu diễn.Đáp án:..........
Ta có 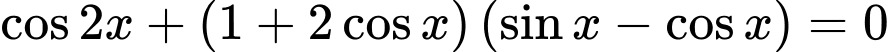
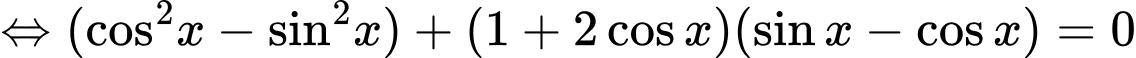

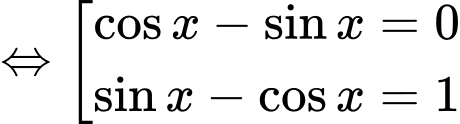
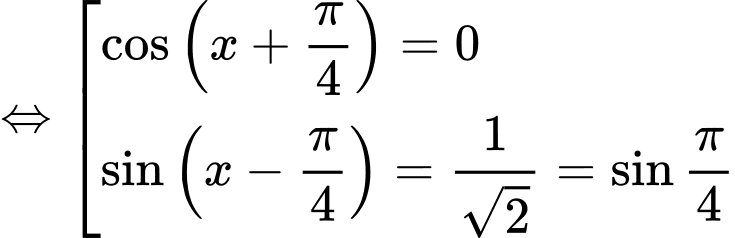
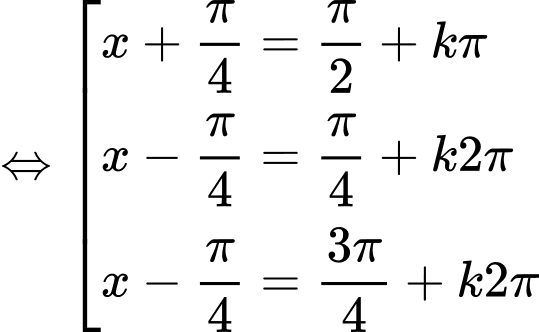
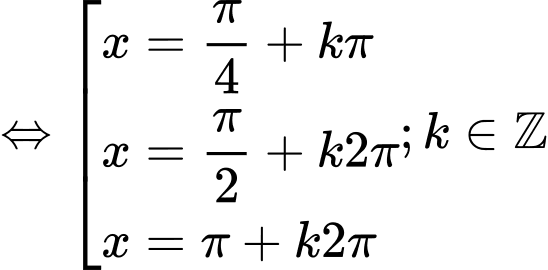
=> Điền:…4….
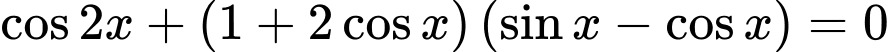
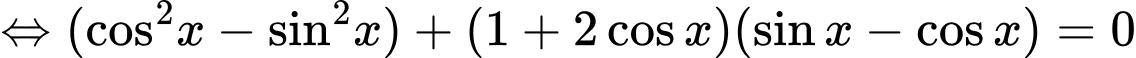

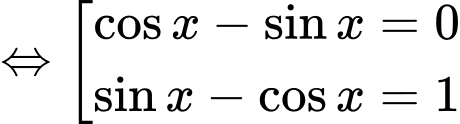
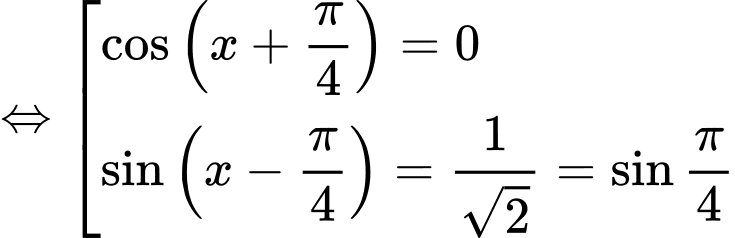
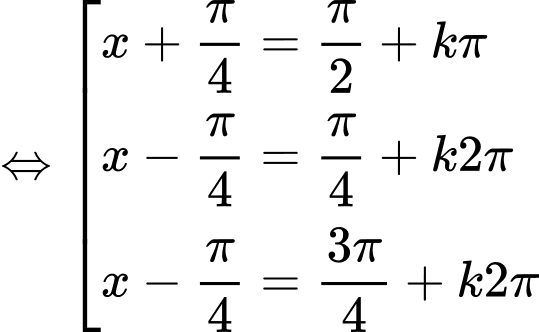
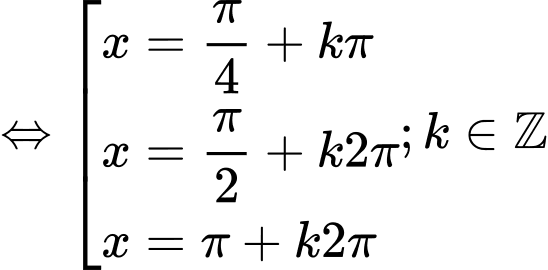
=> Điền:…4….
Câu 26 [583193]: Nghiệm dương nhỏ nhất của 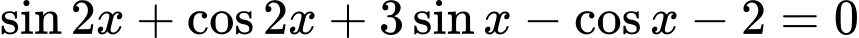 là
là
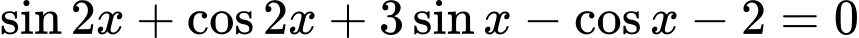 là
là A, 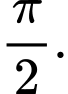
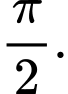
B, 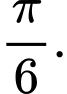
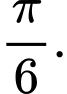
C, 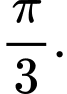
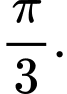
D, 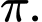
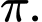
Ta có 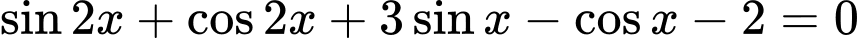
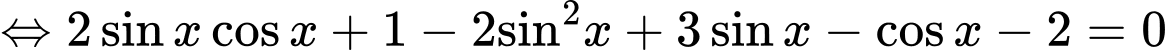

Chú ý : (1) là phương trình bậc 2 với biến
Ta có :
Nghiệm của (1) :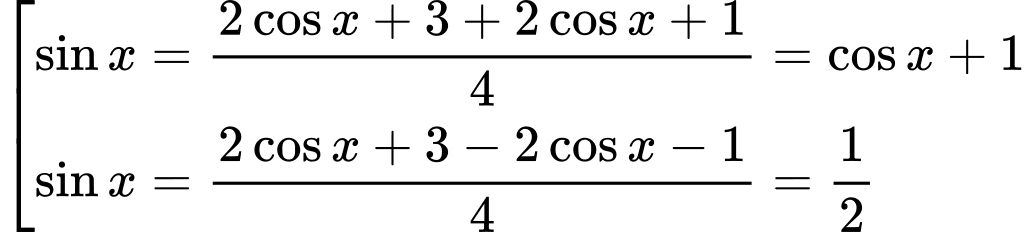
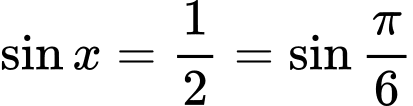
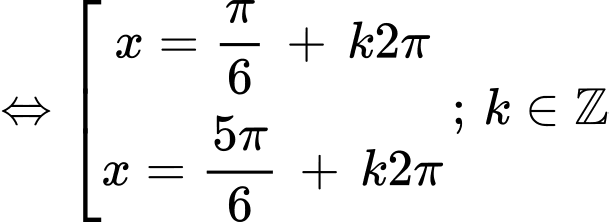
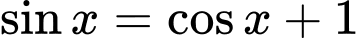
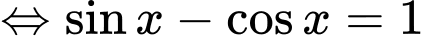
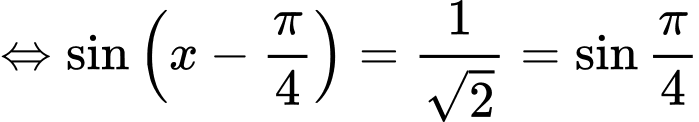
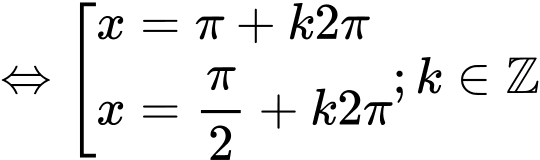
=> Chọn B. Đáp án: B
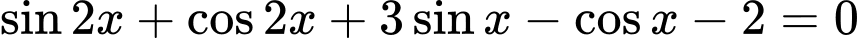
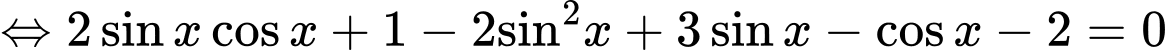

Chú ý : (1) là phương trình bậc 2 với biến

Ta có :

Nghiệm của (1) :
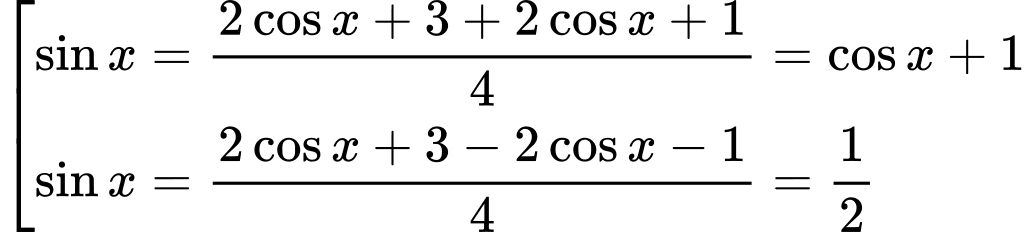
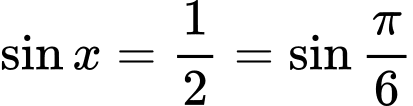
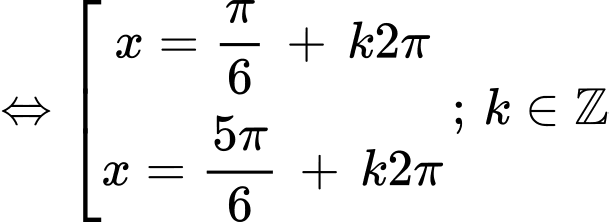
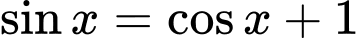
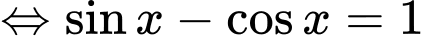
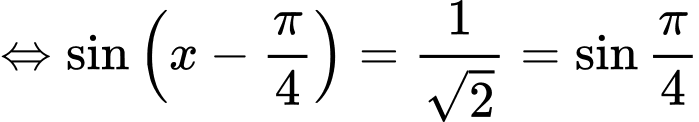
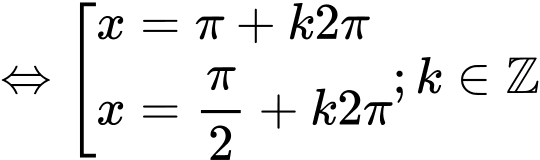
=> Chọn B. Đáp án: B
7.3. Giải phương trình lượng giác sử dụng công thức hạ bậc
Câu 27 [583194]: Trong khoảng 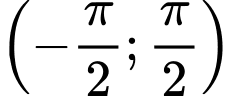 phương trình
phương trình 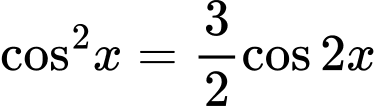 có bao nhiêu nghiệm?
có bao nhiêu nghiệm?
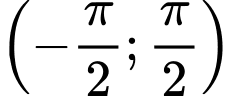 phương trình
phương trình 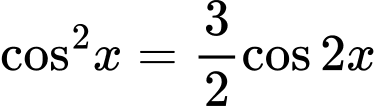 có bao nhiêu nghiệm?
có bao nhiêu nghiệm? A, 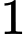 .
.
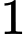 .
.B, 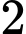 .
.
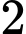 .
.C, 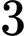 .
.
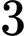 .
.D, 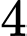 .
.
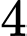 .
.
Giải tự luận:
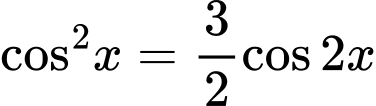
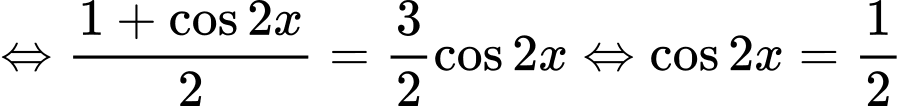
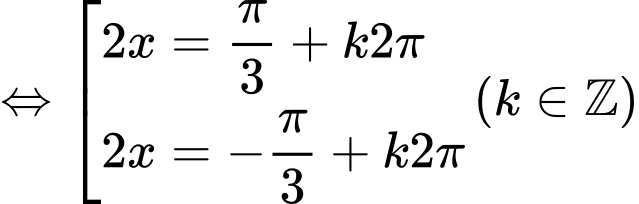
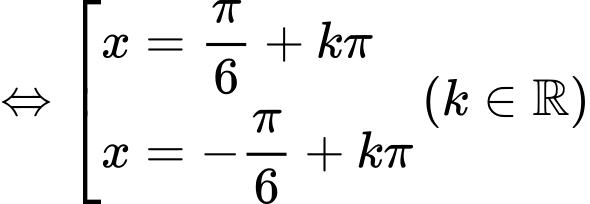
Vì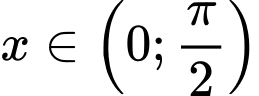
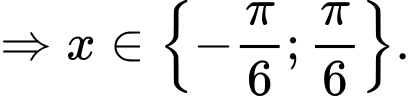 => Chọn B.
=> Chọn B.
Giải trắc nghiệm:
Dùng chức năng TABLE của máy tính cầm tay (như CASIO 570 VN Plus, CASIO FX – 580VN…..).
Kiểm tra máy tính đang để ở hệ nào, nên chuyển sang hệ đơn vị độ cho dễ nhìn. Bấm Shift, bấm Menu, bấm tiếp 2, bấm 1.
Sau đó : Ta bấm MENU Bấm tiếp 8
Sau đó nhập hàm số, ấn dấu =
Rồi nhập bắt đầu: -90; kết thúc: 90; bước: 15
Màn hình xuất hiện
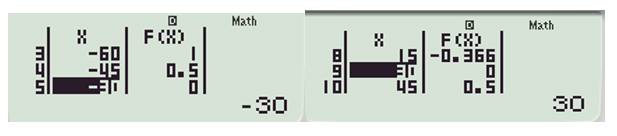
Nhận thấy có hai nghiệm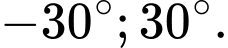 Đáp án: B
Đáp án: B
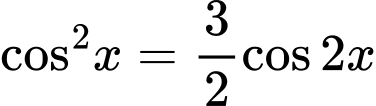
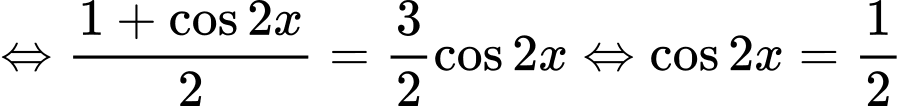
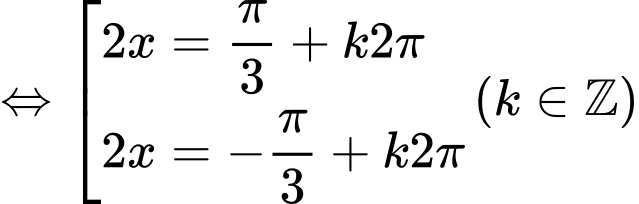
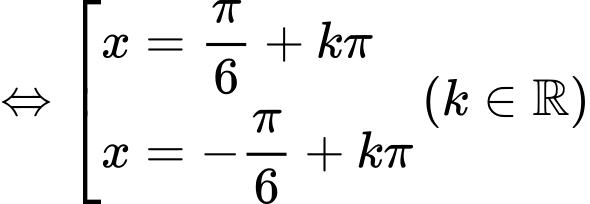
Vì
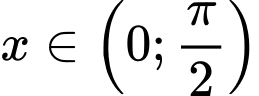
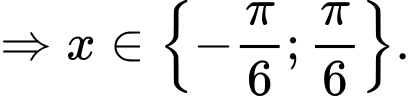 => Chọn B.
=> Chọn B.Giải trắc nghiệm:
Dùng chức năng TABLE của máy tính cầm tay (như CASIO 570 VN Plus, CASIO FX – 580VN…..).
Kiểm tra máy tính đang để ở hệ nào, nên chuyển sang hệ đơn vị độ cho dễ nhìn. Bấm Shift, bấm Menu, bấm tiếp 2, bấm 1.
Sau đó : Ta bấm MENU Bấm tiếp 8
Sau đó nhập hàm số, ấn dấu =
Rồi nhập bắt đầu: -90; kết thúc: 90; bước: 15
Màn hình xuất hiện

Nhận thấy có hai nghiệm
 Đáp án: B
Đáp án: B
Câu 28 [583195]: Họ nghiệm của phương trình 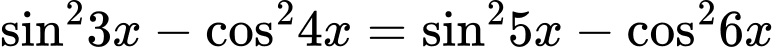 là
là
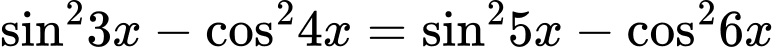 là
là A, 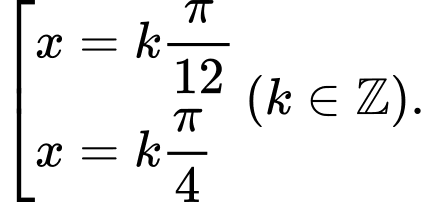
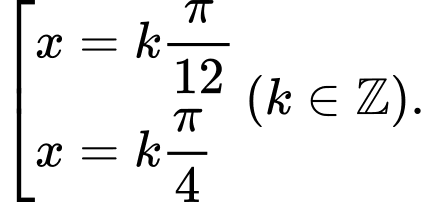
B, 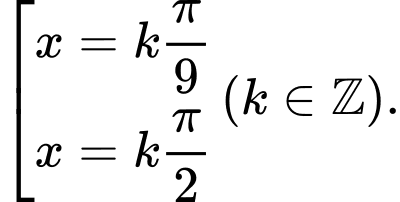
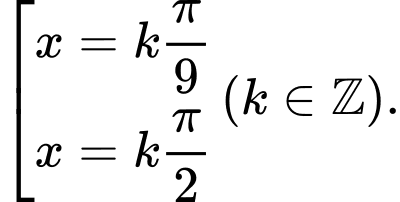
C, 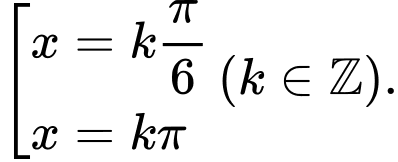
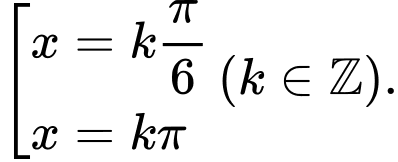
D, 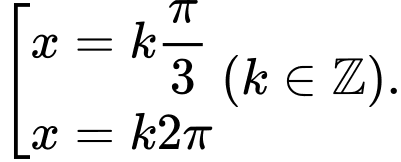
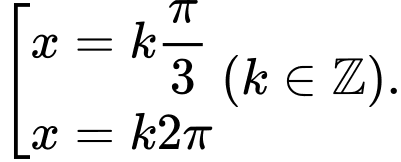
Dùng chức năng CACL của máy tính cầm tay (như CASIO 570 VN Plus, …).
Cho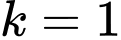 kiểm tra với 4 đáp án:
kiểm tra với 4 đáp án: 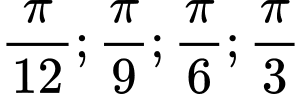 thấy
thấy 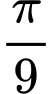 thỏa mãn. => Chọn B. Đáp án: B
thỏa mãn. => Chọn B. Đáp án: B
Cho
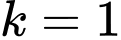 kiểm tra với 4 đáp án:
kiểm tra với 4 đáp án: 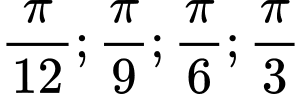 thấy
thấy 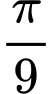 thỏa mãn. => Chọn B. Đáp án: B
thỏa mãn. => Chọn B. Đáp án: B 7.4. Giải phương trình lượng giác đưa về phương trình tích
Câu 29 [583196]: Phương trình 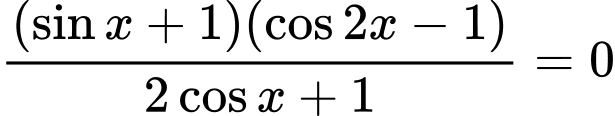 có 2 họ nghiệm là (với
có 2 họ nghiệm là (với 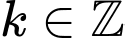 )
)
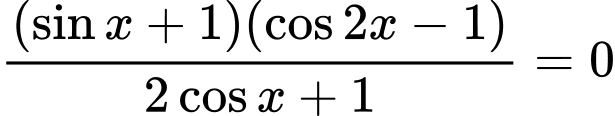 có 2 họ nghiệm là (với
có 2 họ nghiệm là (với 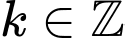 )
) A, 

B, 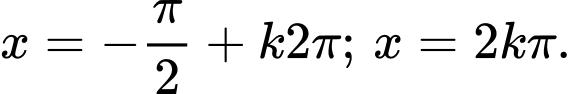
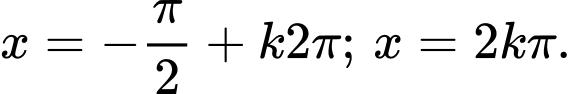
C, 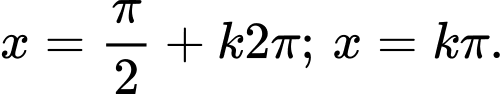
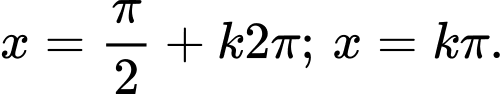
D, 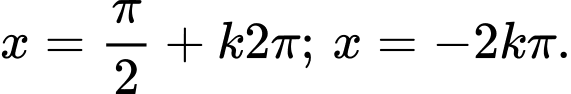
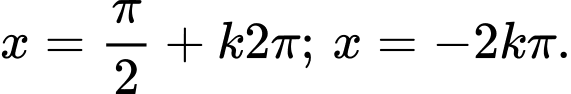
ĐK: 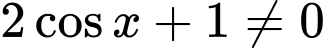
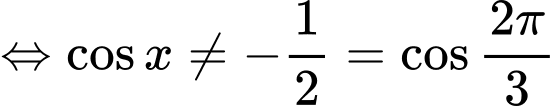
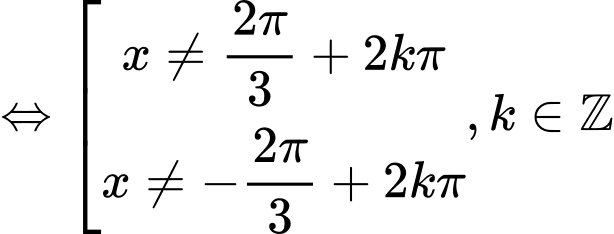
Phương trình:
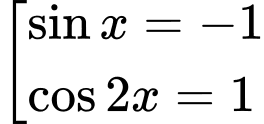
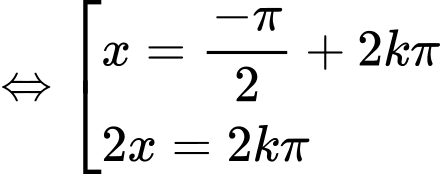
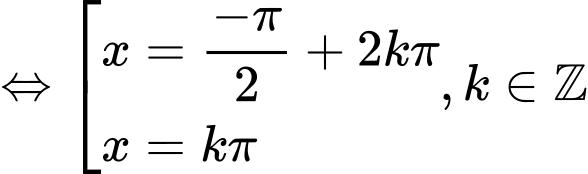
Do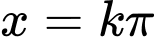 và
và 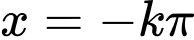 có cùng điểm biểu diễn trên đường tròn lượng giác.
có cùng điểm biểu diễn trên đường tròn lượng giác.
=> Chọn A. Đáp án: A
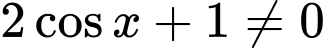
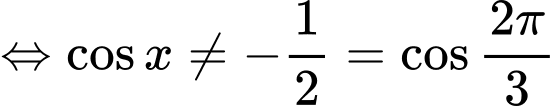
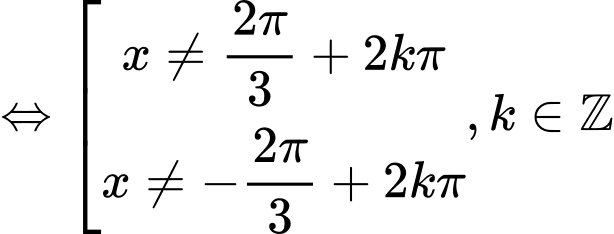
Phương trình:
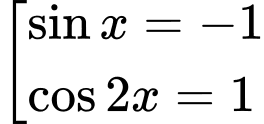
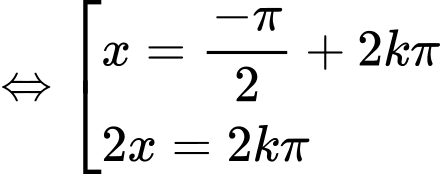
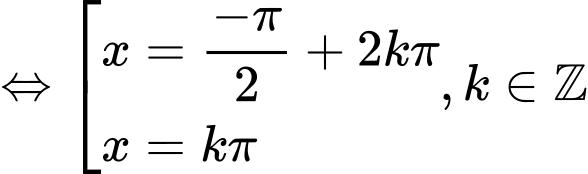
Do
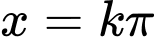 và
và 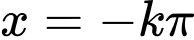 có cùng điểm biểu diễn trên đường tròn lượng giác.
có cùng điểm biểu diễn trên đường tròn lượng giác.=> Chọn A. Đáp án: A
Câu 30 [583197]: Nghiệm của phương trình: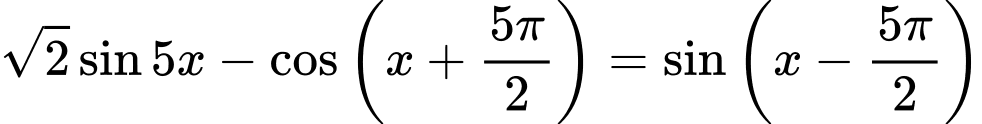 với
với 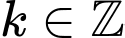 là:
là:
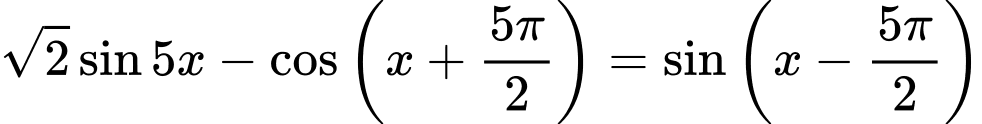 với
với 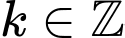 là:
là: A, 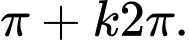
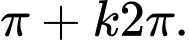
B, 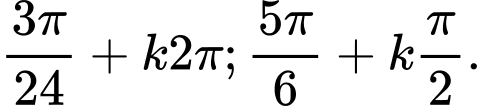
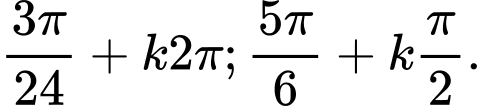
C, 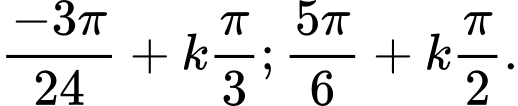
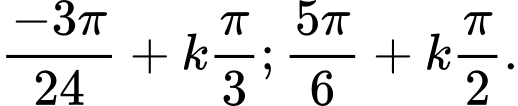
D, 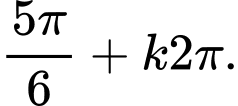
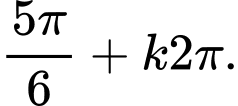
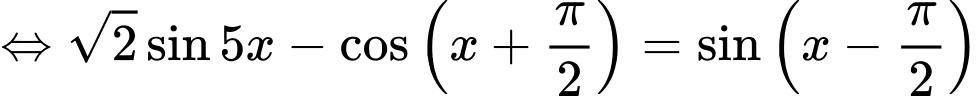


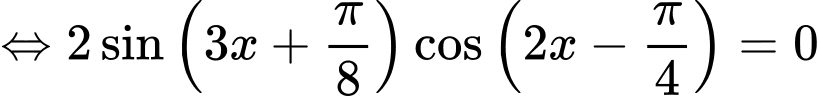
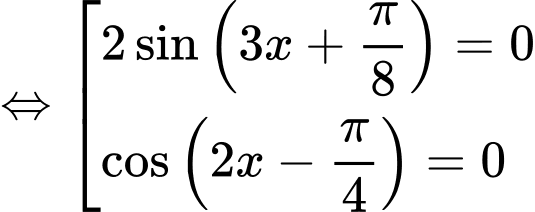
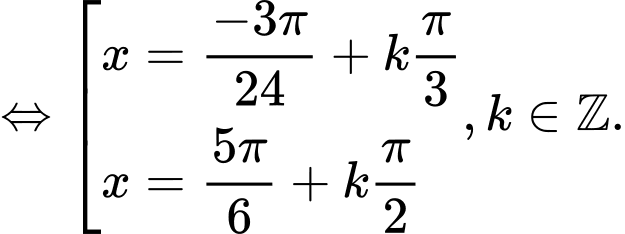
=>Chọn C. Đáp án: C
Câu 31 [583198]: Tổng các nghiệm của phương trình 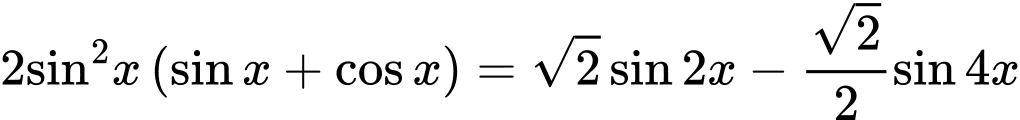 với
với 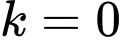 là
là
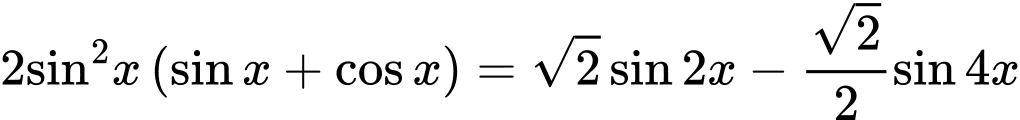 với
với 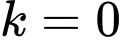 là
là A, 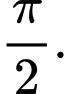
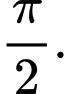
B, 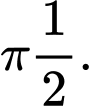
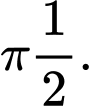
C, 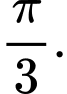
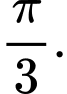
D, 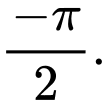
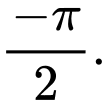
Hướng dẫn giải:
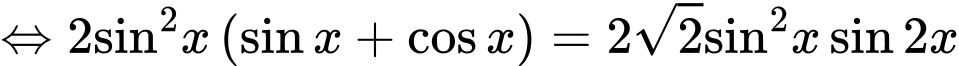
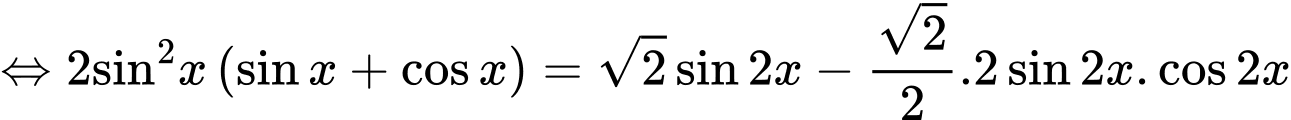
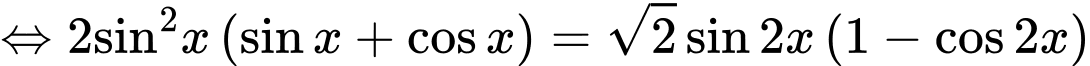
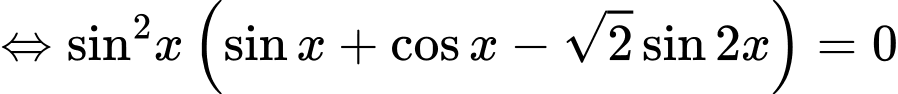
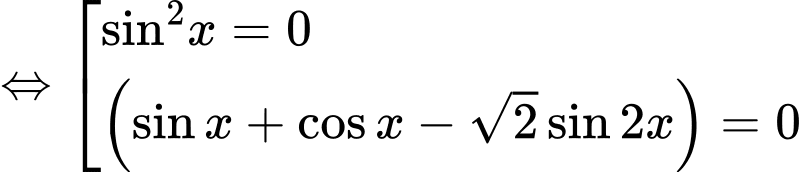
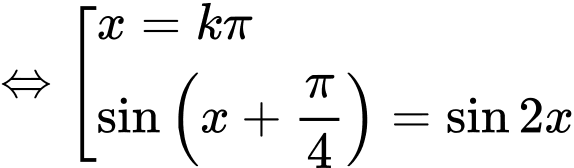
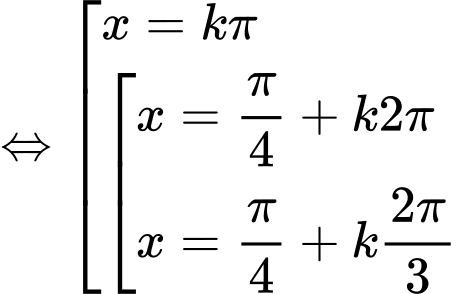
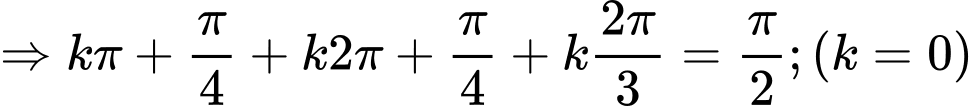
=> Chọn A Đáp án: A
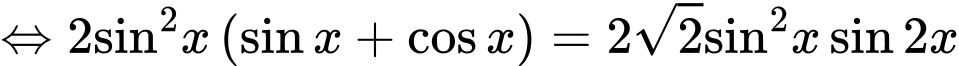
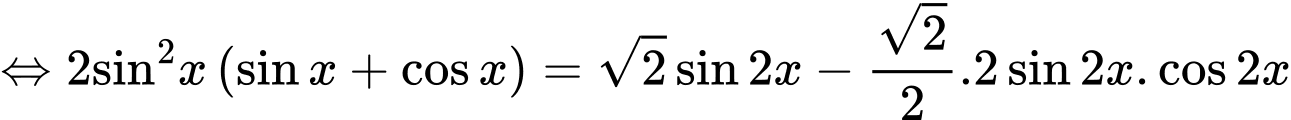
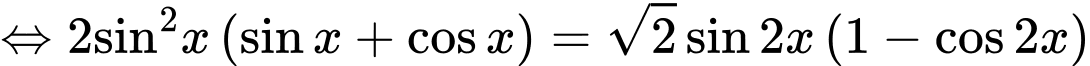
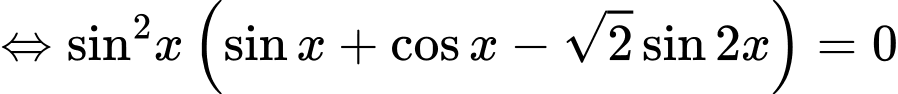
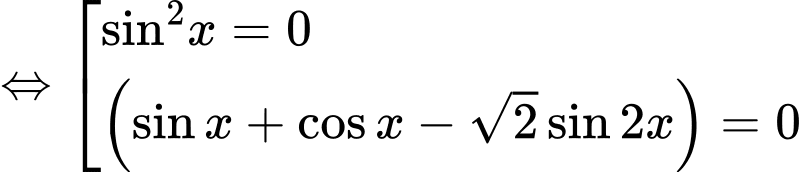
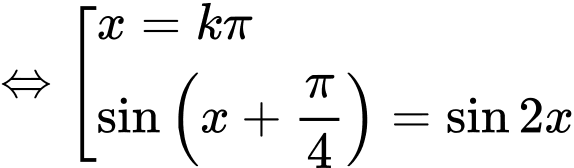
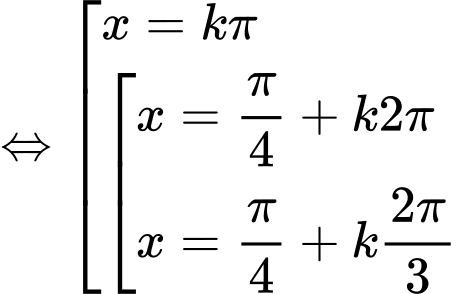
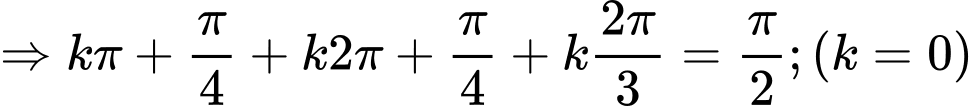
=> Chọn A Đáp án: A