Câu 1 [224675]: Cho cấp số cộng có 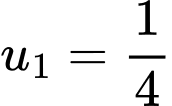 và công sai
và công sai 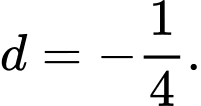 Chọn khẳng định đúng trong các khẳng định sau đây.
Chọn khẳng định đúng trong các khẳng định sau đây.
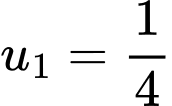 và công sai
và công sai 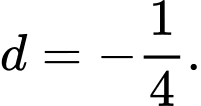 Chọn khẳng định đúng trong các khẳng định sau đây.
Chọn khẳng định đúng trong các khẳng định sau đây. A, 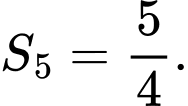
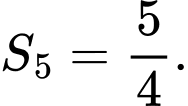
B, 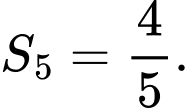
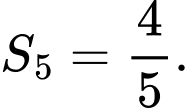
C, 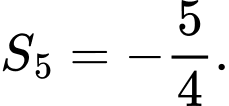
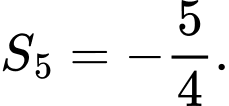
D, 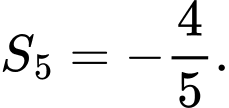
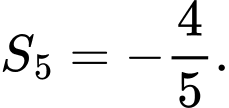
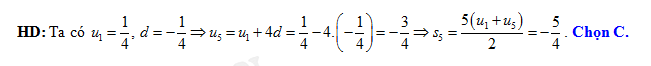 Đáp án: C
Đáp án: C
Câu 2 [806028]: Cho cấp số cộng 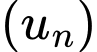 biết
biết 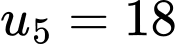 và
và 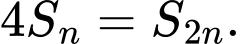 Giá trị
Giá trị 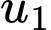 và
và 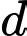 là
là
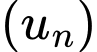 biết
biết 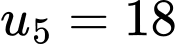 và
và 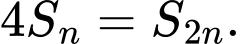 Giá trị
Giá trị 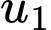 và
và 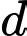 là
là A, 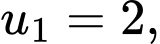

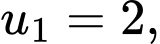

B, 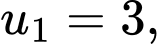

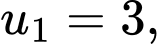

C, 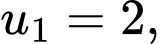

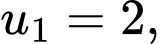

D, 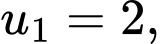

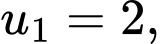

Ta có 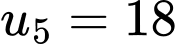

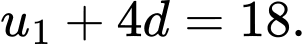
Lại có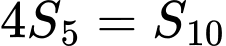
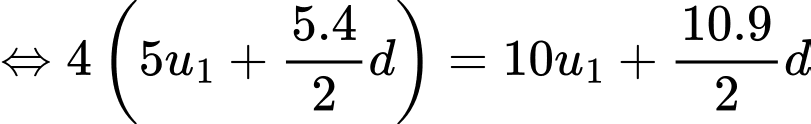

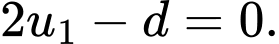
Khi đó ta có hệ phương trình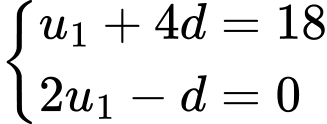
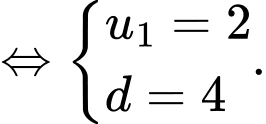 Đáp án: D
Đáp án: D
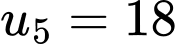

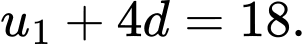
Lại có
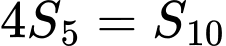
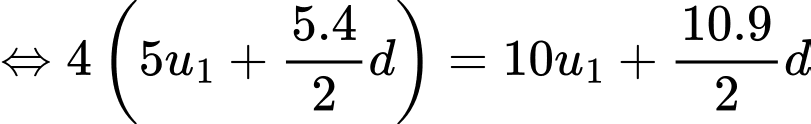

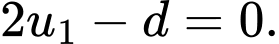
Khi đó ta có hệ phương trình
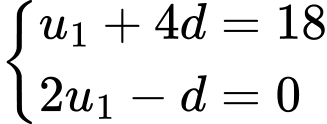
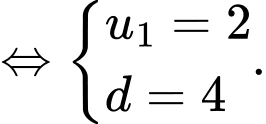 Đáp án: D
Đáp án: D
Câu 3 [224634]: Cho cấp số cộng 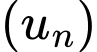 với
với 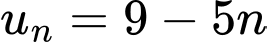 thì
thì  bằng:
bằng:
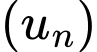 với
với 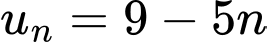 thì
thì  bằng:
bằng: A, 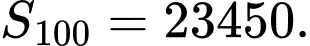
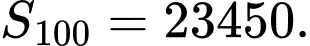
B, 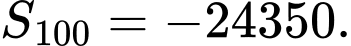
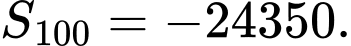
C, 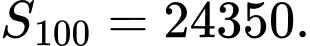
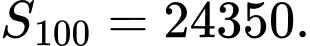
D, 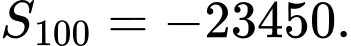
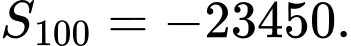
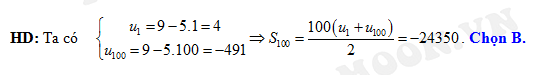 Đáp án: B
Đáp án: B
Câu 4 [224635]: Cho cấp số cộng 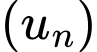 với
với 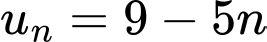 thì
thì 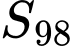 bằng:
bằng:
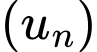 với
với 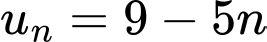 thì
thì 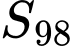 bằng:
bằng: A, 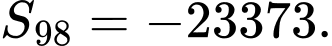
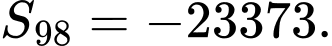
B, 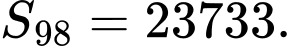
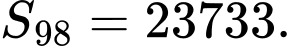
C, 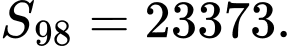
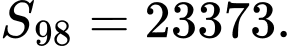
D, 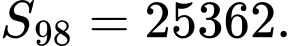
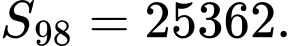
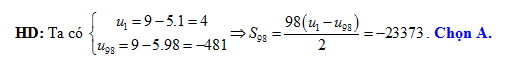 Đáp án: A
Đáp án: A
Câu 5 [805957]: Cho cấp số cộng 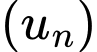 có
có 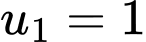 và công sai
và công sai  Tổng
Tổng 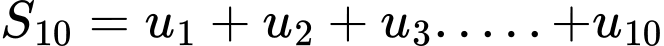 bằng
bằng
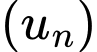 có
có 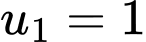 và công sai
và công sai  Tổng
Tổng 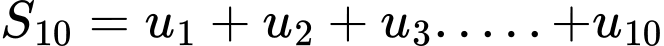 bằng
bằng A, 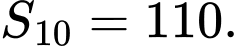
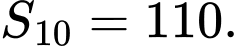
B, 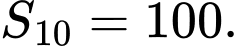
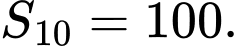
C, 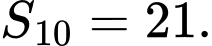
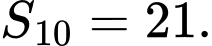
D, 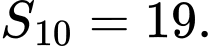
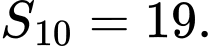
* Áp dụng công thức 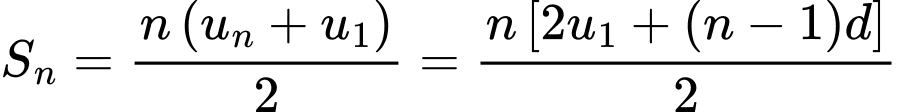 ta được:
ta được:
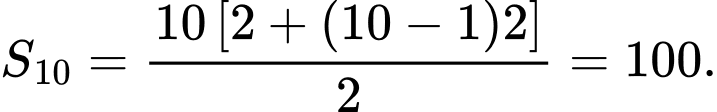 Đáp án: B
Đáp án: B
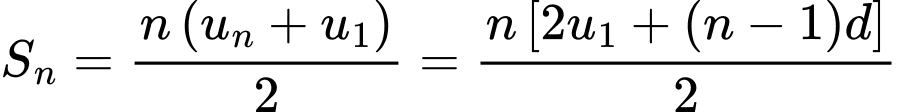 ta được:
ta được: 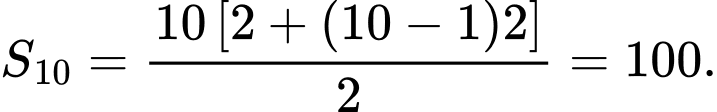 Đáp án: B
Đáp án: B
Câu 6 [805963]: Cho cấp số cộng 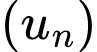 với số hạng đầu
với số hạng đầu 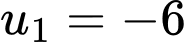 và công sai
và công sai  Tính tổng
Tính tổng 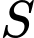 của 14 số hạng đầu tiên của cấp số cộng đó.
của 14 số hạng đầu tiên của cấp số cộng đó.
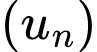 với số hạng đầu
với số hạng đầu 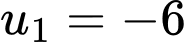 và công sai
và công sai  Tính tổng
Tính tổng 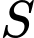 của 14 số hạng đầu tiên của cấp số cộng đó.
của 14 số hạng đầu tiên của cấp số cộng đó. A, 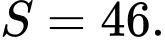
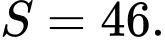
B, 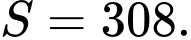
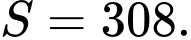
C, 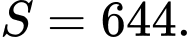
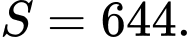
D, 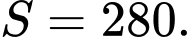
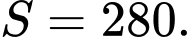
Chọn D
Tổng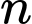 số hạng đầu tiên của một cấp số cộng là
số hạng đầu tiên của một cấp số cộng là 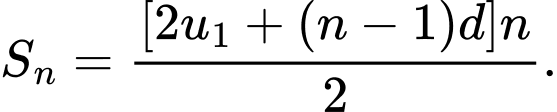
Vậy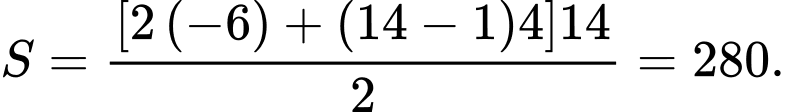 Đáp án: D
Đáp án: D
Tổng
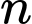 số hạng đầu tiên của một cấp số cộng là
số hạng đầu tiên của một cấp số cộng là 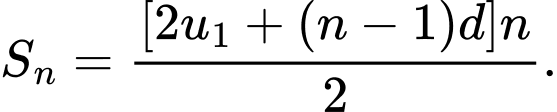
Vậy
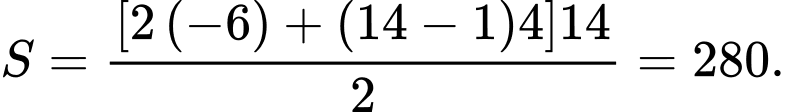 Đáp án: D
Đáp án: D
Câu 7 [806024]: Cho cấp số cộng 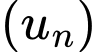 có
có 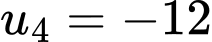 ;
; 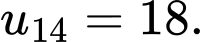 Tổng của 16 số hạng đầu tiên của cấp số cộng là
Tổng của 16 số hạng đầu tiên của cấp số cộng là
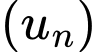 có
có 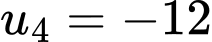 ;
; 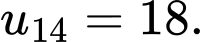 Tổng của 16 số hạng đầu tiên của cấp số cộng là
Tổng của 16 số hạng đầu tiên của cấp số cộng là A, 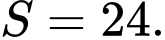
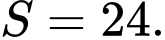
B, 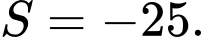
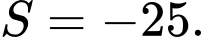
C, 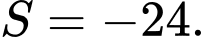
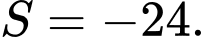
D, 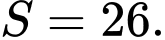
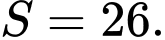
Chọn A
Ta có: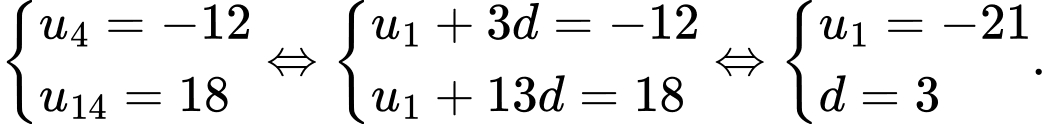
Tổng của 16 số hạng đầu tiên của cấp số cộng là: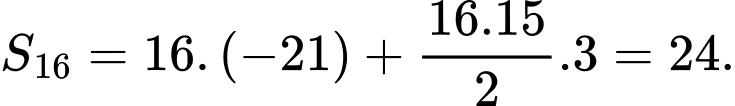 Đáp án: A
Đáp án: A
Ta có:
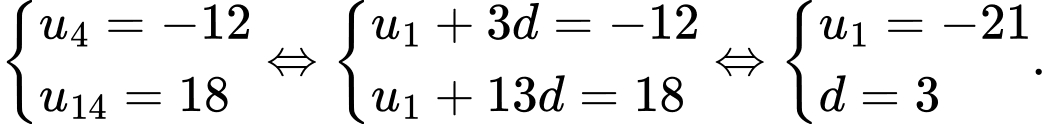
Tổng của 16 số hạng đầu tiên của cấp số cộng là:
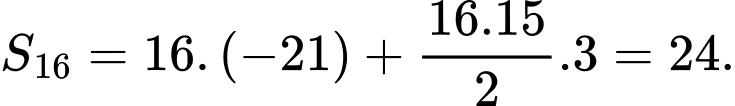 Đáp án: A
Đáp án: A
Câu 8 [806019]: Cho cấp số cộng có công sai  và
và 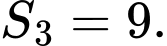 Khi đó tổng 20 số hạng đầu tiên
Khi đó tổng 20 số hạng đầu tiên  là
là
 và
và 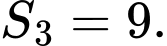 Khi đó tổng 20 số hạng đầu tiên
Khi đó tổng 20 số hạng đầu tiên  là
là A, 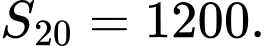
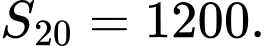
B, 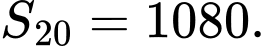
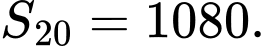
C, 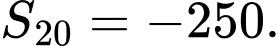
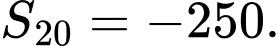
D, 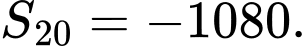
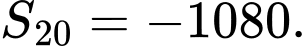
Chọn B.
Ta có: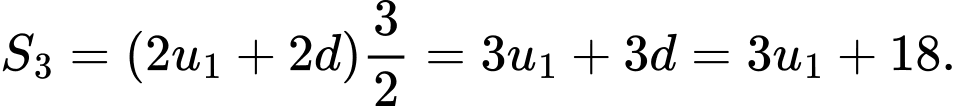
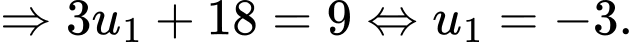
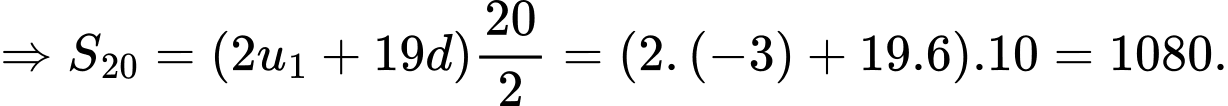 Đáp án: B
Đáp án: B
Ta có:
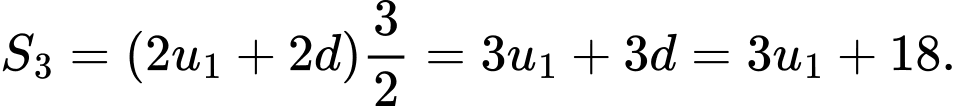
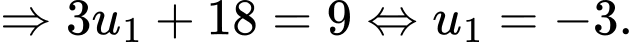
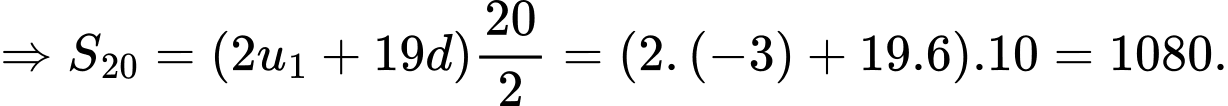 Đáp án: B
Đáp án: B
Câu 9 [805961]: Cho cấp số cộng 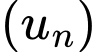 có số hạng đầu
có số hạng đầu 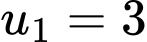 và công sai
và công sai  Tổng của 2019 số hạng đầu bằng
Tổng của 2019 số hạng đầu bằng
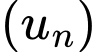 có số hạng đầu
có số hạng đầu 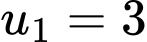 và công sai
và công sai  Tổng của 2019 số hạng đầu bằng
Tổng của 2019 số hạng đầu bằng A, 4 080 399.
B, 4 800 399.
C, 4 399 080.
D, 8 154 741.
Chọn A.
Áp dụng công thức tổng n số hạng đầu của cấp số cộng ta có:
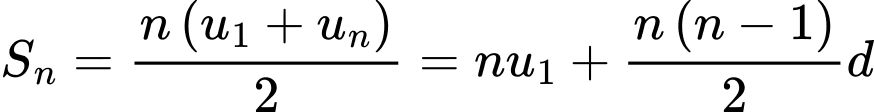
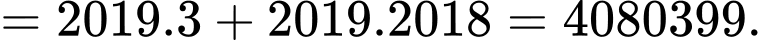 Đáp án: A
Đáp án: A
Áp dụng công thức tổng n số hạng đầu của cấp số cộng ta có:
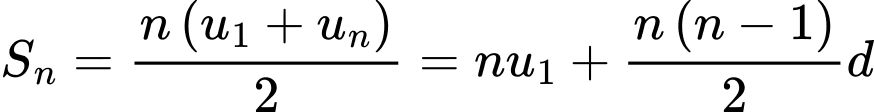
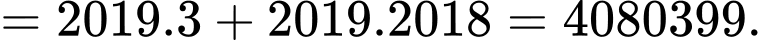 Đáp án: A
Đáp án: A
Câu 10 [224687]: Cho cấp số cộng 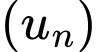 có
có 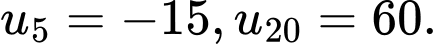 Tổng của 20 số hạng đầu tiên của cấp số cộng là?
Tổng của 20 số hạng đầu tiên của cấp số cộng là?
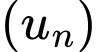 có
có 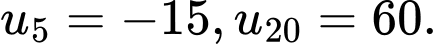 Tổng của 20 số hạng đầu tiên của cấp số cộng là?
Tổng của 20 số hạng đầu tiên của cấp số cộng là? A, 200.
B, –200.
C, 250.
D, –25.
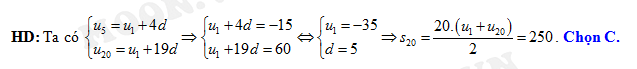 Đáp án: C
Đáp án: C
Câu 11 [805962]: Cho 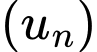 là cấp số cộng biết
là cấp số cộng biết 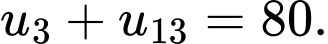 Tổng 15 số hạng đầu của cấp số cộng đó bằng
Tổng 15 số hạng đầu của cấp số cộng đó bằng
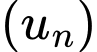 là cấp số cộng biết
là cấp số cộng biết 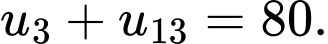 Tổng 15 số hạng đầu của cấp số cộng đó bằng
Tổng 15 số hạng đầu của cấp số cộng đó bằng A, 800.
B, 600.
C, 570.
D, 630.
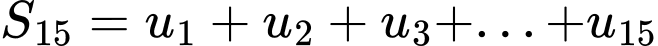
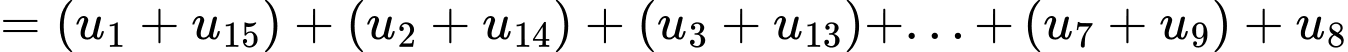
Vì
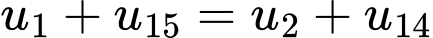
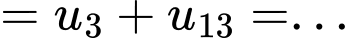
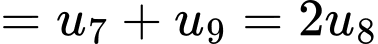 và
và 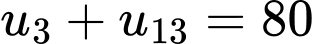
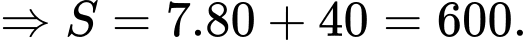 Đáp án: B
Đáp án: B
Câu 12 [806022]: Cho cấp số cộng 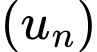 có
có 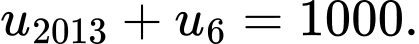 Tổng 2018 số hạng đầu tiên của cấp số cộng đó là
Tổng 2018 số hạng đầu tiên của cấp số cộng đó là
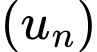 có
có 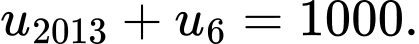 Tổng 2018 số hạng đầu tiên của cấp số cộng đó là
Tổng 2018 số hạng đầu tiên của cấp số cộng đó là A, 1009000.
B, 100800.
C, 1008000.
D, 100900.
Gọi 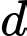 là công sai của cấp số cộng. Khi đó:
là công sai của cấp số cộng. Khi đó:
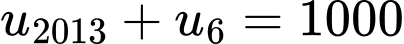
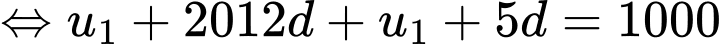
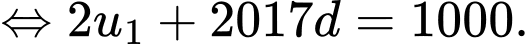
Ta có: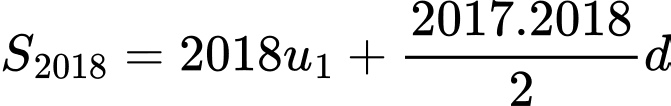
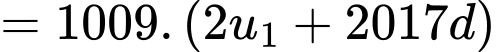
 Đáp án: A
Đáp án: A
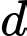 là công sai của cấp số cộng. Khi đó:
là công sai của cấp số cộng. Khi đó: 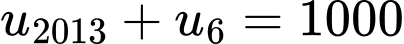
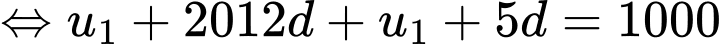
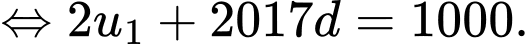
Ta có:
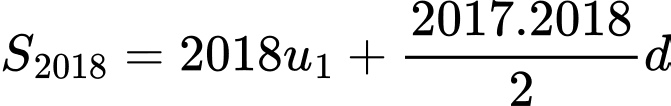
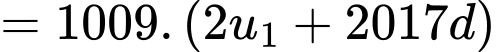
 Đáp án: A
Đáp án: A
Câu 13 [224666]: Tính tổng  số hạng đầu tiên của cấp số cộng
số hạng đầu tiên của cấp số cộng 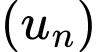 biết
biết 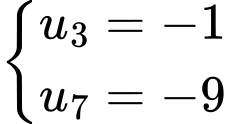 .
.
 số hạng đầu tiên của cấp số cộng
số hạng đầu tiên của cấp số cộng 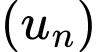 biết
biết 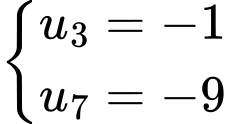 .
. A, 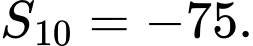
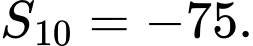
B, 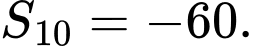
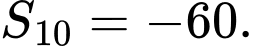
C, 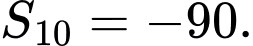
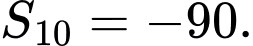
D, 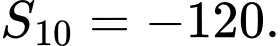
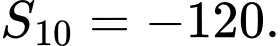
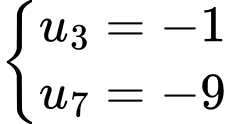
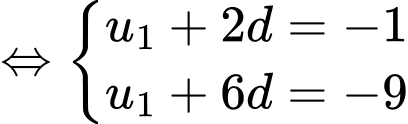
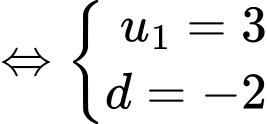
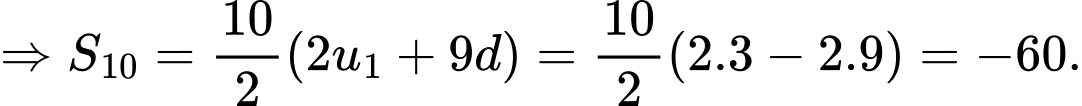 Đáp án: B
Đáp án: B
Câu 14 [224661]: Tính 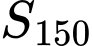 của một cấp số cộng
của một cấp số cộng 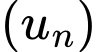 biết
biết 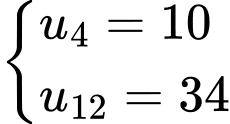 ?
?
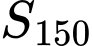 của một cấp số cộng
của một cấp số cộng 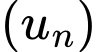 biết
biết 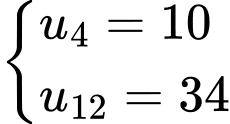 ?
? A, 33 677.
B, 33 657.
C, 46 783.
D, 33 675.
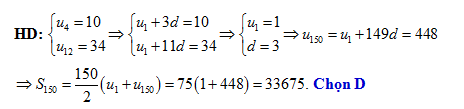 Đáp án: D
Đáp án: D
Câu 15 [806023]: Cho cấp số cộng 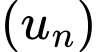 thỏa mãn
thỏa mãn 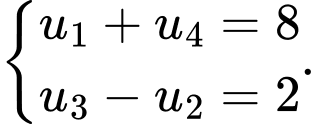 Tính tổng
Tính tổng  số hạng đầu của cấp số cộng trên.
số hạng đầu của cấp số cộng trên.
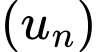 thỏa mãn
thỏa mãn 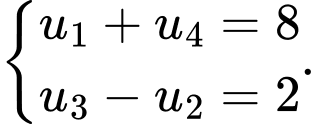 Tính tổng
Tính tổng  số hạng đầu của cấp số cộng trên.
số hạng đầu của cấp số cộng trên. A, 100.
B, 110.
C, 10.
D, 90.
Chọn A
Gọi cấp cố cộng có công sai là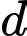 ta có
ta có 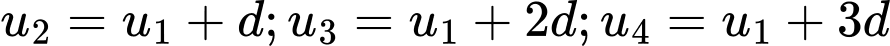
Khi đó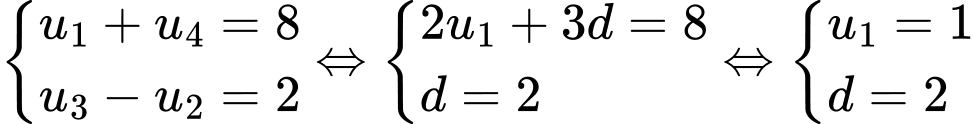
Áp dụng công thức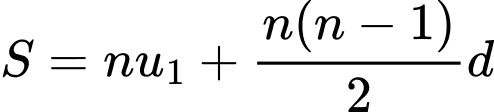
Vậy tổng của số hạng đầu của cấp số cộng là
số hạng đầu của cấp số cộng là 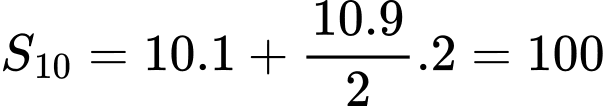 Đáp án: A
Đáp án: A
Gọi cấp cố cộng có công sai là
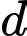 ta có
ta có 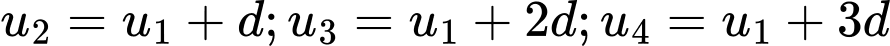
Khi đó
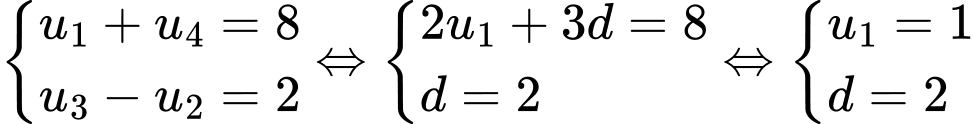
Áp dụng công thức
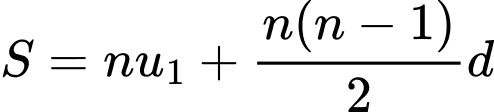
Vậy tổng của
 số hạng đầu của cấp số cộng là
số hạng đầu của cấp số cộng là 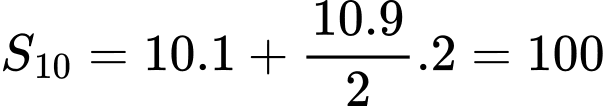 Đáp án: A
Đáp án: A
Câu 16 [805958]: Cho dãy số 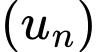 là một cấp số cộng có
là một cấp số cộng có 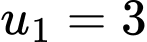 và công sai
và công sai  Biết tổng
Biết tổng 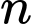 số hạng đầu của dãy số
số hạng đầu của dãy số 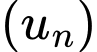 là
là 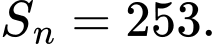 Tìm
Tìm 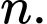
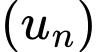 là một cấp số cộng có
là một cấp số cộng có 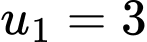 và công sai
và công sai  Biết tổng
Biết tổng 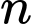 số hạng đầu của dãy số
số hạng đầu của dãy số 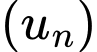 là
là 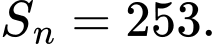 Tìm
Tìm 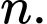
A, 9.
B, 11.
C, 12.
D, 10.
Ta có 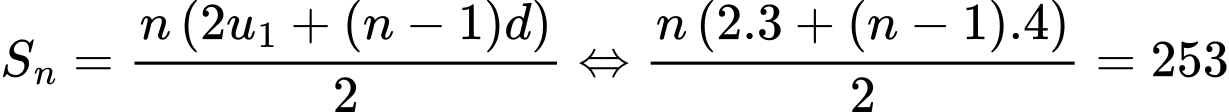
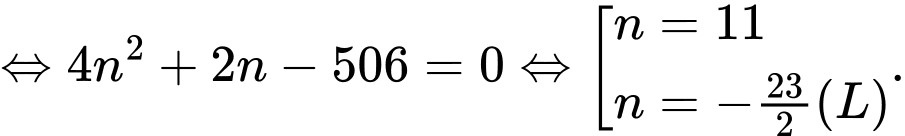 Đáp án: B
Đáp án: B
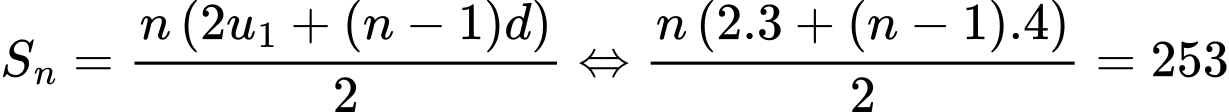
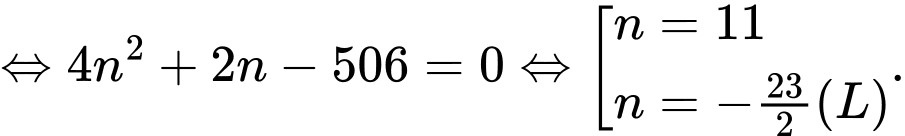 Đáp án: B
Đáp án: B
Câu 17 [806029]: Gọi 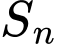 là tổng
là tổng 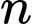 số hạng đầu tiên trong cấp số cộng
số hạng đầu tiên trong cấp số cộng  Biết
Biết 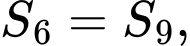 tỉ số
tỉ số 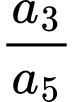 bằng
bằng
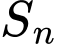 là tổng
là tổng 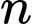 số hạng đầu tiên trong cấp số cộng
số hạng đầu tiên trong cấp số cộng  Biết
Biết 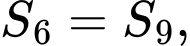 tỉ số
tỉ số 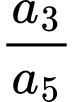 bằng
bằng A, 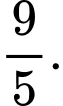
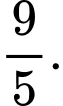
B, 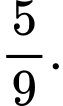
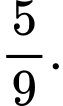
C, 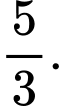
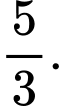
D, 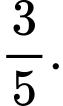
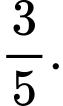
Chọn C
Ta có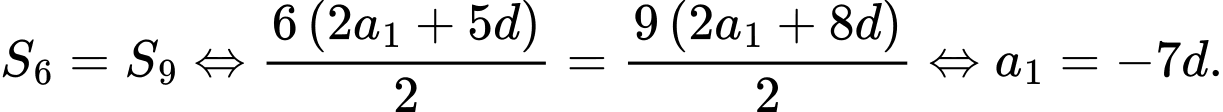
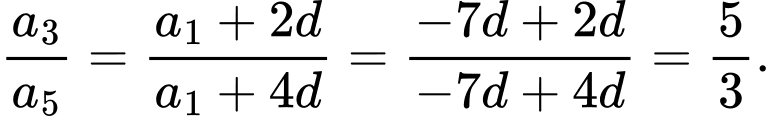 Đáp án: C
Đáp án: C
Ta có
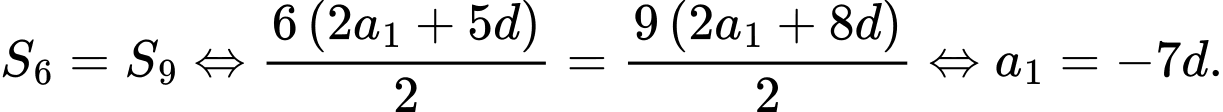
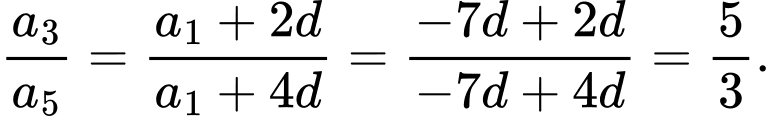 Đáp án: C
Đáp án: C
Câu 18 [224649]: Lập công thức tổng quát của cấp số cộng 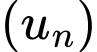 biết:
biết: 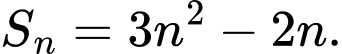
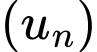 biết:
biết: 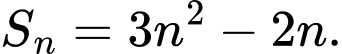
A, 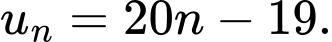
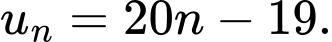
B, 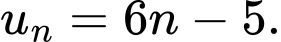
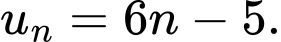
C, 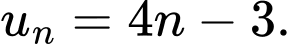
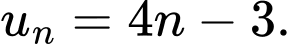
D, 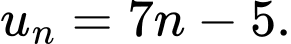
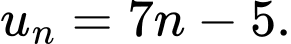
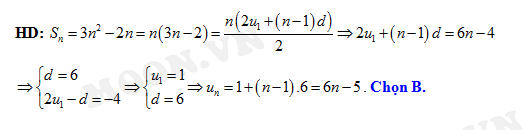 Đáp án: B
Đáp án: B
Câu 19 [806027]: Một cấp số cộng có tổng 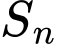 của
của 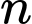 số hạng đầu được tính theo công thức
số hạng đầu được tính theo công thức 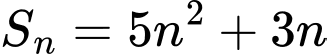
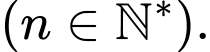 Tìm số hạng đầu
Tìm số hạng đầu 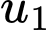 và công sai
và công sai 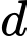 của cấp số cộng đó.
của cấp số cộng đó.
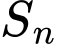 của
của 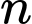 số hạng đầu được tính theo công thức
số hạng đầu được tính theo công thức 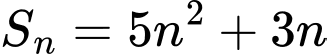
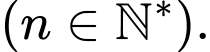 Tìm số hạng đầu
Tìm số hạng đầu 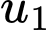 và công sai
và công sai 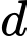 của cấp số cộng đó.
của cấp số cộng đó. A, 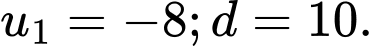
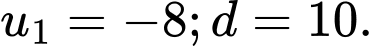
B, 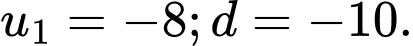
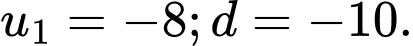
C, 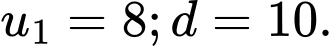
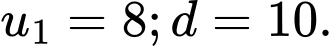
D, 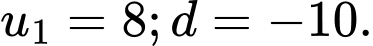
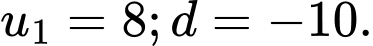
Ta có: 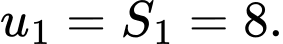
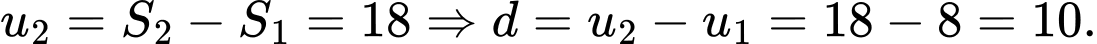 Đáp án: C
Đáp án: C
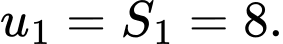
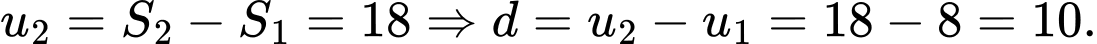 Đáp án: C
Đáp án: C
Câu 20 [806030]: Cho cấp số cộng 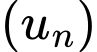 và gọi
và gọi 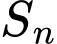 là tổng
là tổng 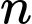 số hạng đầu tiên của nó. Biết
số hạng đầu tiên của nó. Biết 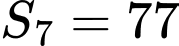 và
và 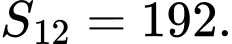 Tìm số hạng tổng quát
Tìm số hạng tổng quát 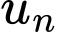 của cấp số cộng đó.
của cấp số cộng đó.
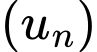 và gọi
và gọi 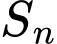 là tổng
là tổng 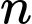 số hạng đầu tiên của nó. Biết
số hạng đầu tiên của nó. Biết 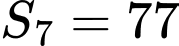 và
và 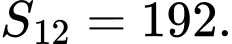 Tìm số hạng tổng quát
Tìm số hạng tổng quát 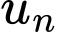 của cấp số cộng đó.
của cấp số cộng đó. A, 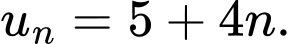
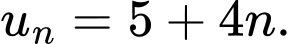
B, 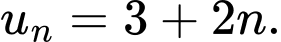
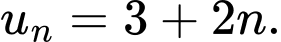
C, 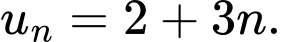
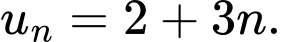
D, 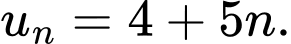
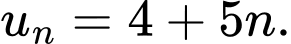
Giả sử cấp số cộng có số hạng đầu là 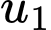 và công sai
và công sai 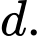
Ta có: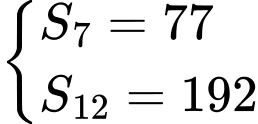
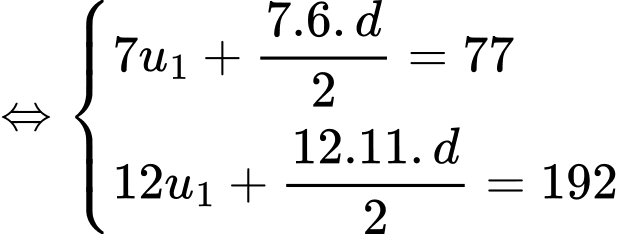
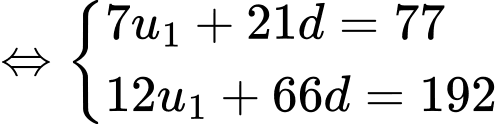
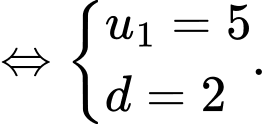
Khi đó:
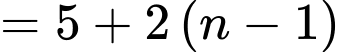
 Đáp án: B
Đáp án: B
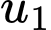 và công sai
và công sai 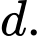
Ta có:
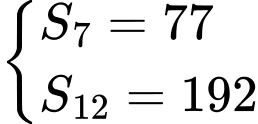
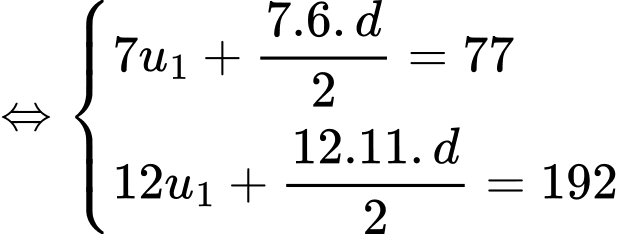
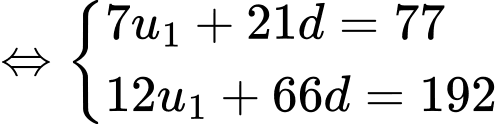
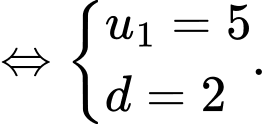
Khi đó:

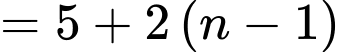
 Đáp án: B
Đáp án: B
Câu 21 [224697]: Cho cấp số cộng có tổng 10 số hạng đầu tiên và 100 số hạng đầu tiên lần lượt là 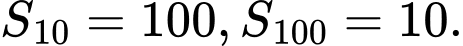 Khi đó, tổng của 110 số hạng đầu tiên là
Khi đó, tổng của 110 số hạng đầu tiên là
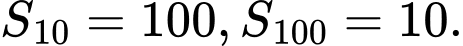 Khi đó, tổng của 110 số hạng đầu tiên là
Khi đó, tổng của 110 số hạng đầu tiên là A, 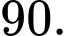
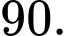
B, 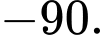
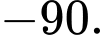
C, 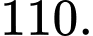
D, 

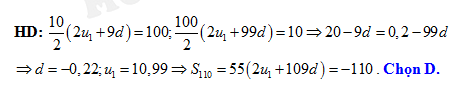 Đáp án: D
Đáp án: D
Câu 22 [224695]: Cho dãy số 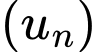 xác định bởi:
xác định bởi: 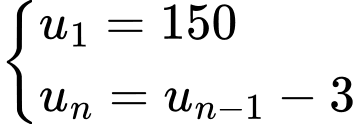 với mọi
với mọi  Khi đó tổng 100 số hạng đầu tiên của dãy số đó bằng
Khi đó tổng 100 số hạng đầu tiên của dãy số đó bằng
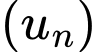 xác định bởi:
xác định bởi: 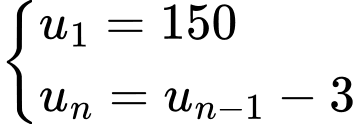 với mọi
với mọi  Khi đó tổng 100 số hạng đầu tiên của dãy số đó bằng
Khi đó tổng 100 số hạng đầu tiên của dãy số đó bằng A, 150.
B, 300.
C, 29 850.
D, 59 700.
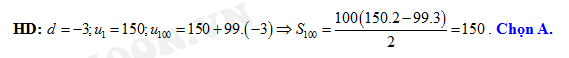 Đáp án: A
Đáp án: A
Câu 23 [806032]: Giải phương trình 

A, 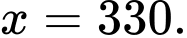
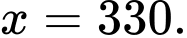
B, 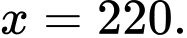
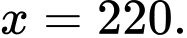
C, 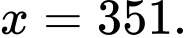
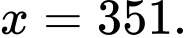
D, 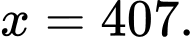
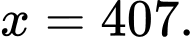
Ta có cấp số cộng với 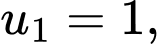
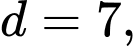
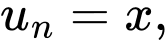
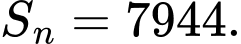
Áp dụng công thức
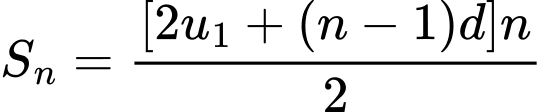
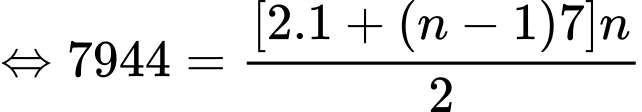
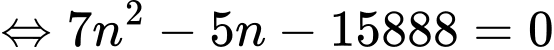
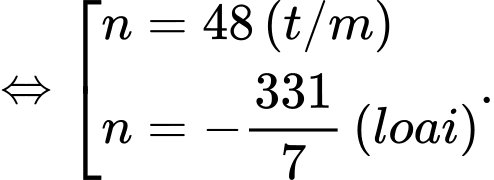
Vậy Đáp án: A
Đáp án: A
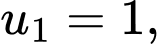
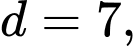
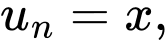
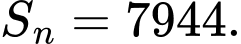
Áp dụng công thức
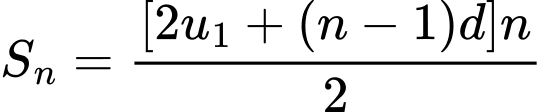
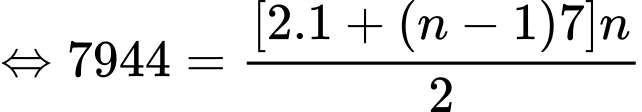
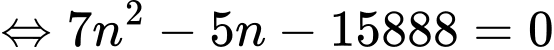
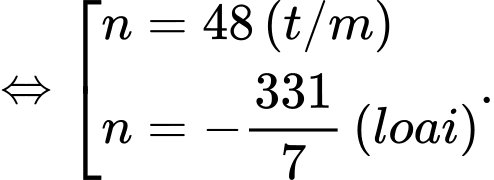
Vậy
 Đáp án: A
Đáp án: A
Câu 24 [398792]: Giải phương trình sau: 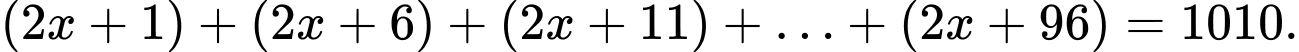
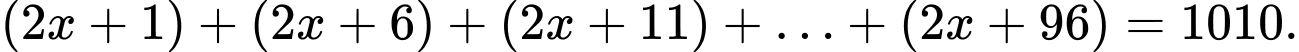
A, 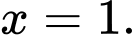
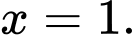
B, 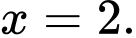
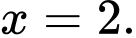
C, 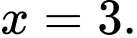
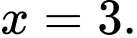
D, 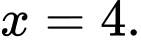
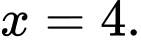
Ta có dãy số 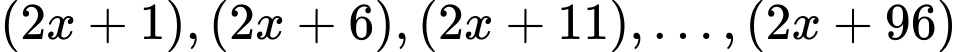 lập thành cấp số cộng có
lập thành cấp số cộng có 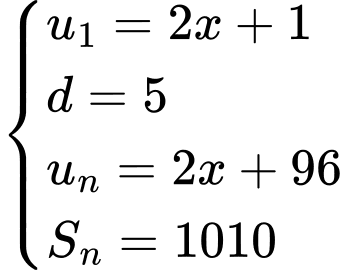
Suy ra: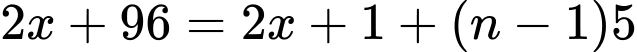
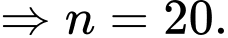
Vậy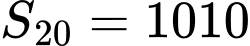
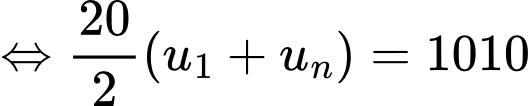
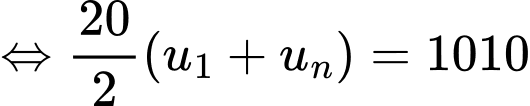
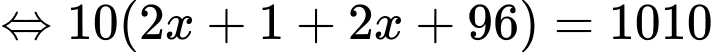
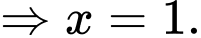 Đáp án: A
Đáp án: A
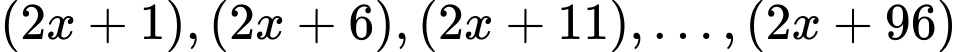 lập thành cấp số cộng có
lập thành cấp số cộng có 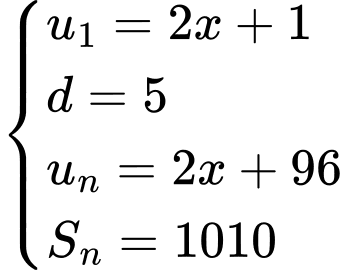
Suy ra:
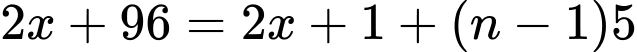
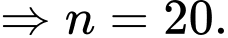
Vậy
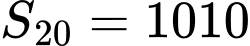
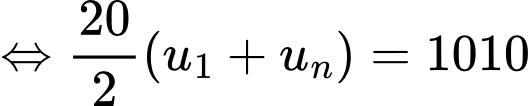
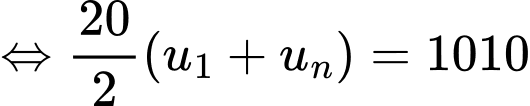
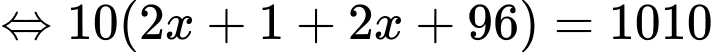
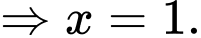 Đáp án: A
Đáp án: A
Câu 25 [224663]: Cho 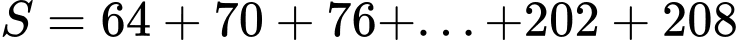 . Tính
. Tính 
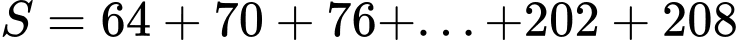 . Tính
. Tính 
A, 3250.
B, 3400.
C, 4200.
D, 4250.
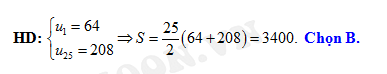 Đáp án: B
Đáp án: B
Câu 26 [224646]: Tỉnh tổng sau : 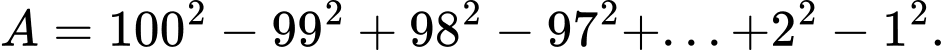
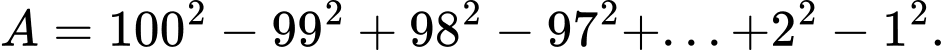
A, 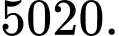
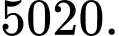
B, 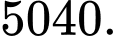
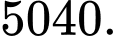
C, 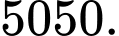
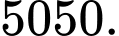
D, 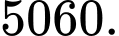
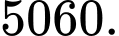
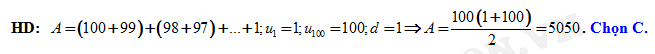 Đáp án: C
Đáp án: C
Câu 27 [224691]: Cho dãy số 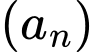 xác định bởi
xác định bởi 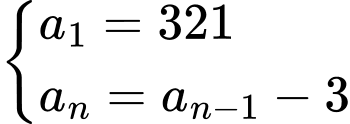 với mọi
với mọi 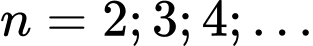 Tổng 125 số hạng đầu tiên của dãy số
Tổng 125 số hạng đầu tiên của dãy số 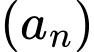 là
là
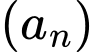 xác định bởi
xác định bởi 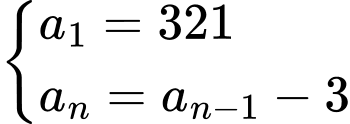 với mọi
với mọi 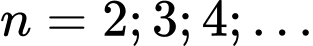 Tổng 125 số hạng đầu tiên của dãy số
Tổng 125 số hạng đầu tiên của dãy số 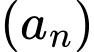 là
là A, 16 875.
B, 63 375.
C, 635 625.
D, 166 875.
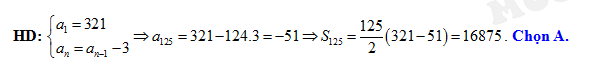 Đáp án: A
Đáp án: A
Câu 28 [806025]: Cho cấp số cộng 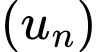 thỏa
thỏa 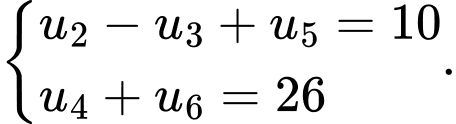 Tính
Tính 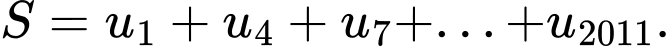
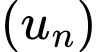 thỏa
thỏa 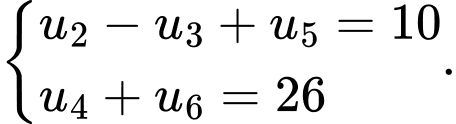 Tính
Tính 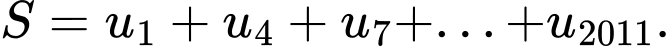
A, 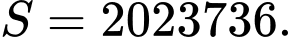
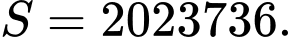
B, 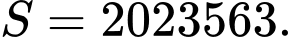
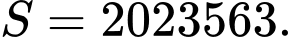
C, 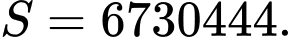
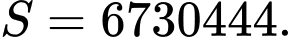
D, 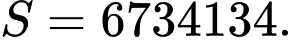
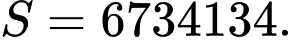
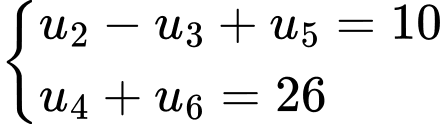
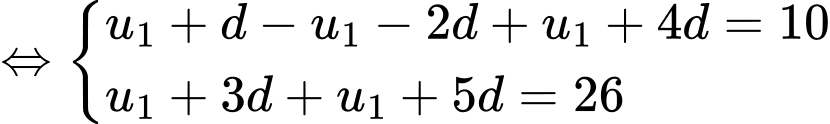
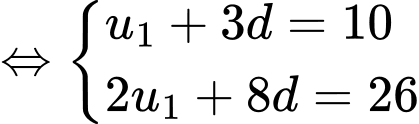
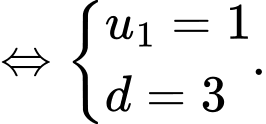
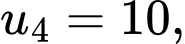
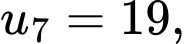
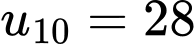 …
… Ta có
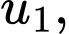
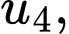
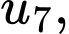
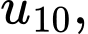 …,
…,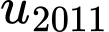 là cấp số cộng có
là cấp số cộng có 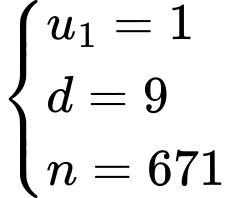
 Đáp án: A
Đáp án: A
Câu 29 [806033]: Cho cấp số cộng 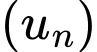 có số hạng đầu bằng 1 và tổng 100 số hạng đầu bằng 14950. Giá trị của tổng
có số hạng đầu bằng 1 và tổng 100 số hạng đầu bằng 14950. Giá trị của tổng 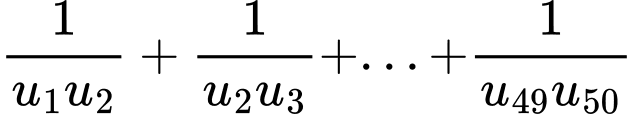 bằng
bằng
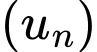 có số hạng đầu bằng 1 và tổng 100 số hạng đầu bằng 14950. Giá trị của tổng
có số hạng đầu bằng 1 và tổng 100 số hạng đầu bằng 14950. Giá trị của tổng 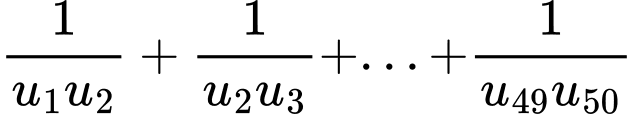 bằng
bằng A, 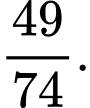
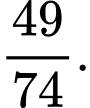
B, 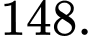
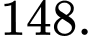
C, 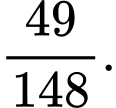
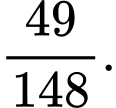
D, 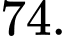
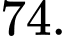
Gọi 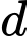 là công sai của cấp số cộng. Ta có
là công sai của cấp số cộng. Ta có 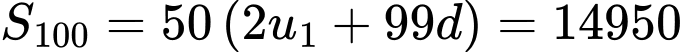 với
với 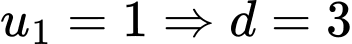
Đặt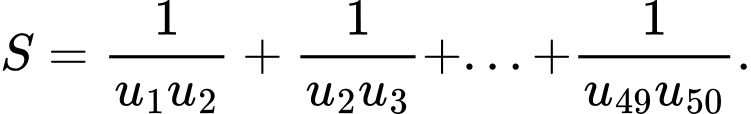
Ta có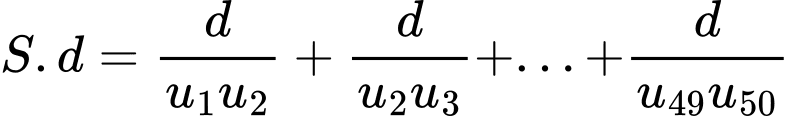
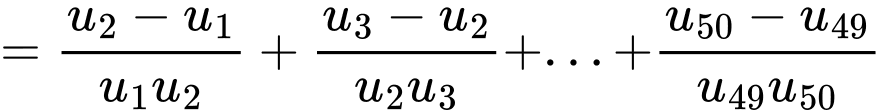
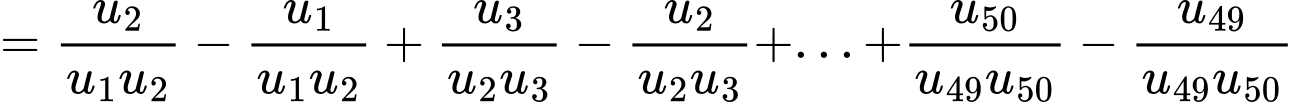
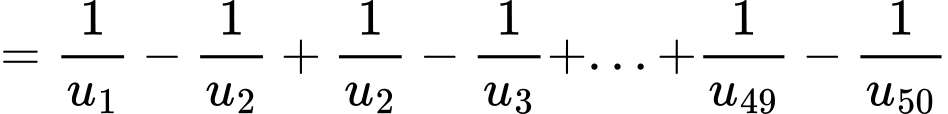
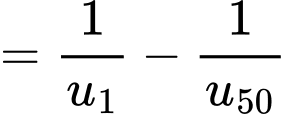
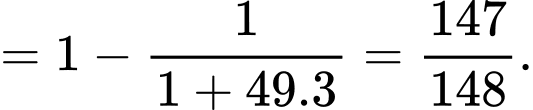
Với nên
nên 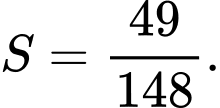 Đáp án: C
Đáp án: C
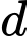 là công sai của cấp số cộng. Ta có
là công sai của cấp số cộng. Ta có 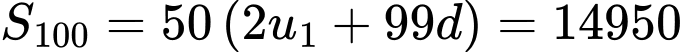 với
với 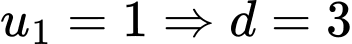
Đặt
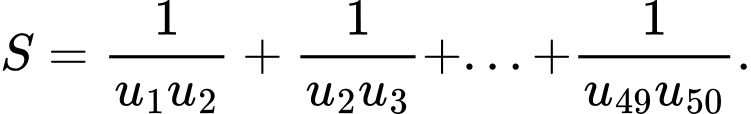
Ta có
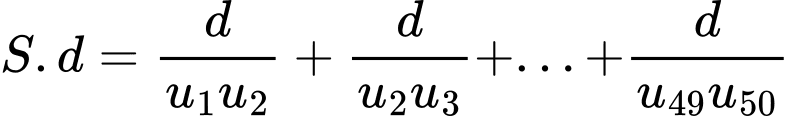
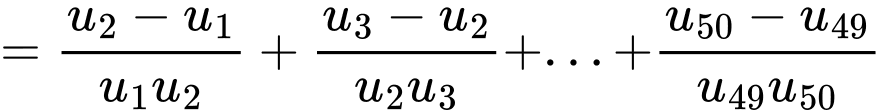
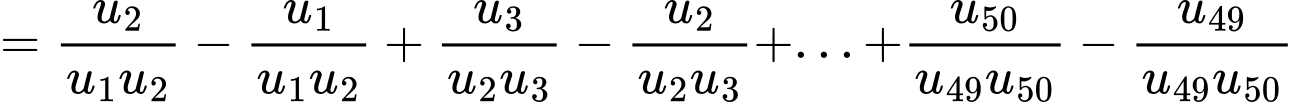
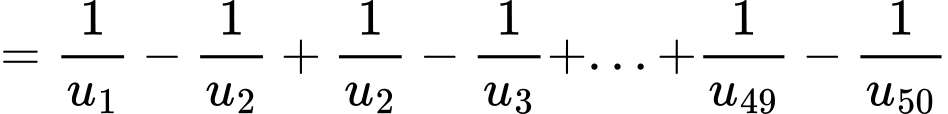
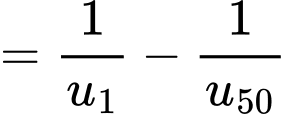
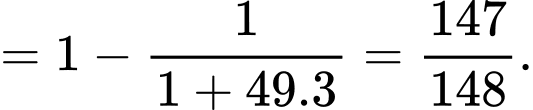
Với
 nên
nên 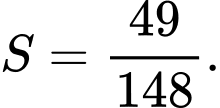 Đáp án: C
Đáp án: C
Câu 30 [806164]: Cho một cấp số cộng 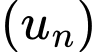 có
có 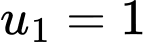 và tổng 100 số hạng đầu bằng 10000. Tính tổng
và tổng 100 số hạng đầu bằng 10000. Tính tổng 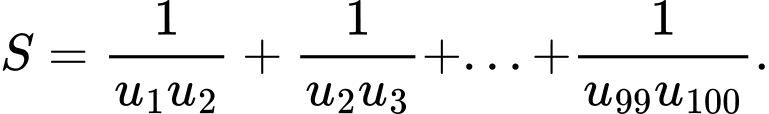
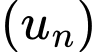 có
có 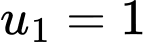 và tổng 100 số hạng đầu bằng 10000. Tính tổng
và tổng 100 số hạng đầu bằng 10000. Tính tổng 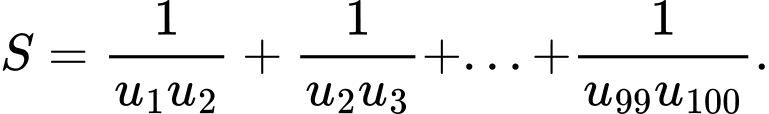
A, 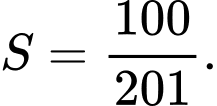
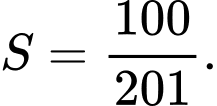
B, 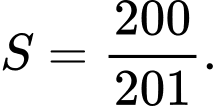
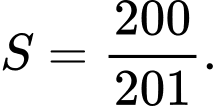
C, 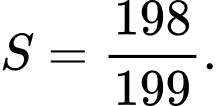
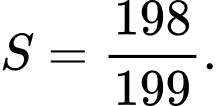
D, 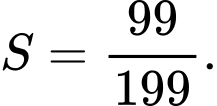
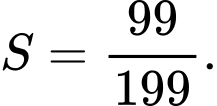
Chọn D
Gọi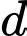 là công sai của cấp số cộng đã cho.
là công sai của cấp số cộng đã cho.
Ta có: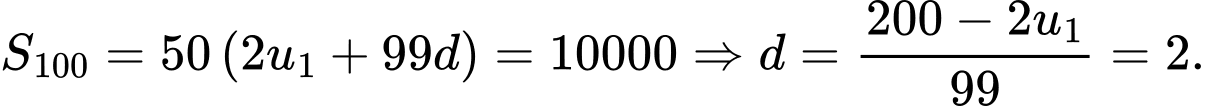
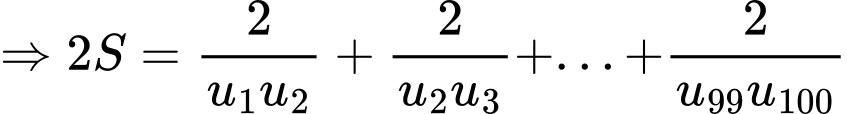
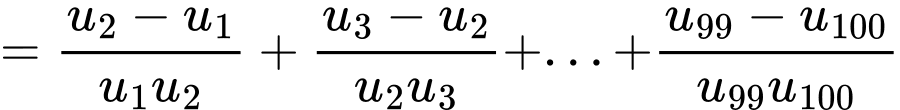
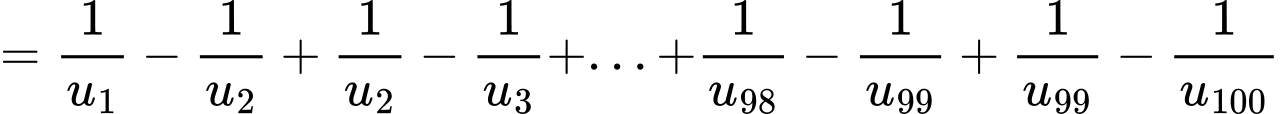
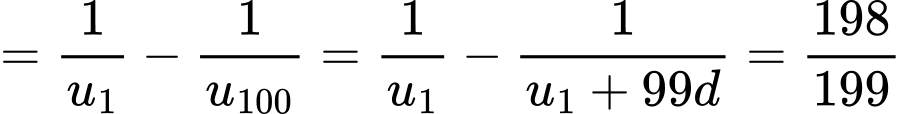
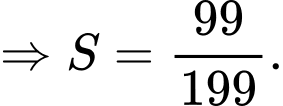 Đáp án: D
Đáp án: D
Gọi
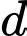 là công sai của cấp số cộng đã cho.
là công sai của cấp số cộng đã cho. Ta có:
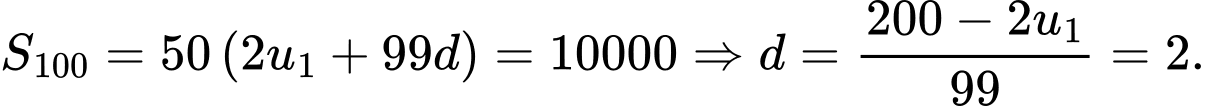
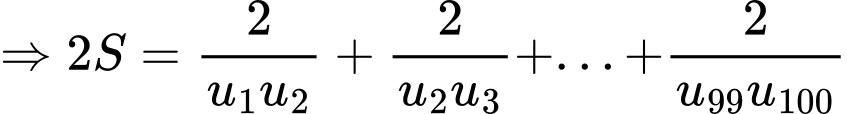
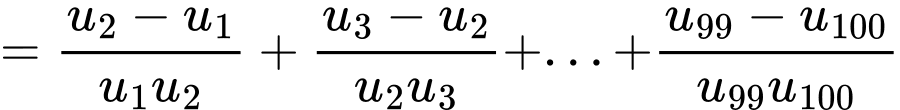
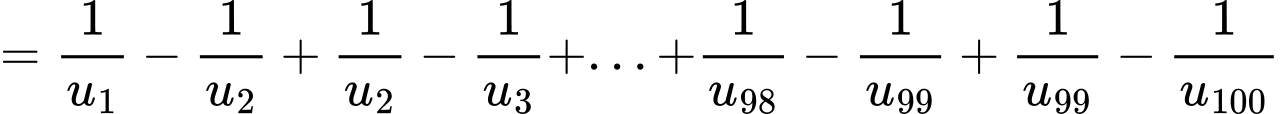
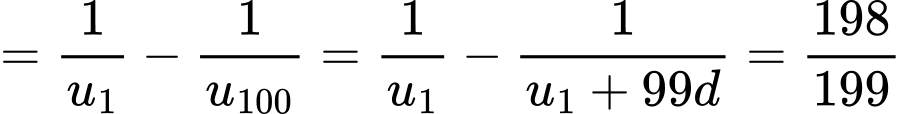
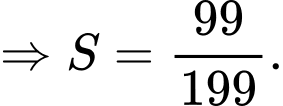 Đáp án: D
Đáp án: D