Câu 1 [804409]: Cấp số nhân 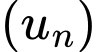 có
có 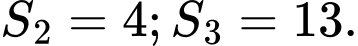 Tìm
Tìm 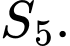
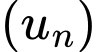 có
có 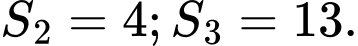 Tìm
Tìm 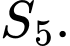
A, 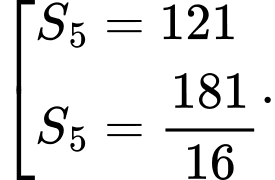
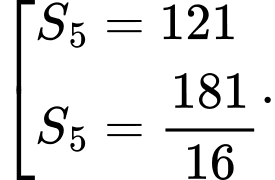
B, 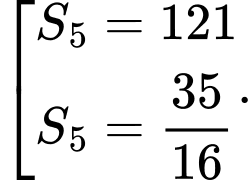
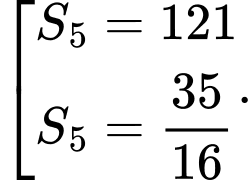
C, 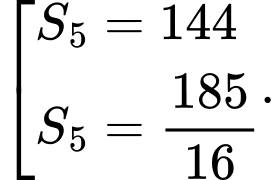
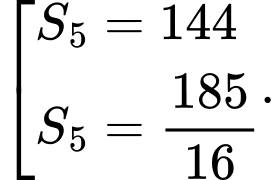
D, 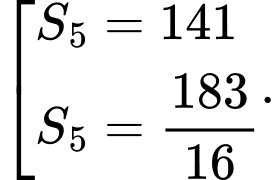
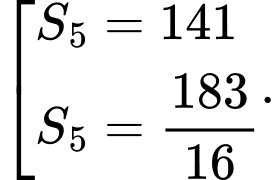
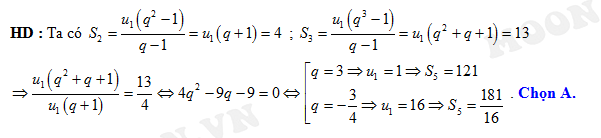 Đáp án: A
Đáp án: A
Câu 2 [804399]: Tổng 10 số hạng đầu tiên của cấp số nhân 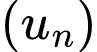 với
với 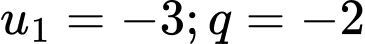 bằng
bằng
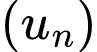 với
với 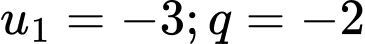 bằng
bằng A, 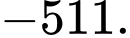
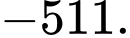
B, 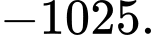
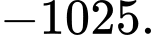
C, 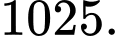
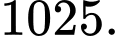
D, 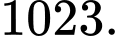
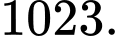
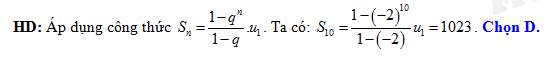 Đáp án: D
Đáp án: D
Câu 3 [806405]: Cho 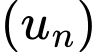 là cấp số nhân, đặt
là cấp số nhân, đặt 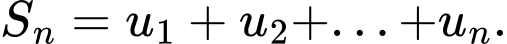 Biết
Biết 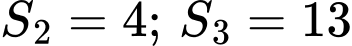 và
và  giá trị
giá trị 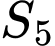 bằng
bằng
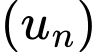 là cấp số nhân, đặt
là cấp số nhân, đặt 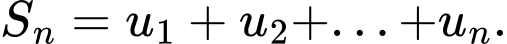 Biết
Biết 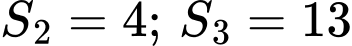 và
và  giá trị
giá trị 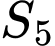 bằng
bằng A, 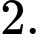
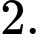
B, 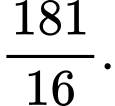
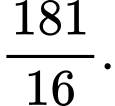
C, 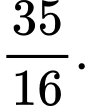
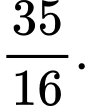
D, 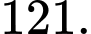
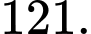
Chọn B
Gọi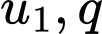 lần lượt là số hạng đầu tiên và công bội của cấp số nhân cần tìm.
lần lượt là số hạng đầu tiên và công bội của cấp số nhân cần tìm.
Từ giả thiết ta có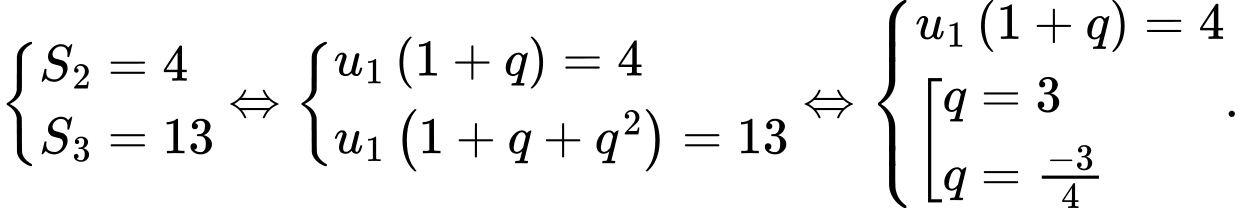
Vì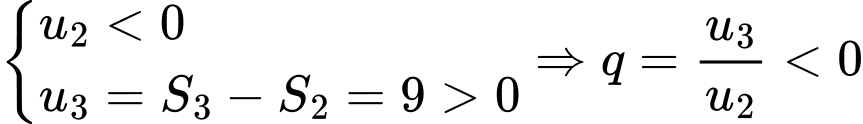 nên cấp số nhân cần tìm có
nên cấp số nhân cần tìm có 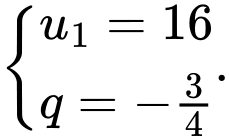
Do đó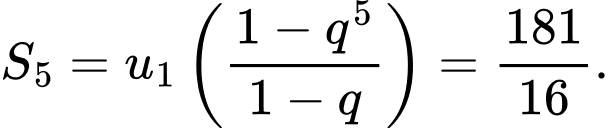 Đáp án: B
Đáp án: B
Gọi
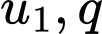 lần lượt là số hạng đầu tiên và công bội của cấp số nhân cần tìm.
lần lượt là số hạng đầu tiên và công bội của cấp số nhân cần tìm. Từ giả thiết ta có
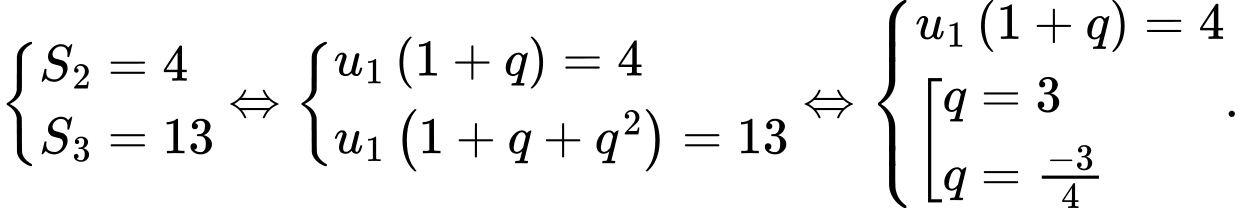
Vì
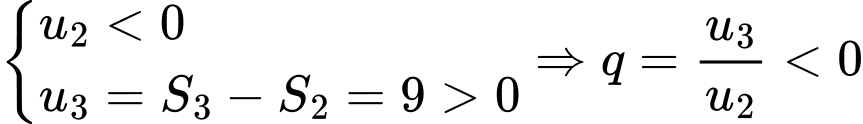 nên cấp số nhân cần tìm có
nên cấp số nhân cần tìm có 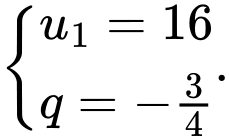
Do đó
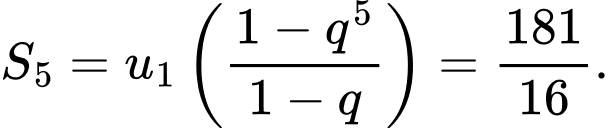 Đáp án: B
Đáp án: B
Câu 4 [804405]: Cho cấp số nhân 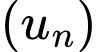 với
với 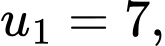 công bội
công bội 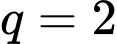 và tổng
và tổng 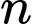 số hạng đầu tiên là
số hạng đầu tiên là 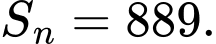 Khi đó số hạng cuối của dãy số bằng
Khi đó số hạng cuối của dãy số bằng
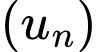 với
với 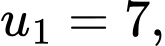 công bội
công bội 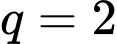 và tổng
và tổng 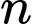 số hạng đầu tiên là
số hạng đầu tiên là 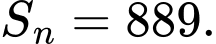 Khi đó số hạng cuối của dãy số bằng
Khi đó số hạng cuối của dãy số bằng A, 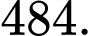
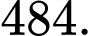
B, 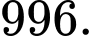
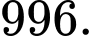
C, 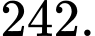
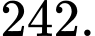
D, 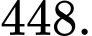
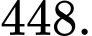
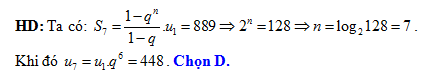 Đáp án: D
Đáp án: D
Câu 5 [806396]: Cho cấp số nhân 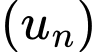 có tổng
có tổng 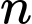 số hạng đầu tiên là
số hạng đầu tiên là 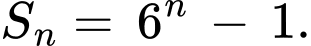 Tìm số hạng thứ 5 của cấp số nhân đã cho.
Tìm số hạng thứ 5 của cấp số nhân đã cho.
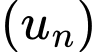 có tổng
có tổng 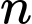 số hạng đầu tiên là
số hạng đầu tiên là 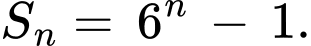 Tìm số hạng thứ 5 của cấp số nhân đã cho.
Tìm số hạng thứ 5 của cấp số nhân đã cho. A, 120 005.
B, 6840.
C, 7775.
D, 6480.
Chọn D
Cấp số nhân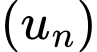 có số hạng đầu
có số hạng đầu 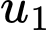 và công bội
và công bội 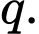
Do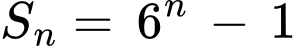 nên
nên 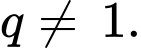 Khi đó
Khi đó 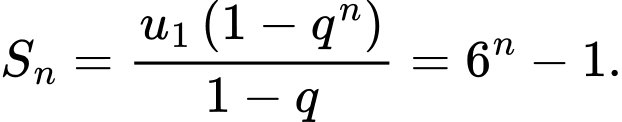
Ta có: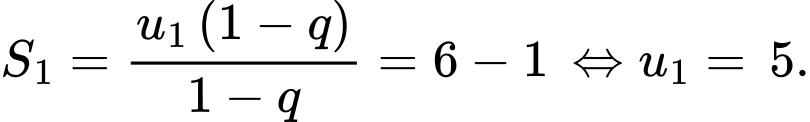
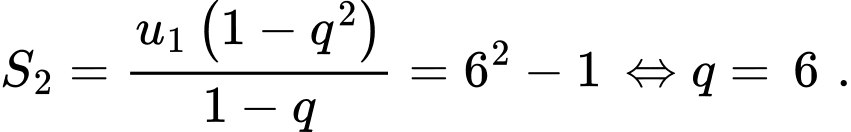
Vậy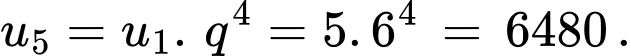 Đáp án: D
Đáp án: D
Cấp số nhân
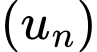 có số hạng đầu
có số hạng đầu 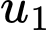 và công bội
và công bội 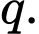
Do
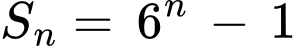 nên
nên 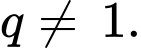 Khi đó
Khi đó 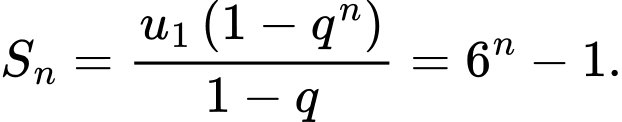
Ta có:
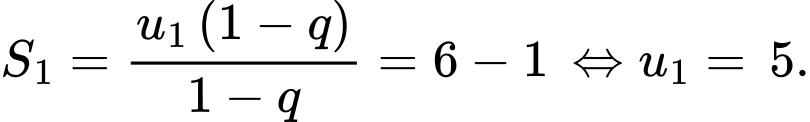
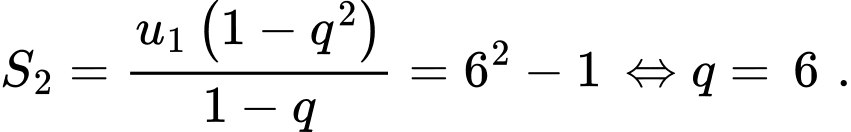
Vậy
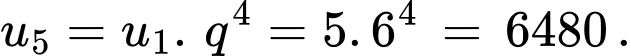 Đáp án: D
Đáp án: D
Câu 6 [804416]: Cho cấp số nhân 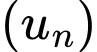 có
có 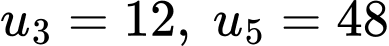 và có công bội âm. Tổng 7 số hạng đầu tiên của cấp số nhân đã cho bằng
và có công bội âm. Tổng 7 số hạng đầu tiên của cấp số nhân đã cho bằng
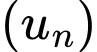 có
có 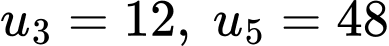 và có công bội âm. Tổng 7 số hạng đầu tiên của cấp số nhân đã cho bằng
và có công bội âm. Tổng 7 số hạng đầu tiên của cấp số nhân đã cho bằng A, 129.
B, –129.
C, 128.
D, –128.
Đáp án: D
Câu 7 [734885]: Xác định 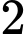 số hạng đầu của một cấp số nhân có tổng số hạng đầu và số hạng thứ
số hạng đầu của một cấp số nhân có tổng số hạng đầu và số hạng thứ 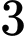 bằng
bằng  , tổng của số hạng thứ
, tổng của số hạng thứ 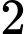 và số hạng thứ
và số hạng thứ 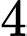 bằng
bằng 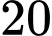 .
.
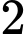 số hạng đầu của một cấp số nhân có tổng số hạng đầu và số hạng thứ
số hạng đầu của một cấp số nhân có tổng số hạng đầu và số hạng thứ 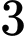 bằng
bằng  , tổng của số hạng thứ
, tổng của số hạng thứ 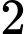 và số hạng thứ
và số hạng thứ 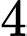 bằng
bằng 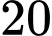 .
. A, 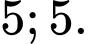
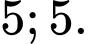
B, 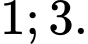
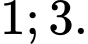
C, 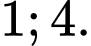
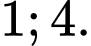
D, 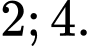
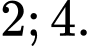
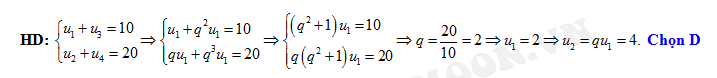 Đáp án: D
Đáp án: D
Câu 8 [518992]: Một cấp số nhân có số hạng đầu 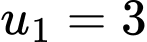 và công bội
và công bội 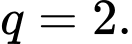 Biết
Biết 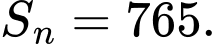 Tìm
Tìm 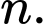
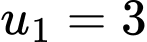 và công bội
và công bội 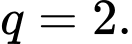 Biết
Biết 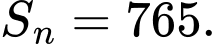 Tìm
Tìm 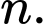
A, 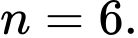
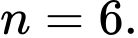
B, 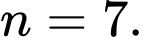
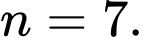
C, 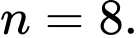
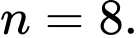
D, 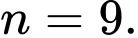
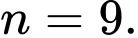
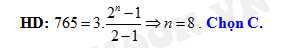 Đáp án: C
Đáp án: C
Câu 9 [806401]: Cho cấp số nhân 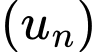 có
có 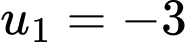 và
và 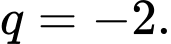 Tính tổng 10 số hạng đầu tiên của cấp số nhân.
Tính tổng 10 số hạng đầu tiên của cấp số nhân.
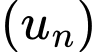 có
có 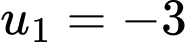 và
và 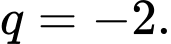 Tính tổng 10 số hạng đầu tiên của cấp số nhân.
Tính tổng 10 số hạng đầu tiên của cấp số nhân. A, 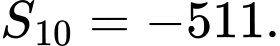
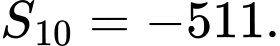
B, 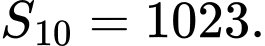
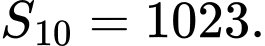
C, 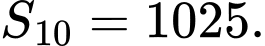
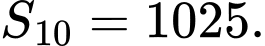
D, 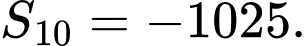
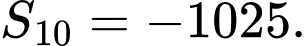
Chọn B
Ta có: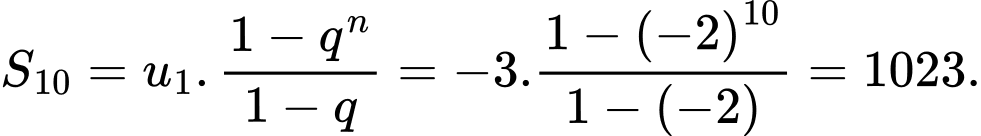 Đáp án: B
Đáp án: B
Ta có:
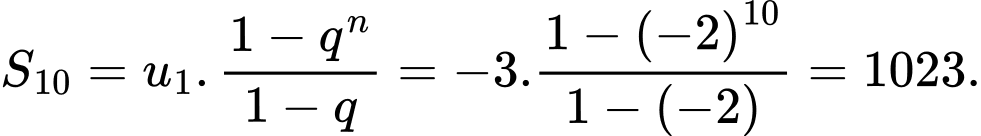 Đáp án: B
Đáp án: B
Câu 10 [748249]: Cho cấp số nhân 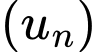 có
có 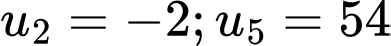 . Khi đó tổng 1000 số hạng đầu tiên của cấp số nhân đó bằng
. Khi đó tổng 1000 số hạng đầu tiên của cấp số nhân đó bằng
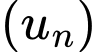 có
có 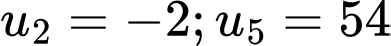 . Khi đó tổng 1000 số hạng đầu tiên của cấp số nhân đó bằng
. Khi đó tổng 1000 số hạng đầu tiên của cấp số nhân đó bằng A, 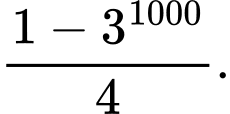
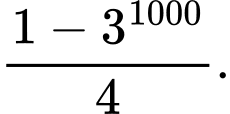
B, 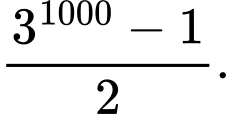
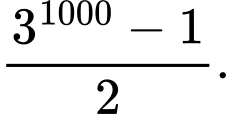
C, 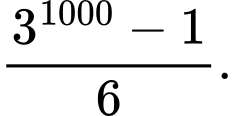
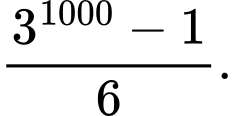
D, 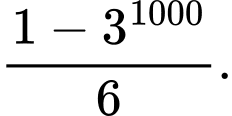
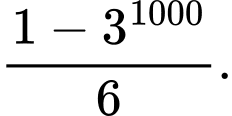
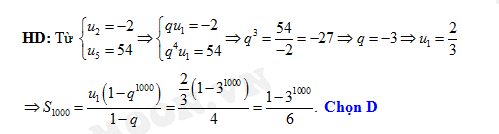 Đáp án: D
Đáp án: D
Câu 11 [806402]: Cho một cấp số nhân có các số hạng đều không âm thỏa mãn 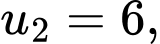
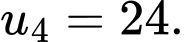 Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó.
Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó.
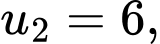
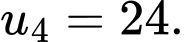 Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó.
Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó. A, 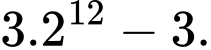
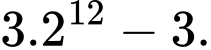
B, 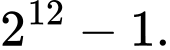
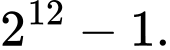
C, 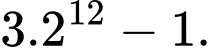
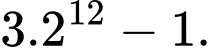
D, 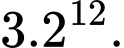
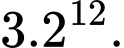
Gọi công bội của CSN bằng 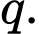 Suy ra
Suy ra 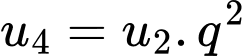
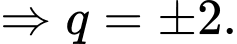 Do CSN có các số hạng không âm nên
Do CSN có các số hạng không âm nên 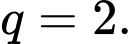
Ta có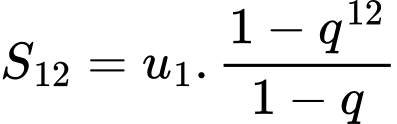
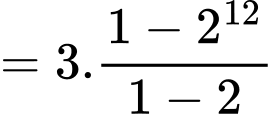
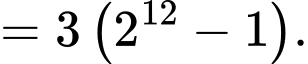 Đáp án: A
Đáp án: A
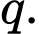 Suy ra
Suy ra 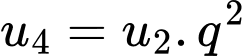
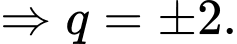 Do CSN có các số hạng không âm nên
Do CSN có các số hạng không âm nên 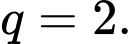
Ta có
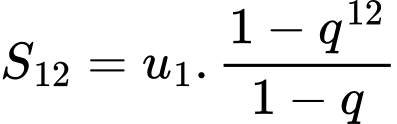
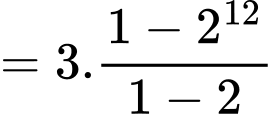
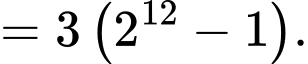 Đáp án: A
Đáp án: A
Câu 12 [519013]: Cho cấp số nhân 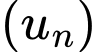 có tổng
có tổng 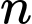 số hạng đầu tiên là:
số hạng đầu tiên là: 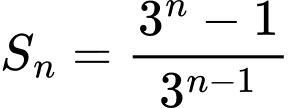 . Số hạng thứ 5 của cấp số nhân đó là
. Số hạng thứ 5 của cấp số nhân đó là
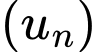 có tổng
có tổng 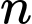 số hạng đầu tiên là:
số hạng đầu tiên là: 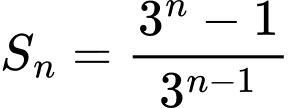 . Số hạng thứ 5 của cấp số nhân đó là
. Số hạng thứ 5 của cấp số nhân đó là A, 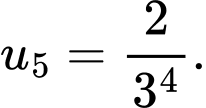
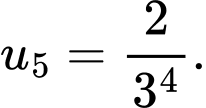
B, 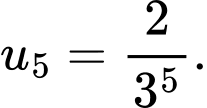
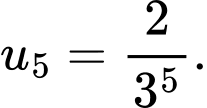
C, 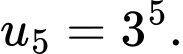
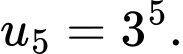
D, 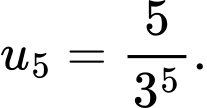
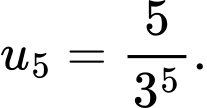
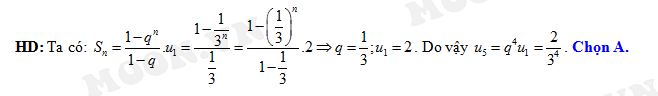 Đáp án: B
Đáp án: B
Câu 13 [806386]: Cho cấp số nhân 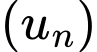 có tổng
có tổng 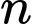 số hạng đầu tiên là
số hạng đầu tiên là 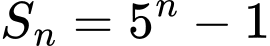 với
với 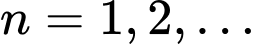 Tìm số hạng đầu
Tìm số hạng đầu 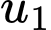 và công bội
và công bội 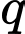 của cấp số nhân đó.
của cấp số nhân đó.
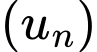 có tổng
có tổng 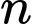 số hạng đầu tiên là
số hạng đầu tiên là 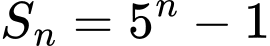 với
với 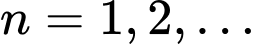 Tìm số hạng đầu
Tìm số hạng đầu 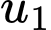 và công bội
và công bội 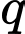 của cấp số nhân đó.
của cấp số nhân đó. A, 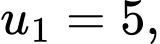
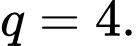
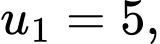
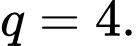
B, 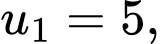
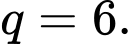
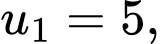
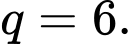
C, 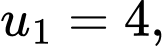
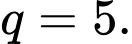
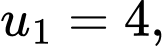
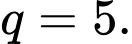
D, 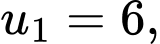
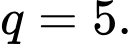
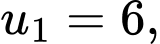
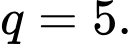
Ta có: 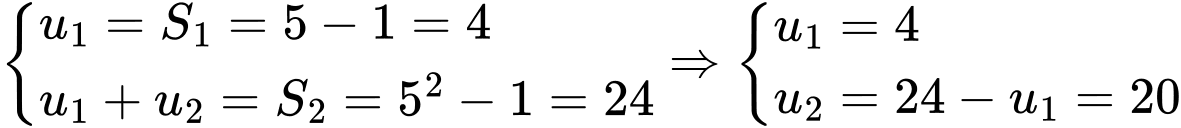
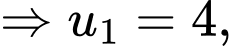
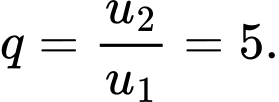 Đáp án: C
Đáp án: C
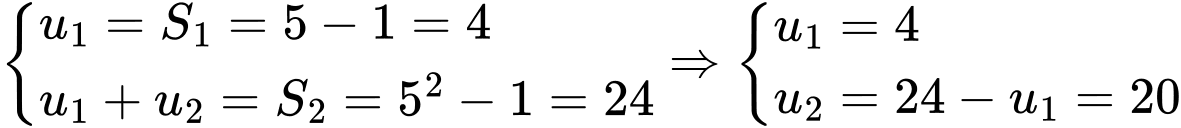
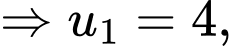
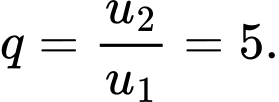 Đáp án: C
Đáp án: C
Câu 14 [806387]: Cho cấp số nhân 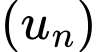 biết
biết 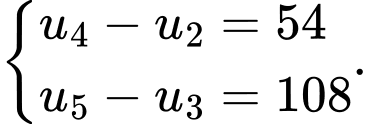 Tìm số hạng đầu
Tìm số hạng đầu 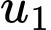 và công bội
và công bội 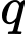 của cấp số nhân trên.
của cấp số nhân trên.
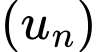 biết
biết 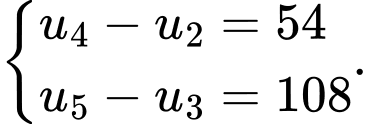 Tìm số hạng đầu
Tìm số hạng đầu 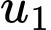 và công bội
và công bội 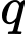 của cấp số nhân trên.
của cấp số nhân trên. A, 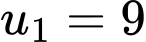 ;
; 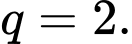
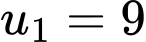 ;
; 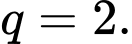
B, 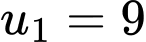 ;
; 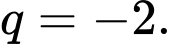
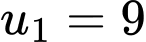 ;
; 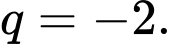
C, 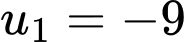 ;
; 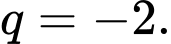
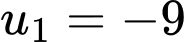 ;
; 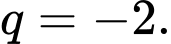
D, 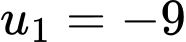 ;
; 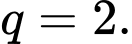
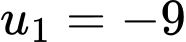 ;
; 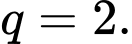
Ta có: 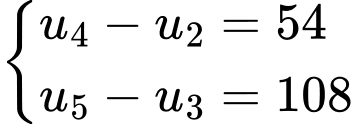
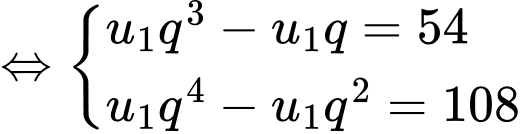
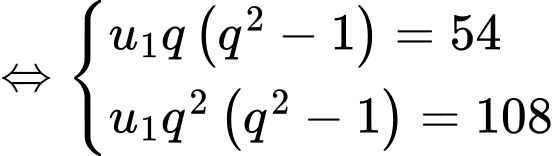
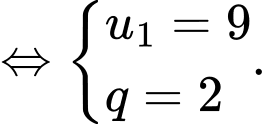
Vậy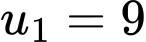 ;
; 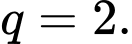 Đáp án: A
Đáp án: A
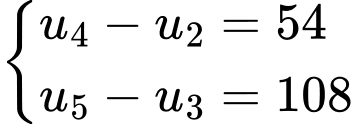
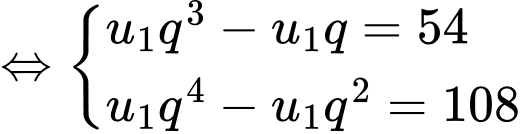
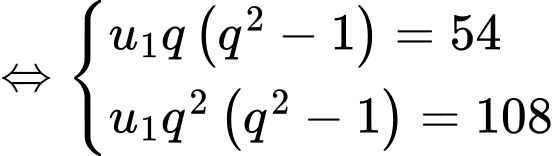
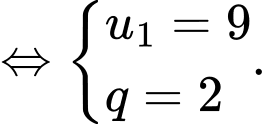
Vậy
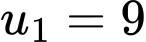 ;
; 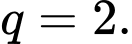 Đáp án: A
Đáp án: A
Câu 15 [806380]: Tìm số hạng đầu 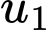 của cấp số nhân
của cấp số nhân 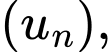 biết rằng
biết rằng 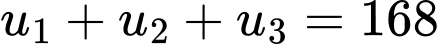 và
và 
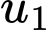 của cấp số nhân
của cấp số nhân 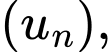 biết rằng
biết rằng 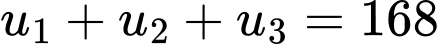 và
và 
A, 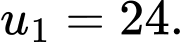
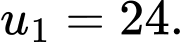
B, 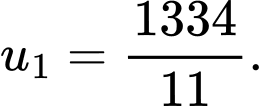
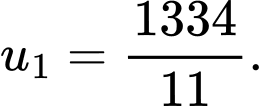
C, 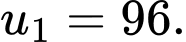
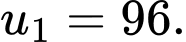
D, 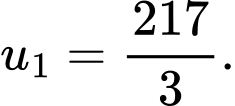
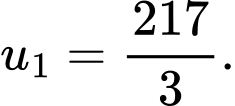
Chọn C
Ta có :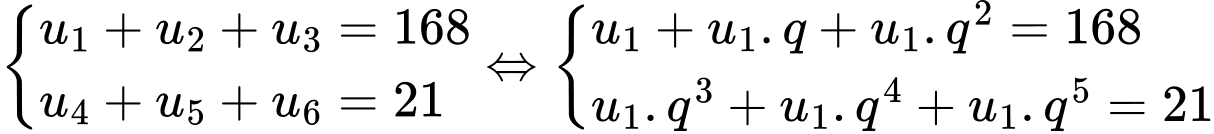
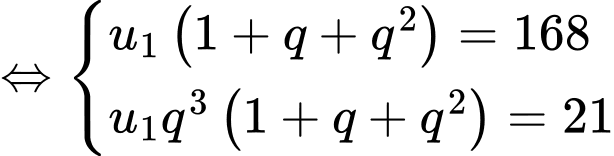
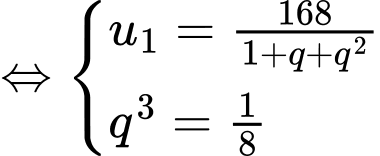
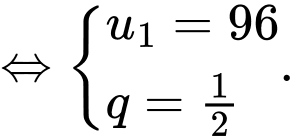
Vậy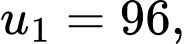 Đáp án: C
Đáp án: C
Ta có :
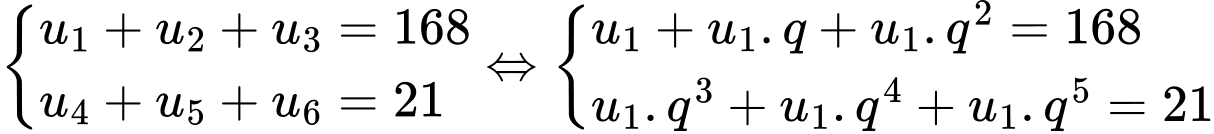
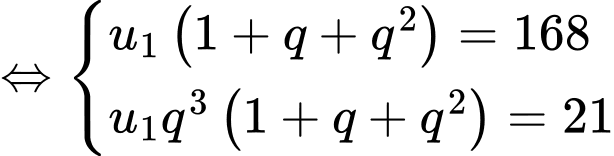
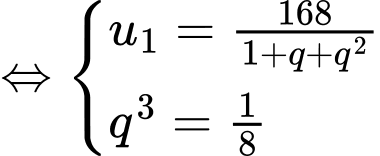
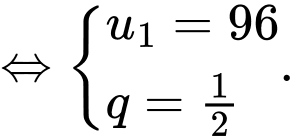
Vậy
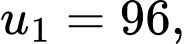 Đáp án: C
Đáp án: C
Câu 16 [806403]: Cho dãy 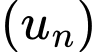 với
với 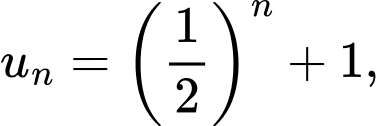
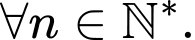 Tính
Tính 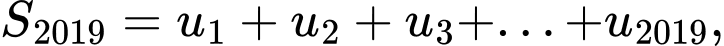 ta được kết quả
ta được kết quả
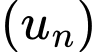 với
với 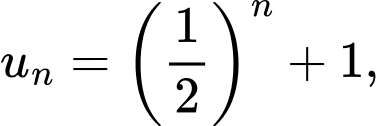
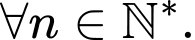 Tính
Tính 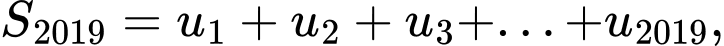 ta được kết quả
ta được kết quả A, 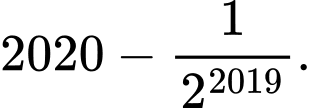
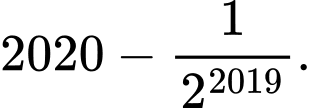
B, 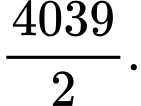
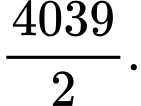
C, 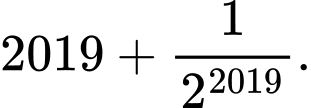
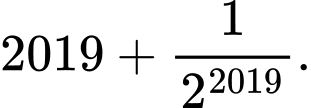
D, 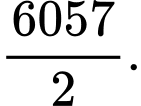
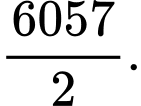
Chọn A
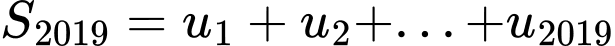
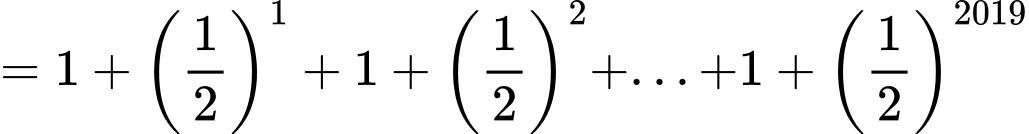
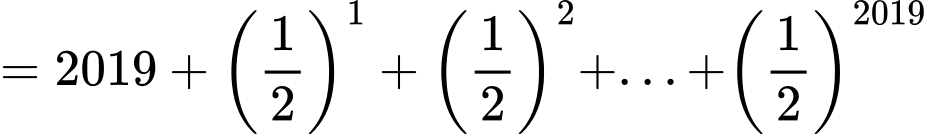
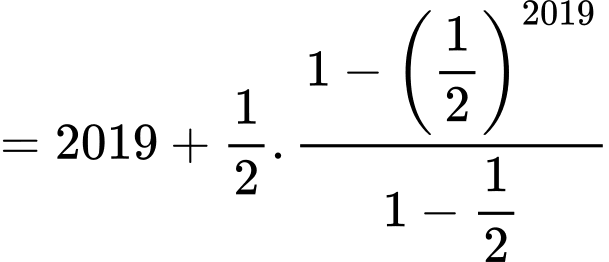
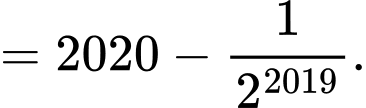
(Ta tính tổng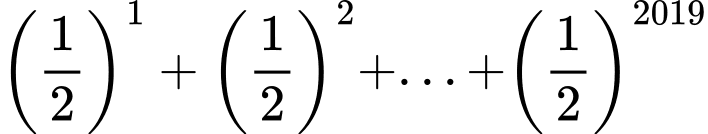 theo CT tính tổng CSN với số hạng đầu là
theo CT tính tổng CSN với số hạng đầu là 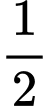 và có công bội
và có công bội 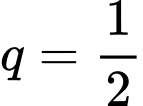 )
Đáp án: A
)
Đáp án: A
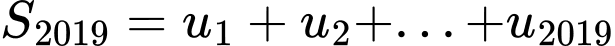
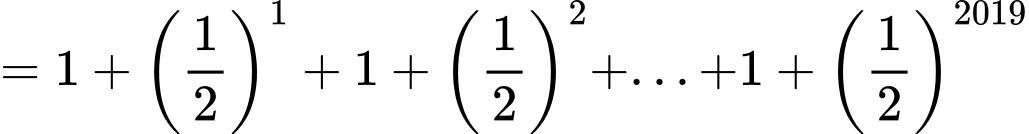
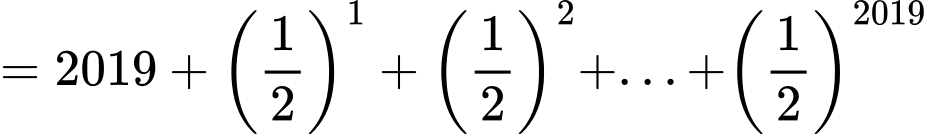
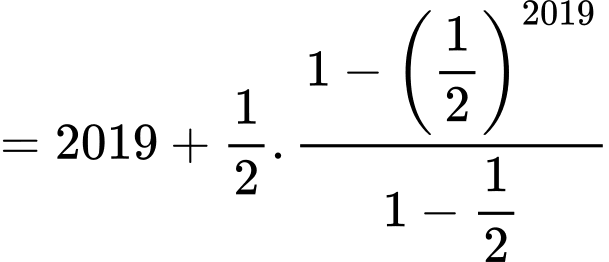
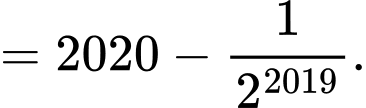
(Ta tính tổng
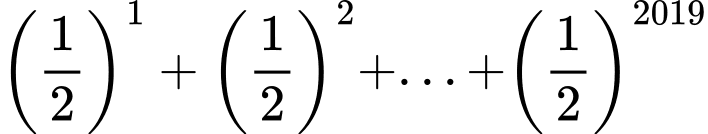 theo CT tính tổng CSN với số hạng đầu là
theo CT tính tổng CSN với số hạng đầu là 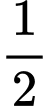 và có công bội
và có công bội 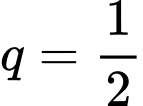 )
Đáp án: A
)
Đáp án: A
Câu 17 [806406]: Giá trị của tổng 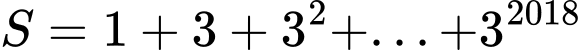 bằng
bằng
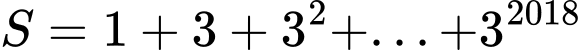 bằng
bằng A, 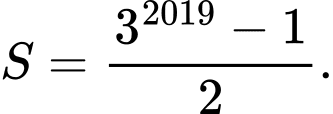
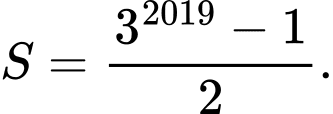
B, 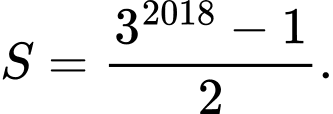
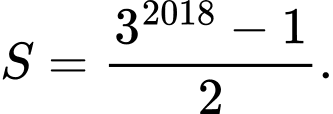
C, 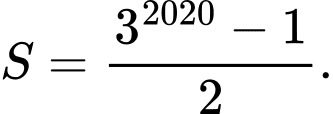
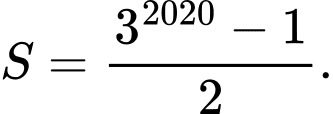
D, 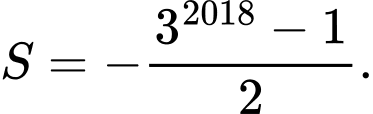
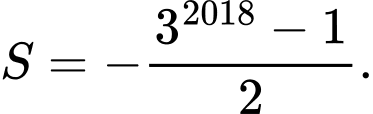
Chọn A
Ta thấy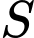 là tổng của 2019 số hạng đầu tiên của cấp số nhân với số hạng đầu là
là tổng của 2019 số hạng đầu tiên của cấp số nhân với số hạng đầu là 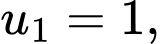 công bội
công bội 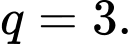
Áp dụng công thức tính tổng của cấp số nhân ta có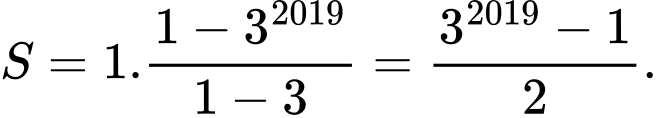 Đáp án: A
Đáp án: A
Ta thấy
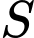 là tổng của 2019 số hạng đầu tiên của cấp số nhân với số hạng đầu là
là tổng của 2019 số hạng đầu tiên của cấp số nhân với số hạng đầu là 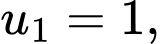 công bội
công bội 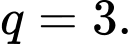
Áp dụng công thức tính tổng của cấp số nhân ta có
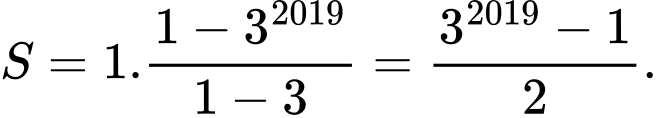 Đáp án: A
Đáp án: A
Câu 18 [806413]: Cho dãy số 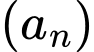 xác định bởi
xác định bởi 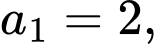
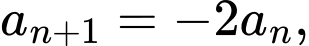
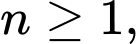
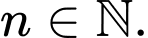 Tính tổng của 10 số hạng đầu tiên của dãy số.
Tính tổng của 10 số hạng đầu tiên của dãy số.
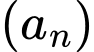 xác định bởi
xác định bởi 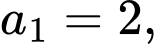
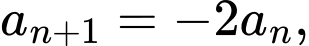
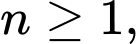
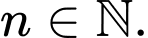 Tính tổng của 10 số hạng đầu tiên của dãy số.
Tính tổng của 10 số hạng đầu tiên của dãy số. A, 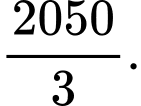
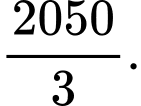
B, 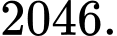
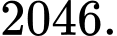
C, 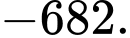
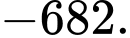
D, 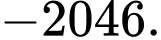
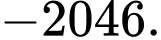
Vì 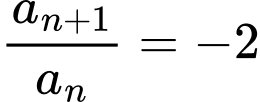 suy ra
suy ra 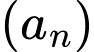 là một cấp số nhân với
là một cấp số nhân với 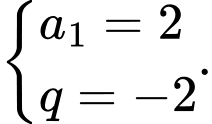
Suy ra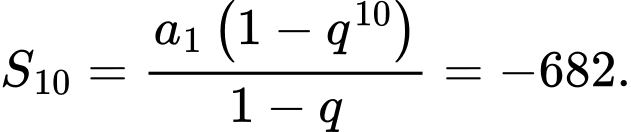 Đáp án: C
Đáp án: C
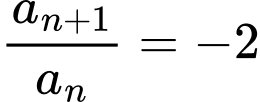 suy ra
suy ra 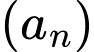 là một cấp số nhân với
là một cấp số nhân với 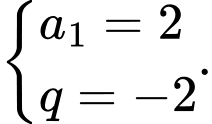
Suy ra
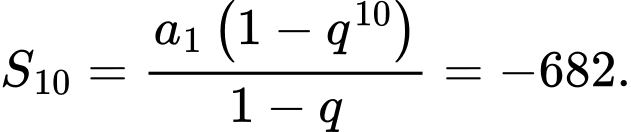 Đáp án: C
Đáp án: C
Câu 19 [806411]: Cho cấp số nhân 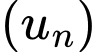 thỏa mãn
thỏa mãn 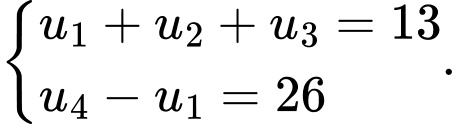 Tổng 8 số hạng đầu của cấp số nhân
Tổng 8 số hạng đầu của cấp số nhân 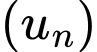 là
là
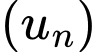 thỏa mãn
thỏa mãn 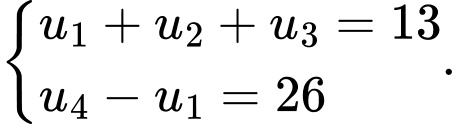 Tổng 8 số hạng đầu của cấp số nhân
Tổng 8 số hạng đầu của cấp số nhân 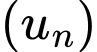 là
là A, 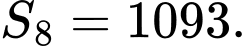
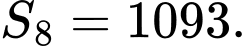
B, 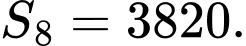
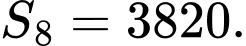
C, 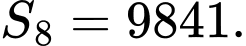
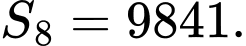
D, 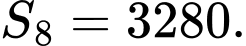
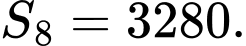
Ta có 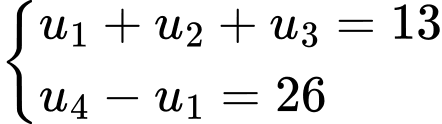
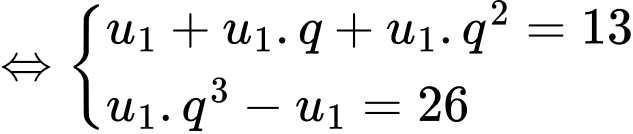
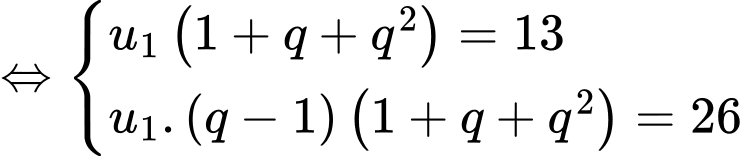
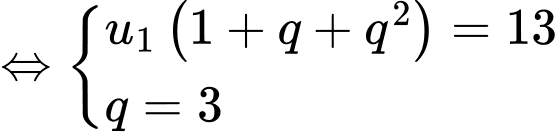
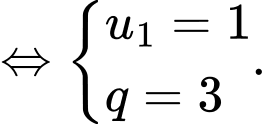
Vậy tổng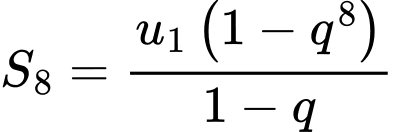
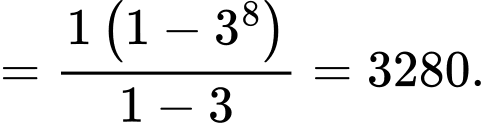 Đáp án: D
Đáp án: D
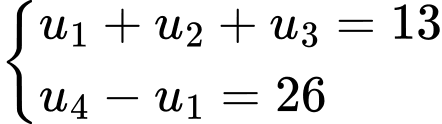
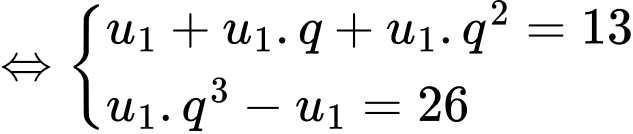
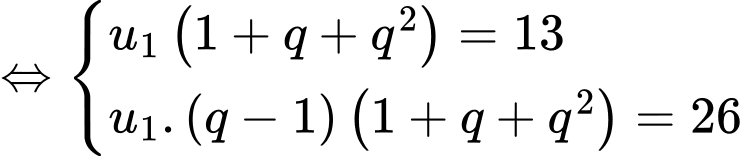
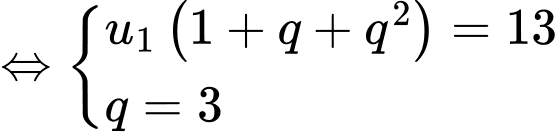
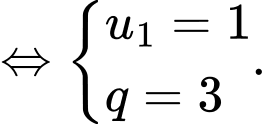
Vậy tổng
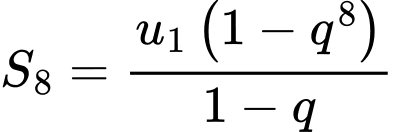
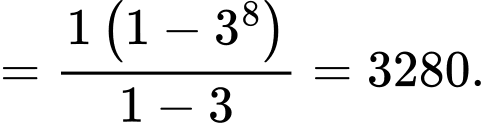 Đáp án: D
Đáp án: D
Câu 20 [690345]: Cho cấp số nhân 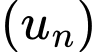 biết rằng
biết rằng 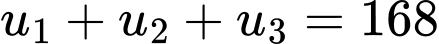 và
và  Khi đó, tổng của 10 số hạng đầu cấp số nhân là
Khi đó, tổng của 10 số hạng đầu cấp số nhân là
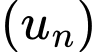 biết rằng
biết rằng 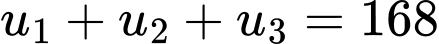 và
và  Khi đó, tổng của 10 số hạng đầu cấp số nhân là
Khi đó, tổng của 10 số hạng đầu cấp số nhân là A, 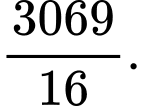
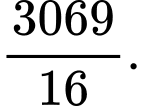
B, 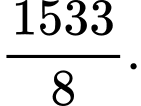
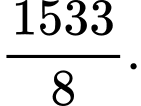
C, 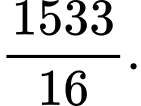
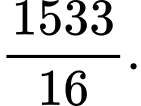
D, 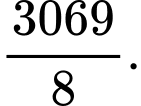
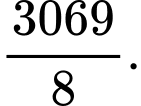
Chọn đáp án A.
Ta có: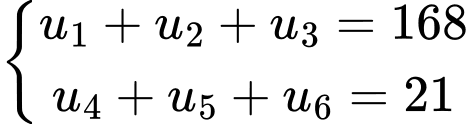
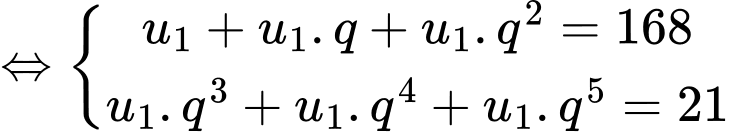
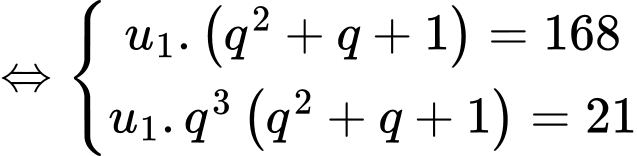
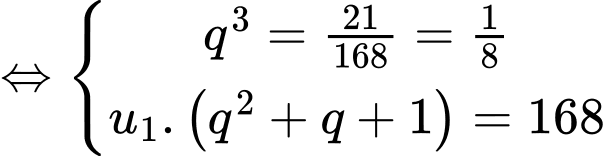
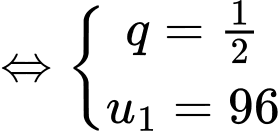
Mà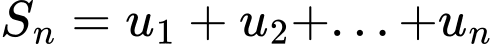
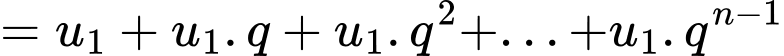
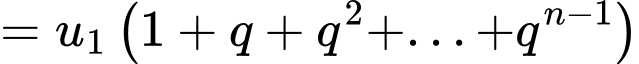
Đặt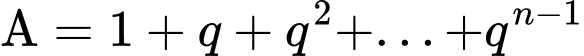
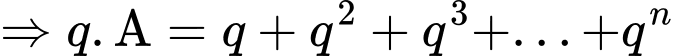
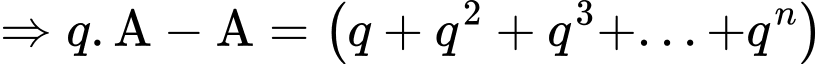
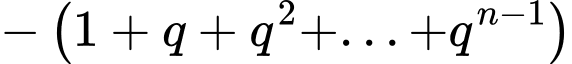
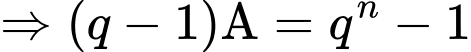
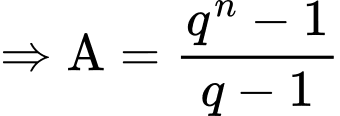
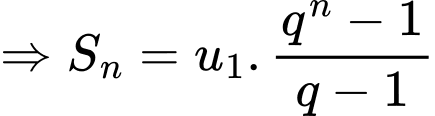
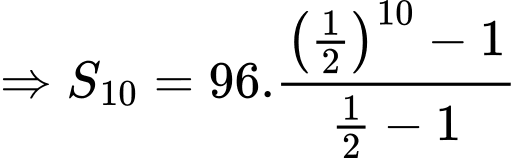
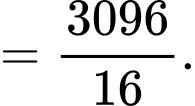 Đáp án: A
Đáp án: A
Ta có:
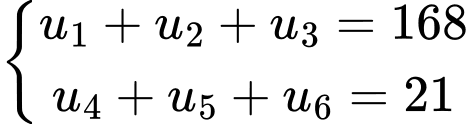
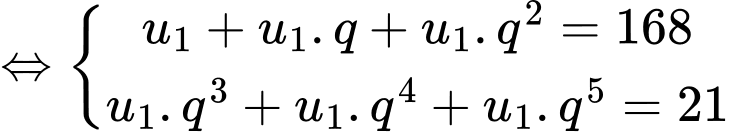
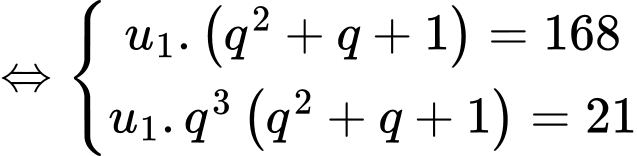
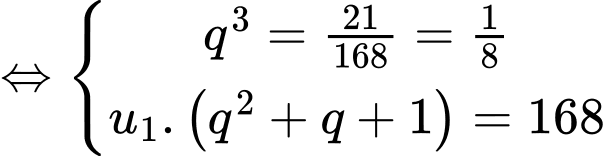
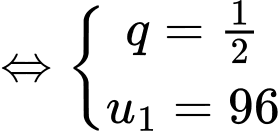
Mà
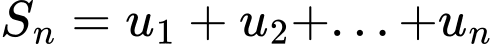
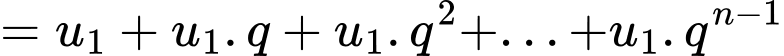
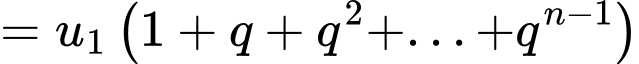
Đặt
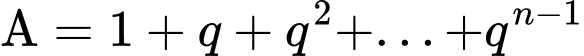
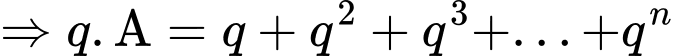
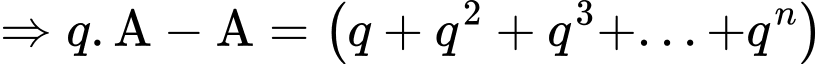
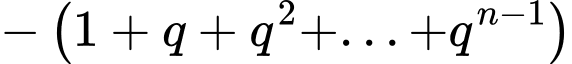
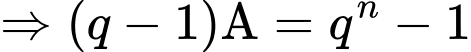
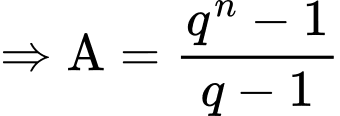
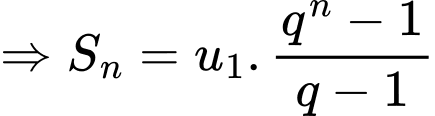
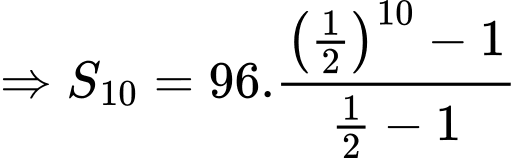
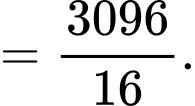 Đáp án: A
Đáp án: A
Câu 21 [806414]: Tính tổng tất cả các số hạng của một cấp số nhân có số hạng đầu là 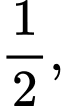 số hạng thứ tư là 32 và số hạng cuối là 2048.
số hạng thứ tư là 32 và số hạng cuối là 2048.
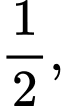 số hạng thứ tư là 32 và số hạng cuối là 2048.
số hạng thứ tư là 32 và số hạng cuối là 2048. A, 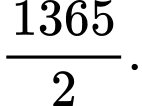
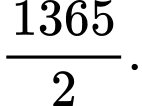
B, 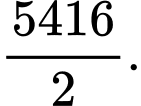
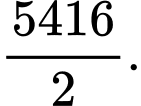
C, 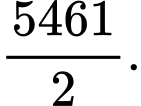
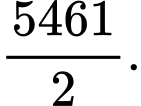
D, 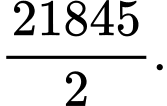
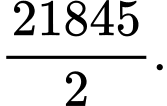
Theo bài ra ta có 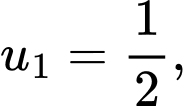
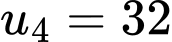 và
và 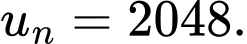
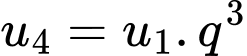
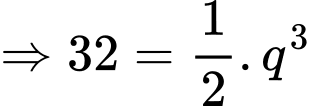
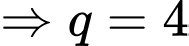
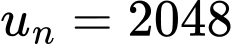
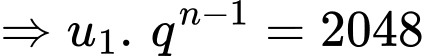
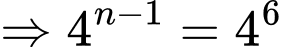
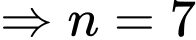
Khi đó tổng của cấp số nhân này là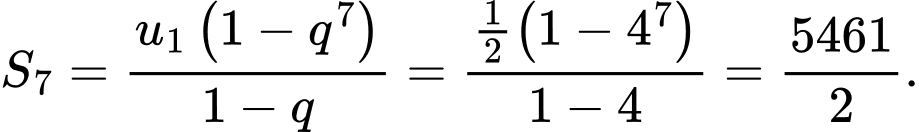 Đáp án: C
Đáp án: C
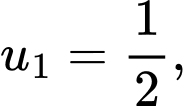
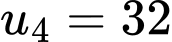 và
và 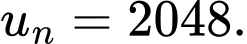
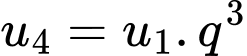
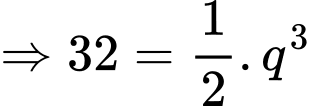
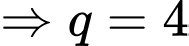
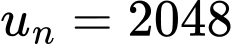
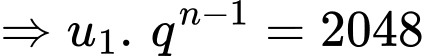
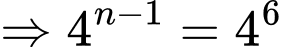
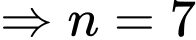
Khi đó tổng của cấp số nhân này là
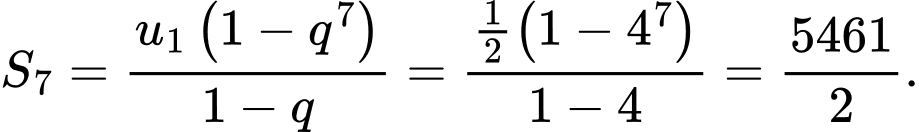 Đáp án: C
Đáp án: C
Câu 22 [806415]: Một cấp số nhân 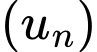 có
có 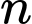 số hạng, số hạng đầu
số hạng, số hạng đầu 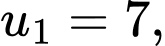 công bội
công bội 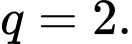 Số hạng thứ
Số hạng thứ 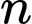 bằng 1792. Tính tổng
bằng 1792. Tính tổng 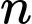 số hạng đầu tiên của cấp số nhân
số hạng đầu tiên của cấp số nhân 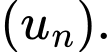
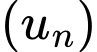 có
có 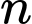 số hạng, số hạng đầu
số hạng, số hạng đầu 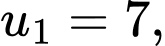 công bội
công bội 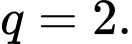 Số hạng thứ
Số hạng thứ 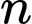 bằng 1792. Tính tổng
bằng 1792. Tính tổng 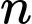 số hạng đầu tiên của cấp số nhân
số hạng đầu tiên của cấp số nhân 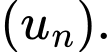
A, 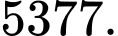
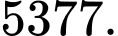
B, 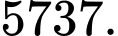
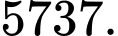
C, 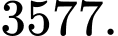
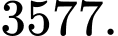
D, 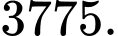
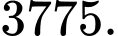
Ta có 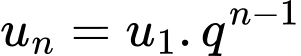
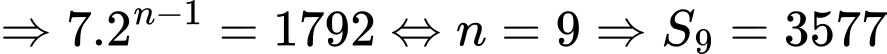
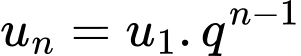
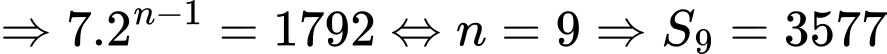
Chọn đáp án C.
Đáp án: C
Câu 23 [806437]: Ba số phân biệt có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, cũng có thể coi là số hạng thứ 2, thứ 9, thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng này để tổng của chúng bằng 820?
A, 20.
B, 42.
C, 21.
D, 17.
Gọi ba số đó là 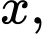
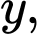
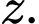
Do ba số là các số hạng thứ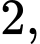 thứ
thứ 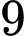 và thứ
và thứ 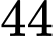 của một cấp số cộng nên ta có:
của một cấp số cộng nên ta có: 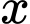 ;
; 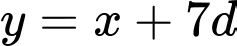 ;
; 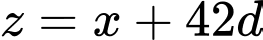 (với
(với 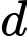 là công sai của cấp số cộng).
là công sai của cấp số cộng).
Theo giả thiết, ta có: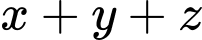
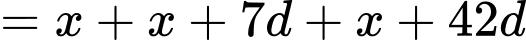
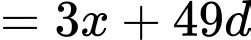
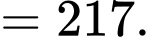
Mặt khác, do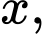
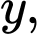
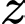 là các số hạng liên tiếp của một cấp số nhân nên:
là các số hạng liên tiếp của một cấp số nhân nên:
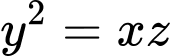
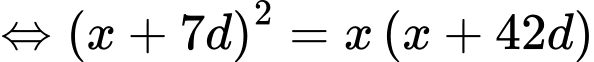
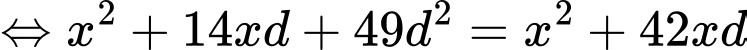
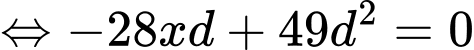
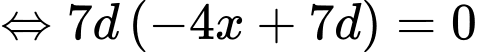
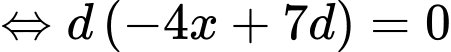
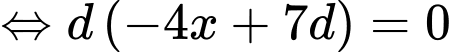
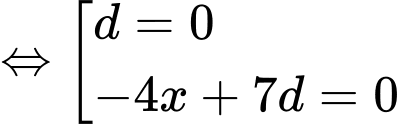
Với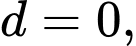 ta có:
ta có: 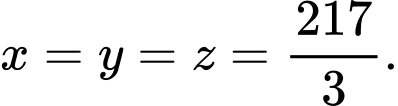 Suy ra
Suy ra 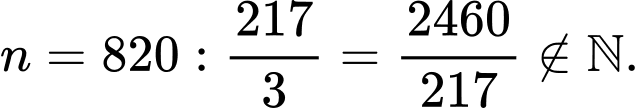
Với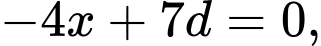 ta có:
ta có: 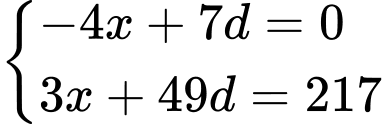
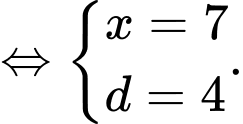 Suy ra
Suy ra 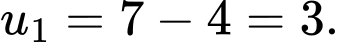
Do đó,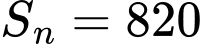
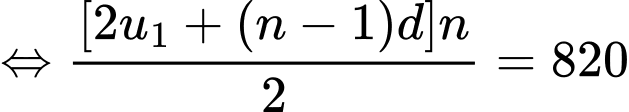
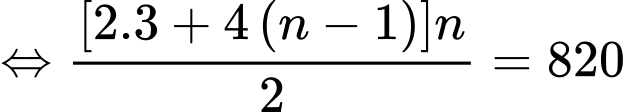
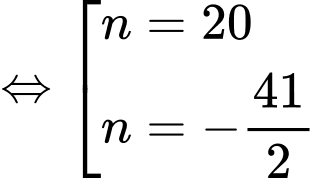
Vậy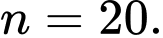 Đáp án: A
Đáp án: A
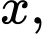
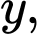
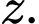
Do ba số là các số hạng thứ
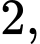 thứ
thứ 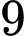 và thứ
và thứ 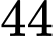 của một cấp số cộng nên ta có:
của một cấp số cộng nên ta có: 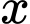 ;
; 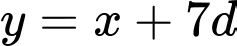 ;
; 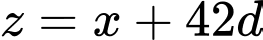 (với
(với 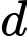 là công sai của cấp số cộng).
là công sai của cấp số cộng). Theo giả thiết, ta có:
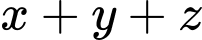
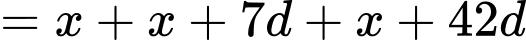
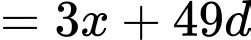
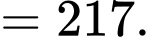
Mặt khác, do
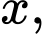
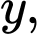
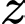 là các số hạng liên tiếp của một cấp số nhân nên:
là các số hạng liên tiếp của một cấp số nhân nên: 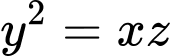
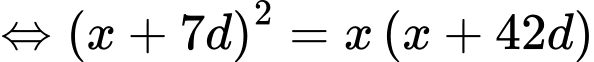
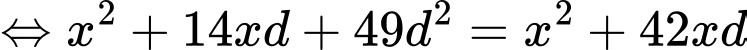
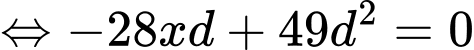
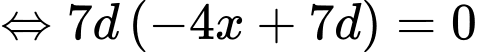
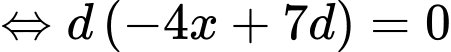
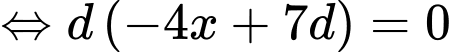
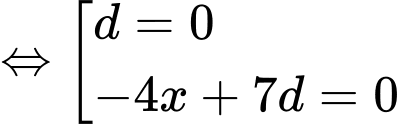
Với
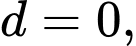 ta có:
ta có: 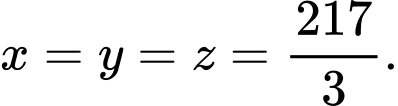 Suy ra
Suy ra 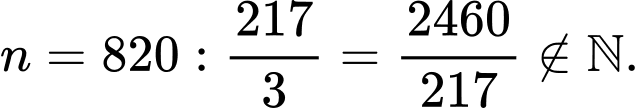
Với
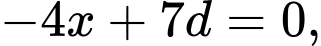 ta có:
ta có: 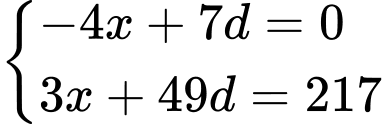
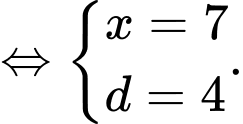 Suy ra
Suy ra 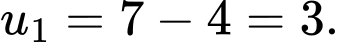
Do đó,
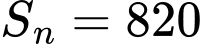
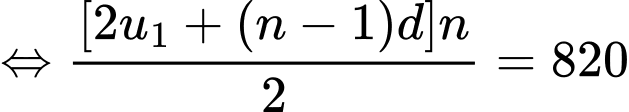
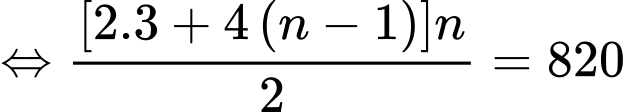
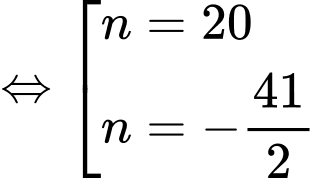
Vậy
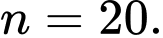 Đáp án: A
Đáp án: A
Câu 24 [735352]: Trong một cấp số nhân gồm các số hạng dương, hiệu số giữa số hạng thứ 5 và thứ 4 là 576 và hiệu số giữa số hạng thứ 2 và số hạng đầu tiên là 9. Tìm tổng 5 số hạng đầu tiên của cấp số nhân này.
A, 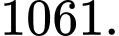
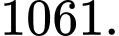
B, 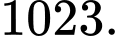
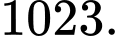
C, 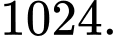
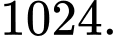
D, 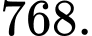
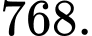
 Đáp án: B
Đáp án: B
Câu 25 [806454]: Cho năm số 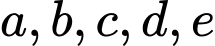 tạo thành một cấp số nhân theo thứ tự đó và các số đều khác 0, biết
tạo thành một cấp số nhân theo thứ tự đó và các số đều khác 0, biết 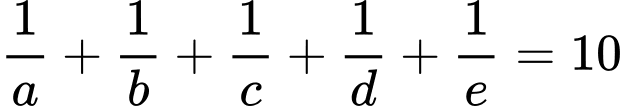 và tổng của chúng bằng 40. Tính giá trị
và tổng của chúng bằng 40. Tính giá trị  với
với 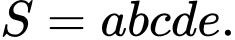
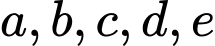 tạo thành một cấp số nhân theo thứ tự đó và các số đều khác 0, biết
tạo thành một cấp số nhân theo thứ tự đó và các số đều khác 0, biết 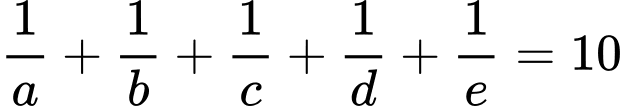 và tổng của chúng bằng 40. Tính giá trị
và tổng của chúng bằng 40. Tính giá trị  với
với 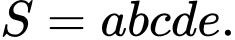
A, 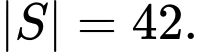
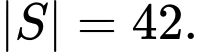
B, 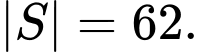
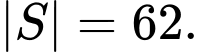
C, 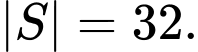
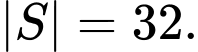
D, 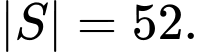
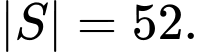
Gọi 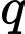
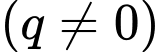 là công bội của cấp số nhân
là công bội của cấp số nhân 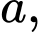
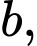
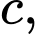
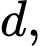
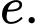 Khi đó
Khi đó 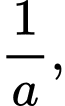
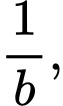
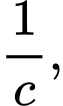
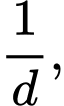
 là cấp số nhân có công bội
là cấp số nhân có công bội 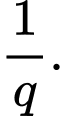
Theo đề bài ta có
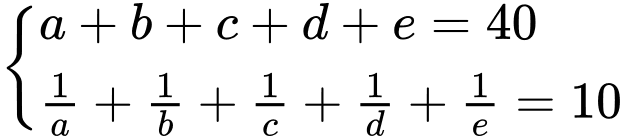
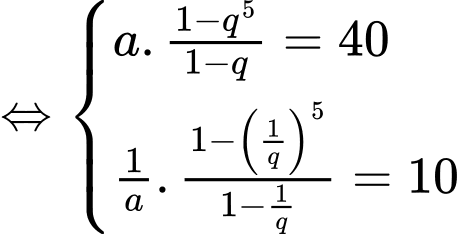
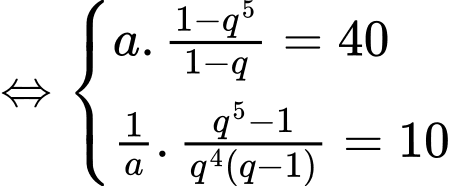
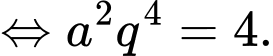
Ta có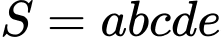
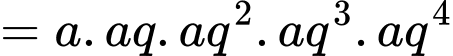
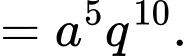
Nên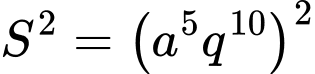
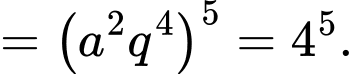
Suy ra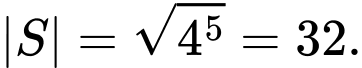 Đáp án: C
Đáp án: C
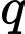
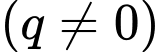 là công bội của cấp số nhân
là công bội của cấp số nhân 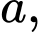
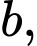
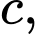
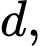
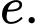 Khi đó
Khi đó 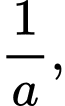
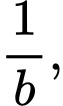
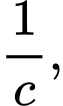
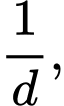
 là cấp số nhân có công bội
là cấp số nhân có công bội 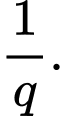
Theo đề bài ta có
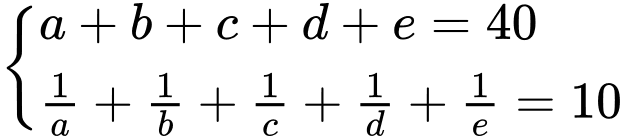
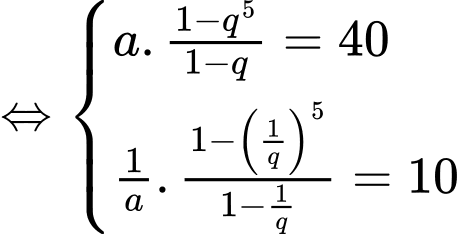
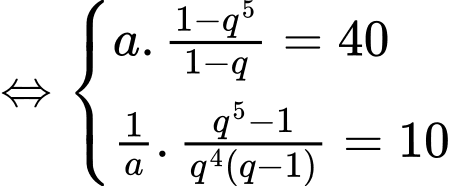
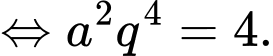
Ta có
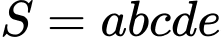
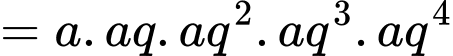
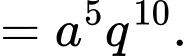
Nên
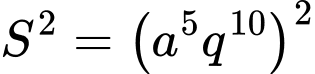
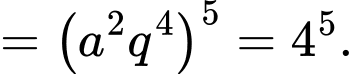
Suy ra
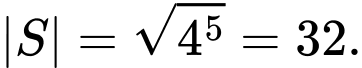 Đáp án: C
Đáp án: C
Câu 26 [804410]: Tính tổng sau 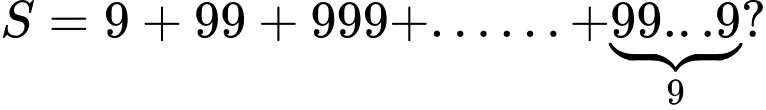
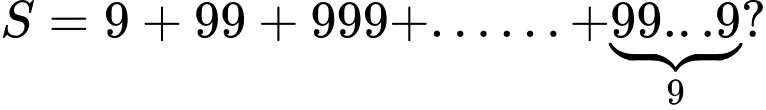
A, 

B, 

C, 

D, 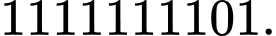
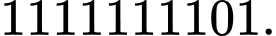
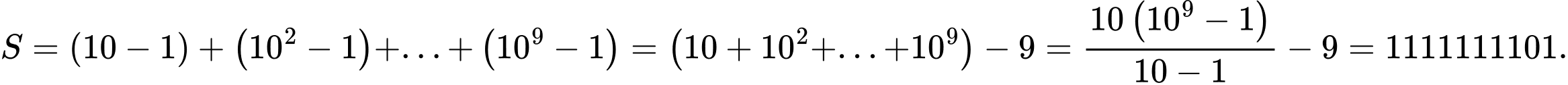 Chọn đáp án D. Đáp án: D
Chọn đáp án D. Đáp án: D
Câu 27 [806417]: Giá trị của tổng 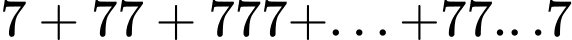 (tổng có 2018 số hạng) bằng
(tổng có 2018 số hạng) bằng
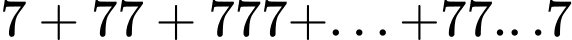 (tổng có 2018 số hạng) bằng
(tổng có 2018 số hạng) bằng A, 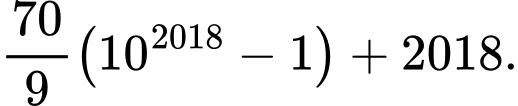
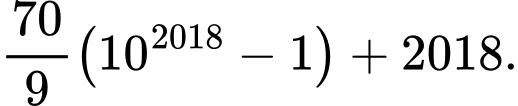
B, 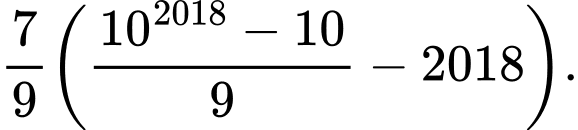
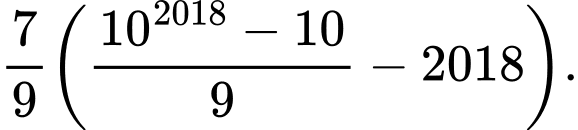
C, 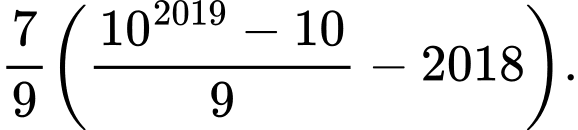
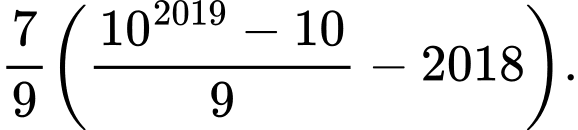
D, 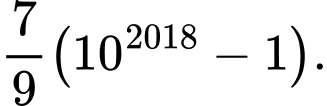
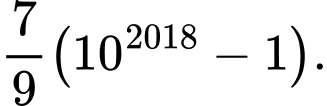
Chọn C
Ta có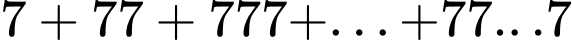
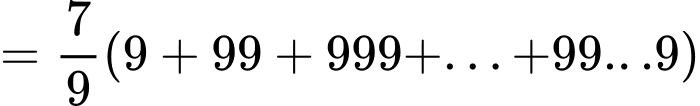
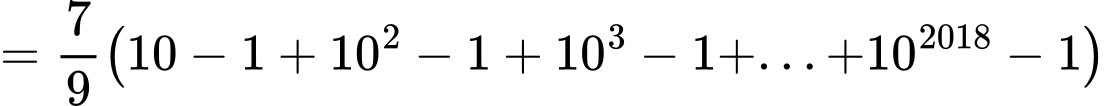
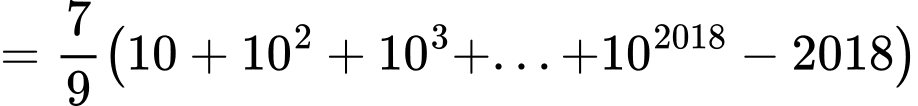
Mặt khác,ta có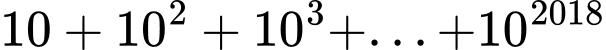 là tổng của một cấp số nhân với
là tổng của một cấp số nhân với 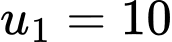 và công bội
và công bội 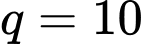
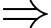
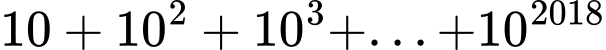
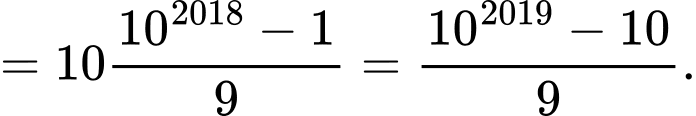
Do đó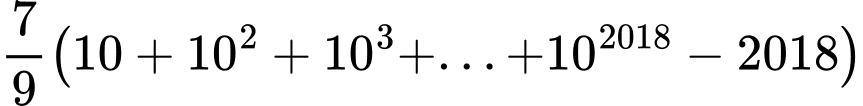
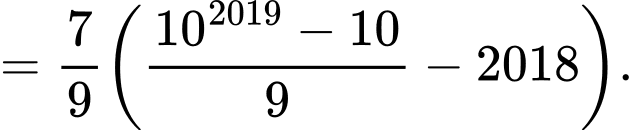 Đáp án: C
Đáp án: C
Ta có
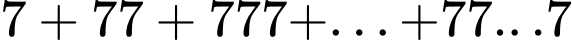
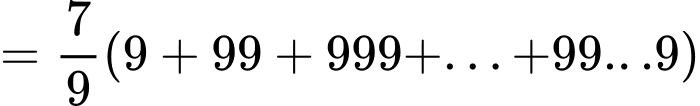
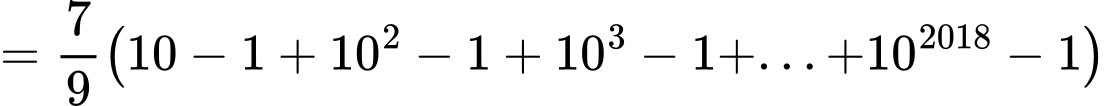
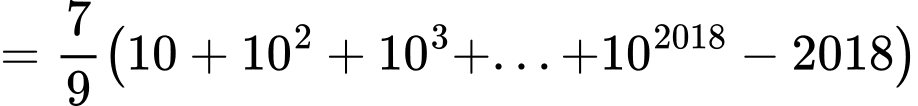
Mặt khác,ta có
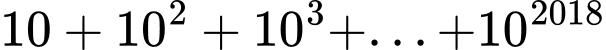 là tổng của một cấp số nhân với
là tổng của một cấp số nhân với 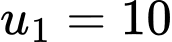 và công bội
và công bội 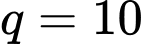
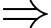
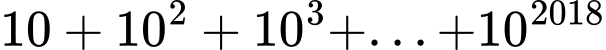
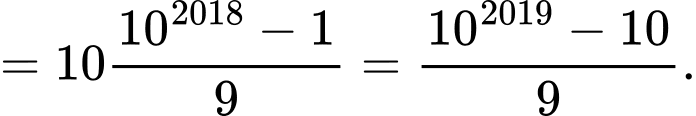
Do đó
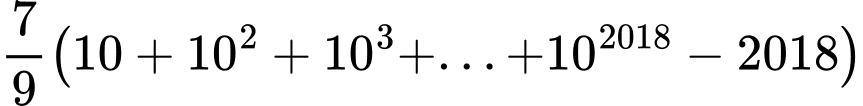
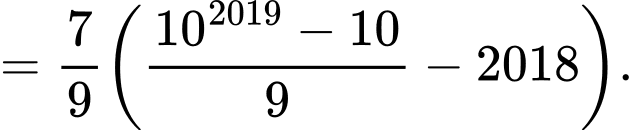
Câu 28 [806418]: Giá trị của tổng 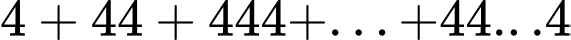 (tổng có 2018 số hạng) bằng
(tổng có 2018 số hạng) bằng
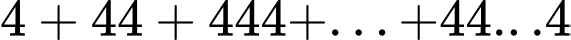 (tổng có 2018 số hạng) bằng
(tổng có 2018 số hạng) bằng A, 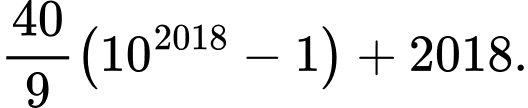
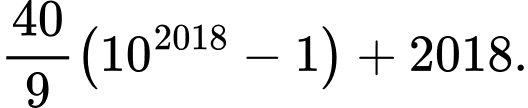
B, 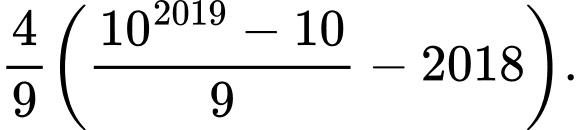
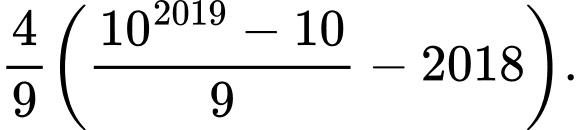
C, 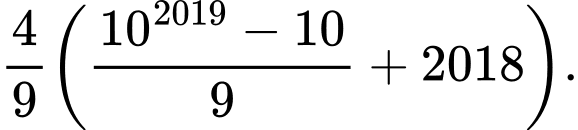
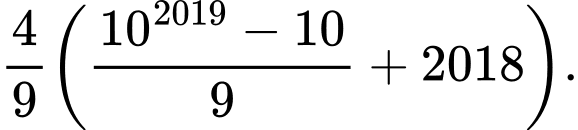
D, 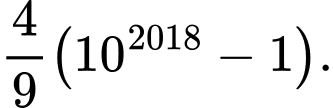
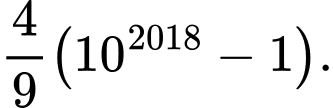
Đặt 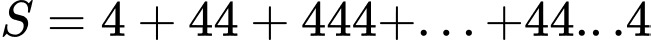 (tổng đó có
(tổng đó có  số hạng). Ta có:
số hạng). Ta có:
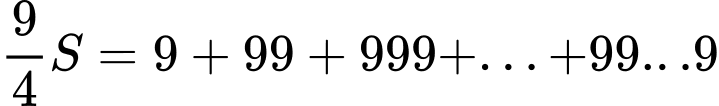
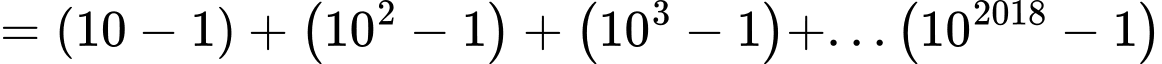
Suy ra: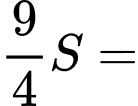
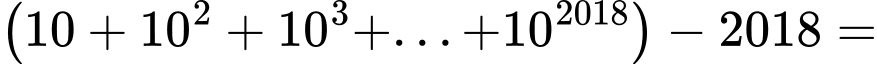
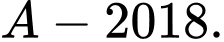
Với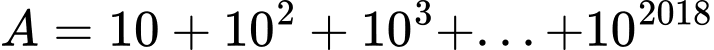 là tổng
là tổng  số hạng của một cấp số nhân có số hạng đầu
số hạng của một cấp số nhân có số hạng đầu 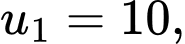 công bội
công bội 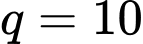 nên ta có
nên ta có 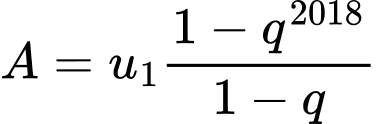
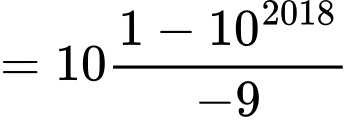
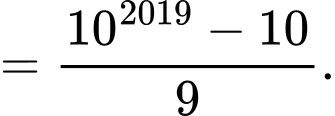
Do đó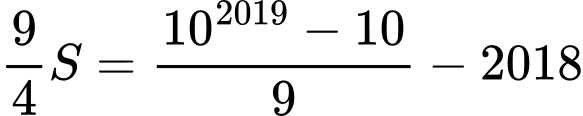
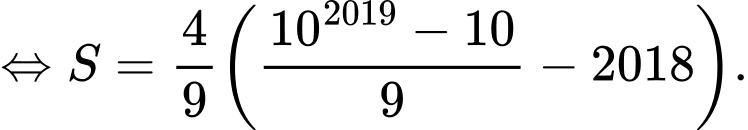 Đáp án: B
Đáp án: B
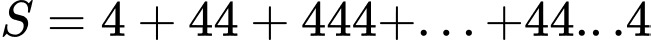 (tổng đó có
(tổng đó có  số hạng). Ta có:
số hạng). Ta có: 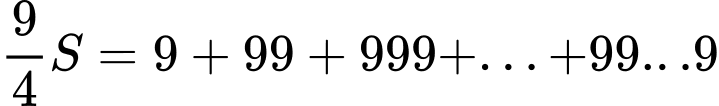
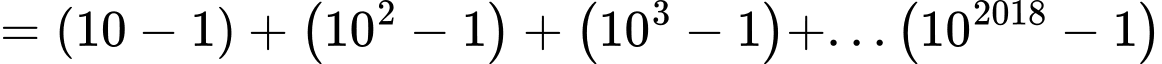
Suy ra:
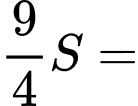
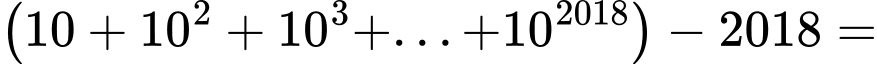
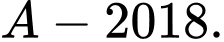
Với
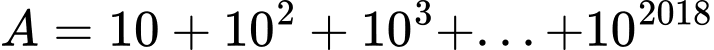 là tổng
là tổng  số hạng của một cấp số nhân có số hạng đầu
số hạng của một cấp số nhân có số hạng đầu 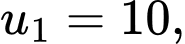 công bội
công bội 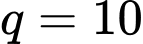 nên ta có
nên ta có 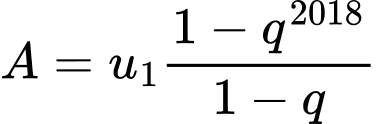
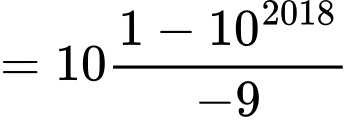
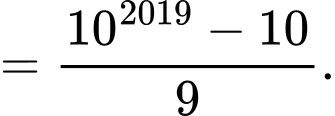
Do đó
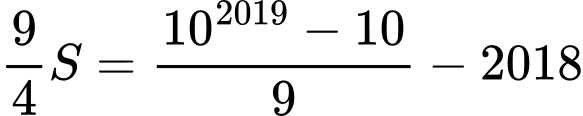
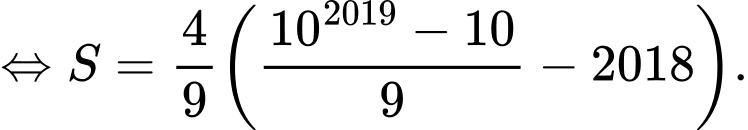
Câu 29 [806439]: Một hình vuông 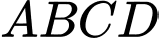 có
có 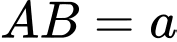 và diện tích là
và diện tích là 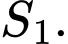 Nối 4 trung điểm
Nối 4 trung điểm 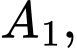
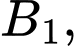
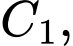
 theo thứ tự của 4 cạnh
theo thứ tự của 4 cạnh 
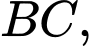
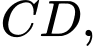
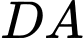 ta được hình vuông thứ hai là
ta được hình vuông thứ hai là 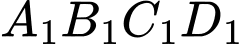 có diện tích
có diện tích 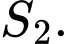 Tiếp tục như thế ta được hình vuông thứ ba
Tiếp tục như thế ta được hình vuông thứ ba 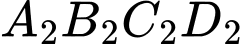 có diện tích
có diện tích 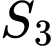 và cứ tiếp tục như thế, ta được diện tích
và cứ tiếp tục như thế, ta được diện tích 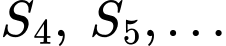 Tính
Tính 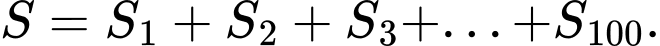
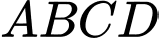 có
có 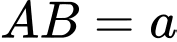 và diện tích là
và diện tích là 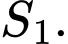 Nối 4 trung điểm
Nối 4 trung điểm 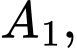
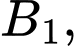
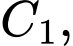
 theo thứ tự của 4 cạnh
theo thứ tự của 4 cạnh 
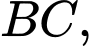
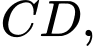
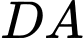 ta được hình vuông thứ hai là
ta được hình vuông thứ hai là 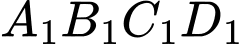 có diện tích
có diện tích 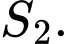 Tiếp tục như thế ta được hình vuông thứ ba
Tiếp tục như thế ta được hình vuông thứ ba 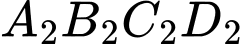 có diện tích
có diện tích 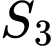 và cứ tiếp tục như thế, ta được diện tích
và cứ tiếp tục như thế, ta được diện tích 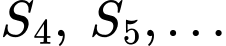 Tính
Tính 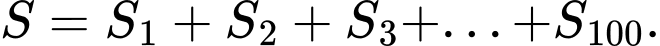
A, 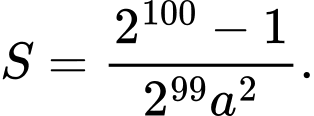
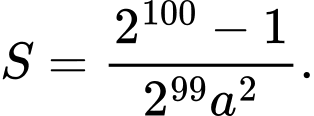
B, 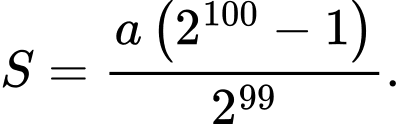
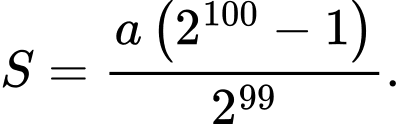
C, 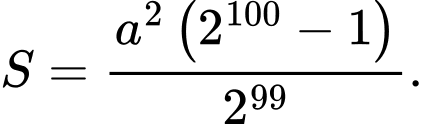
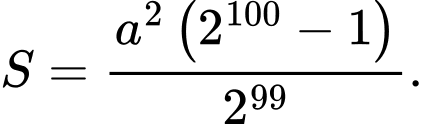
D, 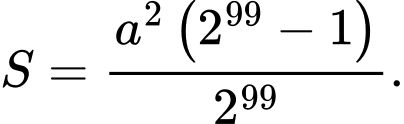
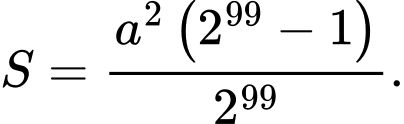
Dễ thấy: 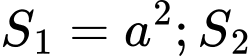
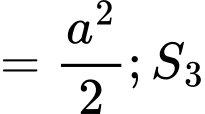
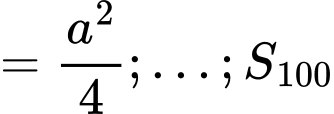
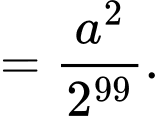
Như vậy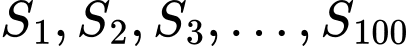 là cấp số nhân với công bội
là cấp số nhân với công bội 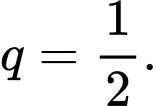
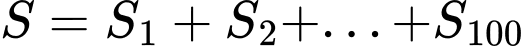
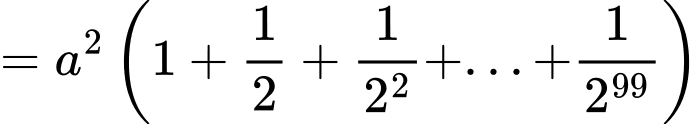
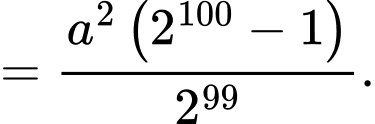 Đáp án: C
Đáp án: C
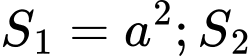
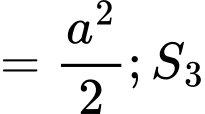
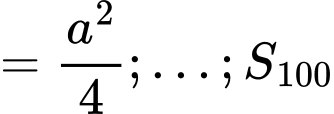
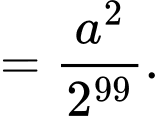
Như vậy
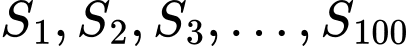 là cấp số nhân với công bội
là cấp số nhân với công bội 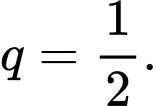
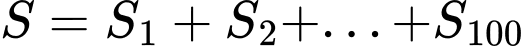
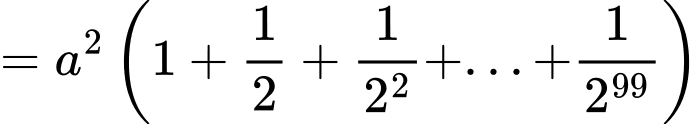
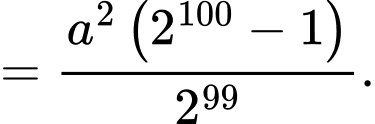 Đáp án: C
Đáp án: C
Câu 30 [806446]: Cho 4 số 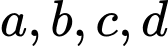 theo thứ tự đó tạo thành cấp số nhân với công bội khác 1. Biết tổng 3 số hạng đầu bằng
theo thứ tự đó tạo thành cấp số nhân với công bội khác 1. Biết tổng 3 số hạng đầu bằng 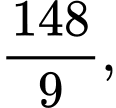 đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng. Tính giá trị biểu thức
đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng. Tính giá trị biểu thức 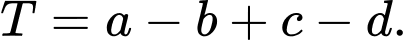
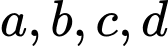 theo thứ tự đó tạo thành cấp số nhân với công bội khác 1. Biết tổng 3 số hạng đầu bằng
theo thứ tự đó tạo thành cấp số nhân với công bội khác 1. Biết tổng 3 số hạng đầu bằng 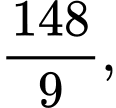 đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng. Tính giá trị biểu thức
đồng thời theo thứ tự đó chúng lần lượt là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng. Tính giá trị biểu thức 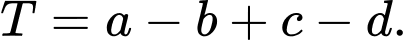
A, 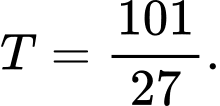
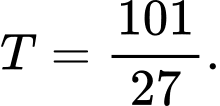
B, 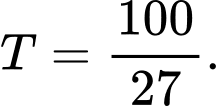
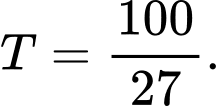
C, 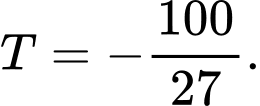
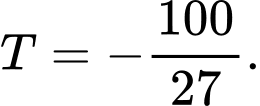
D, 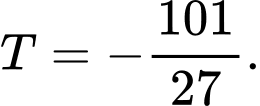
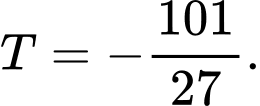
Ta có 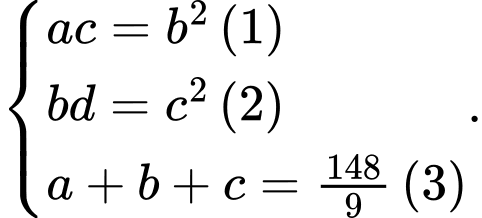
Và cấp số cộng có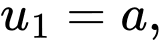
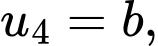
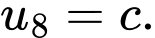 Gọi
Gọi 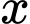 là công sai của cấp số cộng. Vì cấp số nhân có công bội khác
là công sai của cấp số cộng. Vì cấp số nhân có công bội khác 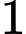 nên
nên 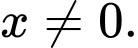
Ta có :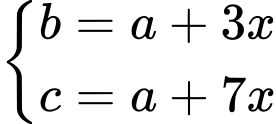
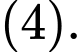
Từ và
và 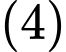 ta được :
ta được : 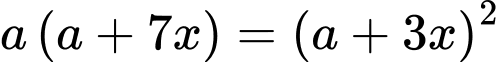
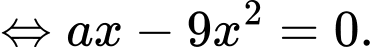
Do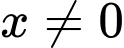 nên
nên 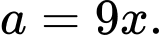
Từ và
và 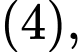 suy ra
suy ra 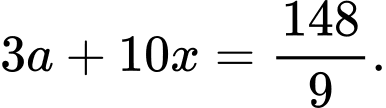
Do đó :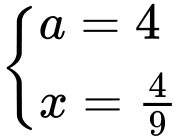
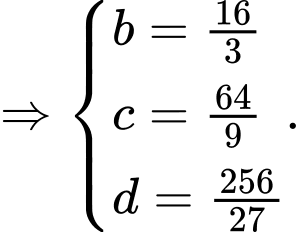
Vậy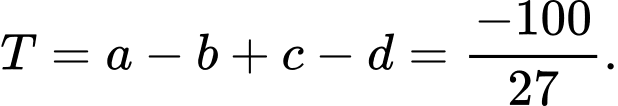 Đáp án: C
Đáp án: C
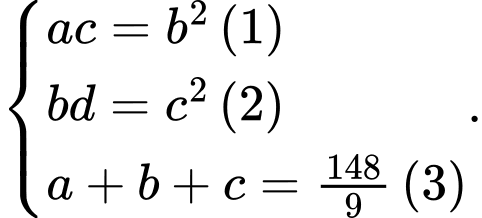
Và cấp số cộng có
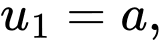
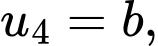
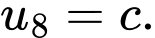 Gọi
Gọi 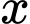 là công sai của cấp số cộng. Vì cấp số nhân có công bội khác
là công sai của cấp số cộng. Vì cấp số nhân có công bội khác 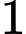 nên
nên 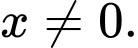
Ta có :
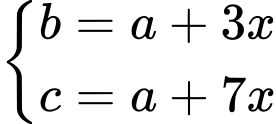
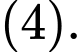
Từ
 và
và 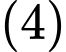 ta được :
ta được : 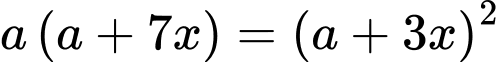
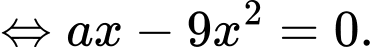
Do
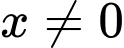 nên
nên 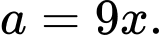
Từ
 và
và 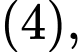 suy ra
suy ra 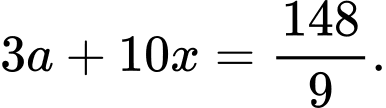
Do đó :
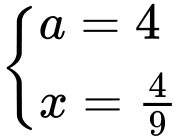
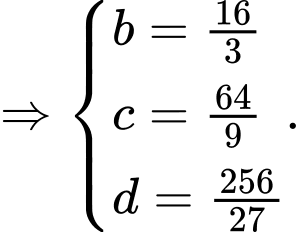
Vậy
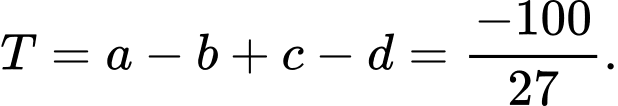 Đáp án: C
Đáp án: C