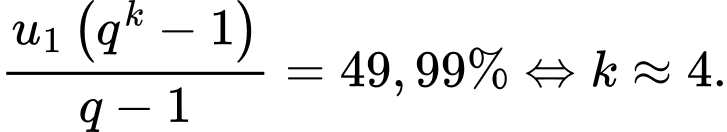Câu 1 [690364]: Cho tứ giác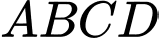 
có 4 góc tạo thành cấp số nhân có công bội 
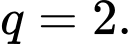Góc có số đo nhỏ nhất trong 4 góc đó là bao nhiêu độ?
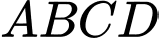có 4 góc tạo thành cấp số nhân có công bội 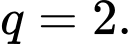Góc có số đo nhỏ nhất trong 4 góc đó là bao nhiêu độ?
Điền đáp án: 24.
Đặt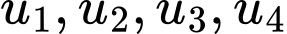
theo thứ tự là số đo bốn góc của tứ giác ABCD , gọi d là công bội của cấp số nhân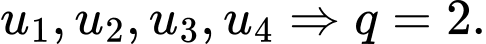 
Ta có: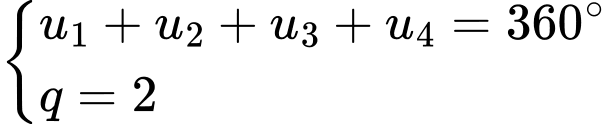
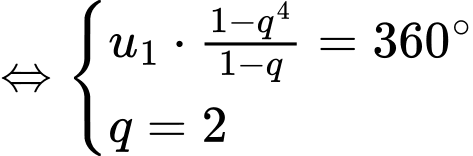
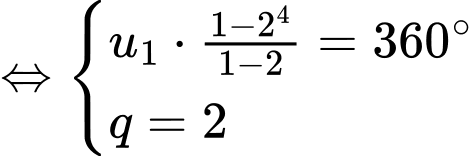
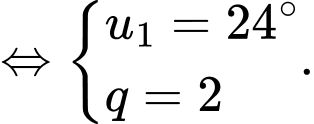
Góc có số đo nhỏ nhất của tứ giác ABCD là: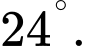
Đặt
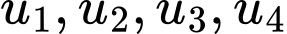theo thứ tự là số đo bốn góc của tứ giác ABCD , gọi d là công bội của cấp số nhân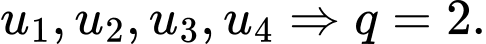 Ta có:
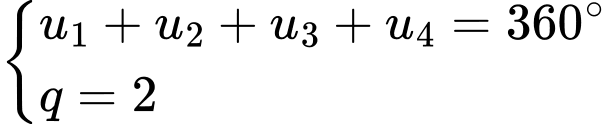
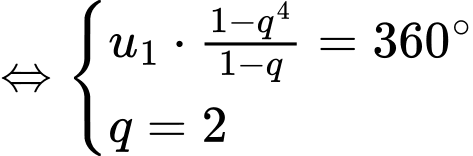
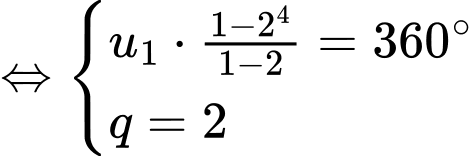
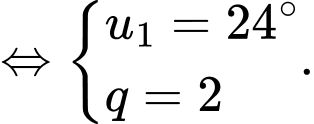
Góc có số đo nhỏ nhất của tứ giác ABCD là:
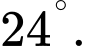
Câu 2 [690365]: Viết thêm 4 số vào giữa hai số 160 và 5 để được một cấp số nhân. Tổng các số hạng của cấp số nhân đó là
Điền đáp án: 315.
Gọi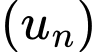
là cấp số nhân lập được và 
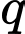là công bội của cấp số nhân đó.
Cấp số nhân cần lập có dạng: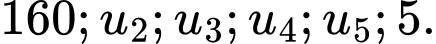
Ta có: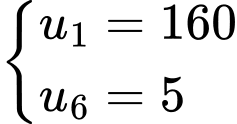
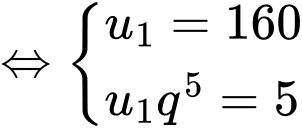
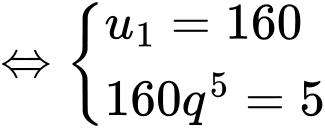
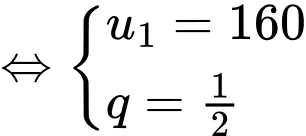
Tổng các số hạng của cấp số nhân là:
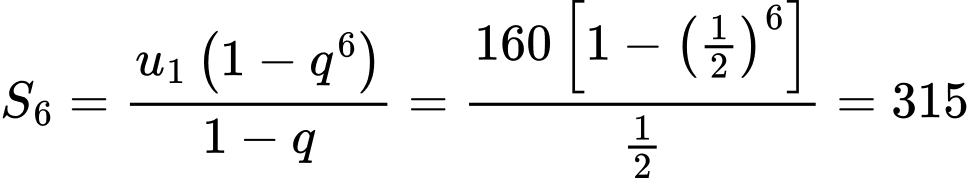
Gọi
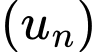là cấp số nhân lập được và 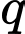là công bội của cấp số nhân đó.Cấp số nhân cần lập có dạng:
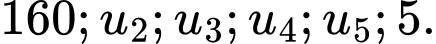
Ta có:
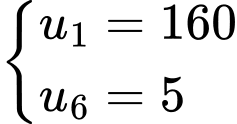
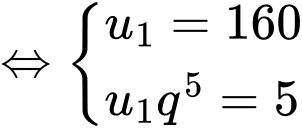
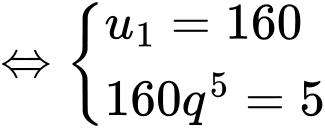
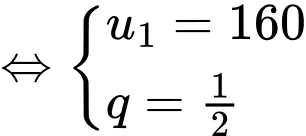
Tổng các số hạng của cấp số nhân là:
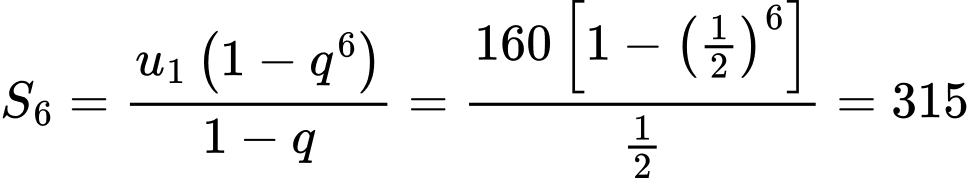
Câu 3 [690366]: Cho một cấp số nhân có số hạng thứ 4 gấp 4096 lần số hạng đầu tiên. Tổng hai số hạng đầu tiên là 34. Số hạng thứ 3 của dãy số có giá trị bằng
Điền đáp án 512.
Theo bài ra ta có: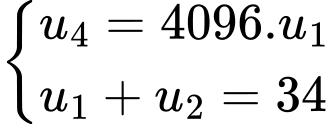
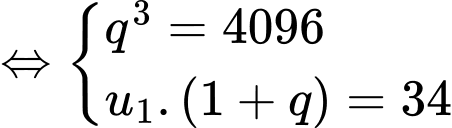
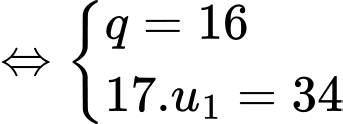
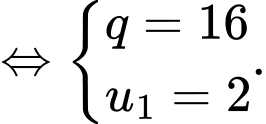
Vậy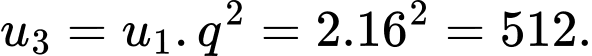
Theo bài ra ta có:
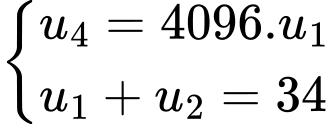
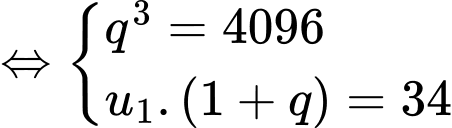
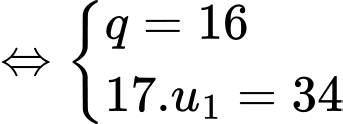
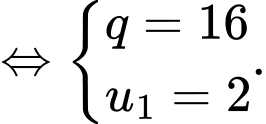
Vậy
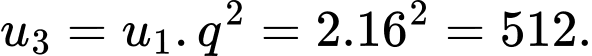
Câu 4 [690367]: Viết thêm 7 số vào giữa 3 và 768 để được một cấp số nhân có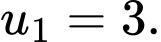 
Khi đó 
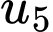bằng
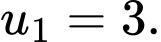Khi đó 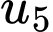bằng
Điền đáp án: 48.
Giả sử viết thêm 7 số nữa vào giữa số 3 và 768 ta được dãy cấp số nhân là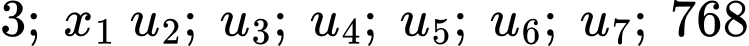
Khi đó số hạng 768 của dãy là số hạng thứ 9 tức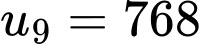
Áp dụng công thức số hạng tổng quát của 1 cấp số nhân: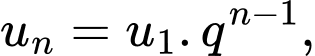
ta có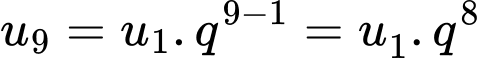 
Vì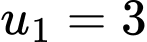
theo giả thiết, nên suy ra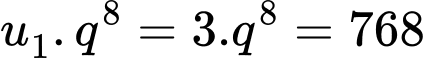 
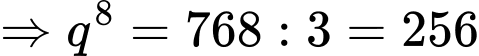
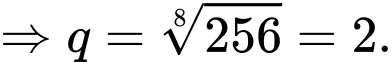
Vậy cấp số nhân tạo thành có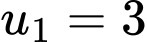
và công bội 
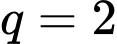suy ra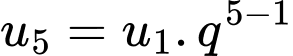 
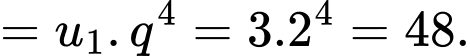
Giả sử viết thêm 7 số nữa vào giữa số 3 và 768 ta được dãy cấp số nhân là
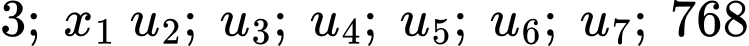
Khi đó số hạng 768 của dãy là số hạng thứ 9 tức
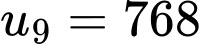
Áp dụng công thức số hạng tổng quát của 1 cấp số nhân:
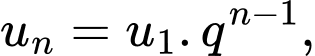ta có 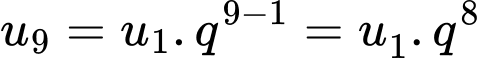Vì
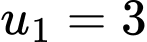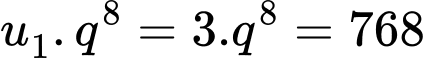
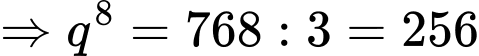
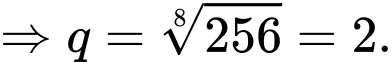
theo giả thiết, nên suy ra Vậy cấp số nhân tạo thành có
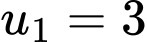và công bội 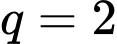suy ra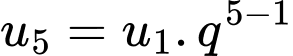
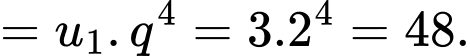
Câu 5 [690368]: Một cấp số nhân có số hạng đầu bằng 5 và công bội bằng 2. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của dãy cấp số nhân này để có tổng bằng 5115?
Điền đáp án: 10.
Dựa vào giả thiết: cấp số nhân có số hạng đầu bằng 5 và công bội bằng 2 suy ra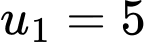
và 
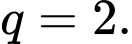
Ta có công thức tổng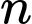
số hạng đầu của cấp số nhân là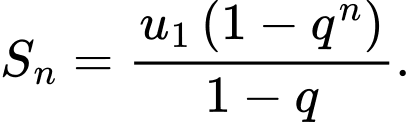 
Để tổng của các số hạng đầu này bằng 5115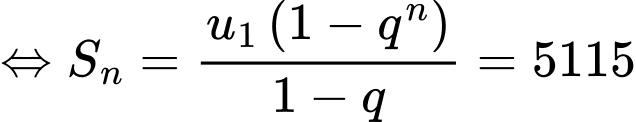
Thay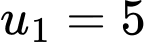
và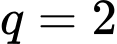 
vào phương trình trên, ta được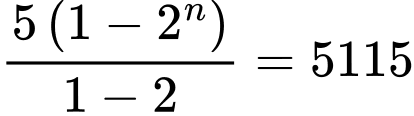 
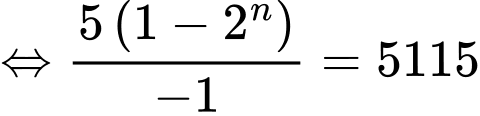
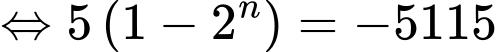
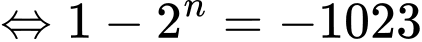
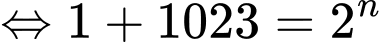
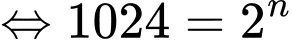
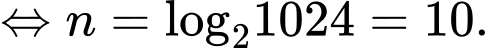
Vậy phải lấy tổng của 10 số hạng đầu của dãy cấp số nhân này để có tổng bằng 5115.
Dựa vào giả thiết: cấp số nhân có số hạng đầu bằng 5 và công bội bằng 2 suy ra
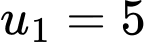và
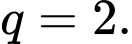
Ta có công thức tổng
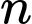số hạng đầu của cấp số nhân là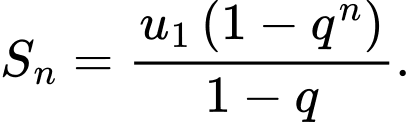
Để tổng của các số hạng đầu này bằng 5115
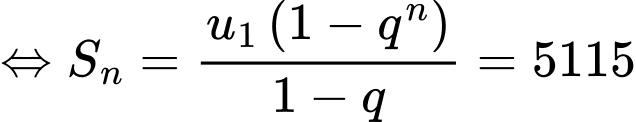
Thay
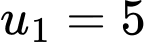và 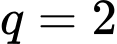vào phương trình trên, ta được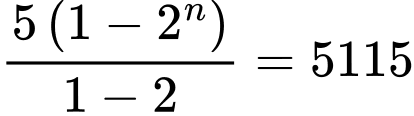
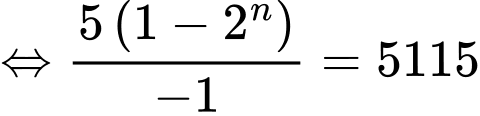
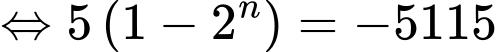
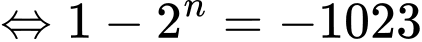
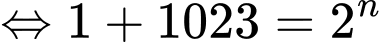
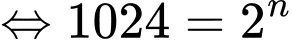
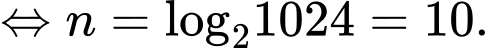
Vậy phải lấy tổng của 10 số hạng đầu của dãy cấp số nhân này để có tổng bằng 5115.
Câu 6 [690369]: Trên một bàn cờ vua kích thước 
người ta đặt số hạt thóc theo cách như sau: Ô thứ nhất đặt một hạt thóc, ô thứ hai đặt hai hạt thóc, các ô tiếp theo đặt số hạt thóc gấp đôi ô đứng liền kề trước nó. Hỏi phải tối thiểu từ ô thứ bao nhiêu thì tổng số hạt thóc từ ô đầu tiên đến ô đó lớn hơn 20 172 018 hạt thóc?
người ta đặt số hạt thóc theo cách như sau: Ô thứ nhất đặt một hạt thóc, ô thứ hai đặt hai hạt thóc, các ô tiếp theo đặt số hạt thóc gấp đôi ô đứng liền kề trước nó. Hỏi phải tối thiểu từ ô thứ bao nhiêu thì tổng số hạt thóc từ ô đầu tiên đến ô đó lớn hơn 20 172 018 hạt thóc?
Điền đáp án: 25.
Gọi ô chứa hạt thóc thỏa mãn đề bài là ô thứ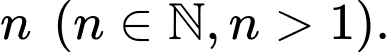
Vì ô đầu tiên đặt 1 hạt thóc và các ô sau đó lại đặt số hạt thóc gấp đôi ô đứng liền kề trước nó tức ta được dãy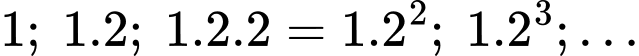
Suy ra dãy tạo thành là một cấp số nhân với số hạng đầu tiên là 
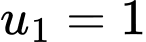và công bội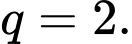 
Áp dụng công thức tổng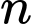
số hạng đầu của cấp số nhân là
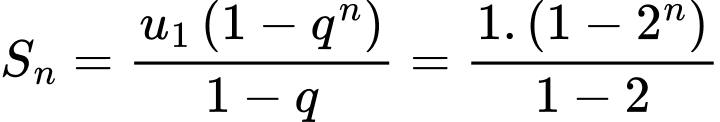
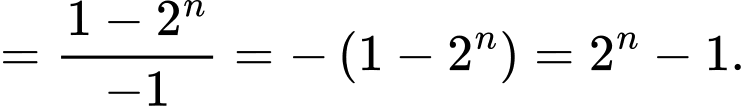
Khi đó yêu cầu bài toán tương đương với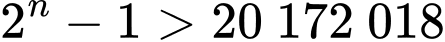
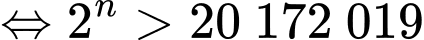
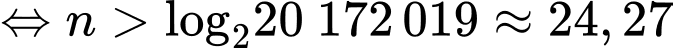
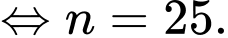
Vậy phải tối thiểu từ ô thứ 25 thì tổng số hạt thóc từ ô đầu tiên đến ô đó lớn hơn 20 172 018 hạt thóc.
Gọi ô chứa hạt thóc thỏa mãn đề bài là ô thứ
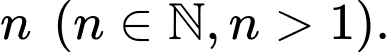
Vì ô đầu tiên đặt 1 hạt thóc và các ô sau đó lại đặt số hạt thóc gấp đôi ô đứng liền kề trước nó tức ta được dãy
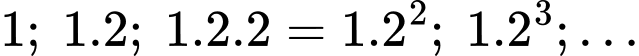Suy ra dãy tạo thành là một cấp số nhân với số hạng đầu tiên là 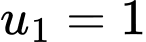và công bội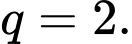
Áp dụng công thức tổng
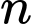số hạng đầu của cấp số nhân là
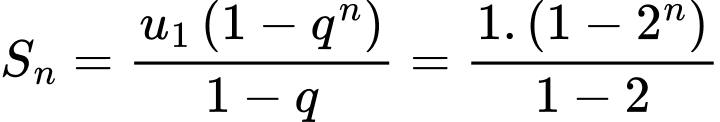
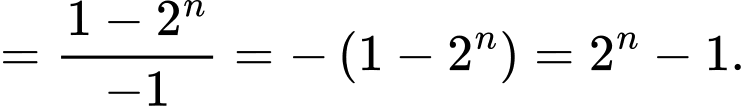
Khi đó yêu cầu bài toán tương đương với
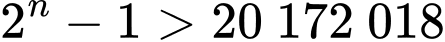
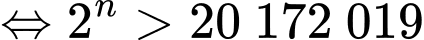
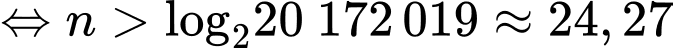
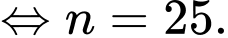
Vậy phải tối thiểu từ ô thứ 25 thì tổng số hạt thóc từ ô đầu tiên đến ô đó lớn hơn 20 172 018 hạt thóc.
Câu 7 [690370]: Một công ty xây dựng mua một chiếc máy ủi với giá 3 tỉ đồng. Cứ sau mỗi năm sử dụng, giá trị của chiếc máy ủi này lại giảm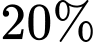 
so với giá trị của nó trong năm liền trước đó. Giá trị còn lại của chiếc máy ủi đó sau 5 năm sử dụng là bao nhiêu tỉ đồng? (Kết quả làm tròn hàng phần trăm).
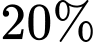so với giá trị của nó trong năm liền trước đó. Giá trị còn lại của chiếc máy ủi đó sau 5 năm sử dụng là bao nhiêu tỉ đồng? (Kết quả làm tròn hàng phần trăm).
Điền đáp án: 0,98.
Cứ sau mỗi năm sử dụng, giá trị của chiếc máy ủi giảm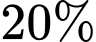
so với giá trị của nó trong năm liền trước đó, tức là giá trị của chiếc máy ủi năm sau thì bằng 
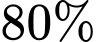giá trị của chiếc máy ủi so với năm liền trước đó.
Giá trị của chiếc máy úi sau 1 năm sử dụng là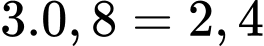
(tỉ đồng).
Giá trị của chiếc máy ủi sau mỗi năm sử dụng lập thành một cấp số nhân với số hạng đầu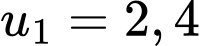
và công bội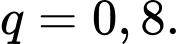 
Áp dụng công thức số hạng tổng quát của cấp số nhân là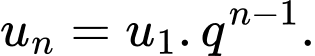
Suy ra giá trị còn lại của chiếc máy ủi sau 5 năm sử dụng là
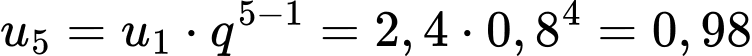(tỉ đồng)
Cứ sau mỗi năm sử dụng, giá trị của chiếc máy ủi giảm
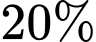so với giá trị của nó trong năm liền trước đó, tức là giá trị của chiếc máy ủi năm sau thì bằng 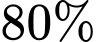giá trị của chiếc máy ủi so với năm liền trước đó.
Giá trị của chiếc máy úi sau 1 năm sử dụng là
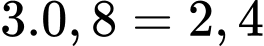(tỉ đồng).
Giá trị của chiếc máy ủi sau mỗi năm sử dụng lập thành một cấp số nhân với số hạng đầu
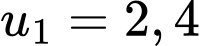và công bội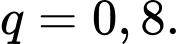
Áp dụng công thức số hạng tổng quát của cấp số nhân là
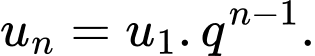Suy ra giá trị còn lại của chiếc máy ủi sau 5 năm sử dụng là
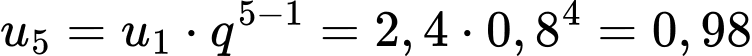(tỉ đồng)
Câu 8 [690371]: Một loại vi khuẩn được nuôi cấy trong phòng thí nghiệm, cứ mỗi phút số lượng lại tăng lên gấp đôi số lượng đang có. Từ một vi khuẩn ban đầu, hãy tính tổng số vi khuẩn có trong ống nghiệm sau 10 phút.
Điền đáp án: 1048575.
Số lượng vi khuẩn sau mỗi phút lập thành một cấp số nhân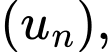
với số hạng đầu 
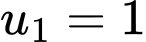(vì ban đầu nuôi cấy từ 1 vi khuẩn) và công bội 
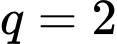(vì cứ mỗi phút số lượng vi khuẩn lại tăng gấp đôi số lượng đang có).
Áp dụng công thức tổng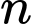
số hạng đầu của cấp số nhân là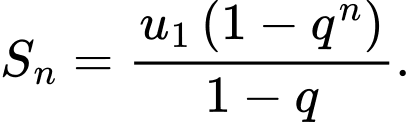 
Ta suy ra sau 20 phút (tức tại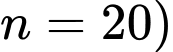
tổng số lượng vi khuẩn trong ống nghiệm là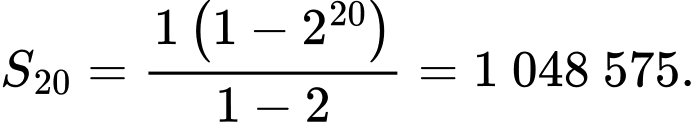
Số lượng vi khuẩn sau mỗi phút lập thành một cấp số nhân
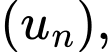với số hạng đầu 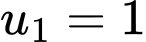(vì ban đầu nuôi cấy từ 1 vi khuẩn) và công bội 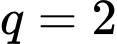(vì cứ mỗi phút số lượng vi khuẩn lại tăng gấp đôi số lượng đang có).
Áp dụng công thức tổng
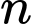số hạng đầu của cấp số nhân là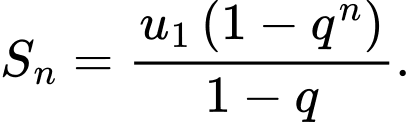
Ta suy ra sau 20 phút (tức tại
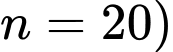tổng số lượng vi khuẩn trong ống nghiệm là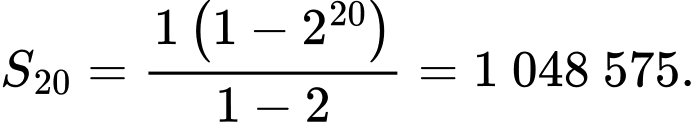
Câu 9 [690372]: Người ta thiết kế một cái tháp 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích của bề mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là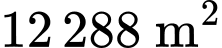 
). Diện tích mặt trên cùng là bao nhiêu mét vuông?
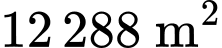). Diện tích mặt trên cùng là bao nhiêu mét vuông?
Điền đáp án: 6.
Diện tích bề mặt của mỗi tầng (kể từ tầng 1) lập thành một cấp số nhân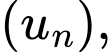
có công bội
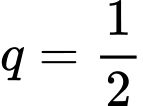và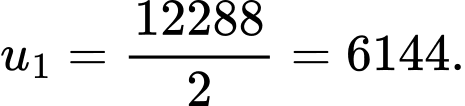 
Khi đó diện tích mặt trên cùng là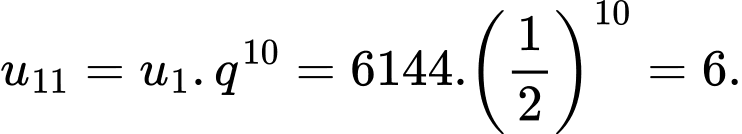
Diện tích bề mặt của mỗi tầng (kể từ tầng 1) lập thành một cấp số nhân
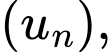có công bội
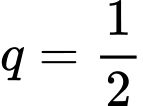và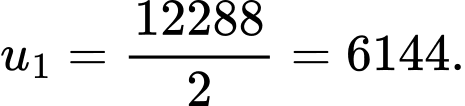
Khi đó diện tích mặt trên cùng là
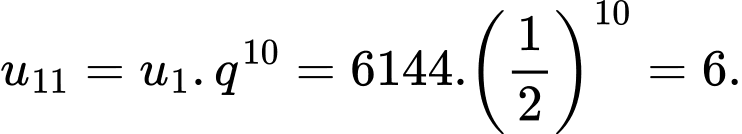
Câu 10 [690373]: E.coli (Escherichia coli) là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau 20 phút thì số lượng vi khuẩn E.coli lại tăng gấp đôi. Ban đầu, chỉ có 60 vi khuẩn E.coli trong đường ruột. Hỏi sau 2 giờ, số lượng vi khuẩn E.coli là bao nhiêu?
Điền đáp án: 3840.
Đổi đơn vị: 2 giờ = 120 phút
Số lần vi khuẩn tăng gấp đôi trong 2 giờ là 120 phút / 20 phút = 6 lần.
Sau 20 phút (hay số lượng vi khuẩn tăng gấp đôi lần 1) thì số lượng vi khuẩn lúc này là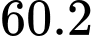
Sau 40 phút (tức số lượng vi khuẩn tăng gấp đôi lần 2) thì số lượng vi khuẩn lúc này là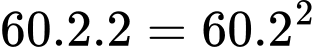
…
Tiếp tục như thế, ta suy ra số lượng vi khuẩn sau 2 giờ (tức tăng gấp đôi lần 6) là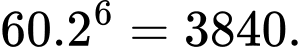
Đổi đơn vị: 2 giờ = 120 phút
Số lần vi khuẩn tăng gấp đôi trong 2 giờ là 120 phút / 20 phút = 6 lần.
Sau 20 phút (hay số lượng vi khuẩn tăng gấp đôi lần 1) thì số lượng vi khuẩn lúc này là
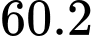
Sau 40 phút (tức số lượng vi khuẩn tăng gấp đôi lần 2) thì số lượng vi khuẩn lúc này là
…
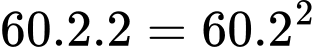
Tiếp tục như thế, ta suy ra số lượng vi khuẩn sau 2 giờ (tức tăng gấp đôi lần 6) là
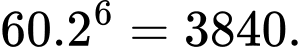
Câu 11 [690374]: Một loại vi khuẩn sau mỗi phút số lượng tăng gấp đôi biết rằng sau 5 phút người ta đếm được có 64 000 con. Hỏi sau bao nhiêu phút thì có được 2 048 000 con?
Điền đáp án: 2048000.
Số lượng vi khuẩn tăng lên là cấp số nhân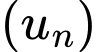
với công bội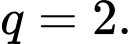 
Ta có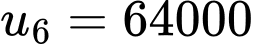
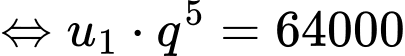
Thay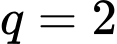
vào ta được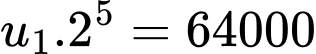 
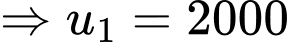
Sau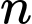
phút thì số lượng vi khuẩn là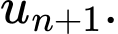 
YCBT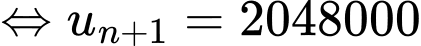
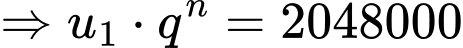
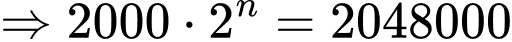
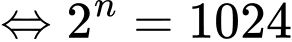
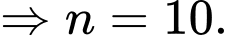
Vậy sau 10 phút thì có được 2048000 con.
Số lượng vi khuẩn tăng lên là cấp số nhân
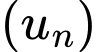với công bội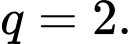
Ta có
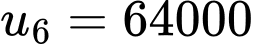
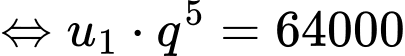
Thay
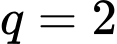vào ta được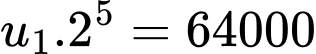
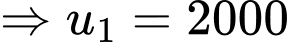
Sau
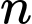phút thì số lượng vi khuẩn là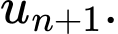
YCBT
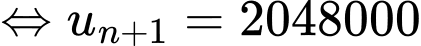
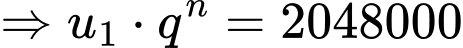
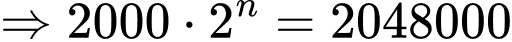
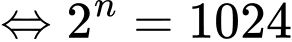
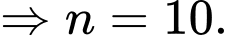
Vậy sau 10 phút thì có được 2048000 con.
Câu 12 [690375]: Vào năm 2020, dân số của một quốc gia là khoảng 97 triệu người và tốc độ tăng trưởng dân số là 0,91%. Nếu tốc độ tăng trưởng dân số này được giữ nguyên hằng năm thì vào năm 2030 dân số của quốc gia này là bao nhiêu triệu dân? (Kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 106.
Giả sử dân số của quốc gia đó là N.
Vì tốc độ tăng trưởng dân số là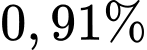
nên sau một năm, số dân tăng thêm là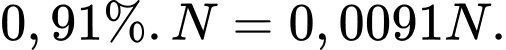 
Vậy dân số của quốc gia đó vào năm 2021 là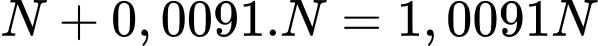
Tương tự, dân số của quốc gia đó vào năm 2022 là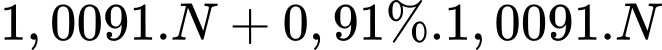
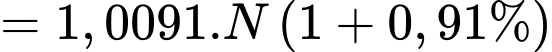
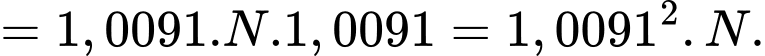
Như vậy, dân số của quốc gia đó sau mỗi năm lập thành một cấp số nhân với số hạng đầu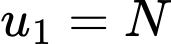
và công bội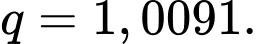 
Theo bài ra ta có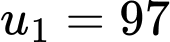
ứng với năm 2020.
Ta có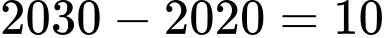
(năm)
Dân số của quốc gia đó vào năm 2030 là dân số của quốc gia sau 10 năm kể từ năm 2020, ứng với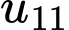
và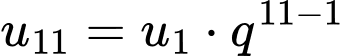 
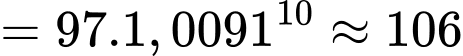(triệu người).
Vậy nếu tốc độ tăng trưởng dân số được giữ nguyên hằng năm thì dân số của quốc gia đó vào năm 2030 xấp xỉ khoảng 106 triệu người.
Giả sử dân số của quốc gia đó là N.
Vì tốc độ tăng trưởng dân số là
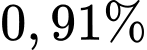nên sau một năm, số dân tăng thêm là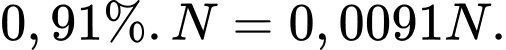 Vậy dân số của quốc gia đó vào năm 2021 là
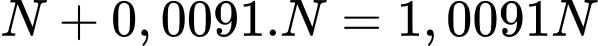
Tương tự, dân số của quốc gia đó vào năm 2022 là
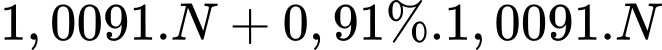
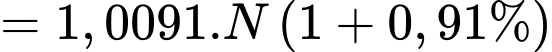
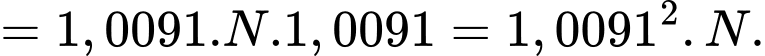
Như vậy, dân số của quốc gia đó sau mỗi năm lập thành một cấp số nhân với số hạng đầu
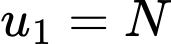và công bội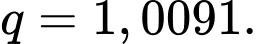 Theo bài ra ta có
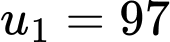ứng với năm 2020.Ta có
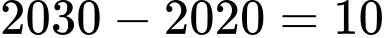(năm)Dân số của quốc gia đó vào năm 2030 là dân số của quốc gia sau 10 năm kể từ năm 2020, ứng với
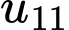và 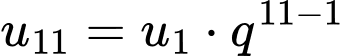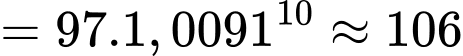(triệu người).Vậy nếu tốc độ tăng trưởng dân số được giữ nguyên hằng năm thì dân số của quốc gia đó vào năm 2030 xấp xỉ khoảng 106 triệu người.
Câu 13 [690376]: Một gia đình mua một chiếc ô tô giá 800 triệu đồng. Trung bình sau mỗi năm sử dụng, giá trị còn lại của ô tô giảm đi 4% (so với năm trước đó). Sau 10 năm, giá trị của ô tô ước tính còn bao nhiêu triệu đồng? (Kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 532.
Dựa vào giả thiết: Giá xe ban đầu là 800 triệu đồng và sau mỗi năm sử dụng, giá trị còn lại của ô tô giảm đi 4% (so với năm trước đó). Ta có:
Sau 1 năm thì giá trị sử dụng của ô tô còn lại là
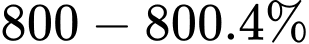
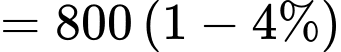
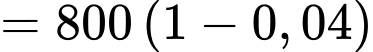(triệu đồng)
Tương tự, ta có sau 2 năm, giá trị sử dụng của ô tô còn lại là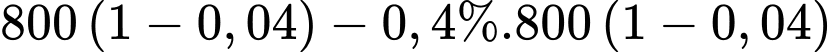
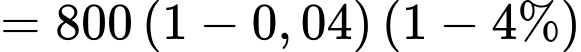
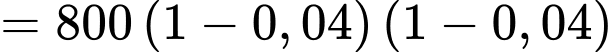
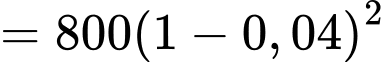(triệu đồng)
…
Vậy sau 10 năm, giá trị của ô tô ước tính còn lại là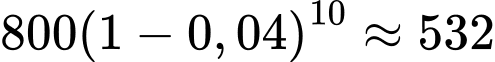
(triệu đồng).
Dựa vào giả thiết: Giá xe ban đầu là 800 triệu đồng và sau mỗi năm sử dụng, giá trị còn lại của ô tô giảm đi 4% (so với năm trước đó). Ta có:
Sau 1 năm thì giá trị sử dụng của ô tô còn lại là
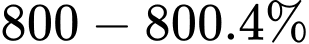
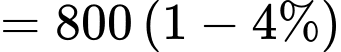
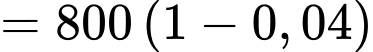(triệu đồng)Tương tự, ta có sau 2 năm, giá trị sử dụng của ô tô còn lại là
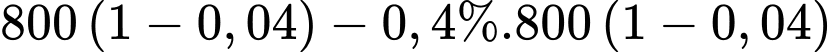
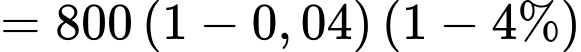
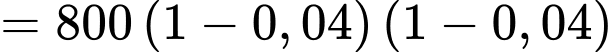
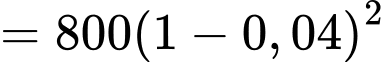(triệu đồng)…
Vậy sau 10 năm, giá trị của ô tô ước tính còn lại là
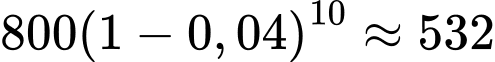(triệu đồng).
Câu 14 [690377]: Giả sử một thành phố có dân số năm 2022 là khoảng 2,1 triệu người và tốc độ gia tăng dân số trung bình mỗi năm là 0,75%. Nếu tốc độ gia tăng dân số vẫn giữ nguyên như trên thì ước tính vào năm nào dân số của thành phố đó sẽ tăng gấp đôi so với năm 2022?
Điền đáp án: 2116.
Khi biết dân số năm 2022 là khoảng 2,1 triệu người và tốc độ gia tăng dân số trung bình mỗi năm là 0,75%, ta có
+) Sau 1 năm tức năm 2023, dân số của thành phố đó là
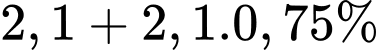
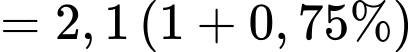
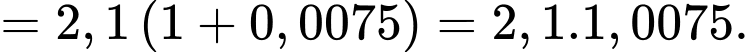
+) Sau 2 năm tức năm 2024, dân số của thành phố đó là
…
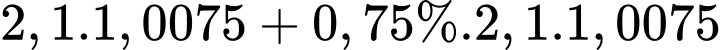
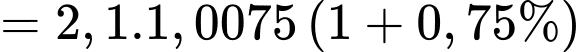
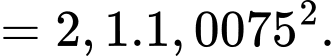
Suy ra sau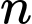
năm thì dân số của thành phố đó là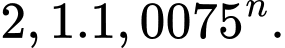 
Vậy dân số của thành phố đó lập thành một cấp số nhân với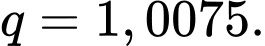
Giả sử sau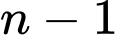
năm thì dân số thành phố đó tăng gấp đôi.
YCBT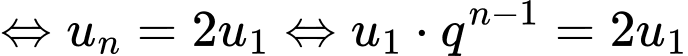
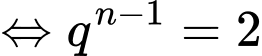
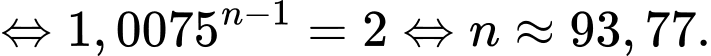
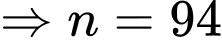
Vậy sau 93 năm thì dân số thành phố đó tăng gấp đôi.
Vậy ước tính vào năm 2115 dân số của thành phố đó sẽ tăng gấp đôi so với năm 2022.
Khi biết dân số năm 2022 là khoảng 2,1 triệu người và tốc độ gia tăng dân số trung bình mỗi năm là 0,75%, ta có
+) Sau 1 năm tức năm 2023, dân số của thành phố đó là
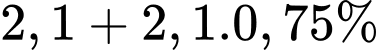
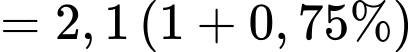
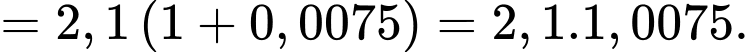
+) Sau 2 năm tức năm 2024, dân số của thành phố đó là
…
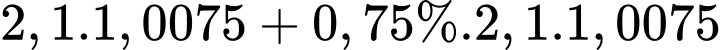
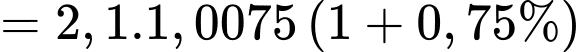
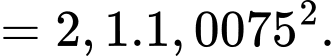
Suy ra sau
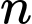năm thì dân số của thành phố đó là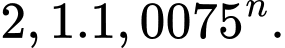 Vậy dân số của thành phố đó lập thành một cấp số nhân với
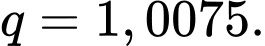
Giả sử sau
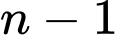năm thì dân số thành phố đó tăng gấp đôi. YCBT
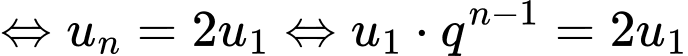
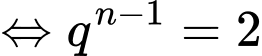
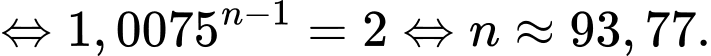
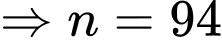
Vậy sau 93 năm thì dân số thành phố đó tăng gấp đôi.
Vậy ước tính vào năm 2115 dân số của thành phố đó sẽ tăng gấp đôi so với năm 2022.
Câu 15 [690378]: Aladin nhặt được cây đèn thần, chàng miết tay vào cây đèn và gọi Thần đèn ra. Thần đèn cho chàng 3 điều ước. Aladin ước 2 điều đầu tiên tùy thích nhưng điều ước thứ 3 của chàng là: “Ước gì ngày mai tôi lại nhặt được cây đèn và Thần cho tôi số điều ước gấp đôi số điều ước ngày hôm nay”. Thần đèn chấp thuận và mỗi ngày Aladin đều thực hiện theo quy tắc như trên: ước hết các điều đầu tiên và luôn chừa lại điều ước cuối cùng để kéo dài thỏa thuận với thần đèn như ngày hôm sau. Vậy sau 10 ngày gặp Thần đèn, Aladin có tổng cộng bao nhiêu điều ước?
Điền đáp án: 3069.
Từ đề bài ta thấy các điều ước của Aladin lập thành một cấp số nhân có số hạng đầu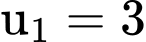
và công bội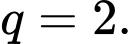 
Tổng số điều ước sau 10 ngày gặp thần đèn là tổng 10 số hạng đầu của cấp số nhân, áp dụng công thức tổng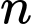
số hạng đầu của cấp số nhân, ta có
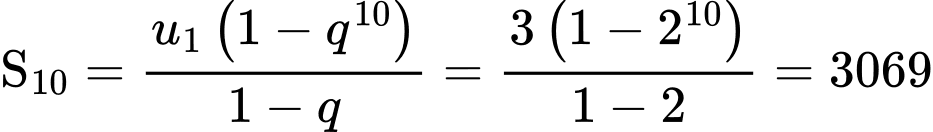(điều ước).
Từ đề bài ta thấy các điều ước của Aladin lập thành một cấp số nhân có số hạng đầu
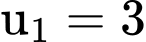và công bội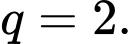
Tổng số điều ước sau 10 ngày gặp thần đèn là tổng 10 số hạng đầu của cấp số nhân, áp dụng công thức tổng
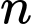số hạng đầu của cấp số nhân, ta có
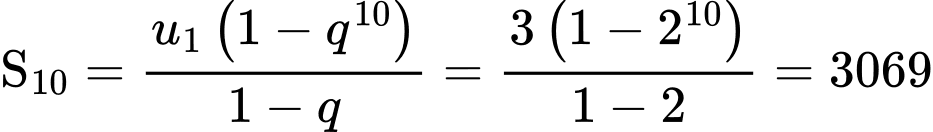(điều ước).
Câu 16 [690379]: Một loại thuốc được dùng mỗi ngày một lần. Lúc đầu, nồng độ thuốc trong máu của bệnh nhân tăng nhanh, nhưng mỗi liều kế tiếp có tác dụng ít hơn liều trước đó. Lượng thuốc trong máu ở ngày thứ nhất là 50 mg và mỗi ngày sau đó giảm chỉ còn một nửa so với ngày kế trước đó. Tính tổng lượng thuốc (tính bằng mg) trong máu của bệnh nhân sau khi dùng thuốc 10 ngày liên tiếp.
Điền đáp án: 25575/256.
Lượng thuốc (tính bằng mg) trong máu của bệnh nhân sau mỗi ngày dùng thuốc lập thành một cấp số nhân với số hạng đầu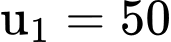
và công bội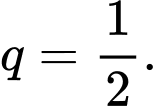 
Tổng lượng thuốc (tính bằng mg) trong máu của bệnh nhân sau khi dùng thuốc 10 ngày liên tiếp chính bằng tổng của 10 số hạng đầu của cấp số nhân trên và bằng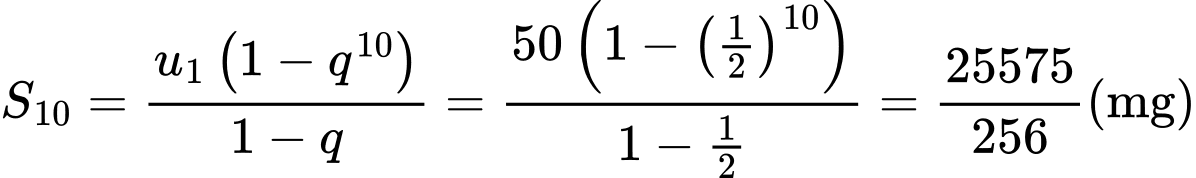
Lượng thuốc (tính bằng mg) trong máu của bệnh nhân sau mỗi ngày dùng thuốc lập thành một cấp số nhân với số hạng đầu
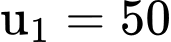và công bội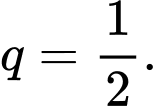
Tổng lượng thuốc (tính bằng mg) trong máu của bệnh nhân sau khi dùng thuốc 10 ngày liên tiếp chính bằng tổng của 10 số hạng đầu của cấp số nhân trên và bằng
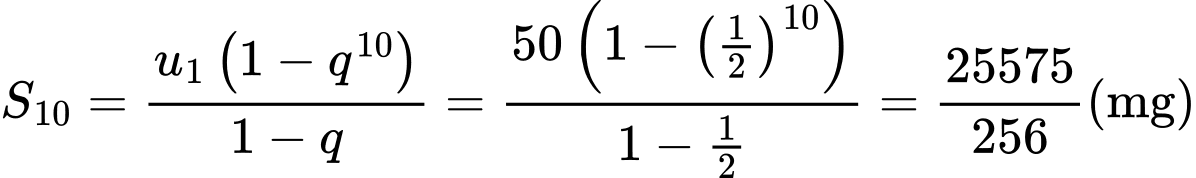
Câu 17 [690380]: Trong trò chơi mạo hiểm nhảy bungee, mỗi lần nhảy, người chơi sẽ được dây an toàn có tính đàn hồi kéo nảy ngược lên 60% chiều sâu của cú nhảy. Một người chơi bungee thực hiện cú nhảy đầu tiên có độ cao nảy ngược lên là 9 m. Độ cao nảy ngược lên của người đó ở lần nhảy thứ ba là bao nhiêu mét?
Điền đáp án: 3,24.
Độ cao nảy ngược lên của người đó là một cấp số nhân có số hạng đầu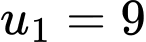
và công bội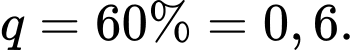 
Độ cao nảy ngược lên của người đó ở lần nảy thứ ba là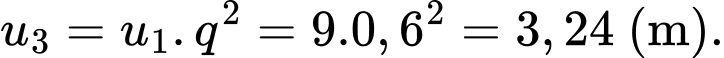
Độ cao nảy ngược lên của người đó là một cấp số nhân có số hạng đầu
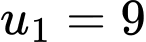và công bội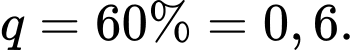 Độ cao nảy ngược lên của người đó ở lần nảy thứ ba là
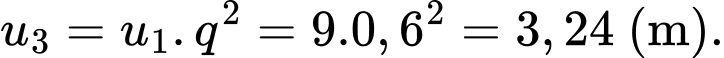
Câu 18 [690381]: Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài 100 m. Sau mỗi lần rơi xuống, nhờ sự đàn hồi của dây, người nhảy được kéo lên một quãng đường có độ dài bằng 75% so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên. Tính tổng quãng đường người đó đi được sau 10 lần kéo lên và lại bị rơi xuống.
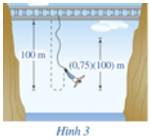
Điền đáp án: 377,5.
Gọi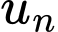
là độ dài dây kéo sau 
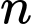lần rơi xuống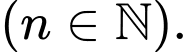 
Ta có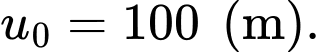
Sau lần rơi đầu tiên độ dài dây kéo còn lại là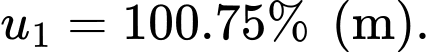
Sau cú nhảy tiếp theo độ dài dây kéo còn lại là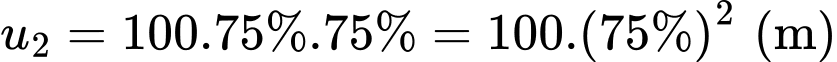
Dãy số này lập thành một cấp số nhân có số hạng đầu là 100 và công bội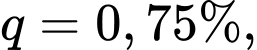
có công thức tổng quát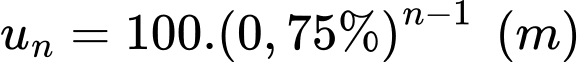 
Tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống là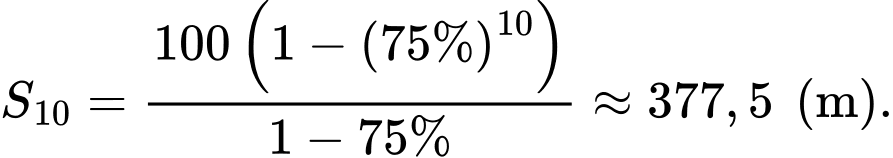
Gọi
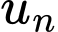là độ dài dây kéo sau 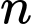lần rơi xuống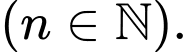 Ta có
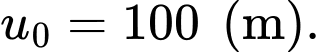
Sau lần rơi đầu tiên độ dài dây kéo còn lại là
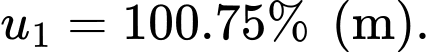
Sau cú nhảy tiếp theo độ dài dây kéo còn lại là
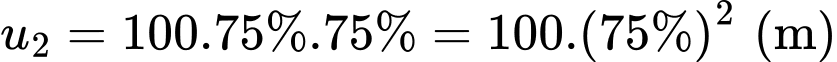
Dãy số này lập thành một cấp số nhân có số hạng đầu là 100 và công bội
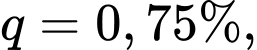có công thức tổng quát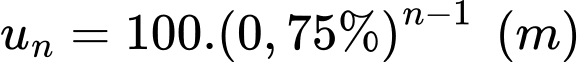 Tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống là
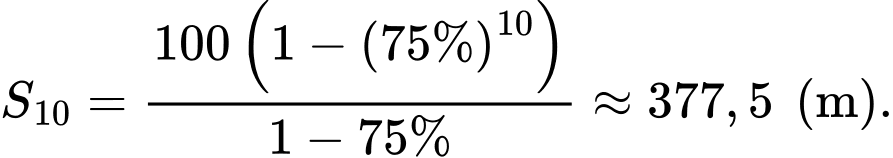
Câu 19 [690382]: Để trang trí cho quán trà sữa sắp mở cửa của mình, bạn Việt quyết định tô màu một mảng tường hình vuông cạnh bằng 
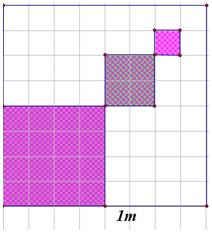
Phần tô màu dự kiến là các hình vuông nhỏ được đánh số lần lượt là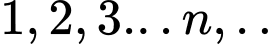 
(các hình vuông được tô màu chấm bi), trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó (hình vẽ). Giả sử quá trình tô màu của Việt có thể diễn ra nhiều giờ. Hỏi bạn Việt tô màu đến hình vuông thứ mấy thì diện tích của hình vuông được tô bắt đầu nhỏ hơn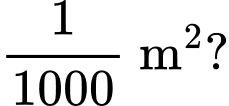 
Phần tô màu dự kiến là các hình vuông nhỏ được đánh số lần lượt là 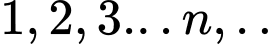(các hình vuông được tô màu chấm bi), trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó (hình vẽ). Giả sử quá trình tô màu của Việt có thể diễn ra nhiều giờ. Hỏi bạn Việt tô màu đến hình vuông thứ mấy thì diện tích của hình vuông được tô bắt đầu nhỏ hơn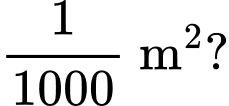
Điền đáp án: 5.
Diện tích hình vuông 1 là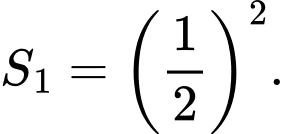
Diện tích hình vuông 2 là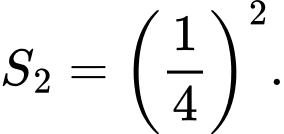
Diện tích hình vuông thứ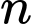
là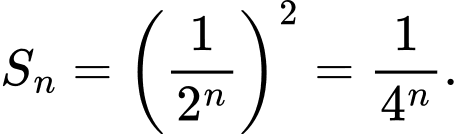 
Theo ra ta có
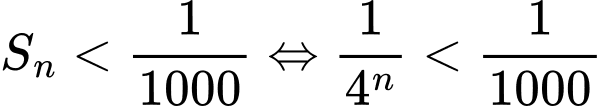
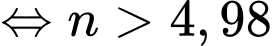
Vậy bạn Việt tô màu đến hình vuông thứ 5 thì diện tích của hình vuông được tô bắt đầu nhỏ hơn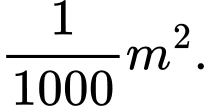
Diện tích hình vuông 1 là
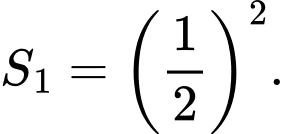
Diện tích hình vuông 2 là
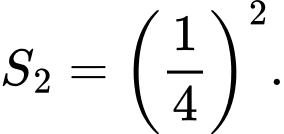
Diện tích hình vuông thứ
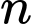là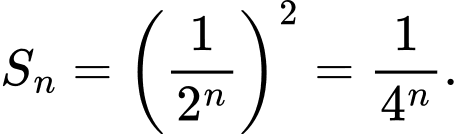
Theo ra ta có
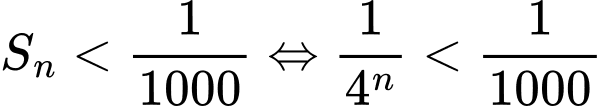
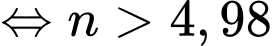
Vậy bạn Việt tô màu đến hình vuông thứ 5 thì diện tích của hình vuông được tô bắt đầu nhỏ hơn
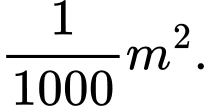
Câu 20 [690383]: Với hình vuông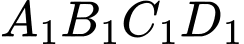 
như hình vẽ bên, cách tô màu như phần gạch sọc được gọi là cách tô màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy trình sau:
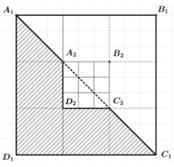
Bước 1: Tô màu “đẹp” cho hình vuông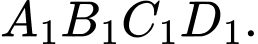
Bước 2: Tô màu “đẹp” cho hình vuông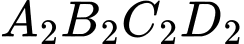
là hình vuông ở chính giữa khi chia hình vuông 
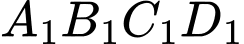thành 9 phần bằng nhau như hình vẽ.
Bước 3: Tô màu “đẹp” cho hình vuông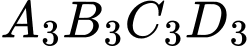
là hình vuông ở chính giữa khi chia hình vuông 
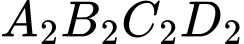thành 9 phần bằng nhau. Cứ tiếp tục như vậy.
Hỏi cần ít nhất bao nhiêu bước để tổng diện tích phần được tô màu chiếm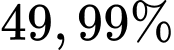
diện tích hình vuông ban đầu?
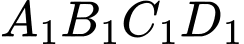như hình vẽ bên, cách tô màu như phần gạch sọc được gọi là cách tô màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy trình sau:Bước 1: Tô màu “đẹp” cho hình vuông
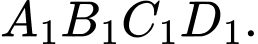
Bước 2: Tô màu “đẹp” cho hình vuông
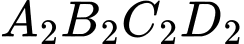là hình vuông ở chính giữa khi chia hình vuông 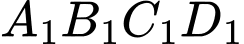thành 9 phần bằng nhau như hình vẽ.Bước 3: Tô màu “đẹp” cho hình vuông
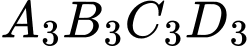là hình vuông ở chính giữa khi chia hình vuông 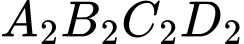thành 9 phần bằng nhau. Cứ tiếp tục như vậy.Hỏi cần ít nhất bao nhiêu bước để tổng diện tích phần được tô màu chiếm
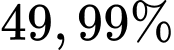diện tích hình vuông ban đầu?
Điền đáp án: 4.
Gọi diện tích được tô màu ở mỗi bước là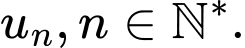
Dễ thấy dãy các giá trị 
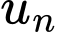là một cấp số nhân với số hạng đầu 
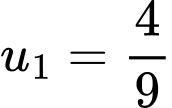và công bội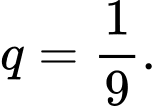 
Gọi
là tổng của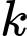 
số hạng đầu trong cấp số nhân đang xét thì 
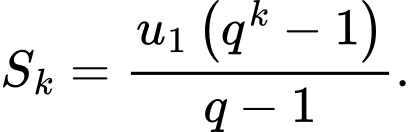Để tổng diện tích phần được tô màu chiếm 
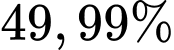phần diện tích hình vuông ban đầu thì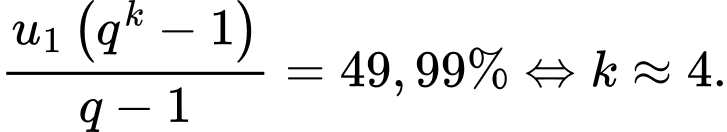 
Gọi diện tích được tô màu ở mỗi bước là
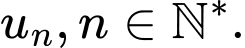Dễ thấy dãy các giá trị 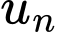là một cấp số nhân với số hạng đầu 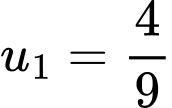và công bội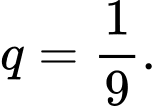
Gọi
là tổng của 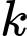số hạng đầu trong cấp số nhân đang xét thì 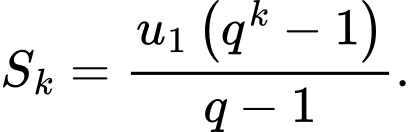Để tổng diện tích phần được tô màu chiếm 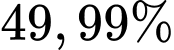phần diện tích hình vuông ban đầu thì