Câu 1 [27836]: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức 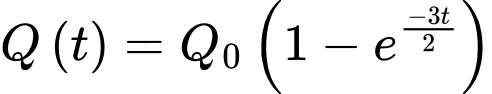 , với
, với 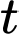 là khoảng thời gian tính bằng giờ và
là khoảng thời gian tính bằng giờ và 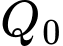 là dung lượng nạp tối đa (pin đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
là dung lượng nạp tối đa (pin đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là  ) thì bao lâu sau sẽ nạp được
) thì bao lâu sau sẽ nạp được 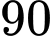 (kết quả làm tròn đến hàng phần trăm)?
(kết quả làm tròn đến hàng phần trăm)?
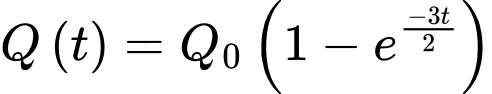 , với
, với 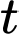 là khoảng thời gian tính bằng giờ và
là khoảng thời gian tính bằng giờ và 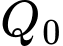 là dung lượng nạp tối đa (pin đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
là dung lượng nạp tối đa (pin đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là  ) thì bao lâu sau sẽ nạp được
) thì bao lâu sau sẽ nạp được 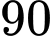 (kết quả làm tròn đến hàng phần trăm)?
(kết quả làm tròn đến hàng phần trăm)? A, 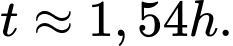
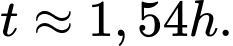
B, 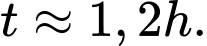
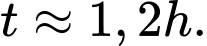
C, 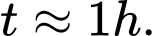
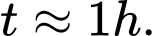
D, 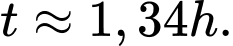
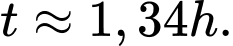
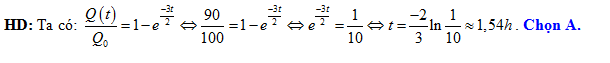 Đáp án: A
Đáp án: A
Câu 2 [27835]: Người ta thả một lá bèo vào một hồ nước. Giả sử sau 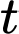 giờ, bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng lá bèo tăng gấp 10 lần lượng lá bèo trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì số lá bèo phủ kín
giờ, bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng lá bèo tăng gấp 10 lần lượng lá bèo trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì số lá bèo phủ kín 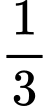 cái hồ?
cái hồ?
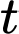 giờ, bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng lá bèo tăng gấp 10 lần lượng lá bèo trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì số lá bèo phủ kín
giờ, bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng lá bèo tăng gấp 10 lần lượng lá bèo trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì số lá bèo phủ kín 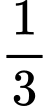 cái hồ?
cái hồ? A, 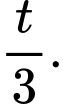
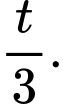
B, 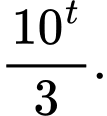
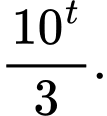
C, 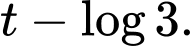
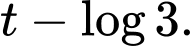
D, 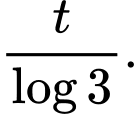
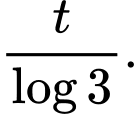
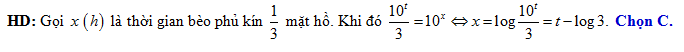 Đáp án: C
Đáp án: C
Câu 3 [27856]: Một người gửi tiết kiệm 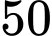 triệu đồng vào một ngân hàng với lãi suất
triệu đồng vào một ngân hàng với lãi suất  một năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu. Sau 5 năm mới rút lãi thì người đó thu được số tiền lãi là
một năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu. Sau 5 năm mới rút lãi thì người đó thu được số tiền lãi là
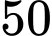 triệu đồng vào một ngân hàng với lãi suất
triệu đồng vào một ngân hàng với lãi suất  một năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu. Sau 5 năm mới rút lãi thì người đó thu được số tiền lãi là
một năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu. Sau 5 năm mới rút lãi thì người đó thu được số tiền lãi là A, 70,128 triệu đồng.
B, 50,7 triệu đồng.
C, 20,128 triệu đồng.
D, 3,5 triệu đồng.
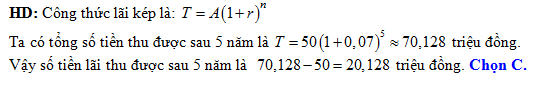 Đáp án: C
Đáp án: C
Câu 4 [27824]: Trong nông nghiệp bèo hoa dâu được dùng làm phân bón, nó rất tốt cho cây trồng. Mới đây một nhóm các nhà khoa học Việt Nam đã phát hiện ra bèo hoa dâu có thể được dùng để chiết xuất ra chất có tác dụng kích thích hệ miễn dịch và hỗ trợ điều trị bệnh ung thư. Bèo hoa dâu được thả nuôi trên mặt nước. Một người đã thả một lượng bèo hoa dâu chiếm 4% diện tích mặt hồ. Biết rằng cứ sau đúng một tuần bèo phát triển thành 3 lần lượng đã có và tốc độ phát triển của bèo ở mọi thời điểm như nhau. Sau bao nhiêu ngày bèo sẽ vừa phủ kín mặt hồ?
A, 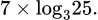
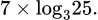
B, 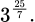
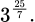
C, 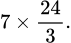
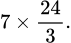
D, 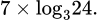
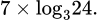
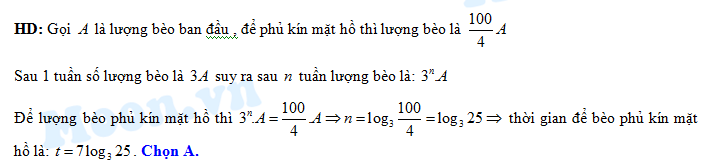 Đáp án: A
Đáp án: A
Câu 5 [27821]: E. Coli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ sau 20 phút thì số lượng vi khuẩn E. Coli tăng gấp đôi. Ban đầu, chỉ có 40 vi khuẩn E. Coli trong đường ruột. Hỏi sau bao lâu, số lượng vi khuẩn E. Coli là 671088640 con?
A, 48 giờ.
B, 24 giờ.
C, 12 giờ.
D, 8 giờ.
 Đáp án: D
Đáp án: D
Câu 6 [27817]: Số lượng của một loại vi khuẩn trong phòng thí nghiệm được tính theo công thức 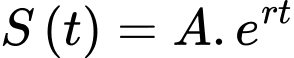 , trong đó
, trong đó 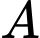 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 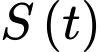 là số lượng vi khuẩn có sau
là số lượng vi khuẩn có sau 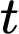 (phút),
(phút), 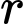 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 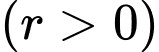 . Biết rằng số lượng vi khuẩn ban đầu là 500 con và sau 5 giờ có 1500 con. Hỏi sau bao lâu, kể từ lúc bắt đầu, số lượng vi khuẩn đạt 121500 con?
. Biết rằng số lượng vi khuẩn ban đầu là 500 con và sau 5 giờ có 1500 con. Hỏi sau bao lâu, kể từ lúc bắt đầu, số lượng vi khuẩn đạt 121500 con?
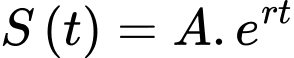 , trong đó
, trong đó 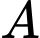 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 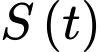 là số lượng vi khuẩn có sau
là số lượng vi khuẩn có sau 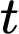 (phút),
(phút), 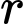 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 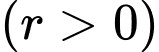 . Biết rằng số lượng vi khuẩn ban đầu là 500 con và sau 5 giờ có 1500 con. Hỏi sau bao lâu, kể từ lúc bắt đầu, số lượng vi khuẩn đạt 121500 con?
. Biết rằng số lượng vi khuẩn ban đầu là 500 con và sau 5 giờ có 1500 con. Hỏi sau bao lâu, kể từ lúc bắt đầu, số lượng vi khuẩn đạt 121500 con? A, 35 (giờ).
B, 45 (giờ).
C, 25 (giờ).
D, 15 (giờ).
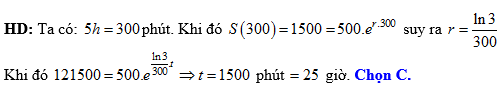 Đáp án: C
Đáp án: C
Câu 7 [27814]: Một người thả một lá bèo vào một cái ao, sau 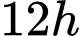 thì bèo sinh sôi phủ kín mặt ao. Hỏi sau mấy giờ thì bèo phủ kín
thì bèo sinh sôi phủ kín mặt ao. Hỏi sau mấy giờ thì bèo phủ kín 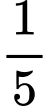 mặt ao, biết rằng sau mỗi giờ thì lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi.
mặt ao, biết rằng sau mỗi giờ thì lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi.
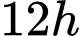 thì bèo sinh sôi phủ kín mặt ao. Hỏi sau mấy giờ thì bèo phủ kín
thì bèo sinh sôi phủ kín mặt ao. Hỏi sau mấy giờ thì bèo phủ kín 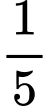 mặt ao, biết rằng sau mỗi giờ thì lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi.
mặt ao, biết rằng sau mỗi giờ thì lượng bèo tăng gấp 10 lần lượng bèo trước đó và tốc độ tăng không đổi. A, 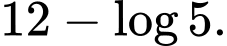
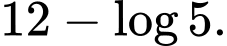
B, 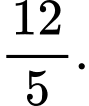
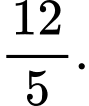
C, 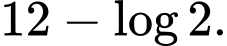
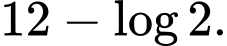
D, 

Ta có: 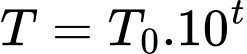 , khi đó sau 12 giờ lượng bèo sẽ là
, khi đó sau 12 giờ lượng bèo sẽ là 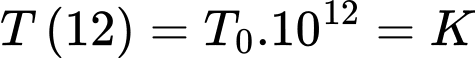
(trong đó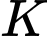 là lượng bèo phủ kín mặt hồ).
là lượng bèo phủ kín mặt hồ).
Gọi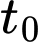 là thời gian bèo phủ
là thời gian bèo phủ 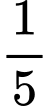 mặt hồ thì ta có:
mặt hồ thì ta có: 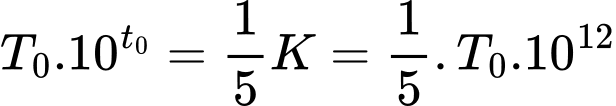
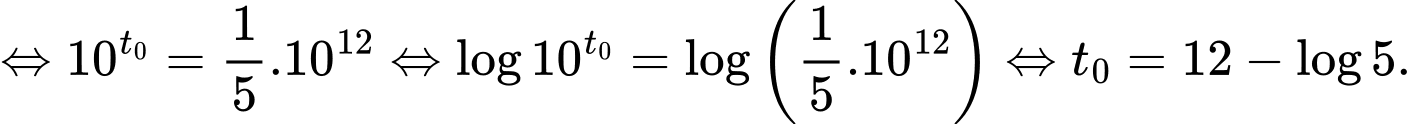 Chọn A. Đáp án: A
Chọn A. Đáp án: A
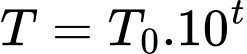 , khi đó sau 12 giờ lượng bèo sẽ là
, khi đó sau 12 giờ lượng bèo sẽ là 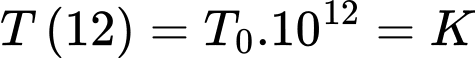
(trong đó
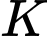 là lượng bèo phủ kín mặt hồ).
là lượng bèo phủ kín mặt hồ).
Gọi
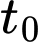 là thời gian bèo phủ
là thời gian bèo phủ 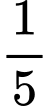 mặt hồ thì ta có:
mặt hồ thì ta có: 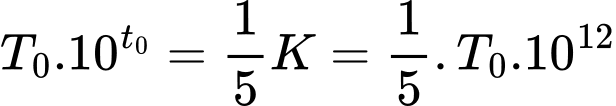
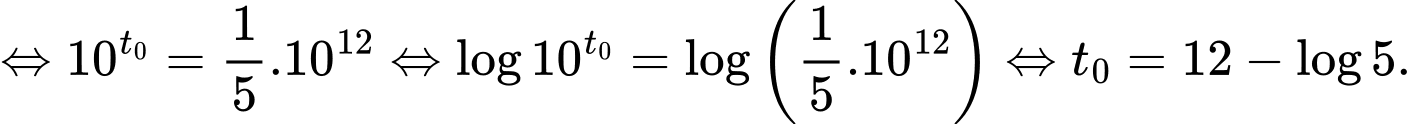 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 8 [27854]: Ông Việt dự định gửi vào ngân hàng một số tiền với lãi suất 6,5 % một năm. Biết rằng, cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Tính số tiền tối thiểu 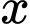 (triệu đồng
(triệu đồng 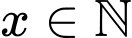 ) ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá 30 triệu đồng.
) ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá 30 triệu đồng.
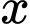 (triệu đồng
(triệu đồng 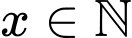 ) ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá 30 triệu đồng.
) ông Việt gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy trị giá 30 triệu đồng. A, 150 triệu đồng.
B, 154 triệu đồng.
C, 145 triệu đồng.
D, 140 triệu đồng.
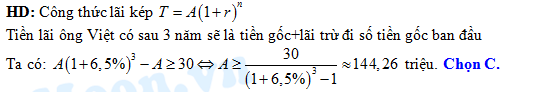 Đáp án: C
Đáp án: C
Câu 9 [27806]: Các khí thải gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm Trái Đất nóng lên. Theo OECD (tổ chức Hợp tác và Phát triển kinh tế thế giới), khi nhiệt độ Trái Đất tăng lên thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính rằng, khi nhiệt độ Trái Đất tăng thêm 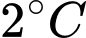 thì tổng giá trị kinh tế toàn cầu giảm
thì tổng giá trị kinh tế toàn cầu giảm 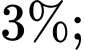 còn khi nhiệt độ Trái Đất tăng thêm
còn khi nhiệt độ Trái Đất tăng thêm 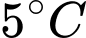 thì tổng giá trị kinh tế toàn cầu giảm
thì tổng giá trị kinh tế toàn cầu giảm 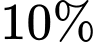 . Biết rằng, nếu nhiệt độ Trái Đất tăng thêm
. Biết rằng, nếu nhiệt độ Trái Đất tăng thêm 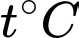 , tổng giá trị kinh tế toàn cầu giảm
, tổng giá trị kinh tế toàn cầu giảm 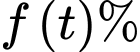 thì
thì 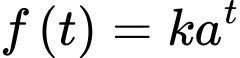 , trong đó
, trong đó 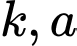 là các hằng số dương. Khi nhiệt độ Trái Đất tăng thêm bao nhiêu oC thì tổng giá trị kinh tế toàn cầu giảm đến
là các hằng số dương. Khi nhiệt độ Trái Đất tăng thêm bao nhiêu oC thì tổng giá trị kinh tế toàn cầu giảm đến 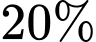 .(kết quả làm tròn đến hàng phần mười).
.(kết quả làm tròn đến hàng phần mười).

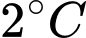 thì tổng giá trị kinh tế toàn cầu giảm
thì tổng giá trị kinh tế toàn cầu giảm 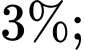 còn khi nhiệt độ Trái Đất tăng thêm
còn khi nhiệt độ Trái Đất tăng thêm 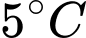 thì tổng giá trị kinh tế toàn cầu giảm
thì tổng giá trị kinh tế toàn cầu giảm 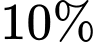 . Biết rằng, nếu nhiệt độ Trái Đất tăng thêm
. Biết rằng, nếu nhiệt độ Trái Đất tăng thêm 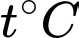 , tổng giá trị kinh tế toàn cầu giảm
, tổng giá trị kinh tế toàn cầu giảm 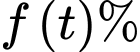 thì
thì 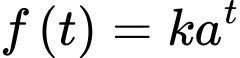 , trong đó
, trong đó 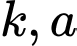 là các hằng số dương. Khi nhiệt độ Trái Đất tăng thêm bao nhiêu oC thì tổng giá trị kinh tế toàn cầu giảm đến
là các hằng số dương. Khi nhiệt độ Trái Đất tăng thêm bao nhiêu oC thì tổng giá trị kinh tế toàn cầu giảm đến 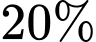 .(kết quả làm tròn đến hàng phần mười).
.(kết quả làm tròn đến hàng phần mười).
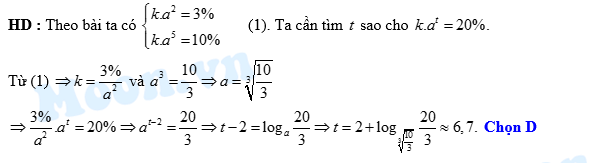
Câu 10 [27802]: Trong vật lí, sự phân rã của các chất phóng xạ được biểu diễn bởi công thức 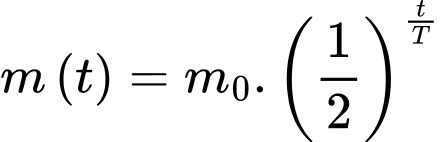 , trong đó
, trong đó 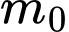 là khối lượng ban đầu của chất phóng xạ (tại thời điểm
là khối lượng ban đầu của chất phóng xạ (tại thời điểm 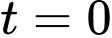 );
); 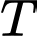 là chu kì bán rã (từ là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất khác). Chu kì bán rã của Cacbon
là chu kì bán rã (từ là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất khác). Chu kì bán rã của Cacbon 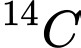 là khoảng 5730 năm. Người ta tìm được trong một mẫu đồ cổ một lượng Cacbon và xác định được nó đã mất khoảng
là khoảng 5730 năm. Người ta tìm được trong một mẫu đồ cổ một lượng Cacbon và xác định được nó đã mất khoảng 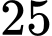 lượng Cacbon ban đầu của nó. Hỏi mẫu đồ cổ có tuổi là bao nhiêu?
lượng Cacbon ban đầu của nó. Hỏi mẫu đồ cổ có tuổi là bao nhiêu?
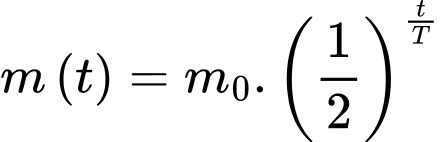 , trong đó
, trong đó 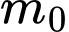 là khối lượng ban đầu của chất phóng xạ (tại thời điểm
là khối lượng ban đầu của chất phóng xạ (tại thời điểm 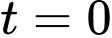 );
); 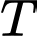 là chu kì bán rã (từ là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất khác). Chu kì bán rã của Cacbon
là chu kì bán rã (từ là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất khác). Chu kì bán rã của Cacbon 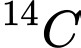 là khoảng 5730 năm. Người ta tìm được trong một mẫu đồ cổ một lượng Cacbon và xác định được nó đã mất khoảng
là khoảng 5730 năm. Người ta tìm được trong một mẫu đồ cổ một lượng Cacbon và xác định được nó đã mất khoảng 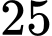 lượng Cacbon ban đầu của nó. Hỏi mẫu đồ cổ có tuổi là bao nhiêu?
lượng Cacbon ban đầu của nó. Hỏi mẫu đồ cổ có tuổi là bao nhiêu? A, 2378 năm.
B, 2300 năm.
C, 2387 năm.
D, 2400 năm.
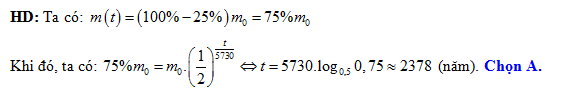 Đáp án: A
Đáp án: A
Câu 11 [27798]: Sự tăng trưởng của một loại vi khuẩn tuân theo công thức 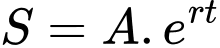 , trong đó
, trong đó 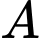 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 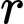 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 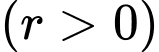 ,
, 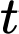 là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Hỏi sau 15 giờ có bao nhiêu con vi khuẩn.
là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Hỏi sau 15 giờ có bao nhiêu con vi khuẩn.
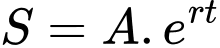 , trong đó
, trong đó 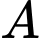 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 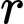 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 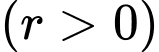 ,
, 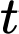 là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Hỏi sau 15 giờ có bao nhiêu con vi khuẩn.
là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Hỏi sau 15 giờ có bao nhiêu con vi khuẩn. A, 900 con.
B, 2700 con.
C, 600 con.
D, 1800 con.
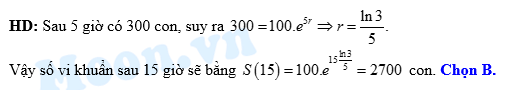 Đáp án: B
Đáp án: B
Câu 12 [27790]: Khi ánh sáng đi qua môi trường (chẳng hạn như không khí, nước, sương mù...), cường độ sẽ giảm dần theo quãng đường truyền 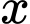 , theo công thức
, theo công thức 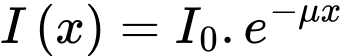 , trong đó
, trong đó 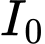 là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và
là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và 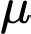 là hệ số hấp thụ của môi trường đó. Biết rằng nước biển có hệ số hấp thụ
là hệ số hấp thụ của môi trường đó. Biết rằng nước biển có hệ số hấp thụ 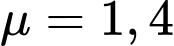 và người ta tính được rằng khi đi từ độ sâu
và người ta tính được rằng khi đi từ độ sâu 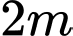 xuống đến độ sâu
xuống đến độ sâu 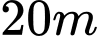 thì cường độ ánh sáng giảm
thì cường độ ánh sáng giảm 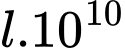 lần. Số nguyên nào sau đây gần với
lần. Số nguyên nào sau đây gần với 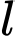 nhất?
nhất?
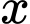 , theo công thức
, theo công thức 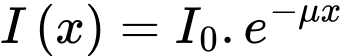 , trong đó
, trong đó 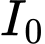 là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và
là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và 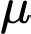 là hệ số hấp thụ của môi trường đó. Biết rằng nước biển có hệ số hấp thụ
là hệ số hấp thụ của môi trường đó. Biết rằng nước biển có hệ số hấp thụ 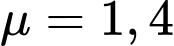 và người ta tính được rằng khi đi từ độ sâu
và người ta tính được rằng khi đi từ độ sâu 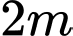 xuống đến độ sâu
xuống đến độ sâu 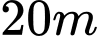 thì cường độ ánh sáng giảm
thì cường độ ánh sáng giảm 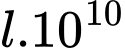 lần. Số nguyên nào sau đây gần với
lần. Số nguyên nào sau đây gần với 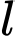 nhất?
nhất?
Ta có: Ở độ sâu 2m: 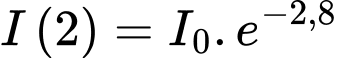
Ở độ sâu 20 m: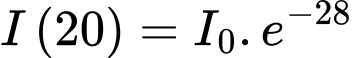
Theo giả thiết ta có: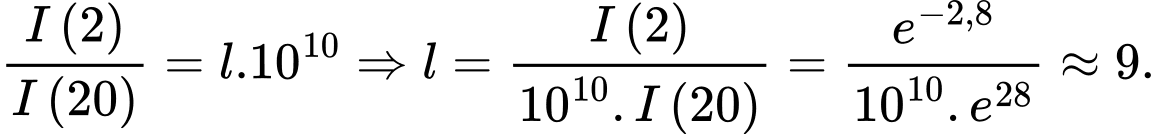
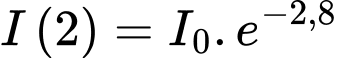
Ở độ sâu 20 m:
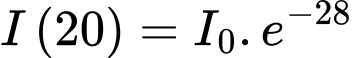
Theo giả thiết ta có:
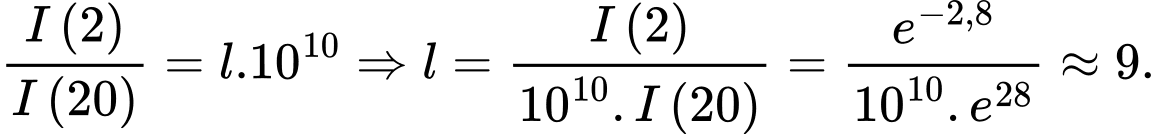
Câu 13 [27780]: Theo số liệu của Tổng cục thống kế, năm 2016 dân số Việt Nam ước tính khoảng 94.444.200 người. Tỉ lệ tăng dân số hàng năm ở Việt Nam được duy trì ở mức 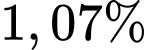 . Cho biết sự tăng dân số được tính theo công thức
. Cho biết sự tăng dân số được tính theo công thức 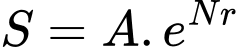 (trong đó
(trong đó 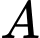 là dân số của năm lấy làm mốc tính,
là dân số của năm lấy làm mốc tính, 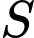 là dân số sau
là dân số sau 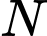 năm,
năm, 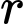 là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người
là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người
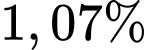 . Cho biết sự tăng dân số được tính theo công thức
. Cho biết sự tăng dân số được tính theo công thức 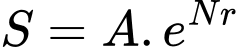 (trong đó
(trong đó 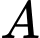 là dân số của năm lấy làm mốc tính,
là dân số của năm lấy làm mốc tính, 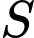 là dân số sau
là dân số sau 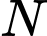 năm,
năm, 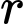 là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người
là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người A, 2040.
B, 2037.
C, 2038.
D, 2039.
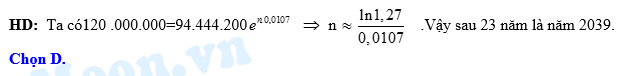 Đáp án: D
Đáp án: D
Câu 14 [27777]: Số lượng của loại virut 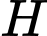 trong một phòng thí nghiệm được tính theo công thức
trong một phòng thí nghiệm được tính theo công thức 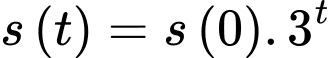 trong đó
trong đó  là số lượng virut
là số lượng virut 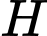 lúc ban đầu,
lúc ban đầu, 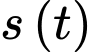 là số lượng virut
là số lượng virut 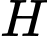 có sau thời gian
có sau thời gian 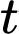 phút. Biết sau 5 phút thì số lượng virut
phút. Biết sau 5 phút thì số lượng virut 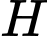 là 815.000 con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng virut
là 815.000 con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng virut 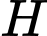 là 22.005.000 con?
là 22.005.000 con?
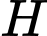 trong một phòng thí nghiệm được tính theo công thức
trong một phòng thí nghiệm được tính theo công thức 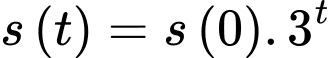 trong đó
trong đó  là số lượng virut
là số lượng virut 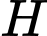 lúc ban đầu,
lúc ban đầu, 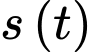 là số lượng virut
là số lượng virut 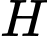 có sau thời gian
có sau thời gian 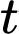 phút. Biết sau 5 phút thì số lượng virut
phút. Biết sau 5 phút thì số lượng virut 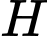 là 815.000 con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng virut
là 815.000 con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng virut 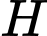 là 22.005.000 con?
là 22.005.000 con? A, 8 phút.
B, 30 phút.
C, 27 phút.
D, 15 phút.
 Đáp án: A
Đáp án: A
Câu 15 [27756]: Sự tăng trưởng của một loại vi khuẩn theo công thức 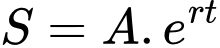 , trong đó
, trong đó 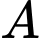 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 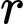 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 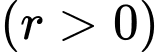 ,
, 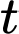 là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Khi đó sau thời gian bao lâu thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng ban đầu
là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Khi đó sau thời gian bao lâu thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng ban đầu
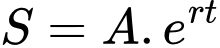 , trong đó
, trong đó 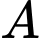 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 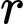 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 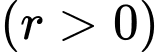 ,
, 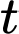 là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Khi đó sau thời gian bao lâu thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng ban đầu
là thời gian tăng trưởng. Biết số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ là 300 con. Khi đó sau thời gian bao lâu thì số lượng vi khuẩn tăng gấp 10 lần so với số lượng ban đầu A, 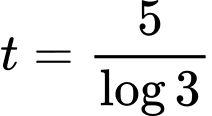 (giờ).
(giờ).
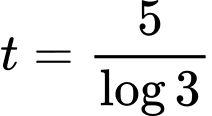 (giờ).
(giờ).B, 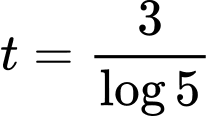 (giờ).
(giờ).
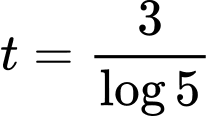 (giờ).
(giờ).C, 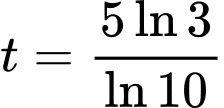 (giờ).
(giờ).
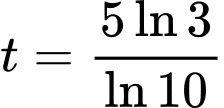 (giờ).
(giờ).D, 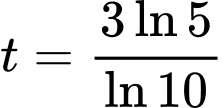 (giờ).
(giờ).
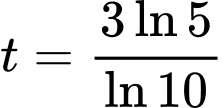 (giờ).
(giờ).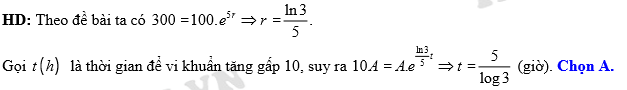 Đáp án: A
Đáp án: A
Câu 16 [27754]: Cho một lượng vi khuẩn bắt đầu với 500 con và phát triển với vận tốc tỷ lệ thuận với số lượng. Biết sau 3 giờ, có 8000 con vi khuẩn. Hỏi sau 4 giờ, số lượng vi khuẩn là bao nhiêu?
A, Khoảng 463521 con.
B, Khoảng 40235 con.
C, Khoảng 20159 con.
D, Khoảng 322539 con.
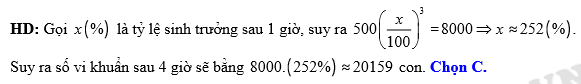 Đáp án: C
Đáp án: C
Câu 17 [27752]: Năng lượng của một trận động đất được tính bằng 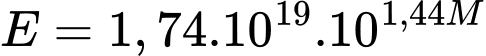 với
với 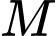 là độ chấn động theo thang Richter. Thành phố
là độ chấn động theo thang Richter. Thành phố 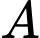 xảy ra một trận động đất 8 độ Richter và năng lượng của nó gấp 14 lần năng lượng của trận động đất xảy ra ở thành phố
xảy ra một trận động đất 8 độ Richter và năng lượng của nó gấp 14 lần năng lượng của trận động đất xảy ra ở thành phố 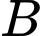 . Hỏi khi đó độ chấn động của trận động đất tại thành phố
. Hỏi khi đó độ chấn động của trận động đất tại thành phố 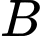 là bao nhiêu?
là bao nhiêu?
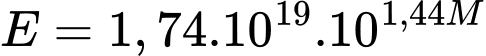 với
với 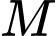 là độ chấn động theo thang Richter. Thành phố
là độ chấn động theo thang Richter. Thành phố 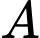 xảy ra một trận động đất 8 độ Richter và năng lượng của nó gấp 14 lần năng lượng của trận động đất xảy ra ở thành phố
xảy ra một trận động đất 8 độ Richter và năng lượng của nó gấp 14 lần năng lượng của trận động đất xảy ra ở thành phố 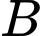 . Hỏi khi đó độ chấn động của trận động đất tại thành phố
. Hỏi khi đó độ chấn động của trận động đất tại thành phố 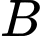 là bao nhiêu?
là bao nhiêu? A,
B,
C,
D,
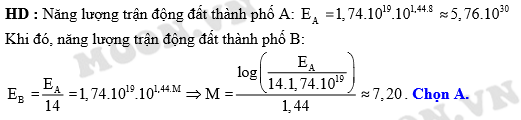 Đáp án: A
Đáp án: A
Câu 18 [27751]: Độ chấn động 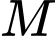 của một cơn địa chấn được đo bằng thang Richter xác định bởi công thức:
của một cơn địa chấn được đo bằng thang Richter xác định bởi công thức: 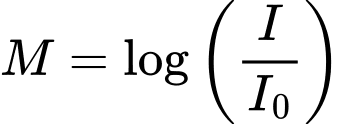 , trong đó
, trong đó 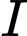 là biên độ tối đa đo được bằng địa kế chấn,
là biên độ tối đa đo được bằng địa kế chấn, 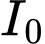 là biên độ chuẩn. Năng lượng giải tỏa
là biên độ chuẩn. Năng lượng giải tỏa 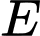 (tính theo đơn vị Jun) từ tâm địa chấn khi cơn địa chấn đạt
(tính theo đơn vị Jun) từ tâm địa chấn khi cơn địa chấn đạt 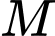 độ Richter được xác định bởi công thức
độ Richter được xác định bởi công thức 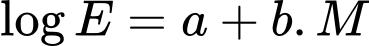 (trong đó
(trong đó 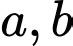 là hai hàng số đã cho). Xác định
là hai hàng số đã cho). Xác định 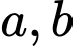 (tính chính xác đến hàng phần chục) biết rằng một trận động đất 8 độ Richter giải phóng ra một nguồn năng lượng gấp 30.000 lần một cơn địa chấn 5 độ Richter (địa chấn ở 5 độ Richter nó sản sinh khoảng
(tính chính xác đến hàng phần chục) biết rằng một trận động đất 8 độ Richter giải phóng ra một nguồn năng lượng gấp 30.000 lần một cơn địa chấn 5 độ Richter (địa chấn ở 5 độ Richter nó sản sinh khoảng 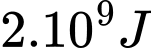 ).
).
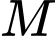 của một cơn địa chấn được đo bằng thang Richter xác định bởi công thức:
của một cơn địa chấn được đo bằng thang Richter xác định bởi công thức: 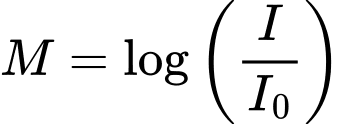 , trong đó
, trong đó 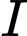 là biên độ tối đa đo được bằng địa kế chấn,
là biên độ tối đa đo được bằng địa kế chấn, 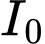 là biên độ chuẩn. Năng lượng giải tỏa
là biên độ chuẩn. Năng lượng giải tỏa 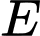 (tính theo đơn vị Jun) từ tâm địa chấn khi cơn địa chấn đạt
(tính theo đơn vị Jun) từ tâm địa chấn khi cơn địa chấn đạt 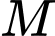 độ Richter được xác định bởi công thức
độ Richter được xác định bởi công thức 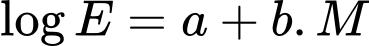 (trong đó
(trong đó 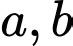 là hai hàng số đã cho). Xác định
là hai hàng số đã cho). Xác định 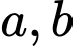 (tính chính xác đến hàng phần chục) biết rằng một trận động đất 8 độ Richter giải phóng ra một nguồn năng lượng gấp 30.000 lần một cơn địa chấn 5 độ Richter (địa chấn ở 5 độ Richter nó sản sinh khoảng
(tính chính xác đến hàng phần chục) biết rằng một trận động đất 8 độ Richter giải phóng ra một nguồn năng lượng gấp 30.000 lần một cơn địa chấn 5 độ Richter (địa chấn ở 5 độ Richter nó sản sinh khoảng 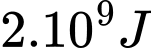 ).
). A, 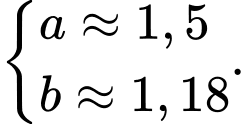
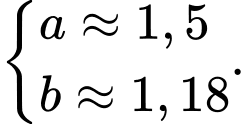
B, 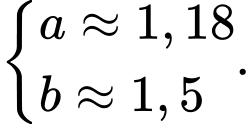
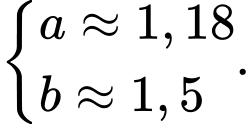
C, 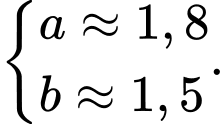
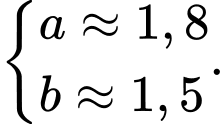
D, 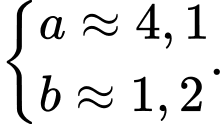
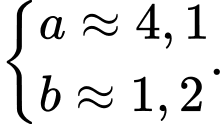
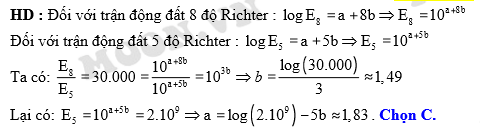 Đáp án: C
Đáp án: C
Câu 19 [27738]: Một người gửi vào ngân hàng theo hình thức lãi kép với lãi suất 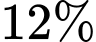 một năm, kỳ hạn
một năm, kỳ hạn 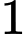 tháng. Hỏi sau bao nhiêu lâu, số tiền trong tài khoản của người đó gấp
tháng. Hỏi sau bao nhiêu lâu, số tiền trong tài khoản của người đó gấp 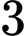 lần số tiền ban đầu?
lần số tiền ban đầu?
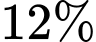 một năm, kỳ hạn
một năm, kỳ hạn 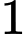 tháng. Hỏi sau bao nhiêu lâu, số tiền trong tài khoản của người đó gấp
tháng. Hỏi sau bao nhiêu lâu, số tiền trong tài khoản của người đó gấp 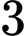 lần số tiền ban đầu?
lần số tiền ban đầu? A, 12 năm 5 tháng.
B, 9 năm 3 tháng.
C, 11 năm.
D, 10 năm 2 tháng.
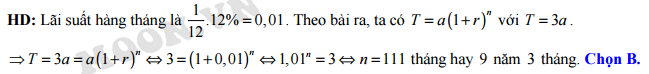 Đáp án: B
Đáp án: B
Câu 20 [27722]: Trong môi trường nuôi cấy ổn định người ta nhận thấy cứ sau 5 ngày số lượng loài vi khuẩn A tăng lên gấp đôi, còn sau đúng 10 ngày số lượng loài vi khuẩn B tăng lên gấp ba. Giả sử ban đầu có 100 con vi khuẩn A và 200 con vi khuẩn B, hỏi sau bao nhiêu ngày nuôi cấy trong môi trường đó thì số lượng hai loài bằng nhau, biết rằng tốc độ tăng trưởng của mỗi loài ở mọi thời điểm là như nhau?
A, 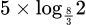 ngày.
ngày.
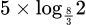 ngày.
ngày.B, 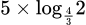 ngày.
ngày.
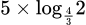 ngày.
ngày.C, 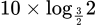 ngày.
ngày.
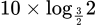 ngày.
ngày.D, 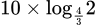 ngày
ngày
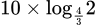 ngày
ngày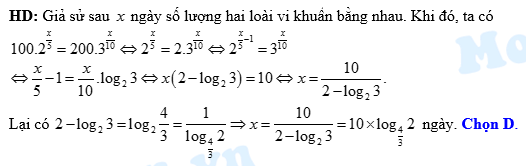 Đáp án: D
Đáp án: D
Câu 21 [27720]: Sự tăng trưởng của một loài vi khuẩn được tính theo công thức 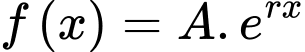 , trong đó
, trong đó 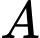 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 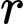 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 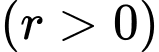 ,
, 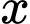 (tính theo giờ) là thời gian tăng trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sau bao lâu thì số lượng vi khuẩn tăng gấp 10 lần
(tính theo giờ) là thời gian tăng trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sau bao lâu thì số lượng vi khuẩn tăng gấp 10 lần
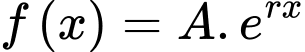 , trong đó
, trong đó 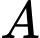 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 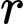 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 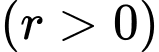 ,
, 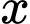 (tính theo giờ) là thời gian tăng trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sau bao lâu thì số lượng vi khuẩn tăng gấp 10 lần
(tính theo giờ) là thời gian tăng trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sau bao lâu thì số lượng vi khuẩn tăng gấp 10 lần A, 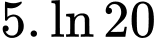 (giờ).
(giờ).
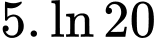 (giờ).
(giờ).B, 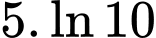 (giờ).
(giờ).
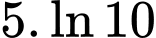 (giờ).
(giờ).C, 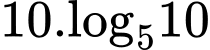 (giờ).
(giờ).
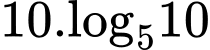 (giờ).
(giờ).D, 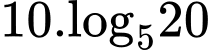 (giờ).
(giờ).
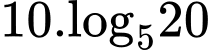 (giờ).
(giờ).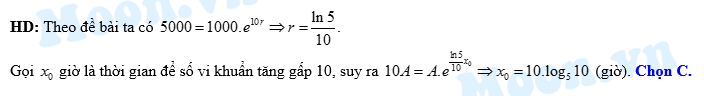 Đáp án: C
Đáp án: C
Câu 22 [27716]: Các nhà nghiên cứu cho biết dân số của thế giới năm 1950 là 2,56 tỉ người và năm 1960 là 3,04 tỉ người. Đồng thời các nhà nghiên cứu còn công bố rằng dân số của thế giới tăng hàng năm theo một hàm mũ theo thời gian có dạng như sau 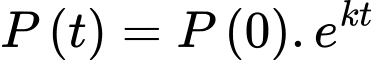 trong đó
trong đó 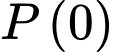 là dân số thế giới tại thời điểm chọn làm mốc,
là dân số thế giới tại thời điểm chọn làm mốc, 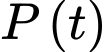 là dân số thế giới tại thời điểm
là dân số thế giới tại thời điểm 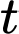 (năm) và hệ số
(năm) và hệ số 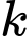 là hằng số. Hãy ước lượng dân số thế giới vào năm 2020 có khoảng bao nhiêu tỉ người
là hằng số. Hãy ước lượng dân số thế giới vào năm 2020 có khoảng bao nhiêu tỉ người
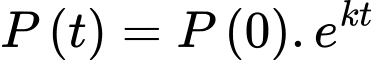 trong đó
trong đó 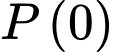 là dân số thế giới tại thời điểm chọn làm mốc,
là dân số thế giới tại thời điểm chọn làm mốc, 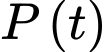 là dân số thế giới tại thời điểm
là dân số thế giới tại thời điểm 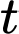 (năm) và hệ số
(năm) và hệ số 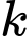 là hằng số. Hãy ước lượng dân số thế giới vào năm 2020 có khoảng bao nhiêu tỉ người
là hằng số. Hãy ước lượng dân số thế giới vào năm 2020 có khoảng bao nhiêu tỉ người A, 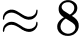 tỉ người.
tỉ người.
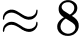 tỉ người.
tỉ người.B, 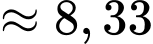 tỉ người.
tỉ người.
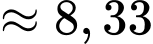 tỉ người.
tỉ người.C, 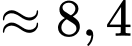 tỉ người.
tỉ người.
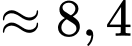 tỉ người.
tỉ người.D, 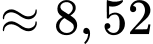 tỉ người.
tỉ người.
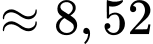 tỉ người.
tỉ người.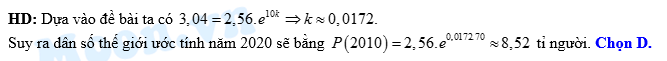 Đáp án: D
Đáp án: D
Câu 23 [27709]: Số lượng của một loại vi khuẩn tuân theo công thức 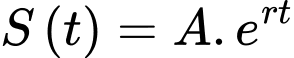 , trong đó
, trong đó 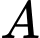 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 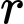 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 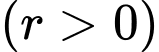 ,
, 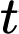 là thời gian tăng trưởng (tính theo đơn vị là giờ). Biết số vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Thời gian để vi khuẩn tăng gấp đôi số ban đầu gần đúng nhất với kết quả nào trong các kết quả sau?
là thời gian tăng trưởng (tính theo đơn vị là giờ). Biết số vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Thời gian để vi khuẩn tăng gấp đôi số ban đầu gần đúng nhất với kết quả nào trong các kết quả sau?
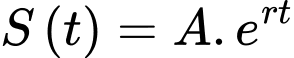 , trong đó
, trong đó 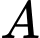 là số lượng vi khuẩn ban đầu,
là số lượng vi khuẩn ban đầu, 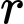 là tỉ lệ tăng trưởng
là tỉ lệ tăng trưởng 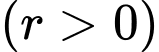 ,
, 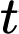 là thời gian tăng trưởng (tính theo đơn vị là giờ). Biết số vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Thời gian để vi khuẩn tăng gấp đôi số ban đầu gần đúng nhất với kết quả nào trong các kết quả sau?
là thời gian tăng trưởng (tính theo đơn vị là giờ). Biết số vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Thời gian để vi khuẩn tăng gấp đôi số ban đầu gần đúng nhất với kết quả nào trong các kết quả sau? A, 3 giờ 20 phút.
B, 3 giờ 9 phút.
C, 3 giờ 40 phút.
D, 3 giờ 2 phút.
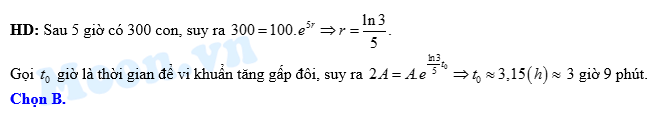 Đáp án: B
Đáp án: B
Câu 24 [27708]: Số lượng của loại vi khuẩn X trong một phòng thí nghiệm được tính theo công thức 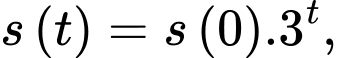 trong đó
trong đó  là số lượng vi khuẩn lúc ban đầu,
là số lượng vi khuẩn lúc ban đầu, 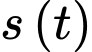 là số lượng vi khuẩn
là số lượng vi khuẩn 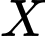 có sau
có sau 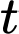 phút. Biết rằng sau 3 phút thì số lượng vi khuẩn X là 20 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn X là 540 nghìn con?
phút. Biết rằng sau 3 phút thì số lượng vi khuẩn X là 20 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn X là 540 nghìn con?
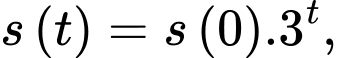 trong đó
trong đó  là số lượng vi khuẩn lúc ban đầu,
là số lượng vi khuẩn lúc ban đầu, 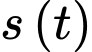 là số lượng vi khuẩn
là số lượng vi khuẩn 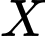 có sau
có sau 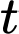 phút. Biết rằng sau 3 phút thì số lượng vi khuẩn X là 20 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn X là 540 nghìn con?
phút. Biết rằng sau 3 phút thì số lượng vi khuẩn X là 20 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn X là 540 nghìn con? A, 81 phút.
B, 6 phút.
C, 12 phút.
D, 9 phút.
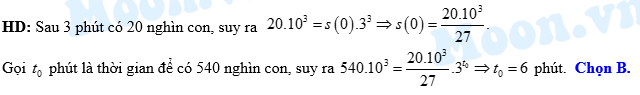 Đáp án: B
Đáp án: B
Câu 25 [27954]: Bác Hiếu đầu tư 99 triệu đồng vào một công ti theo thể thức lãi kép với lãi suất 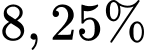 một năm. Hỏi sau 5 năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (giả sử rằng lãi suất hàng năm không đổi)
một năm. Hỏi sau 5 năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (giả sử rằng lãi suất hàng năm không đổi)
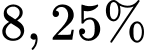 một năm. Hỏi sau 5 năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (giả sử rằng lãi suất hàng năm không đổi)
một năm. Hỏi sau 5 năm mới rút tiền lãi thì bác Hiếu thu được bao nhiêu tiền lãi? (giả sử rằng lãi suất hàng năm không đổi) A, 48,155 triệu đồng.
B, 147,155 triệu đồng.
C, 58,004 triệu đồng.
D, 8,7 triệu đồng.
 Đáp án: A
Đáp án: A
Câu 26 [27920]: Số lượng của một số loài vi khuẩn sau 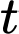 (giờ) được xấp xỉ bởi đẳng thức
(giờ) được xấp xỉ bởi đẳng thức 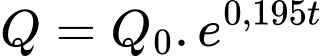 , trong đó
, trong đó 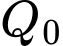 là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn đầu là 5000 con thì sau bao lâu có 100.000 con.
là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn đầu là 5000 con thì sau bao lâu có 100.000 con.
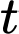 (giờ) được xấp xỉ bởi đẳng thức
(giờ) được xấp xỉ bởi đẳng thức 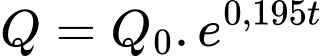 , trong đó
, trong đó 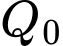 là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn đầu là 5000 con thì sau bao lâu có 100.000 con.
là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn đầu là 5000 con thì sau bao lâu có 100.000 con. A, 24 giờ.
B, 3,55 giờ.
C, 20 giờ.
D, 15,36 giờ.
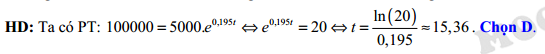 Đáp án: D
Đáp án: D
Câu 27 [27912]: Đầu năm 2016, ông A thành lập một công ty. Tổng số tiền ông A dùng để trả lương cho nhân viên trong năm 2016 là 1 tỷ đồng. Biết rằng biết sau mỗi năm thì số tiền dùng để trả cho nhân viên trong cả năm đó tăng thêm 15% so với năm trước. Hỏi năm nào dưới đây là năm đầu tiên mà tổng số tiền ông A dùng để trả lương cho nhân viên trong cả năm lớn hơn 2 tỷ đồng?
A, Năm 2022.
B, Năm 2021.
C, Năm 2020.
D, Năm 2023.
HD: Số tiền mà ông A phải trả cho nhân viên sau năm thứ n là 1.(1+15\%) tỷ đồng.
Theo bài ra, ta có
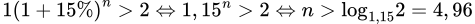
Vậy năm đầu tiên mà tổng số tiền ông A dùng để trả lớn hơn 2 tỷ đồng là 2016+5=2021. Chọn B.
Đáp án: B
Câu 28 [27910]: Một nguồn âm đẳng hướng đặt tại điểm  có công suất truyền âm không đổi. Mức cường độ âm tại điểm
có công suất truyền âm không đổi. Mức cường độ âm tại điểm 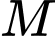 cách
cách  một khoảng
một khoảng 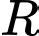 được tính bởi công thức
được tính bởi công thức 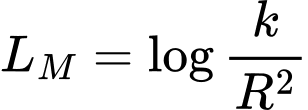 (Ben), với
(Ben), với 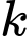 là hằng số. Biết điểm
là hằng số. Biết điểm  thuộc đoạn thẳng
thuộc đoạn thẳng  và mức cường độ âm tại
và mức cường độ âm tại 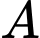 và
và 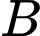 là
là 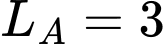 Ben và
Ben và 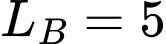 Ben. Tính mức cường độ âm tại trung điểm
Ben. Tính mức cường độ âm tại trung điểm  (làm tròn đến hai chữ số sau dấu phẩy)
(làm tròn đến hai chữ số sau dấu phẩy)
 có công suất truyền âm không đổi. Mức cường độ âm tại điểm
có công suất truyền âm không đổi. Mức cường độ âm tại điểm 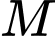 cách
cách  một khoảng
một khoảng 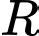 được tính bởi công thức
được tính bởi công thức 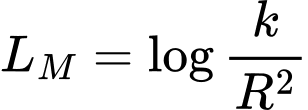 (Ben), với
(Ben), với 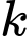 là hằng số. Biết điểm
là hằng số. Biết điểm  thuộc đoạn thẳng
thuộc đoạn thẳng  và mức cường độ âm tại
và mức cường độ âm tại 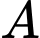 và
và 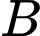 là
là 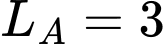 Ben và
Ben và 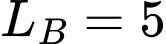 Ben. Tính mức cường độ âm tại trung điểm
Ben. Tính mức cường độ âm tại trung điểm  (làm tròn đến hai chữ số sau dấu phẩy)
(làm tròn đến hai chữ số sau dấu phẩy) A, 3,59 Ben.
B, 3,06 Ben.
C, 3,69 Ben.
D, 4 Ben.
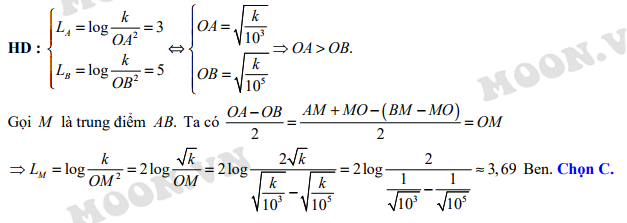 Đáp án: C
Đáp án: C
Câu 29 [981666]: Khi một kim loại được làm nóng đến 6000 C, độ bền kéo của nó giảm đi 50%. Sau khi kim loại vượt qua ngưỡng 6000 C, nếu nhiệt độ tăng thêm 50 C thì độ bền kéo của nó giảm đi 35% hiện có. Biết kim loại này có độ bền kéo là 280Mpa dưới 6000 C, được sử dụng trong việc xây dựng các lò công nghiệp. Nếu mức an toàn tối thiểu của độ bền kéo của vật liệu này là 38Mpa, thì nhiệt độ an toàn tối đa của lò công nghiệp bằng bao nhiêu, tính theo độ Celsius?(kết quả làm tròn đến hàng đơn vị)?

Câu 30 [27676]: Một người gửi tiết kiệm với số tiền gửi là A đồng với lãi suất là 6% một năm, biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Sau 10 năm người đó rút ra được số tiền cả gốc lẫn lãi nhiều hơn số tiền ban đầu là 100 triệu đồng. Hỏi người đó phải gửi số tiền A bằng bao nhiêu?
A, 145037058,3 đồng.
B, 55839477,69 đồng.
C, 126446589 đồng.
D, 111321563,5 đồng.
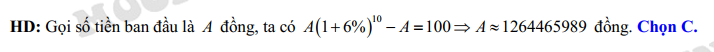 Đáp án: C
Đáp án: C
Câu 31 [27602]: Độ 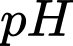 của một dung dịch được tính theo công thức
của một dung dịch được tính theo công thức 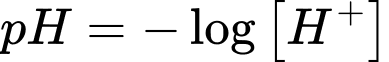 , với
, với 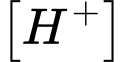 là nồng độ ion
là nồng độ ion 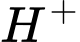 trong dung dịch đó. Cho dung dịch
trong dung dịch đó. Cho dung dịch 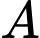 có độ
có độ 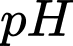 ban đầu bằng 6. Nếu nồng độ ion
ban đầu bằng 6. Nếu nồng độ ion 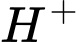 trong dung dịch
trong dung dịch 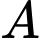 tăng lên 4 lần thì độ
tăng lên 4 lần thì độ 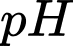 trong dung dịch mới gần bằng giá trị nào dưới đây?
trong dung dịch mới gần bằng giá trị nào dưới đây?
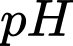 của một dung dịch được tính theo công thức
của một dung dịch được tính theo công thức 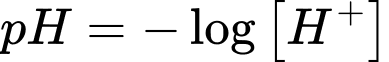 , với
, với 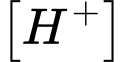 là nồng độ ion
là nồng độ ion 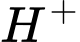 trong dung dịch đó. Cho dung dịch
trong dung dịch đó. Cho dung dịch 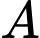 có độ
có độ 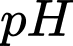 ban đầu bằng 6. Nếu nồng độ ion
ban đầu bằng 6. Nếu nồng độ ion 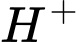 trong dung dịch
trong dung dịch 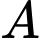 tăng lên 4 lần thì độ
tăng lên 4 lần thì độ 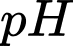 trong dung dịch mới gần bằng giá trị nào dưới đây?
trong dung dịch mới gần bằng giá trị nào dưới đây? A, 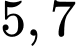 .
.
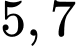 .
.B, 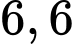 .
.
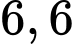 .
.C, 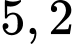 .
.
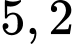 .
.D, 5,4
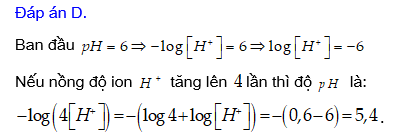 Đáp án: D
Đáp án: D
Câu 32 [27590]: Trong 1 bản hợp ca, coi mọi ca sĩ đều hát với cùng một cường độ âm và cùng một tần số. Khi một ca sĩ hát thì mức cường độ âm là 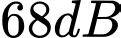 . Khi cả ban hợp ca cùng hát thì đo được mức cường độ âm là
. Khi cả ban hợp ca cùng hát thì đo được mức cường độ âm là 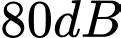 . Biết mức cường độ âm
. Biết mức cường độ âm 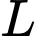 được tính theo công thức:
được tính theo công thức: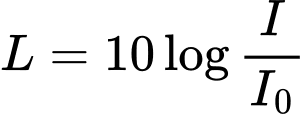 , trong đó
, trong đó 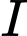 : là cường độ âm,
: là cường độ âm, 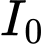 là cường độ âm chuẩn. Số ca sĩ trong ban hợp ca đó gần nhất với kết quả nào sau đây:
là cường độ âm chuẩn. Số ca sĩ trong ban hợp ca đó gần nhất với kết quả nào sau đây:
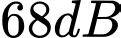 . Khi cả ban hợp ca cùng hát thì đo được mức cường độ âm là
. Khi cả ban hợp ca cùng hát thì đo được mức cường độ âm là 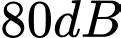 . Biết mức cường độ âm
. Biết mức cường độ âm 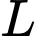 được tính theo công thức:
được tính theo công thức: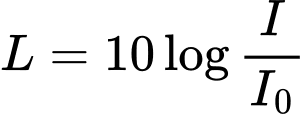 , trong đó
, trong đó 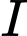 : là cường độ âm,
: là cường độ âm, 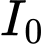 là cường độ âm chuẩn. Số ca sĩ trong ban hợp ca đó gần nhất với kết quả nào sau đây:
là cường độ âm chuẩn. Số ca sĩ trong ban hợp ca đó gần nhất với kết quả nào sau đây: A, 19 người.
B, 16 người.
C, 8 người.
D, 10 người.
 Đáp án: B
Đáp án: B
Câu 33 [29277]: Cường độ một trận động đất M được cho bởi công thức 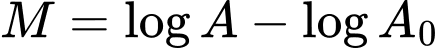 , đơn vị richter với
, đơn vị richter với 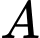 là biên độ rung chấn tối đa và
là biên độ rung chấn tối đa và 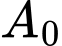 là biên độ chuẩn (hằng số). Vào tháng 2 năm 2010, một trận động đất ở Chile có cường độ 8,8 độ rrichter. Biết rằng trận động đất năm 2004 gây ra sóng thần tại Bắc Sumatra, Indonexia ngày 26.12.2004 có biên độ rung chấn manh gấp 3,26 lần so với biên độ rung chấn tối đa của trận động đất Chile. Tính cường độ trận động đất ở Bắc Sumatra.
là biên độ chuẩn (hằng số). Vào tháng 2 năm 2010, một trận động đất ở Chile có cường độ 8,8 độ rrichter. Biết rằng trận động đất năm 2004 gây ra sóng thần tại Bắc Sumatra, Indonexia ngày 26.12.2004 có biên độ rung chấn manh gấp 3,26 lần so với biên độ rung chấn tối đa của trận động đất Chile. Tính cường độ trận động đất ở Bắc Sumatra.
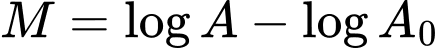 , đơn vị richter với
, đơn vị richter với 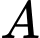 là biên độ rung chấn tối đa và
là biên độ rung chấn tối đa và 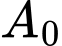 là biên độ chuẩn (hằng số). Vào tháng 2 năm 2010, một trận động đất ở Chile có cường độ 8,8 độ rrichter. Biết rằng trận động đất năm 2004 gây ra sóng thần tại Bắc Sumatra, Indonexia ngày 26.12.2004 có biên độ rung chấn manh gấp 3,26 lần so với biên độ rung chấn tối đa của trận động đất Chile. Tính cường độ trận động đất ở Bắc Sumatra.
là biên độ chuẩn (hằng số). Vào tháng 2 năm 2010, một trận động đất ở Chile có cường độ 8,8 độ rrichter. Biết rằng trận động đất năm 2004 gây ra sóng thần tại Bắc Sumatra, Indonexia ngày 26.12.2004 có biên độ rung chấn manh gấp 3,26 lần so với biên độ rung chấn tối đa của trận động đất Chile. Tính cường độ trận động đất ở Bắc Sumatra. A, 9,3 độ richter.
B, 9,2 độ richter.
C, 9,1 độ richter.
D, 9,4 độ richter.
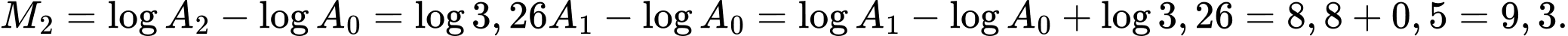
Chọn đáp án A.
Đáp án: A
Câu 34 [29285]: Một trận động đất có cường độ 8,5 richter có biên độ mạnh gấp mấy lần biên độ của một trận động đất có cường độ 6,5 richter? Biết rằng cường độ một trận động đất 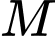 được cho bởi công thức
được cho bởi công thức 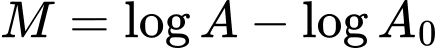 , đơn vị richter với
, đơn vị richter với 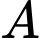 là biên độ rung chấn tối đa và
là biên độ rung chấn tối đa và 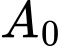 là biên độ chuẩn (hằng số).
là biên độ chuẩn (hằng số).
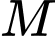 được cho bởi công thức
được cho bởi công thức 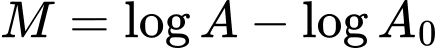 , đơn vị richter với
, đơn vị richter với 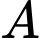 là biên độ rung chấn tối đa và
là biên độ rung chấn tối đa và 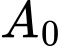 là biên độ chuẩn (hằng số).
là biên độ chuẩn (hằng số). A, 1000 lần.
B, 100 lần.
C, 2 lần.
D, 1024 lần.
Ta có: 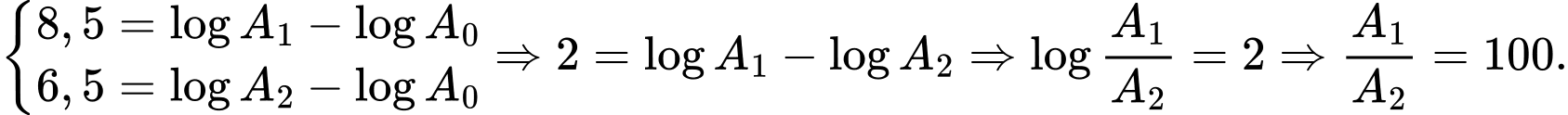
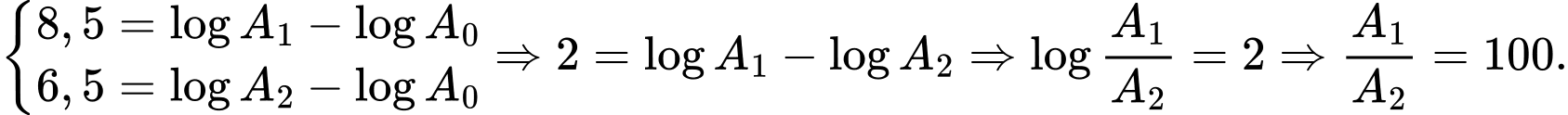
Chọn đáp án B.
Đáp án: B
Câu 35 [28868]: Người ta thả một lá bèo vào một hồ nước. Kinh nghiệm cho thấy sau 14 giờ, bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, lượng lá bèo tăng gấp 10 lần lượng lá bèo trước đó và tốc độ tăng không đổi. Hỏi sau mấy giờ thì số lá bèo phủ kín 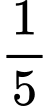 mặt hồ?
mặt hồ?
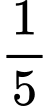 mặt hồ?
mặt hồ? A, 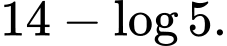
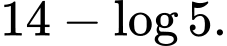
B, 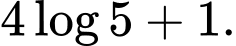
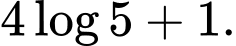
C, 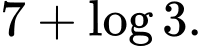
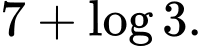
D, 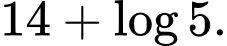
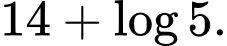
Ta có: 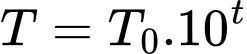 , khi đó sau 14 giờ lượng bèo sẽ là
, khi đó sau 14 giờ lượng bèo sẽ là 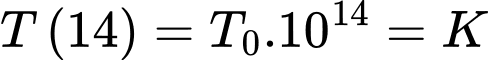 (trong đó
(trong đó 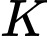 là lượng bèo phủ kín mặt hồ).
là lượng bèo phủ kín mặt hồ). 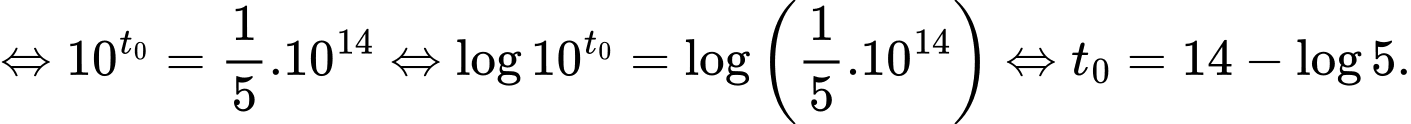 Đáp án: A
Đáp án: A
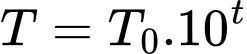 , khi đó sau 14 giờ lượng bèo sẽ là
, khi đó sau 14 giờ lượng bèo sẽ là 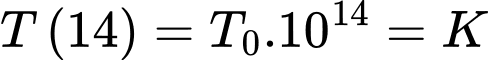 (trong đó
(trong đó 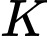 là lượng bèo phủ kín mặt hồ).
là lượng bèo phủ kín mặt hồ). Gọi 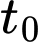 là thời gian bèo phủ
là thời gian bèo phủ 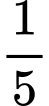 mặt hồ thì ta có:
mặt hồ thì ta có: 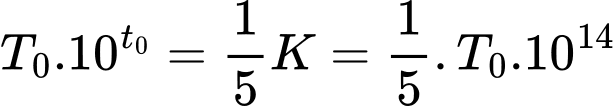
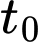 là thời gian bèo phủ
là thời gian bèo phủ 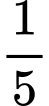 mặt hồ thì ta có:
mặt hồ thì ta có: 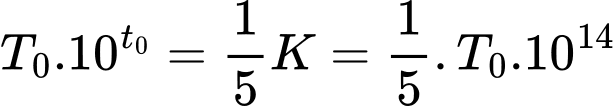
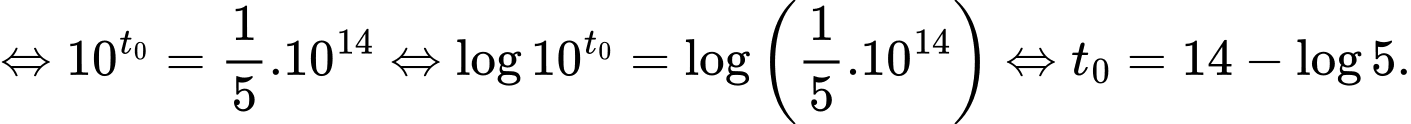
Chọn A.
Câu 36 [28918]: Sự phân rã của các chất phóng xạ được biểu diễn theo công thức hàm số mũ 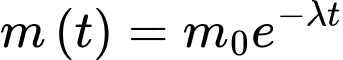 ,
, 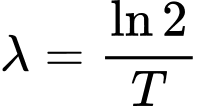 , trong đó
, trong đó 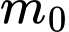 là khối lượng ban đầu của chất phóng xạ,
là khối lượng ban đầu của chất phóng xạ, 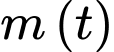 là khối lượng chất phóng xạ tại thời điểm
là khối lượng chất phóng xạ tại thời điểm 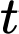 ,
, 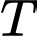 là chu kỳ bán rã. Khi phân tích một mẫu gỗ từ công trình kiến trúc cổ, các nhà khoa học thấy rằng khối lượng cacbon phóng xạ
là chu kỳ bán rã. Khi phân tích một mẫu gỗ từ công trình kiến trúc cổ, các nhà khoa học thấy rằng khối lượng cacbon phóng xạ 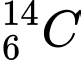 trong mẫu gỗ đó đã mất
trong mẫu gỗ đó đã mất 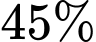 so với lượng
so với lượng 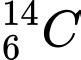 ban đầu của nó. Hỏi công trình kiến trúc đó có niên đại khoảng bao nhiêu năm? Cho biết chu kỳ bán rã của
ban đầu của nó. Hỏi công trình kiến trúc đó có niên đại khoảng bao nhiêu năm? Cho biết chu kỳ bán rã của 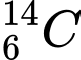 là khoảng
là khoảng 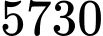 năm.
năm.
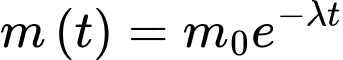 ,
, 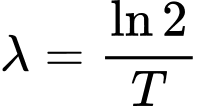 , trong đó
, trong đó 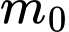 là khối lượng ban đầu của chất phóng xạ,
là khối lượng ban đầu của chất phóng xạ, 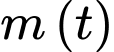 là khối lượng chất phóng xạ tại thời điểm
là khối lượng chất phóng xạ tại thời điểm 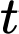 ,
, 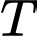 là chu kỳ bán rã. Khi phân tích một mẫu gỗ từ công trình kiến trúc cổ, các nhà khoa học thấy rằng khối lượng cacbon phóng xạ
là chu kỳ bán rã. Khi phân tích một mẫu gỗ từ công trình kiến trúc cổ, các nhà khoa học thấy rằng khối lượng cacbon phóng xạ 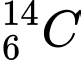 trong mẫu gỗ đó đã mất
trong mẫu gỗ đó đã mất 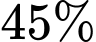 so với lượng
so với lượng 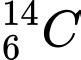 ban đầu của nó. Hỏi công trình kiến trúc đó có niên đại khoảng bao nhiêu năm? Cho biết chu kỳ bán rã của
ban đầu của nó. Hỏi công trình kiến trúc đó có niên đại khoảng bao nhiêu năm? Cho biết chu kỳ bán rã của 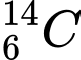 là khoảng
là khoảng 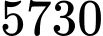 năm.
năm. A, 5157.
B, 3561.
C, 6601.
D, 4942.
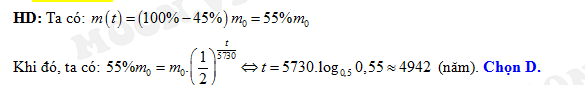 Đáp án: D
Đáp án: D
Câu 37 [28922]: Một sóng âm truyền trong không khí với mức cường độ âm được tính theo công thức 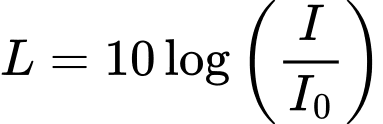 , đợi vị đề xi ben
, đợi vị đề xi ben 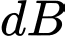 , trong đó
, trong đó 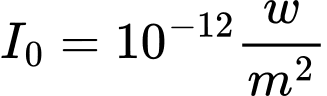 là cường độ ẩm chuẩn. Mức cường độ âm tại điểm
là cường độ ẩm chuẩn. Mức cường độ âm tại điểm 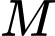 và tại điểm
và tại điểm 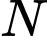 lần lượt là
lần lượt là 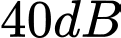 và
và 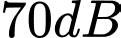 . Cường độ âm tại
. Cường độ âm tại 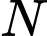 lớn hơn cường độ âm tại
lớn hơn cường độ âm tại 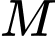 bao nhiêu lần?
bao nhiêu lần?
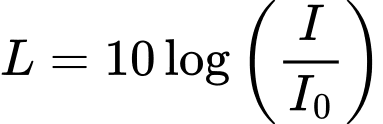 , đợi vị đề xi ben
, đợi vị đề xi ben 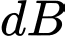 , trong đó
, trong đó 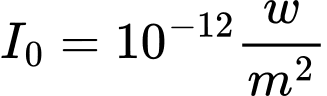 là cường độ ẩm chuẩn. Mức cường độ âm tại điểm
là cường độ ẩm chuẩn. Mức cường độ âm tại điểm 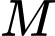 và tại điểm
và tại điểm 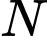 lần lượt là
lần lượt là 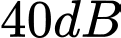 và
và 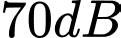 . Cường độ âm tại
. Cường độ âm tại 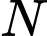 lớn hơn cường độ âm tại
lớn hơn cường độ âm tại 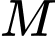 bao nhiêu lần?
bao nhiêu lần? A, 10000 lần.
B, 1000 lần.
C, 40 lần.
D, 20 lần.
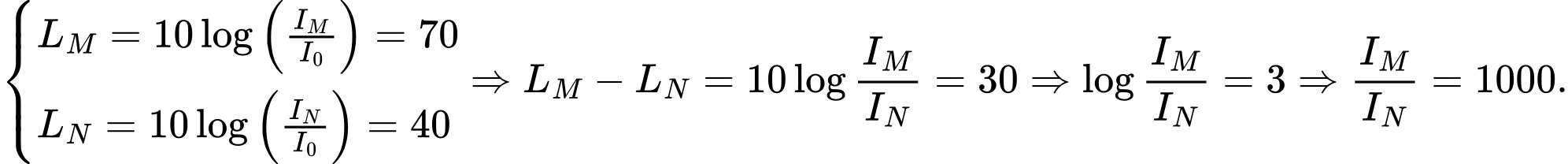 Chọn đáp án B.
Đáp án: B
Chọn đáp án B.
Đáp án: B
Câu 38 [28926]: Gọi 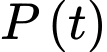 là số phần trăm cacbon 14 còn lại trong một bộ phận của một cây sinh trưởng từ
là số phần trăm cacbon 14 còn lại trong một bộ phận của một cây sinh trưởng từ 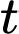 năm trước đây thì ta có công thức
năm trước đây thì ta có công thức 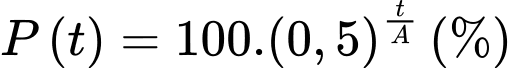 với
với 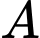 là hằng số. Biết rằng một mẩu gỗ có tuổi khoảng 3574 năm thì lượng cacbon 14 còn lại là 65%. Phân tích mẩu gỗ từ một công trình kiến trúc cổ người ta thấy lượng cacbon 14 còn lại trong mẩu gỗ đó là 63%. Hãy xác định tuổi của mẩu gỗ được lấy từ công trình đó.
là hằng số. Biết rằng một mẩu gỗ có tuổi khoảng 3574 năm thì lượng cacbon 14 còn lại là 65%. Phân tích mẩu gỗ từ một công trình kiến trúc cổ người ta thấy lượng cacbon 14 còn lại trong mẩu gỗ đó là 63%. Hãy xác định tuổi của mẩu gỗ được lấy từ công trình đó.
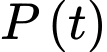 là số phần trăm cacbon 14 còn lại trong một bộ phận của một cây sinh trưởng từ
là số phần trăm cacbon 14 còn lại trong một bộ phận của một cây sinh trưởng từ 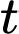 năm trước đây thì ta có công thức
năm trước đây thì ta có công thức 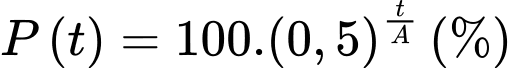 với
với 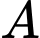 là hằng số. Biết rằng một mẩu gỗ có tuổi khoảng 3574 năm thì lượng cacbon 14 còn lại là 65%. Phân tích mẩu gỗ từ một công trình kiến trúc cổ người ta thấy lượng cacbon 14 còn lại trong mẩu gỗ đó là 63%. Hãy xác định tuổi của mẩu gỗ được lấy từ công trình đó.
là hằng số. Biết rằng một mẩu gỗ có tuổi khoảng 3574 năm thì lượng cacbon 14 còn lại là 65%. Phân tích mẩu gỗ từ một công trình kiến trúc cổ người ta thấy lượng cacbon 14 còn lại trong mẩu gỗ đó là 63%. Hãy xác định tuổi của mẩu gỗ được lấy từ công trình đó. A, 3874 năm.
B, 3833 năm.
C, 3834 năm.
D, 3596 năm.
 Đáp án: B
Đáp án: B
Câu 39 [981103]: Khi ánh sáng đi qua một môi trường (chẳng hạn như không khí, nước, sương mù,…) cường độ sẽ giảm dần theo quãng đường truyền 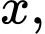 theo công thức
theo công thức 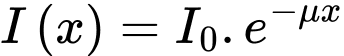 trong đó
trong đó 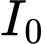 là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và
là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và 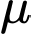 là hệ số hấp thu của môi trường đó. Biết rằng nước biển có hệ số hấp thu
là hệ số hấp thu của môi trường đó. Biết rằng nước biển có hệ số hấp thu 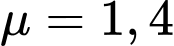 và người ta tính được rằng khi đi từ độ sâu
và người ta tính được rằng khi đi từ độ sâu 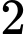 m xuống đến độ sâu 20 m thì cường độ ánh sáng giảm
m xuống đến độ sâu 20 m thì cường độ ánh sáng giảm 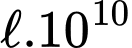 lần. Số nguyên nào sau đây gần với
lần. Số nguyên nào sau đây gần với 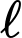 nhất?
nhất?
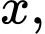 theo công thức
theo công thức 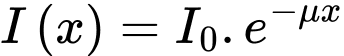 trong đó
trong đó 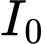 là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và
là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và 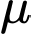 là hệ số hấp thu của môi trường đó. Biết rằng nước biển có hệ số hấp thu
là hệ số hấp thu của môi trường đó. Biết rằng nước biển có hệ số hấp thu 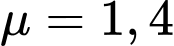 và người ta tính được rằng khi đi từ độ sâu
và người ta tính được rằng khi đi từ độ sâu 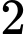 m xuống đến độ sâu 20 m thì cường độ ánh sáng giảm
m xuống đến độ sâu 20 m thì cường độ ánh sáng giảm 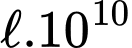 lần. Số nguyên nào sau đây gần với
lần. Số nguyên nào sau đây gần với 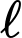 nhất?
nhất? A, 8.
B, 9.
C, 10.
D, 90.
Chọn đáp án B.
Ta có: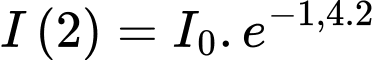
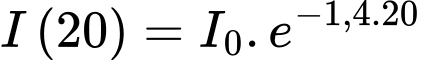
Người ta tính được rằng khi đi từ độ sâu xuống đến độ sâu 20 m thì cường độ ánh sáng giảm
xuống đến độ sâu 20 m thì cường độ ánh sáng giảm 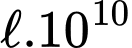 lần.
lần.
Suy ra: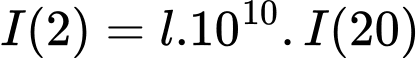
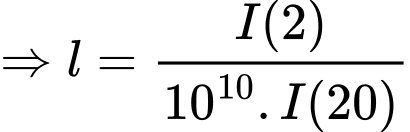
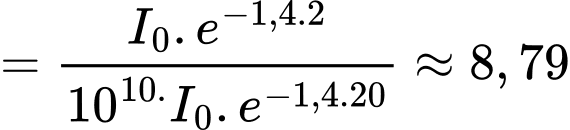 Đáp án: B
Đáp án: B
Ta có:
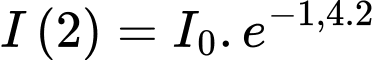
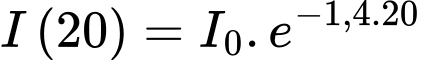
Người ta tính được rằng khi đi từ độ sâu
 xuống đến độ sâu 20 m thì cường độ ánh sáng giảm
xuống đến độ sâu 20 m thì cường độ ánh sáng giảm 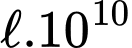 lần.
lần.Suy ra:
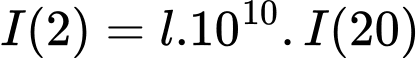
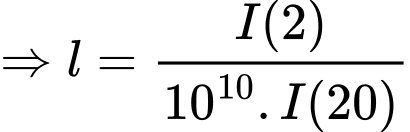
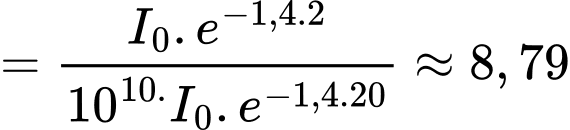 Đáp án: B
Đáp án: B
Câu 40 [981105]: Cho biết chu kì bán rã của chất phóng xạ radi 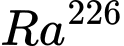 là
là 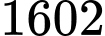 năm (tức là một lượng
năm (tức là một lượng 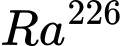 sau
sau 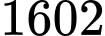 năm phân hủy thì chỉ còn lại một nửa). Sự phân hủy được tính theo công thức
năm phân hủy thì chỉ còn lại một nửa). Sự phân hủy được tính theo công thức 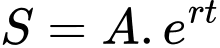 trong đó
trong đó 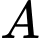 là lượng chất phóng xạ ban đầu,
là lượng chất phóng xạ ban đầu, 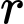 là tỉ lệ phân hủy hàng năm
là tỉ lệ phân hủy hàng năm 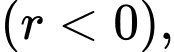
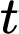 là thời gian phân hủy,
là thời gian phân hủy, 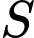 là lượng còn lại sau thời gian phân hủy. Hỏi
là lượng còn lại sau thời gian phân hủy. Hỏi 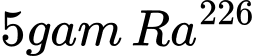 sau
sau  năm phân hủy sẽ còn lại bao nhiêu gam? (làm tròn đến
năm phân hủy sẽ còn lại bao nhiêu gam? (làm tròn đến 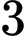 chữ số thập phân).
chữ số thập phân).
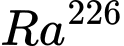 là
là 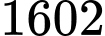 năm (tức là một lượng
năm (tức là một lượng 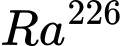 sau
sau 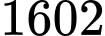 năm phân hủy thì chỉ còn lại một nửa). Sự phân hủy được tính theo công thức
năm phân hủy thì chỉ còn lại một nửa). Sự phân hủy được tính theo công thức 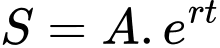 trong đó
trong đó 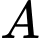 là lượng chất phóng xạ ban đầu,
là lượng chất phóng xạ ban đầu, 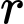 là tỉ lệ phân hủy hàng năm
là tỉ lệ phân hủy hàng năm 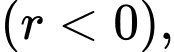
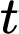 là thời gian phân hủy,
là thời gian phân hủy, 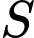 là lượng còn lại sau thời gian phân hủy. Hỏi
là lượng còn lại sau thời gian phân hủy. Hỏi 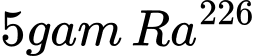 sau
sau  năm phân hủy sẽ còn lại bao nhiêu gam? (làm tròn đến
năm phân hủy sẽ còn lại bao nhiêu gam? (làm tròn đến 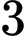 chữ số thập phân).
chữ số thập phân). A, . 

B, 

C, 

D, 

Lời giải: Đầu tiên ta sẽ tính 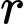 :
: 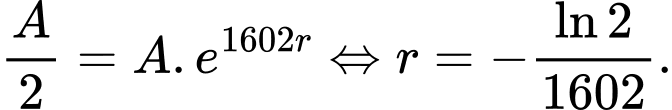 Thay
Thay 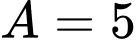 (gam),
(gam), 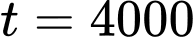 ,
, 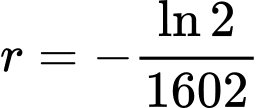 vào công thức
vào công thức  Tìm được
Tìm được 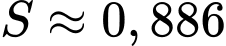 (gam). Chọn A.
Đáp án: A
(gam). Chọn A.
Đáp án: A
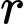 :
: 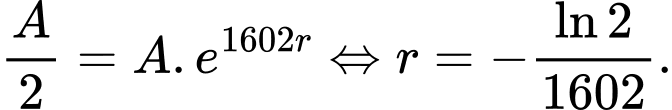 Thay
Thay 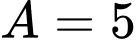 (gam),
(gam), 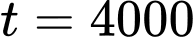 ,
, 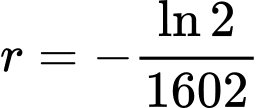 vào công thức
vào công thức  Tìm được
Tìm được 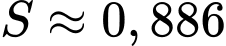 (gam). Chọn A.
Đáp án: A
(gam). Chọn A.
Đáp án: A
Câu 41 [944211]: Áp suất không khí P (đo bằng milimet thủy ngân, kí hiệu mmHg) theo công thức 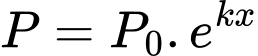 (mmHg), trong đó
(mmHg), trong đó 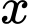 là độ cao (đo bằng mét),
là độ cao (đo bằng mét), 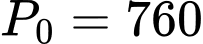 (mmHg) là áp suất không khí ở mức nước biển
(mmHg) là áp suất không khí ở mức nước biển 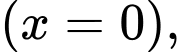 k là hệ số suy giảm. Biết rằng ở độ cao 1000 m thì áp suất không khí là 672,71 (mmHg). Tính áp suất của không khí ở độ cao 3000 m.
k là hệ số suy giảm. Biết rằng ở độ cao 1000 m thì áp suất không khí là 672,71 (mmHg). Tính áp suất của không khí ở độ cao 3000 m.
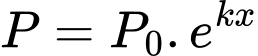 (mmHg), trong đó
(mmHg), trong đó 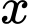 là độ cao (đo bằng mét),
là độ cao (đo bằng mét), 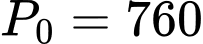 (mmHg) là áp suất không khí ở mức nước biển
(mmHg) là áp suất không khí ở mức nước biển 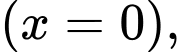 k là hệ số suy giảm. Biết rằng ở độ cao 1000 m thì áp suất không khí là 672,71 (mmHg). Tính áp suất của không khí ở độ cao 3000 m.
k là hệ số suy giảm. Biết rằng ở độ cao 1000 m thì áp suất không khí là 672,71 (mmHg). Tính áp suất của không khí ở độ cao 3000 m. A, 527,06 (mmHg).
B, 530,23 (mmHg).
C, 530,73 (mmHg).
D, 545,01 (mmHg).
Lời giải: Ở độ cao 1000 m ta có: 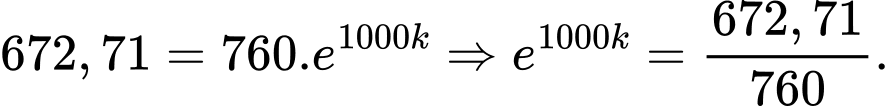 Áp suất không khí ở độ cao 3000 m là:
Áp suất không khí ở độ cao 3000 m là:
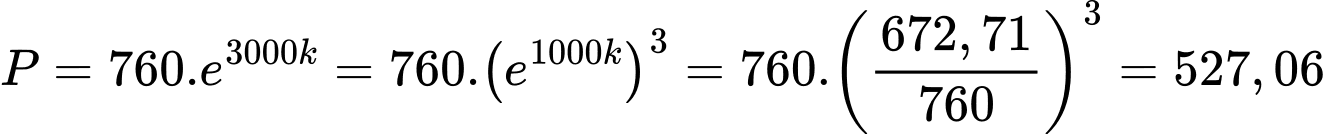 (mmHg). Chọn A.
Đáp án: A
(mmHg). Chọn A.
Đáp án: A
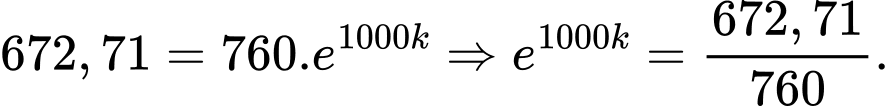 Áp suất không khí ở độ cao 3000 m là:
Áp suất không khí ở độ cao 3000 m là:
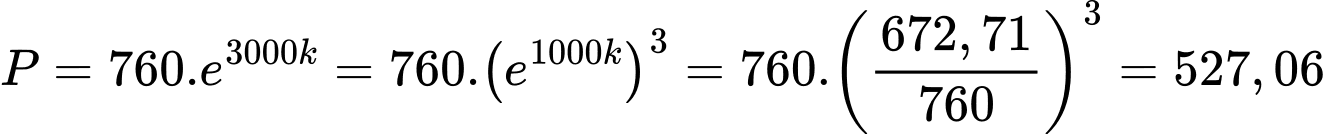 (mmHg). Chọn A.
Đáp án: A
(mmHg). Chọn A.
Đáp án: A
Câu 42 [981671]: Số lượng của loại vi khuẩn A trong một phòng thí nghiệm được tính theo công thức 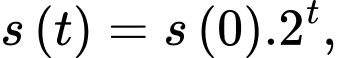 trong đó
trong đó  là số lượng vi khuẩn A lúc ban đầu,
là số lượng vi khuẩn A lúc ban đầu, 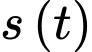 là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con?
là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con?
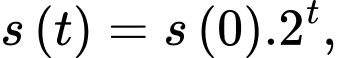 trong đó
trong đó  là số lượng vi khuẩn A lúc ban đầu,
là số lượng vi khuẩn A lúc ban đầu, 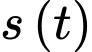 là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con?
là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con? A, 48 phút.
B, 19 phút.
C, 7 phút.
D, 12 phút.
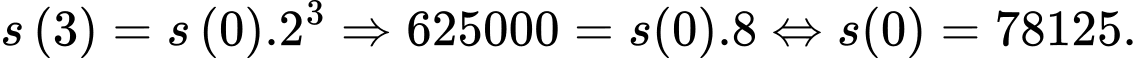

Chọn đáp án C.
Câu 43 [981674]: [Đề thi tham khảo 2020]: Để quảng bá cho sản phẩm A, một công ty dự định tổ chức quảng cáo theo hình thức quảng cáo trên truyền hình. Nghiên cứu của công ty cho thấy: nếu sau n lần quảng cáo được phát thì tỉ lệ người xem quảng cáo đó mua sản phẩm A tuân theo công thức 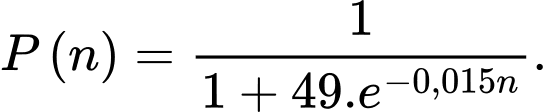 Hỏi cần phát ít nhất bao nhiêu lần quảng cáo để tỉ lệ người xem mua sản phẩm đạt trên 30%?
Hỏi cần phát ít nhất bao nhiêu lần quảng cáo để tỉ lệ người xem mua sản phẩm đạt trên 30%?
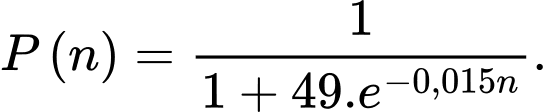 Hỏi cần phát ít nhất bao nhiêu lần quảng cáo để tỉ lệ người xem mua sản phẩm đạt trên 30%?
Hỏi cần phát ít nhất bao nhiêu lần quảng cáo để tỉ lệ người xem mua sản phẩm đạt trên 30%? 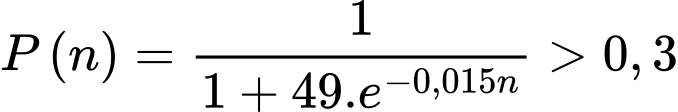
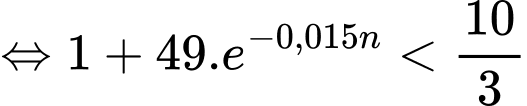
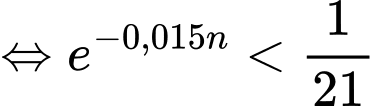
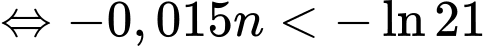
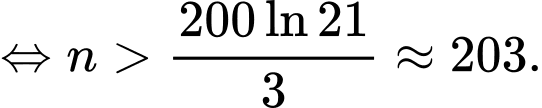
Câu 44 [690318]: Sắt 55 là một nguyên tố phóng xạ được sử dụng trong khoa học thí nghiệm. Nó có chu kỳ bán rã khoảng 2,75 năm. Giả sử một phòng thí nghiệm có 100 gam sắt 55, nếu các nhà khoa học không sử dụng nó thì sau 11 năm sẽ còn bao nhiêu gam sắt 55?
A, 50.
B, 25.
C, 12,5.
D, 6,25.
Chọn đáp án D.
Chu kì bán rã của chất phóng xạ là 2,75 năm (tức là một lượng chất này sau 2,75 năm phân hủy thì chỉ còn một nửa)
Coi lượng chất ban đầu là 100\% , lượng chất giảm đi phân hủy mỗi năm là x\% nta có:
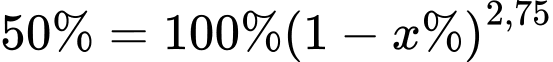
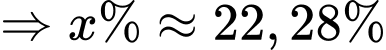
100 gam sắt 55, nếu các nhà khoa học không sử dụng nó thì sau 11 năm sẽ còn:
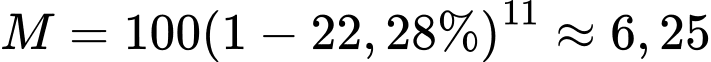
Chu kì bán rã của chất phóng xạ là 2,75 năm (tức là một lượng chất này sau 2,75 năm phân hủy thì chỉ còn một nửa)
Coi lượng chất ban đầu là 100\% , lượng chất giảm đi phân hủy mỗi năm là x\% nta có:
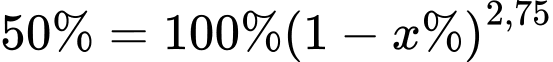
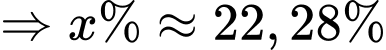
100 gam sắt 55, nếu các nhà khoa học không sử dụng nó thì sau 11 năm sẽ còn:
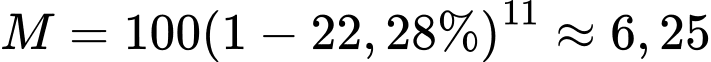
Câu 45 [690319]: Coban 60 là một nguyên tố phóng xạ được sử dụng trong khoa học thí nghiệm. Nó có chu kỳ bán rã khoảng 5,4 năm. Giả sử một phòng thí nghiệm có 150 gam Coban 60. Nếu các nhà khoa học không sử dụng nó thì sau 27 năm nữa lượng Coban 60 vẫn còn bao nhiêu gam?
A, 37,5.
B, 18,75.
C, 9,37.
D, 4,69.
Chọn đáp án D.
Chu kì bán rã của chất phóng xạ là 5,4 năm (tức là một lượng chất này sau 5,4 năm phân hủy thì chỉ còn một nửa)
Coi lượng chất ban đầu là 100\% , lượng chất giảm đi phân hủy mỗi năm là x\% nta có: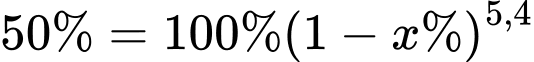
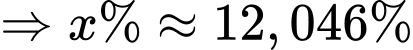
150 gam Coban 60. Nếu các nhà khoa học không sử dụng nó thì sau 27 năm nữa lượng Coban 60 vẫn còn: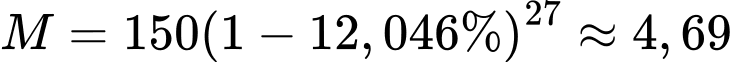 Đáp án: D
Đáp án: D
Chu kì bán rã của chất phóng xạ là 5,4 năm (tức là một lượng chất này sau 5,4 năm phân hủy thì chỉ còn một nửa)
Coi lượng chất ban đầu là 100\% , lượng chất giảm đi phân hủy mỗi năm là x\% nta có:
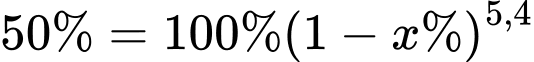
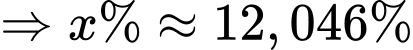
150 gam Coban 60. Nếu các nhà khoa học không sử dụng nó thì sau 27 năm nữa lượng Coban 60 vẫn còn:
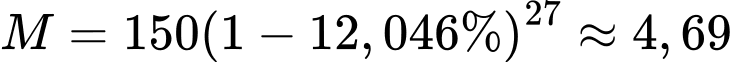 Đáp án: D
Đáp án: D