Câu 1 [583431]: [Đường lên đỉnh Olympia năm thứ 16]: Một lớp có 30 học sinh, biết 25 học sinh thi Toán, 15 học sinh thi Văn. Hỏi có ít nhất bao nhiêu học sinh vừa thi Toán vừa thi Văn?
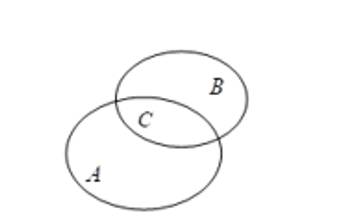
Gọi
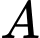 là tập hợp các học sinh chỉ thích môn Toán.
là tập hợp các học sinh chỉ thích môn Toán.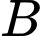 là tập hợp các học sinh chỉ thích môn Văn.
là tập hợp các học sinh chỉ thích môn Văn. là tập hợp các học sinh thích cả hai môn Toán và Văn.
là tập hợp các học sinh thích cả hai môn Toán và Văn.Ta có hệ phương trình:
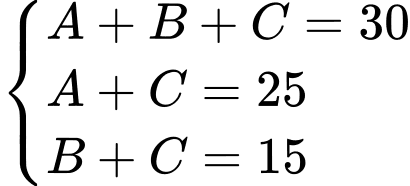
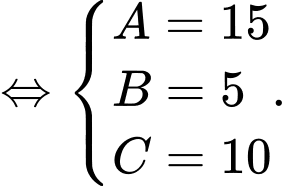
Vậy số học sinh vừa thi Toán vừa thi Văn là: 10 (học sinh).
Câu 2 [583432]: [Đường lên đỉnh Olympia năm thứ 19]: Lớp 9A có 30 học sinh tham gia dạ hội tiếng Anh và tiếng Trung, trong đó có 25 em nói được tiếng Anh, 18 em nói được tiếng Trung. Hỏi có bao nhiêu em nói được hai thứ tiếng?
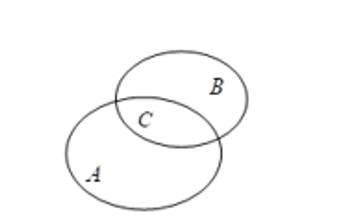
Gọi
 là tập hợp các học sinh chỉ nói được tiếng Anh.
là tập hợp các học sinh chỉ nói được tiếng Anh. là tập hợp các học sinh chỉ nói được tiếng Trung.
là tập hợp các học sinh chỉ nói được tiếng Trung. là tập hợp các học sinh nói được cả hai thứ tiếng.
là tập hợp các học sinh nói được cả hai thứ tiếng.Ta có hệ phương trình:
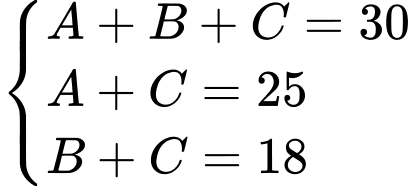
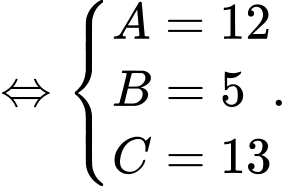
Vậy số học sinh nói được cả hai thứ tiếng là: 13 (học sinh).
Câu 3 [583433]: [Đường lên đỉnh Olympia năm thứ 14]:Lớp 4A có 42 học sinh, trong đó 25 học sinh giỏi toán, 23 học sinh giỏi văn, và 2 học sinh không giỏi môn nào. Hỏi có bao nhiêu học sinh giỏi cả 2 môn?
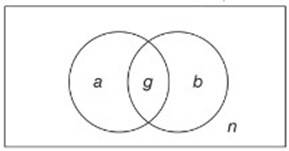
Gọi
 là tập hợp các học sinh chỉ học giỏi Toán.
là tập hợp các học sinh chỉ học giỏi Toán.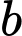 là tập hợp các học sinh chỉ học giỏi Văn.
là tập hợp các học sinh chỉ học giỏi Văn.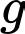 là tập hợp các học sinh giỏi cả hai môn.
là tập hợp các học sinh giỏi cả hai môn. 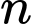 là tập hợp các học sinh không giỏi môn nào.
là tập hợp các học sinh không giỏi môn nào.Từ dữ kiện đề bài cho, ta có hệ phương trình:
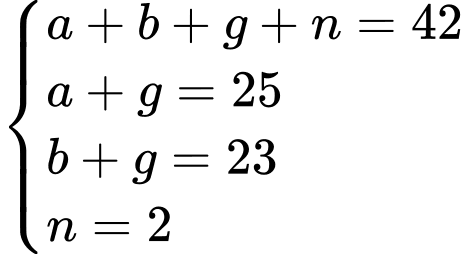
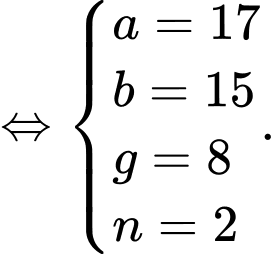
Vậy số học sinh giỏi cả hai môn là: 8 (học sinh).
Câu 4 [583434]: [Đường lên đỉnh Olympia năm thứ 17]: Một khối lớp học hai ngôn ngữ Anh và Pháp, trong đó 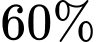 học sinh học tiếng Anh,
học sinh học tiếng Anh, 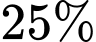 học sinh học tiếng Pháp,
học sinh học tiếng Pháp, 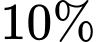 học cả hai thứ tiếng và 35 học sinh không học hai thứ tiếng trên. Hỏi khối lớp này có bao nhiêu học sinh?
học cả hai thứ tiếng và 35 học sinh không học hai thứ tiếng trên. Hỏi khối lớp này có bao nhiêu học sinh?
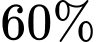 học sinh học tiếng Anh,
học sinh học tiếng Anh, 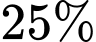 học sinh học tiếng Pháp,
học sinh học tiếng Pháp, 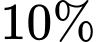 học cả hai thứ tiếng và 35 học sinh không học hai thứ tiếng trên. Hỏi khối lớp này có bao nhiêu học sinh?
học cả hai thứ tiếng và 35 học sinh không học hai thứ tiếng trên. Hỏi khối lớp này có bao nhiêu học sinh? 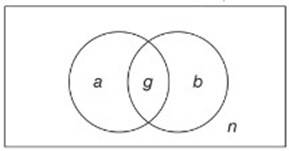
Gọi
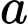 là tập hợp các học sinh chỉ học tiếng Anh.
là tập hợp các học sinh chỉ học tiếng Anh.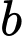 là tập hợp các học sinh chỉ học tiếng Pháp.
là tập hợp các học sinh chỉ học tiếng Pháp.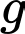 là tập hợp các học sinh học cả hai thứ tiếng.
là tập hợp các học sinh học cả hai thứ tiếng. 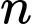 là tập hợp các học sinh không học hai thứ tiếng trên.
là tập hợp các học sinh không học hai thứ tiếng trên.Từ dữ kiện đề bài cho, ta có hệ phương trình:
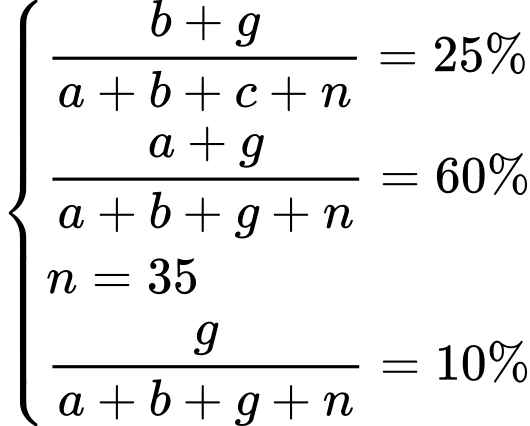
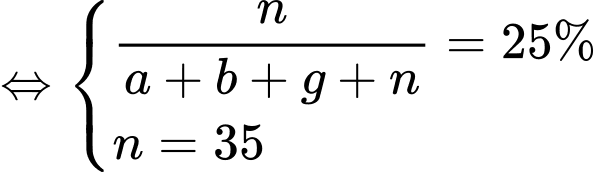
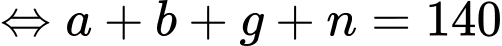
Vậy tổng số học sinh của khối lớp đó là:
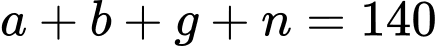 (học sinh).
(học sinh).
Câu 5 [583435]: [Đường lên đỉnh Olympia năm thứ 15 và 19]: Lớp học có 100 bạn. Số bạn đăng kí học bơi là 85. Số bạn đăng kí học bóng chuyền là 70. Số bạn đăng kí bóng rổ là 75. Số bạn đăng kí các môn điền kinh là 80. Hỏi trong lớp có bao nhiêu bạn đăng ký cả bốn nội dung?
Điền đáp án: 10.
Câu 6 [379559]: Biểu đồ ven thể hiện thông số của một cuộc khảo sát. Hình tròn thể hiện tất cả những người thích uống nước khoáng Lavie, hình vuông thể hiện tất cả những người thích uống Coca-Cola, hình tam giác thể hiện tất cả những người thích uống Mirinda, hình chữ nhật thể hiện tất cả những người thích uống Pepsi. Danh sách nào dưới đây đại diện cho những người thích uống nước khoáng Lavie và Coca-Cola?
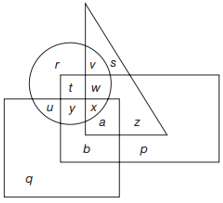

A, u, r, w.
B, v, w, x.
C, b, a, x.
D, u, y, x.
Chọn đáp án D.
Đáp án A sai vì r không thuộc hình chữ nhật.
Đáp án B sai vì v không thuộc hình chữ nhật.
Đáp án C sai vì a, b không thuộc hình tròn. Đáp án: D
Đáp án A sai vì r không thuộc hình chữ nhật.
Đáp án B sai vì v không thuộc hình chữ nhật.
Đáp án C sai vì a, b không thuộc hình tròn. Đáp án: D
Câu 7 [288947]: Moon.vn thực hiện 1 cuộc khảo sát về môn học yêu thích của các bạn 2006 và kết quả nhận được là: 25% học sinh thích môn Văn, 50% học sinh thích môn Toán và 40% học sinh không thích môn Văn và Toán. Vậy có bao nhiêu phần trăm học sinh thích cả 2 môn trên?
A, 10%.
B, 15%.
C, 20%.
D, 25%.
Chọn đáp án B.
Số học sinh thích môn Văn hoặc Toán là: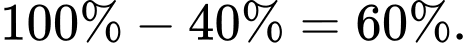
Số học sinh thích cả 2 môn Văn và Toán là: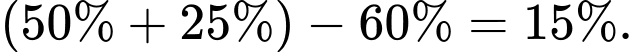
Cách khác:
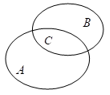
Gọi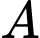 là tập hợp các học sinh chỉ thích môn Toán.
là tập hợp các học sinh chỉ thích môn Toán.
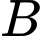 là tập hợp các học sinh chỉ thích môn Văn.
là tập hợp các học sinh chỉ thích môn Văn.
 là tập hợp các học sinh thích cả hai môn Toán và Văn.
là tập hợp các học sinh thích cả hai môn Toán và Văn.
Số học sinh thích môn Văn hoặc Toán là: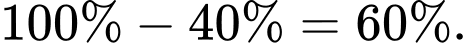
Theo sơ đồ Ven ta có: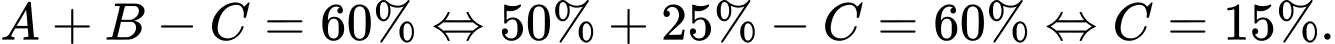
Do vậy số học sinh thích cả 2 môn Văn và Toán là: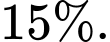 Đáp án: B
Đáp án: B
Số học sinh thích môn Văn hoặc Toán là:
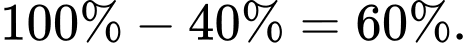
Số học sinh thích cả 2 môn Văn và Toán là:
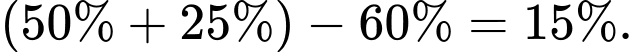
Cách khác:

Gọi
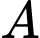 là tập hợp các học sinh chỉ thích môn Toán.
là tập hợp các học sinh chỉ thích môn Toán. là tập hợp các học sinh chỉ thích môn Văn.
là tập hợp các học sinh chỉ thích môn Văn. là tập hợp các học sinh thích cả hai môn Toán và Văn.
là tập hợp các học sinh thích cả hai môn Toán và Văn.Số học sinh thích môn Văn hoặc Toán là:
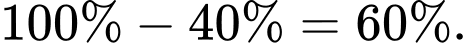
Theo sơ đồ Ven ta có:
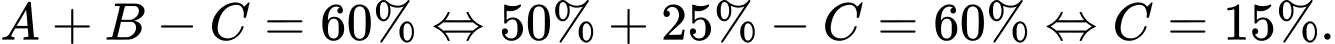
Do vậy số học sinh thích cả 2 môn Văn và Toán là:
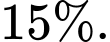 Đáp án: B
Đáp án: B
Câu 8 [290999]: Một cuộc khảo sát được thực hiện với các bệnh nhân mắc Covid-19 tại một thị trấn. Người ta phát hiện ra rằng 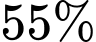 số bệnh nhân mắc Covid-19 mắc bệnh tiểu đường,
số bệnh nhân mắc Covid-19 mắc bệnh tiểu đường, 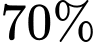 mắc bệnh tim và
mắc bệnh tim và 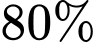 mắc bệnh trầm cảm. Tỷ lệ phần trăm tối thiểu bệnh nhân mắc cả ba bệnh tiểu đường, bệnh tim và trầm cảm là bao nhiêu?
mắc bệnh trầm cảm. Tỷ lệ phần trăm tối thiểu bệnh nhân mắc cả ba bệnh tiểu đường, bệnh tim và trầm cảm là bao nhiêu?
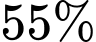 số bệnh nhân mắc Covid-19 mắc bệnh tiểu đường,
số bệnh nhân mắc Covid-19 mắc bệnh tiểu đường, 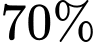 mắc bệnh tim và
mắc bệnh tim và 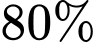 mắc bệnh trầm cảm. Tỷ lệ phần trăm tối thiểu bệnh nhân mắc cả ba bệnh tiểu đường, bệnh tim và trầm cảm là bao nhiêu?
mắc bệnh trầm cảm. Tỷ lệ phần trăm tối thiểu bệnh nhân mắc cả ba bệnh tiểu đường, bệnh tim và trầm cảm là bao nhiêu? A, 5%.
B, 10%.
C, 15%.
D, 20%.
Chọn đáp án A.
Tỷ lệ phần trăm tối thiểu bệnh nhân mắc cả ba bệnh tiểu đường, bệnh tim và trầm cảm là:
 Đáp án: A
Đáp án: A
Tỷ lệ phần trăm tối thiểu bệnh nhân mắc cả ba bệnh tiểu đường, bệnh tim và trầm cảm là:
 Đáp án: A
Đáp án: A
Câu 9 [379564]: Khảo sát 150 sinh viên đang theo học ngành khoa học máy tính tại một trường Đại học về việc sinh viên đó sử dụng phương thức xét tuyển nào để đỗ vào ngành học. Kết quả cho thấy có 45 sinh viên xét tuyển thẳng/xét tuyển ưu tiên, có 65 sinh viên sử dụng kết quả của bài thi ĐGNL (Đánh giá năng lực) và 10 sinh viên sử dụng kết hợp của hai phương thức này để xét tuyển. Vậy có bao nhiêu sinh viên không sử dụng hai phương thức xét tuyển trên để đỗ vào ngành học đó?
A, 20.
B, 30.
C, 40.
D, 50.
Chọn đáp án D.
Gọi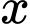 là tập hợp các sinh viên chỉ xét tuyển thẳng/xét tuyển ưu tiên.
là tập hợp các sinh viên chỉ xét tuyển thẳng/xét tuyển ưu tiên.
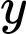 là tập hợp các sinh viên chỉ sử dụng kết quả của bài thi ĐGNL.
là tập hợp các sinh viên chỉ sử dụng kết quả của bài thi ĐGNL.
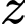 là tập hợp các sinh viên sử dụng kết hợp của hai phương thức.
là tập hợp các sinh viên sử dụng kết hợp của hai phương thức.
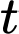 là tập hợp các sinh viên không sử dụng hai phương thức xét tuyển trên.
là tập hợp các sinh viên không sử dụng hai phương thức xét tuyển trên.
Từ dữ kiện đề bài cho, ta có hệ phương trình:
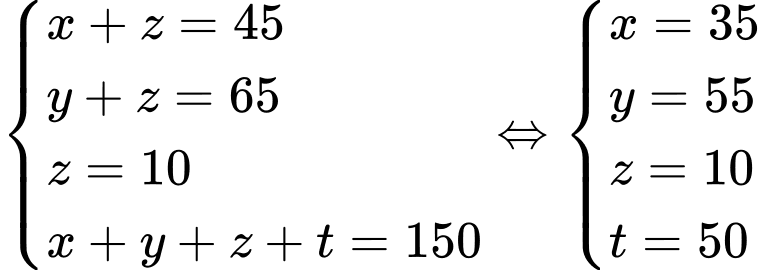
Vậy có 50 sinh viên không sử dụng hai phương thức xét tuyển trên để đỗ vào ngành học. Đáp án: D

Gọi
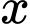 là tập hợp các sinh viên chỉ xét tuyển thẳng/xét tuyển ưu tiên.
là tập hợp các sinh viên chỉ xét tuyển thẳng/xét tuyển ưu tiên. 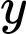 là tập hợp các sinh viên chỉ sử dụng kết quả của bài thi ĐGNL.
là tập hợp các sinh viên chỉ sử dụng kết quả của bài thi ĐGNL. 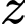 là tập hợp các sinh viên sử dụng kết hợp của hai phương thức.
là tập hợp các sinh viên sử dụng kết hợp của hai phương thức. 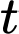 là tập hợp các sinh viên không sử dụng hai phương thức xét tuyển trên.
là tập hợp các sinh viên không sử dụng hai phương thức xét tuyển trên.Từ dữ kiện đề bài cho, ta có hệ phương trình:
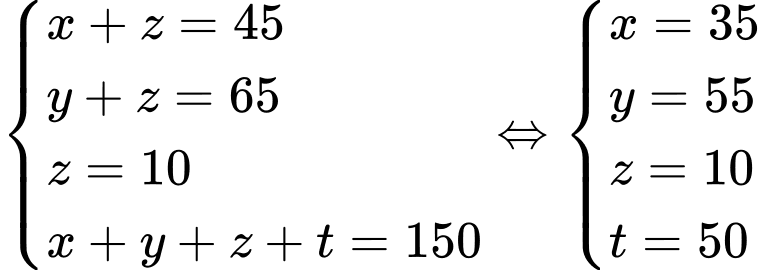
Vậy có 50 sinh viên không sử dụng hai phương thức xét tuyển trên để đỗ vào ngành học. Đáp án: D
Câu 10 [379560]: Lớp 12A1 có 32 học sinh thuộc đội tuyển Toán, 35 học sinh thuộc đội tuyển Lý và có 22 học sinh thuộc cả hai đội tuyển Toán và Lý. Vậy lớp 12A1 có bao nhiêu học sinh thuộc đội tuyển Toán hoặc Lý?
A, 86 học sinh.
B, 78 học sinh.
C, 60 học sinh.
D, 45 học sinh.
Chọn đáp án D.
Gọi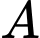 là tập hợp các học sinh chỉ thuộc đội tuyển Toán.
là tập hợp các học sinh chỉ thuộc đội tuyển Toán.
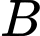 là tập hợp các học sinh chỉ thuộc đội tuyển Lý.
là tập hợp các học sinh chỉ thuộc đội tuyển Lý.
 là tập hợp các học sinh thuộc cả hai đội tuyển Toán và Lý.
là tập hợp các học sinh thuộc cả hai đội tuyển Toán và Lý.
Từ dữ kiện đề bài, ta có hệ phương trình:
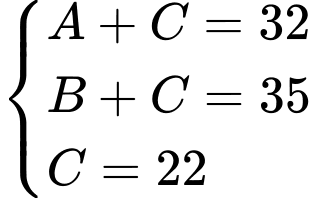
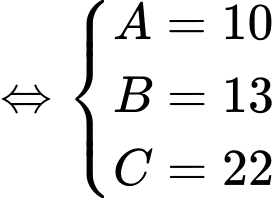
Số học sinh của lớp 12A thuộc đội tuyển Toán hoặc Lý là: (học sinh). Đáp án: D
(học sinh). Đáp án: D

Gọi
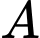 là tập hợp các học sinh chỉ thuộc đội tuyển Toán.
là tập hợp các học sinh chỉ thuộc đội tuyển Toán.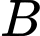 là tập hợp các học sinh chỉ thuộc đội tuyển Lý.
là tập hợp các học sinh chỉ thuộc đội tuyển Lý. là tập hợp các học sinh thuộc cả hai đội tuyển Toán và Lý.
là tập hợp các học sinh thuộc cả hai đội tuyển Toán và Lý.Từ dữ kiện đề bài, ta có hệ phương trình:
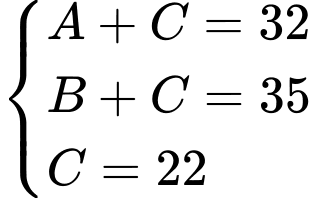
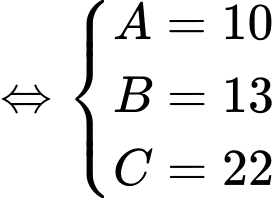
Số học sinh của lớp 12A thuộc đội tuyển Toán hoặc Lý là:
 (học sinh). Đáp án: D
(học sinh). Đáp án: D
Câu 11 [289429]: Bạn Hưng về nghỉ hè ở quê một số ngày, trong đó có 10 ngày mưa. Biết rằng có 11 buổi sáng không mưa, có 9 buổi chiều không mưa và không bao giờ trời mưa cả sáng lẫn chiều. Hỏi bạn Hưng về quê có bao nhiêu ngày mưa buổi sáng?
A, 4 ngày.
B, 8 ngày.
C, 10 ngày.
D, 19 ngày.
Đặt 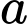 là số ngày chỉ mưa buổi sáng.
là số ngày chỉ mưa buổi sáng.
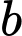 là số ngày chỉ mưa buổi chiều.
là số ngày chỉ mưa buổi chiều.
 là số ngày không mưa.
là số ngày không mưa.
Theo đề bài, ta có hệ phương trình:
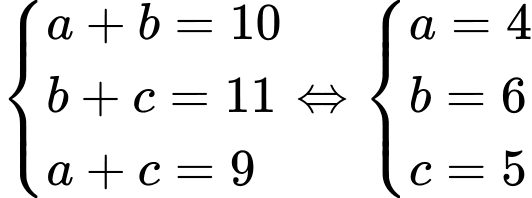
Chọn đáp án A.
Cách khác:
Theo giả thiết: 10 ngày mưa mà không bao giờ trời mưa cả sáng lẫn chiều
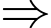 bạn Hưng về quê nghỉ hè có 10 buổi mưa.
bạn Hưng về quê nghỉ hè có 10 buổi mưa.
Mà có 11 buổi sáng không mưa, có 9 buổi chiều không mưa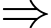 bạn Hưng về quê số buổi là:
bạn Hưng về quê số buổi là:  buổi.
buổi.
Do 1 ngày có 2 buổi sáng và chiều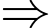 bạn Hưng về quê số ngày là:
bạn Hưng về quê số ngày là: 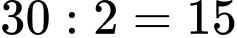 ngày.
ngày.
Mà bạn Hưng về quê có 11 buổi sáng không mưa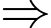 bạn Hưng về quê có số ngày mưa buổi sáng là:
bạn Hưng về quê có số ngày mưa buổi sáng là:  ngày. Đáp án: A
ngày. Đáp án: A
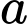 là số ngày chỉ mưa buổi sáng.
là số ngày chỉ mưa buổi sáng.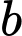 là số ngày chỉ mưa buổi chiều.
là số ngày chỉ mưa buổi chiều. là số ngày không mưa.
là số ngày không mưa.Theo đề bài, ta có hệ phương trình:
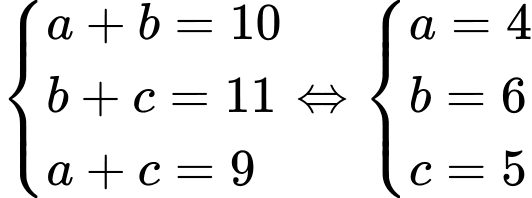
Chọn đáp án A.
Cách khác:
Theo giả thiết: 10 ngày mưa mà không bao giờ trời mưa cả sáng lẫn chiều
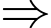 bạn Hưng về quê nghỉ hè có 10 buổi mưa.
bạn Hưng về quê nghỉ hè có 10 buổi mưa.Mà có 11 buổi sáng không mưa, có 9 buổi chiều không mưa
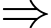 bạn Hưng về quê số buổi là:
bạn Hưng về quê số buổi là:  buổi.
buổi.Do 1 ngày có 2 buổi sáng và chiều
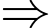 bạn Hưng về quê số ngày là:
bạn Hưng về quê số ngày là: 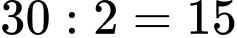 ngày.
ngày.Mà bạn Hưng về quê có 11 buổi sáng không mưa
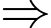 bạn Hưng về quê có số ngày mưa buổi sáng là:
bạn Hưng về quê có số ngày mưa buổi sáng là:  ngày. Đáp án: A
ngày. Đáp án: A
Câu 12 [379561]: Trong một lớp chọn có 30% học sinh tham gia đội tuyển Văn và 75% học sinh tham gia đội tuyển Toán. Lớp đó có 6 học sinh tham gia cả 2 hai đội Văn và Toán; có 3 học sinh không tham gia cả 2 đội tuyển Văn và Toán. Vậy lớp đó có bao nhiêu học sinh?
A, 100.
B, 75.
C, 60.
D, 80.
Chọn đáp án C.
Cách 1:
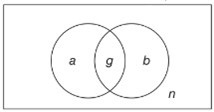
Gọi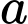 là tập hợp các học sinh chỉ thuộc đội tuyển Toán.
là tập hợp các học sinh chỉ thuộc đội tuyển Toán.
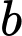 là tập hợp các học sinh chỉ thuộc đội tuyển Văn.
là tập hợp các học sinh chỉ thuộc đội tuyển Văn.
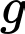 là tập hợp các học sinh thuộc cả hai đội tuyển Toán và Văn.
là tập hợp các học sinh thuộc cả hai đội tuyển Toán và Văn.
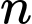 là tập hợp các học sinh không tham gia cả hai đội tuyển.
là tập hợp các học sinh không tham gia cả hai đội tuyển.
Từ dữ kiện đề bài cho, ta có hệ phương trình:
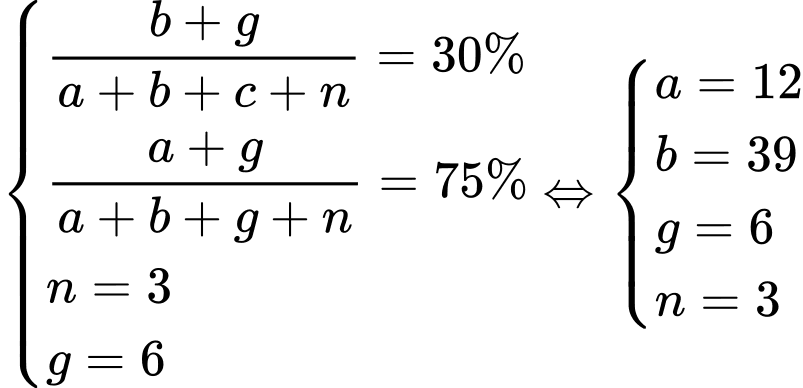
Vậy tổng số học sinh của lớp đó là: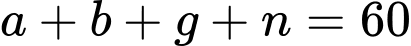 (học sinh).
(học sinh).
Cách 2:
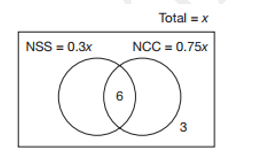
Gọi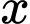 là số học sinh của lớp chọn đó.
là số học sinh của lớp chọn đó.
Ta có: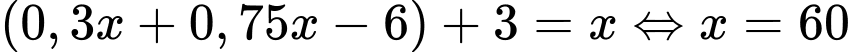 (học sinh) Đáp án: C
(học sinh) Đáp án: C
Cách 1:

Gọi
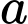 là tập hợp các học sinh chỉ thuộc đội tuyển Toán.
là tập hợp các học sinh chỉ thuộc đội tuyển Toán.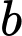 là tập hợp các học sinh chỉ thuộc đội tuyển Văn.
là tập hợp các học sinh chỉ thuộc đội tuyển Văn.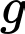 là tập hợp các học sinh thuộc cả hai đội tuyển Toán và Văn.
là tập hợp các học sinh thuộc cả hai đội tuyển Toán và Văn. 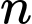 là tập hợp các học sinh không tham gia cả hai đội tuyển.
là tập hợp các học sinh không tham gia cả hai đội tuyển.Từ dữ kiện đề bài cho, ta có hệ phương trình:
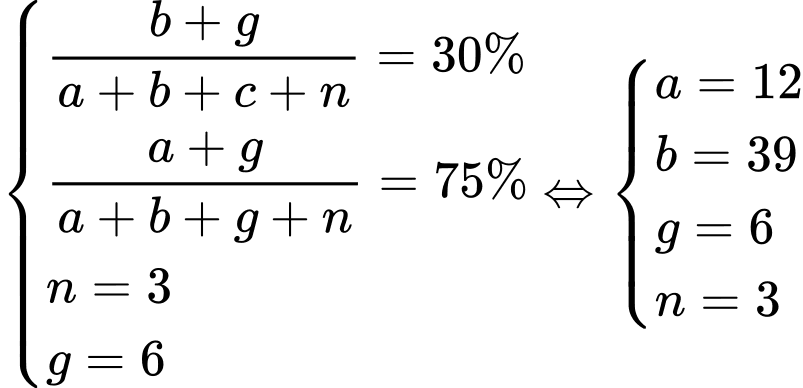
Vậy tổng số học sinh của lớp đó là:
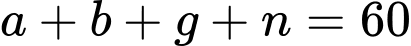 (học sinh).
(học sinh).Cách 2:

Gọi
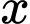 là số học sinh của lớp chọn đó.
là số học sinh của lớp chọn đó.Ta có:
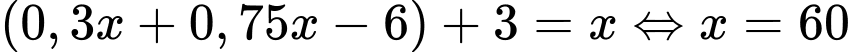 (học sinh) Đáp án: C
(học sinh) Đáp án: C
Câu 13 [379562]: Trong một hội nghị có 100 đại biểu tham dự. Mỗi đại biểu nói được ít nhất một trong ba thứ tiếng: Nga, Anh hoặc Pháp. Biết rằng có 39 đại biểu chỉ nói được tiếng Anh, 35 đại biểu nói được tiếng Pháp, 8 đại biểu nói được đúng hai thứ tiếng là tiếng Anh và tiếng Nga. Hỏi có bao nhiêu đại biểu chỉ nói được tiếng Nga?
A, 18 đại biểu.
B, 26 đại biểu.
C, 36 đại biểu.
D, 61 đại biểu.
Chọn đáp án A.
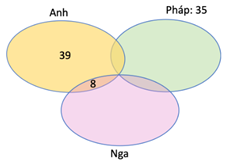
Dựa vào biểu đồ Venn, ta suy ra số đại biểu nói được tiếng Pháp và tiếng Nga là:
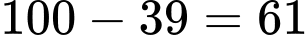 (đại biểu)
(đại biểu)
Số đại biểu nói được tiếng Nga nhưng không nói được tiếng Pháp là:
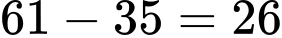 (đại biểu)
(đại biểu)
Số đại biểu chỉ nói được tiếng Nga là:
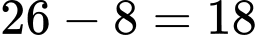 (đại biểu)
(đại biểu)
Vậy có 18 đại biểu chỉ nói được tiếng Nga. Đáp án: A

Dựa vào biểu đồ Venn, ta suy ra số đại biểu nói được tiếng Pháp và tiếng Nga là:
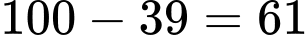 (đại biểu)
(đại biểu)Số đại biểu nói được tiếng Nga nhưng không nói được tiếng Pháp là:
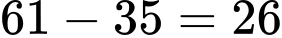 (đại biểu)
(đại biểu)Số đại biểu chỉ nói được tiếng Nga là:
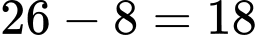 (đại biểu)
(đại biểu)Vậy có 18 đại biểu chỉ nói được tiếng Nga. Đáp án: A
Câu 14 [379563]: Trường THPT X có 30 học sinh thi học sinh giỏi (HSG) cấp huyện hai môn Toán và Lý. Có 10 học sinh được giải HSG môn Toán, có 4 học sinh không được giải môn gì cả, có 8 học sinh chỉ được giải HSG môn Toán. Vậy có bao nhiêu học sinh chỉ đạt giải đúng một trong hai môn trên?
A, 5.
B, 16.
C, 24.
D, 28.
Chọn đáp án C.
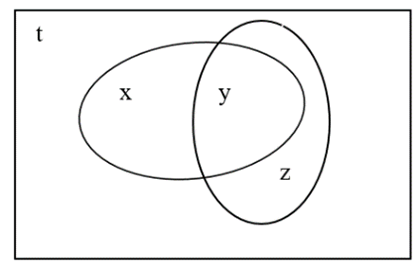
Gọi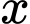 là tập hợp các học sinh chỉ được giải HSG môn Toán.
là tập hợp các học sinh chỉ được giải HSG môn Toán.
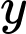 là tập hợp các học sinh chỉ được giải HSG môn Lý.
là tập hợp các học sinh chỉ được giải HSG môn Lý.
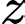 là tập hợp các học sinh được giải cả hai môn.
là tập hợp các học sinh được giải cả hai môn.
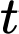 là tập hợp các học sinh không được giải môn nào.
là tập hợp các học sinh không được giải môn nào.
Từ dữ kiện đề bài cho, ta có hệ phương trình:
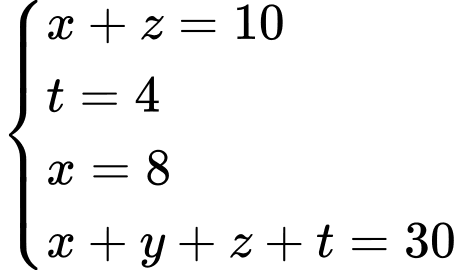
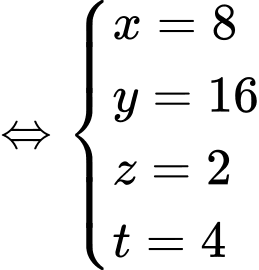
Vậy số học sinh đạt đúng một giải trong hai môn là: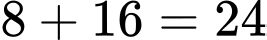 (học sinh). Đáp án: C
(học sinh). Đáp án: C

Gọi
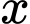 là tập hợp các học sinh chỉ được giải HSG môn Toán.
là tập hợp các học sinh chỉ được giải HSG môn Toán.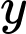 là tập hợp các học sinh chỉ được giải HSG môn Lý.
là tập hợp các học sinh chỉ được giải HSG môn Lý.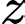 là tập hợp các học sinh được giải cả hai môn.
là tập hợp các học sinh được giải cả hai môn. 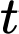 là tập hợp các học sinh không được giải môn nào.
là tập hợp các học sinh không được giải môn nào.Từ dữ kiện đề bài cho, ta có hệ phương trình:
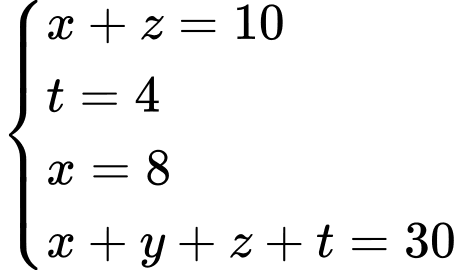
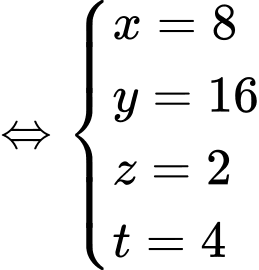
Vậy số học sinh đạt đúng một giải trong hai môn là:
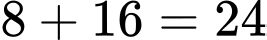 (học sinh). Đáp án: C
(học sinh). Đáp án: C
Câu 15 [379566]: Một cuộc khảo sát được thực hiện với 2000 đàn ông tại một huyện, người ta thấy có 48% thích uống cà phê; 54% thích uống chè và 64% thích hút thuốc; có 28% số người thích uống cả cà phê và chè; 32% thích hút thuốc và uống chè; 30% thích hút thuốc và uống cà phê; có 6% số đàn ông không thích ba thứ trên. Tỉ lệ giữa số người chỉ thích uống cà phê và hút thuốc so với số người chỉ thích uống trà là
A, 1: 2.
B, 1: 1.
C, 3: 1.
D, 2: 1.
Chọn đáp án B.
Gọi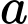 là số người chỉ thích uống cà phê.
là số người chỉ thích uống cà phê.
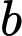 là số người chỉ thích uống chè.
là số người chỉ thích uống chè.
 là số người chỉ thích hút thuốc.
là số người chỉ thích hút thuốc.
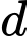 là số người chỉ thích uống cà phê và chè.
là số người chỉ thích uống cà phê và chè.
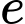 là số người chỉ thích hút thuốc và uống chè.
là số người chỉ thích hút thuốc và uống chè.
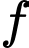 là số người chỉ thích hút thuốc và uống cà phê.
là số người chỉ thích hút thuốc và uống cà phê.
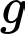 là số người thích cả ba thứ.
là số người thích cả ba thứ.
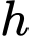 là số người không thích cả ba thứ
là số người không thích cả ba thứ 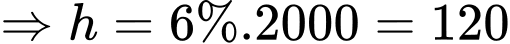 (người).
(người).
Dựa vào dữ kiện đề bài, ta có hệ phương trình:

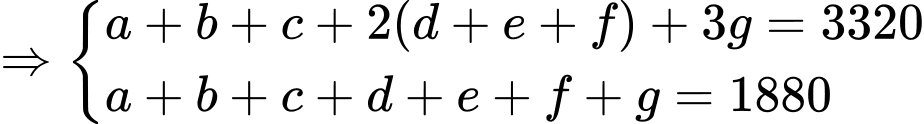
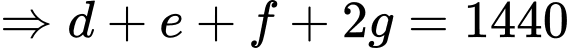

Có: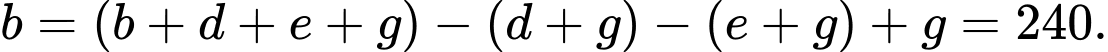
Vậy tỉ lệ giữa số người chỉ thích uống cà phê và hút thuốc so với số người chỉ thích uống chè là: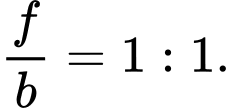 Đáp án: B
Đáp án: B
Gọi
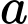 là số người chỉ thích uống cà phê.
là số người chỉ thích uống cà phê. 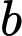 là số người chỉ thích uống chè.
là số người chỉ thích uống chè.  là số người chỉ thích hút thuốc.
là số người chỉ thích hút thuốc. 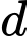 là số người chỉ thích uống cà phê và chè.
là số người chỉ thích uống cà phê và chè. 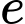 là số người chỉ thích hút thuốc và uống chè.
là số người chỉ thích hút thuốc và uống chè. 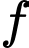 là số người chỉ thích hút thuốc và uống cà phê.
là số người chỉ thích hút thuốc và uống cà phê. 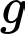 là số người thích cả ba thứ.
là số người thích cả ba thứ. 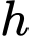 là số người không thích cả ba thứ
là số người không thích cả ba thứ 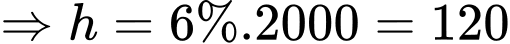 (người).
(người).Dựa vào dữ kiện đề bài, ta có hệ phương trình:

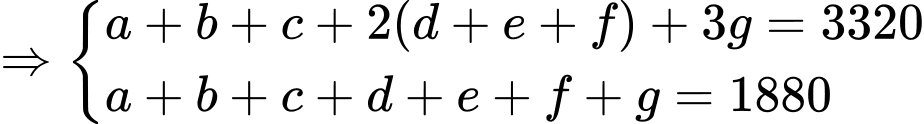
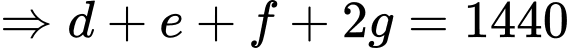

Có:
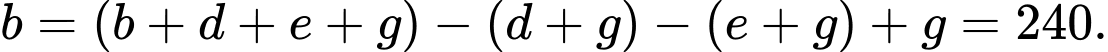
Vậy tỉ lệ giữa số người chỉ thích uống cà phê và hút thuốc so với số người chỉ thích uống chè là:
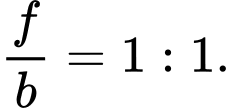 Đáp án: B
Đáp án: B
Câu 16 [379565]: Dữ liệu ghi nhận trong một ngày tại một quán Buffet cho thấy có 5% số bàn không gọi hoa quả, nước ngọt và kem; có 10% số bàn gọi cả ba thứ này; có 20% số bàn gọi hoa quả và nước ngọt; 25% gọi hoa quả và kem; 25% gọi nước ngọt và kem; 50% gọi hoa quả và 50% số bàn gọi kem. Số bàn chỉ gọi hoa quả nhiều hơn bao nhiêu phần trăm so với số bàn chỉ gọi kem?
A, 50%.
B, 100%.
C, 0%.
D, 5%.
Chọn đáp án A.
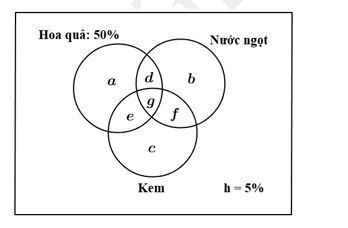
Gọi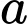 là số bàn chỉ gọi hoa quả.
là số bàn chỉ gọi hoa quả.
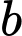 là số bàn chỉ gọi nước ngọt.
là số bàn chỉ gọi nước ngọt.
 là số bàn chỉ gọi kem.
là số bàn chỉ gọi kem.
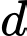 là số bàn chỉ gọi hoa quả và nước ngọt.
là số bàn chỉ gọi hoa quả và nước ngọt.
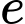 là số bàn chỉ gọi hoa quả và kem.
là số bàn chỉ gọi hoa quả và kem.
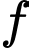 là số bàn chỉ gọi nước ngọt và kem.
là số bàn chỉ gọi nước ngọt và kem.
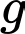 là số bàn gọi cả ba thứ
là số bàn gọi cả ba thứ 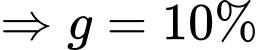
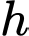 là số bàn không gọi cả ba thứ
là số bàn không gọi cả ba thứ 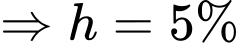
Từ dữ kiện đề bài, ta có hệ phương trình: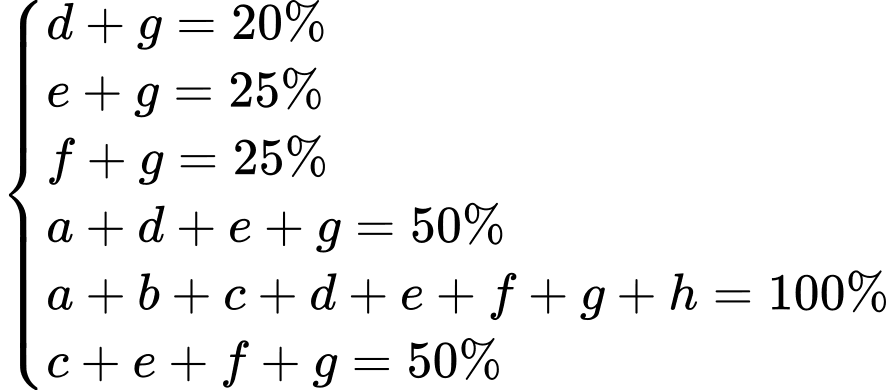
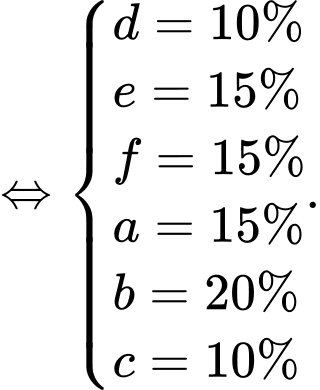
Số bàn chỉ gọi hoa quả nhiều hơn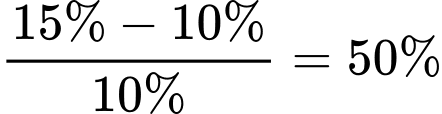 so với số bàn chỉ gọi kem. Đáp án: A
so với số bàn chỉ gọi kem. Đáp án: A

Gọi
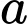 là số bàn chỉ gọi hoa quả.
là số bàn chỉ gọi hoa quả.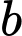 là số bàn chỉ gọi nước ngọt.
là số bàn chỉ gọi nước ngọt. là số bàn chỉ gọi kem.
là số bàn chỉ gọi kem.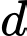 là số bàn chỉ gọi hoa quả và nước ngọt.
là số bàn chỉ gọi hoa quả và nước ngọt.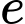 là số bàn chỉ gọi hoa quả và kem.
là số bàn chỉ gọi hoa quả và kem.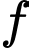 là số bàn chỉ gọi nước ngọt và kem.
là số bàn chỉ gọi nước ngọt và kem.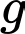 là số bàn gọi cả ba thứ
là số bàn gọi cả ba thứ 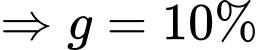
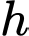 là số bàn không gọi cả ba thứ
là số bàn không gọi cả ba thứ 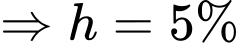
Từ dữ kiện đề bài, ta có hệ phương trình:
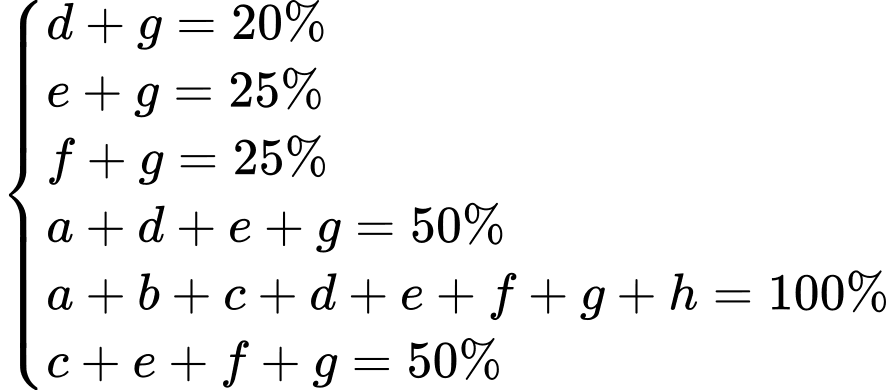
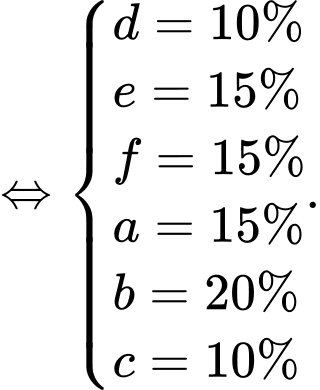
Số bàn chỉ gọi hoa quả nhiều hơn
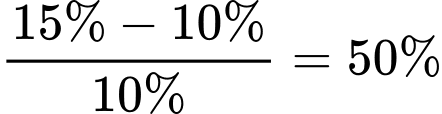 so với số bàn chỉ gọi kem. Đáp án: A
so với số bàn chỉ gọi kem. Đáp án: A
Câu 17 [379567]: Trong một cuộc khảo sát 1000 bạn sinh viên của trường X về việc lựa chọn ít nhất 1 trong 3 môn đại cương mà các bạn đấy cảm thấy dễ học nhất. Nếu 320 bạn chọn môn triết học, 480 bạn chọn môn pháp luật đại cương, 360 bạn chọn môn xác suất thống kê thì tối đa có bao nhiêu bạn chọn cả 3 môn?
A, 60.
B, 80.
C, 100.
D, 120.
Chọn đáp án B.
Gọi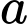 là số sinh viên chỉ chọn triết học.
là số sinh viên chỉ chọn triết học.
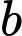 là số sinh viên chỉ chọn pháp luật đại cương (PLDC).
là số sinh viên chỉ chọn pháp luật đại cương (PLDC).
 là số sinh viên chỉ chọn xác suất thống kê (XSTK).
là số sinh viên chỉ chọn xác suất thống kê (XSTK).
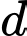 là số sinh viên chỉ chọn triết học và PLDC.
là số sinh viên chỉ chọn triết học và PLDC.
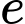 là số sinh viên chỉ chọn triết học và XSTK.
là số sinh viên chỉ chọn triết học và XSTK.
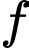 là số sinh viên chỉ chọn XSTK và PLDC.
là số sinh viên chỉ chọn XSTK và PLDC.
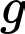 là số sinh viên chọn cả ba môn.
là số sinh viên chọn cả ba môn.
Dựa vào dữ kiện đề bài, ta có hệ phương trình:
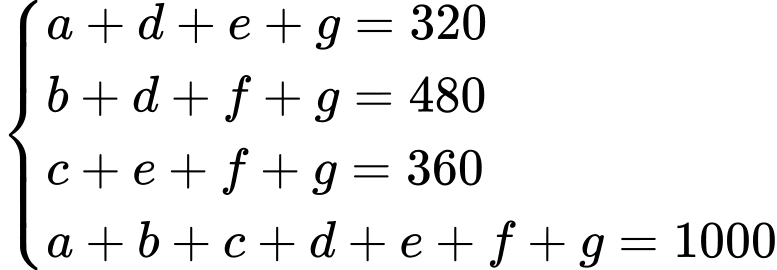
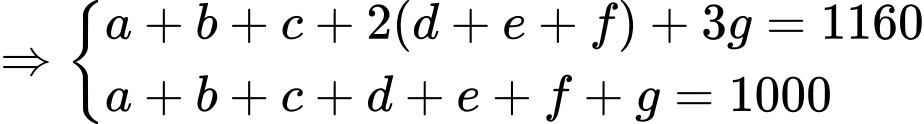
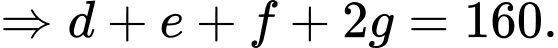
Ta thấy:
Dấu “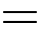 ” xảy ra khi và chỉ khi không có bạn sinh viên nào chỉ chọn 2 trong số 3 môn.
” xảy ra khi và chỉ khi không có bạn sinh viên nào chỉ chọn 2 trong số 3 môn.
Vậy tối đa có 80 bạn chọn cả 3 môn. Đáp án: B
Gọi
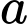 là số sinh viên chỉ chọn triết học.
là số sinh viên chỉ chọn triết học. 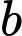 là số sinh viên chỉ chọn pháp luật đại cương (PLDC).
là số sinh viên chỉ chọn pháp luật đại cương (PLDC).  là số sinh viên chỉ chọn xác suất thống kê (XSTK).
là số sinh viên chỉ chọn xác suất thống kê (XSTK). 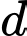 là số sinh viên chỉ chọn triết học và PLDC.
là số sinh viên chỉ chọn triết học và PLDC. 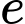 là số sinh viên chỉ chọn triết học và XSTK.
là số sinh viên chỉ chọn triết học và XSTK. 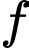 là số sinh viên chỉ chọn XSTK và PLDC.
là số sinh viên chỉ chọn XSTK và PLDC. 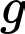 là số sinh viên chọn cả ba môn.
là số sinh viên chọn cả ba môn.Dựa vào dữ kiện đề bài, ta có hệ phương trình:
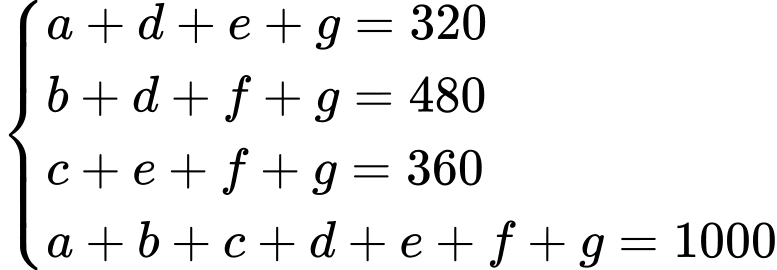
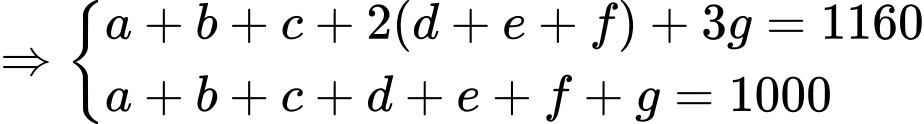
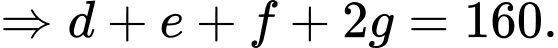
Ta thấy:

Dấu “
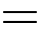 ” xảy ra khi và chỉ khi không có bạn sinh viên nào chỉ chọn 2 trong số 3 môn.
” xảy ra khi và chỉ khi không có bạn sinh viên nào chỉ chọn 2 trong số 3 môn.Vậy tối đa có 80 bạn chọn cả 3 môn. Đáp án: B
Câu 18 [379568]: Khảo sát các hộ gia đình trong một thị trấn, có 30 gia đình cập nhật tin tức qua truyền hình và qua cả các nền tảng mạng xã hội, 40 gia đình cập nhật tin tức không qua hai phương tiện trên. Thị trấn có 40% các hộ gia đình cập nhật tin tức qua các nền tảng mạng xã hội và 55% các hộ gia đình cập nhật tin tức qua truyền hình. Vậy thị trấn này có bao nhiêu hộ gia đình?
A, 150.
B, 200.
C, 160.
D, 250.
Chọn đáp án B.
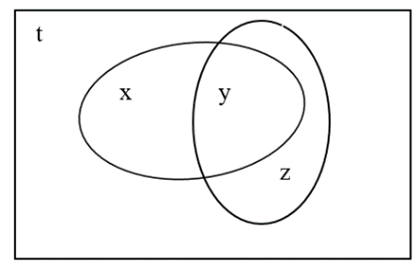
Gọi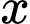 là tập hợp các hộ gia đình chỉ cập nhật tin tức qua truyền hình.
là tập hợp các hộ gia đình chỉ cập nhật tin tức qua truyền hình.
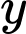 là tập hợp các hộ gia đình cập nhật tin tức thông qua các nền tảng mạng xã hội.
là tập hợp các hộ gia đình cập nhật tin tức thông qua các nền tảng mạng xã hội.
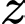 là tập hợp các hộ gia đình cập nhật tin tức thông qua cả hai phương tiện.
là tập hợp các hộ gia đình cập nhật tin tức thông qua cả hai phương tiện.
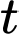 là tập hợp các hộ gia đình cập nhật tin tức không qua hai phương tiện trên.
là tập hợp các hộ gia đình cập nhật tin tức không qua hai phương tiện trên.
Từ dữ kiện đề bài cho, ta có hệ phương trình:
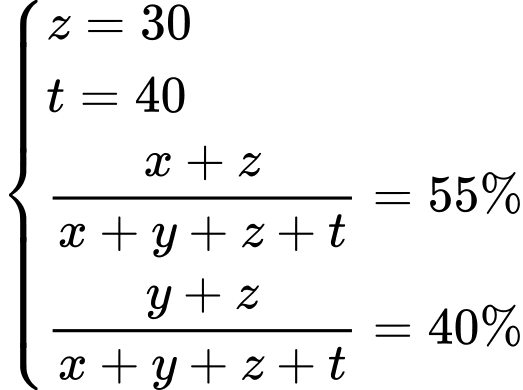
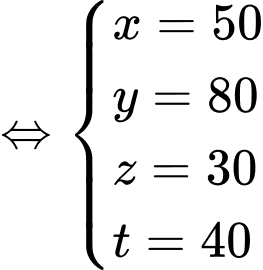
Vậy thị trấn có: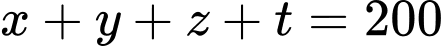 (hộ gia đình). Đáp án: B
(hộ gia đình). Đáp án: B

Gọi
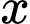 là tập hợp các hộ gia đình chỉ cập nhật tin tức qua truyền hình.
là tập hợp các hộ gia đình chỉ cập nhật tin tức qua truyền hình. 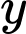 là tập hợp các hộ gia đình cập nhật tin tức thông qua các nền tảng mạng xã hội.
là tập hợp các hộ gia đình cập nhật tin tức thông qua các nền tảng mạng xã hội. 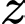 là tập hợp các hộ gia đình cập nhật tin tức thông qua cả hai phương tiện.
là tập hợp các hộ gia đình cập nhật tin tức thông qua cả hai phương tiện. 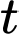 là tập hợp các hộ gia đình cập nhật tin tức không qua hai phương tiện trên.
là tập hợp các hộ gia đình cập nhật tin tức không qua hai phương tiện trên. Từ dữ kiện đề bài cho, ta có hệ phương trình:
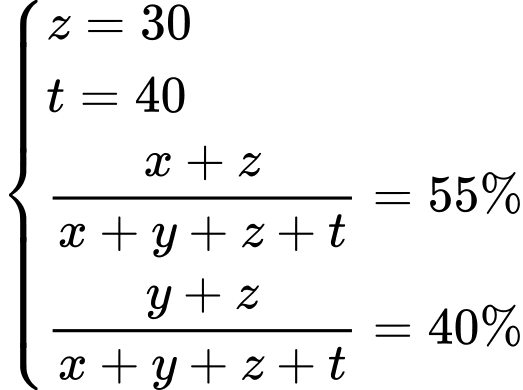
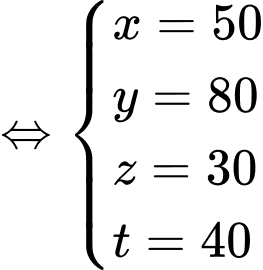
Vậy thị trấn có:
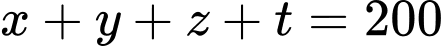 (hộ gia đình). Đáp án: B
(hộ gia đình). Đáp án: B
Câu 19 [379569]: Trong số 450 nhân viên của một công ty có 195 nhân viên là thành viên của câu lạc bộ A, 175 nhân viên là thành viên của câu lạc bộ B và 185 nhân viên là thành viên của câu lạc bộ C. 55 nhân viên là thành viên câu lạc bộ A và B. 40 nhân viên là thành viên câu lạc bộ B và C. 45 nhân viên là thành viên của câu lạc bộ A và C. 25 nhân viên là thành viên của ba câu lạc bộ A, B và C. Nếu 20 nhân viên là thành viên câu lạc bộ A chuyển sang câu lạc bộ C thì số lượng nhân viên là thành viên của cả hai câu lạc bộ A và B ít nhất có thể là
A, 20.
B, 10.
C, 15.
D, 35.
Chọn đáp án D.
Kết hợp các dữ kiện:
• 55 nhân viên là thành viên câu lạc bộ A và B.
• 20 nhân viên là thành viên câu lạc bộ A chuyển sang câu lạc bộ C.
Trường hợp để số lượng nhân viên là thành viên của cả hai câu lạc bộ A và B ít nhất là toàn bộ số nhân viên được chuyển đi đều là thành viên của cả hai câu lạc bộ.
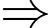 Số lượng nhân viên là thành viên của cả hai câu lạc bộ A và B ít nhất có thể là:
Số lượng nhân viên là thành viên của cả hai câu lạc bộ A và B ít nhất có thể là:
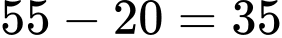 (nhân viên). Đáp án: D
(nhân viên). Đáp án: D
Kết hợp các dữ kiện:
• 55 nhân viên là thành viên câu lạc bộ A và B.
• 20 nhân viên là thành viên câu lạc bộ A chuyển sang câu lạc bộ C.
Trường hợp để số lượng nhân viên là thành viên của cả hai câu lạc bộ A và B ít nhất là toàn bộ số nhân viên được chuyển đi đều là thành viên của cả hai câu lạc bộ.
 Số lượng nhân viên là thành viên của cả hai câu lạc bộ A và B ít nhất có thể là:
Số lượng nhân viên là thành viên của cả hai câu lạc bộ A và B ít nhất có thể là: 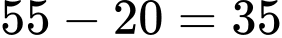 (nhân viên). Đáp án: D
(nhân viên). Đáp án: D
Câu 20 [379570]: Một cuộc khảo sát được thực hiện với 100 sinh viên về tuổi thơ của họ đã từng đọc truyện Doremon hay Conan hay đã từng đọc cả hai truyện này. Sau khi khảo sát xong do một vài yếu tố dẫn đến kết quả của bảng dữ kiện khảo sát chỉ còn lại các thông tin sau:

Người thực hiện khảo sát cung cấp thêm thông tin rằng: có 37% sinh viên tham gia khảo sát đã từng đọc cả hai truyện trên. Số sinh viên nam và nữ được khảo sát là bằng nhau và có 50% sinh viên nữ đọc cả hai truyện. Vậy có bao nhiêu sinh viên nam tham gia khảo sát mà tuổi thơ của họ mới chỉ đọc truyện Doremon?

Người thực hiện khảo sát cung cấp thêm thông tin rằng: có 37% sinh viên tham gia khảo sát đã từng đọc cả hai truyện trên. Số sinh viên nam và nữ được khảo sát là bằng nhau và có 50% sinh viên nữ đọc cả hai truyện. Vậy có bao nhiêu sinh viên nam tham gia khảo sát mà tuổi thơ của họ mới chỉ đọc truyện Doremon?
A, 12.
B, 15.
C, 27.
D, 35.
Dựa vào dữ kiện:
• Một cuộc khảo sát được thực hiện với 100 sinh viên về tuổi thơ của họ đã từng đọc truyện Doremon hay Conan hay đã từng đọc cả hai truyện này.
• Có 37% sinh viên tham gia khảo sát đã từng đọc cả hai truyện trên Có 37 sinh viên tham gia khảo sát đã đọc truyện Doremon hoặc Conan.
Có 37 sinh viên tham gia khảo sát đã đọc truyện Doremon hoặc Conan.
• Số sinh viên nam và nữ được khảo sát là bằng nhau và có 50% sinh viên nữ đọc cả hai truyện Có 50 sinh viên nam và 50 sinh viên nữ tham gia khảo sát; có 25 sinh viên nữ đã từng đọc cả hai truyện.
Có 50 sinh viên nam và 50 sinh viên nữ tham gia khảo sát; có 25 sinh viên nữ đã từng đọc cả hai truyện.
Kết hợp với các dữ kiện của bảng thông tin còn sót lại ta có biểu đồ sau:
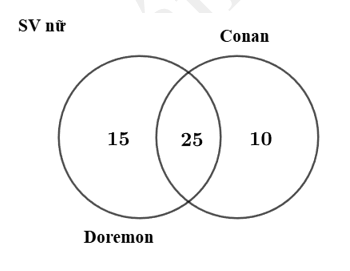
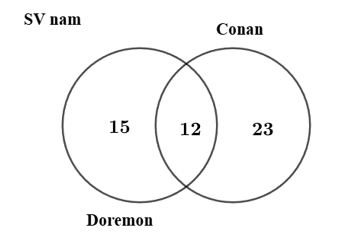
 Có 15 sinh viên nam tham gia khảo sát mà tuổi thơ của họ mới chỉ đọc truyện Doremon
Có 15 sinh viên nam tham gia khảo sát mà tuổi thơ của họ mới chỉ đọc truyện Doremon
 Chọn đáp án B.
Chọn đáp án B.
Bảng số liệu đầy đủ như sau:
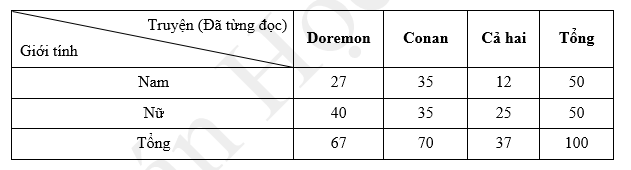 Đáp án: B
Đáp án: B
• Một cuộc khảo sát được thực hiện với 100 sinh viên về tuổi thơ của họ đã từng đọc truyện Doremon hay Conan hay đã từng đọc cả hai truyện này.
• Có 37% sinh viên tham gia khảo sát đã từng đọc cả hai truyện trên
 Có 37 sinh viên tham gia khảo sát đã đọc truyện Doremon hoặc Conan.
Có 37 sinh viên tham gia khảo sát đã đọc truyện Doremon hoặc Conan.• Số sinh viên nam và nữ được khảo sát là bằng nhau và có 50% sinh viên nữ đọc cả hai truyện
 Có 50 sinh viên nam và 50 sinh viên nữ tham gia khảo sát; có 25 sinh viên nữ đã từng đọc cả hai truyện.
Có 50 sinh viên nam và 50 sinh viên nữ tham gia khảo sát; có 25 sinh viên nữ đã từng đọc cả hai truyện.Kết hợp với các dữ kiện của bảng thông tin còn sót lại ta có biểu đồ sau:


 Có 15 sinh viên nam tham gia khảo sát mà tuổi thơ của họ mới chỉ đọc truyện Doremon
Có 15 sinh viên nam tham gia khảo sát mà tuổi thơ của họ mới chỉ đọc truyện Doremon  Chọn đáp án B.
Chọn đáp án B. Bảng số liệu đầy đủ như sau:
 Đáp án: B
Đáp án: B
Câu 21 [379571]: Bảng dữ liệu cho biết kết quả của một cuộc khảo sát một nhóm người có sử dụng hai nền tảng mạng xã hội:
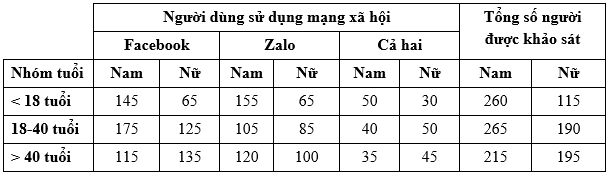
Dựa vào bảng dữ liệu, hãy cho biết có bao nhiêu phần trăm nữ dưới 18 tuổi không sử dụng hai nền tảng mạng xã hội Facebook và Zalo so với tổng số nữ giới không sử dụng hai nền tảng mạng xã hội này?

Dựa vào bảng dữ liệu, hãy cho biết có bao nhiêu phần trăm nữ dưới 18 tuổi không sử dụng hai nền tảng mạng xã hội Facebook và Zalo so với tổng số nữ giới không sử dụng hai nền tảng mạng xã hội này?
A, 30%.
B, 60%.
C, 40%.
D, 20%.
Chọn đáp án A.
Dựa vào bảng dữ liệu, ta có:
Số nữ giới không sử dụng hai nền tảng mạng xã hội Facebook và Zalo dưới 18 tuổi là:
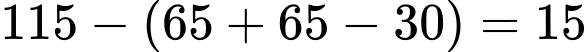 ( người).
( người).
Số nữ giới không sử dụng hai nền tảng mạng xã hội Facebook và Zalo ở độ tuổi từ 18 đến 40 tuổi là: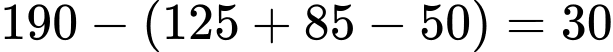 (người).
(người).
Số nữ giới không sử dụng hai nền tảng mạng xã hội Facebook và Zalo trên 40 tuổi là:
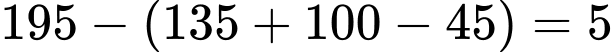 (người).
(người).
Vậy phần trăm nữ giới không sử dụng hai nền tảng mạng xã hội Facebook và Zalo dưới 18 tuổi là: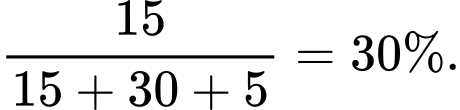 Đáp án: A
Đáp án: A
Dựa vào bảng dữ liệu, ta có:
Số nữ giới không sử dụng hai nền tảng mạng xã hội Facebook và Zalo dưới 18 tuổi là:
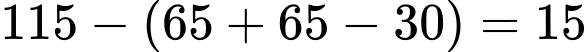 ( người).
( người).Số nữ giới không sử dụng hai nền tảng mạng xã hội Facebook và Zalo ở độ tuổi từ 18 đến 40 tuổi là:
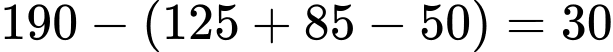 (người).
(người).Số nữ giới không sử dụng hai nền tảng mạng xã hội Facebook và Zalo trên 40 tuổi là:
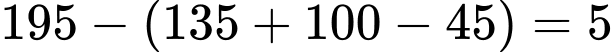 (người).
(người).Vậy phần trăm nữ giới không sử dụng hai nền tảng mạng xã hội Facebook và Zalo dưới 18 tuổi là:
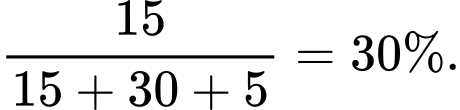 Đáp án: A
Đáp án: A
Câu 22 [379572]: Khảo sát tại trường THCS X có 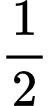 số học sinh học chính xác một môn võ trong ba môn: Kung Fu, Karate và Judo;
số học sinh học chính xác một môn võ trong ba môn: Kung Fu, Karate và Judo; 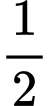 số học sinh học Karate không học Kung Fu và Judo. Số học sinh học cả 3 môn võ bằng
số học sinh học Karate không học Kung Fu và Judo. Số học sinh học cả 3 môn võ bằng 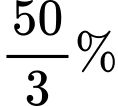 số học sinh học 2 trong 3 môn võ và bằng
số học sinh học 2 trong 3 môn võ và bằng 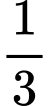 số học sinh không học môn võ nào. Nếu 50 học sinh học cả ba môn võ thì có bao nhiêu học sinh học đúng một trong ba môn võ?
số học sinh không học môn võ nào. Nếu 50 học sinh học cả ba môn võ thì có bao nhiêu học sinh học đúng một trong ba môn võ?
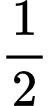 số học sinh học chính xác một môn võ trong ba môn: Kung Fu, Karate và Judo;
số học sinh học chính xác một môn võ trong ba môn: Kung Fu, Karate và Judo; 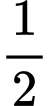 số học sinh học Karate không học Kung Fu và Judo. Số học sinh học cả 3 môn võ bằng
số học sinh học Karate không học Kung Fu và Judo. Số học sinh học cả 3 môn võ bằng 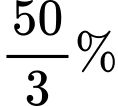 số học sinh học 2 trong 3 môn võ và bằng
số học sinh học 2 trong 3 môn võ và bằng 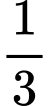 số học sinh không học môn võ nào. Nếu 50 học sinh học cả ba môn võ thì có bao nhiêu học sinh học đúng một trong ba môn võ?
số học sinh không học môn võ nào. Nếu 50 học sinh học cả ba môn võ thì có bao nhiêu học sinh học đúng một trong ba môn võ? A, 480.
B, 500.
C, 700.
D, 550.
Chọn đáp án B.
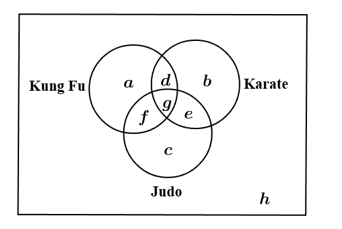
Gọi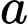 là số học sinh chỉ học Kung Fu.
là số học sinh chỉ học Kung Fu.
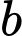 là số học sinh chỉ học Karate.
là số học sinh chỉ học Karate.
 là số học sinh chỉ học Judo.
là số học sinh chỉ học Judo.
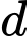 là số học sinh chỉ học Judo và Karate.
là số học sinh chỉ học Judo và Karate.
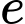 là số học sinh chỉ học Judo và Kung Fu.
là số học sinh chỉ học Judo và Kung Fu.
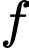 là số học sinh chỉ học Kung Fu và Karate.
là số học sinh chỉ học Kung Fu và Karate.
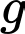 là số học sinh học cả ba môn võ
là số học sinh học cả ba môn võ 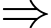
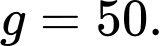
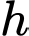 là số học sinh không học môn võ nào.
là số học sinh không học môn võ nào.
Dựa vào các dữ kiện bài cho, ta có hệ phương trình:
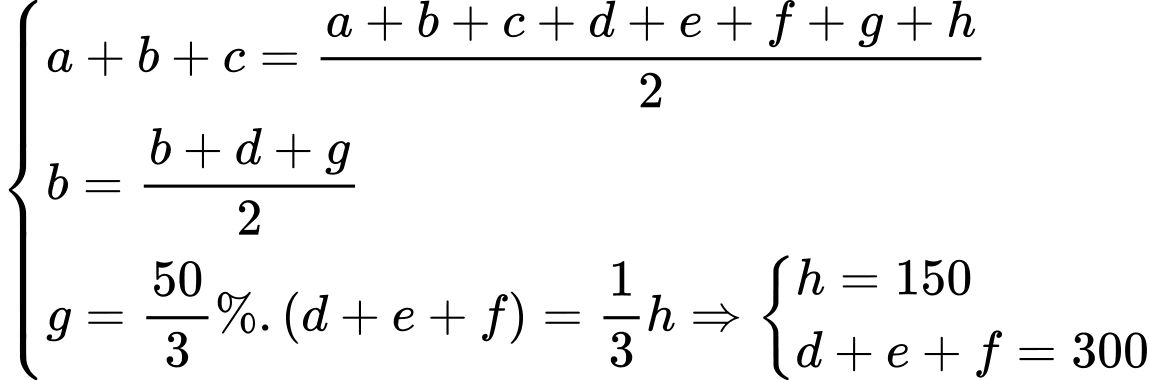
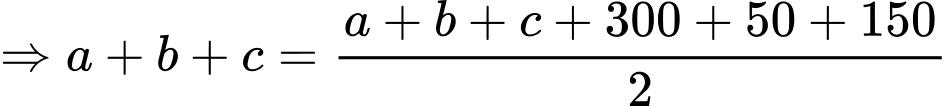

Vậy có 500 học sinh học đúng một trong ba môn võ. Đáp án: B

Gọi
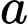 là số học sinh chỉ học Kung Fu.
là số học sinh chỉ học Kung Fu. 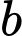 là số học sinh chỉ học Karate.
là số học sinh chỉ học Karate.  là số học sinh chỉ học Judo.
là số học sinh chỉ học Judo. 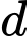 là số học sinh chỉ học Judo và Karate.
là số học sinh chỉ học Judo và Karate. 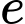 là số học sinh chỉ học Judo và Kung Fu.
là số học sinh chỉ học Judo và Kung Fu. 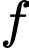 là số học sinh chỉ học Kung Fu và Karate.
là số học sinh chỉ học Kung Fu và Karate. 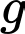 là số học sinh học cả ba môn võ
là số học sinh học cả ba môn võ 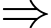
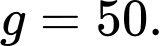
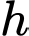 là số học sinh không học môn võ nào.
là số học sinh không học môn võ nào.Dựa vào các dữ kiện bài cho, ta có hệ phương trình:
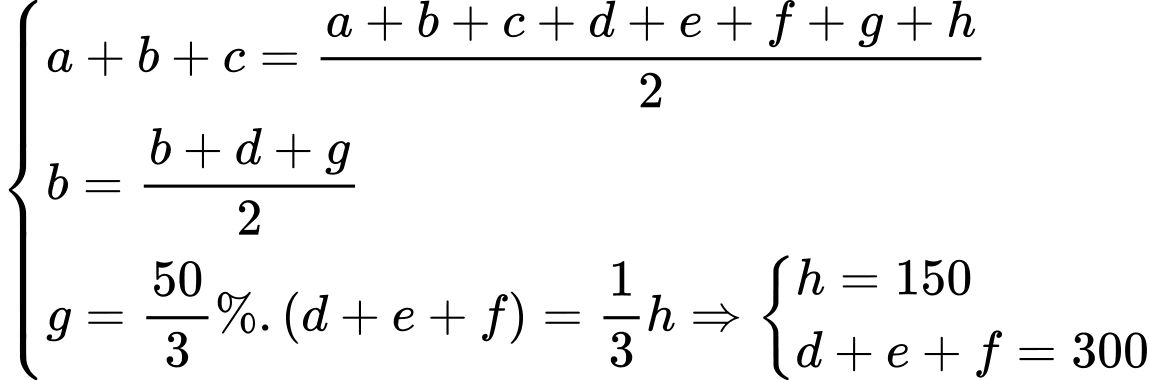
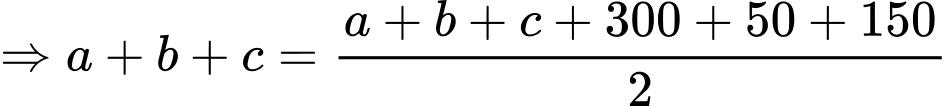

Vậy có 500 học sinh học đúng một trong ba môn võ. Đáp án: B
Câu 23 [379573]: Trường THPT X khảo sát toàn bộ học sinh khối 12 về nguyện vọng các ngành nghề mà học sinh muốn theo đuổi, kết quả cho thấy có 60% học sinh có nguyện vọng học khối ngành kinh tế. Trong số những học sinh có nguyện vọng theo khối ngành kinh tế có 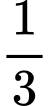 cũng muốn theo cả khối ngành kĩ thuật; 150 học sinh không có nguyện vọng theo đuổi hai khối ngành trên;
cũng muốn theo cả khối ngành kĩ thuật; 150 học sinh không có nguyện vọng theo đuổi hai khối ngành trên; 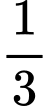 số học sinh có nguyện vọng theo đuổi khối ngành kĩ thuật không có nguyện vọng theo đuổi khối ngành kinh tế. Vậy khối học sinh lớp 12 có bao nhiêu học sinh?
số học sinh có nguyện vọng theo đuổi khối ngành kĩ thuật không có nguyện vọng theo đuổi khối ngành kinh tế. Vậy khối học sinh lớp 12 có bao nhiêu học sinh?
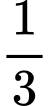 cũng muốn theo cả khối ngành kĩ thuật; 150 học sinh không có nguyện vọng theo đuổi hai khối ngành trên;
cũng muốn theo cả khối ngành kĩ thuật; 150 học sinh không có nguyện vọng theo đuổi hai khối ngành trên; 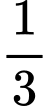 số học sinh có nguyện vọng theo đuổi khối ngành kĩ thuật không có nguyện vọng theo đuổi khối ngành kinh tế. Vậy khối học sinh lớp 12 có bao nhiêu học sinh?
số học sinh có nguyện vọng theo đuổi khối ngành kĩ thuật không có nguyện vọng theo đuổi khối ngành kinh tế. Vậy khối học sinh lớp 12 có bao nhiêu học sinh? A, 350.
B, 660.
C, 550.
D, 500.
Chọn đáp án D.
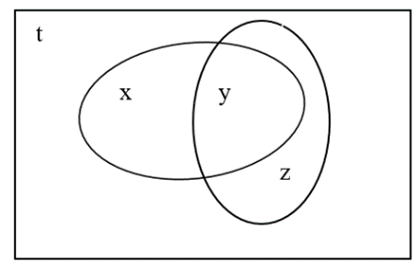
Gọi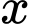 là tập hợp các học sinh chỉ có nguyện vọng học khối ngành kinh tế.
là tập hợp các học sinh chỉ có nguyện vọng học khối ngành kinh tế.
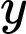 là tập hợp các học sinh chỉ có nguyện vọng học khối ngành kĩ thuật.
là tập hợp các học sinh chỉ có nguyện vọng học khối ngành kĩ thuật.
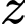 là tập hợp các học sinh có nguyện vọng học cả hai khối ngành.
là tập hợp các học sinh có nguyện vọng học cả hai khối ngành.
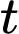 là tập hợp các học sinh không có nguyện vọng theo đuổi hai khối ngành trên.
là tập hợp các học sinh không có nguyện vọng theo đuổi hai khối ngành trên.
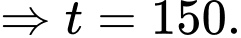
Dựa vào dữ kiện đề bài, ta có hệ phương trình:
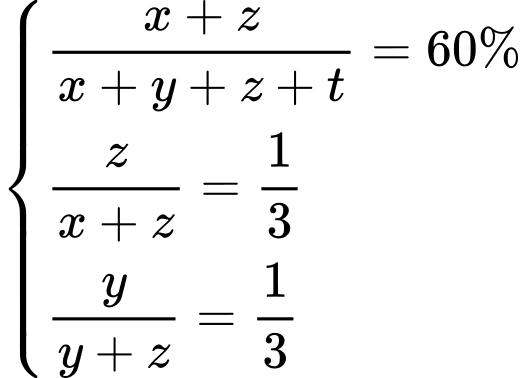
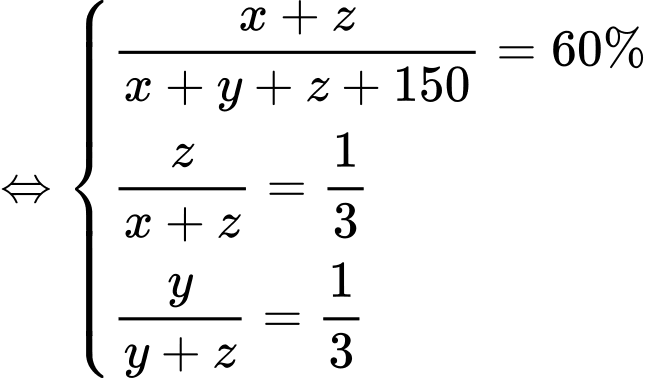
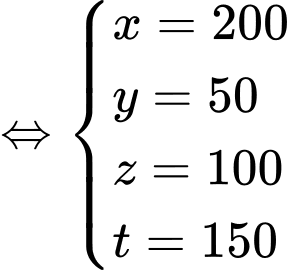
Vậy số học sinh lớp 12 là: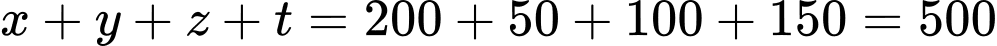 (học sinh). Đáp án: D
(học sinh). Đáp án: D

Gọi
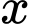 là tập hợp các học sinh chỉ có nguyện vọng học khối ngành kinh tế.
là tập hợp các học sinh chỉ có nguyện vọng học khối ngành kinh tế. 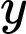 là tập hợp các học sinh chỉ có nguyện vọng học khối ngành kĩ thuật.
là tập hợp các học sinh chỉ có nguyện vọng học khối ngành kĩ thuật. 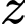 là tập hợp các học sinh có nguyện vọng học cả hai khối ngành.
là tập hợp các học sinh có nguyện vọng học cả hai khối ngành. 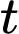 là tập hợp các học sinh không có nguyện vọng theo đuổi hai khối ngành trên.
là tập hợp các học sinh không có nguyện vọng theo đuổi hai khối ngành trên. 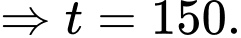
Dựa vào dữ kiện đề bài, ta có hệ phương trình:
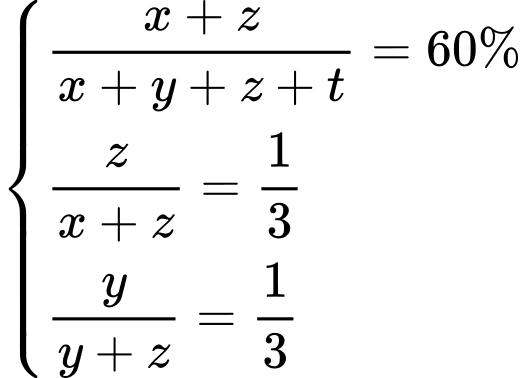
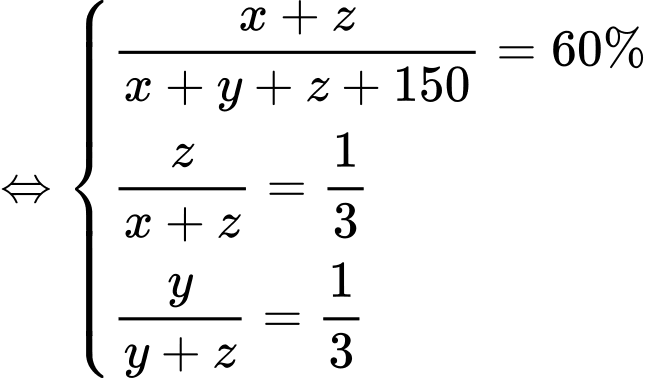
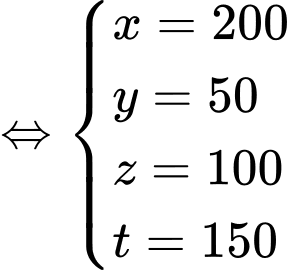
Vậy số học sinh lớp 12 là:
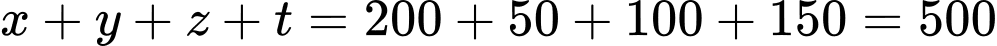 (học sinh). Đáp án: D
(học sinh). Đáp án: D
Câu 24 [379574]: Tại một trại hè gồm 1000 học sinh, mỗi học sinh tham gia ít nhất 2 hoạt động trong số 5 hoạt động là vẽ tranh, bơi lội, khiêu vũ, ca hát và võ thuật. Biết rằng số học sinh tham gia đúng 2 hoạt động gấp ba lần số học sinh tham gia đúng 3 hoạt động. Số học sinh tham gia cả 5 hoạt động bằng 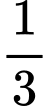 số học sinh tham gia đúng 4 hoạt động. Nếu số học sinh tham gia cả 5 hoạt động là 100 học sinh thì số học sinh chỉ tham gia vẽ tranh và võ thuật là
số học sinh tham gia đúng 4 hoạt động. Nếu số học sinh tham gia cả 5 hoạt động là 100 học sinh thì số học sinh chỉ tham gia vẽ tranh và võ thuật là
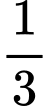 số học sinh tham gia đúng 4 hoạt động. Nếu số học sinh tham gia cả 5 hoạt động là 100 học sinh thì số học sinh chỉ tham gia vẽ tranh và võ thuật là
số học sinh tham gia đúng 4 hoạt động. Nếu số học sinh tham gia cả 5 hoạt động là 100 học sinh thì số học sinh chỉ tham gia vẽ tranh và võ thuật là A, 150.
B, 45.
C, 450.
D, Không thể xác định.
Chọn đáp án D.
Dựa vào các dữ kiện:
• Số học sinh tham gia cả 5 hoạt động bằng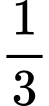 số học sinh tham gia đúng 4 hoạt động.
số học sinh tham gia đúng 4 hoạt động.
• Số học sinh tham gia cả 5 hoạt động là 100.
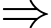 Số học sinh tham gia đúng 4 hoạt động là:
Số học sinh tham gia đúng 4 hoạt động là: 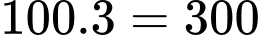 (học sinh).
(học sinh).
Gọi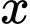 là số học sinh tham gia đúng 2 hoạt động.
là số học sinh tham gia đúng 2 hoạt động.
 là số học sinh tham gia đúng 3 hoạt động.
là số học sinh tham gia đúng 3 hoạt động.
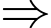
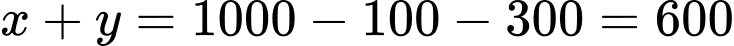 (học sinh).
(học sinh).
Số học sinh tham gia đúng 2 hoạt động gấp ba lần số học sinh tham gia đúng 3 hoạt động.
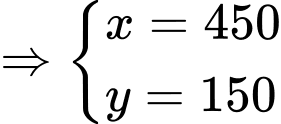
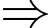 Không đủ dữ kiện để xác định số học sinh chỉ tham gia vẽ tranh và võ thuật. Đáp án: D
Không đủ dữ kiện để xác định số học sinh chỉ tham gia vẽ tranh và võ thuật. Đáp án: D
Dựa vào các dữ kiện:
• Số học sinh tham gia cả 5 hoạt động bằng
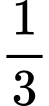 số học sinh tham gia đúng 4 hoạt động.
số học sinh tham gia đúng 4 hoạt động.• Số học sinh tham gia cả 5 hoạt động là 100.
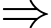 Số học sinh tham gia đúng 4 hoạt động là:
Số học sinh tham gia đúng 4 hoạt động là: 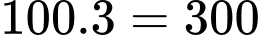 (học sinh).
(học sinh).Gọi
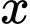 là số học sinh tham gia đúng 2 hoạt động.
là số học sinh tham gia đúng 2 hoạt động.  là số học sinh tham gia đúng 3 hoạt động.
là số học sinh tham gia đúng 3 hoạt động.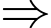
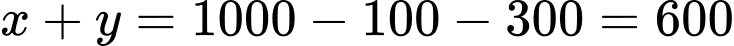 (học sinh).
(học sinh).Số học sinh tham gia đúng 2 hoạt động gấp ba lần số học sinh tham gia đúng 3 hoạt động.
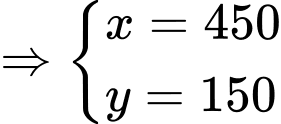
 Không đủ dữ kiện để xác định số học sinh chỉ tham gia vẽ tranh và võ thuật. Đáp án: D
Không đủ dữ kiện để xác định số học sinh chỉ tham gia vẽ tranh và võ thuật. Đáp án: D
Câu 25 [379575]: Thực hiện một cuộc khảo sát với các hộ gia đình tại một thị trấn về 3 loại phương tiện mà gia đình họ đang sở hữu gồm ô tô, xe máy và xe đạp. Kết quả cho thấy số hộ gia đình sở hữu cả 3 loại phương tiện trên bằng số hộ gia đình không sở hữu 3 loại phương tiện trên. Số hộ gia đình chỉ sở hữu 2 loại phương tiện bất kỳ trong 3 loại phương tiện trên đều bằng nhau. Số hộ gia đình chỉ sở hữu xe máy bằng số hộ gia đình chỉ sở hữu ô tô và gấp đôi số hộ gia đình chỉ sở hữu xe đạp. Một nửa số hộ gia đình sở hữu xe đạp, sở hữu thêm ít nhất một trong hai phương tiện còn lại. Nếu số hộ gia đình chỉ sở hữu xe đạp là 150 thì tổng số hộ gia đình của thị trấn này là bao nhiêu?
A, 500.
B, 1000.
C, 750.
D, 1250.
Dựa vào hình minh họa phân tích giả thiết:
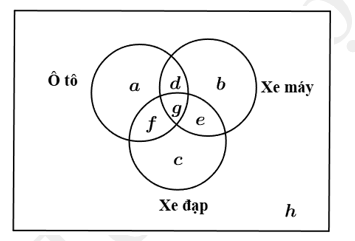
Gọi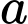 là số hộ gia đình chỉ sở hữu ô tô.
là số hộ gia đình chỉ sở hữu ô tô.
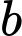 là số hộ gia đình chỉ sở hữu xe máy.
là số hộ gia đình chỉ sở hữu xe máy.
 là số hộ gia đình chỉ sở hữu xe đạp
là số hộ gia đình chỉ sở hữu xe đạp 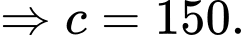
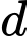 là số hộ gia đình chỉ sở hữu ô tô và xe máy.
là số hộ gia đình chỉ sở hữu ô tô và xe máy.
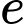 là số hộ gia đình chỉ sở hữu xe máy và xe đạp.
là số hộ gia đình chỉ sở hữu xe máy và xe đạp.
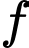 là số hộ gia đình chỉ sở hữu ô tô và xe máy.
là số hộ gia đình chỉ sở hữu ô tô và xe máy.
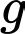 là số hộ gia đình sở hữu cả ba phương tiện.
là số hộ gia đình sở hữu cả ba phương tiện.
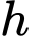 là số hộ gia đình không sở hữu phương tiện nào.
là số hộ gia đình không sở hữu phương tiện nào.
Dựa vào các dữ kiện đề cho, ta có hệ phương trình: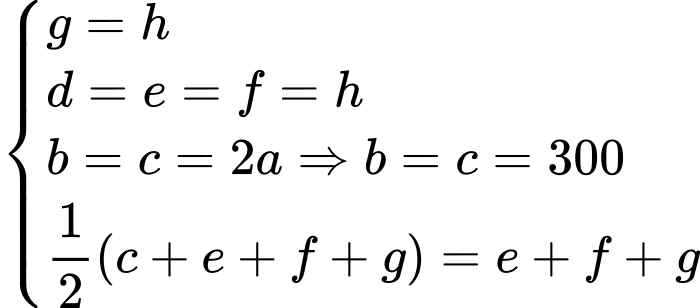
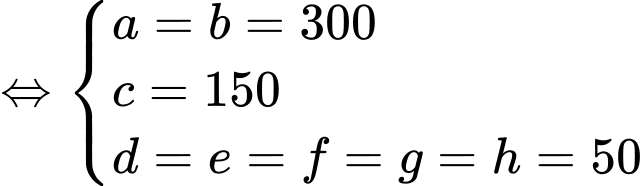
Vậy tổng số hộ gia đình của thị trấn này là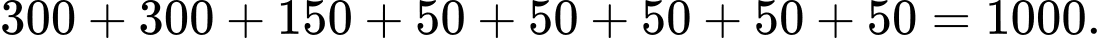 Đáp án: B
Đáp án: B

Gọi
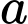 là số hộ gia đình chỉ sở hữu ô tô.
là số hộ gia đình chỉ sở hữu ô tô.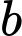 là số hộ gia đình chỉ sở hữu xe máy.
là số hộ gia đình chỉ sở hữu xe máy. là số hộ gia đình chỉ sở hữu xe đạp
là số hộ gia đình chỉ sở hữu xe đạp 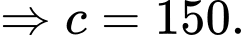
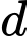 là số hộ gia đình chỉ sở hữu ô tô và xe máy.
là số hộ gia đình chỉ sở hữu ô tô và xe máy.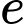 là số hộ gia đình chỉ sở hữu xe máy và xe đạp.
là số hộ gia đình chỉ sở hữu xe máy và xe đạp.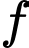 là số hộ gia đình chỉ sở hữu ô tô và xe máy.
là số hộ gia đình chỉ sở hữu ô tô và xe máy.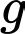 là số hộ gia đình sở hữu cả ba phương tiện.
là số hộ gia đình sở hữu cả ba phương tiện.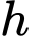 là số hộ gia đình không sở hữu phương tiện nào.
là số hộ gia đình không sở hữu phương tiện nào.Dựa vào các dữ kiện đề cho, ta có hệ phương trình:
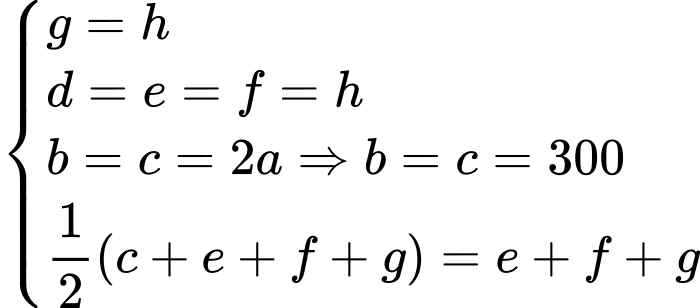
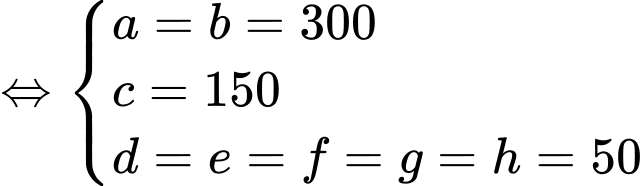
Vậy tổng số hộ gia đình của thị trấn này là
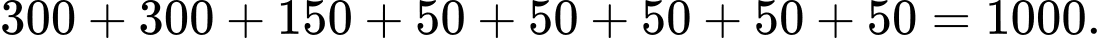 Đáp án: B
Đáp án: B