Logic tình huống – bài đọc số 1
Trong một lớp học có 150 học sinh, 45 học sinh học Lịch sử, 65 học sinh học Địa lý và 10 học sinh học cả Lịch sử và Địa lý.
Câu 1 [583716]: Có bao nhiêu học sinh chỉ học Địa lý?
A, 45.
B, 10.
C, 55.
D, 65.
Chọn đáp án C.
Số học sinh chỉ học Địa lý là: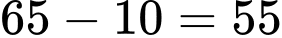 (học sinh).
Đáp án: C
(học sinh).
Đáp án: C
Số học sinh chỉ học Địa lý là:
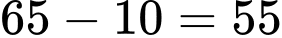 (học sinh).
Đáp án: C
(học sinh).
Đáp án: C
Câu 2 [583717]: Có bao nhiêu học sinh chỉ học Lịch sử?
A, 65.
B, 35.
C, 10.
D, 45.
Chọn đáp án B.
Số học sinh chỉ học Địa lý là: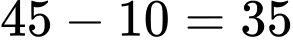 (học sinh).
Đáp án: B
(học sinh).
Đáp án: B
Số học sinh chỉ học Địa lý là:
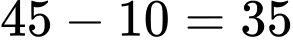 (học sinh).
Đáp án: B
(học sinh).
Đáp án: B
Câu 3 [583718]: Có bao nhiêu học sinh không học Lịch sử hoặc Địa lý?
A, 10.
B, 35.
C, 100.
D, 140.
Chọn đáp án D.
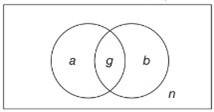
Gọi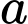 là tập hợp các học sinh chỉ học Địa lý
là tập hợp các học sinh chỉ học Địa lý
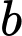 là tập hợp các học sinh chỉ học Lịch sử
là tập hợp các học sinh chỉ học Lịch sử
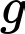 là tập hợp các học sinh học cả Địa lý và Lịch sử.
là tập hợp các học sinh học cả Địa lý và Lịch sử.
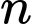 là tập hợp các học sinh không học cả Địa lý và Lịch sử.
là tập hợp các học sinh không học cả Địa lý và Lịch sử.
Từ dữ kiện đề bài cho, ta có hệ phương trình:
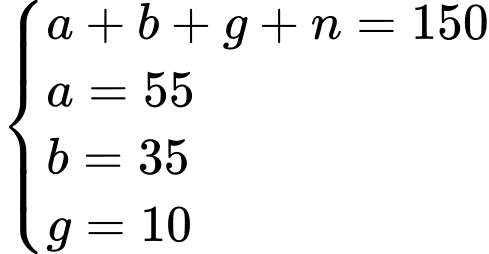
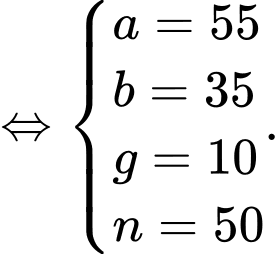
 Số học sinh không học Lịch sử hoặc Địa lý là:
Số học sinh không học Lịch sử hoặc Địa lý là: 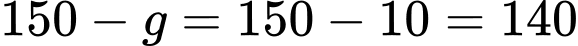 (học sinh). Đáp án: D
(học sinh). Đáp án: D

Gọi
 là tập hợp các học sinh chỉ học Địa lý
là tập hợp các học sinh chỉ học Địa lý là tập hợp các học sinh chỉ học Lịch sử
là tập hợp các học sinh chỉ học Lịch sử là tập hợp các học sinh học cả Địa lý và Lịch sử.
là tập hợp các học sinh học cả Địa lý và Lịch sử. 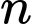 là tập hợp các học sinh không học cả Địa lý và Lịch sử.
là tập hợp các học sinh không học cả Địa lý và Lịch sử.Từ dữ kiện đề bài cho, ta có hệ phương trình:
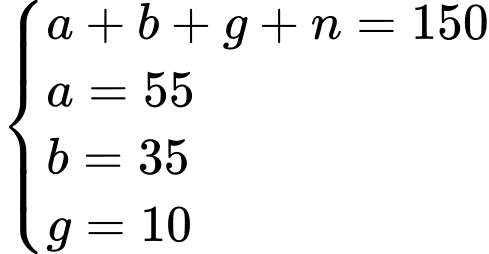
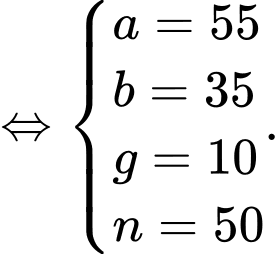
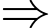 Số học sinh không học Lịch sử hoặc Địa lý là:
Số học sinh không học Lịch sử hoặc Địa lý là: 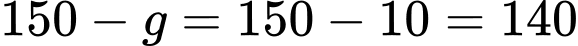 (học sinh). Đáp án: D
(học sinh). Đáp án: D
Câu 4 [583719]: Có bao nhiêu học sinh học ít nhất một môn?
A, 10.
B, 90.
C, 50.
D, 100.
Chọn đáp án D.
Số học sinh học ít nhất một môn là: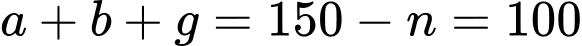 (học sinh).
Đáp án: D
(học sinh).
Đáp án: D
Số học sinh học ít nhất một môn là:
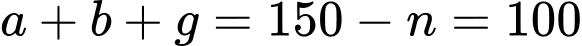 (học sinh).
Đáp án: D
(học sinh).
Đáp án: D
Câu 5 [583720]: Có bao nhiêu học sinh không học bất kỳ môn nào trong hai môn?
A, 90.
B, 10.
C, 50.
D, 100.
Chọn đáp án C.
Số học sinh không học bất kỳ môn nào trong hai môn là: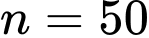 (học sinh).
Đáp án: C
(học sinh).
Đáp án: C
Số học sinh không học bất kỳ môn nào trong hai môn là:
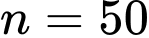 (học sinh).
Đáp án: C
(học sinh).
Đáp án: C Logic tình huống – bài đọc số 2
Khảo sát toàn bộ học sinh trong một lớp học, có học sinh thích đá bóng và thích bơi lội, có 6 học sinh thích cả hai môn thể thao và có 3 học sinh không thích hai môn thể thao này.
Câu 6 [583721]: Lớp học có bao nhiêu học sinh?
A, 100.
B, 75.
C, 60.
D, 80.
Chọn đáp án C.
Gọi là tập hợp các học sinh chỉ thích đá bóng.
là tập hợp các học sinh chỉ thích đá bóng.
 là tập hợp các học sinh chỉ thích bơi lội.
là tập hợp các học sinh chỉ thích bơi lội.
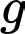 là tập hợp các học sinh thích cả hai môn.
là tập hợp các học sinh thích cả hai môn.
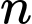 là tập hợp các học sinh không thích hai môn thể thao này.
là tập hợp các học sinh không thích hai môn thể thao này.
Từ dữ kiện đề bài cho, ta có hệ phương trình:
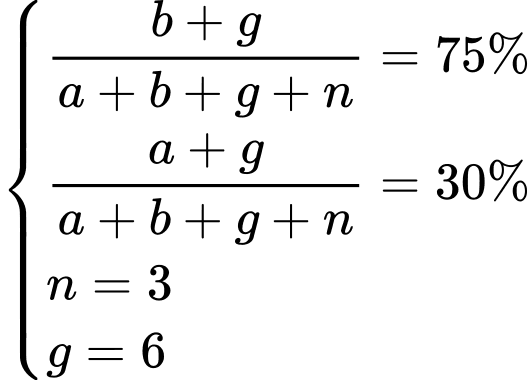
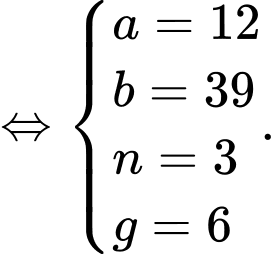
Số học sinh của lớp học là: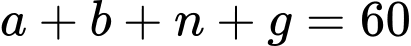 (học sinh). Đáp án: C
(học sinh). Đáp án: C

Gọi
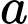 là tập hợp các học sinh chỉ thích đá bóng.
là tập hợp các học sinh chỉ thích đá bóng.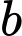 là tập hợp các học sinh chỉ thích bơi lội.
là tập hợp các học sinh chỉ thích bơi lội.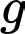 là tập hợp các học sinh thích cả hai môn.
là tập hợp các học sinh thích cả hai môn. 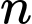 là tập hợp các học sinh không thích hai môn thể thao này.
là tập hợp các học sinh không thích hai môn thể thao này.Từ dữ kiện đề bài cho, ta có hệ phương trình:
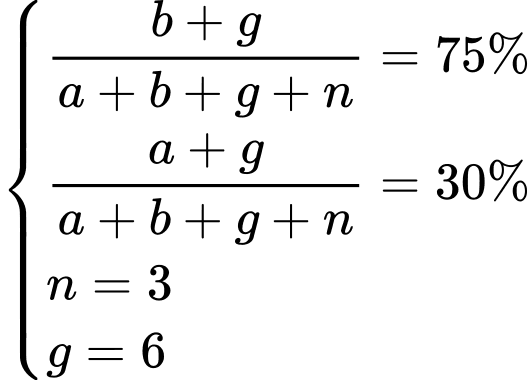
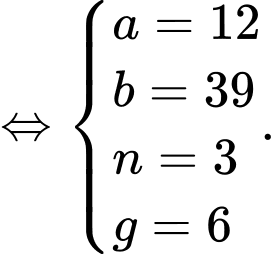
Số học sinh của lớp học là:
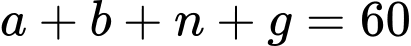 (học sinh). Đáp án: C
(học sinh). Đáp án: C
Câu 7 [583722]: Tỷ lệ phần trăm học sinh chỉ thích bóng đá là
A, 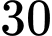
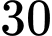
B, 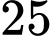
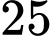
C, 

D, 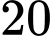
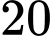
Chọn đáp án D.
Tỷ lệ phần trăm học sinh chỉ thích bóng đá là: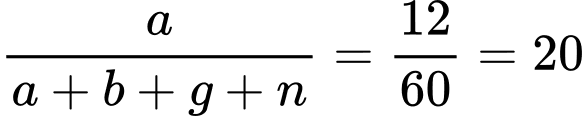 Đáp án: D
Đáp án: D
Tỷ lệ phần trăm học sinh chỉ thích bóng đá là:
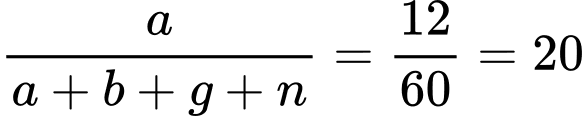 Đáp án: D
Đáp án: D
Câu 8 [583723]: Tỷ lệ phần trăm học sinh chỉ thích một môn thể thao là
A, 
B, 
C, 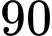
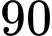
D, 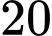
Chọn đáp án A.
Tỷ lệ phần trăm học sinh chỉ thích một môn thể thao là:
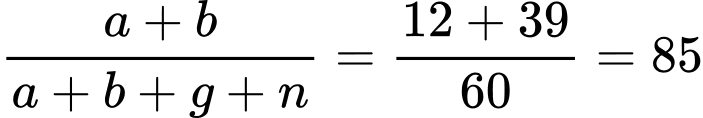 Đáp án: A
Đáp án: A
Tỷ lệ phần trăm học sinh chỉ thích một môn thể thao là:
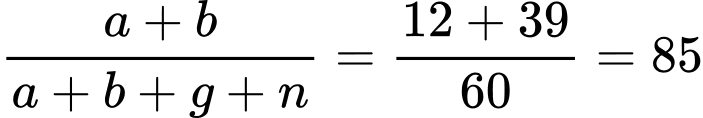 Đáp án: A
Đáp án: A
Câu 9 [583724]: Có bao nhiêu học sinh thích ít nhất một môn thể thao?
A, 97.
B, 87.
C, 147.
D, 57.
Chọn đáp án D.
Số học sinh chỉ thích ít nhất một môn thể thao là: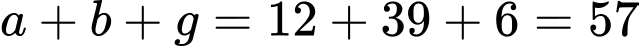 (học sinh).
Đáp án: D
(học sinh).
Đáp án: D
Số học sinh chỉ thích ít nhất một môn thể thao là:
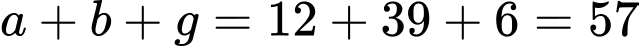 (học sinh).
Đáp án: D
(học sinh).
Đáp án: D Logic tình huống – bài đọc số 3
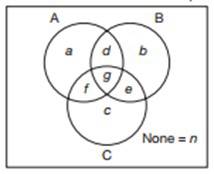
Sơ đồ Venn hình bên biểu thị 1200 nhân viên của một công ty. Mỗi nhân viên là thành viên của ít nhất một trong ba câu lạc bộ A, B và C.
Biết rằng:
▪ Tổng số thành viên câu lạc bộ A là 420.
▪ Tổng số thành viên câu lạc bộ B là 590.
▪ Tổng số thành viên câu lạc bộ C là 340.
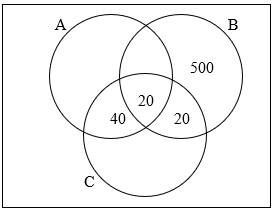
▪ Tổng số thành viên câu lạc bộ A là 420.
▪ Tổng số thành viên câu lạc bộ B là 590.
▪ Tổng số thành viên câu lạc bộ C là 340.

Câu 10 [289514]: Có bao nhiêu nhân viên chỉ tham gia một câu lạc bộ là câu lạc bộ C?
A, 250.
B, 240.
C, 180.
D, 260.
Chọn đáp án D. 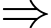 Số nhân viên chỉ tham gia câu lạc bộ C là:
Số nhân viên chỉ tham gia câu lạc bộ C là: 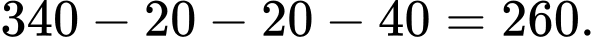 Đáp án: D
Đáp án: D
Dựa vào dữ kiện:
• Mỗi nhân viên là thành viên của ít nhất một trong ba câu lạc bộ A, B và C.
• Tổng số thành viên câu lạc bộ C là 340.
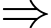 Số nhân viên chỉ tham gia câu lạc bộ C là:
Số nhân viên chỉ tham gia câu lạc bộ C là: 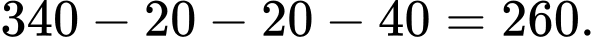
Câu 11 [289515]: Có bao nhiêu nhân viên không phải là thành viên của câu lạc bộ B?
A, 650.
B, 610.
C, 630.
D, 570.
Chọn đáp án B
Dựa vào dữ kiện:
• Sơ đồ Venn sau đây biểu thị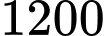 nhân viên của một công ty.
nhân viên của một công ty.
• Mỗi nhân viên là thành viên của ít nhất một trong ba câu lạc bộ A, B và C.
• Tổng số thành viên câu lạc bộ B là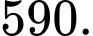
 Số nhân viên không phải là thành viên của câu lạc bộ B là:
Số nhân viên không phải là thành viên của câu lạc bộ B là: 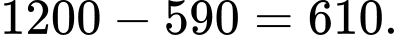 (Đây là tổng số nhân viên là thành viên câu lạc bộ A và câu lạc bộ C). Đáp án: B
(Đây là tổng số nhân viên là thành viên câu lạc bộ A và câu lạc bộ C). Đáp án: B
Dựa vào dữ kiện:
• Sơ đồ Venn sau đây biểu thị
 nhân viên của một công ty.
nhân viên của một công ty.• Mỗi nhân viên là thành viên của ít nhất một trong ba câu lạc bộ A, B và C.
• Tổng số thành viên câu lạc bộ B là
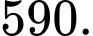
 Số nhân viên không phải là thành viên của câu lạc bộ B là:
Số nhân viên không phải là thành viên của câu lạc bộ B là: 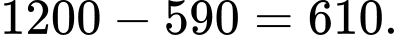 (Đây là tổng số nhân viên là thành viên câu lạc bộ A và câu lạc bộ C). Đáp án: B
(Đây là tổng số nhân viên là thành viên câu lạc bộ A và câu lạc bộ C). Đáp án: B
Câu 12 [289516]: Có bao nhiêu nhân viên là thành viên của câu lạc bộ A hoặc câu lạc bộ C?
A, 850.
B, 700.
C, 975.
D, 675.
Chọn đáp án B.
Dựa vào dữ kiện:
• Sơ đồ Venn sau đây biểu thị 1200 nhân viên của một công ty.
• Mỗi nhân viên là thành viên của ít nhất một trong ba câu lạc bộ A, B và C.
• Kết hợp với biểu đồ Venn ta thấy được có 500 nhân viên chỉ là thành viên câu lạc bộ C.
Số nhân viên là thành viên câu lạc bộ A hoặc câu lạc bộ C là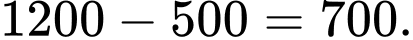 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Dựa vào dữ kiện:
• Sơ đồ Venn sau đây biểu thị 1200 nhân viên của một công ty.
• Mỗi nhân viên là thành viên của ít nhất một trong ba câu lạc bộ A, B và C.
• Kết hợp với biểu đồ Venn ta thấy được có 500 nhân viên chỉ là thành viên câu lạc bộ C.
Số nhân viên là thành viên câu lạc bộ A hoặc câu lạc bộ C là
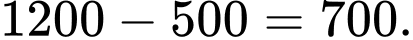 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 13 [289517]: Có bao nhiêu nhân viên là thành viên của đúng hai câu lạc bộ?
A, 110.
B, 130.
C, 98.
D, 78.
Chọn đáp án A.
Dựa vào dữ kiện:
• Sơ đồ Venn sau đây biểu thị 1200 nhân viên của một công ty.
• Mỗi nhân viên là thành viên của ít nhất một trong ba câu lạc bộ A, B và C.
• Kết hợp với biểu đồ Venn ta thấy được có 500 nhân viên chỉ là thành viên câu lạc bộ C.
 Số nhân viên là thành viên câu lạc bộ A và câu lạc bộ B là:
Số nhân viên là thành viên câu lạc bộ A và câu lạc bộ B là: 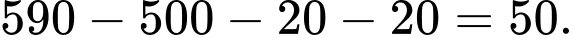 Số nhân viên là thành viên của đúng hai câu lạc bộ là:
Số nhân viên là thành viên của đúng hai câu lạc bộ là: 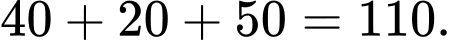 Đáp án: A
Đáp án: A
Dựa vào dữ kiện:
• Sơ đồ Venn sau đây biểu thị 1200 nhân viên của một công ty.
• Mỗi nhân viên là thành viên của ít nhất một trong ba câu lạc bộ A, B và C.
• Kết hợp với biểu đồ Venn ta thấy được có 500 nhân viên chỉ là thành viên câu lạc bộ C.
 Số nhân viên là thành viên câu lạc bộ A và câu lạc bộ B là:
Số nhân viên là thành viên câu lạc bộ A và câu lạc bộ B là: 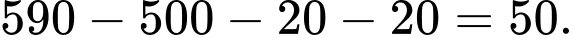 Số nhân viên là thành viên của đúng hai câu lạc bộ là:
Số nhân viên là thành viên của đúng hai câu lạc bộ là: 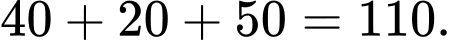 Đáp án: A
Đáp án: A Logic tình huống – bài đọc số 4
Trong bữa tráng miệng với 200 người tham dự tiệc sinh nhật có 120 người uống nước ngọt, 100 người ăn kem, 80 người ăn bánh; 10 người không ăn bữa tráng miệng và 100 người chỉ dùng một trong ba bữa tráng miệng trên.
Câu 14 [583725]: Có bao nhiêu người dùng hai trong ba món tráng miệng trên?
A, 70.
B, 80.
C, 110.
D, 85.
Chọn đáp án B.
Gọi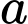 là số người chỉ uống nước ngọt.
là số người chỉ uống nước ngọt.
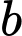 là số người chỉ ăn kem.
là số người chỉ ăn kem.
 là số người chỉ ăn bánh.
là số người chỉ ăn bánh.
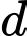 là số người uống nước ngọt và ăn kem.
là số người uống nước ngọt và ăn kem.
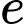 là số người ăn bánh và ăn kem.
là số người ăn bánh và ăn kem.
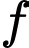 là số người uống nước ngọt và ăn bánh.
là số người uống nước ngọt và ăn bánh.
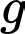 là số người dùng cả 3 món trên.
là số người dùng cả 3 món trên.
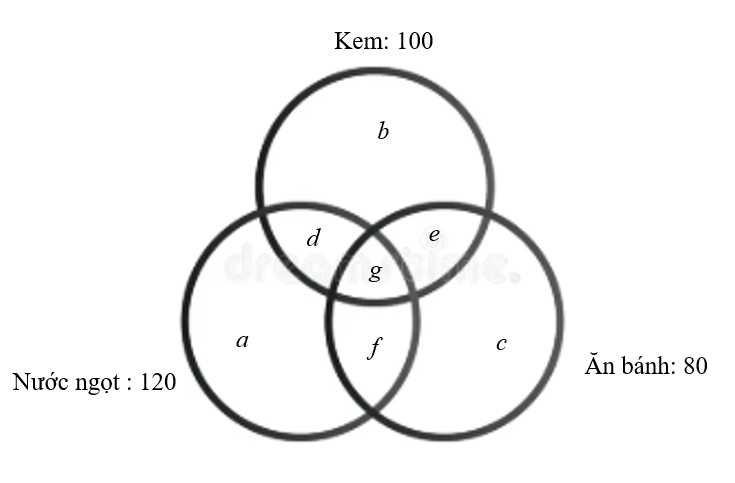
Theo dữ kiện của đề bài ta có hệ phương trình:
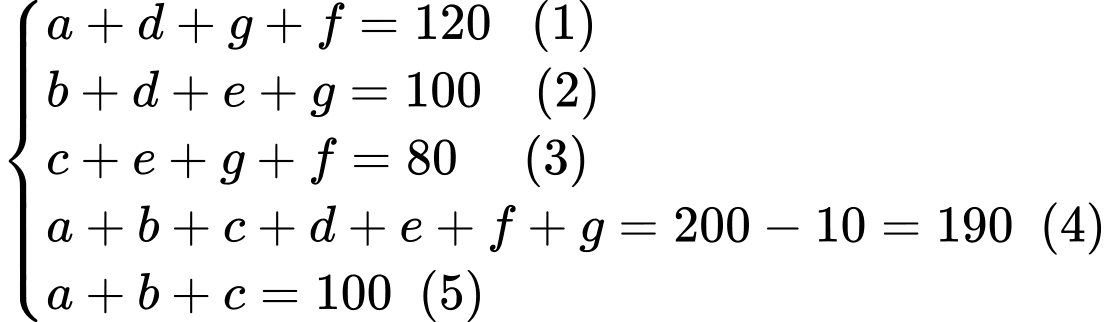
Cộng (1), (2) và (3) ta được: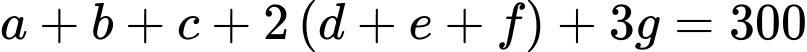
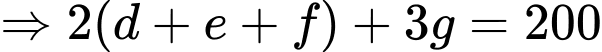 (6)
(6)
Từ (4) và (5)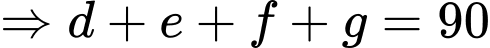 (7)
(7)
Từ (6) và (7)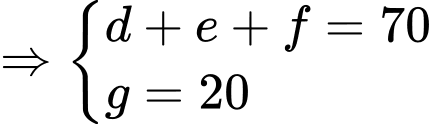 Đáp án: B
Đáp án: B
Gọi
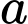 là số người chỉ uống nước ngọt.
là số người chỉ uống nước ngọt.
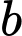 là số người chỉ ăn kem.
là số người chỉ ăn kem.
 là số người chỉ ăn bánh.
là số người chỉ ăn bánh.
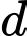 là số người uống nước ngọt và ăn kem.
là số người uống nước ngọt và ăn kem.
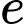 là số người ăn bánh và ăn kem.
là số người ăn bánh và ăn kem.
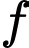 là số người uống nước ngọt và ăn bánh.
là số người uống nước ngọt và ăn bánh.
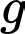 là số người dùng cả 3 món trên.
là số người dùng cả 3 món trên.
Theo dữ kiện của đề bài ta có hệ phương trình:
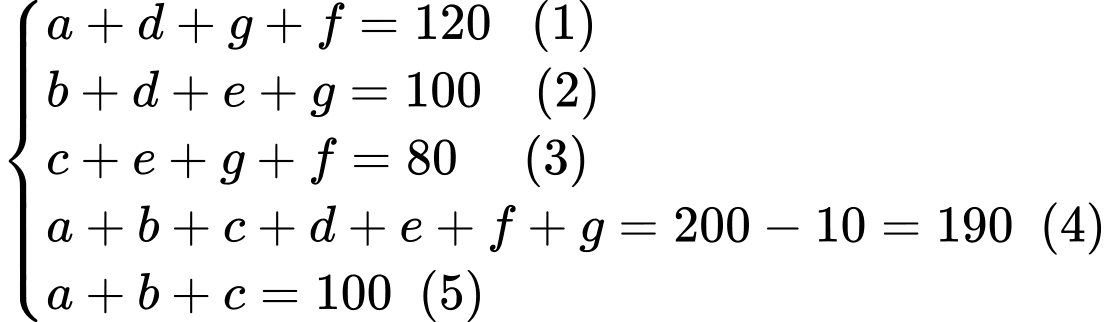
Cộng (1), (2) và (3) ta được:
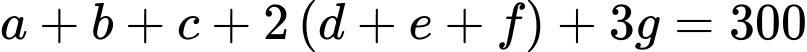
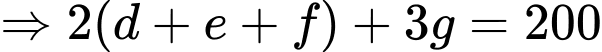 (6)
(6)
Từ (4) và (5)
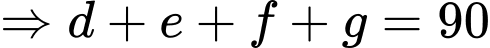 (7)
(7)
Từ (6) và (7)
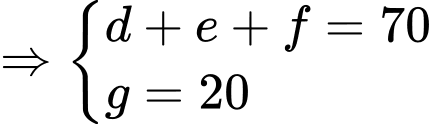 Đáp án: B
Đáp án: B
Câu 15 [583726]: Nếu 20 người chỉ uống nước ngọt và ăn kem thì có bao nhiêu người ăn bánh?
A, 12.
B, 18.
C, 20.
D, 10.
Chọn đáp án D.
Theo dữ kiện câu hỏi IDL: 583725 ta có: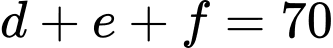
Mà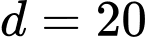 nên
nên 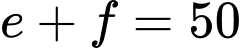
Có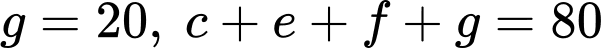
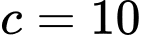 Đáp án: D
Đáp án: D
Theo dữ kiện câu hỏi IDL: 583725 ta có:
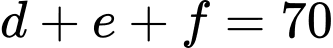
Mà
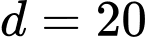 nên
nên 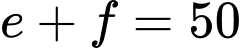
Có
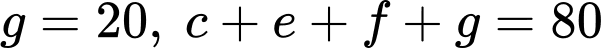
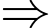
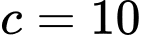 Đáp án: D
Đáp án: D
Câu 16 [583727]: Nếu 15 người chỉ ăn trái cây và ăn bánh; 5 người dùng cả 3 món tráng miệng thì có bao nhiêu người dùng ít nhất hai trong ba món tráng miệng?
A, 135.
B, 105.
C, 78.
D, 119.
Đáp án: B
Câu 17 [583728]: Nếu 30 người chỉ ăn kem thì có bao nhiêu người dùng ít nhất một trong hai món là bánh và trái cây nhưng không ăn kem?
A, 105.
B, 98.
C, 87.
D, 90.
Đáp án: D
Câu 18 [583729]: Số lượng người chỉ ăn trái cây tối đa có thể là
A, 90.
B, 87.
C, 118.
D, 120.
Đáp án: A
Logic tình huống – bài đọc số 5
Trong một cuộc khảo sát được thực hiện với 200 hộ gia đình sử dụng các hãng điện thoại di động và kết quả cho thấy có 140 gia đình sử dụng Iphone, 120 gia đình sử dụng Nokia và 143 gia đình sử dụng Samsung, 95 gia đình sử dụng cả Iphone và Nokia, 85 gia đình sử dụng cả Nokia và Samsung và 93 gia đình sử dụng cả Iphone và Samsung. 70 gia đình sử dụng điện thoại di động của cả 3 hãng trên.
Câu 19 [379865]: Có bao nhiêu gia đình chỉ sử dụng điện thoại di động của Samsung?
A, 50.
B, 35.
C, 70.
D, 143.
Chọn đáp án B.
Gọi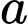 là số hộ gia đình chỉ sử dụng Iphone
là số hộ gia đình chỉ sử dụng Iphone
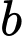 là số hộ gia đình chỉ sử dụng Nokia.
là số hộ gia đình chỉ sử dụng Nokia.
 là số hộ gia đình chỉ sử dụng Samsung.
là số hộ gia đình chỉ sử dụng Samsung.
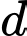 là số hộ gia đình chỉ sử dụng Samsung và Nokia.
là số hộ gia đình chỉ sử dụng Samsung và Nokia.
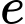 là số hộ gia đình chỉ sử dụng Samsung và Iphone.
là số hộ gia đình chỉ sử dụng Samsung và Iphone.
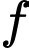 là số hộ gia đình chỉ sử dụng Nokia và Iphone.
là số hộ gia đình chỉ sử dụng Nokia và Iphone.
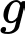 là số hộ gia đình sử dụng điện thoại của cả ba hãng trên
là số hộ gia đình sử dụng điện thoại của cả ba hãng trên 
 là số hộ gia đình không sử dụng điện thoại di động của ba hãng trên.
là số hộ gia đình không sử dụng điện thoại di động của ba hãng trên.
Dựa vào các dữ kiện của đề bài, ta có hệ phương trình:
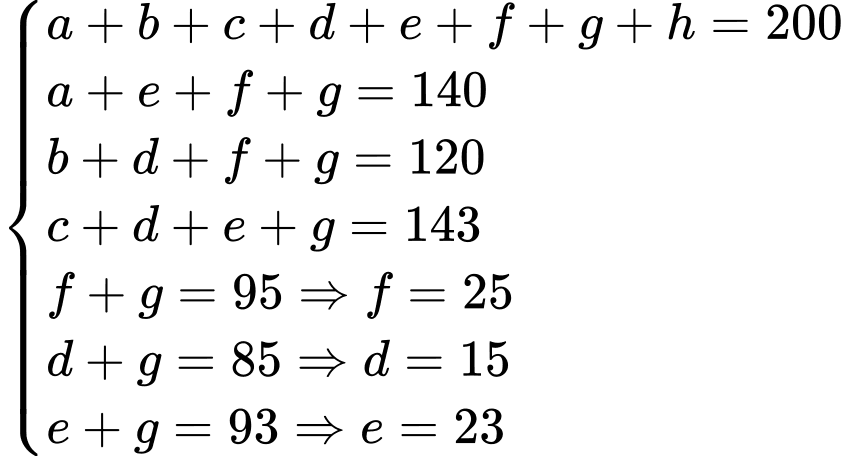
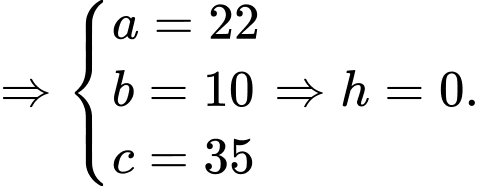
Minh họa:
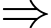 Có 35 hộ gia đình chỉ sử dụng điện thoại diđộng của Samsung. Đáp án: B
Có 35 hộ gia đình chỉ sử dụng điện thoại diđộng của Samsung. Đáp án: B
Gọi
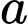 là số hộ gia đình chỉ sử dụng Iphone
là số hộ gia đình chỉ sử dụng Iphone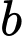 là số hộ gia đình chỉ sử dụng Nokia.
là số hộ gia đình chỉ sử dụng Nokia. là số hộ gia đình chỉ sử dụng Samsung.
là số hộ gia đình chỉ sử dụng Samsung.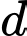 là số hộ gia đình chỉ sử dụng Samsung và Nokia.
là số hộ gia đình chỉ sử dụng Samsung và Nokia.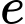 là số hộ gia đình chỉ sử dụng Samsung và Iphone.
là số hộ gia đình chỉ sử dụng Samsung và Iphone.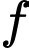 là số hộ gia đình chỉ sử dụng Nokia và Iphone.
là số hộ gia đình chỉ sử dụng Nokia và Iphone.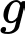 là số hộ gia đình sử dụng điện thoại của cả ba hãng trên
là số hộ gia đình sử dụng điện thoại của cả ba hãng trên 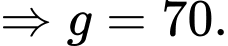
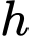 là số hộ gia đình không sử dụng điện thoại di động của ba hãng trên.
là số hộ gia đình không sử dụng điện thoại di động của ba hãng trên.Dựa vào các dữ kiện của đề bài, ta có hệ phương trình:
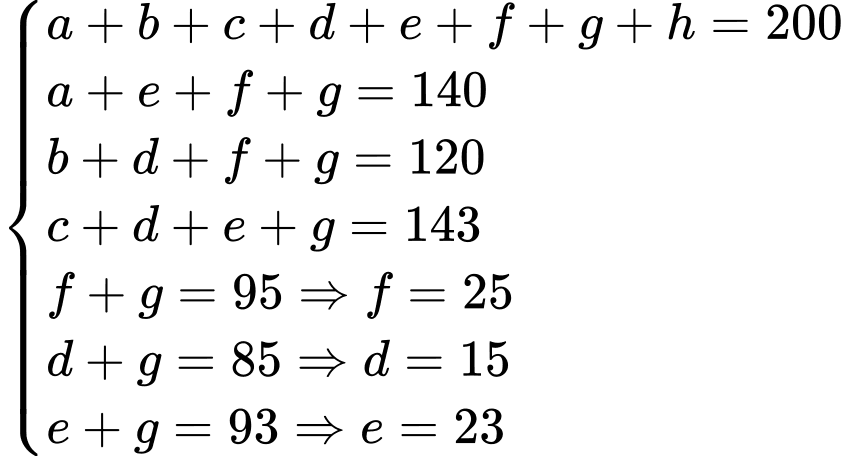
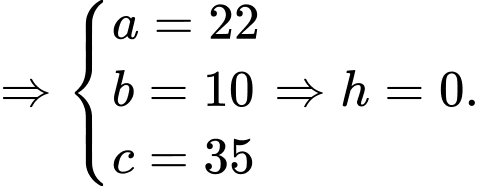
Minh họa:

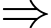 Có 35 hộ gia đình chỉ sử dụng điện thoại diđộng của Samsung. Đáp án: B
Có 35 hộ gia đình chỉ sử dụng điện thoại diđộng của Samsung. Đáp án: B
Câu 20 [379866]: Có bao nhiêu gia đình sử dụng điện thoại di động của hai hãng Iphone và Nokia mà không sử dụng điện thoại của Samsung?
A, 25.
B, 57.
C, 163.
D, 95.
Dựa vào hình minh họa phân tích giả thiết:
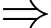 Có 25 hộ gia đình chỉ sử dụng điện thoại của hai hãng Iphone và Nokia.
Có 25 hộ gia đình chỉ sử dụng điện thoại của hai hãng Iphone và Nokia.  Chọn đáp án A.
Đáp án: A
Chọn đáp án A.
Đáp án: A

 Có 25 hộ gia đình chỉ sử dụng điện thoại của hai hãng Iphone và Nokia.
Có 25 hộ gia đình chỉ sử dụng điện thoại của hai hãng Iphone và Nokia.  Chọn đáp án A.
Chọn đáp án A.
Câu 21 [379867]: Có bao nhiêu gia đình sử dụng điện thoại di động của đúng một hãng?
A, 63.
B, 67.
C, 70.
D, 200.
Chọn đáp án B.
Dựa vào hình minh họa phân tích giả thiết:

Số gia đình sử dụng điện thoại di động của đúng một hãng là: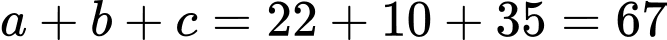 (gia đình). Đáp án: B
(gia đình). Đáp án: B
Dựa vào hình minh họa phân tích giả thiết:

Số gia đình sử dụng điện thoại di động của đúng một hãng là:
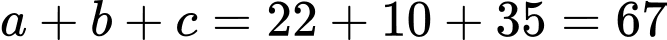 (gia đình). Đáp án: B
(gia đình). Đáp án: B
Câu 22 [379868]: Có bao nhiêu gia đình không sử dụng điện thoại di động của ba hãng trên?
A, 10.
B, 70.
C, 0.
D, Không thể xác định được.
Chọn đáp án C.
Dựa vào hình minh họa phân tích giả thiết:


 Trong số hộ gia đình được khảo sát, không có gia đình nào không sử dụng điện thoại di động của ba hãng trên. Đáp án: C
Trong số hộ gia đình được khảo sát, không có gia đình nào không sử dụng điện thoại di động của ba hãng trên. Đáp án: C
Dựa vào hình minh họa phân tích giả thiết:


 Trong số hộ gia đình được khảo sát, không có gia đình nào không sử dụng điện thoại di động của ba hãng trên. Đáp án: C
Trong số hộ gia đình được khảo sát, không có gia đình nào không sử dụng điện thoại di động của ba hãng trên. Đáp án: C Logic tình huống – bài đọc số 6
Trong một huyện, cư dân đọc các tờ báo khác nhau trong số báo Dân trí, báo Lao động và báo Thanh niên. Người ta biết rằng $52%$ cư dân đọc nhiều nhất một tờ báo. $42%$ cư dân đọc báo Lao động hoặc báo Thanh niên nhưng không đọc báo Dân trí. $54%$ cư dân đọc báo Lao động. $24%$ cư dân đọc cả báo Dân trí và báo Lao động. $36%$ cư dân đọc đúng hai tờ báo. $10%$ cư dân chỉ đọc báo Dân trí và báo Thanh niên. Số lượng cư dân đọc cả ba tờ báo gấp đôi số lượng cư dân không đọc bất kỳ tờ báo nào trong số này. $2\text{ }800$ cư dân chỉ đọc báo Lao động và báo Thanh niên.
Câu 23 [583730]: Có bao nhiêu cư dân chỉ đọc báo Dân trí?
A, 4000.
B, 3600.
C, 3200.
D, 3400.
Đáp án: B
Câu 24 [583731]: Có bao nhiêu cư dân không đọc bất kỳ tờ báo nào?
A, 1 800.
B, 1 600.
C, 1 450.
D, 1 200.
Chọn đáp án D.
Số cư dân không đọc bất kỳ tờ báo nào là: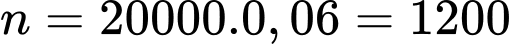 (cư dân). Đáp án: D
(cư dân). Đáp án: D
Số cư dân không đọc bất kỳ tờ báo nào là:
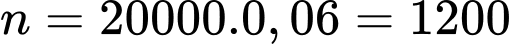 (cư dân). Đáp án: D
(cư dân). Đáp án: D
Câu 25 [583732]: Có bao nhiêu cư dân đọc ít nhất hai tờ báo?
A, 9 600.
B, 8 000.
C, 8 400.
D, 10 200.
Chọn đáp án A.
Số cư dân không đọc ít nhất hai tờ báo là:
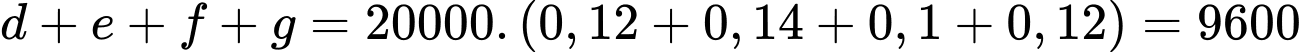 (cư dân).
Đáp án: A
(cư dân).
Đáp án: A
Số cư dân không đọc ít nhất hai tờ báo là:
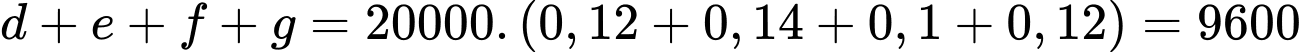 (cư dân).
Đáp án: A
(cư dân).
Đáp án: A
Câu 26 [583733]: Có bao nhiêu cư dân trong huyện này?
A, 22 000.
B, 16 000.
C, 20 000.
D, 18 000.
Chọn đáp án C.
Số cư dân trong huyện này là: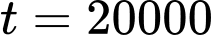 (cư dân).
Đáp án: C
(cư dân).
Đáp án: C
Số cư dân trong huyện này là:
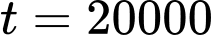 (cư dân).
Đáp án: C
(cư dân).
Đáp án: C Logic tình huống – bài đọc số 7
Một cuộc khảo sát với số lượng A học sinh tham gia ít nhất một trong các nội dung trong hội khỏe phù đổng là nhảy cao, nhảy xa và chạy nước rút $100\text{ m}.$ 27 học sinh tham gia nhảy cao, 27 học sinh tham gia nhảy xa và 52 học sinh tham gia chạy nước rút $100\text{ m}.$
Câu 27 [583734]: Nếu số học sinh tham gia đúng một trong ba nội dung là 51 thì số học sinh tham gia đúng hai trong ba nội dung nhiều nhất có thể là
A, 22.
B, 30.
C, 34.
D, 26.
Chọn đáp án D.
Gọi là tập hợp học sinh chỉ tham gia nhảy cao.
là tập hợp học sinh chỉ tham gia nhảy cao.
 là tập hợp học sinh chỉ tham gia nhảy xa.
là tập hợp học sinh chỉ tham gia nhảy xa.
 là tập hợp học sinh chỉ tham gia chạy nước rút 100m.
là tập hợp học sinh chỉ tham gia chạy nước rút 100m.
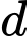 là tập hợp học sinh chỉ tham gia nhảy cao và nhảy xa.
là tập hợp học sinh chỉ tham gia nhảy cao và nhảy xa.
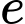 là tập hợp học sinh chỉ tham gia nhảy xa và chạy nước rút 100m.
là tập hợp học sinh chỉ tham gia nhảy xa và chạy nước rút 100m.
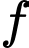 là tập hợp học sinh chỉ tham gia chạy nước rút 100m và nhảy cao.
là tập hợp học sinh chỉ tham gia chạy nước rút 100m và nhảy cao.
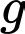 là tập hợp học sinh tham gia cả ba nội dung.
là tập hợp học sinh tham gia cả ba nội dung.

Từ dữ kiện đề bài cho, ta có hệ phương trình:
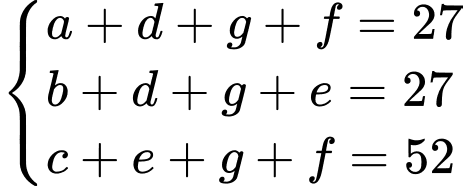
Kết hợp dữ kiện: Số học sinh tham gia đúng một trong ba nội dung là 51.
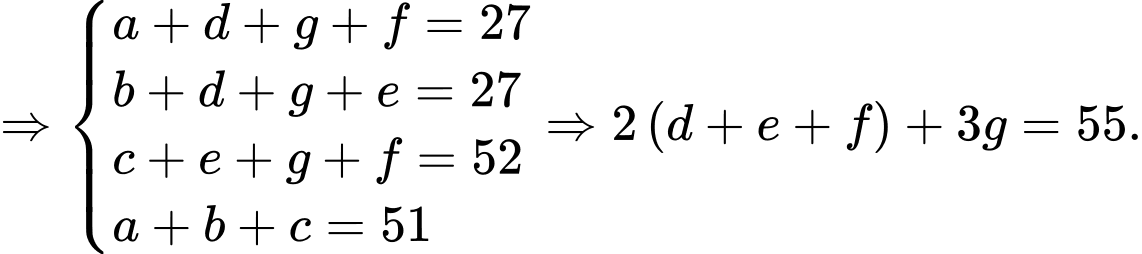
Để số học sinh tham gia đúng hai trong ba nội dung nhiều nhất
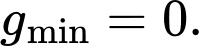
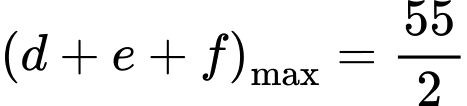 (Loại).
(Loại).
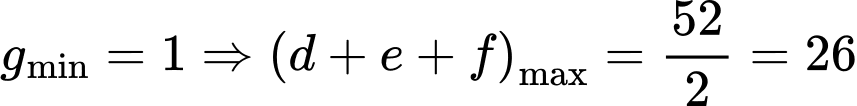 (học sinh). Đáp án: D
(học sinh). Đáp án: D

Gọi
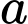 là tập hợp học sinh chỉ tham gia nhảy cao.
là tập hợp học sinh chỉ tham gia nhảy cao.
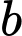 là tập hợp học sinh chỉ tham gia nhảy xa.
là tập hợp học sinh chỉ tham gia nhảy xa.
 là tập hợp học sinh chỉ tham gia chạy nước rút 100m.
là tập hợp học sinh chỉ tham gia chạy nước rút 100m.
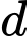 là tập hợp học sinh chỉ tham gia nhảy cao và nhảy xa.
là tập hợp học sinh chỉ tham gia nhảy cao và nhảy xa.
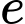 là tập hợp học sinh chỉ tham gia nhảy xa và chạy nước rút 100m.
là tập hợp học sinh chỉ tham gia nhảy xa và chạy nước rút 100m.
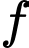 là tập hợp học sinh chỉ tham gia chạy nước rút 100m và nhảy cao.
là tập hợp học sinh chỉ tham gia chạy nước rút 100m và nhảy cao.
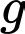 là tập hợp học sinh tham gia cả ba nội dung.
là tập hợp học sinh tham gia cả ba nội dung.

Từ dữ kiện đề bài cho, ta có hệ phương trình:
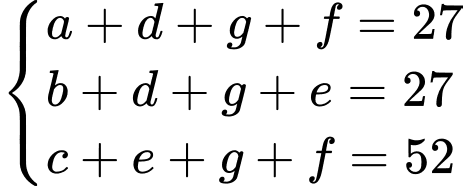
Kết hợp dữ kiện: Số học sinh tham gia đúng một trong ba nội dung là 51.
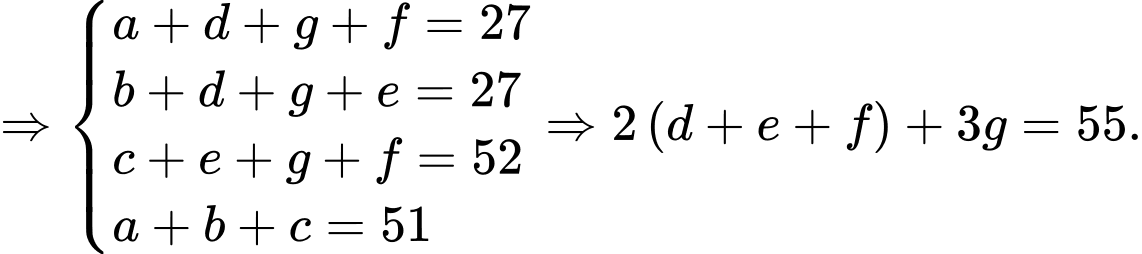
Để số học sinh tham gia đúng hai trong ba nội dung nhiều nhất
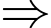
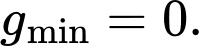
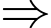
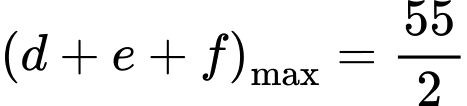 (Loại).
(Loại).
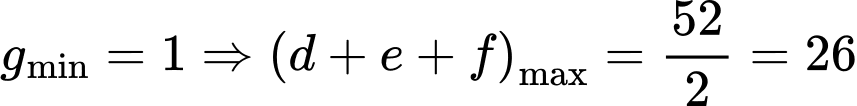 (học sinh). Đáp án: D
(học sinh). Đáp án: D
Câu 28 [583735]: Số học sinh tham gia đúng một trong ba sự kiện lớn hơn hoặc bằng số học sinh tham gia đúng hai trong ba sự kiện, số học sinh tham gia đúng hai trong ba sự kiện lớn hơn hoặc bằng số học sinh tham gia cả ba sự kiện. Tìm số học sinh tham gia cả ba sự kiện nhiều nhất có thể?
A, 16.
B, 18.
C, 17.
D, 19.
Chọn đáp án C.
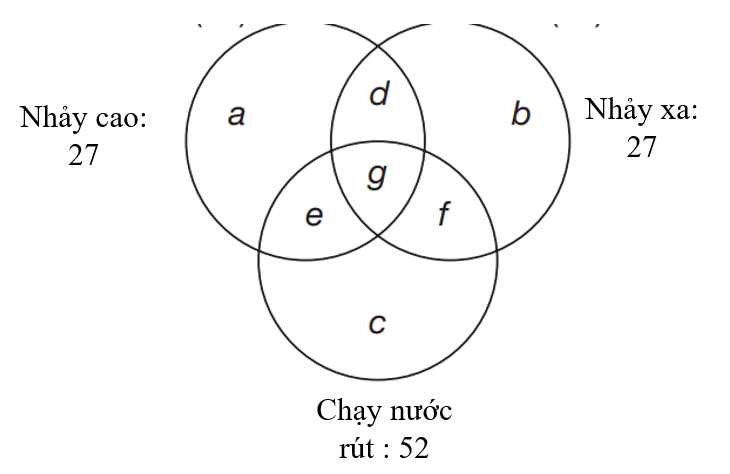
Vì số học sinh tham gia đúng một trong ba sự kiện lớn hơn hoặc bằng số học sinh tham gia đúng hai trong ba sự kiện lớn hơn hoặc bằng số học sinh tham gia cả ba sự kiện nên ta có: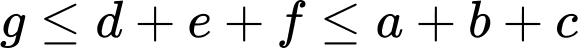
+)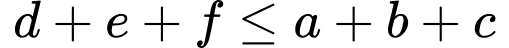
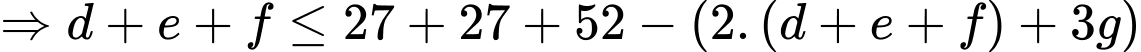
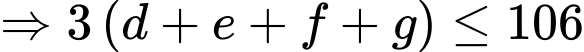
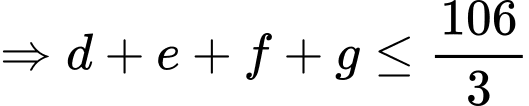
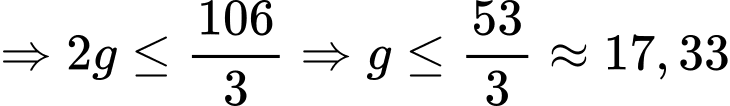
Số học sinh tham gia cả ba sự kiện nhiều nhất có thể là 17. Đáp án: C

Vì số học sinh tham gia đúng một trong ba sự kiện lớn hơn hoặc bằng số học sinh tham gia đúng hai trong ba sự kiện lớn hơn hoặc bằng số học sinh tham gia cả ba sự kiện nên ta có:
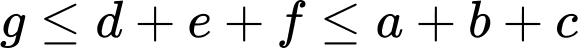
+)
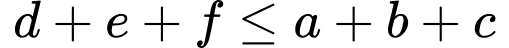
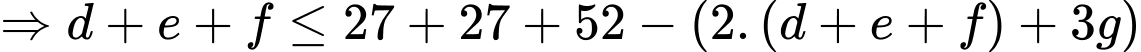
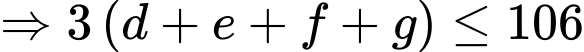
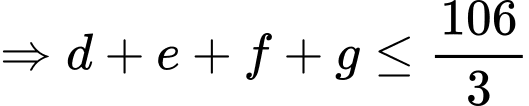
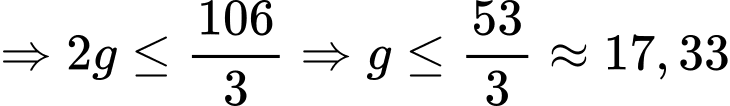
Số học sinh tham gia cả ba sự kiện nhiều nhất có thể là 17. Đáp án: C
Câu 29 [583736]: Nếu số học sinh tham gia ít nhất hai trong ba nội dung là 26 thì giá trị nhỏ nhất có thể của A là
A, 50.
B, 54.
C, 52.
D, 46.
Chọn đáp án B.
Kết hợp dữ kiện: Số học sinh tham gia ít nhất hai trong ba nội dung là 26.
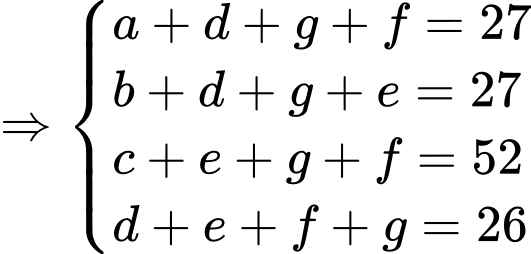
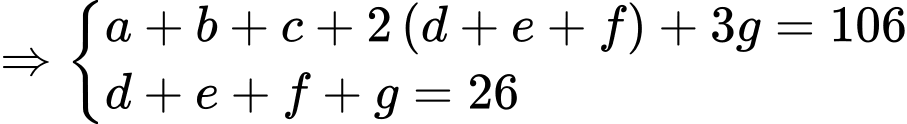
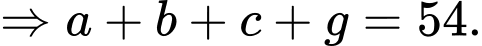
Nhận xét:
Để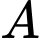 nhỏ nhất
nhỏ nhất
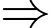
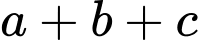 nhỏ nhất.
nhỏ nhất.
Lại có: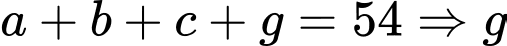 phải lớn nhất.
phải lớn nhất.
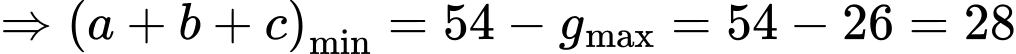
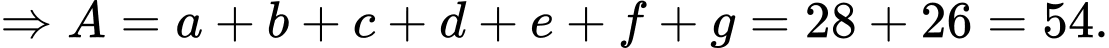 Đáp án: B
Đáp án: B
Kết hợp dữ kiện: Số học sinh tham gia ít nhất hai trong ba nội dung là 26.
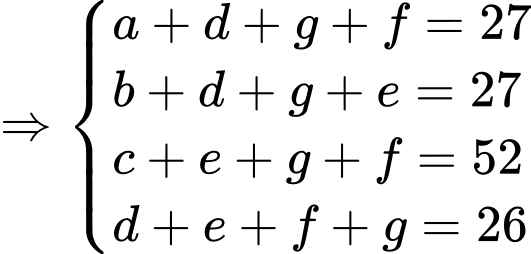
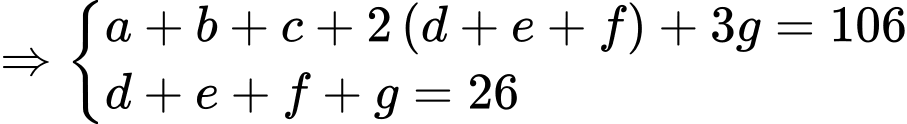
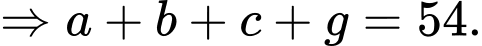
Nhận xét:

Để
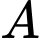 nhỏ nhất
nhỏ nhất 
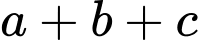 nhỏ nhất.
nhỏ nhất.Lại có:
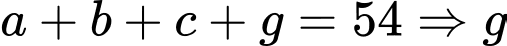 phải lớn nhất.
phải lớn nhất.
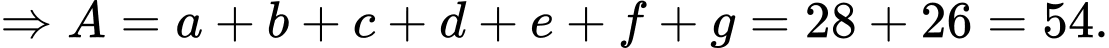 Đáp án: B
Đáp án: B Logic tình huống – bài đọc số 8
Một cuộc khảo sát được tiến hành để đánh giá về mức độ phổ biến của bốn hãng Laptop là Lenovo, Asus, Dell và HP với 800 người tham gia. Mỗi người tham gia sở hữu ít nhất một trong bốn hãng Laptop. Số người sở hữu Latop HP là 450, số người sở hữu Dell là 270 và số người sở hữu Laptop Lenovo là 325. 100 người chỉ sở hữu Latop Asus, 50 chỉ sở hữu Latop Dell và 90 chỉ sở hữu Latop HP. 50 người sở hữu đúng hai hãng Latop Lenovo và Asus, 60 người sở hữu đúng hai hãng Latop Lenovo và Dell, 90 người sở hữu đúng hai hãng Lenovo và HP, 30 người sở hữu đúng hai hãng Laptop Asus và Dell, 120 người sở hữu đúng hai hãng Laptop Asus và HP, 60 người sở hữu đúng hai hãng Laptop Dell và HP. 20 người sở hữu đúng ba hãng Laptop Lenovo, Asus và Dell, 15 người sở hữu đúng ba hãng Laptop Lenovo, Dell và HP; 25 người sở hữu đúng ba hãng Laptop Asus, Dell và HP.
Câu 30 [583737]: Có bao nhiêu người sở hữu hai hãng Laptop Lenovo và Asus nhưng không sở hữu hãng Laptop Dell?
A, 50.
B, 90.
C, 100.
D, 70.
Chọn đáp án B.
Gọi là tập hợp người chỉ sở hữu hãng Laptop Lenovo.
là tập hợp người chỉ sở hữu hãng Laptop Lenovo.
 là tập hợp người sở hữu cả bốn hãng Laptop.
là tập hợp người sở hữu cả bốn hãng Laptop.
 là tập hợp người sở hữu đúng ba hãng Laptop Lenovo, HP và Asus.
là tập hợp người sở hữu đúng ba hãng Laptop Lenovo, HP và Asus.
Từ các dữ kiện đề bài, ta có biểu đồ:
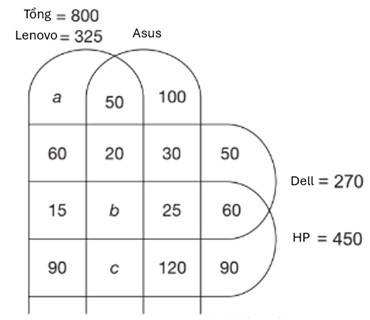
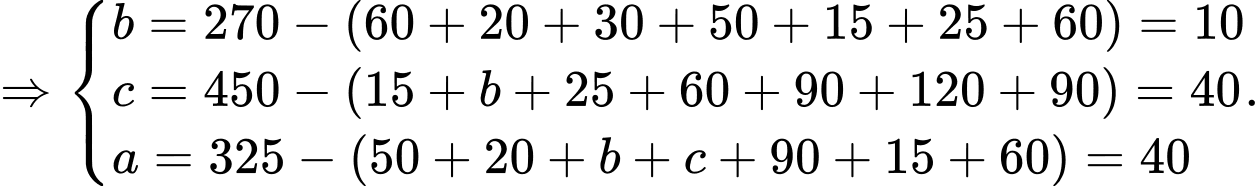
Số người sở hữu hai hãng Laptop Lenovo và Asus nhưng không sở hữu hãng Laptop Dell là:
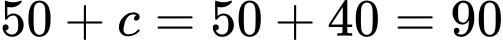 (người). Đáp án: B
(người). Đáp án: B
Gọi
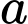 là tập hợp người chỉ sở hữu hãng Laptop Lenovo.
là tập hợp người chỉ sở hữu hãng Laptop Lenovo.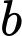 là tập hợp người sở hữu cả bốn hãng Laptop.
là tập hợp người sở hữu cả bốn hãng Laptop. là tập hợp người sở hữu đúng ba hãng Laptop Lenovo, HP và Asus.
là tập hợp người sở hữu đúng ba hãng Laptop Lenovo, HP và Asus.Từ các dữ kiện đề bài, ta có biểu đồ:

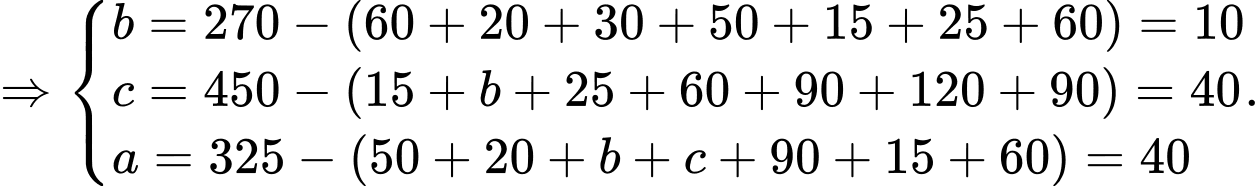
Số người sở hữu hai hãng Laptop Lenovo và Asus nhưng không sở hữu hãng Laptop Dell là:
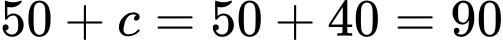 (người). Đáp án: B
(người). Đáp án: B
Câu 31 [583738]: Có bao nhiêu người sở hữu ít nhất hai hãng Laptop?
A, 480.
B, 560.
C, 600.
D, 520.
Chọn đáp án D.
Số người chỉ sở hữu một hãng Laptop là: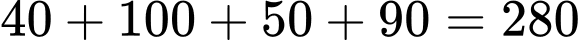 (người)
(người)
Số người sở hữu ít nhất hai hãng Laptop là: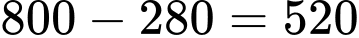 (người).
Đáp án: D
(người).
Đáp án: D
Số người chỉ sở hữu một hãng Laptop là:
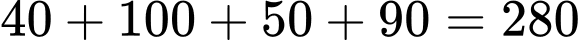 (người)
(người)
Số người sở hữu ít nhất hai hãng Laptop là:
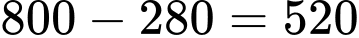 (người).
Đáp án: D
(người).
Đáp án: D
Câu 32 [583739]: Có bao nhiêu người không sở hữu hãng Laptop Lenovo cũng không sở hữu hãng Laptop Asus?
A, 200.
B, 250.
C, 180.
D, 150.
Chọn đáp án A.
Số người không sở hữu hãng Laptop Lenovo cũng không sở hữu hãng Laptop Asus là:
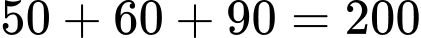 (người).
Đáp án: A
(người).
Đáp án: A
Số người không sở hữu hãng Laptop Lenovo cũng không sở hữu hãng Laptop Asus là:
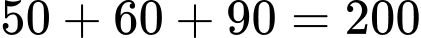 (người).
Đáp án: A
(người).
Đáp án: A
Câu 33 [583740]: Có bao nhiêu người sở hữu hãng Laptop Dell hoặc HP?
A, 590.
B, 630.
C, 570.
D, 610.
Chọn đáp án D.
Số người không sở hữu cả hai hãng Laptop Dell và HP là: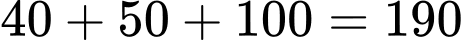 (người)
(người)
Số người không sở hữu hãng Laptop Dell hoặc HP là: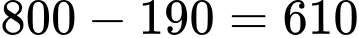 (người).
Đáp án: D
(người).
Đáp án: D
Số người không sở hữu cả hai hãng Laptop Dell và HP là:
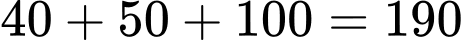 (người)
(người)
Số người không sở hữu hãng Laptop Dell hoặc HP là:
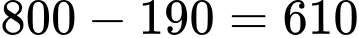 (người).
Đáp án: D
(người).
Đáp án: D Logic tình huống – bài đọc số 9
Toàn bộ học sinh trong một thị trấn đều thích ít nhất một trong bốn thương hiệu đồ uống sau Coca-Cola, Fanta, 7Up và Sprite. 65 học sinh thích Fanta và Coca-Cola. 77 học sinh thích Sprite và Fanta. 73 học sinh thích Coca-Cola và 7Up. 76 học sinh thích 7Up và Fanta. 74 học sinh thích Sprite và Coca-Cola. Có 67 học sinh thích đúng một thương hiệu. Số học sinh chỉ thích 7Up, Fanta và Coca-Cola bằng số học sinh chỉ thích Sprite, Fanta và Coca-Cola. Số học sinh thích Sprite, 7Up và Fanta nhưng không thích Coca-Cola bằng số học sinh thích Sprite, 7Up và Coca-Cola nhưng không thích Fanta. Số lượng học sinh chỉ thích Coca-Cola và Sprite là 14. Số lượng học sinh chỉ thích Sprite và 7Up và chỉ Fanta và Coca-Cola lần lượt là 10 và 15. Tổng số học sinh thích Fanta, số lượng học sinh thích Coca-Cola, số lượng học sinh thích Sprite và số lượng học sinh thích 7Up là 557.
Câu 34 [583741]: Có bao nhiêu học sinh thích cả Sprite và 7Up nhưng không thích cả bốn thương hiệu?
A, 60.
B, 50.
C, 55.
D, 44.
Chọn đáp án A.
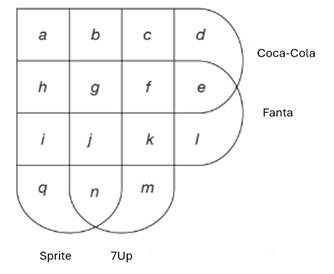
Từ các dữ kiện đề bài cho, ta có hệ phương trình:
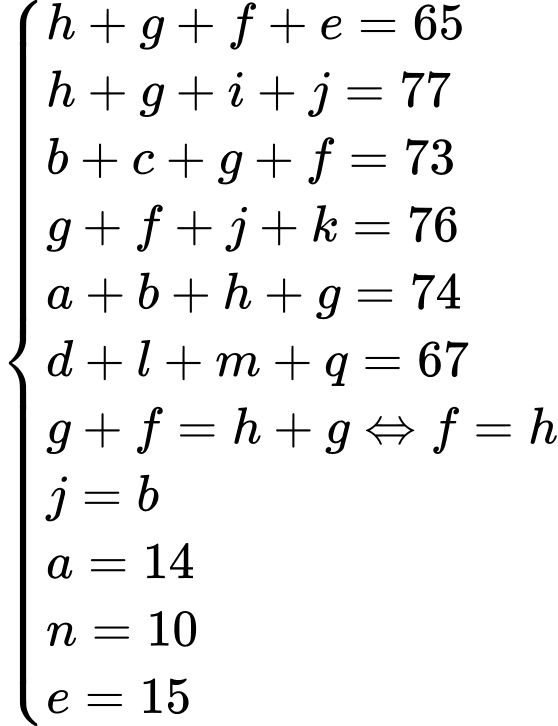
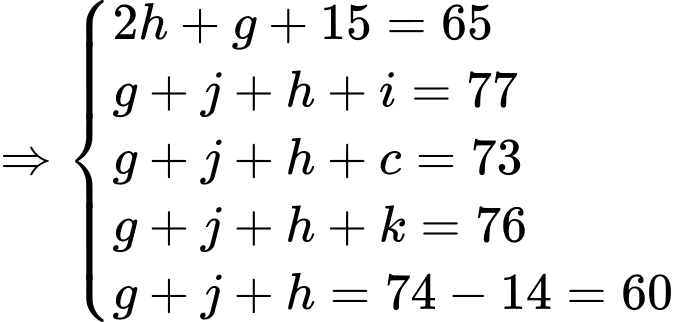
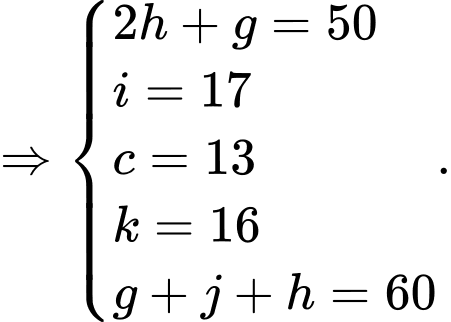
Gọi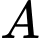 là tập hợp học sinh thích chính xác một đồ uống.
là tập hợp học sinh thích chính xác một đồ uống.
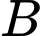 là tập hợp học sinh thích chính xác hai đồ uống.
là tập hợp học sinh thích chính xác hai đồ uống.
 là tập hợp học sinh thích chính xác ba đồ uống.
là tập hợp học sinh thích chính xác ba đồ uống.
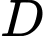 là tập hợp học sinh thích chính xác bốn đồ uống.
là tập hợp học sinh thích chính xác bốn đồ uống.
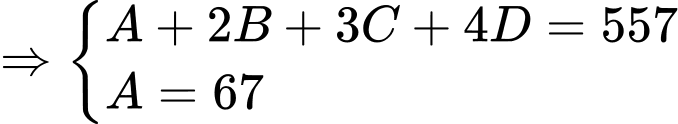
Có:
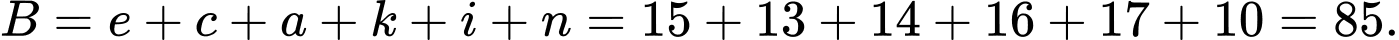
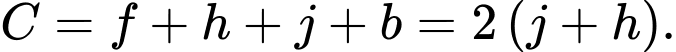
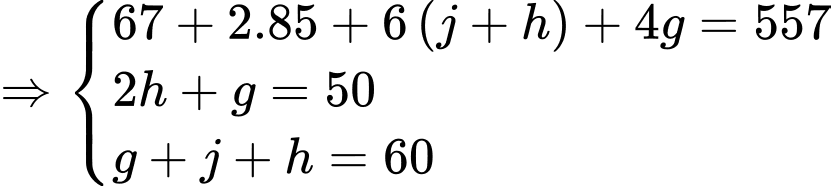
 Đáp án: A
Đáp án: A

Từ các dữ kiện đề bài cho, ta có hệ phương trình:
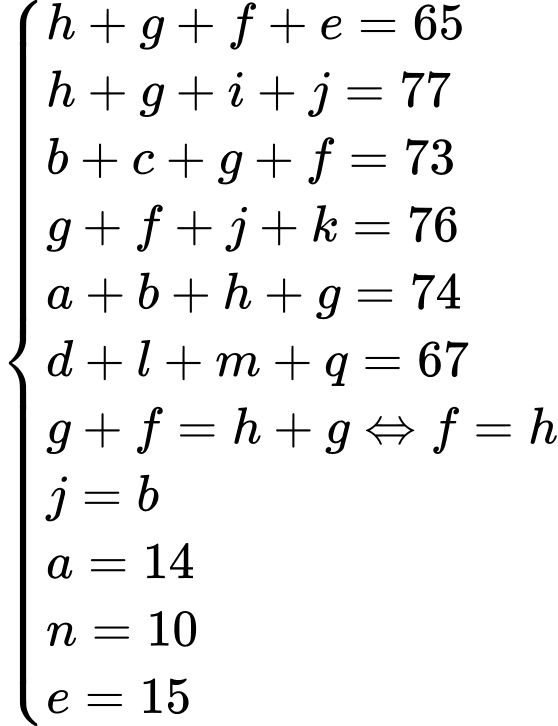
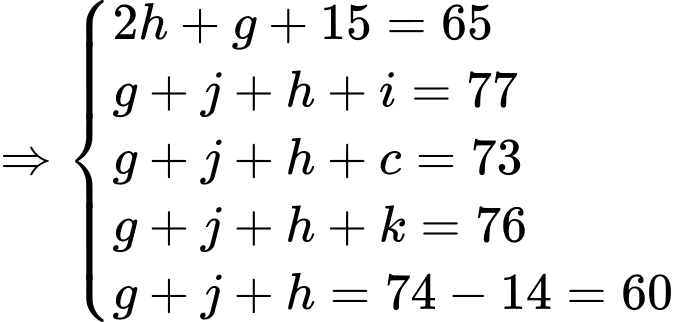
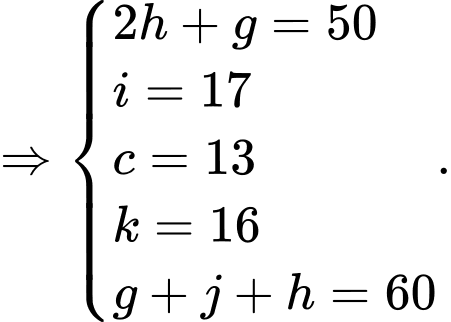
Gọi
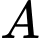 là tập hợp học sinh thích chính xác một đồ uống.
là tập hợp học sinh thích chính xác một đồ uống.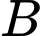 là tập hợp học sinh thích chính xác hai đồ uống.
là tập hợp học sinh thích chính xác hai đồ uống. là tập hợp học sinh thích chính xác ba đồ uống.
là tập hợp học sinh thích chính xác ba đồ uống.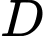 là tập hợp học sinh thích chính xác bốn đồ uống.
là tập hợp học sinh thích chính xác bốn đồ uống.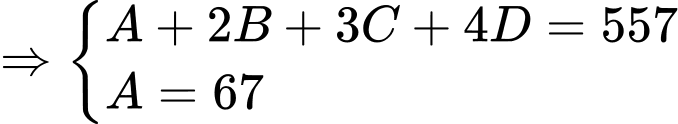
Có:
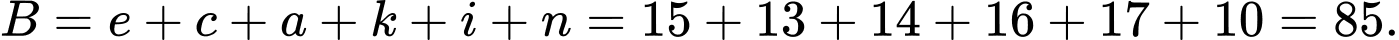
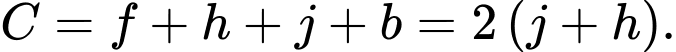
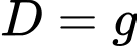
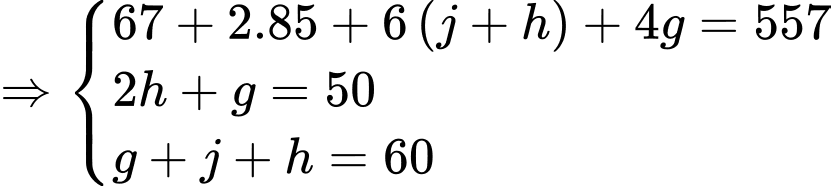
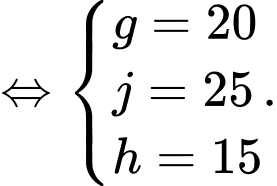 Đáp án: A
Đáp án: A
Câu 35 [583742]: Tổng số học sinh tham gia khảo sát là
A, 247.
B, 250.
C, 235.
D, 252.
Chọn đáp án D.
Tổng số học sinh tham gia khảo sát là: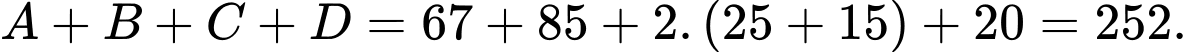 Đáp án: D
Đáp án: D
Tổng số học sinh tham gia khảo sát là:
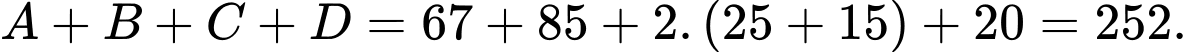 Đáp án: D
Đáp án: D
Câu 36 [583743]: Có bao nhiêu học sinh chỉ thích Coca-Cola và 7Up?
A, 16.
B, 17.
C, 13.
D, 15.
Chọn đáp án C.
Số học sinh chỉ thích Coca-Cola và 7Up là: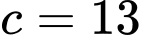 (học sinh).
Đáp án: C
(học sinh).
Đáp án: C
Số học sinh chỉ thích Coca-Cola và 7Up là:
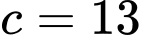 (học sinh).
Đáp án: C
(học sinh).
Đáp án: C
Câu 37 [583744]: Nếu 25 học sinh chỉ thích Fanta hoặc chỉ thích Sprite thì có bao nhiêu học sinh thích Coca-Cola hoặc 7Up?
A, 42.
B, 208.
C, 152.
D, 210.
Chọn đáp án D.
Dựa vào dữ kiện: 25 học sinh chỉ thích Fanta hoặc chỉ thích Sprite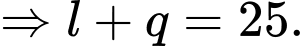
Số học sinh chỉ thích Coca-Cola hoặc 7Up là: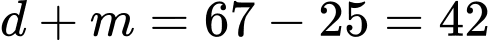 (học sinh).
(học sinh).
Số học sinh thích Coca-Cola hoặc 7Up là: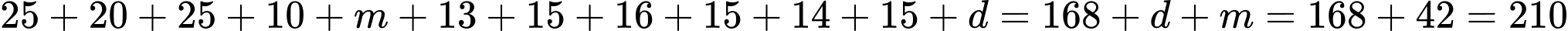 (học sinh).
Đáp án: D
(học sinh).
Đáp án: D
Dựa vào dữ kiện: 25 học sinh chỉ thích Fanta hoặc chỉ thích Sprite
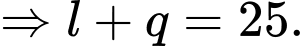
Số học sinh chỉ thích Coca-Cola hoặc 7Up là:
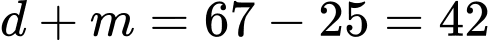 (học sinh).
(học sinh).
Số học sinh thích Coca-Cola hoặc 7Up là:
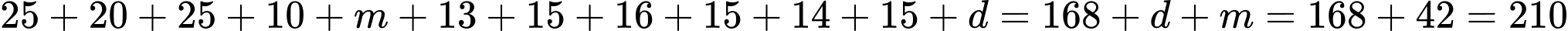 (học sinh).
Đáp án: D
(học sinh).
Đáp án: D Logic tình huống – bài đọc số 10
Một cuộc khảo sát được thực hiện giữa một nhóm người hâm mộ bóng đá để biết bao nhiêu người trong số họ thích các đội bóng Barcelona, Liverpool, Real Madrid, Manchester United và Bayern Munich.
(i) 57 trong số 125 người hâm mộ thích Real Madrid cũng thích Manchester United.
(ii) 10 người hâm mộ thích chính xác 3 câu lạc bộ.
(iii) 10 người hâm mộ chỉ thích Liverpool.
(iv) Được biết, không ai thích Barcelona mà thích Real Madrid và Manchester United.
(v) Số lượng người hâm mộ thích Bayern Munich và Barcelona bằng với số người chỉ thích Real Madrid và Manchester United và nhiều hơn 4 người so với số lượng người thích Barcelona và Liverpool.
(vi) Số lượng người hâm mộ thích Bayern Munich và Manchester United cũng bằng với số lượng người chỉ thích Liverpool và Real Madrid và bằng 1/3 số người chỉ thích Real Madrid.
(vii) Số lượng người hâm mộ Barcelona, Bayern Munich, Manchester United và Liverpool lần lượt là 112, 75, 88 và 92.
(viii) Không ai thích Bayern Munich mà thích Liverpool và Real Madrid.
(i) 57 trong số 125 người hâm mộ thích Real Madrid cũng thích Manchester United.
(ii) 10 người hâm mộ thích chính xác 3 câu lạc bộ.
(iii) 10 người hâm mộ chỉ thích Liverpool.
(iv) Được biết, không ai thích Barcelona mà thích Real Madrid và Manchester United.
(v) Số lượng người hâm mộ thích Bayern Munich và Barcelona bằng với số người chỉ thích Real Madrid và Manchester United và nhiều hơn 4 người so với số lượng người thích Barcelona và Liverpool.
(vi) Số lượng người hâm mộ thích Bayern Munich và Manchester United cũng bằng với số lượng người chỉ thích Liverpool và Real Madrid và bằng 1/3 số người chỉ thích Real Madrid.
(vii) Số lượng người hâm mộ Barcelona, Bayern Munich, Manchester United và Liverpool lần lượt là 112, 75, 88 và 92.
(viii) Không ai thích Bayern Munich mà thích Liverpool và Real Madrid.
Câu 38 [379873]: Có bao nhiêu người thích chính xác hai câu lạc bộ?
A, 183.
B, 152.
C, 137.
D, 154.
Chọn đáp án A.
Dựa vào dữ kiện:
• Không ai thích Barcelona mà thích Real Madrid và Manchester United.
• Không ai thích Bayern Munich mà thích Liverpool và Real Madrid.
Ta có biểu đồ Venn như sau:
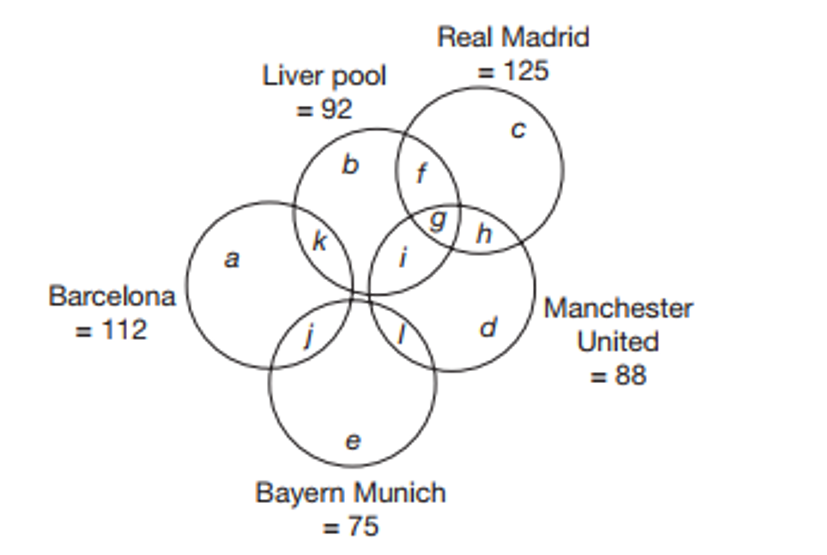
• 57 trong số 125 người hâm mộ thích Real Madrid cũng thích Manchester United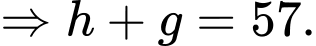
• 10 người hâm mộ thích chính xác 3 câu lạc bộ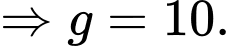
• 10 người hâm mộ chỉ thích Liverpool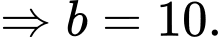
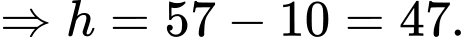 <
<
• Số lượng người hâm mộ thích Bayern Munich và Barcelona bằng với số người chỉ thích Real Madrid và Manchester United và nhiều hơn 4 người so với số lượng người thích Barcelona và Liverpool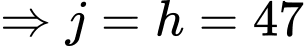 và
và 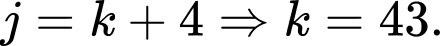
• Số lượng người hâm mộ thích Bayern Munich và Manchester United cũng bằng với số lượng người chỉ thích Liverpool và Real Madrid và bằng 1/3 số người chỉ thích Real Madrid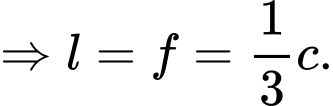
Có số người hâm mộ Real Madrid là 125.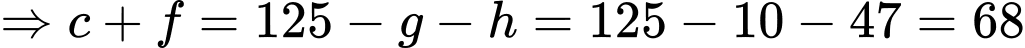
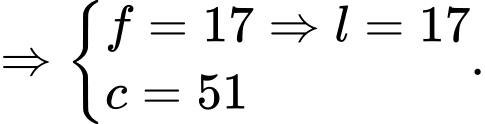
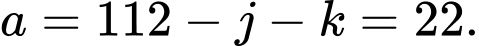
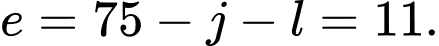
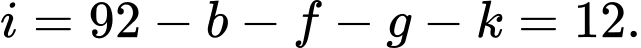
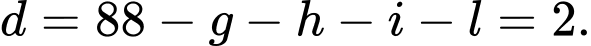
Minh họa:
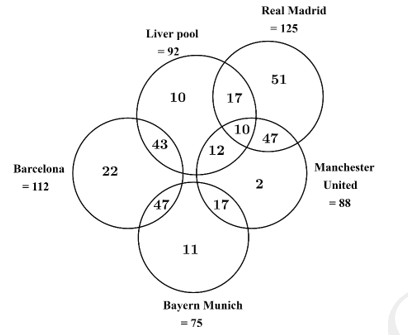
Số người thích chính xác hai câu lạc bộ là: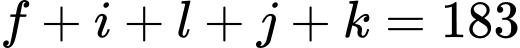 (người). Đáp án: A
(người). Đáp án: A
Dựa vào dữ kiện:
• Không ai thích Barcelona mà thích Real Madrid và Manchester United.
• Không ai thích Bayern Munich mà thích Liverpool và Real Madrid.
Ta có biểu đồ Venn như sau:

• 57 trong số 125 người hâm mộ thích Real Madrid cũng thích Manchester United
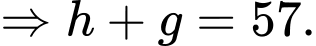
• 10 người hâm mộ thích chính xác 3 câu lạc bộ
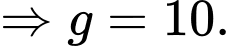
• 10 người hâm mộ chỉ thích Liverpool
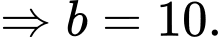
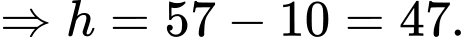 <
<• Số lượng người hâm mộ thích Bayern Munich và Barcelona bằng với số người chỉ thích Real Madrid và Manchester United và nhiều hơn 4 người so với số lượng người thích Barcelona và Liverpool
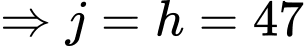 và
và 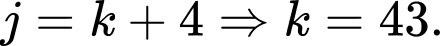
• Số lượng người hâm mộ thích Bayern Munich và Manchester United cũng bằng với số lượng người chỉ thích Liverpool và Real Madrid và bằng 1/3 số người chỉ thích Real Madrid
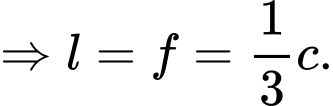
Có số người hâm mộ Real Madrid là 125.
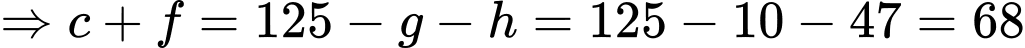
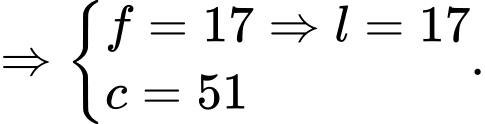
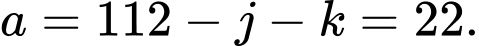
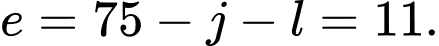
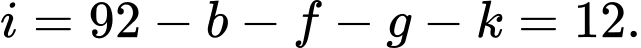
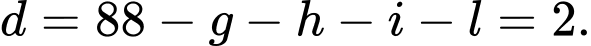
Minh họa:

Số người thích chính xác hai câu lạc bộ là:
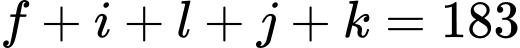 (người). Đáp án: A
(người). Đáp án: A
Câu 39 [379874]: Có bao nhiêu người chỉ thích một trong hai câu lạc bộ Bayern Munich, Barcelona?
A, 45.
B, 51.
C, 33.
D, Không thể xác định được.
Chọn đáp án C.
Dựa vào hình minh họa phân tích giả thiết:

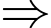 Số người mà chỉ thích một trong hai câu lạc bộ Bayern Munich, Barcelona là:
Số người mà chỉ thích một trong hai câu lạc bộ Bayern Munich, Barcelona là: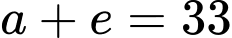 (người). Đáp án: C
(người). Đáp án: C
Dựa vào hình minh họa phân tích giả thiết:

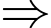 Số người mà chỉ thích một trong hai câu lạc bộ Bayern Munich, Barcelona là:
Số người mà chỉ thích một trong hai câu lạc bộ Bayern Munich, Barcelona là: (người). Đáp án: C
(người). Đáp án: C
Câu 40 [379875]: Có bao nhiêu người thích câu lạc bộ Manchester United nhưng không thích Liverpool?
A, 66.
B, 72.
C, 81.
D, 71.
Chọn đáp án A.
Dựa vào hình minh họa phân tích giả thiết:

 Số người thích câu lạc bộ Manchester United nhưng không thích Liverpool là:
Số người thích câu lạc bộ Manchester United nhưng không thích Liverpool là: (người). Đáp án: A
(người). Đáp án: A
Dựa vào hình minh họa phân tích giả thiết:

 Số người thích câu lạc bộ Manchester United nhưng không thích Liverpool là:
Số người thích câu lạc bộ Manchester United nhưng không thích Liverpool là: (người). Đáp án: A
(người). Đáp án: A
Câu 41 [379876]: Trong số những người hâm mộ Barcelona, có bao nhiêu người thích ít nhất hai câu lạc bộ nữa?
A, 90.
B, 64.
C, 57.
D, 0.
Chọn đáp án D.
Đáp án: D
Dựa vào hình minh họa phân tích giả thiết:

Dựa vào biểu đồ Venn, ta thấy không có người nào hâm mộ Barcelona và thích ít nhất hai câu lạc bộ nữa.