Logic tình huống – bài đọc số 1
Một khối lập phương lớn được sơn cả sáu mặt và đưa cắt thành 27 khối lập phương nhỏ hơn giống hệt nhau.
Câu 1 [583692]: Có bao nhiêu khối lập phương nhỏ không có mặt nào được sơn?
A, 0.
B, 1.
C, 3.
D, 4.
Chọn đáp án B.
Khối lập phương nhỏ duy nhất không có mặt
nào được sơn là khối lập phương không có mặt nào thuộc mặt lớn của khối lập
phương lớn.
Câu 2 [583693]: Có bao nhiêu khối lập phương nhỏ hơn có đúng một mặt được sơn?
A, 3.
B, 6.
C, 12.
D, 15.
Chọn đáp án B.
Những khối lập phương nhỏ có đúng một mặt được sơn là những khối không nằm ở cạnh của khối lập phương lớn. Đồng thời, chúng phải có một mặt thuộc mặt lớn của khối lập phương lớn.
 Số khối lập phương nhỏ có đúng một mặt được sơn là:
Số khối lập phương nhỏ có đúng một mặt được sơn là: 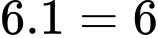 (khối).
Đáp án: B
(khối).
Đáp án: B
Những khối lập phương nhỏ có đúng một mặt được sơn là những khối không nằm ở cạnh của khối lập phương lớn. Đồng thời, chúng phải có một mặt thuộc mặt lớn của khối lập phương lớn.
 Số khối lập phương nhỏ có đúng một mặt được sơn là:
Số khối lập phương nhỏ có đúng một mặt được sơn là: 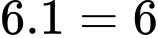 (khối).
Đáp án: B
(khối).
Đáp án: B
Câu 3 [583694]: Có bao nhiêu khối lập phương nhỏ hơn có đúng hai mặt được sơn?
A, 36.
B, 6.
C, 12.
D, 15.
Chọn đáp án C.
Những khối lập phương nhỏ có đúng hai mặt được sơn là những khối nằm ở cạnh của khối lập phương lớn.
Đồng thời, chúng không chứa góc của khối lập phương lớn.
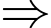 Số khối lập phương nhỏ có đúng hai mặt được sơn là:
Số khối lập phương nhỏ có đúng hai mặt được sơn là: 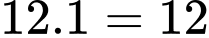 (khối).
Đáp án: C
(khối).
Đáp án: C
Những khối lập phương nhỏ có đúng hai mặt được sơn là những khối nằm ở cạnh của khối lập phương lớn.
Đồng thời, chúng không chứa góc của khối lập phương lớn.
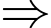 Số khối lập phương nhỏ có đúng hai mặt được sơn là:
Số khối lập phương nhỏ có đúng hai mặt được sơn là: 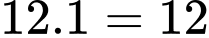 (khối).
Đáp án: C
(khối).
Đáp án: C Logic tình huống – bài đọc số 2
Một khối lập phương lớn được sơn trên cả sáu mặt và sau đó cắt thành một số khối lập phương nhỏ hơn bằng nhau. Người ta thấy trong số các khối lập phương nhỏ có 8 khối lập phương không được sơn mặt nào cả.
Câu 4 [583695]: Khối lập phương lớn ban đầu được cắt thành bao nhiêu khối lập phương nhỏ?
A, 27.
B, 48.
C, 64.
D, 125.
Chọn đáp án C.
Những khối lập phương không có mặt nào được sơn là những khối lập phương không có mặt nào thuộc mặt lớn của khối lập phương lớn.
Có: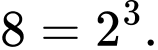
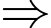 Số khối lập phương nhỏ nhận được khi cắt khối lập phương lớn là:
Số khối lập phương nhỏ nhận được khi cắt khối lập phương lớn là: 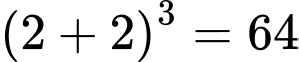 (khối).
Đáp án: C
(khối).
Đáp án: C
Những khối lập phương không có mặt nào được sơn là những khối lập phương không có mặt nào thuộc mặt lớn của khối lập phương lớn.
Có:
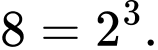
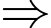 Số khối lập phương nhỏ nhận được khi cắt khối lập phương lớn là:
Số khối lập phương nhỏ nhận được khi cắt khối lập phương lớn là: 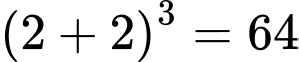 (khối).
Đáp án: C
(khối).
Đáp án: C
Câu 5 [583696]: Có bao nhiêu khối lập phương nhỏ có đúng một mặt được sơn?
A, 12.
B, 24.
C, 16.
D, 32.
Chọn đáp án B.
Những khối lập phương nhỏ có đúng một mặt được sơn là những khối không nằm ở cạnh của khối lập phương lớn. Đồng thời, chúng phải có một mặt thuộc mặt lớn của khối lập phương lớn.
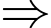 Số khối lập phương nhỏ có đúng một mặt được sơn là:
Số khối lập phương nhỏ có đúng một mặt được sơn là: 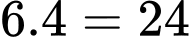 (khối).
Đáp án: B
(khối).
Đáp án: B
Những khối lập phương nhỏ có đúng một mặt được sơn là những khối không nằm ở cạnh của khối lập phương lớn. Đồng thời, chúng phải có một mặt thuộc mặt lớn của khối lập phương lớn.
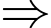 Số khối lập phương nhỏ có đúng một mặt được sơn là:
Số khối lập phương nhỏ có đúng một mặt được sơn là: 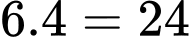 (khối).
Đáp án: B
(khối).
Đáp án: B
Câu 6 [583697]: Có bao nhiêu khối lập phương nhỏ có đúng hai mặt được sơn?
A, 6.
B, 12.
C, 18.
D, 24.
Chọn đáp án D.
Những khối lập phương nhỏ có đúng hai mặt được sơn là những khối nằm ở cạnh của khối lập phương lớn.
Đồng thời, chúng không chứa góc của khối lập phương lớn.
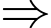 Số khối lập phương nhỏ có đúng hai mặt được sơn là:
Số khối lập phương nhỏ có đúng hai mặt được sơn là: 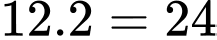 (khối).
Đáp án: D
(khối).
Đáp án: D
Những khối lập phương nhỏ có đúng hai mặt được sơn là những khối nằm ở cạnh của khối lập phương lớn.
Đồng thời, chúng không chứa góc của khối lập phương lớn.
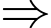 Số khối lập phương nhỏ có đúng hai mặt được sơn là:
Số khối lập phương nhỏ có đúng hai mặt được sơn là: 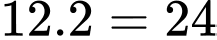 (khối).
Đáp án: D
(khối).
Đáp án: D Logic tình huống – bài đọc số 3
Có một khối lập phương trong đó một cặp mặt kề nhau được sơn màu đỏ, cặp mặt kề thứ hai được sơn màu xanh nước biển và cặp mặt kề nhau thứ ba được sơn màu xanh lá cây. Khối lập phương được cắt thành 216 khối lập phương nhỏ bằng nhau.
Câu 7 [583698]: Có bao nhiêu khối lập phương nhỏ có một mặt được sơn màu đỏ?
A, 64.
B, 81.
C, 60.
D, 120.
Chọn đáp án C.
Có: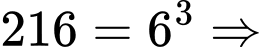 Mỗi mặt của hình lập phương lớn được cắt 5 nhát (được 6 phần).
Mỗi mặt của hình lập phương lớn được cắt 5 nhát (được 6 phần).
Số khối lập phương có mặt đỏ là: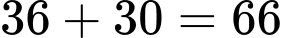 (khối).
(khối).
Có 6 khối lập phương có hai mặt được sơn màu đỏ.
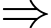 Số hình lập phương chỉ có một mặt được sơn màu đỏ là:
Số hình lập phương chỉ có một mặt được sơn màu đỏ là: 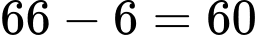 (khối).
Đáp án: C
(khối).
Đáp án: C
Có:
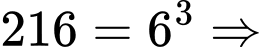 Mỗi mặt của hình lập phương lớn được cắt 5 nhát (được 6 phần).
Mỗi mặt của hình lập phương lớn được cắt 5 nhát (được 6 phần).
Số khối lập phương có mặt đỏ là:
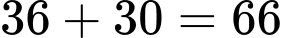 (khối).
(khối).
Có 6 khối lập phương có hai mặt được sơn màu đỏ.
 Số hình lập phương chỉ có một mặt được sơn màu đỏ là:
Số hình lập phương chỉ có một mặt được sơn màu đỏ là: 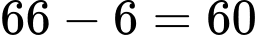 (khối).
Đáp án: C
(khối).
Đáp án: C
Câu 8 [583699]: Có bao nhiêu khối lập phương nhỏ được sơn cả màu đỏ và màu xanh lá cây?
A, 8.
B, 12.
C, 16.
D, 32.
Chọn đáp án C.
Mặt màu đỏ và màu xanh lá cây của khối lập phương lớn có 3 cạnh chung.
 Số khối lập phương nhỏ được sơn cả màu đỏ và màu xanh lá cây là:
Số khối lập phương nhỏ được sơn cả màu đỏ và màu xanh lá cây là: 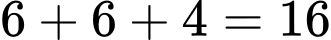 (khối).
Đáp án: C
(khối).
Đáp án: C
Mặt màu đỏ và màu xanh lá cây của khối lập phương lớn có 3 cạnh chung.
 Số khối lập phương nhỏ được sơn cả màu đỏ và màu xanh lá cây là:
Số khối lập phương nhỏ được sơn cả màu đỏ và màu xanh lá cây là: 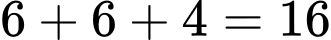 (khối).
Đáp án: C
(khối).
Đáp án: C
Câu 9 [583700]: Có bao nhiêu khối lập phương nhỏ được sơn đúng màu xanh lá cây hoặc màu xanh nước biển?
A, 64.
B, 72.
C, 81.
D, 96.
Chọn đáp án B.
Những khối lập phương nhỏ được sơn đúng một màu xanh lá cây hoặc màu xanh nước biển sẽ thuộc hai trường hợp:
• Hình vuông 4x4 ở giữa mỗi mặt tương ứng Tạo thành 16 khối.
Tạo thành 16 khối.
• Cạnh chung của hai mặt cùng màu Tạo thành 4 khối.
Tạo thành 4 khối.
• Mỗi màu được sơn hai mặt liền kề.
 Số khối lập phương nhỏ được sơn đúng một màu xanh lá cây hoặc màu xanh nước biển là:
Số khối lập phương nhỏ được sơn đúng một màu xanh lá cây hoặc màu xanh nước biển là:
 (khối).
Đáp án: B
(khối).
Đáp án: B
Những khối lập phương nhỏ được sơn đúng một màu xanh lá cây hoặc màu xanh nước biển sẽ thuộc hai trường hợp:
• Hình vuông 4x4 ở giữa mỗi mặt tương ứng
 Tạo thành 16 khối.
Tạo thành 16 khối.
• Cạnh chung của hai mặt cùng màu
 Tạo thành 4 khối.
Tạo thành 4 khối.
• Mỗi màu được sơn hai mặt liền kề.
 Số khối lập phương nhỏ được sơn đúng một màu xanh lá cây hoặc màu xanh nước biển là:
Số khối lập phương nhỏ được sơn đúng một màu xanh lá cây hoặc màu xanh nước biển là:
 (khối).
Đáp án: B
(khối).
Đáp án: B Logic tình huống – bài đọc số 4
Một khối lập phương được sơn màu đen và xanh lá cây sao cho các mặt được sơn màu đen không chung một đỉnh. Khối lập phương này được cắt thành 60 khối nhỏ bằng nhau sử dụng 2, 3 và 4 đường cắt song song với các mặt khác nhau.
Câu 10 [583745]: Có bao nhiêu khối nhỏ có đúng hai mặt được sơn màu đen?
A, 5.
B, 9.
C, 18.
D, 27.
Đáp án: B
Câu 11 [583746]: Có bao nhiêu khối nhỏ được sơn cả hai màu?
A, 9.
B, 18.
C, 6.
D, 24.
Đáp án: B
Câu 12 [583747]: Có bao nhiêu khối nhỏ không được sơn mặt nào?
A, 6.
B, 9.
C, 11.
D, 1.
Đáp án: A
Logic tình huống – bài đọc số 5
Một mặt của một khối lập phương được sơn màu xanh lá cây, hai mặt được sơn màu vàng và ba mặt được sơn màu trắng. Khối lập phương được cắt thành 512 khối lập phương nhỏ bằng nhau.
Câu 13 [583704]: Số khối lập phương nhỏ ít nhất có thể được sơn hai mặt màu vàng là
A, 0.
B, 9.
C, 7.
D, 16.
Chọn đáp án A.
Khối lập phương có thể được sơn theo các trường hợp sau:

Có: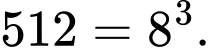 Mỗi mặt của khối lập phương được chia thành 8 phần bằng nhau. Ta có bảng phân tích sự phân bố màu của khối lập phương lớn như sau:
Mỗi mặt của khối lập phương được chia thành 8 phần bằng nhau. Ta có bảng phân tích sự phân bố màu của khối lập phương lớn như sau:
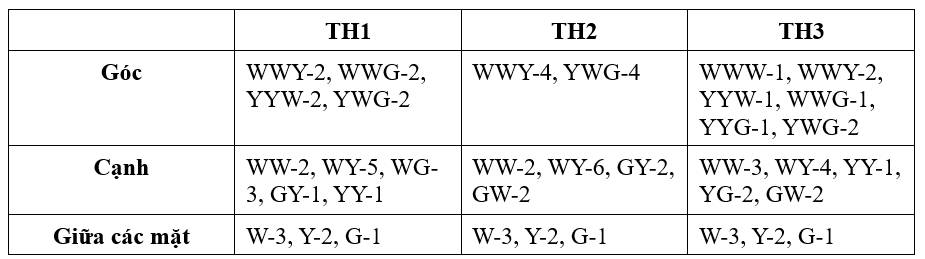
Số khối lập phương nhỏ được sơn hai mặt màu vàng là:
TH1: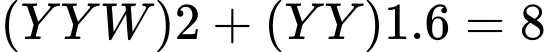 (khối)
(khối)
TH2: Không có khối nào thỏa mãn.
TH3: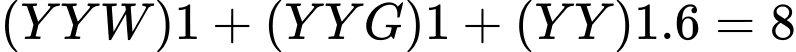 (khối)
(khối)
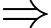 Số khối lập phương nhỏ ít nhất có thể được sơn hai mặt màu vàng là 0.
Đáp án: A
Số khối lập phương nhỏ ít nhất có thể được sơn hai mặt màu vàng là 0.
Đáp án: A
Khối lập phương có thể được sơn theo các trường hợp sau:

Có:
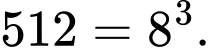 Mỗi mặt của khối lập phương được chia thành 8 phần bằng nhau. Ta có bảng phân tích sự phân bố màu của khối lập phương lớn như sau:
Mỗi mặt của khối lập phương được chia thành 8 phần bằng nhau. Ta có bảng phân tích sự phân bố màu của khối lập phương lớn như sau:

Số khối lập phương nhỏ được sơn hai mặt màu vàng là:
TH1:
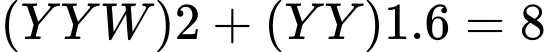 (khối)
(khối)
TH2: Không có khối nào thỏa mãn.
TH3:
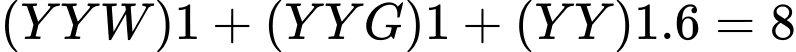 (khối)
(khối)
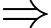 Số khối lập phương nhỏ ít nhất có thể được sơn hai mặt màu vàng là 0.
Đáp án: A
Số khối lập phương nhỏ ít nhất có thể được sơn hai mặt màu vàng là 0.
Đáp án: A
Câu 14 [583705]: Số khối lập phương nhỏ nhiều nhất có thể được sơn hai màu xanh lá cây và màu vàng là
A, 12.
B, 6.
C, 14.
D, 13.
Đáp án: D
Câu 15 [583706]: Số khối lập phương nhỏ nhiều nhất và ít nhất có thể được sơn một màu là
A, 241, 228.
B, 234, 228.
C, 241, 234.
D, 241, 226.
Chọn đáp án A.
Số khối lập phương được sơn một màu là:
TH1: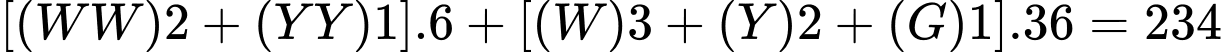 (khối)
(khối)
TH2: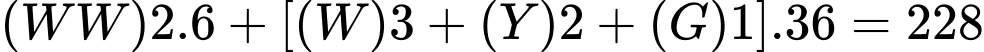 (khối)
(khối)
TH3: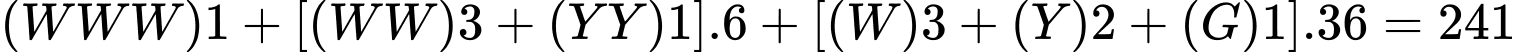 (khối)
(khối)
Số khối lập phương nhỏ được sơn một màu nhiều nhất và ít nhất có thể lần lượt là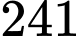 và
và 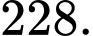 Đáp án: A
Đáp án: A
Số khối lập phương được sơn một màu là:
TH1:
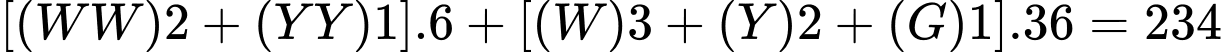 (khối)
(khối)
TH2:
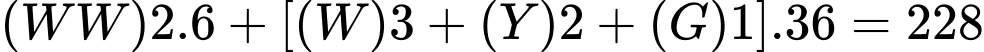 (khối)
(khối)
TH3:
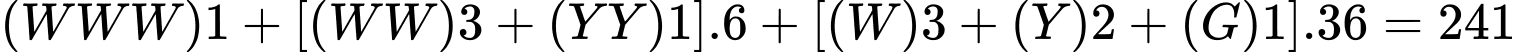 (khối)
(khối)
Số khối lập phương nhỏ được sơn một màu nhiều nhất và ít nhất có thể lần lượt là
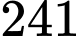 và
và 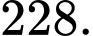 Đáp án: A
Đáp án: A
Câu 16 [583707]: Có bao nhiêu khối lập phương nhỏ có ít nhất hai mặt được sơn nhưng chỉ có màu trắng trên đó?
A, 18.
B, 15.
C, 17.
D, 12.
Chọn đáp án D.
Số khối lập phương nhỏ có ít nhất hai mặt được sơn nhưng chỉ có màu trắng là:
TH1: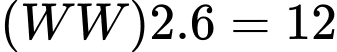 (khối)
(khối)
TH2: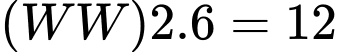 (khối)
(khối)
TH3: (khối)
(khối)
Số khối lập phương cần tìm ít nhất có thể là: (khối).
Đáp án: D
(khối).
Đáp án: D
Số khối lập phương nhỏ có ít nhất hai mặt được sơn nhưng chỉ có màu trắng là:
TH1:
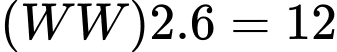 (khối)
(khối)
TH2:
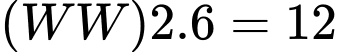 (khối)
(khối)
TH3:
 (khối)
(khối)
Số khối lập phương cần tìm ít nhất có thể là:
 (khối).
Đáp án: D
(khối).
Đáp án: D Logic tình huống – bài đọc số 6
Một khối lập phương được sơn sao cho một mặt được sơn màu đen, một mặt được sơn màu trắng và một mặt được sơn màu đỏ. Ba mặt còn lại không được sơn. Khối lập phương được cắt thành 729 khối lập phương nhỏ bằng nhau.
Câu 17 [583708]: Số khối lập phương nhỏ được sơn cả 3 màu là
A, 1.
B, 2.
C, 4.
D, 5.
Đáp án: A
Câu 18 [583709]: Số khối lập phương nhỏ ít nhất có thể được sơn màu đen và trắng là
A, 1.
B, 5.
C, 6.
D, 0.
Chọn đáp án D.
Trong hình (ii), mặt đen và trắng đối diện nhau.
 Số khối lập phương nhỏ ít nhất có thể được sơn màu đen và trắng là 0.
Đáp án: D
Số khối lập phương nhỏ ít nhất có thể được sơn màu đen và trắng là 0.
Đáp án: D
Trong hình (ii), mặt đen và trắng đối diện nhau.
 Số khối lập phương nhỏ ít nhất có thể được sơn màu đen và trắng là 0.
Đáp án: D
Số khối lập phương nhỏ ít nhất có thể được sơn màu đen và trắng là 0.
Đáp án: D
Câu 19 [583710]: Số khối lập phương nhỏ ít nhất có thể được sơn màu đỏ là
A, 72.
B, 81.
C, 63.
D, 80.
Chọn đáp án B.
Số khối lập phương nhỏ được sơn màu đỏ là: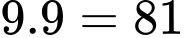 (khối).
Đáp án: B
(khối).
Đáp án: B
Số khối lập phương nhỏ được sơn màu đỏ là:
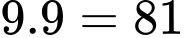 (khối).
Đáp án: B
(khối).
Đáp án: B
Câu 20 [583711]: Có bao nhiêu khối lập phương nhỏ được sơn màu trắng?
A, 75.
B, 85.
C, 72.
D, 81.
Chọn đáp án D.
Số khối lập phương nhỏ được sơn màu trắng là: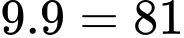 (khối).
Đáp án: D
(khối).
Đáp án: D
Số khối lập phương nhỏ được sơn màu trắng là:
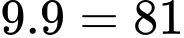 (khối).
Đáp án: D
(khối).
Đáp án: D
Câu 21 [583712]: Số khối lập phương nhỏ ít nhất có thể không được sơn màu là
A, 343.
B, 512.
C, 504.
D, 269.
Chọn đáp án C.
Số khối lập phương nhỏ không màu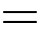 Số khối lập phương nhỏ nằm trong
Số khối lập phương nhỏ nằm trong  Số khối lập phương nhỏ từ ba mặt không màu.
Số khối lập phương nhỏ từ ba mặt không màu.
Trong hình (i), số khối lập phương nhỏ không màu là: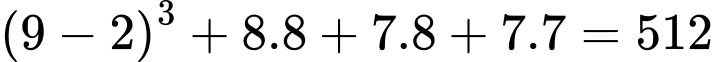 (khối).
(khối).
Trong hình (i), (ii), (iii) và (iv), số khối lập phương nhỏ không màu là:
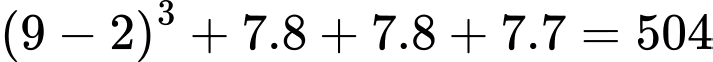 (khối).
(khối).
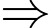 Số khối lập phương nhỏ ít nhất có thể không được sơn màu là
Số khối lập phương nhỏ ít nhất có thể không được sơn màu là 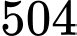 khối.
Đáp án: C
khối.
Đáp án: C
Số khối lập phương nhỏ không màu
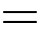 Số khối lập phương nhỏ nằm trong
Số khối lập phương nhỏ nằm trong  Số khối lập phương nhỏ từ ba mặt không màu.
Số khối lập phương nhỏ từ ba mặt không màu.
Trong hình (i), số khối lập phương nhỏ không màu là:
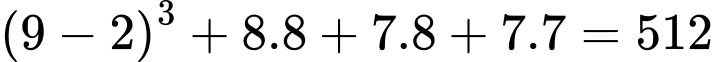 (khối).
(khối).
Trong hình (i), (ii), (iii) và (iv), số khối lập phương nhỏ không màu là:
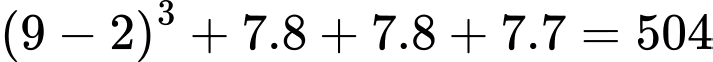 (khối).
(khối).
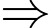 Số khối lập phương nhỏ ít nhất có thể không được sơn màu là
Số khối lập phương nhỏ ít nhất có thể không được sơn màu là 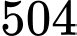 khối.
Đáp án: C
khối.
Đáp án: C Logic tình huống – bài đọc số 7
Mỗi mặt của xúc xắc được đánh dấu bằng một số khác nhau từ 1 đến 6. Các số trên mặt con xúc xắc được đánh dấu thỏa mãn hai mặt đối diện bất kỳ có tổng bằng 7. Hai con xúc xắc như vậy được người ta ném ra. Giả sử, người ta luôn ở một góc có thể nhìn thấy chính xác ba mặt của mỗi con súc sắc.
Câu 22 [379885]: Tổng các số người ta có thể nhìn thấy tối đa là
A, 6.
B, 12.
C, 30.
D, 36.
Chọn đáp án C.
Dựa vào các dữ kiện:
• Các số trên mặt con xúc xắc được đánh dấu thỏa mãn hai mặt đối diện bất kỳ có tổng bằng 7.
• Người ta luôn ở một góc có thể nhìn thấy chính xác ba mặt của mỗi con xúc xắc.
 Để tổng các số ở ba mặt của xúc xắc nhìn được lớn nhất thì ba mặt của xúc xắc là các số 4, 5, 6.
Để tổng các số ở ba mặt của xúc xắc nhìn được lớn nhất thì ba mặt của xúc xắc là các số 4, 5, 6.
 Tổng các số người ta có thể nhìn thấy tối đa là:
Tổng các số người ta có thể nhìn thấy tối đa là:  Đáp án: C
Đáp án: C
Dựa vào các dữ kiện:
• Các số trên mặt con xúc xắc được đánh dấu thỏa mãn hai mặt đối diện bất kỳ có tổng bằng 7.
• Người ta luôn ở một góc có thể nhìn thấy chính xác ba mặt của mỗi con xúc xắc.
 Để tổng các số ở ba mặt của xúc xắc nhìn được lớn nhất thì ba mặt của xúc xắc là các số 4, 5, 6.
Để tổng các số ở ba mặt của xúc xắc nhìn được lớn nhất thì ba mặt của xúc xắc là các số 4, 5, 6. Tổng các số người ta có thể nhìn thấy tối đa là:
Tổng các số người ta có thể nhìn thấy tối đa là:  Đáp án: C
Đáp án: C
Câu 23 [379886]: Có bao nhiêu trường hợp về tổng các số nhìn thấy có thể xảy ra?
A, 16.
B, 36.
C, 48.
D, 64.
Chọn đáp án D.
Dựa vào các dữ kiện:
• Các số trên mặt con xúc xắc được đánh dấu thỏa mãn hai mặt đối diện bất kỳ có tổng bằng 7.
• Người ta luôn ở một góc có thể nhìn thấy chính xác ba mặt của mỗi con xúc xắc Có 8 góc nhìn với một con xúc xắc
Có 8 góc nhìn với một con xúc xắc  Số trường hợp xảy ra là:
Số trường hợp xảy ra là: 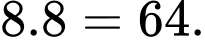 Đáp án: D
Đáp án: D
Dựa vào các dữ kiện:
• Các số trên mặt con xúc xắc được đánh dấu thỏa mãn hai mặt đối diện bất kỳ có tổng bằng 7.
• Người ta luôn ở một góc có thể nhìn thấy chính xác ba mặt của mỗi con xúc xắc
 Có 8 góc nhìn với một con xúc xắc
Có 8 góc nhìn với một con xúc xắc  Số trường hợp xảy ra là:
Số trường hợp xảy ra là: 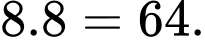 Đáp án: D
Đáp án: D
Câu 24 [379887]: Có bao nhiêu trường hợp để người ta nhìn thấy tổng các số là 20 khi ném ra hai con xúc xắc?
A, 2.
B, 6.
C, 3.
D, 5.
Chọn đáp án D.
Dựa vào các dữ kiện:
• Các số trên mặt con xúc xắc được đánh dấu thỏa mãn hai mặt đối diện bất kỳ có tổng bằng 7.
• Người ta luôn ở một góc có thể nhìn thấy chính xác ba mặt của mỗi con xúc xắc.
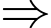 Các trường hợp về 3 mặt của một con xúc xắc có thể xảy ra là:
Các trường hợp về 3 mặt của một con xúc xắc có thể xảy ra là:
• 6, 4 và 5 (tổng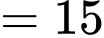 )
)
• 6, 5 và 3 (tổng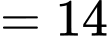 )
)
• 6, 4 và 2 (tổng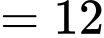 )
)
• 6, 3 và 2 (tổng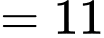 )
)
• 5, 4 và 1 (tổng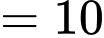 )
)
• 5, 3 và 1 (tổng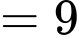 )
)
• 4, 2 và 1 (tổng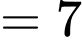 )
)
• 3, 2 và 1 (tổng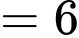 )
)
Để tổng là 20 thì tổng các số của hai con xúc xắc lần lượt là:
• 6 và 14
• 14 và 6
• 9 và 11
• 11 và 9
• 10 và 10
 Có 5 trường hợp. Đáp án: D
Có 5 trường hợp. Đáp án: D
Dựa vào các dữ kiện:
• Các số trên mặt con xúc xắc được đánh dấu thỏa mãn hai mặt đối diện bất kỳ có tổng bằng 7.
• Người ta luôn ở một góc có thể nhìn thấy chính xác ba mặt của mỗi con xúc xắc.
 Các trường hợp về 3 mặt của một con xúc xắc có thể xảy ra là:
Các trường hợp về 3 mặt của một con xúc xắc có thể xảy ra là:• 6, 4 và 5 (tổng
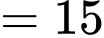 )
)• 6, 5 và 3 (tổng
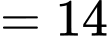 )
)• 6, 4 và 2 (tổng
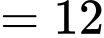 )
)• 6, 3 và 2 (tổng
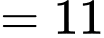 )
)• 5, 4 và 1 (tổng
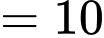 )
)• 5, 3 và 1 (tổng
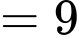 )
)• 4, 2 và 1 (tổng
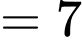 )
)• 3, 2 và 1 (tổng
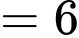 )
)Để tổng là 20 thì tổng các số của hai con xúc xắc lần lượt là:
• 6 và 14
• 14 và 6
• 9 và 11
• 11 và 9
• 10 và 10
 Có 5 trường hợp. Đáp án: D
Có 5 trường hợp. Đáp án: D
Câu 25 [379888]: Số trường hợp để người ta nhìn thấy tổng các số từ 25 trở lên ít hơn số trường hợp để người nhìn thấy tổng các số dưới 26 là
A, 32.
B, 46.
C, 51.
D, 40.
Chọn đáp án D.  Các trường hợp về 3 mặt của một con xúc xắc có thể xảy ra là:
Các trường hợp về 3 mặt của một con xúc xắc có thể xảy ra là:  Có 14 trường hợp.
Có 14 trường hợp.  Có 10 trường hợp.
Có 10 trường hợp. 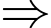 Số trường hợp để người nhìn thấy tổng các số dưới 26 là:
Số trường hợp để người nhìn thấy tổng các số dưới 26 là: 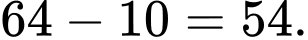
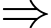 Số trường hợp để người ta nhìn thấy tổng các số từ 25 trở lên ít hơn số trường hợp để người nhìn thấy tổng các số dưới 26 là:
Số trường hợp để người ta nhìn thấy tổng các số từ 25 trở lên ít hơn số trường hợp để người nhìn thấy tổng các số dưới 26 là: 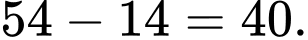 Đáp án: A
Đáp án: A
Dựa vào các dữ kiện:
• Các số trên mặt con xúc xắc được đánh dấu thỏa mãn hai mặt đối diện bất kỳ có tổng bằng 7.
• Người ta luôn ở một góc có thể nhìn thấy chính xác ba mặt của mỗi con xúc xắc.
 Các trường hợp về 3 mặt của một con xúc xắc có thể xảy ra là:
Các trường hợp về 3 mặt của một con xúc xắc có thể xảy ra là: • 6, 4 và 5 (tổng 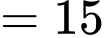 )
)
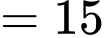 )
) • 6, 5 và 3 (tổng 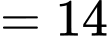 )
)
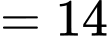 )
) • 6, 4 và 2 (tổng 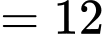 )
)
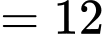 )
) • 6, 3 và 2 (tổng 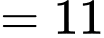 )
)
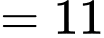 )
) • 5, 4 và 1 (tổng 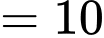 )
)
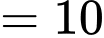 )
) • 5, 3 và 1 (tổng 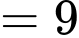 )
)
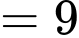 )
) • 4, 2 và 1 (tổng 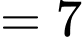 )
)
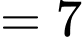 )
) • 3, 2 và 1 (tổng 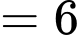 )
)
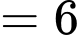 )
) Các trường hợp để người ta nhìn thấy tổng các số từ 25 trở lên là:
1. 15 và 10
2. 10 và 15
3. 15 và 11
4. 11 và 15
5. 15 và 12
6. 12 và 15
7. 15 và 14
8. 14 và 15
9. 15 và 15
10. 14 và 11
11. 11 và 14
12. 14 và 12
13. 12 và 14
14. 14 và 14
 Có 14 trường hợp.
Có 14 trường hợp. Các trường hợp để người ta nhìn thấy tổng các số từ 26 trở lên là:
1. 15 và 11
2. 11 và 15
3. 15 và 12
4. 12 và 15
5. 15 và 14
6. 14 và 15
7. 15 và 15
8. 14 và 12
9. 12 và 14
10. 14 và 14
 Có 10 trường hợp.
Có 10 trường hợp.  Số trường hợp để người nhìn thấy tổng các số dưới 26 là:
Số trường hợp để người nhìn thấy tổng các số dưới 26 là: 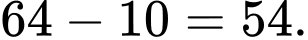
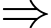 Số trường hợp để người ta nhìn thấy tổng các số từ 25 trở lên ít hơn số trường hợp để người nhìn thấy tổng các số dưới 26 là:
Số trường hợp để người ta nhìn thấy tổng các số từ 25 trở lên ít hơn số trường hợp để người nhìn thấy tổng các số dưới 26 là: 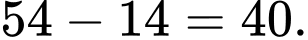
Logic tình huống – bài đọc số 8
Một khối lập phương được sơn sao cho hai mặt liền kề được sơn màu xanh, hai mặt đối diện được sơn màu vàng và hai mặt còn lại được sơn màu đỏ. Sau đó, người ta cắt khối lập phương lớn thành 125 khối lập phương nhỏ giống hệt nhau.
Câu 26 [379889]: Có bao nhiêu hình lập phương nhỏ có đúng hai mặt được sơn màu xanh?
A, 10.
B, 7.
C, 5.
D, 8.
Chọn đáp án C.
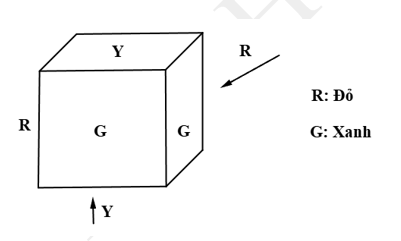
Những hình lập phương nhỏ có đúng hai mặt được sơn màu xanh được cắt dọc theo phần cạnh G-G tạo bởi hai mặt liền kề sơn màu xanh.
Lại có: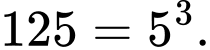
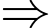 Có 5 hình lập phương nhỏ có đúng hai mặt được sơn màu xanh. Đáp án: C
Có 5 hình lập phương nhỏ có đúng hai mặt được sơn màu xanh. Đáp án: C

Những hình lập phương nhỏ có đúng hai mặt được sơn màu xanh được cắt dọc theo phần cạnh G-G tạo bởi hai mặt liền kề sơn màu xanh.
Lại có:
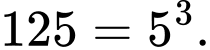
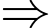 Có 5 hình lập phương nhỏ có đúng hai mặt được sơn màu xanh. Đáp án: C
Có 5 hình lập phương nhỏ có đúng hai mặt được sơn màu xanh. Đáp án: C
Câu 27 [379890]: Có bao nhiêu hình lập phương nhỏ có ít nhất hai màu khác nhau trên mặt?
A, 30.
B, 38.
C, 36.
D, 42.
Chọn đáp án B.
Nhận xét: Số hình lập phương nhỏ có ít nhất hai màu khác nhau bằng tổng của số hình lập phương nhỏ nằm ở góc có hai hoặc ba màu và số hình lập phương nhỏ dọc theo các cạnh của hình lập phương lớn ngoại trừ cạnh G-G và R-R vì chúng chỉ được sơn một màu.
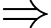 Số hình lập phương nhỏ có ít nhất hai màu khác nhau trên mặt là:
Số hình lập phương nhỏ có ít nhất hai màu khác nhau trên mặt là: 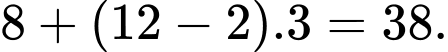 Đáp án: B
Đáp án: B
Nhận xét: Số hình lập phương nhỏ có ít nhất hai màu khác nhau bằng tổng của số hình lập phương nhỏ nằm ở góc có hai hoặc ba màu và số hình lập phương nhỏ dọc theo các cạnh của hình lập phương lớn ngoại trừ cạnh G-G và R-R vì chúng chỉ được sơn một màu.
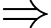 Số hình lập phương nhỏ có ít nhất hai màu khác nhau trên mặt là:
Số hình lập phương nhỏ có ít nhất hai màu khác nhau trên mặt là: 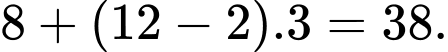 Đáp án: B
Đáp án: B
Câu 28 [379891]: Có bao nhiêu hình lập phương nhỏ không có màu xanh nhưng có màu vàng hoặc màu đỏ trên đó?
A, 40.
B, 75.
C, 80.
D, 53.
Chọn đáp án D.
Số hình lập phương nhỏ không có màu xanh nhưng có màu vàng hoặc màu đỏ trên đó = Tổng số hình lập phương nhỏ - Số hình lập phương có màu xanh – Số hình lập phương không có màu.
Màu xanh có hai mặt nên số hình lập phương nhỏ có màu xanh là: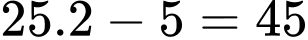 (Vì có 5 hình ở phần tiếp giáp 2 mặt).
(Vì có 5 hình ở phần tiếp giáp 2 mặt).
Số hình lập phương không có màu là: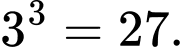
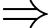 Số hình lập phương nhỏ không có màu xanh nhưng có màu vàng hoặc màu đỏ trên đó là:
Số hình lập phương nhỏ không có màu xanh nhưng có màu vàng hoặc màu đỏ trên đó là: 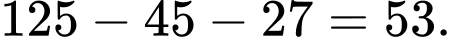 Đáp án: D
Đáp án: D
Số hình lập phương nhỏ không có màu xanh nhưng có màu vàng hoặc màu đỏ trên đó = Tổng số hình lập phương nhỏ - Số hình lập phương có màu xanh – Số hình lập phương không có màu.
Màu xanh có hai mặt nên số hình lập phương nhỏ có màu xanh là:
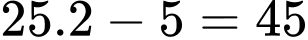 (Vì có 5 hình ở phần tiếp giáp 2 mặt).
(Vì có 5 hình ở phần tiếp giáp 2 mặt).Số hình lập phương không có màu là:
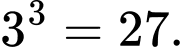
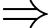 Số hình lập phương nhỏ không có màu xanh nhưng có màu vàng hoặc màu đỏ trên đó là:
Số hình lập phương nhỏ không có màu xanh nhưng có màu vàng hoặc màu đỏ trên đó là: 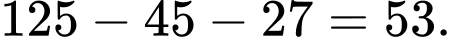 Đáp án: D
Đáp án: D
Câu 29 [379892]: Có bao nhiêu hình lập phương nhỏ được sơn đúng hai mặt trên đó?
A, 36.
B, 30.
C, 24.
D, 34.
Chọn đáp án A.
Số hình lập phương nhỏ được sơn đúng hai màu = Số hình lập phương nhỏ dọc theo các cạnh của hình lập phương lớn =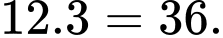 Đáp án: A
Đáp án: A
Số hình lập phương nhỏ được sơn đúng hai màu = Số hình lập phương nhỏ dọc theo các cạnh của hình lập phương lớn =
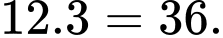 Đáp án: A
Đáp án: A Logic tình huống – bài đọc số 9
Một khối lập phương có cả sáu mặt được sơn bằng sáu màu khác nhau là trắng, xanh nước biển, đỏ, vàng, xanh lá cây và hồng theo cách mà màu hồng và xanh lá cây nằm trên hai mặt đối diện.
Khối lập phương được đặt trên bàn với mặt màu hồng chạm vào mặt bàn. Mặt màu đỏ hướng về phía bạn, các mặt màu trắng và xanh nước biển đối diện nhau. Khối lập phương được cắt thành 120 khối giống hệt nhau bằng cách thực hiện số lần cắt ít nhất có thể, trong đó tất cả các lần cắt đều song song với các mặt của khối lập phương. Số lần cắt ít nhất có thể được thực hiện theo hướng ngang và số lần cắt tối đa có thể được thực hiện song song với mặt màu đỏ.
Câu 30 [583713]: Có bao nhiêu khối nhỏ có màu trắng trên các mặt của chúng?
A, 36.
B, 42.
C, 30.
D, 24.
Chọn đáp án D.
Dựa vào các dữ kiện:
• Màu hồng và xanh lá cây nằm trên hai mặt đối diện.
• Mặt màu hồng chạm vào mặt bàn.
• Mặt màu đỏ hướng về phía bạn, các mặt màu trắng và xanh nước biển đối diện nhau.
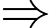 Ta có hình minh họa:
Ta có hình minh họa:
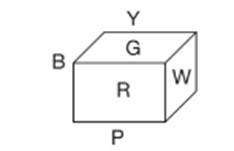
Có: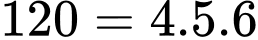
 Người ta thực hiện 12 nhát cắt như sau:
Người ta thực hiện 12 nhát cắt như sau:
• 1 mặt ta cắt: 3 nhát (được 4 phần).
• 1 mặt ta cắt: 4 nhát (được 5 phần).
• 1 mặt ta cắt: 5 nhát (được 6 phần).
Kết hợp dữ kiện:
• Số lần cắt ít nhất có thể được thực hiện theo hướng ngang.
• Số lần cắt tối đa có thể được thực hiện song song với mặt màu đỏ.
 Ta có hình minh họa:
Ta có hình minh họa:
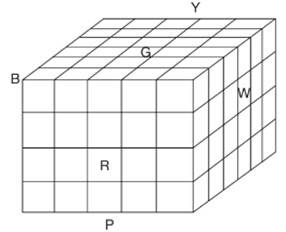
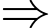 Số khối lập phương nhỏ có mặt màu trắng là:
Số khối lập phương nhỏ có mặt màu trắng là: 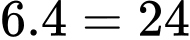 (khối). Đáp án: D
(khối). Đáp án: D
Dựa vào các dữ kiện:
• Màu hồng và xanh lá cây nằm trên hai mặt đối diện.
• Mặt màu hồng chạm vào mặt bàn.
• Mặt màu đỏ hướng về phía bạn, các mặt màu trắng và xanh nước biển đối diện nhau.
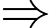 Ta có hình minh họa:
Ta có hình minh họa:

Có:
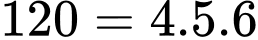
 Người ta thực hiện 12 nhát cắt như sau:
Người ta thực hiện 12 nhát cắt như sau:
• 1 mặt ta cắt: 3 nhát (được 4 phần).
• 1 mặt ta cắt: 4 nhát (được 5 phần).
• 1 mặt ta cắt: 5 nhát (được 6 phần).
Kết hợp dữ kiện:
• Số lần cắt ít nhất có thể được thực hiện theo hướng ngang.
• Số lần cắt tối đa có thể được thực hiện song song với mặt màu đỏ.
 Ta có hình minh họa:
Ta có hình minh họa:

 Số khối lập phương nhỏ có mặt màu trắng là:
Số khối lập phương nhỏ có mặt màu trắng là: 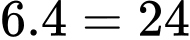 (khối). Đáp án: D
(khối). Đáp án: D
Câu 31 [583714]: Có bao nhiêu khối nhỏ có ít nhất hai màu khác nhau trên các mặt của chúng?
A, 44.
B, 28.
C, 38.
D, 30.
Chọn đáp án A.
Số khối lập phương nhỏ chỉ có hai màu khác nhau là: (khối)
(khối)
Số khối lập phương nhỏ có ba màu khác nhau là: 8 (khối)
Số khối lập phương nhỏ có ít nhất hai màu khác nhau là: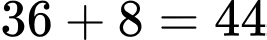 (khối).
Đáp án: A
(khối).
Đáp án: A
Số khối lập phương nhỏ chỉ có hai màu khác nhau là:
 (khối)
(khối)
Số khối lập phương nhỏ có ba màu khác nhau là: 8 (khối)
Số khối lập phương nhỏ có ít nhất hai màu khác nhau là:
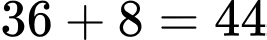 (khối).
Đáp án: A
(khối).
Đáp án: A
Câu 32 [583715]: Có bao nhiêu khối nhỏ không được sơn màu?
A, 42.
B, 24.
C, 36.
D, 27.
Chọn đáp án B.
Coi khối lập phương ban đầu có kích thước: 4x5x6
 Khối lập phương nằm bên trong khối lập phương ban đầu và không được tô màu có kích thước: 2x3x4.
Khối lập phương nằm bên trong khối lập phương ban đầu và không được tô màu có kích thước: 2x3x4.
 Số khối lập phương nhỏ không được tô màu là:
Số khối lập phương nhỏ không được tô màu là: 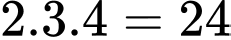 (khối).
Đáp án: B
(khối).
Đáp án: B
Coi khối lập phương ban đầu có kích thước: 4x5x6
 Khối lập phương nằm bên trong khối lập phương ban đầu và không được tô màu có kích thước: 2x3x4.
Khối lập phương nằm bên trong khối lập phương ban đầu và không được tô màu có kích thước: 2x3x4.
 Số khối lập phương nhỏ không được tô màu là:
Số khối lập phương nhỏ không được tô màu là: 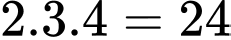 (khối).
Đáp án: B
(khối).
Đáp án: B Logic tình huống – bài đọc số 10
Hai khối gỗ hình lập phương P và Q giống hệt nhau đặt đối diện nhau, các mặt của mỗi khối gỗ đều được sơn màu. Một cặp mặt đối diện của khối P được sơn cùng màu đỏ và một cặp mặt đối diện khác được sơn màu xanh nước biển. Hai mặt còn lại được sơn màu vàng và màu nâu. Một cặp mặt đối diện của khối gỗ Q được sơn màu xanh nước biển. Đối diện mặt được sơn màu nâu là mặt được sơn màu xanh lá cây. Hai mặt còn lại được sơn màu đen và màu vàng. Trong các câu hỏi dưới đây đề cập tới hai mặt tiếp xúc với nhau có nghĩa là toàn bộ diện tích của mặt thứ nhất tiếp xúc vào toàn bộ diện tích của mặt thứ hai.
Câu 33 [379893]: Nếu người ta ở một góc nào đó nhìn thấy 3 mặt của mỗi khối gỗ P lần lượt là đỏ, vàng, xanh nước biển và 3 mặt của khối gỗ Q lần lượt là xanh nước biển, nâu, vàng thì khi người ta đứng ở góc nhìn đối diện sẽ nhìn thấy?
A, 3 mặt của khối gỗ P có màu lần lượt là đỏ, xanh nước biển, nâu và 3 mặt của khối gỗ Q có các màu lần lượt là xanh nước biển, đen, xanh lá cây.
B, 3 mặt của khối gỗ P có màu lần lượt là đỏ, xanh nước biển, vàng và 3 mặt của khối gỗ Q có các màu lần lượt là xanh nước biển, đen, nâu.
C, 3 mặt của khối gỗ P có màu lần lượt là đỏ, xanh nước biển, vàng và 3 mặt của khối gỗ Q có các màu lần lượt là xanh nước biển, đen, nâu.
D, 3 mặt của khối gỗ P có màu lần lượt là đỏ, xanh nước biển, vàng và 3 mặt của khối gỗ Q có các màu lần lượt là xanh nước biển, vàng, xanh lá cây.
Chọn đáp án A.
Dựa vào các dữ kiện:
• Một cặp mặt đối diện của khối P được sơn cùng màu đỏ và một cặp mặt đối diện khác được sơn màu xanh nước biển.
• Hai mặt còn lại được sơn màu vàng và màu nâu.
• Người ta ở một góc nào đó nhìn thấy 3 mặt của mỗi khối gỗ P lần lượt là đỏ, vàng, xanh nước biển.
 Người ở góc đối diện sẽ nhìn thấy các mặt của khối P có màu đỏ, nâu và xanh nước biển.
Người ở góc đối diện sẽ nhìn thấy các mặt của khối P có màu đỏ, nâu và xanh nước biển.
Dựa vào các dữ kiện:
• Một cặp mặt đối diện của khối gỗ Q được sơn màu xanh nước biển.
• Đối diện mặt được sơn màu nâu là mặt được sơn màu xanh lá cây.
• Hai mặt còn lại được sơn màu đen và màu vàng Hai mặt đen và vàng đối diện.• Người ta ở một góc nào đó nhìn thấy 3 mặt của khối gỗ Q lần lượt là xanh nước biển, nâu, vàng.
Hai mặt đen và vàng đối diện.• Người ta ở một góc nào đó nhìn thấy 3 mặt của khối gỗ Q lần lượt là xanh nước biển, nâu, vàng.
 Người ở góc đối diện sẽ nhìn thấy các mặt của khối Q có màu xanh nước biển, xanh lá cây và đen. Đáp án: A
Người ở góc đối diện sẽ nhìn thấy các mặt của khối Q có màu xanh nước biển, xanh lá cây và đen. Đáp án: A
Dựa vào các dữ kiện:
• Một cặp mặt đối diện của khối P được sơn cùng màu đỏ và một cặp mặt đối diện khác được sơn màu xanh nước biển.
• Hai mặt còn lại được sơn màu vàng và màu nâu.
• Người ta ở một góc nào đó nhìn thấy 3 mặt của mỗi khối gỗ P lần lượt là đỏ, vàng, xanh nước biển.
 Người ở góc đối diện sẽ nhìn thấy các mặt của khối P có màu đỏ, nâu và xanh nước biển.
Người ở góc đối diện sẽ nhìn thấy các mặt của khối P có màu đỏ, nâu và xanh nước biển.Dựa vào các dữ kiện:
• Một cặp mặt đối diện của khối gỗ Q được sơn màu xanh nước biển.
• Đối diện mặt được sơn màu nâu là mặt được sơn màu xanh lá cây.
• Hai mặt còn lại được sơn màu đen và màu vàng
 Hai mặt đen và vàng đối diện.• Người ta ở một góc nào đó nhìn thấy 3 mặt của khối gỗ Q lần lượt là xanh nước biển, nâu, vàng.
Hai mặt đen và vàng đối diện.• Người ta ở một góc nào đó nhìn thấy 3 mặt của khối gỗ Q lần lượt là xanh nước biển, nâu, vàng. Người ở góc đối diện sẽ nhìn thấy các mặt của khối Q có màu xanh nước biển, xanh lá cây và đen. Đáp án: A
Người ở góc đối diện sẽ nhìn thấy các mặt của khối Q có màu xanh nước biển, xanh lá cây và đen. Đáp án: A
Câu 34 [379894]: Hai khối gỗ được đặt cạnh nhau trên bàn sao cho dù vị trí của P và Q đổi chỗ hay để nguyên thì hai mặt của P và Q tiếp xúc với nhau đều cùng màu. Nếu các mặt trên của cả P và Q phải có cùng màu thì điều nào sau đây phải đúng?
A, Các mặt trước của khối P và Q lần lượt có màu đỏ và vàng.
B, Hai mặt của khối P và Q tiếp xúc với mặt bàn lần lượt có màu nâu và đen.
C, Mặt trước của khối P có màu đỏ.
D, Mặt trên của khối P và Q lần lượt có màu đỏ và vàng.
Dựa vào các dữ kiện:
• Hai khối gỗ được đặt cạnh nhau trên bàn sao cho dù vị trí của P và Q đổi chỗ hay để nguyên thì hai mặt của P và Q tiếp xúc với nhau đều cùng màu Mặt tiếp xúc của P và Q phải có màu xanh nước biển.
Mặt tiếp xúc của P và Q phải có màu xanh nước biển.
• Các mặt trên của cả P và Q phải có cùng màu Đó phải là vàng hoặc nâu.
Đó phải là vàng hoặc nâu.
Kết hợp với các đáp án Chọn đáp án C. Đáp án: C
Chọn đáp án C. Đáp án: C
• Hai khối gỗ được đặt cạnh nhau trên bàn sao cho dù vị trí của P và Q đổi chỗ hay để nguyên thì hai mặt của P và Q tiếp xúc với nhau đều cùng màu
 Mặt tiếp xúc của P và Q phải có màu xanh nước biển.
Mặt tiếp xúc của P và Q phải có màu xanh nước biển.• Các mặt trên của cả P và Q phải có cùng màu
 Đó phải là vàng hoặc nâu.
Đó phải là vàng hoặc nâu.Kết hợp với các đáp án
 Chọn đáp án C. Đáp án: C
Chọn đáp án C. Đáp án: C
Câu 35 [379895]: Khối gỗ Q được đặt trên P sao cho không có mặt xanh nước biển nào của cả hai khối lập phương nằm trên cùng một mặt phẳng. Nếu màu nâu và màu xanh nước biển lần lượt là mặt trước của P và Q thì khẳng định nào sau đây là sai?
A, Hai mặt của hai hình lập phương tiếp xúc với nhau có màu đỏ và xanh lá cây.
B, Hai mặt của hai hình lập phương tiếp xúc với nhau có màu đỏ và nâu.
C, Nếu mặt bên phải của hai hình khối là màu xanh nước biển và màu xanh là cây thì mặt bên trái của hai hình khối sẽ lần lượt có màu xanh nước biển và màu nâu.
D, Các mặt của hai hình lập phương tiếp xúc với nhau có màu vàng và nâu.
Chọn đáp án D.
Dựa vào các dữ kiện:
• Khối gỗ Q được đặt trên P sao cho không có mặt xanh nước biển nào của cả hai khối lập phương nằm trên cùng một mặt phẳng.
• Màu nâu và màu xanh nước biển lần lượt là mặt trước của P và Q.
Kết hợp với các đáp án Mặt tiếp xúc với Q của P chỉ có thể là màu đỏ
Mặt tiếp xúc với Q của P chỉ có thể là màu đỏ  Đáp án D sai. Đáp án: D
Đáp án D sai. Đáp án: D
Dựa vào các dữ kiện:
• Khối gỗ Q được đặt trên P sao cho không có mặt xanh nước biển nào của cả hai khối lập phương nằm trên cùng một mặt phẳng.
• Màu nâu và màu xanh nước biển lần lượt là mặt trước của P và Q.
Kết hợp với các đáp án
 Mặt tiếp xúc với Q của P chỉ có thể là màu đỏ
Mặt tiếp xúc với Q của P chỉ có thể là màu đỏ  Đáp án D sai. Đáp án: D
Đáp án D sai. Đáp án: D
Câu 36 [379896]: Nếu khối gỗ Q đặt sau khối P sao cho mặt màu vàng của P đối diện với mặt màu nâu của khối Q và các mặt tiếp xúc với bàn có màu đỏ và đen, thì mặt nào của cả hai khối có cùng màu?
A, Mặt trên.
B, Mặt trên và mặt dưới.
C, Mặt bên trái và bên phải.
D, Mặt trên và mặt trước.
Chọn đáp án C.
Ta có hình minh họa cho trường hợp trên:
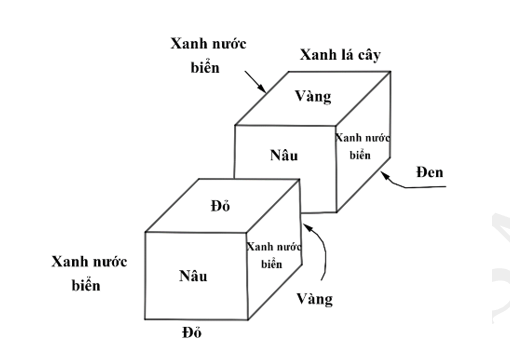
 Mặt bên trái và mặt bên phải của hai khối có cùng màu là xanh nước biển. Đáp án: C
Mặt bên trái và mặt bên phải của hai khối có cùng màu là xanh nước biển. Đáp án: C
Ta có hình minh họa cho trường hợp trên:

 Mặt bên trái và mặt bên phải của hai khối có cùng màu là xanh nước biển. Đáp án: C
Mặt bên trái và mặt bên phải của hai khối có cùng màu là xanh nước biển. Đáp án: C