Đáp án Bài tập tự luyện
Câu 1 [379675]: Bảng số liệu cung cấp chi phí cho việc di chuyển giữa các ga đường sắt (đơn vị: nghìn đồng).
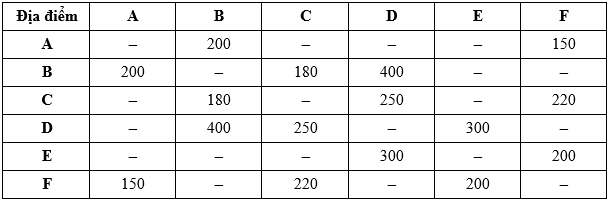
Chi phí rẻ nhất để đi từ ga A đến ga D là

Chi phí rẻ nhất để đi từ ga A đến ga D là
A, 600.000 đồng.
B, 550.000 đồng.
C, 770.000 đồng.
D, 650.000 đồng.
Chọn đáp án A.
Dựa vào bảng số liệu, ta có:
• Từ A có các quãng đường tới B, F.
• Từ D có các quãng đường tới B, C, E.
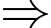 Các quãng đường từ A đến D có thể có chi phí rẻ nhất là:
Các quãng đường từ A đến D có thể có chi phí rẻ nhất là:
•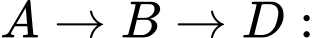 600.000 đồng.
600.000 đồng.
•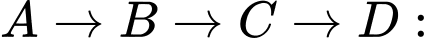 630.000 đồng.
630.000 đồng.
•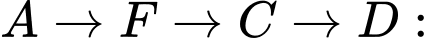 620.000 đồng.
620.000 đồng.
•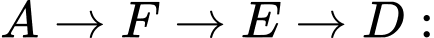 650.000 đồng.
650.000 đồng.
 Chi phí rẻ nhất để đi từ ga A đến ga D là: 600.000 đồng. Đáp án: A
Chi phí rẻ nhất để đi từ ga A đến ga D là: 600.000 đồng. Đáp án: A
Dựa vào bảng số liệu, ta có:
• Từ A có các quãng đường tới B, F.
• Từ D có các quãng đường tới B, C, E.
 Các quãng đường từ A đến D có thể có chi phí rẻ nhất là:
Các quãng đường từ A đến D có thể có chi phí rẻ nhất là:•
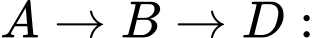 600.000 đồng.
600.000 đồng.•
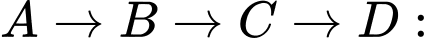 630.000 đồng.
630.000 đồng.•
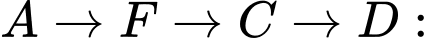 620.000 đồng.
620.000 đồng.•
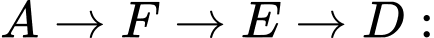 650.000 đồng.
650.000 đồng. Chi phí rẻ nhất để đi từ ga A đến ga D là: 600.000 đồng. Đáp án: A
Chi phí rẻ nhất để đi từ ga A đến ga D là: 600.000 đồng. Đáp án: A
Câu 2 [379676]: Một mạng cáp quang dùng để kết nối giữa năm thị trấn. Bảng số liệu bên dưới cho biết về chi phí để lắp đặt (đơn vị: triệu đồng).
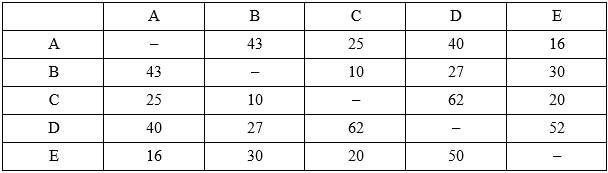
Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là

Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là
A, 63 triệu đồng.
B, 73 triệu đồng.
C, 87 triệu đồng.
D, 97 triệu đồng.
Chọn đáp án B.
Ta mô phỏng bài toán trên dưới dạng đồ thị với năm thị trấn là năm đỉnh, chi phí để lắp đặt giữa các thị trấn là trọng số của các cạnh.
 Yêu cầu của bài toán là tìm cây khung nhỏ nhất.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất.
Ta tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không tạo thành chu trình):
• Cạnh BC: 10 triệu đồng.
• Cạnh AE: 16 triệu đồng.
• Cạnh EC: 20 triệu đồng.
• Cạnh AC: 25 triệu đồng (loại vì tạo thành chu trình).
• Cạnh BD: 27 triệu đồng.
 Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là:
Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là: 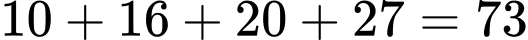 (triệu đồng).
(triệu đồng).
Minh họa:
 Đáp án: B
Đáp án: B
Ta mô phỏng bài toán trên dưới dạng đồ thị với năm thị trấn là năm đỉnh, chi phí để lắp đặt giữa các thị trấn là trọng số của các cạnh.
 Yêu cầu của bài toán là tìm cây khung nhỏ nhất.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất.Ta tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không tạo thành chu trình):
• Cạnh BC: 10 triệu đồng.
• Cạnh AE: 16 triệu đồng.
• Cạnh EC: 20 triệu đồng.
• Cạnh AC: 25 triệu đồng (loại vì tạo thành chu trình).
• Cạnh BD: 27 triệu đồng.
 Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là:
Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là: 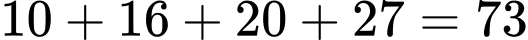 (triệu đồng).
(triệu đồng).Minh họa:
 Đáp án: B
Đáp án: B
Câu 3 [379677]: Một thanh tra đang sinh sống ở thành phố A phải đến các trung tâm bán hàng ở các thành phố B, C, D, E và F và quay trở lại nhà. Khoảng cách giữa các thành phố được thể hiện ở bảng minh họa bên dưới (đơn vị: km).
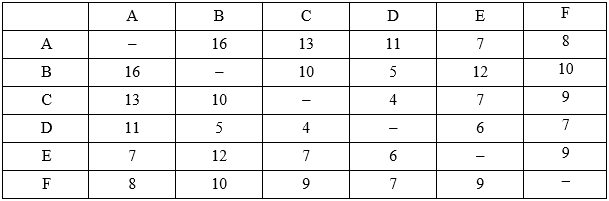
Quãng đường ngắn nhất thanh tra phải đi là

Quãng đường ngắn nhất thanh tra phải đi là
A, 50 km.
B, 52 km.
C, 45 km.
D, 54 km.
Chọn đáp án B.
Áp dụng kĩ thuật láng giềng gần nhất, thanh tra sẽ đến những trung tâm bán hàng ở các thành phố gần nhất và chưa đi đến trước đó.
 Quãng đường đi của thanh tra là:
Quãng đường đi của thanh tra là: 
 Quãng đường ngắn nhất thanh tra phải đi là: 52 km. Đáp án: B
Quãng đường ngắn nhất thanh tra phải đi là: 52 km. Đáp án: B
Áp dụng kĩ thuật láng giềng gần nhất, thanh tra sẽ đến những trung tâm bán hàng ở các thành phố gần nhất và chưa đi đến trước đó.
 Quãng đường đi của thanh tra là:
Quãng đường đi của thanh tra là: 
 Quãng đường ngắn nhất thanh tra phải đi là: 52 km. Đáp án: B
Quãng đường ngắn nhất thanh tra phải đi là: 52 km. Đáp án: B
Câu 4 [583840]: Cây khung nhỏ nhất của đồ thị bên có trọng số bằng bao nhiêu?
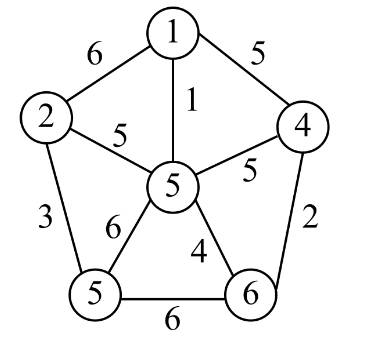

A, 15.
B, 21.
C, 27.
D, 18.
Chọn đáp án A.
Nhận xét: đồ thị có 6 đỉnh.
Áp dụng thuật toán Kruskal, cây khung nhỏ nhất có tổng trọng số là 15 và thứ tự ghép cây khung là:
 Đáp án: A
Đáp án: A
Nhận xét: đồ thị có 6 đỉnh.
Áp dụng thuật toán Kruskal, cây khung nhỏ nhất có tổng trọng số là 15 và thứ tự ghép cây khung là:
 Đáp án: A
Đáp án: A
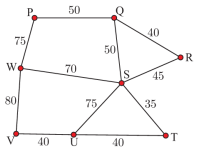
Câu 5 [379678]: Sơ đồ bên thể hiện thời gian di chuyển của An giữa các địa điểm (tính bằng phút). Vậy An mất ít nhất bao nhiêu phút để đi từ P đến R mà phải qua Q?
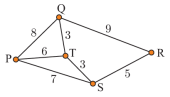

A, 12.
B, 14.
C, 17.
D, 18.
Chọn đáp án C.
Các quãng đường mà An có thể di chuyển là:
• 17 phút.
17 phút.
•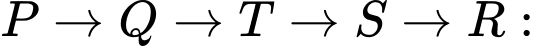 19 phút.
19 phút.
•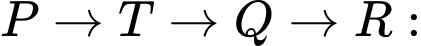 18 phút.
18 phút.
•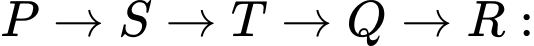 22 phút.
22 phút.
 An mất ít nhất 17 phút để đi từ P đến R mà phải qua Q. Đáp án: C
An mất ít nhất 17 phút để đi từ P đến R mà phải qua Q. Đáp án: C
Các quãng đường mà An có thể di chuyển là:
•
 17 phút.
17 phút.•
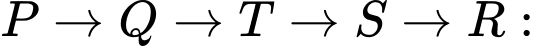 19 phút.
19 phút.•
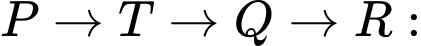 18 phút.
18 phút.•
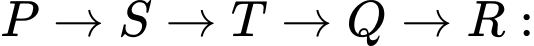 22 phút.
22 phút. An mất ít nhất 17 phút để đi từ P đến R mà phải qua Q. Đáp án: C
An mất ít nhất 17 phút để đi từ P đến R mà phải qua Q. Đáp án: C
Câu 6 [379679]: Sơ đồ bên thể hiện thời gian di chuyển của Bình giữa các địa điểm (tính bằng phút). Tính tổng thời gian tất cả các quãng đường mà Bình có thể di chuyển từ P đến T mà phải đi qua thêm đúng 2 địa điểm nữa?
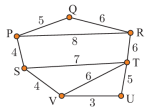

A, 17 phút.
B, 25 phút.
C, 31 phút.
D, 33 phút.
Chọn đáp án C.
Các quãng đường mà Bình có thể di chuyển là:
•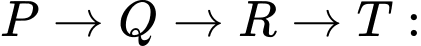 17 phút.
17 phút.
•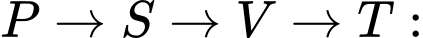 14 phút.
14 phút.
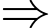 Tổng thời gian tất cả các quãng đường mà Bình có thể di chuyển từ P đến T mà phải đi qua thêm đúng 2 địa điểm nữa là:
Tổng thời gian tất cả các quãng đường mà Bình có thể di chuyển từ P đến T mà phải đi qua thêm đúng 2 địa điểm nữa là: 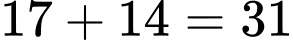 (phút). Đáp án: C
(phút). Đáp án: C
Các quãng đường mà Bình có thể di chuyển là:
•
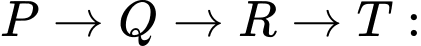 17 phút.
17 phút.•
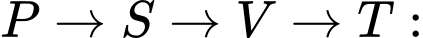 14 phút.
14 phút. Tổng thời gian tất cả các quãng đường mà Bình có thể di chuyển từ P đến T mà phải đi qua thêm đúng 2 địa điểm nữa là:
Tổng thời gian tất cả các quãng đường mà Bình có thể di chuyển từ P đến T mà phải đi qua thêm đúng 2 địa điểm nữa là: 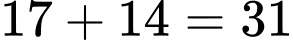 (phút). Đáp án: C
(phút). Đáp án: C
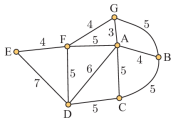
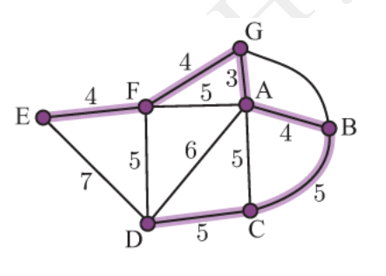
Câu 7 [379680]: Thời gian di chuyển của các tuyến xe lửa giữa các nhà ga được mô phỏng như hình vẽ bên (đơn vị: giờ). Có một tuyến xe lửa đi qua tất cả các nhà ga, bỏ qua thời gian dừng nghỉ đón khách. Vậy thời gian ngắn nhất của tuyến xe lửa đó kể từ lúc xuất phát cho đến nhà ga cuối cùng là

A, 33 giờ.
B, 32 giờ.
C, 31 giờ.
D, 25 giờ.
Chọn đáp án D.
Bài toán trên được mô phỏng dưới dạng đồ thị với bảy nhà ga là bảy đỉnh, thời gian di chuyển của các tuyến xe là trọng số của các cạnh.
Nhận thấy các đỉnh đều là bặc chẵn, ta sử dụng thuật toán Prim: (Xuất phát tại 1 đỉnh đi tới đỉnh kế tiếp với các cạnh có trọng số nhỏ nhất và thực hiện liên tiếp cho tới đỉnh cuối cùng sao cho không tạo thành chu trình tại bất kỳ điểm nào).
Hành trình của tuyến xe lửa từ lúc xuất phát đến nhà ga cuối cùng là: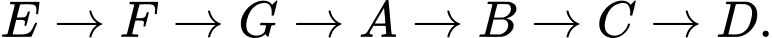
 Thời gian ngắn nhất của tuyến xe lửa đó kể từ lúc xuất phát cho đến đến nhà ga cuối cùng là:
Thời gian ngắn nhất của tuyến xe lửa đó kể từ lúc xuất phát cho đến đến nhà ga cuối cùng là: 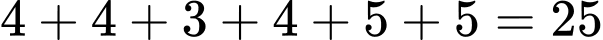 (giờ).
(giờ).
Minh họa:
 Đáp án: D
Đáp án: D
Bài toán trên được mô phỏng dưới dạng đồ thị với bảy nhà ga là bảy đỉnh, thời gian di chuyển của các tuyến xe là trọng số của các cạnh.
Nhận thấy các đỉnh đều là bặc chẵn, ta sử dụng thuật toán Prim: (Xuất phát tại 1 đỉnh đi tới đỉnh kế tiếp với các cạnh có trọng số nhỏ nhất và thực hiện liên tiếp cho tới đỉnh cuối cùng sao cho không tạo thành chu trình tại bất kỳ điểm nào).
Hành trình của tuyến xe lửa từ lúc xuất phát đến nhà ga cuối cùng là:
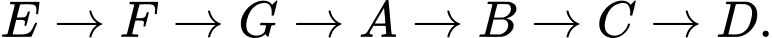
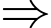 Thời gian ngắn nhất của tuyến xe lửa đó kể từ lúc xuất phát cho đến đến nhà ga cuối cùng là:
Thời gian ngắn nhất của tuyến xe lửa đó kể từ lúc xuất phát cho đến đến nhà ga cuối cùng là: 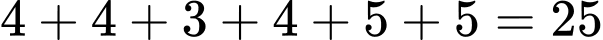 (giờ).
(giờ).Minh họa:
 Đáp án: D
Đáp án: D
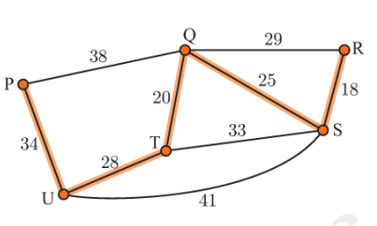
Câu 8 [379681]: Chiều dài đoạn dây điện được nối giữa các cột điện được mô phỏng như hình vẽ bên ( đơn vị là km). Vậy chiều dài ngắn nhất của dây điện để nối qua cả sáu cột điện là
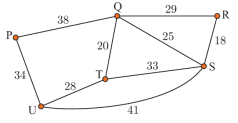

A, 120 km.
B, 125 km.
C, 142 km.
D, 151 km.
Chọn đáp án B.
Bài toán trên được mô phỏng dưới dạng đồ thị với sáu cột điện là sáu đỉnh, chiều dài dây điện là trọng số của các cạnh.
 Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Sử dụng thuật toán Prim/Kruskal: tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không được tạo thành chu trình với các cạnh đã được thêm lúc trước):
• Cạnh SR: 18 km.
• Cạnh TQ: 20 km.
• Cạnh QS: 25 km.
• Cạnh UT: 28 km.
• Cạnh PU: 34 km.
 Chiều dài ngắn nhất của dây điện để nối qua cả sáu cột điện là 125 (km).
Chiều dài ngắn nhất của dây điện để nối qua cả sáu cột điện là 125 (km).
Minh họa:
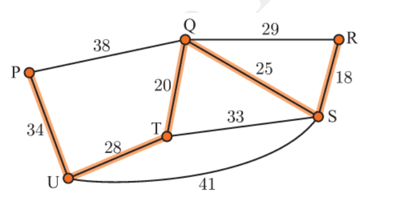 Đáp án: B
Đáp án: B
Bài toán trên được mô phỏng dưới dạng đồ thị với sáu cột điện là sáu đỉnh, chiều dài dây điện là trọng số của các cạnh.
 Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.Sử dụng thuật toán Prim/Kruskal: tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không được tạo thành chu trình với các cạnh đã được thêm lúc trước):
• Cạnh SR: 18 km.
• Cạnh TQ: 20 km.
• Cạnh QS: 25 km.
• Cạnh UT: 28 km.
• Cạnh PU: 34 km.
 Chiều dài ngắn nhất của dây điện để nối qua cả sáu cột điện là 125 (km).
Chiều dài ngắn nhất của dây điện để nối qua cả sáu cột điện là 125 (km).Minh họa:
 Đáp án: B
Đáp án: B
Câu 9 [379682]: Biểu đồ thể hiện khoảng cách giữa các thị trấn ở khu vực núi cao (tính bằng km). Sau khi tuyết rơi dày, cơ quan quản lý đường bộ mong muốn kết nối lại các thị trấn càng nhanh càng tốt bằng cách dọn sạch các đoạn đường có chiều dài tối thiểu. Tổng chiều dài đoạn đường cần dọn là
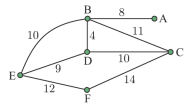

A, 44 km.
B, 53 km.
C, 43 km.
D, 78 km.
Chọn đáp án C.
Bài toán trên được mô phỏng dưới dạng đồ thị với sáu thị trấn là sáu đỉnh, khoảng cách giữa các thị trấn là trọng số của các cạnh.
 Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Sử dụng thuật toán Prim/Kruskal: tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không được tạo thành chu trình với các cạnh đã được thêm lúc trước):
• Cạnh BD: 4 km.
• Cạnh BA: 8 km.
• Cạnh ED: 9 km.
• Cạnh DC: 10 km.
• Cạnh EF: 12 km.
 Tổng chiều dài đoạn đường cần dọn là 43 (km). Đáp án: C
Tổng chiều dài đoạn đường cần dọn là 43 (km). Đáp án: C
Bài toán trên được mô phỏng dưới dạng đồ thị với sáu thị trấn là sáu đỉnh, khoảng cách giữa các thị trấn là trọng số của các cạnh.
 Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.Sử dụng thuật toán Prim/Kruskal: tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không được tạo thành chu trình với các cạnh đã được thêm lúc trước):
• Cạnh BD: 4 km.
• Cạnh BA: 8 km.
• Cạnh ED: 9 km.
• Cạnh DC: 10 km.
• Cạnh EF: 12 km.
 Tổng chiều dài đoạn đường cần dọn là 43 (km). Đáp án: C
Tổng chiều dài đoạn đường cần dọn là 43 (km). Đáp án: C
Câu 10 [379683]: Biểu đồ thể hiện các con đường nối giữa các thị trấn (đơn vị: km). Cán bộ thanh tra xuất phát từ thị trấn L đi kiểm tra tất cả các tuyến đường nối giữa các thị trấn và quay lại L. Chiều dài quãng đường tối thiểu thanh tra cần phải đi là
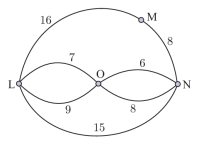

A, 59 km.
B, 69 km.
C, 82 km.
D, 86 km.
Chọn đáp án B.
Nhận thấy đồ thị trên đều là bậc chẵn ( không có đỉnh bậc lẻ).
 Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu).
Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu).
 Chiều dài quãng đường tối thiểu thanh tra cần phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên: 69 (km). Đáp án: B
Chiều dài quãng đường tối thiểu thanh tra cần phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên: 69 (km). Đáp án: B
Nhận thấy đồ thị trên đều là bậc chẵn ( không có đỉnh bậc lẻ).
 Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu).
Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu). Chiều dài quãng đường tối thiểu thanh tra cần phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên: 69 (km). Đáp án: B
Chiều dài quãng đường tối thiểu thanh tra cần phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên: 69 (km). Đáp án: B
Câu 11 [379684]: Xe xúc tuyết phải dọn tuyết bằng cách lái xe dọc tất cả các con đường được hiển thị như hình vẽ bên (đơn vị: km). Quãng đường ngắn nhất xe xúc tuyết phải đi là
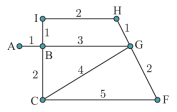

A, 21 km.
B, 22 km.
C, 23 km.
D, 24 km.
Chọn đáp án A.
Nhận thấy đây là đồ thị vô hướng có hai đỉnh bậc lẻ Có đường đi Euler.
Có đường đi Euler.
Để xe xúc tuyết đi được quãng đường ngắn nhất thì xe chỉ đi qua các con đường đúng một lần. Một trong số các cách đi của xe là:

 Quãng đường ngắn nhất xe xúc tuyết phải đi là:
Quãng đường ngắn nhất xe xúc tuyết phải đi là:

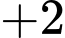
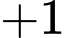
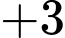
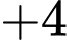
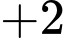
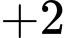
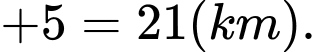 Đáp án: A
Đáp án: A
Nhận thấy đây là đồ thị vô hướng có hai đỉnh bậc lẻ
 Có đường đi Euler.
Có đường đi Euler.Để xe xúc tuyết đi được quãng đường ngắn nhất thì xe chỉ đi qua các con đường đúng một lần. Một trong số các cách đi của xe là:


 Quãng đường ngắn nhất xe xúc tuyết phải đi là:
Quãng đường ngắn nhất xe xúc tuyết phải đi là: 
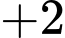
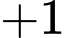
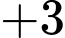
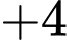
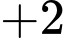
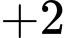
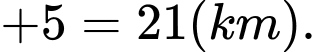 Đáp án: A
Đáp án: A
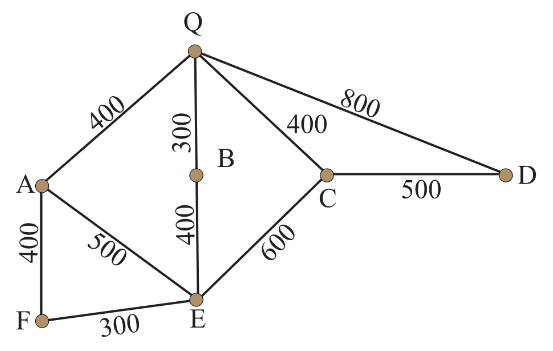
Câu 12 [379685]: Một công nhân cần kiểm tra tất cả các đường hầm trong mạng lưới thoát nước như hình vẽ (đơn vị: mét). Anh ta sẽ đi vào và đi ra qua hố ga Q. Quãng đường ngắn nhất anh ta có thể đi là

A, 4, 6 km.
B, 5 km.
C, 5,1 km.
D, 5,4 km.
Chọn đáp án D.
Nhận thấy đây là đồ thị vô hướng có hai đỉnh bậc lẻ Có đường đi Euler.
Có đường đi Euler.
Nhưng anh ta đi vào và đi ra qua hố ga Q nên sẽ không có đường đi Euler thỏa mãn.
Nên anh ấy phải đi lặp lại các quãng đường tới Q và quãng đường ngắn nhất anh ta đi là:
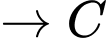
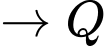

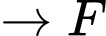
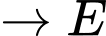

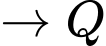
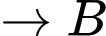
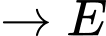
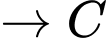
 Quãng đường ngắn nhất anh ta có thể đi là:
Quãng đường ngắn nhất anh ta có thể đi là:

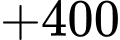
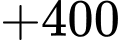
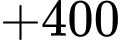
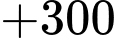
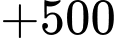
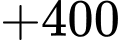
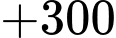
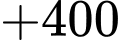
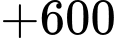
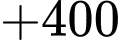
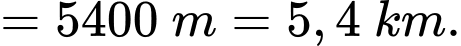 Đáp án: D
Đáp án: D
Nhận thấy đây là đồ thị vô hướng có hai đỉnh bậc lẻ
 Có đường đi Euler.
Có đường đi Euler.Nhưng anh ta đi vào và đi ra qua hố ga Q nên sẽ không có đường đi Euler thỏa mãn.
Nên anh ấy phải đi lặp lại các quãng đường tới Q và quãng đường ngắn nhất anh ta đi là:



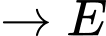
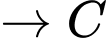
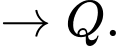
 Quãng đường ngắn nhất anh ta có thể đi là:
Quãng đường ngắn nhất anh ta có thể đi là: 
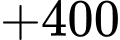
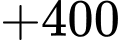
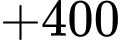
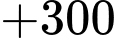
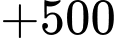
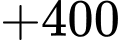
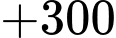
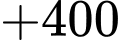
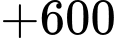
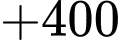
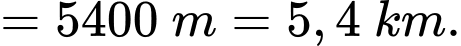 Đáp án: D
Đáp án: D
Câu 13 [379686]: Khoảng cách giữa những thành phố được mô phỏng như hình vẽ bên ( đơn vị: km). Một nhà cung cấp gạo có trụ sở tại thành phố P, họ phải giao gạo tới các thành phố trước khi quay lại P. Do thành phố Q cần gạo gấp nên nhà cung cấp phải đến thành phố Q đầu tiên, quãng đường ngắn nhất mà nhà cung cấp gạo phải đi là

A, 405 km.
B, 460 km.
C, 330 km.
D, 600 km.
Chọn đáp án A.
Đồ thị tồn tại chu trình Hamilton để nhà cung cấp gạo xuất phát và kết thúc tại thành phố P. Quãng đường nhà cung cấp gạo đi là:
Quãng đường nhà cung cấp gạo đi là: 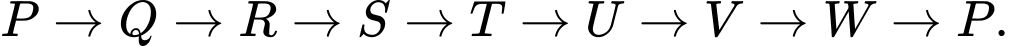
 Độ dài quãng đường là:
Độ dài quãng đường là:  Đáp án: A
Đáp án: A
Đồ thị tồn tại chu trình Hamilton để nhà cung cấp gạo xuất phát và kết thúc tại thành phố P.
 Quãng đường nhà cung cấp gạo đi là:
Quãng đường nhà cung cấp gạo đi là: 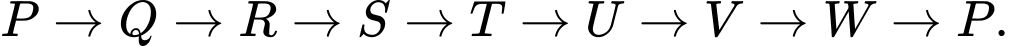
 Độ dài quãng đường là:
Độ dài quãng đường là:  Đáp án: A
Đáp án: A
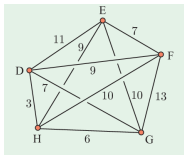
Câu 14 [379687]: Từ kho D xe bưu chính đến lấy thư từ các hộp thư tại E, F, G và H rồi quay lại kho. Sơ đồ bên hiển thị thời gian di chuyển giữa các hộp thư (đơn vị: phút). Thời gian ngắn nhất để xe bưu chính thực hiện điều đó là

A, 32 phút.
B, 35 phút.
C, 47 phút.
D, 65 phút.
Chọn đáp án B.
Áp dụng thuật toán láng giềng gần nhất, ta sẽ ưu tiên cho xe bưu chính di chuyển đến những hộp thư gần nhất và chưa được đi đến trước đó.
 Quãng đường đi của xe là:
Quãng đường đi của xe là: 
 Thời gian ngắn nhất để xe bưu chính thực hiện điều đó là: 35 phút. Đáp án: B
Thời gian ngắn nhất để xe bưu chính thực hiện điều đó là: 35 phút. Đáp án: B
Áp dụng thuật toán láng giềng gần nhất, ta sẽ ưu tiên cho xe bưu chính di chuyển đến những hộp thư gần nhất và chưa được đi đến trước đó.
 Quãng đường đi của xe là:
Quãng đường đi của xe là: 
 Thời gian ngắn nhất để xe bưu chính thực hiện điều đó là: 35 phút. Đáp án: B
Thời gian ngắn nhất để xe bưu chính thực hiện điều đó là: 35 phút. Đáp án: B
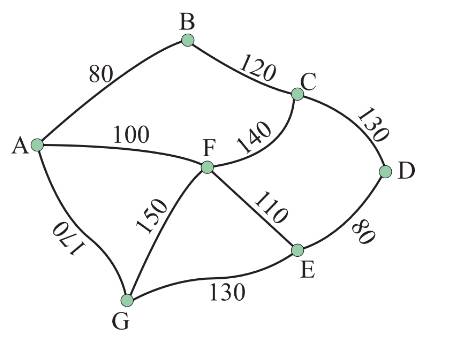
Câu 15 [379688]: Một đoàn rước lễ hội muốn diễu hành dọc theo tất cả các con đường được hiển thị như hình vẽ và quay lại điểm xuất phát E (đơn vị: mét). Quãng đường ngắn nhất mà đoàn rước lễ hội phải đi là
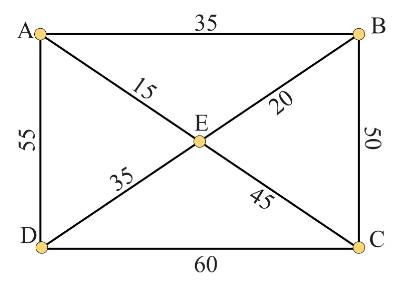

A, 315 m.
B, 370 m.
C, 375 m.
D, 410 m.
Chọn đáp án D.
Nhận thấy đây là đồ thị vô hướng có bốn đỉnh bậc lẻ Đồ thị không có chu trình và đường đi Euler.
Đồ thị không có chu trình và đường đi Euler.
Đoàn rước lễ hội muốn diễn hành dọc theo tất cả các con đường thì những cạnh có trọng số nhỏ sẽ được lặp lại và những cạnh có trọng số lớn sẽ diễu hành 1 lần.
Hành trình của đoàn diễn hành xuất phát từ E và kết thúc ở E là:



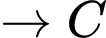
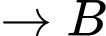
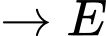
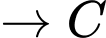

 Quãng đường ngắn nhất anh ta có thể đi là:
Quãng đường ngắn nhất anh ta có thể đi là:

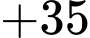
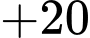
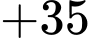
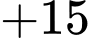
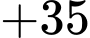
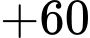
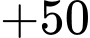
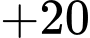
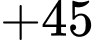
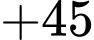
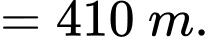 Đáp án: D
Đáp án: D
Nhận thấy đây là đồ thị vô hướng có bốn đỉnh bậc lẻ
 Đồ thị không có chu trình và đường đi Euler.
Đồ thị không có chu trình và đường đi Euler.Đoàn rước lễ hội muốn diễn hành dọc theo tất cả các con đường thì những cạnh có trọng số nhỏ sẽ được lặp lại và những cạnh có trọng số lớn sẽ diễu hành 1 lần.
Hành trình của đoàn diễn hành xuất phát từ E và kết thúc ở E là:


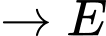
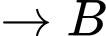

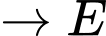

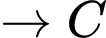
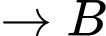
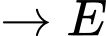
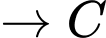

 Quãng đường ngắn nhất anh ta có thể đi là:
Quãng đường ngắn nhất anh ta có thể đi là: 
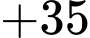
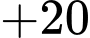
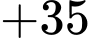
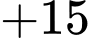
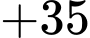
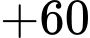
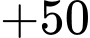
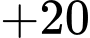
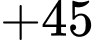
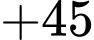
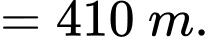 Đáp án: D
Đáp án: D
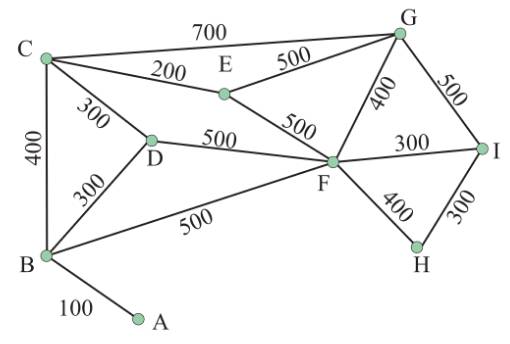
Câu 16 [379689]: Biểu đồ thể hiện chiều dài các con đường trong tuyến đường gửi thư của người đưa thư (đơn vị: m). Người đưa thư xuất phát và kết thúc tại nhà riêng của mình tại điểm A và phải đi qua tất cả các tuyến đường để đưa thư. Tính quãng đường ngắn nhất mà người đưa thư phải đi?

A, 3,3 km.
B, 7,9 km.
C, 7,1 km.
D, 8,5 km.
Chọn đáp án C.
Nhận thấy đây là đồ thị vô hướng có bốn đỉnh bậc lẻ Đồ thị không có chu trình và đường đi Euler.
Đồ thị không có chu trình và đường đi Euler.
Người đưa thư xuất phát và kết thúc tại nhà riêng của mình tại điểm A và phải đi qua tất cả các tuyến đường để đưa thư thì những cạnh có trọng số nhỏ sẽ được lặp lại và những cạnh có trọng số lớn sẽ diễu hành 1 lần.
Hành trình của người đưa thư xuất phát từ A và kết thúc ở A là:



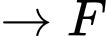
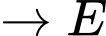
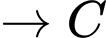
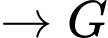


 Quãng đường ngắn nhất anh ta có thể đi là:
Quãng đường ngắn nhất anh ta có thể đi là:

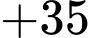
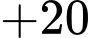
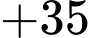
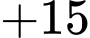
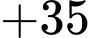
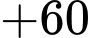
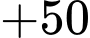
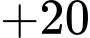
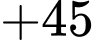
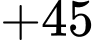
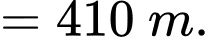 Đáp án: C
Đáp án: C
Nhận thấy đây là đồ thị vô hướng có bốn đỉnh bậc lẻ
 Đồ thị không có chu trình và đường đi Euler.
Đồ thị không có chu trình và đường đi Euler.Người đưa thư xuất phát và kết thúc tại nhà riêng của mình tại điểm A và phải đi qua tất cả các tuyến đường để đưa thư thì những cạnh có trọng số nhỏ sẽ được lặp lại và những cạnh có trọng số lớn sẽ diễu hành 1 lần.
Hành trình của người đưa thư xuất phát từ A và kết thúc ở A là:

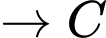

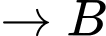

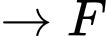
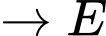
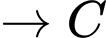
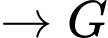
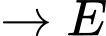


 Quãng đường ngắn nhất anh ta có thể đi là:
Quãng đường ngắn nhất anh ta có thể đi là:
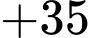
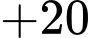
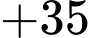
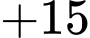
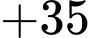
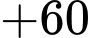
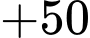
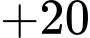
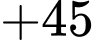
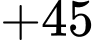
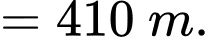 Đáp án: C
Đáp án: C
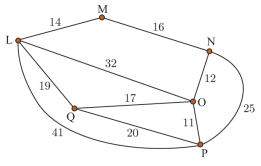
Câu 17 [379690]: Các khu cắm trại tại một công viên được mô phỏng như hình vẽ bên (đơn vị: mét). Bác bảo vệ đang ở khu cắm tại A và phải kiểm tra tất cả các khu cắm trại khác. Vậy quãng đường ngắn nhất bác bảo vệ có thể đi và điểm kiểm tra cuối cùng ở khu cắm tại D là

A, 690 m.
B, 700 m.
C, 840 m.
D, 820 m.
Chọn đáp án B.
Áp dụng kĩ thuật người láng giềng gần nhất, bác bảo vệ sẽ ưu tiên di chuyển đến những khu cắm trại gần nhất và chưa được đi đến trước đó.
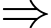 Quãng đường đi của bác bảo vệ là:
Quãng đường đi của bác bảo vệ là: 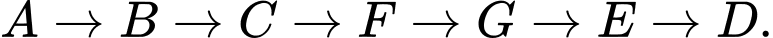
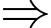 Vậy quãng đường ngắn nhất bác bảo vệ có thể đi là: 700 m. Đáp án: B
Vậy quãng đường ngắn nhất bác bảo vệ có thể đi là: 700 m. Đáp án: B
Áp dụng kĩ thuật người láng giềng gần nhất, bác bảo vệ sẽ ưu tiên di chuyển đến những khu cắm trại gần nhất và chưa được đi đến trước đó.
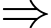 Quãng đường đi của bác bảo vệ là:
Quãng đường đi của bác bảo vệ là: 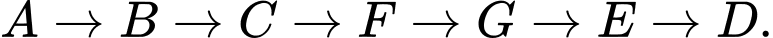
 Vậy quãng đường ngắn nhất bác bảo vệ có thể đi là: 700 m. Đáp án: B
Vậy quãng đường ngắn nhất bác bảo vệ có thể đi là: 700 m. Đáp án: B
Câu 18 [379691]: Năm thị trấn sẽ được kết nối với một nhà máy thủy điện L. Biểu đồ bên cạnh cho thấy chi phí tính bằng tỉ đồng cho các kết nối giữa chúng.Vậy chi phí tối thiểu để kết nối giữa nhà máy và tất cả các thị trấn là

A, 86 tỉ đồng.
B, 98 tỉ đồng.
C, 117 tỉ đồng.
D, 70 tỉ đồng.
Chọn đáp án D.
Bài toán trên được mô phỏng dưới dạng đồ thị với năm thị trấn là năm đỉnh, chi phí kết nối giữa các thị trấn là trọng số của các cạnh.
 Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Sử dụng thuật toán Prim/Kruskal: tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không được tạo thành chu trình với các cạnh đã được thêm lúc trước):
• Cạnh OP: 11 tỉ đồng.
• Cạnh ON: 12 tỉ đồng.
• Cạnh LM: 14 tỉ đồng.
• Cạnh MN: 16 tỉ đồng.
• Cạnh QO: 17 tỉ đồng.
 Chi phí tối thiểu để kết nối giữa nhà máy và tất cả các thị trấn là 70 tỉ đồng. Đáp án: D
Chi phí tối thiểu để kết nối giữa nhà máy và tất cả các thị trấn là 70 tỉ đồng. Đáp án: D
Bài toán trên được mô phỏng dưới dạng đồ thị với năm thị trấn là năm đỉnh, chi phí kết nối giữa các thị trấn là trọng số của các cạnh.
 Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.Sử dụng thuật toán Prim/Kruskal: tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không được tạo thành chu trình với các cạnh đã được thêm lúc trước):
• Cạnh OP: 11 tỉ đồng.
• Cạnh ON: 12 tỉ đồng.
• Cạnh LM: 14 tỉ đồng.
• Cạnh MN: 16 tỉ đồng.
• Cạnh QO: 17 tỉ đồng.
 Chi phí tối thiểu để kết nối giữa nhà máy và tất cả các thị trấn là 70 tỉ đồng. Đáp án: D
Chi phí tối thiểu để kết nối giữa nhà máy và tất cả các thị trấn là 70 tỉ đồng. Đáp án: D
Câu 19 [379692]: Các tòa nhà của một trường đại học vừa được xây dựng như hình vẽ. Khoảng cách giữa các tòa nhà được tính bằng mét. Tất cả các tòa nhà được kết nối với mạng máy tính của trường bằng dây cáp. Để giảm thiểu chi phí thì chiều dài dây cáp tối thiểu nhà trường phải sử dụng là
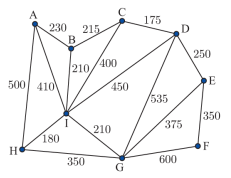

A, 2750 m.
B, 2460 m.
C, 2005 m.
D, 1820 m.
Chọn đáp án D.
Bài toán trên được mô phỏng dưới dạng đồ thị với chín tòa nhà là chín đỉnh, khoảng cách giữa các tòa nhà là trọng số của các cạnh.
 Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Sử dụng thuật toán Prim/Kruskal: tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không được tạo thành chu trình với các cạnh đã được thêm lúc trước):
• Cạnh CD: 175 m.
• Cạnh HI: 180 m.
• Cạnh IG: 210 m.
• Cạnh IB: 210 m.
• Cạnh BC: 215 m.
• Cạnh AB: 230 m.
• Cạnh DE: 250 m.
• Cạnh EF: 350m.
 Chiều dài dây cáp tối thiểu nhà trường phải sử dụng là 1820m. Đáp án: D
Chiều dài dây cáp tối thiểu nhà trường phải sử dụng là 1820m. Đáp án: D
Bài toán trên được mô phỏng dưới dạng đồ thị với chín tòa nhà là chín đỉnh, khoảng cách giữa các tòa nhà là trọng số của các cạnh.
 Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất của đồ thị.Sử dụng thuật toán Prim/Kruskal: tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không được tạo thành chu trình với các cạnh đã được thêm lúc trước):
• Cạnh CD: 175 m.
• Cạnh HI: 180 m.
• Cạnh IG: 210 m.
• Cạnh IB: 210 m.
• Cạnh BC: 215 m.
• Cạnh AB: 230 m.
• Cạnh DE: 250 m.
• Cạnh EF: 350m.
 Chiều dài dây cáp tối thiểu nhà trường phải sử dụng là 1820m. Đáp án: D
Chiều dài dây cáp tối thiểu nhà trường phải sử dụng là 1820m. Đáp án: D
Câu 20 [379693]: Giả sử bạn là một người công nhân dọn đường, những con đường cần được dọn có chiều dài được mô phỏng như hình vẽ bên (đơn vị: mét). Bạn xuất phát từ 1 điểm nào đó thực hiện công việc của mình và hoàn thành công việc khi quay lại điểm xuất phát. Vậy tổng chiều dài tối thiểu bạn phải đi là
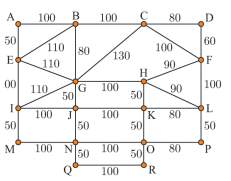

A, 2350 m.
B, 2970 m.
C, 2750 m.
D, 3270 m.
Chọn đáp án B.
Nhận thấy đồ thị trên đều là bậc chẵn ( không có đỉnh bậc lẻ).
 Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu).
Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu).
 Tổng chiều dài tối thiểu bạn phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên: 2970 (m). Đáp án: B
Tổng chiều dài tối thiểu bạn phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên: 2970 (m). Đáp án: B
Nhận thấy đồ thị trên đều là bậc chẵn ( không có đỉnh bậc lẻ).
 Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu).
Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu). Tổng chiều dài tối thiểu bạn phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên: 2970 (m). Đáp án: B
Tổng chiều dài tối thiểu bạn phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên: 2970 (m). Đáp án: B