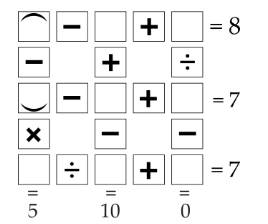
Đáp án Bài tập tự luyện số 4
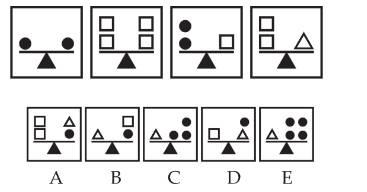
Câu 1 [584208]: [Đường lên đỉnh Olympia năm thứ 23]: Quả nặng cần tìm có khối lượng là bao nhiêu đơn vị để cân thăng bằng?
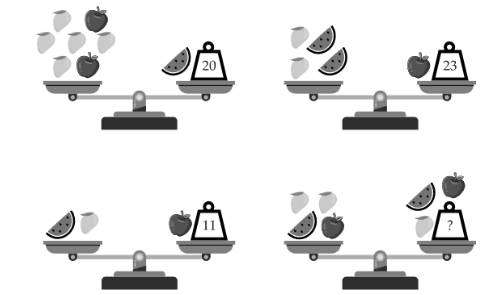

Gọi 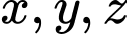 lần lượt tượng trưng cho cân nặng của một quả xoài, táo, dưa hấu.
lần lượt tượng trưng cho cân nặng của một quả xoài, táo, dưa hấu.
Dựa vào hình trên, ta có hệ phương trình:
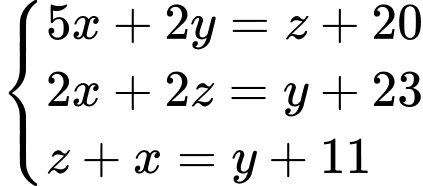
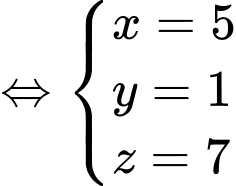
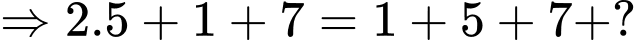
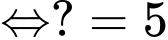
Đáp án: 5.
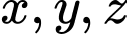 lần lượt tượng trưng cho cân nặng của một quả xoài, táo, dưa hấu.
lần lượt tượng trưng cho cân nặng của một quả xoài, táo, dưa hấu.
Dựa vào hình trên, ta có hệ phương trình:
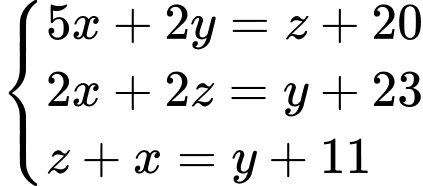
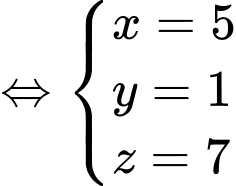
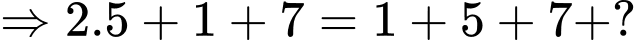
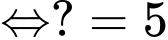
Đáp án: 5.
Câu 2 [584209]: [Đường lên đỉnh Olympia năm thứ 22]: Điền số thích hợp vào dấu “?”
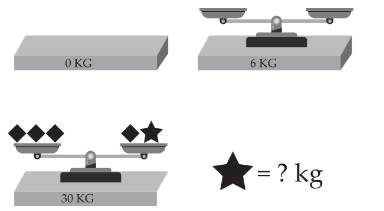

Gọi 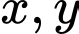 lần lượt là khối lượng của hình vuông và hình sao.
lần lượt là khối lượng của hình vuông và hình sao.
Từ hình đã cho, ta có hệ phương trình:
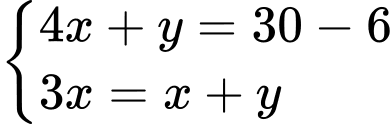
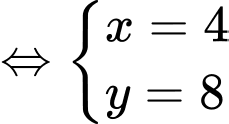
Đáp án: 8.
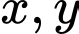 lần lượt là khối lượng của hình vuông và hình sao.
lần lượt là khối lượng của hình vuông và hình sao.
Từ hình đã cho, ta có hệ phương trình:
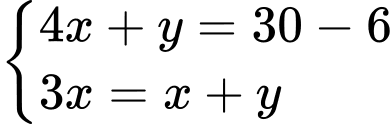
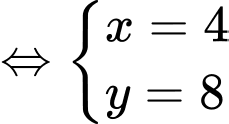
Đáp án: 8.
Câu 3 [584210]: [Đường lên đỉnh Olympia năm thứ 22]: Chiếc bàn trong hình vẽ cao bao nhiêu cm?
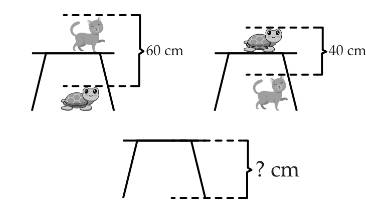

Gọi 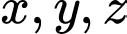 lần lượt là chiều cao của chiếc bàn, mèo và rùa.
lần lượt là chiều cao của chiếc bàn, mèo và rùa.
Dựa vào hình đã cho, ta có hệ phương trình:
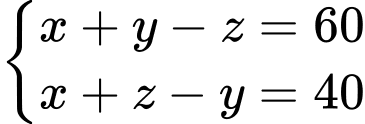
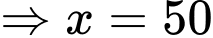
Đáp án: 50.
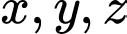 lần lượt là chiều cao của chiếc bàn, mèo và rùa.
lần lượt là chiều cao của chiếc bàn, mèo và rùa.
Dựa vào hình đã cho, ta có hệ phương trình:
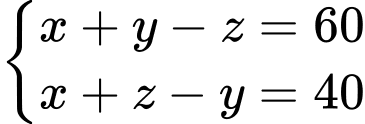
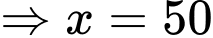
Đáp án: 50.
Câu 4 [584211]: [Đường lên đỉnh Olympia năm thứ 22]: Tìm phương án thích hợp để chắc chắn hai đĩa của cân số 2 thăng bằng.
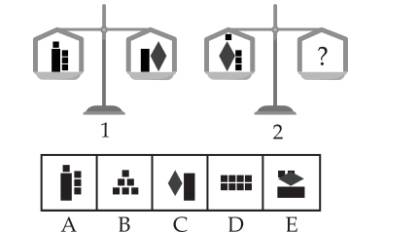

Từ hình 1  Khối lượng của hình thoi bằng tổng khối lượng của 4 hình vuông nhỏ.
Khối lượng của hình thoi bằng tổng khối lượng của 4 hình vuông nhỏ.
Đáp án: D.
 Khối lượng của hình thoi bằng tổng khối lượng của 4 hình vuông nhỏ.
Khối lượng của hình thoi bằng tổng khối lượng của 4 hình vuông nhỏ.
Đáp án: D.
Câu 5 [584212]: [Đường lên đỉnh Olympia năm thứ 22]: Đĩa cân bên phải nặng bao nhiêu kg?
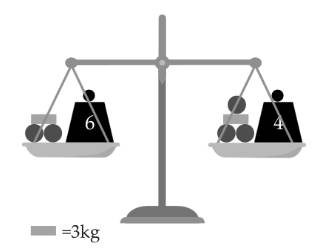

Từ hình vẽ  Vật hình tròn có cân nặng 2kg.
Vật hình tròn có cân nặng 2kg.
 Cân nặng của đĩa cân bên phải là:
Cân nặng của đĩa cân bên phải là:
 (kg)
(kg)
Đáp án: 13.
 Vật hình tròn có cân nặng 2kg.
Vật hình tròn có cân nặng 2kg.
 Cân nặng của đĩa cân bên phải là:
Cân nặng của đĩa cân bên phải là:  (kg)
(kg)
Đáp án: 13.
Câu 6 [584213]: [Đường lên đỉnh Olympia năm thứ 22]: Tìm số thích hợp điền vào dấu “?”
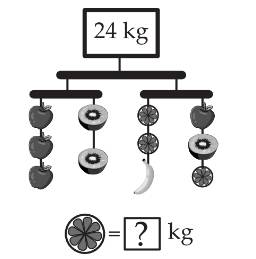

Từ hình vẽ  Cân nặng của mỗi dây quả là:
Cân nặng của mỗi dây quả là: 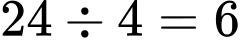 (kg)
(kg)
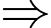 Cân nặng của một quả táo là:
Cân nặng của một quả táo là: 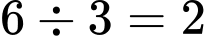 (kg)
(kg)
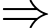 Cân nặng của một quả kiwi là:
Cân nặng của một quả kiwi là: 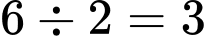 (kg)
(kg)
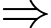 Cân nặng của một quả cam là:
Cân nặng của một quả cam là: 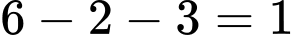 (kg)
(kg)
Đáp án: 1.
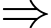 Cân nặng của mỗi dây quả là:
Cân nặng của mỗi dây quả là: 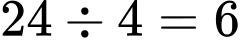 (kg)
(kg)
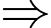 Cân nặng của một quả táo là:
Cân nặng của một quả táo là: 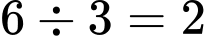 (kg)
(kg)
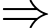 Cân nặng của một quả kiwi là:
Cân nặng của một quả kiwi là: 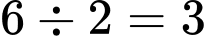 (kg)
(kg)
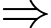 Cân nặng của một quả cam là:
Cân nặng của một quả cam là: 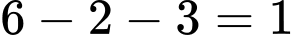 (kg)
(kg)
Đáp án: 1.
Câu 7 [584214]: [Đường lên đỉnh Olympia năm thứ 22]: Cần đặt bao nhiêu quả táo vào đĩa bên phải để cân số 3 thăng bằng?
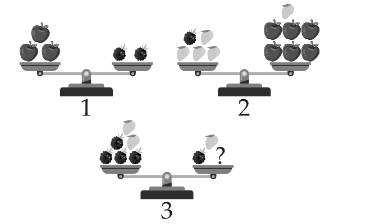

Giả sử một quả táo có khối lượng 2kg.
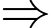 Khối lượng của một chùm nho là:
Khối lượng của một chùm nho là: 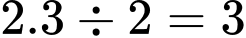 (kg)
(kg)
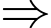 Khối lượng của một quả xoài là:
Khối lượng của một quả xoài là: 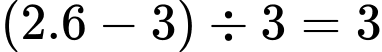 (kg)
(kg)
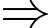 Số quả táo cần cho đĩa cân bên phải của cân số 3 là:
Số quả táo cần cho đĩa cân bên phải của cân số 3 là: 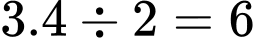 (quả).
(quả).
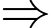 Khối lượng của một chùm nho là:
Khối lượng của một chùm nho là: 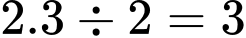 (kg)
(kg)
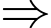 Khối lượng của một quả xoài là:
Khối lượng của một quả xoài là: 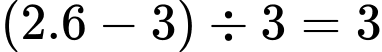 (kg)
(kg)
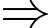 Số quả táo cần cho đĩa cân bên phải của cân số 3 là:
Số quả táo cần cho đĩa cân bên phải của cân số 3 là: 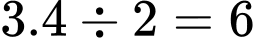 (quả).
(quả).
Câu 8 [584215]: [Đường lên đỉnh Olympia năm thứ 23]: Theo thông tin phía trên, chiếc cân nào bên dưới đang ở đúng vị trí?

Theo hình ảnh đã cho 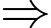 Cân nặng của hình vuông gấp 2 lần hình tròn, cân nặng hình tam giác gấp 2 lần hình vuông
Cân nặng của hình vuông gấp 2 lần hình tròn, cân nặng hình tam giác gấp 2 lần hình vuông 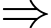 Cân nặng của hình tam giác gấp 4 lần hình tròn.
Cân nặng của hình tam giác gấp 4 lần hình tròn.
Đáp án: E.
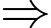 Cân nặng của hình vuông gấp 2 lần hình tròn, cân nặng hình tam giác gấp 2 lần hình vuông
Cân nặng của hình vuông gấp 2 lần hình tròn, cân nặng hình tam giác gấp 2 lần hình vuông  Cân nặng của hình tam giác gấp 4 lần hình tròn.
Cân nặng của hình tam giác gấp 4 lần hình tròn.
Đáp án: E.
Câu 9 [584216]: [Đường lên đỉnh Olympia năm thứ 21]: Đâu là hình ảnh của cân số 3 khi nó ở trạng thái thăng bằng?
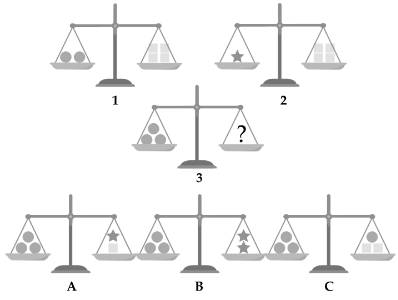

Theo hình ảnh đã cho  Cân nặng của hình tròn gấp 2 lần hình vuông, cân nặng hình sao gấp 3 lần hình vuông.
Cân nặng của hình tròn gấp 2 lần hình vuông, cân nặng hình sao gấp 3 lần hình vuông.
Đáp án: B.
 Cân nặng của hình tròn gấp 2 lần hình vuông, cân nặng hình sao gấp 3 lần hình vuông.
Cân nặng của hình tròn gấp 2 lần hình vuông, cân nặng hình sao gấp 3 lần hình vuông.
Đáp án: B.
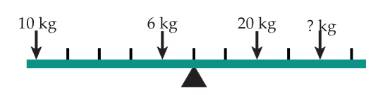
Câu 10 [584217]: [Đường lên đỉnh Olympia năm thứ 21]: Khi cân bằng, đĩa bên phải của chiếc cân số 4 nặng bao nhiêu?
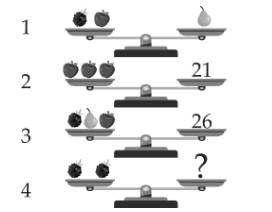

Cân nặng của một quả táo là: 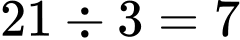
Từ đĩa cân 1 và 3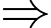 Cân nặng của một quả lê là:
Cân nặng của một quả lê là: 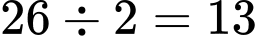
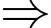 Cân nặng của một quả nho là:
Cân nặng của một quả nho là: 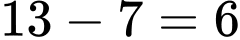
Đáp án: 12.
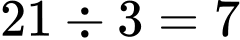
Từ đĩa cân 1 và 3
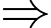 Cân nặng của một quả lê là:
Cân nặng của một quả lê là: 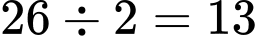
 Cân nặng của một quả nho là:
Cân nặng của một quả nho là: 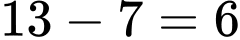
Đáp án: 12.
Câu 11 [584218]: [Đường lên đỉnh Olympia năm thứ 17]: Tìm khối lượng phù hợp để cân được thăng bằng?

Từ hình đã cho, ta có phương trình: 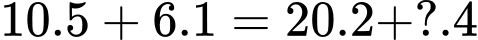
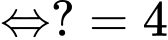
Đáp án: 4.
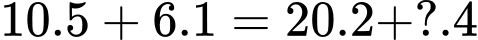
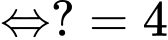
Đáp án: 4.
Câu 12 [584219]: [Đường lên đỉnh Olympia năm thứ 15]: Bên phía dấu chấm hỏi có bao nhiêu hình phong bì?
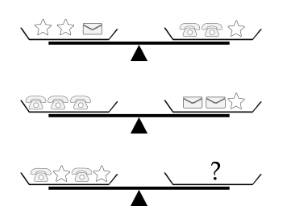

Giả sử khối lượng của một chiếc điện thoại là 2
Từ cân thứ hai Khối lượng của một chiếc phong bì là:
Khối lượng của một chiếc phong bì là: 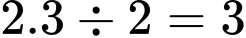
Từ cân thứ nhất Khối lượng của một hình sao là:
Khối lượng của một hình sao là: 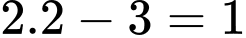
 Đĩa bên phải của cân thứ 3 cần số phong bì là:
Đĩa bên phải của cân thứ 3 cần số phong bì là: 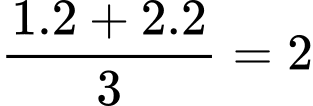 (chiếc)
(chiếc)
Đáp án: 2.
Từ cân thứ hai
 Khối lượng của một chiếc phong bì là:
Khối lượng của một chiếc phong bì là: 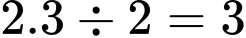
Từ cân thứ nhất
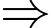 Khối lượng của một hình sao là:
Khối lượng của một hình sao là: 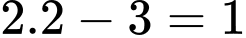
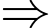 Đĩa bên phải của cân thứ 3 cần số phong bì là:
Đĩa bên phải của cân thứ 3 cần số phong bì là: 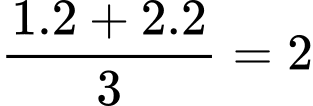 (chiếc)
(chiếc)
Đáp án: 2.
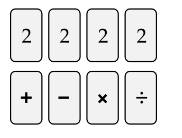
Câu 13 [584220]: [Đường lên đỉnh Olympia năm thứ 23]: Chỉ sử dụng các chữ số và dấu phép tính dưới đây, hãy tạo ra một phép toán có kết quả là 9.

Đáp án: 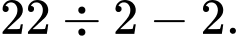
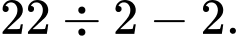
Câu 14 [584221]: [Đường lên đỉnh Olympia năm thứ 22]: Điền lần lượt các số 4, 5, 6 vào vị trí thích hợp (A, B, C) để tổng các số trên mỗi cạnh tam giác đều bằng nhau.
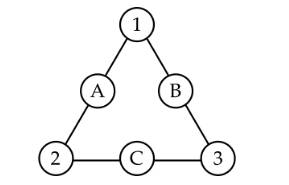

Ta thấy: Cạnh có chứa C có tổng hai số ở góc là lớn nhất 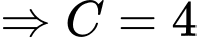
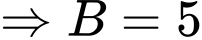
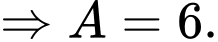
Đáp án: 6, 5, 4.
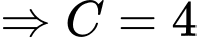
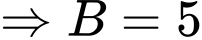
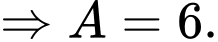
Đáp án: 6, 5, 4.
Câu 15 [584222]: [Đường lên đỉnh Olympia năm thứ 23]: Điền số từ 1-8, mỗi số chỉ sử dụng 1 lần sao cho tổng các số trên 1 cạnh bằng 12.
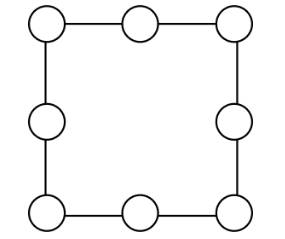

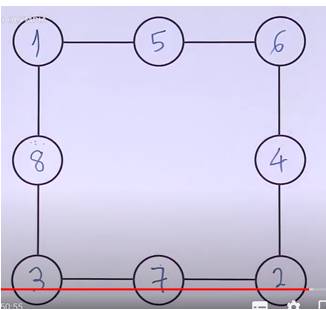
Câu 16 [584223]: [Đường lên đỉnh Olympia năm thứ 23]: Điền số từ 1-6, không trùng nhau.
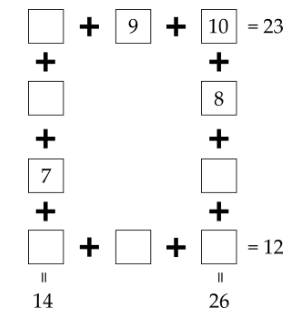


Câu 17 [584224]: [Đường lên đỉnh Olympia năm thứ 23]: Điền số từ 1-6, mỗi số 1 lần, sao cho tổng các số trên cùng 1 cạnh của tam giác bằng 26.
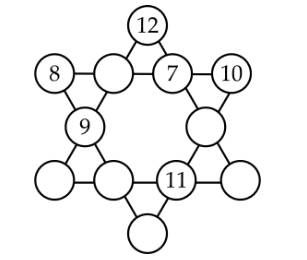

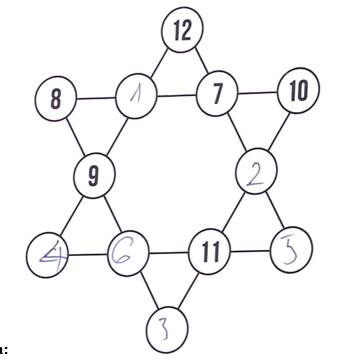
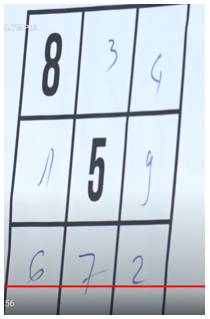
Câu 18 [584225]: [Đường lên đỉnh Olympia năm thứ 23]: Điền số từ 1-9 vào ô trống, mỗi số 1 lần, 3 số trên hàng ngang, dọc, chéo bất kì bằng nhau.
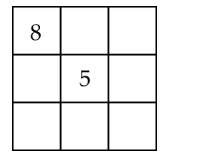

Ta thấy: Tổng các số từ 1 đến 9 bằng 45  Tổng của 3 số theo hàng ngang, hàng dọc bất kỳ phải bằng:
Tổng của 3 số theo hàng ngang, hàng dọc bất kỳ phải bằng: 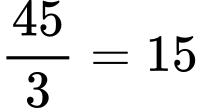
 Tổng của 3 số theo hàng ngang, hàng dọc bất kỳ phải bằng:
Tổng của 3 số theo hàng ngang, hàng dọc bất kỳ phải bằng: 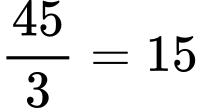

Câu 19 [584226]: [Đường lên đỉnh Olympia năm thứ 23]: Điền số từ ô vuông vào các vị trí đã đánh dấu để tổng các số trong đường tròn bằng 0.
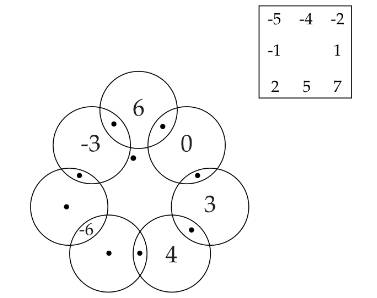

Ta thấy: Có đường tròn chứa số 0 nên sẽ có 3 trường hợp cho 2 chỗ trống còn lại cho đường tròn đó. Đó là  và
và 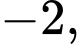
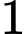 và
và 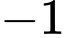 hoặc
hoặc 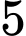 và
và 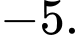
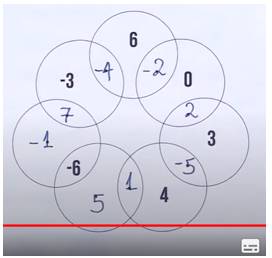
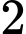 và
và 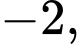
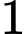 và
và 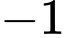 hoặc
hoặc 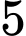 và
và 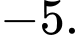

Câu 20 [584227]: [Đường lên đỉnh Olympia năm thứ 23]: Điền số từ 1-7, mỗi số điền một lần.
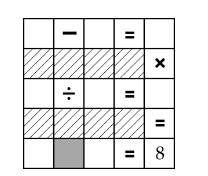


Câu 21 [584228]: [Đường lên đỉnh Olympia năm thứ 23]: Điền số từ 2-7, mỗi số sử dụng một lần.
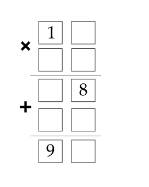


Câu 22 [584229]: [Đường lên đỉnh Olympia năm thứ 23]: Điền các số từ 1-9. Sao cho tổng các số nằm trên cạnh bằng nhau.
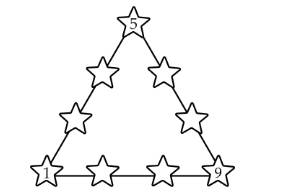


Câu 23 [584230]: [Đường lên đỉnh Olympia năm thứ 22]: Điền số từ 1-9, ngoại trừ 8.
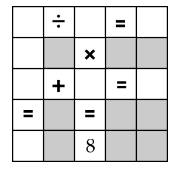

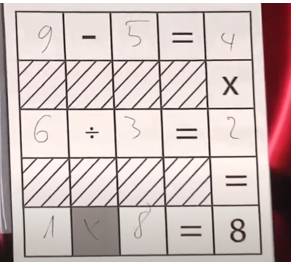
Câu 24 [584231]: [Đường lên đỉnh Olympia năm thứ 22]: Điền các số sau vào các ô tròn: 2, 4, 5, 6, 7, 8, 9. Sao cho tổng t cả các số ở các đỉnh mỗi tam giác bằng 16.
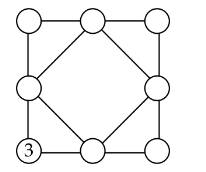

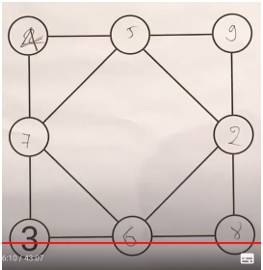
Câu 25 [584232]: [Đường lên đỉnh Olympia năm thứ 22]: Điền số từ 1-7, tổng các số trên mỗi đường tròn bằng 17.
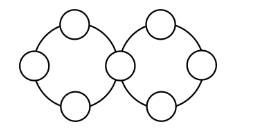

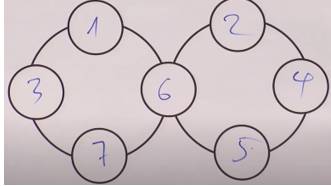
Câu 26 [584233]: [Đường lên đỉnh Olympia năm thứ 22]: Dùng các số 1, 3, 5, 7 sao cho tổng trong mỗi đường tròn bằng 15.

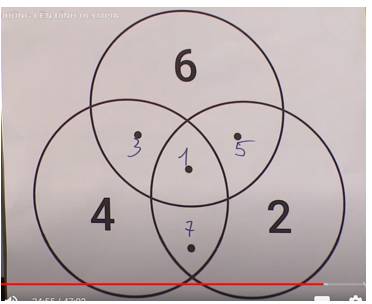
Câu 27 [584234]: [Đường lên đỉnh Olympia năm thứ 24]: Điền số từ 4-12 sao cho trên cùng đoạn, tổng 3 số bằng 21.
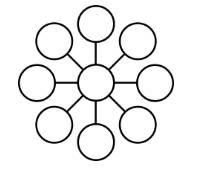

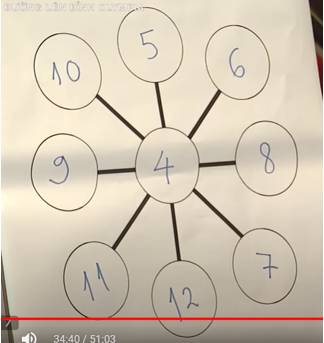
Câu 28 [584235]: [Đường lên đỉnh Olympia năm thứ 24]: Điền các số từ 1- 9, mỗi số 1 lần.
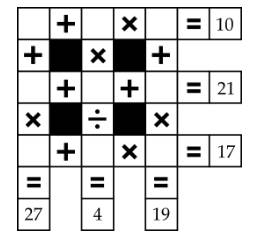


Câu 29 [584236]: [Đường lên đỉnh Olympia năm thứ 19]: Ta cần đổi vị trí của 2 chú heo nào cho nhau để tổng các con số trên 3 chú heo cùng trên một đường thẳng đều bằng 12?
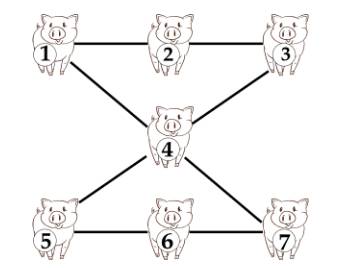

Đáp án: 1 và 7.
Câu 30 [584237]: [Đường lên đỉnh Olympia năm thứ 24]: Điền số từ 1-9. Ngoặc đơn chỉ áp dụng trong cột dọc.