Đáp án Bài tập tự luyện số 1
Câu 1 [583990]: [Đường lên đỉnh Olympia năm thứ 16]: Dãy số gồm 9 số tự nhiên khác nhau có tổng là 45, số tự nhiên lớn nhất trong dãy là số mấy?
Có: 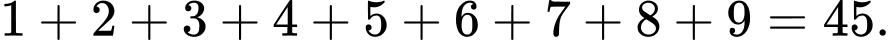
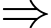 Số tự nhiên lớn nhất trong dãy là 9.
Số tự nhiên lớn nhất trong dãy là 9.
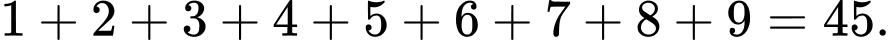
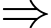 Số tự nhiên lớn nhất trong dãy là 9.
Số tự nhiên lớn nhất trong dãy là 9.
Câu 2 [583991]: [Đường lên đỉnh Olympia năm thứ 23]: Số tự nhiên có hai chữ số nào khi đem nhân với 3 và trừ đi 2 thì sẽ cho ra đáp án là số đảo ngược của chính nó ?
Theo đề bài, ta có phương trình:
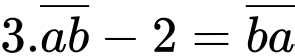

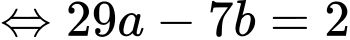
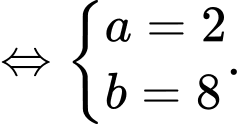
Đáp án: 28.
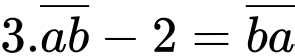

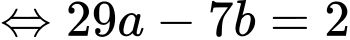
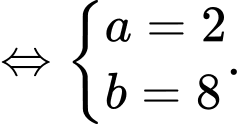
Đáp án: 28.
Câu 3 [289261]: Vẽ 12 đoạn thẳng bằng nhau lên giấy có thể tạo ra tối đa bao nhiêu hình vuông?
A, 
B, 
C, 
D, 
Từ 12 đoạn thẳng ta vẽ các đoạn giao với nhanh tạo thành các hình vuông con tạo thành ma trận 5x5.
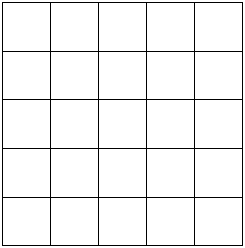
Hình vuông kích thước có:
có: 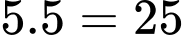 hình vuông
hình vuông
Hình vuông kích thước có :
có : 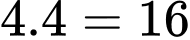 hình vuông
hình vuông
Hình vuông kích thước có:
có: 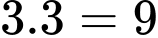 hình vuông
hình vuông
Hình vuông kích thước có:
có: 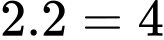 hình vuông
hình vuông
Hình vuông kích thước có:
có: 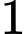 hình vuông
hình vuông
Từ 12 đoạn thẳng bằng nhau ta có thể vẽ tối đa: hình vuông.
hình vuông.
 Chọn đáp án B. Đáp án: B
Chọn đáp án B. Đáp án: B

Hình vuông kích thước
 có:
có: 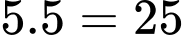 hình vuông
hình vuôngHình vuông kích thước
 có :
có : 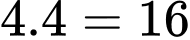 hình vuông
hình vuôngHình vuông kích thước
 có:
có: 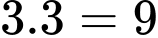 hình vuông
hình vuôngHình vuông kích thước
 có:
có: 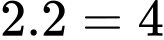 hình vuông
hình vuôngHình vuông kích thước
 có:
có: 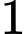 hình vuông
hình vuông
Từ 12 đoạn thẳng bằng nhau ta có thể vẽ tối đa:
 hình vuông.
hình vuông. Chọn đáp án B. Đáp án: B
Chọn đáp án B. Đáp án: B
Câu 4 [289917]: Cầu thang nhà ông T có 13 bậc, ông T vừa sửa lại 1 bậc cầu thang. Con trai cả nhà ông T bước lên bậc thứ nhất và lần lượt sau đó bước cách 2 bậc so với lần bước trước đó, thực hiện liên tiếp cho đến khi lên được tầng trên. Cậu con trai út nghịch ngợm bước đầu tiên bước đến bậc thứ ba rồi lại bước lùi 1 bậc sau đó lại bước tiếp 3 bậc, rồi lại lùi lại 1 bậc, thực hiện như thế cho đến khi lên được tầng trên. Biết rằng, cả 2 cậu con trai nhà ô T không ai bước vào bậc cầu thang vừa sửa. Hỏi bậc vừa sửa là bậc thứ?
A, 4.
B, 6.
C, 10.
D, 12.
Chọn đáp án D.
Người con trai cả bước vào các bậc: 1, 3, 5, 7, 9, 11, 13.
Người con trái út bước từ nền lên bậc 3, xuống 2 lên 5, xuống 4 lên 7, xuống 6 lên 9, xuống 8 lên 11, xuống 10 lên 13 Người con trai út bước vào các bậc: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13.
Người con trai út bước vào các bậc: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13.
Nên chỉ còn bậc thứ 12 là chưa ai bước đến. Mà, cả 2 cậu con trai nhà ô T không ai bước vào bậc cầu thang vừa sửa.
Suy ra, bậc 12 vừa được sửa. Đáp án: D
Người con trai cả bước vào các bậc: 1, 3, 5, 7, 9, 11, 13.
Người con trái út bước từ nền lên bậc 3, xuống 2 lên 5, xuống 4 lên 7, xuống 6 lên 9, xuống 8 lên 11, xuống 10 lên 13
 Người con trai út bước vào các bậc: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13.
Người con trai út bước vào các bậc: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13.Nên chỉ còn bậc thứ 12 là chưa ai bước đến. Mà, cả 2 cậu con trai nhà ô T không ai bước vào bậc cầu thang vừa sửa.
Suy ra, bậc 12 vừa được sửa. Đáp án: D
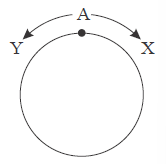
Câu 5 [290566]: Hai xe X và Y xuất phát lúc 7 giờ sáng từ vị trí ‘A’ nhưng di chuyển ngược chiều nhau dọc theo một đường tròn dài 100 km như hình vẽ dưới. Vận tốc của X gấp 1,5 lần vận tốc của Y tại điểm xuất phát ‘A’. Nếu lúc 8 giờ 15 sáng họ gặp nhau lần thứ nhất thì vận tốc trung bình của Y?

A, 32 km/h.
B, 40 km/h.
C, 50 km/h.
D, 60 km/h.
Chọn đáp án A.
Cách 1: Gọi vận tốc trung bình của Y là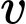 (
(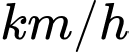 )
) 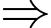 Vận tốc trung bình của X là
Vận tốc trung bình của X là 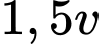 (
(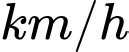 )
)
Từ 7 giờ sáng đến 8 giờ 15 sáng là 1 giờ 15 phút.
Đổi: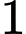 giờ
giờ  phút =
phút = 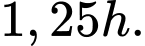
Ta có phương trình: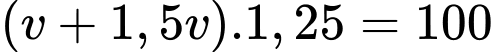
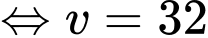 (
(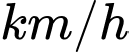 ).
).
Cách 2: Vì vận tốc của X gấp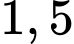 lần (
lần (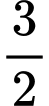 lần) vận tốc của Y tại điểm xuất phát
lần) vận tốc của Y tại điểm xuất phát 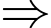 Quãng đường X đi được cũng gấp
Quãng đường X đi được cũng gấp 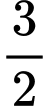 lần quãng đường Y đi được.
lần quãng đường Y đi được.
Ta chia đường tròn ra thành 5 phần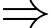 2 xe gặp nhau lần thứ nhất ở vị trí D (như hình vẽ).
2 xe gặp nhau lần thứ nhất ở vị trí D (như hình vẽ).
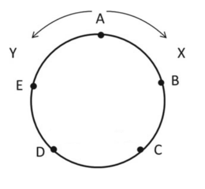
Quãng đường xe Y đi được là: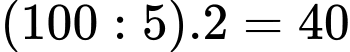 (
(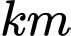 )
)
Từ 7 giờ sáng đến 8 giờ 15 sáng là 1 giờ 15 phút.
Đổi: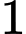 giờ
giờ  phút
phút 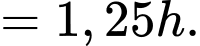
Vận tốc trung bình của Y là: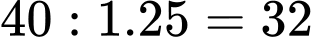 (
(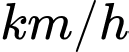 ). Đáp án: A
). Đáp án: A
Cách 1: Gọi vận tốc trung bình của Y là
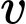 (
(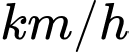 )
)  Vận tốc trung bình của X là
Vận tốc trung bình của X là 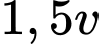 (
(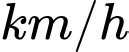 )
)Từ 7 giờ sáng đến 8 giờ 15 sáng là 1 giờ 15 phút.
Đổi:
 giờ
giờ  phút =
phút = 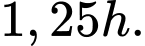
Ta có phương trình:
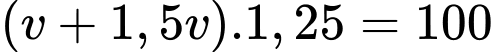
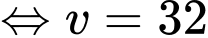 (
(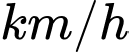 ).
).Cách 2: Vì vận tốc của X gấp
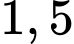 lần (
lần (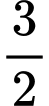 lần) vận tốc của Y tại điểm xuất phát
lần) vận tốc của Y tại điểm xuất phát 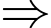 Quãng đường X đi được cũng gấp
Quãng đường X đi được cũng gấp 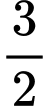 lần quãng đường Y đi được.
lần quãng đường Y đi được.Ta chia đường tròn ra thành 5 phần
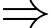 2 xe gặp nhau lần thứ nhất ở vị trí D (như hình vẽ).
2 xe gặp nhau lần thứ nhất ở vị trí D (như hình vẽ).
Quãng đường xe Y đi được là:
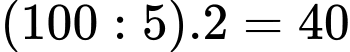 (
(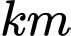 )
)Từ 7 giờ sáng đến 8 giờ 15 sáng là 1 giờ 15 phút.
Đổi:
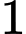 giờ
giờ  phút
phút 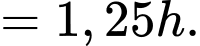
Vận tốc trung bình của Y là:
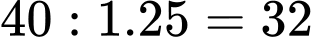 (
(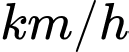 ). Đáp án: A
). Đáp án: A
Câu 6 [379667]: Hai cây nến có chiều dài khác nhau, cháy với tốc độ khác nhau. Mỗi ngọn nến cháy đúng một giờ. Chúng ta có thể đo khoảng thời gian nào sau đây bằng cách đốt những ngọn nến này?
A, 20 phút.
B, 10 phút.
C, 15 phút.
D, 24 phút.
Chọn đáp án C.
Đầu tiên, với cây nến thứ nhất ta đốt từ hai đầu và cây nến thứ hai được đốt từ một đầu. Sau 30 phút cây nến thứ nhất cháy hết và cây nến thứ hai cháy được một nửa.
Ta tiếp tục đốt cây nến thứ hai từ hai đầu Ta có thể do khoảng thời gian 15 phút. Đáp án: C
Ta có thể do khoảng thời gian 15 phút. Đáp án: C
Đầu tiên, với cây nến thứ nhất ta đốt từ hai đầu và cây nến thứ hai được đốt từ một đầu. Sau 30 phút cây nến thứ nhất cháy hết và cây nến thứ hai cháy được một nửa.
Ta tiếp tục đốt cây nến thứ hai từ hai đầu
 Ta có thể do khoảng thời gian 15 phút. Đáp án: C
Ta có thể do khoảng thời gian 15 phút. Đáp án: C
Câu 7 [379669]: Trong một hộp có 34 viên bi, hai người bạn An và Bình chơi một trò chơi, mỗi người lấy ra 2 hoặc 3 viên bi từ hộp đó. Người lấy ra viên bi cuối cùng là người thua cuộc. Vậy An nên lấy ra bao nhiêu viên bi để chắc chắn bạn đấy thắng nếu An là người lấy bi đầu tiên?
A, 2 viên.
B, 3 viên.
C, 2 hoặc 3 viên.
D, An không thể thắng.
Chọn đáp án B.
An nên lấy ra sao cho luôn còn lại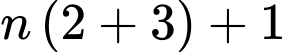 viên bi, sao cho Bình lấy được 3 viên bi thì An lấy được 2 viên bi và ngược lại.
viên bi, sao cho Bình lấy được 3 viên bi thì An lấy được 2 viên bi và ngược lại.
 Cần phải còn lại 30 + 1 viên bi
Cần phải còn lại 30 + 1 viên bi  An nên lấy 3 viên bi trong lần lấy đầu tiên. Đáp án: B
An nên lấy 3 viên bi trong lần lấy đầu tiên. Đáp án: B
An nên lấy ra sao cho luôn còn lại
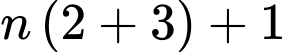 viên bi, sao cho Bình lấy được 3 viên bi thì An lấy được 2 viên bi và ngược lại.
viên bi, sao cho Bình lấy được 3 viên bi thì An lấy được 2 viên bi và ngược lại. Cần phải còn lại 30 + 1 viên bi
Cần phải còn lại 30 + 1 viên bi  An nên lấy 3 viên bi trong lần lấy đầu tiên. Đáp án: B
An nên lấy 3 viên bi trong lần lấy đầu tiên. Đáp án: B
Câu 8 [583992]: Có hai vòng tròn có bán kính lần lượt là  và
và  Sự chêch lệch số vòng quay nếu quay vòng tròn nhỏ bên ngoài và bên trong hết một vòng tròn lớn là
Sự chêch lệch số vòng quay nếu quay vòng tròn nhỏ bên ngoài và bên trong hết một vòng tròn lớn là
 và
và  Sự chêch lệch số vòng quay nếu quay vòng tròn nhỏ bên ngoài và bên trong hết một vòng tròn lớn là
Sự chêch lệch số vòng quay nếu quay vòng tròn nhỏ bên ngoài và bên trong hết một vòng tròn lớn là A, 0.
B, 1.
C, 2.
D, 3.
Câu 9 [583993]: Một chai soda có giá 1 đô. Sau khi uống, hai chai rỗng sẽ được đổi lấy một chai soda. Bạn có thể uống nhiều nhất bao nhiêu chai soda nếu bạn có 20 đô?
A, 20 chai.
B, 30 chai.
C, 39 chai.
D, 40 chai.
Câu 10 [290967]: Có 4 người và 1 đèn pin muốn qua sông phải đi qua 1 cây cầu. Biết cây cầu chỉ đi 1 lần tối đa 2 người, phải có đèn pin nên phải đi đi về về. A đi qua cầu hết 1 phút, B hết 2 phút, C 5 phút, D 10 phút. Hai người đi cùng nhau thì phải đi với tốc độ của người đi chậm hơn. Hỏi mất ít nhất bao nhiêu phút để tất cả đều qua được sông?
A, 16.
B, 17.
C, 18.
D, 19.
Chọn đáp án B.
Để mất ít thời gian nhất ta sẽ cho 4 người đi như sau:

Tổng thời gian: phút. Đáp án: B
phút. Đáp án: B
Để mất ít thời gian nhất ta sẽ cho 4 người đi như sau:

Tổng thời gian:
 phút. Đáp án: B
phút. Đáp án: B
Câu 11 [289508]: Ở đất nước nọ, khi di chuyển từ thành này qua thành khác sẽ có lính gác các cổng thành kiểm tra. Ông Quỳnh là một thương nhân buôn rượu khôn khéo. Khi qua các cổng, ông sẽ hối lộ lính canh bằng cách đưa cho họ một chai rượu trong mỗi thùng hàng. Biết mỗi thùng hàng chứa được tối đa 15 chai rượu. Nếu phải vượt qua 10 cổng thành và cung cấp 50 chai rượu cho khách hàng thì lúc xuất phát ông cần mang tối thiểu bao nhiêu chai rượu?
A, 99.
B, 60.
C, 101.
D, 107.
Giải quyết bài toán bằng tư duy ngược:
Vì ông Quỳnh cần cung cấp 50 chai rượu nên ta sẽ khai thác từ con số 50 trở ra.
Do phải vượt qua 10 cổng thành và khi qua các cổng, ông sẽ hối lộ lính canh bằng cách đưa cho họ một chai rượu trong mỗi thùng hàng nên để ông Quỳnh mang ít nhất số chai rượu thì đồng nghĩa với việc ông sẽ cho lính canh số rượu ít nhất.
Có nghĩa ra: Khi qua mỗi cổng, ông sẽ phải bỏ số chai rượu từ thùng ít hơn sang các thùng nhiều hơn để làm đầy các thùng đó (đồng nghĩa với việc khi qua các cổng thành sau số chai rượu hối lộ lính canh sẽ giảm).
Vì “số chai rượu cần cung cấp là 50 chai mà 1 thùng chứa tối đa được 15 chai”
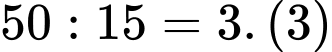 (vậy cần tối thiểu 4 thùng để chứa, 3 thùng 15 chai và 1 thùng 5 chai).
(vậy cần tối thiểu 4 thùng để chứa, 3 thùng 15 chai và 1 thùng 5 chai).
Trước khi qua cổng thành số 10 số chai rượu ông Quỳnh mang theo là: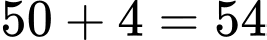 chai (do cần tối thiểu 4 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 10: 4 chai)
chai (do cần tối thiểu 4 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 10: 4 chai)
Trước khi qua cổng thành số 9 số chai rượu ông Quỳnh mang theo là: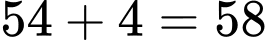 chai (do cần tối thiểu 4 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 9: 4 chai)
chai (do cần tối thiểu 4 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 9: 4 chai)
Trước khi qua cổng thành số 8 số chai rượu ông Quỳnh mang theo là: chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 8: 4+1 chai)
chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 8: 4+1 chai)
Trước khi qua cổng thành số 7 số chai rượu ông Quỳnh mang theo là: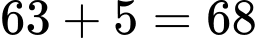 chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 7: 5 chai)
chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 7: 5 chai)
Trước khi qua cổng thành số 6 số chai rượu ông Quỳnh mang theo là: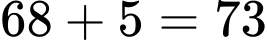 chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 6: 5 chai)
chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 6: 5 chai)
Trước khi qua cổng thành số 5 số chai rượu ông Quỳnh mang theo là: chai (do cần tối thiểu 6 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 5: 5+1 chai)
chai (do cần tối thiểu 6 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 5: 5+1 chai)
Trước khi qua cổng thành số 4 số chai rượu ông Quỳnh mang theo là: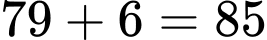 chai (do cần tối thiểu 6 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 5: 6 chai)
chai (do cần tối thiểu 6 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 5: 6 chai)
Trước khi qua cổng thành số 3 số chai rượu ông Quỳnh mang theo là: chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)
chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)
Trước khi qua cổng thành số 2 số chai rượu ông Quỳnh mang theo là: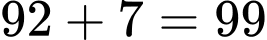 chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)
chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)
Trước khi qua cổng thành số 1 số chai rượu ông Quỳnh mang theo là: chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)
chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)
Minh họa:
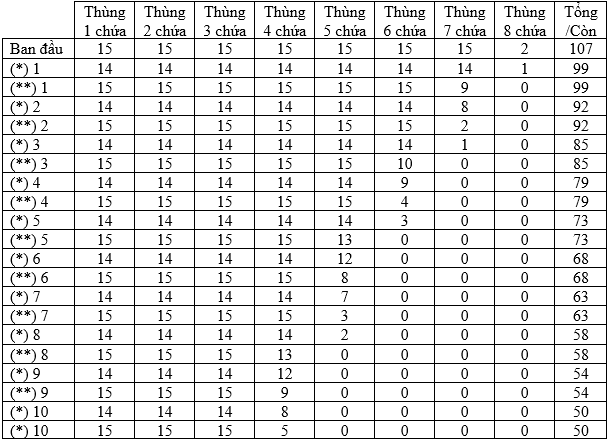
(*): Số chai rượu trong mỗi thùng khi qua cổng thành số
(**): Ông Quỳnh xếp lại số chai rượu vào các thùng khi ở thành số Đáp án: D
Vì ông Quỳnh cần cung cấp 50 chai rượu nên ta sẽ khai thác từ con số 50 trở ra.
Do phải vượt qua 10 cổng thành và khi qua các cổng, ông sẽ hối lộ lính canh bằng cách đưa cho họ một chai rượu trong mỗi thùng hàng nên để ông Quỳnh mang ít nhất số chai rượu thì đồng nghĩa với việc ông sẽ cho lính canh số rượu ít nhất.
Có nghĩa ra: Khi qua mỗi cổng, ông sẽ phải bỏ số chai rượu từ thùng ít hơn sang các thùng nhiều hơn để làm đầy các thùng đó (đồng nghĩa với việc khi qua các cổng thành sau số chai rượu hối lộ lính canh sẽ giảm).
Vì “số chai rượu cần cung cấp là 50 chai mà 1 thùng chứa tối đa được 15 chai”
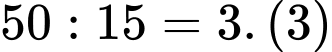 (vậy cần tối thiểu 4 thùng để chứa, 3 thùng 15 chai và 1 thùng 5 chai).
(vậy cần tối thiểu 4 thùng để chứa, 3 thùng 15 chai và 1 thùng 5 chai).Trước khi qua cổng thành số 10 số chai rượu ông Quỳnh mang theo là:
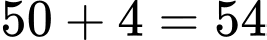 chai (do cần tối thiểu 4 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 10: 4 chai)
chai (do cần tối thiểu 4 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 10: 4 chai)Trước khi qua cổng thành số 9 số chai rượu ông Quỳnh mang theo là:
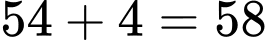 chai (do cần tối thiểu 4 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 9: 4 chai)
chai (do cần tối thiểu 4 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 9: 4 chai)Trước khi qua cổng thành số 8 số chai rượu ông Quỳnh mang theo là:
 chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 8: 4+1 chai)
chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 8: 4+1 chai)Trước khi qua cổng thành số 7 số chai rượu ông Quỳnh mang theo là:
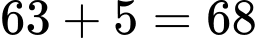 chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 7: 5 chai)
chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 7: 5 chai)Trước khi qua cổng thành số 6 số chai rượu ông Quỳnh mang theo là:
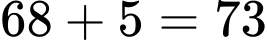 chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 6: 5 chai)
chai (do cần tối thiểu 5 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 6: 5 chai)Trước khi qua cổng thành số 5 số chai rượu ông Quỳnh mang theo là:
 chai (do cần tối thiểu 6 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 5: 5+1 chai)
chai (do cần tối thiểu 6 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 5: 5+1 chai)Trước khi qua cổng thành số 4 số chai rượu ông Quỳnh mang theo là:
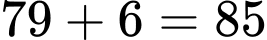 chai (do cần tối thiểu 6 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 5: 6 chai)
chai (do cần tối thiểu 6 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 5: 6 chai)Trước khi qua cổng thành số 3 số chai rượu ông Quỳnh mang theo là:
 chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)
chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)Trước khi qua cổng thành số 2 số chai rượu ông Quỳnh mang theo là:
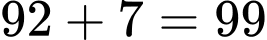 chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)
chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)Trước khi qua cổng thành số 1 số chai rượu ông Quỳnh mang theo là:
 chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)
chai (do cần tối thiểu 7 thùng để chứa nên phải hối lộ lính canh ở cổng thành số 3: 7 chai)Minh họa:

(*): Số chai rượu trong mỗi thùng khi qua cổng thành số
(**): Ông Quỳnh xếp lại số chai rượu vào các thùng khi ở thành số Đáp án: D
Câu 12 [379671]: A, B, C, D và E là 5 chữ số khác nhau và khác 0, thỏa mãn 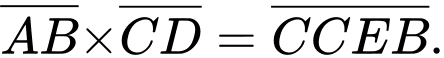 Biết rằng
Biết rằng 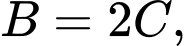
 và
và 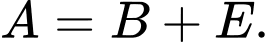 Giá trị của A là
Giá trị của A là
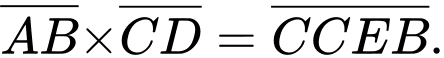 Biết rằng
Biết rằng 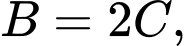
 và
và 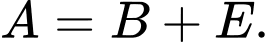 Giá trị của A là
Giá trị của A là A, 1.
B, 2.
C, 7.
D, 4.
Chọn đáp án C.
Vì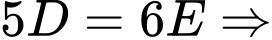
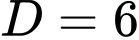 và
và 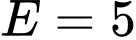
Vì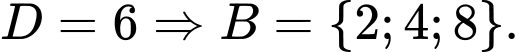
Vì loại giá trị
loại giá trị 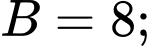
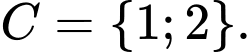
Kết hợp với dữ kiện: A, B, C, D và E là 5 chữ số khác nhau và khác 0 và các phép thử ta có duy nhất 1 trường hợp thỏa mãn: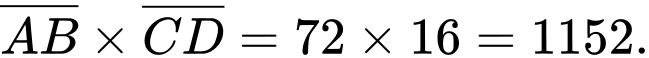
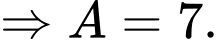 Đáp án: C
Đáp án: C
Vì
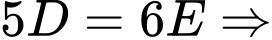
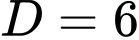 và
và 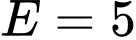
Vì
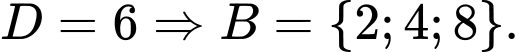
Vì
 loại giá trị
loại giá trị 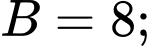
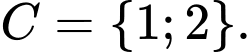
Kết hợp với dữ kiện: A, B, C, D và E là 5 chữ số khác nhau và khác 0 và các phép thử ta có duy nhất 1 trường hợp thỏa mãn:
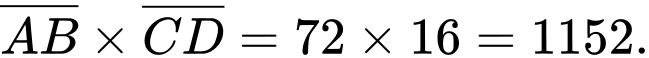
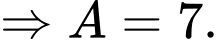 Đáp án: C
Đáp án: C
Câu 13 [291211]: Mỗi chữ cái A, B và C là một chữ số khác nhau từ 1 đến 9. Tổng giá trị A, B, C lớn nhất là bao nhiêu nếu 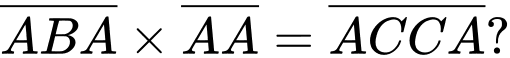
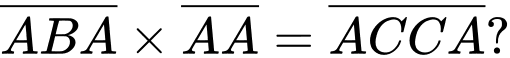
A, 27.
B, 18.
C, 9.
D, 15.
Chọn đáp án B.
Vì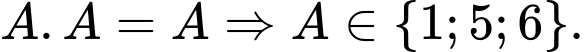
TH1: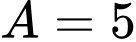
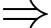 tích
tích 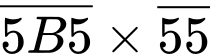 có 5 chữ số. (mâu thuẫn với dữ kiện đề bài).
có 5 chữ số. (mâu thuẫn với dữ kiện đề bài).
TH2: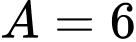
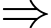 tích
tích 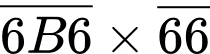 có 5 chữ số. (mâu thuẫn với dữ kiện đề bài).
có 5 chữ số. (mâu thuẫn với dữ kiện đề bài).
TH3: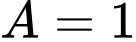
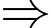 tích:
tích: 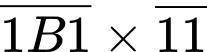 có 4 chữ số. (thỏa mãn).
có 4 chữ số. (thỏa mãn).
Mà, mỗi chữ cái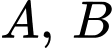 và
và  là một chữ số khác nhau từ 1 đến 9 nên
là một chữ số khác nhau từ 1 đến 9 nên 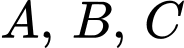 lớn nhất là:
lớn nhất là: 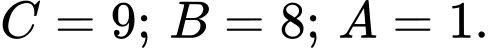
Tổng giá trị của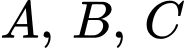 là:
là: 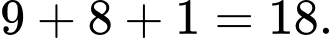 Đáp án: B
Đáp án: B
Vì
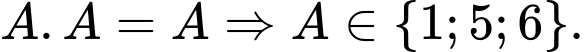
TH1:
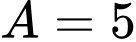
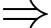 tích
tích 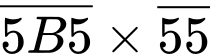 có 5 chữ số. (mâu thuẫn với dữ kiện đề bài).
có 5 chữ số. (mâu thuẫn với dữ kiện đề bài).TH2:
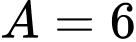
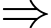 tích
tích 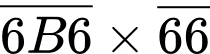 có 5 chữ số. (mâu thuẫn với dữ kiện đề bài).
có 5 chữ số. (mâu thuẫn với dữ kiện đề bài).TH3:
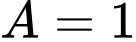
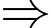 tích:
tích: 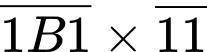 có 4 chữ số. (thỏa mãn).
có 4 chữ số. (thỏa mãn).Mà, mỗi chữ cái
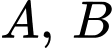 và
và  là một chữ số khác nhau từ 1 đến 9 nên
là một chữ số khác nhau từ 1 đến 9 nên 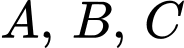 lớn nhất là:
lớn nhất là: 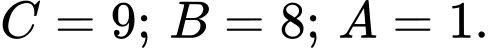
Tổng giá trị của
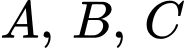 là:
là: 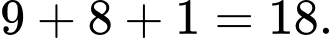 Đáp án: B
Đáp án: B
Câu 14 [290505]: 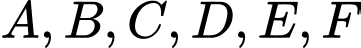 và
và  là 7 chữ số khác nhau và khác 0, thỏa mãn
là 7 chữ số khác nhau và khác 0, thỏa mãn 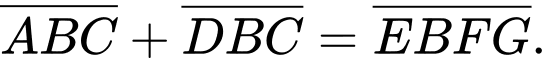 Biết rằng
Biết rằng  là số chẵn,
là số chẵn,  lớn hơn 4,
lớn hơn 4,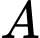 lớn hơn
lớn hơn 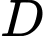 và
và 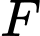 là số lẻ lớn hơn 5. Giá trị của
là số lẻ lớn hơn 5. Giá trị của 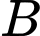 là
là
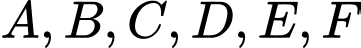 và
và  là 7 chữ số khác nhau và khác 0, thỏa mãn
là 7 chữ số khác nhau và khác 0, thỏa mãn 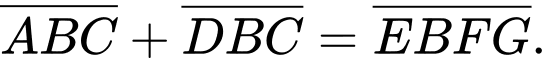 Biết rằng
Biết rằng  là số chẵn,
là số chẵn,  lớn hơn 4,
lớn hơn 4,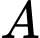 lớn hơn
lớn hơn 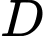 và
và 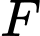 là số lẻ lớn hơn 5. Giá trị của
là số lẻ lớn hơn 5. Giá trị của 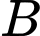 là
là A, 3.
B, 4.
C, 7.
D, 8.
Chọn đáp án A.
Ta có biểu thức sau:
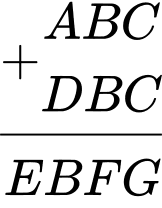
Dựa vào dữ kiện:
 là số chẵn
là số chẵn 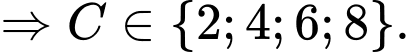 (1)
(1)
Mà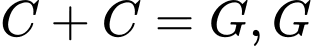 lớn hơn 4
lớn hơn 4 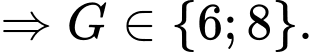 (2)
(2)
Từ (1) và (2) suy ra: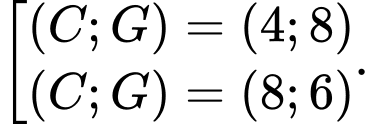
Kết hợp với dữ kiện: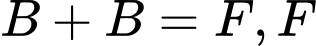 là số lẻ lớn hơn 5
là số lẻ lớn hơn 5 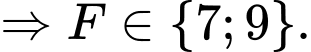
Suy ra: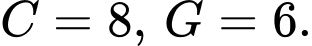
TH1: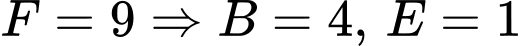 . Ta có:
. Ta có: 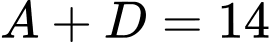 và
và 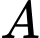 lớn hơn
lớn hơn 
TH1.1: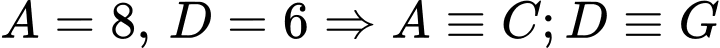 (không thỏa mãn, mẫu thuẫn với dữ kiện:
(không thỏa mãn, mẫu thuẫn với dữ kiện: 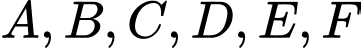 và
và  là 7 chữ số khác nhau và khác 0 ).
là 7 chữ số khác nhau và khác 0 ).
TH1.2: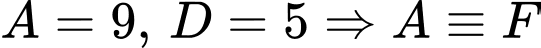 (không thỏa mãn, mẫu thuẫn với dữ kiện:
(không thỏa mãn, mẫu thuẫn với dữ kiện: 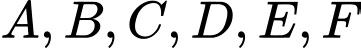 và
và  là 7 chữ số khác nhau và khác 0 ).
là 7 chữ số khác nhau và khác 0 ).
TH2: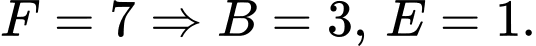 Ta có:
Ta có: 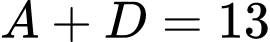 và A lớn hơn D.
và A lớn hơn D.
TH2.1: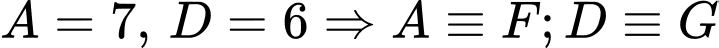 (không thỏa mãn, mẫu thuẫn với dữ kiện:
(không thỏa mãn, mẫu thuẫn với dữ kiện: 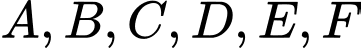 và
và  là 7 chữ số khác nhau và khác 0 ).
là 7 chữ số khác nhau và khác 0 ).
TH2.2: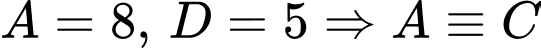 (không thỏa mãn, mẫu thuẫn với dữ kiện:
(không thỏa mãn, mẫu thuẫn với dữ kiện: 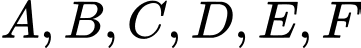 và
và  là 7 chữ số khác nhau và khác 0 ).
là 7 chữ số khác nhau và khác 0 ).
TH2.3: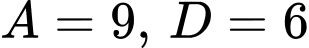 (thỏa mãn).
(thỏa mãn).
Phép tính thỏa mãn:
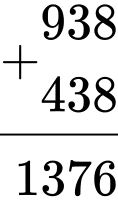
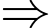 Giá trị của B là: 3 Đáp án: A
Giá trị của B là: 3 Đáp án: A
Ta có biểu thức sau:
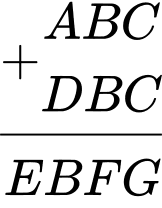
Dựa vào dữ kiện:
 là số chẵn
là số chẵn 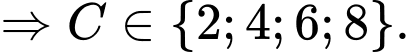 (1)
(1)Mà
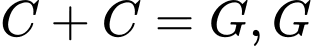 lớn hơn 4
lớn hơn 4 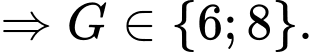 (2)
(2)Từ (1) và (2) suy ra:
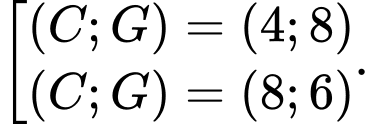
Kết hợp với dữ kiện:
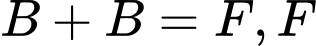 là số lẻ lớn hơn 5
là số lẻ lớn hơn 5 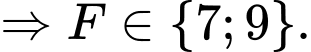
Suy ra:
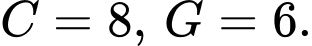
TH1:
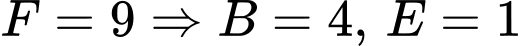 . Ta có:
. Ta có: 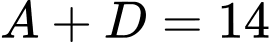 và
và 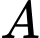 lớn hơn
lớn hơn 
TH1.1:
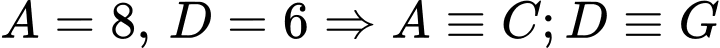 (không thỏa mãn, mẫu thuẫn với dữ kiện:
(không thỏa mãn, mẫu thuẫn với dữ kiện: 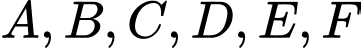 và
và  là 7 chữ số khác nhau và khác 0 ).
là 7 chữ số khác nhau và khác 0 ).TH1.2:
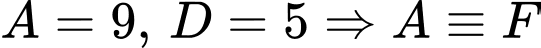 (không thỏa mãn, mẫu thuẫn với dữ kiện:
(không thỏa mãn, mẫu thuẫn với dữ kiện: 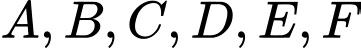 và
và  là 7 chữ số khác nhau và khác 0 ).
là 7 chữ số khác nhau và khác 0 ).TH2:
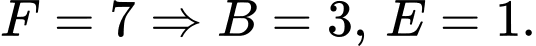 Ta có:
Ta có: 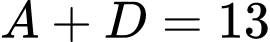 và A lớn hơn D.
và A lớn hơn D.TH2.1:
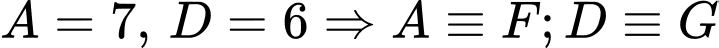 (không thỏa mãn, mẫu thuẫn với dữ kiện:
(không thỏa mãn, mẫu thuẫn với dữ kiện: 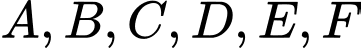 và
và  là 7 chữ số khác nhau và khác 0 ).
là 7 chữ số khác nhau và khác 0 ).TH2.2:
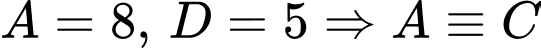 (không thỏa mãn, mẫu thuẫn với dữ kiện:
(không thỏa mãn, mẫu thuẫn với dữ kiện: 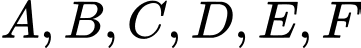 và
và  là 7 chữ số khác nhau và khác 0 ).
là 7 chữ số khác nhau và khác 0 ).TH2.3:
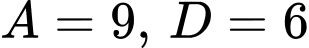 (thỏa mãn).
(thỏa mãn).Phép tính thỏa mãn:
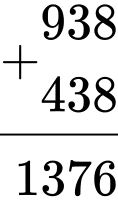
 Giá trị của B là: 3 Đáp án: A
Giá trị của B là: 3 Đáp án: A
Câu 15 [289956]: 4 đội bóng A, B, C, D thi đấu vòng tròn một lượt. Thắng được 3 điểm, hòa được 1 điểm và thua không được điểm nào. Kết quả điểm các đội sau vòng đấu như sau: 5 điểm, 1 điểm, x điểm và 6 điểm. Giá trị của x là
A, 2.
B, 3.
C, 4.
D, 5.
Chọn đáp án C.
Dựa vào dữ kiện:
• Thắng được 3 điểm, hòa được 1 điểm và thua không được điểm nào.
• 4 đội bóng thi đấu vòng tròn một lượt mỗi đội phải đấu 3 trận.
mỗi đội phải đấu 3 trận.
• Kết quả của 1 đội nào đó là 5 điểm
Đội đó sẽ có: 1 trận thắng,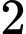 trận hòa.
trận hòa.
• Kết quả của 1 đội nào đó là 1 điểm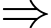 Đội đó sẽ có: 1 trận hòa, 2 trận thua.
Đội đó sẽ có: 1 trận hòa, 2 trận thua.
• Kết quả của 1 đội nào đó là 6 điểm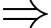 Đội đó sẽ có: 2 trận thắng, 1 trận thua.
Đội đó sẽ có: 2 trận thắng, 1 trận thua.
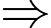 Thiếu 1 trận thắng (do đội có 1 điểm mới thua đội có 6 điểm, cần 1 trận thắng để đội có 1 điểm thua); thiếu 1 trận hòa (do đội có 5 điểm mới hòa 1 trận với đội có 1 điểm nên cần thêm 1 trận hòa) và thiếu 1 trận thua (do đội 6 điểm mới thắng đội có 1 điểm nên cần thắng thêm 1 trận).
Thiếu 1 trận thắng (do đội có 1 điểm mới thua đội có 6 điểm, cần 1 trận thắng để đội có 1 điểm thua); thiếu 1 trận hòa (do đội có 5 điểm mới hòa 1 trận với đội có 1 điểm nên cần thêm 1 trận hòa) và thiếu 1 trận thua (do đội 6 điểm mới thắng đội có 1 điểm nên cần thắng thêm 1 trận).
 Điểm của đội còn lại là:
Điểm của đội còn lại là: 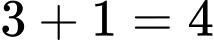 điểm. Đáp án: C
điểm. Đáp án: C
Dựa vào dữ kiện:
• Thắng được 3 điểm, hòa được 1 điểm và thua không được điểm nào.
• 4 đội bóng thi đấu vòng tròn một lượt
 mỗi đội phải đấu 3 trận.
mỗi đội phải đấu 3 trận.• Kết quả của 1 đội nào đó là 5 điểm
Đội đó sẽ có: 1 trận thắng,
 trận hòa.
trận hòa.• Kết quả của 1 đội nào đó là 1 điểm
 Đội đó sẽ có: 1 trận hòa, 2 trận thua.
Đội đó sẽ có: 1 trận hòa, 2 trận thua.• Kết quả của 1 đội nào đó là 6 điểm
 Đội đó sẽ có: 2 trận thắng, 1 trận thua.
Đội đó sẽ có: 2 trận thắng, 1 trận thua. Thiếu 1 trận thắng (do đội có 1 điểm mới thua đội có 6 điểm, cần 1 trận thắng để đội có 1 điểm thua); thiếu 1 trận hòa (do đội có 5 điểm mới hòa 1 trận với đội có 1 điểm nên cần thêm 1 trận hòa) và thiếu 1 trận thua (do đội 6 điểm mới thắng đội có 1 điểm nên cần thắng thêm 1 trận).
Thiếu 1 trận thắng (do đội có 1 điểm mới thua đội có 6 điểm, cần 1 trận thắng để đội có 1 điểm thua); thiếu 1 trận hòa (do đội có 5 điểm mới hòa 1 trận với đội có 1 điểm nên cần thêm 1 trận hòa) và thiếu 1 trận thua (do đội 6 điểm mới thắng đội có 1 điểm nên cần thắng thêm 1 trận). Điểm của đội còn lại là:
Điểm của đội còn lại là: 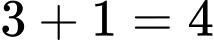 điểm. Đáp án: C
điểm. Đáp án: C
Câu 16 [379672]: Trong một giải đấu, sáu đội tuyển thi đấu vòng tròn một lượt. Ở mỗi trận đấu, đội thắng sẽ được hai điểm, đội thua sẽ không có điểm và nếu hòa thì mỗi đội được một điểm. Điểm của sáu đội A, B, C, D, E và F lần lượt là 9, 8, 7, 3, 2 và 1 điểm. Có đúng hai trận hòa. Vậy đội D hòa với đội nào sau đây?
A, Đội A.
B, Đội C.
C, Đội F.
D, Chưa đủ dữ kiện.
Dựa vào dữ kiện:
• Trong một giải đấu, mỗi bảng có 6 đội và các đội phải thi đấu vòng trong một lượt Mỗi đội thi đấu với nhau 1 lần (mỗi đội thi đấu 5 trận).
Mỗi đội thi đấu với nhau 1 lần (mỗi đội thi đấu 5 trận).
• Trong trận đấu giữa hai đội bất kỳ, đội thắng được hai điểm, đội thua không có điểm và nếu hòa thì mỗi đội được một điểm.
• Điểm của A, B, C, D, E và F là lần lượt là 9, 8, 7, 3, 2 và 1 điểm A, C, D và F có số điểm lẻ nên mỗi đội có 1 trận hòa.
A, C, D và F có số điểm lẻ nên mỗi đội có 1 trận hòa.
• Có đúng hai trận hòa.
Bảng minh họa:
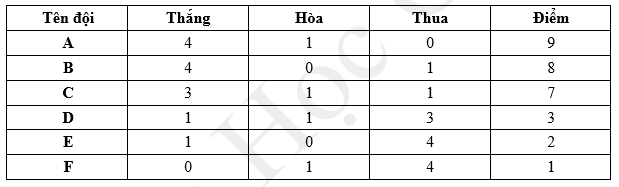
Nếu D có một trận hòa với A hoặc C, thì F cũng phải có một trận hòa với A hoặc C Cả D và E đều thắng F
Cả D và E đều thắng F  D và DE thi đấu với nhau tạo ra mâu thuẫn vì không có trường hợp xảy ra
D và DE thi đấu với nhau tạo ra mâu thuẫn vì không có trường hợp xảy ra  D có một trận hòa với F.
D có một trận hòa với F. Chọn đáp án C. Đáp án: C
Chọn đáp án C. Đáp án: C
• Trong một giải đấu, mỗi bảng có 6 đội và các đội phải thi đấu vòng trong một lượt
 Mỗi đội thi đấu với nhau 1 lần (mỗi đội thi đấu 5 trận).
Mỗi đội thi đấu với nhau 1 lần (mỗi đội thi đấu 5 trận).• Trong trận đấu giữa hai đội bất kỳ, đội thắng được hai điểm, đội thua không có điểm và nếu hòa thì mỗi đội được một điểm.
• Điểm của A, B, C, D, E và F là lần lượt là 9, 8, 7, 3, 2 và 1 điểm
 A, C, D và F có số điểm lẻ nên mỗi đội có 1 trận hòa.
A, C, D và F có số điểm lẻ nên mỗi đội có 1 trận hòa.• Có đúng hai trận hòa.
Bảng minh họa:

Nếu D có một trận hòa với A hoặc C, thì F cũng phải có một trận hòa với A hoặc C
 Cả D và E đều thắng F
Cả D và E đều thắng F  D và DE thi đấu với nhau tạo ra mâu thuẫn vì không có trường hợp xảy ra
D và DE thi đấu với nhau tạo ra mâu thuẫn vì không có trường hợp xảy ra  D có một trận hòa với F.
D có một trận hòa với F. Chọn đáp án C. Đáp án: C
Chọn đáp án C. Đáp án: C
Câu 17 [290203]: Một vận động viên thi bắn súng, vận động viên đã bắn hơn 11 viên và đều bắn trúng vào các vòng 8, 9, 10 điểm. Tổng số điểm là 100. Số viên 9 điểm chênh lệch với số viên 10 điểm là
A, 1 viên.
B, 2 viên.
C, 3 viên.
D, 4 viên.
Chọn đáp án A.
Vì vận động viên đã bắn hơn 11 viên và đều bắn súng vào các vòng 8, 9, 10 điểm nhưng tổng số điểm là 100 vận đông viên đã bắn 12 viên (Nếu bắn 13 viên thì tổng số điểm ít nhất là:
vận đông viên đã bắn 12 viên (Nếu bắn 13 viên thì tổng số điểm ít nhất là: 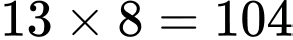 điểm không thỏa mãn).
điểm không thỏa mãn).
Nếu tất cả đều trúng vòng 8 điểm thì số điểm đạt được là: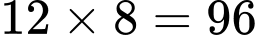 (điểm).
(điểm).
So với 100 điểm thì còn thiếu :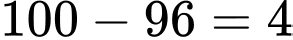 (điểm).
(điểm).
Phân tích: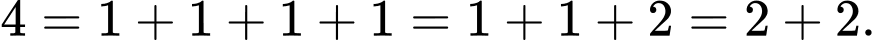
Vì tất cả các vòng đều có viên trúng nên phải thay 1 viên vòng 8 bằng 1 viên vòng 10 và 2 viên vòng 8 bằng 2 viên vòng 9.
Vậy người đó đã bắn 12 viên trong đó có 9 viên trúng vòng 8, có 2 viên trúng vòng 9 và 1 viên trúng vòng 10.
Số viên 9 điểm và số viên điểm điểm 10 chênh nhau 1 viên. Đáp án: A
Vì vận động viên đã bắn hơn 11 viên và đều bắn súng vào các vòng 8, 9, 10 điểm nhưng tổng số điểm là 100
 vận đông viên đã bắn 12 viên (Nếu bắn 13 viên thì tổng số điểm ít nhất là:
vận đông viên đã bắn 12 viên (Nếu bắn 13 viên thì tổng số điểm ít nhất là: 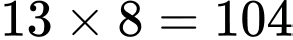 điểm không thỏa mãn).
điểm không thỏa mãn).Nếu tất cả đều trúng vòng 8 điểm thì số điểm đạt được là:
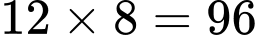 (điểm).
(điểm).So với 100 điểm thì còn thiếu :
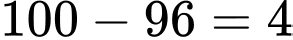 (điểm).
(điểm).Phân tích:
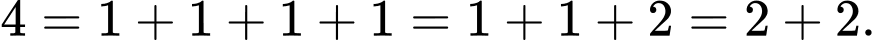
Vì tất cả các vòng đều có viên trúng nên phải thay 1 viên vòng 8 bằng 1 viên vòng 10 và 2 viên vòng 8 bằng 2 viên vòng 9.
Vậy người đó đã bắn 12 viên trong đó có 9 viên trúng vòng 8, có 2 viên trúng vòng 9 và 1 viên trúng vòng 10.
Số viên 9 điểm và số viên điểm điểm 10 chênh nhau 1 viên. Đáp án: A
Câu 18 [583994]: Nhân dịp khai trương, cửa hàng có một chương trình tri ân dành cho 50 người đầu tiên đứng xếp hàng (theo thứ tự từ 1 đến 50). Chủ cửa hàng sẽ tặng cho người cuối cùng một món quà và thể thức cuộc chơi như sau. Chủ cửa hàng nói “ Các khách hàng số lẻ sẽ bị loại”. Các khách hàng còn lại sẽ sắp xếp lại (từ 1 đến hết), cuộc chơi sẽ dừng khi tìm được người cuối cùng. Vậy người may mắn nhận được quà thì ban đầu họ đứng số mấy?
A, 25.
B, 32.
C, 22.
D, 28.
Chọn đáp án B.
Ban đầu có 50 người, đánh số từ 1 đến 50.
Đầu tiên, những người có vị trí là số lẻ sẽ bị loại bỏ.
Những người còn lại có số thứ tự: 2, 4, 6, 8, ..., 50 (tức là còn lại 25 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 4, 8, 12, ..., 48 (tức là còn lại 12 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 8, 16, 24, 32, 40, 48 (tức là còn lại 6 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 16, 32, 48 (còn lại 3 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 32 (chỉ còn lại 1 người).
Vậy người may mắn nhận được quà ban đầu đứng vị trí số 32. Đáp án: B
Ban đầu có 50 người, đánh số từ 1 đến 50.
Đầu tiên, những người có vị trí là số lẻ sẽ bị loại bỏ.
Những người còn lại có số thứ tự: 2, 4, 6, 8, ..., 50 (tức là còn lại 25 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 4, 8, 12, ..., 48 (tức là còn lại 12 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 8, 16, 24, 32, 40, 48 (tức là còn lại 6 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 16, 32, 48 (còn lại 3 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 32 (chỉ còn lại 1 người).
Vậy người may mắn nhận được quà ban đầu đứng vị trí số 32. Đáp án: B
Câu 19 [379673]: Trên đường Mạnh đi từ nhà đến công ty (C) có điểm A đang sửa chữa nên không thể đi qua A. Biết rằng toàn bộ cung đường theo bản đồ từ dưới lên trên và từ phải qua trái là đường một chiều vì vậy Mạnh chỉ được phép đi lên hoặc đi sang phải. Vậy Mạnh có bao nhiêu cách đến công ty?
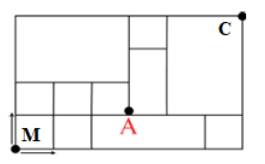

A, 12.
B, 15.
C, 24.
D, 25.
Số cách Mạnh đến công ty là: 15 cách.
Minh họa:
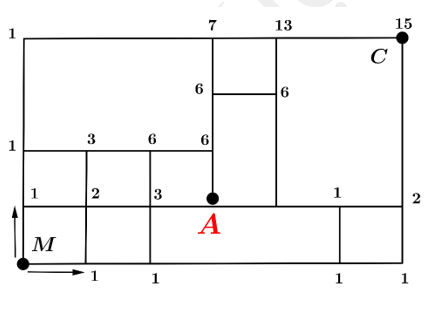
Chọn đáp án B. Đáp án: B
Minh họa:

Chọn đáp án B. Đáp án: B
Câu 20 [289676]: Trong tiết mục biểu diễn của rạp xiếc, có 6 con chim khác nhau đang giữ thăng bằng như hình vẽ. Biết rằng, trọng lượng của các con chim nặng từ 2 đến 9 kg và không con nào có số cân nặng bằng nhau. Cân nặng của các con chim đều là các số tự nhiên. Con chim đứng ở B nặng bao nhiêu kg?


A, 2.
B, 5.
C, 6.
D, 7.
Chọn đáp án C.
Dựa vào hình vẽ ta dễ dành nhận thấy:
Con chim đứng ở C nặng gấp 3 lần con chim đứng ở D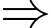
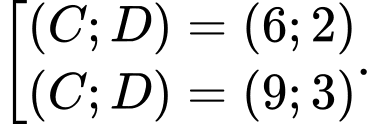
Con chim đứng ở E nặng gấp 2 lần con chim đứng ở F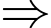
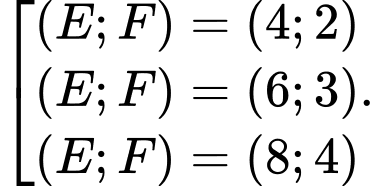
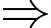
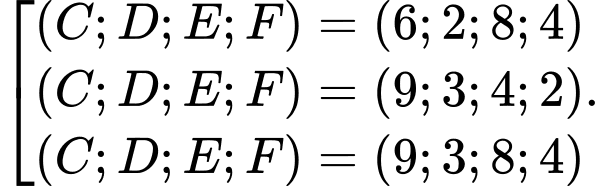
Ta có: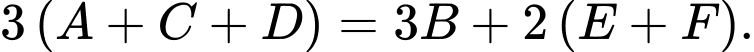
TH1: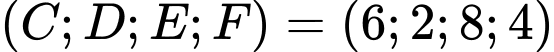
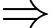
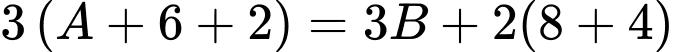

 (không thỏa mãn do mâu thuẫn với dữ kiện “không có con nào có số cân nặng bằng nhau”).
(không thỏa mãn do mâu thuẫn với dữ kiện “không có con nào có số cân nặng bằng nhau”).
TH2: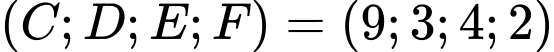
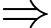
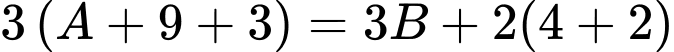

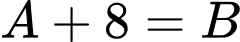 (không thỏa mãn do mâu thuẫn với dữ kiện “trọng lượng của các con chim nặng từ 2 đến 9 kg”).
(không thỏa mãn do mâu thuẫn với dữ kiện “trọng lượng của các con chim nặng từ 2 đến 9 kg”).
TH3: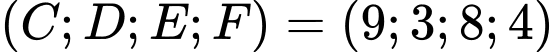
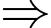
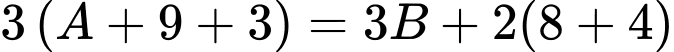

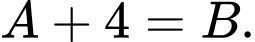
Mà “trọng lượng của các con chim nặng từ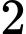 đến
đến 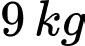 và không con nào có số cân nặng bằng nhau”
và không con nào có số cân nặng bằng nhau” 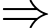
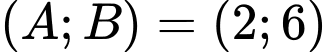
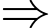 Con chim đứng ở B nặng
Con chim đứng ở B nặng 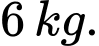 Đáp án: C
Đáp án: C
Dựa vào hình vẽ ta dễ dành nhận thấy:
Con chim đứng ở C nặng gấp 3 lần con chim đứng ở D
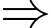
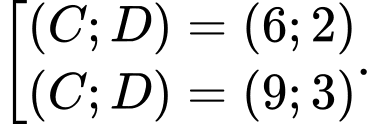
Con chim đứng ở E nặng gấp 2 lần con chim đứng ở F
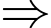
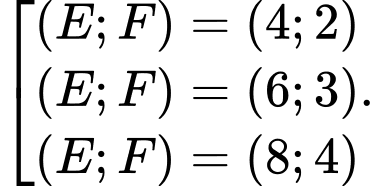
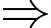
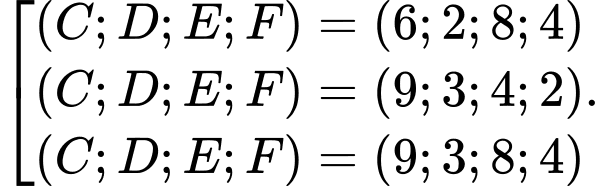
Ta có:
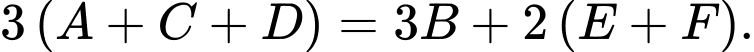
TH1:
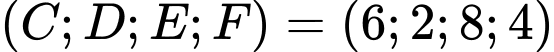
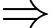
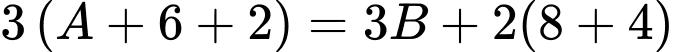

 (không thỏa mãn do mâu thuẫn với dữ kiện “không có con nào có số cân nặng bằng nhau”).
(không thỏa mãn do mâu thuẫn với dữ kiện “không có con nào có số cân nặng bằng nhau”).TH2:
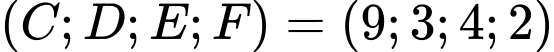
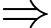
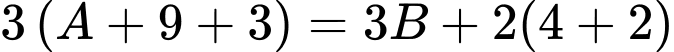

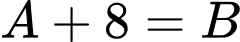 (không thỏa mãn do mâu thuẫn với dữ kiện “trọng lượng của các con chim nặng từ 2 đến 9 kg”).
(không thỏa mãn do mâu thuẫn với dữ kiện “trọng lượng của các con chim nặng từ 2 đến 9 kg”).TH3:
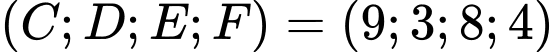
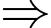
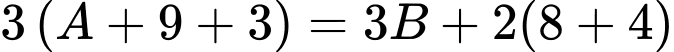

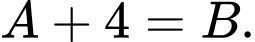
Mà “trọng lượng của các con chim nặng từ
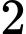 đến
đến 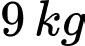 và không con nào có số cân nặng bằng nhau”
và không con nào có số cân nặng bằng nhau” 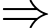
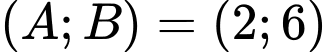
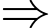 Con chim đứng ở B nặng
Con chim đứng ở B nặng 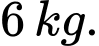 Đáp án: C
Đáp án: C