Đáp án Bài tập tự luyện số 2
Câu 1 [583995]: [Đường lên đỉnh Olympia năm thứ 23] : Năm đầu tiên trong thế kỷ XX có tổng các chữ số bằng 20 là năm nào ?
Năm trong thế kỷ XX có dạng: 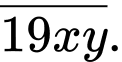
Năm cần tìm phải là năm đầu tiên và có tổng các chữ số bằng 20.
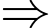
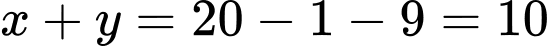 và
và 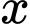 nhỏ nhất có thể, sau đó đến
nhỏ nhất có thể, sau đó đến 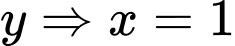 và
và 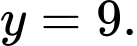
Đáp án: 1919.
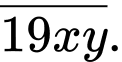
Năm cần tìm phải là năm đầu tiên và có tổng các chữ số bằng 20.
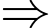
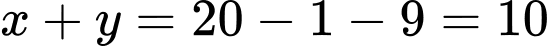 và
và 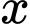 nhỏ nhất có thể, sau đó đến
nhỏ nhất có thể, sau đó đến 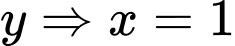 và
và 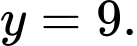
Đáp án: 1919.
Câu 2 [583996]: [Đường lên đỉnh Olympia năm thứ 23] : Tìm số lớn nhất có các chữ số khác nhau và tổng của các chữ số đó là 6.
Để số cần tìm là lớn nhất thì nó phải có nhiều chữ số nhất có thể.
Có: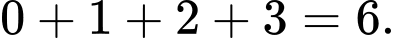
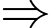 Đáp án: 3210.
Đáp án: 3210.
Có:
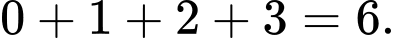
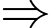 Đáp án: 3210.
Đáp án: 3210.
Câu 3 [583997]: [Đường lên đỉnh Olympia năm thứ 15]: Số nguyên tố nào có 3 chữ số tạo nên nó giống hệt nhau?
Không có số nguyên tố thỏa mãn vì số có 3 chữ số giống nhau sẽ chia hết cho 3.
Câu 4 [583998]: [Đường lên đỉnh Olympia năm thứ 23]: Trong đợt trồng cây đầu năm, lớp 11A1 cử một số bạn đi trồng cây và trồng được 180 cây, mỗi học sinh trồng được 8 hoặc 9 cây. Tính số học sinh tham gia trồng cây, biết số học sinh tham gia là một số chia hết cho 3.
Gọi 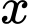 là số học sinh trồng được 8 cây,
là số học sinh trồng được 8 cây, 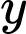 là số học sinh trồng được 9 cây.
là số học sinh trồng được 9 cây.
Từ đề bài, ta có: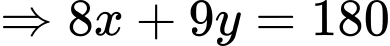 và
và  chia hết cho 3.
chia hết cho 3.
Ta thấy: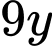 và 180 đều chia hết cho 9
và 180 đều chia hết cho 9 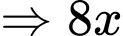 cũng phải chia hết cho 9, ta có các trường hợp:
cũng phải chia hết cho 9, ta có các trường hợp:

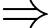 Đáp án: 21.
Đáp án: 21.
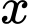 là số học sinh trồng được 8 cây,
là số học sinh trồng được 8 cây, 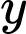 là số học sinh trồng được 9 cây.
là số học sinh trồng được 9 cây.
Từ đề bài, ta có:
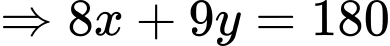 và
và  chia hết cho 3.
chia hết cho 3.
Ta thấy:
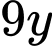 và 180 đều chia hết cho 9
và 180 đều chia hết cho 9 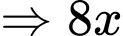 cũng phải chia hết cho 9, ta có các trường hợp:
cũng phải chia hết cho 9, ta có các trường hợp: 
 Đáp án: 21.
Đáp án: 21.
Câu 5 [583999]: [Đường lên đỉnh Olympia năm thứ 23]: Số viên bi của Dũng chia hết cho cả 3 và 5 và ít hơn 2000. Hỏi Dũng có thể có nhiều nhất bao nhiêu viên bi?
Gọi 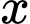 là số viên bi của Dũng.
là số viên bi của Dũng.
Theo đề bài, ta có: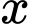 chia hết cho cả 3 và 5 và
chia hết cho cả 3 và 5 và 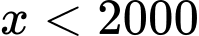
 chia hết cho 15 và
chia hết cho 15 và 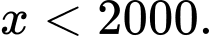
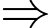 Giá trị lớn nhất có thể của
Giá trị lớn nhất có thể của 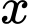 là: 1995.
là: 1995.
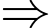 Dũng có thể có nhiều nhất 1995 viên bi.
Dũng có thể có nhiều nhất 1995 viên bi.
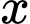 là số viên bi của Dũng.
là số viên bi của Dũng.
Theo đề bài, ta có:
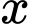 chia hết cho cả 3 và 5 và
chia hết cho cả 3 và 5 và 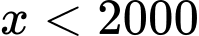
 chia hết cho 15 và
chia hết cho 15 và 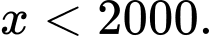
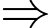 Giá trị lớn nhất có thể của
Giá trị lớn nhất có thể của 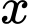 là: 1995.
là: 1995.
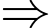 Dũng có thể có nhiều nhất 1995 viên bi.
Dũng có thể có nhiều nhất 1995 viên bi.
Câu 6 [584000]: [Đường lên đỉnh Olympia năm thứ 23]: Số ngày nằm trong phạm vi các số tự nhiên từ 1 đến 58. Khi viết “nó” không sử dụng các chữ số 1, 2, 3. Ngoài ra “nó” là số lẻ và không chia hết cho các số 3, 5, 7. Vậy “nó” là số nào?
Gọi 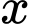 là số cần tìm.
là số cần tìm.
Dựa vào các dữ kiện:
• Khi viết “nó” không sử dụng các chữ số 1, 2, 3.
• Ngoài ra “nó” là số lẻ và không chia hết cho các số 3, 5, 7.
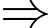
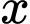 là số có chữ số hàng chục là 4 hoặc 5 và chữ số hàng đơn vị khác 1, 2, 3.
là số có chữ số hàng chục là 4 hoặc 5 và chữ số hàng đơn vị khác 1, 2, 3.
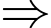 Đáp án: 47.
Đáp án: 47.
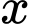 là số cần tìm.
là số cần tìm.
Dựa vào các dữ kiện:
• Khi viết “nó” không sử dụng các chữ số 1, 2, 3.
• Ngoài ra “nó” là số lẻ và không chia hết cho các số 3, 5, 7.
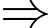
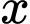 là số có chữ số hàng chục là 4 hoặc 5 và chữ số hàng đơn vị khác 1, 2, 3.
là số có chữ số hàng chục là 4 hoặc 5 và chữ số hàng đơn vị khác 1, 2, 3.
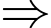 Đáp án: 47.
Đáp án: 47.
Câu 7 [584001]: [Đường lên đỉnh Olympia năm thứ 19]: Tìm số tự nhiên nhỏ nhất sao cho số đó chia 3 dư 2, chia 5 dư 3, chia 7 dư 5.
Gọi 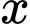 là số cần tìm.
là số cần tìm.
Từ đề bài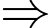
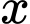 chia 5 dư 3 nên
chia 5 dư 3 nên 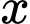 sẽ có chữ số tận cùng là 3 hoặc 8.
sẽ có chữ số tận cùng là 3 hoặc 8.
Ngoài ra,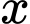 chia 7 dư 5, chia 3 dư 2 nên ta có các trường hợp:
chia 7 dư 5, chia 3 dư 2 nên ta có các trường hợp:
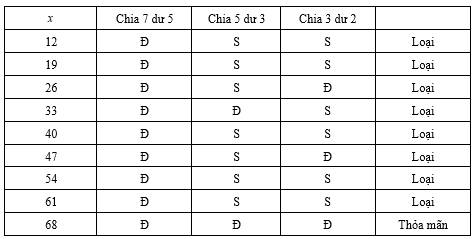
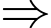 Đáp án: 68.
Đáp án: 68.
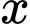 là số cần tìm.
là số cần tìm.
Từ đề bài
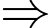
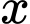 chia 5 dư 3 nên
chia 5 dư 3 nên 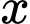 sẽ có chữ số tận cùng là 3 hoặc 8.
sẽ có chữ số tận cùng là 3 hoặc 8.
Ngoài ra,
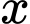 chia 7 dư 5, chia 3 dư 2 nên ta có các trường hợp:
chia 7 dư 5, chia 3 dư 2 nên ta có các trường hợp: 
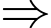 Đáp án: 68.
Đáp án: 68.
Câu 8 [584002]: [Đường lên đỉnh Olympia năm thứ 19]: Hãy tìm số tự nhiên nhỏ nhất tạo thành từ các số 3 và 7 (có đủ cả hai chữ số này) và chia hết cho cả 3 và 7.
Gọi 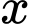 là số cần tìm.
là số cần tìm.
Dựa vào các dữ kiện:
• Số tự nhiên nhỏ nhất tạo thành từ các số 3 và 7 (có đủ cả hai chữ số này) và chia hết cho cả 3 và 7.
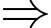
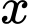 chia hết cho 3 nên cần ít nhất 3 số 7.
chia hết cho 3 nên cần ít nhất 3 số 7.
Để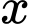 chia hết cho 7 thì tổng số dư khi chia 7 của các số 30..0 phải chia hết cho 7.
chia hết cho 7 thì tổng số dư khi chia 7 của các số 30..0 phải chia hết cho 7.
Nhận xét: Dễ thấy 1, 10, 100, 1000, 10000, 100000 chia 7 có số dư lần lượt là: 1 3 2 6 4 5; còn 3, 30, 300, 3000, 30000, 300000 chia 7 có số dư lần lượt là 3, 2, 6, 4, 5, 1.
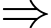
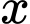 cần có ít nhất 2 chữ số 3
cần có ít nhất 2 chữ số 3
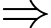
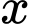 là số có 5 chữ số.
là số có 5 chữ số.
Để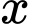 đạt giá trị nhỏ nhất
đạt giá trị nhỏ nhất 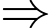 Các chữ số 3 phải ở vị trí cao nhất có thể nên chúng sẽ ở vị trí hàng chục nghìn và hàng chục, tương ứng với hai số dư là 5 và 2.
Các chữ số 3 phải ở vị trí cao nhất có thể nên chúng sẽ ở vị trí hàng chục nghìn và hàng chục, tương ứng với hai số dư là 5 và 2.
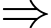 Đáp án: 37737.
Đáp án: 37737.
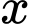 là số cần tìm.
là số cần tìm.
Dựa vào các dữ kiện:
• Số tự nhiên nhỏ nhất tạo thành từ các số 3 và 7 (có đủ cả hai chữ số này) và chia hết cho cả 3 và 7.
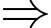
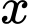 chia hết cho 3 nên cần ít nhất 3 số 7.
chia hết cho 3 nên cần ít nhất 3 số 7. Để
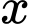 chia hết cho 7 thì tổng số dư khi chia 7 của các số 30..0 phải chia hết cho 7.
chia hết cho 7 thì tổng số dư khi chia 7 của các số 30..0 phải chia hết cho 7.
Nhận xét: Dễ thấy 1, 10, 100, 1000, 10000, 100000 chia 7 có số dư lần lượt là: 1 3 2 6 4 5; còn 3, 30, 300, 3000, 30000, 300000 chia 7 có số dư lần lượt là 3, 2, 6, 4, 5, 1.
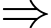
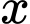 cần có ít nhất 2 chữ số 3
cần có ít nhất 2 chữ số 3 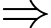
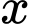 là số có 5 chữ số.
là số có 5 chữ số.
Để
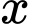 đạt giá trị nhỏ nhất
đạt giá trị nhỏ nhất 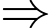 Các chữ số 3 phải ở vị trí cao nhất có thể nên chúng sẽ ở vị trí hàng chục nghìn và hàng chục, tương ứng với hai số dư là 5 và 2.
Các chữ số 3 phải ở vị trí cao nhất có thể nên chúng sẽ ở vị trí hàng chục nghìn và hàng chục, tương ứng với hai số dư là 5 và 2.
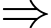 Đáp án: 37737.
Đáp án: 37737.
Câu 9 [584003]: [Đường lên đỉnh Olympia năm thứ 14]: Một số chia 5 dư 1, chia 4 dư 2, hỏi số đó chia 20 dư mấy?
Dựa vào dữ kiện:
• Một số chia 5 dư 1.
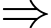 Số đó có dạng:
Số đó có dạng: 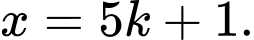
Kết hợp dữ kiện:
• Số đó chia 4 dư 2.
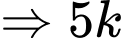 chia 4 dư 1
chia 4 dư 1
 chia 4 dư 1
chia 4 dư 1
 có dạng:
có dạng: 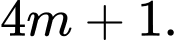
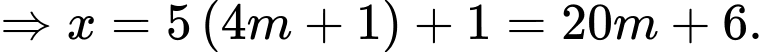
 Đáp án: 6.
Đáp án: 6.
• Một số chia 5 dư 1.
 Số đó có dạng:
Số đó có dạng: 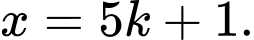
Kết hợp dữ kiện:
• Số đó chia 4 dư 2.
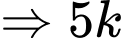 chia 4 dư 1
chia 4 dư 1  chia 4 dư 1
chia 4 dư 1  có dạng:
có dạng: 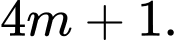
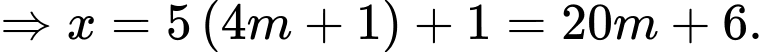
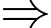 Đáp án: 6.
Đáp án: 6.
Câu 10 [584004]: [Đường lên đỉnh Olympia năm thứ 22]: Hãy thay x và y vào 1996xy để được số chia hết cho 2, 5, 9.
Số chia hết cho 2 và 5 sẽ có tận cùng bằng 0 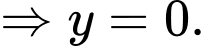
Số chia hết cho 9 sẽ có tổng các chữ số chia hết cho 9.
Tổng các chữ số của 1996x0 là: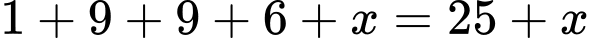
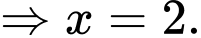
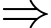 Đáp án:
Đáp án: 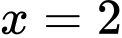 và
và 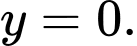
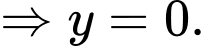
Số chia hết cho 9 sẽ có tổng các chữ số chia hết cho 9.
Tổng các chữ số của 1996x0 là:
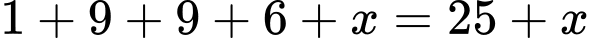
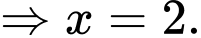
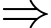 Đáp án:
Đáp án: 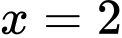 và
và 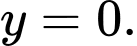
Câu 11 [584005]: [Đường lên đỉnh Olympia năm thứ 19]: Tìm tất cả các số tự nhiên có 2 chữ số vừa chia hết cho 2 vừa chia hết cho 3 lại vừa chia hết cho 5.
Số chia hết cho 2 và 5 sẽ có tận cùng bằng 0.
Số chia hết cho 3 sẽ có tổng các chữ số chia hết cho 3.
 Đáp án: 30, 60, 90.
Đáp án: 30, 60, 90.
Số chia hết cho 3 sẽ có tổng các chữ số chia hết cho 3.
 Đáp án: 30, 60, 90.
Đáp án: 30, 60, 90.
Câu 12 [584006]: [Đường lên đỉnh Olympia năm thứ 17]: Tìm số bé nhất khác 1 mà khi chia cho 2, 3, 4, 5, 6 cùng có số dư bằng 1.
Số bé nhất khác 1 mà khi chia cho 2, 3, 4, 5, 6 cùng có số dư bằng 1 là số liền sau của bội chung nhỏ nhất của 2, 3, 4, 5, 6. |Bội chung nhỏ nhất của 2, 3, 4, 5, 6 là 60.
 Đáp án: 61.
Đáp án: 61.
 Đáp án: 61.
Đáp án: 61.
Câu 13 [584007]: [Đường lên đỉnh Olympia năm thứ 24]: Số nào là số tự nhiên khác không nhỏ nhất chia hết cho tất cả các số nguyên từ 1 đến 10?
Số cần tìm là bội chung nhỏ nhất của các số nguyên từ 1 đến 10.
Số đó là: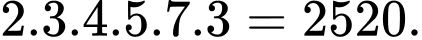
Số đó là:
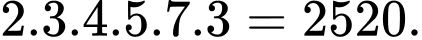
Câu 14 [584008]: [Đường lên đỉnh Olympia năm thứ 22]: Tuổi của A chia 3 dư 2, chia 5 dư 3, chia 7 dư 4. Hỏi A bao nhiêu tuổi (Biết rằng tuổi của A nhỏ hơn 100)?
Gọi 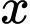 là số tuổi của A.
là số tuổi của A.
Từ đề bài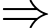
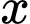 chia 5 dư 3 nên
chia 5 dư 3 nên 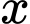 sẽ có chữ số tận cùng là 3 hoặc 8.
sẽ có chữ số tận cùng là 3 hoặc 8.
Ngoài ra,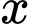 chia 7 dư 4, chia 3 dư 2 nên ta có các trường hợp:
chia 7 dư 4, chia 3 dư 2 nên ta có các trường hợp:
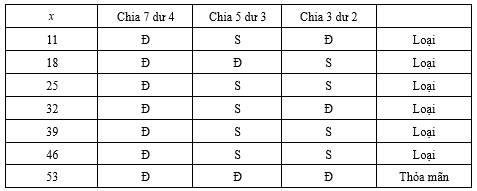
 Đáp án: 53.
Đáp án: 53.
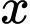 là số tuổi của A.
là số tuổi của A.
Từ đề bài
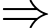
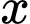 chia 5 dư 3 nên
chia 5 dư 3 nên 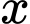 sẽ có chữ số tận cùng là 3 hoặc 8.
sẽ có chữ số tận cùng là 3 hoặc 8.
Ngoài ra,
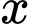 chia 7 dư 4, chia 3 dư 2 nên ta có các trường hợp:
chia 7 dư 4, chia 3 dư 2 nên ta có các trường hợp: 
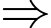 Đáp án: 53.
Đáp án: 53.
Câu 15 [584009]: [Đường lên đỉnh Olympia năm thứ 17]: Cho X là một số nguyên lớn hơn 1. Khi chia X cho các số từ 2 đến 9 đều có số dư là 1. Tìm giá trị nhỏ nhất của X.
Giá trị nhỏ nhất của X là số liền sau của bội chung nhỏ nhất của các số từ 2 đến 9.
Số đó là: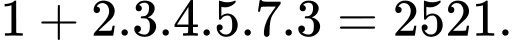
Số đó là:
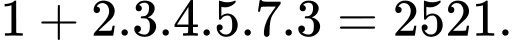
Câu 16 [584010]: [Đường lên đỉnh Olympia năm thứ 23]: Năm đầu tiên của thế kỉ 21 chia hết cho 167 là năm nào?
Năm cần tìm ở thế kỉ 21 nên nó có dạng: 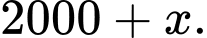
Có 2000 chia 167 dư 163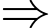 2004 là số nhỏ nhất cần tìm.
2004 là số nhỏ nhất cần tìm.
 Đáp án: 2004.
Đáp án: 2004.
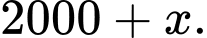
Có 2000 chia 167 dư 163
 2004 là số nhỏ nhất cần tìm.
2004 là số nhỏ nhất cần tìm.
 Đáp án: 2004.
Đáp án: 2004.
Câu 17 [584011]: [Đường lên đỉnh Olympia năm thứ 17]: Một số tự nhiên lẻ có hai chữ số và chia hết cho 5. Hiệu của nó và chữ số hàng chục của nó là 68. Số đó là số nào?
Số cần tìm là số lẻ có hai chữ số và chia hết cho 5 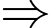 Chữ số hàng đơn vị là 5.
Chữ số hàng đơn vị là 5.
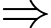 Số cần tìm có dạng:
Số cần tìm có dạng: 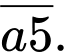
Từ đề bài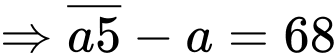

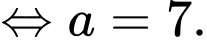
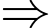 Đáp án: 75.
Đáp án: 75.
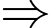 Chữ số hàng đơn vị là 5.
Chữ số hàng đơn vị là 5.
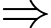 Số cần tìm có dạng:
Số cần tìm có dạng: 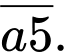
Từ đề bài
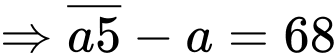

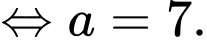
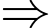 Đáp án: 75.
Đáp án: 75.
Câu 18 [584012]: [Đường lên đỉnh Olympia năm thứ 24] : A là số tự nhiên có 2004 chữ số. A là số chia hết cho 9, B là tổng các chữ số của A, C là tổng các chữ số của B, D là tổng các chữ số của C. Tìm D.
Dựa vào các dữ kiện:
• A là số tự nhiên có 2004 chữ số. A là số chia hết cho 9.
• B là tổng các chữ số của A.
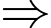 Giá trị lớn nhất mà B có thể nhận là:
Giá trị lớn nhất mà B có thể nhận là: 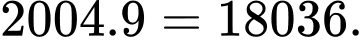
Kết hợp dữ kiện:
• C là tổng các chữ số của B.
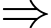 Giá trị lớn nhất của C cũng chỉ có thể là một số có hai chữ số nhỏ hơn:
Giá trị lớn nhất của C cũng chỉ có thể là một số có hai chữ số nhỏ hơn: 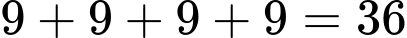 và C cũng sẽ chia hết cho 9.
và C cũng sẽ chia hết cho 9.
• D là tổng các chữ số của C.
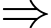 D cũng phải chia hết cho 9
D cũng phải chia hết cho 9
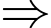 D
D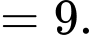
• A là số tự nhiên có 2004 chữ số. A là số chia hết cho 9.
• B là tổng các chữ số của A.
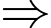 Giá trị lớn nhất mà B có thể nhận là:
Giá trị lớn nhất mà B có thể nhận là: 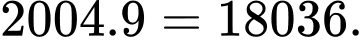
Kết hợp dữ kiện:
• C là tổng các chữ số của B.
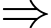 Giá trị lớn nhất của C cũng chỉ có thể là một số có hai chữ số nhỏ hơn:
Giá trị lớn nhất của C cũng chỉ có thể là một số có hai chữ số nhỏ hơn: 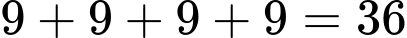 và C cũng sẽ chia hết cho 9.
và C cũng sẽ chia hết cho 9.
• D là tổng các chữ số của C.
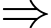 D cũng phải chia hết cho 9
D cũng phải chia hết cho 9 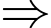 D
D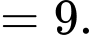
Câu 19 [584013]: [Đường lên đỉnh Olympia năm thứ 22]: Tang tảng lúc trời mới rạng đông. Rủ nhau đi hái mấy quả hồng. Mỗi người 5 quả thừa 5 quả. Mỗi người 6 quả, một người không. Hỏi có bao nhiêu người, bao nhiêu quả hồng?
Gọi 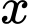 là số người,
là số người, 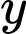 là số quả hồng.
là số quả hồng.
Từ đề bài, ta có hệ phương trình: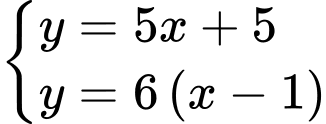
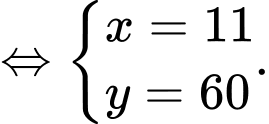
 Có 11 người và 60 quả hồng.
Có 11 người và 60 quả hồng.
 là số người,
là số người, 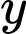 là số quả hồng.
là số quả hồng.
Từ đề bài, ta có hệ phương trình:
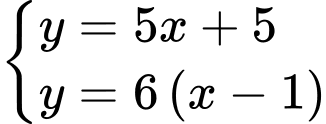
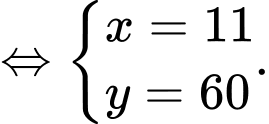
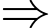 Có 11 người và 60 quả hồng.
Có 11 người và 60 quả hồng.
Câu 20 [584014]: [Đường lên đỉnh Olympia năm thứ 23] : Anh Huy hỏi anh Dũng: “Các con của anh năm nay bao nhiêu tuổi?”. Anh Dũng trả lời: “Tuổi tôi gấp 7 lần đứa nhỏ và gấp 4 lần đứa lớn”. Hỏi anh Dũng bao nhiêu tuổi, biết anh Dũng nhỏ hơn 30 tuổi ?
Gọi 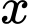 là số tuổi của anh Dũng.
là số tuổi của anh Dũng.
Từ đề bài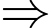
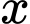 chia hết cho 7 và 4 đồng thời nhỏ hơn 30
chia hết cho 7 và 4 đồng thời nhỏ hơn 30 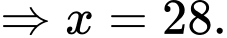
Đáp án: 28 tuổi.
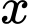 là số tuổi của anh Dũng.
là số tuổi của anh Dũng.
Từ đề bài
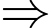
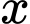 chia hết cho 7 và 4 đồng thời nhỏ hơn 30
chia hết cho 7 và 4 đồng thời nhỏ hơn 30 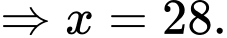
Đáp án: 28 tuổi.
Câu 21 [584015]: [Đường lên đỉnh Olympia năm thứ 23]: Dũng và Huy có 260 quả chuối. Biết rằng nếu gạch bỏ chữ số hàng đơn vị trong số chuối của Dũng sẽ được số chuối của Huy. Hỏi mỗi người có bao nhiêu quả chuối nếu số được gạch bỏ là số 7 ?
Dựa vào dữ kiện:
• Nếu gạch bỏ chữ số hàng đơn vị trong số chuối của Dũng sẽ được số chuối của Huy.
• Số được gạch bỏ là số 7. Gọi là số chuối của Dũng
là số chuối của Dũng
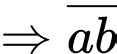 là số chuối của Huy.
là số chuối của Huy.
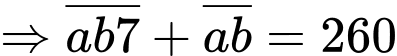
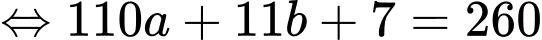
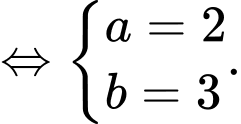
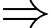 Dũng có 237 quả chuối, Huy có 23 quả chuối.
Dũng có 237 quả chuối, Huy có 23 quả chuối.
• Nếu gạch bỏ chữ số hàng đơn vị trong số chuối của Dũng sẽ được số chuối của Huy.
• Số được gạch bỏ là số 7. Gọi
 là số chuối của Dũng
là số chuối của Dũng 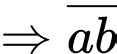 là số chuối của Huy.
là số chuối của Huy.
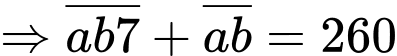
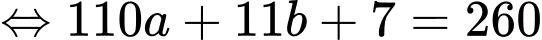
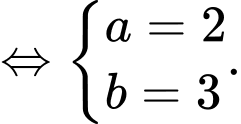
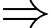 Dũng có 237 quả chuối, Huy có 23 quả chuối.
Dũng có 237 quả chuối, Huy có 23 quả chuối.
Câu 22 [584016]: [Đường lên đỉnh Olympia năm thứ 16]: Tìm số tự nhiên có ba chữ số sao cho tổng các chữ số tạo nên nó lớn gấp ba lần tích các chữ số tạo nên nó ?
Gọi 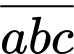 là số cần tìm.
là số cần tìm.
Theo đề bài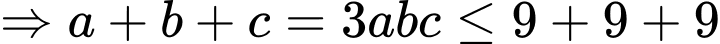
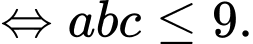
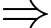 Ta thử với các trường hợp
Ta thử với các trường hợp 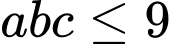
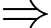 Chỉ có
Chỉ có 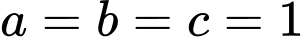 thỏa mãn.
thỏa mãn.
Đáp án: 111.
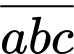 là số cần tìm.
là số cần tìm.
Theo đề bài
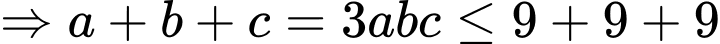
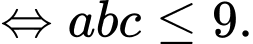
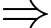 Ta thử với các trường hợp
Ta thử với các trường hợp 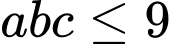
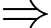 Chỉ có
Chỉ có 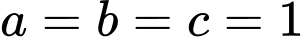 thỏa mãn.
thỏa mãn.
Đáp án: 111.
Câu 23 [584017]: [Đường lên đỉnh Olympia năm thứ 17]: Hãy tìm số lớn nhất có ba chữ số, biết rằng nếu lấy số đó chia cho 11 thì được một số nguyên dương có tổng các chữ số là 5.
Để số cần tìm đạt giá trị lớn nhất thì số nguyên dương có tổng các chữ số là 5 cũng phải đạt giá trị lớn nhất.
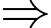 Số cần tìm là:
Số cần tìm là: 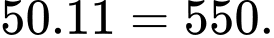
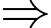 Số cần tìm là:
Số cần tìm là: 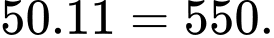
Câu 24 [584018]: [Đường lên đỉnh Olympia năm thứ 16]: Tính tổng các số tự nhiên thỏa mãn điều kiện những số này khác nhau và khi chia mỗi số này cho 10 đều được thương là 10.
Các số khác nhau thỏa mãn khi chia mỗi số này cho 10 đều được thương là 10 là: 100, 101, 102, 103, ..., 109.
Tổng các số đó là: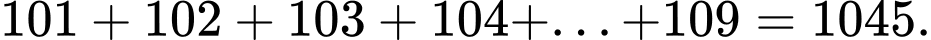
Tổng các số đó là:
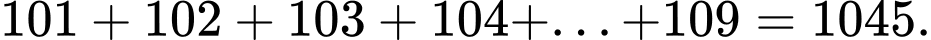
Câu 25 [584019]: [Đường lên đỉnh Olympia năm thứ 15]: Tìm số X có hai chữ số, biết chữ số hàng chục là 4 và nếu đổi chữ số hàng chục và hàng đơn vị cho nhau ta sẽ được số mới có giá trị bằng X cộng với 1/5 X.
Dựa vào dữ kiện: “số X có hai chữ số, biết chữ số hàng chục là 4”.
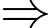 X có dạng:
X có dạng: 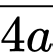
Theo đề bài, ta có phương trình: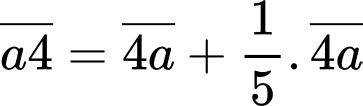
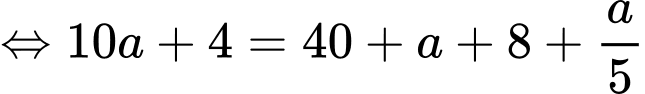
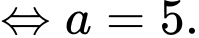
Đáp án: 45.
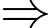 X có dạng:
X có dạng: 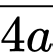
Theo đề bài, ta có phương trình:
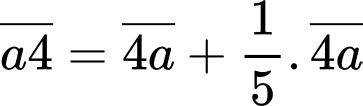
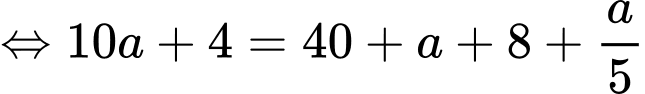
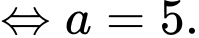
Đáp án: 45.
Câu 26 [584020]: [Đường lên đỉnh Olympia năm thứ 16]: Tích hai số giảm đi 1176 đơn vị. Nếu thừa số thứ nhất giảm đi 12 đơn vị, vậy thừa số thứ hai là số mấy ?
Gọi 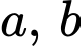 lần lượt là thừa số thứ nhất và thứ hai.
lần lượt là thừa số thứ nhất và thứ hai.
Từ đề bài, ta có: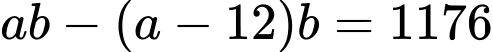
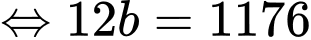
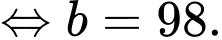
Đáp án: 98.
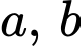 lần lượt là thừa số thứ nhất và thứ hai.
lần lượt là thừa số thứ nhất và thứ hai.
Từ đề bài, ta có:
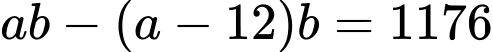
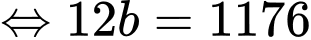
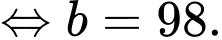
Đáp án: 98.
Câu 27 [584021]: [Đường lên đỉnh Olympia năm thứ 17]: Tìm số tự nhiên có hai chữ số sao cho thỏa mãn điều kiện: đem số tự nhiên này cộng với các chữ số cấu thành nên nó, ta được kết quả là 65.
Gọi số tự nhiên cần tìm là: 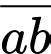
Theo đề bài, ta có:

Nhận xét: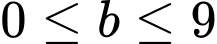
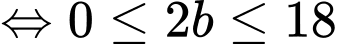
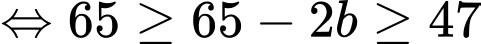
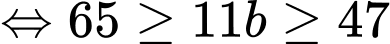
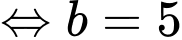
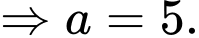
Đáp án: 55.
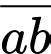
Theo đề bài, ta có:


Nhận xét:
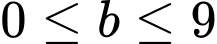
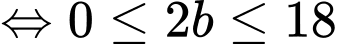
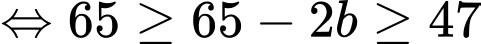
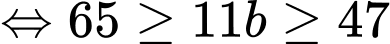
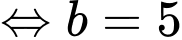
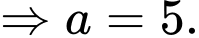
Đáp án: 55.
Câu 28 [584022]: [Đường lên đỉnh Olympia năm thứ 16]: Tìm số có ba chữ số biết tổng các chữ số bằng 26 và khi đổi chỗ chữ số hàng trăm với chữ số hàng đơn vị thì số đó không thay đổi.
Gọi số có ba chữ số cần tìm là: 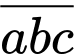
Theo đề bài, ta có: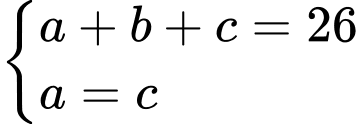

Nhận xét: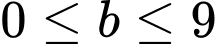
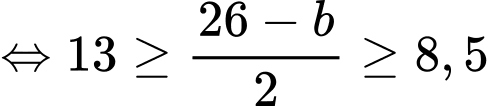
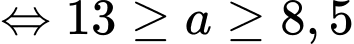
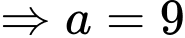
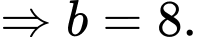
Đáp án: 989.
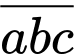
Theo đề bài, ta có:
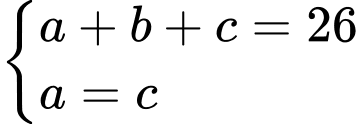

Nhận xét:
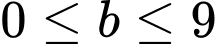
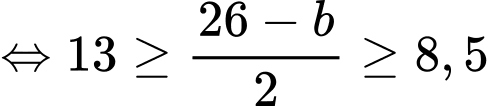
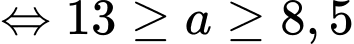
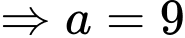
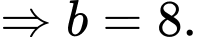
Đáp án: 989.
Câu 29 [584023]: [Đường lên đỉnh Olympia năm thứ 21]: Một học sinh viết lên bảng 10 số tự nhiên từ 1 đến 10 rồi chơi trò chơi sau: Mỗi lần học sinh đó xóa đi hai số a và b bất kỳ rồi viết lên bảng số (a+b+1). Hỏi sau 9 lần chơi liên tiếp thì trên bảng còn lại số nào?
Dựa vào các dữ kiện:
• Mỗi lần học sinh đó xóa đi hai số a và b bất kỳ rồi viết lên bảng số (a+b+1).
 Mỗi lần đó, tổng của các số trên bảng tăng thêm 1.
Mỗi lần đó, tổng của các số trên bảng tăng thêm 1.
Ta lại thấy lúc đầu khi trên bảng có 10 số tự nhiên từ 1 đến 10 thì tổng của các số đó là 55.
 Sau 9 lần chơi liên tiếp, tổng của các số tự nhiên trên bảng, hay cũng chính là số tự nhiên duy nhất còn lại là:
Sau 9 lần chơi liên tiếp, tổng của các số tự nhiên trên bảng, hay cũng chính là số tự nhiên duy nhất còn lại là: 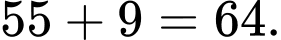
Đáp án: 64.
• Mỗi lần học sinh đó xóa đi hai số a và b bất kỳ rồi viết lên bảng số (a+b+1).
 Mỗi lần đó, tổng của các số trên bảng tăng thêm 1.
Mỗi lần đó, tổng của các số trên bảng tăng thêm 1.Ta lại thấy lúc đầu khi trên bảng có 10 số tự nhiên từ 1 đến 10 thì tổng của các số đó là 55.
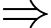 Sau 9 lần chơi liên tiếp, tổng của các số tự nhiên trên bảng, hay cũng chính là số tự nhiên duy nhất còn lại là:
Sau 9 lần chơi liên tiếp, tổng của các số tự nhiên trên bảng, hay cũng chính là số tự nhiên duy nhất còn lại là: 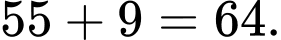
Đáp án: 64.
Câu 30 [584024]: [Đường lên đỉnh Olympia năm thứ 19]: Tổng của một số tự nhiên và một số thập phân là 62, 42. Khi cộng hai số này bạn An quên mất dấu phẩy ở số thập phân và đặt tính cộng như số tự nhiên nên kết quả sai là 3569. Tìm số thập phân và số tự nhiên đã cho.
Gọi 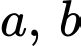 lần lượt là số thập phân và số tự nhiên cần tìm.
lần lượt là số thập phân và số tự nhiên cần tìm.
Dựa vào các dữ kiện:
• Tổng của một số tự nhiên và một số thập phân là 62,42.
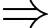
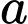 có hai chữ số sau dấu phẩy.
có hai chữ số sau dấu phẩy.
• Khi cộng hai số này bạn An quên mất dấu phẩy ở số thập phân và đặt tính cộng như số tự nhiên nên kết quả sai là 3569.
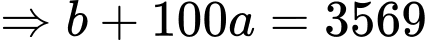
Ta có hệ phương trình: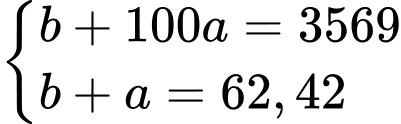
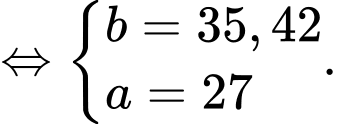
Đáp án: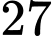 và
và 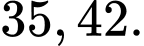
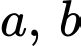 lần lượt là số thập phân và số tự nhiên cần tìm.
lần lượt là số thập phân và số tự nhiên cần tìm.
Dựa vào các dữ kiện:
• Tổng của một số tự nhiên và một số thập phân là 62,42.
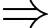
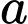 có hai chữ số sau dấu phẩy.
có hai chữ số sau dấu phẩy.
• Khi cộng hai số này bạn An quên mất dấu phẩy ở số thập phân và đặt tính cộng như số tự nhiên nên kết quả sai là 3569.
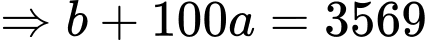
Ta có hệ phương trình:
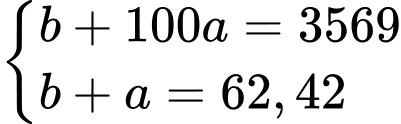
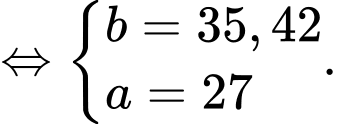
Đáp án:
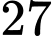 và
và 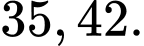
Câu 31 [584025]: [Đường lên đỉnh Olympia năm thứ 22]: A nhân một số với 2002 nhưng “đãng trí” quên viết hai chữ số 0 của số 2002 nên kết quả “bị” giảm đi 3965940 đơn vị. Hỏi A đã định nhân số nào với 2002?
Gọi số cần tìm là 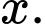
Dựa vào các dữ kiện:
• A nhân một số với 2002 nhưng “đãng trí” quên viết hai chữ số 0 của số 2002 nên kết quả “bị” giảm đi 3965940 đơn vị.
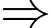 Phương trình:
Phương trình: 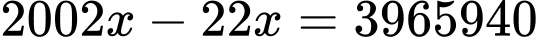
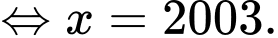
Đáp án: 2003.
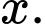
Dựa vào các dữ kiện:
• A nhân một số với 2002 nhưng “đãng trí” quên viết hai chữ số 0 của số 2002 nên kết quả “bị” giảm đi 3965940 đơn vị.
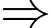 Phương trình:
Phương trình: 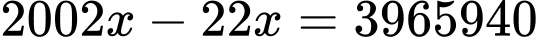
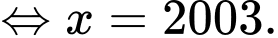
Đáp án: 2003.
Câu 32 [584026]: [Đường lên đỉnh Olympia năm thứ 19]: Khi làm phép nhân một số với 102, một bạn học sinh đã quên mất chữ số 0 ở số 102 nên tích giảm đi 1170 đơn vị. Hỏi bạn đó đã nhân số nào với 102?
Gọi số cần tìm là 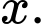
Dựa vào các dữ kiện:
• Khi làm phép nhân một số với 102, một bạn học sinh đã quên mất chữ số 0 ở số 102 nên tích giảm đi 1170 đơn vị.
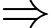 Phương trình:
Phương trình: 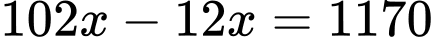
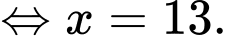
Đáp án: 13.
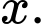
Dựa vào các dữ kiện:
• Khi làm phép nhân một số với 102, một bạn học sinh đã quên mất chữ số 0 ở số 102 nên tích giảm đi 1170 đơn vị.
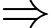 Phương trình:
Phương trình: 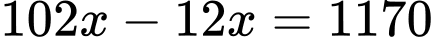
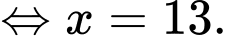
Đáp án: 13.
Câu 33 [584027]: [Đường lên đỉnh Olympia năm thứ 22]: Bạn hãy giải bài toán sau: Ba số trong một phép chia/ Đem cộng chúng lại ra kìa 95/ “Số chia” cho biết bằng 5/ Hỏi “thương” bằng mấy ? Đây khâm phục tài! (Lưu ý: Đây là phép chia hết)
Gọi 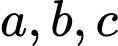 lần lượt là số bị chia, số chia và thương của phép chia.
lần lượt là số bị chia, số chia và thương của phép chia.
Dựa vào các dữ kiện:
• Đem cộng chúng lại ra kìa 95.
• “Số chia” cho biết bằng 5.
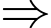 Ta có hệ phương trình:
Ta có hệ phương trình: 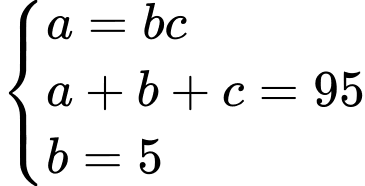
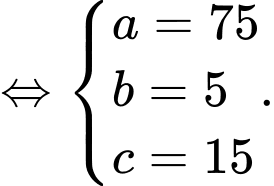
Đáp án: 15.
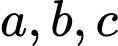 lần lượt là số bị chia, số chia và thương của phép chia.
lần lượt là số bị chia, số chia và thương của phép chia.
Dựa vào các dữ kiện:
• Đem cộng chúng lại ra kìa 95.
• “Số chia” cho biết bằng 5.
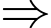 Ta có hệ phương trình:
Ta có hệ phương trình: 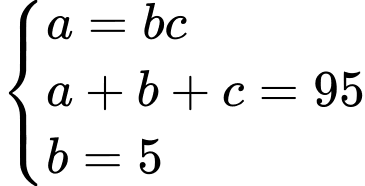
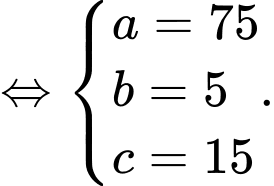
Đáp án: 15.
Câu 34 [584028]: [Đường lên đỉnh Olympia năm thứ 16]: Đức và Huy có tổng cộng 162 viên bi. Hỏi mỗi bạn có bao nhiêu viên bi, biết số bi của Đức có chữ số hàng đơn vị là 8 và nếu gạch số này đi thì số bi của Đức và Huy bằng nhau?
Dựa vào dữ kiện:
• Số bi của Đức có chữ số hàng đơn vị là 8 và nếu gạch số này đi thì số bi của Đức và Huy bằng nhau.
Gọi là số bi của Đức
là số bi của Đức 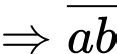 là số bi của Huy.
là số bi của Huy.
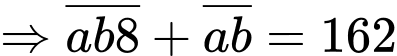
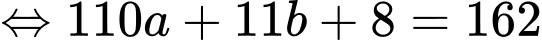
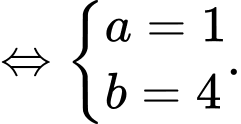
Đáp án: Đức có 148 quả chuối, Huy có 14 quả chuối.
• Số bi của Đức có chữ số hàng đơn vị là 8 và nếu gạch số này đi thì số bi của Đức và Huy bằng nhau.
Gọi
 là số bi của Đức
là số bi của Đức 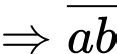 là số bi của Huy.
là số bi của Huy.
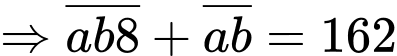
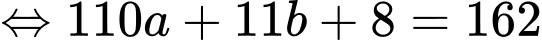
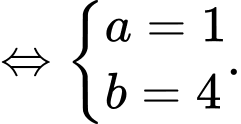
Đáp án: Đức có 148 quả chuối, Huy có 14 quả chuối.
Câu 35 [584029]: [Đường lên đỉnh Olympia năm thứ 24] : Một hôm Minh hỏi ông về số tuổi của những người trong gia đình, ông liền nói: “Tuổi cháu có bao nhiêu ngày thì tuổi bố cháu có bấy nhiêu tuần, tuổi cháu có bao nhiêu tháng thì tuổi ông có bấy nhiêu năm”. Hỏi năm nay ông của Minh bao nhiêu tuổi, biết rằng tổng số tuổi của 3 người bằng 140?
Gọi 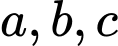 lần lượt là số tuổi của ông, bố của Minh và Minh.
lần lượt là số tuổi của ông, bố của Minh và Minh.
Dựa vào các dữ kiện:
• Tuổi cháu có bao nhiêu ngày thì tuổi bố cháu có bấy nhiêu tuần.
• Tuổi cháu có bao nhiêu tháng thì tuổi ông có bấy nhiêu năm.
• Rổng số tuổi của 3 người bằng 140.
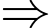 Ta có hệ phương trình:
Ta có hệ phương trình:
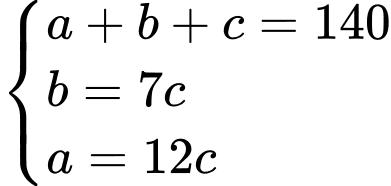
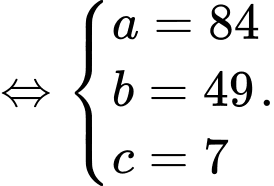
Đáp án: 84 tuổi.
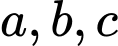 lần lượt là số tuổi của ông, bố của Minh và Minh.
lần lượt là số tuổi của ông, bố của Minh và Minh.
Dựa vào các dữ kiện:
• Tuổi cháu có bao nhiêu ngày thì tuổi bố cháu có bấy nhiêu tuần.
• Tuổi cháu có bao nhiêu tháng thì tuổi ông có bấy nhiêu năm.
• Rổng số tuổi của 3 người bằng 140.
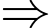 Ta có hệ phương trình:
Ta có hệ phương trình: 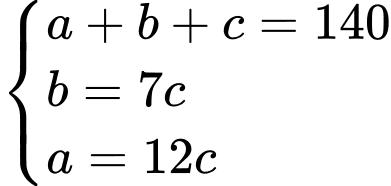
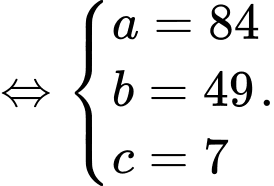
Đáp án: 84 tuổi.