Đáp án Ví dụ minh hoạ Chương 4
Câu 1 [379594]: Ba trong bốn số dưới đây giống nhau theo một quy luật nào đó. Chọn đáp án chữ số khác ba số còn lại
A, 16.
B, 9.
C, 49.
D, 121.
Chọn đáp án A.
16 là số chẵn; 9, 49, 121 là số lẻ. Đáp án: A
16 là số chẵn; 9, 49, 121 là số lẻ. Đáp án: A
Câu 2 [379598]: Theo logic quy luật, sau số 25 là số 36. Vậy sau số 49 là số….
A, 61.
B, 63.
C, 65.
D, 60.
Chọn đáp án D.
Ta thấy: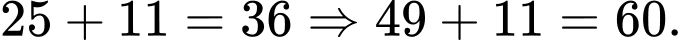 Đáp án: D
Đáp án: D
Ta thấy:
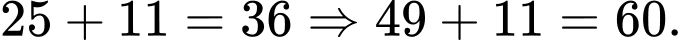 Đáp án: D
Đáp án: D
Câu 3 [379604]: Số thích hợp để điền vào ô trống trong dãy 5, 120, 6, 210, …, 8, ☐ là
A, 520.
B, 504.
C, 448.
D, 512.
Chọn đáp án B.
Ta thấy: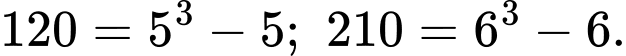
 Số cần điền vào ô trống là:
Số cần điền vào ô trống là: 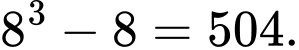 Đáp án: B
Đáp án: B
Ta thấy:
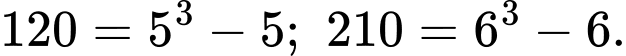
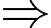 Số cần điền vào ô trống là:
Số cần điền vào ô trống là: 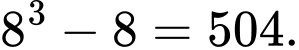 Đáp án: B
Đáp án: B
Câu 4 [379609]: Số bị sai quy luật trong dãy 24, 25, 29, 36, 54, 79, 115 là
A, 24.
B, 29.
C, 79.
D, 36.
Chọn đáp án D.
Ta thấy:
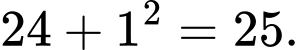
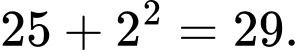
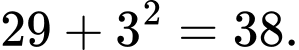
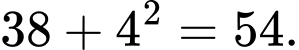
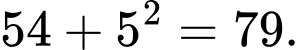
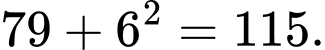
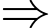 Số bị sai quy luật là số 36.
Số bị sai quy luật là số 36.
Đáp án: A Ta thấy:
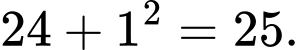
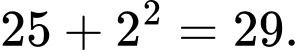
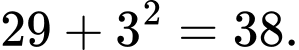
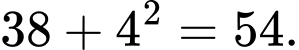
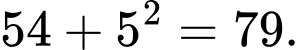
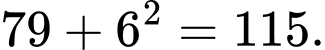
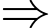 Số bị sai quy luật là số 36.
Số bị sai quy luật là số 36.
Câu 5 [379610]: Trong dãy sau có hai số bị sai quy luật, hãy chọn đáp án chứa số bị sai quy luật lớn hơn số còn lại 434, 629, 774, 874, 938, 972, 990 là
A, 629.
B, 774.
C, 874.
D, 972.
Chọn đáp án D.
Ta thấy:
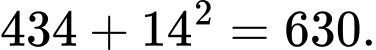
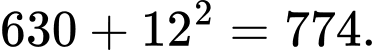
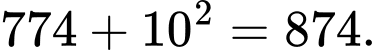
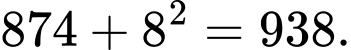
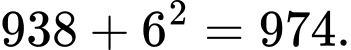
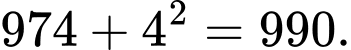
 Hai số bị sai quy luật là 629 và 972
Hai số bị sai quy luật là 629 và 972  Đáp án là 972. Đáp án: D
Đáp án là 972. Đáp án: D
Ta thấy:
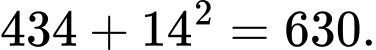
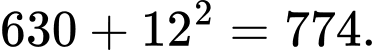
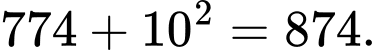
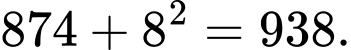
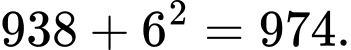
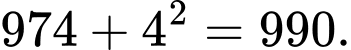
 Hai số bị sai quy luật là 629 và 972
Hai số bị sai quy luật là 629 và 972  Đáp án là 972. Đáp án: D
Đáp án là 972. Đáp án: D
Câu 6 [379632]: Sau 15 phút, kim giờ quay được một góc bằng
A, 5°.
B, 7,5°.
C, 10°.
D, 12,5°.
Góc quay của kim giờ sau 15 phút là: 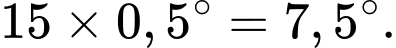
Chọn đáp án B. Đáp án: B
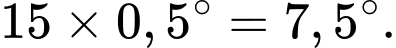
Chọn đáp án B. Đáp án: B
Câu 7 [379633]: Góc giữa kim phút và kim giờ của đồng hồ lúc 3 giờ 40 phút là bao nhiêu độ?
A, 120°.
B, 130°.
C, 140°.
D, 150°.
Góc giữa kim phút và kim giờ của đồng hồ được tính bằng công thức: 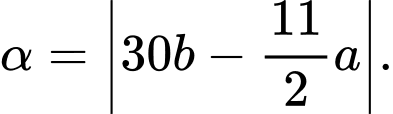
Trong đó: a = phút và b = giờ.
Vậy góc giữa kim phút và kim giờ của đồng hồ lúc 3 giờ 40 phút là:
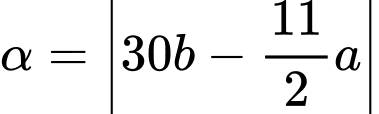
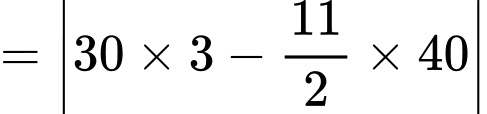
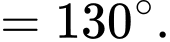
Chọn đáp án B. Đáp án: B
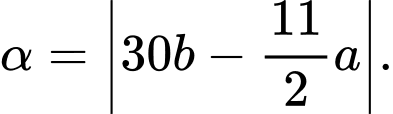
Trong đó: a = phút và b = giờ.
Vậy góc giữa kim phút và kim giờ của đồng hồ lúc 3 giờ 40 phút là:
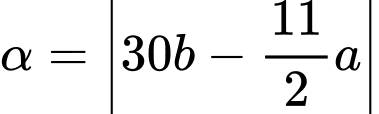
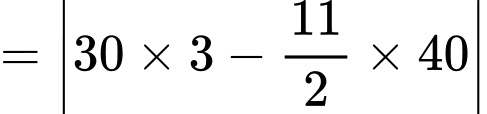
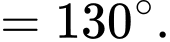
Chọn đáp án B. Đáp án: B
Câu 8 [379635]: Trong một khoảng thời gian, nếu kim giờ quay được một góc 6° thì kim phút sẽ quay được một góc bao nhiêu độ?
A, 54°.
B, 84°.
C, 72°.
D, 60°.
Ta có mỗi phút kim giờ quay được 1 góc bằng 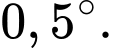
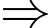 Sau
Sau 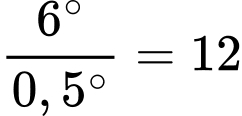 phút thì kim giờ sẽ quay được 1 góc bằng
phút thì kim giờ sẽ quay được 1 góc bằng 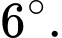
Lại có kim phút quay được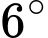 mỗi phút.
mỗi phút.
Vậy nếu kim giờ quay tạo được một góc 6° thì kim phút sẽ quay tạo được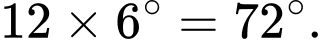
Chọn đáp án C. Đáp án: C
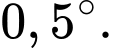
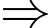 Sau
Sau 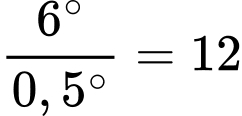 phút thì kim giờ sẽ quay được 1 góc bằng
phút thì kim giờ sẽ quay được 1 góc bằng 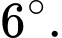
Lại có kim phút quay được
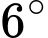 mỗi phút.
mỗi phút.Vậy nếu kim giờ quay tạo được một góc 6° thì kim phút sẽ quay tạo được
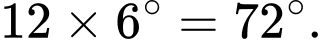
Chọn đáp án C. Đáp án: C
Câu 9 [379639]: Vào thời điểm nào trong khoảng thời gian từ 9 đến 10 giờ, kim giờ và kim phút trùng nhau?
A, 9 giờ 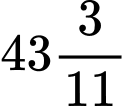 phút.
phút.
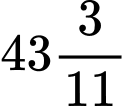 phút.
phút.B, 9 giờ 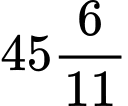 phút.
phút.
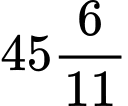 phút.
phút.C, 9 giờ 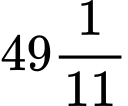 phút.
phút.
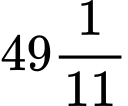 phút.
phút.D, 9 giờ 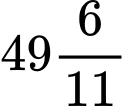 phút.
phút.
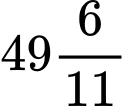 phút.
phút.
Khi kim giờ và kim phút trùng nhau thì góc giữa chúng bằng 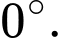 Do đó, góc giữa kim giờ và kim phút được xác định bằng công thức:
Do đó, góc giữa kim giờ và kim phút được xác định bằng công thức:
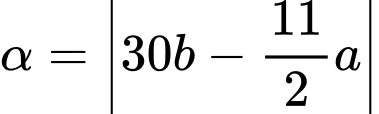
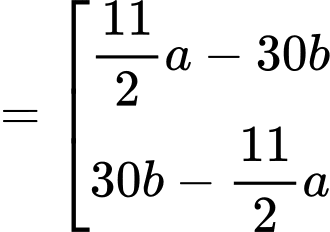
Trong đó: a = phút và b = giờ.
Ở đây b = 9 và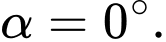
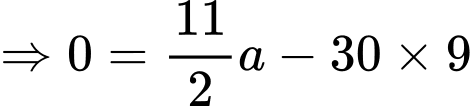 hoặc
hoặc 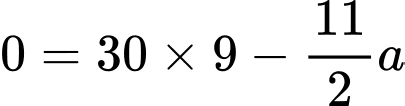
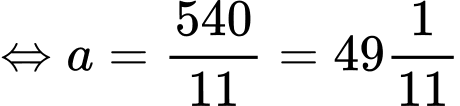 phút.
phút.
Vậy tại 9 giờ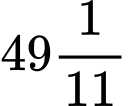 phút kim giờ và kim phút trùng nhau.
phút kim giờ và kim phút trùng nhau.
Chọn đáp án C. Đáp án: C
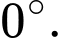 Do đó, góc giữa kim giờ và kim phút được xác định bằng công thức:
Do đó, góc giữa kim giờ và kim phút được xác định bằng công thức: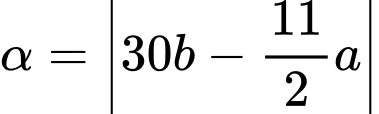
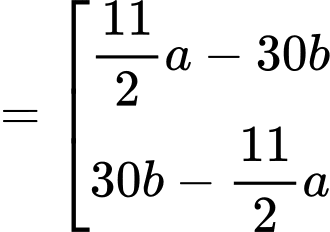
Trong đó: a = phút và b = giờ.
Ở đây b = 9 và
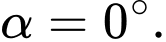
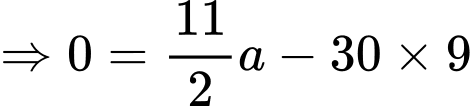 hoặc
hoặc 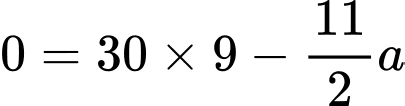
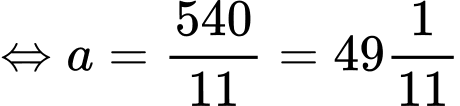 phút.
phút.Vậy tại 9 giờ
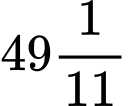 phút kim giờ và kim phút trùng nhau.
phút kim giờ và kim phút trùng nhau.Chọn đáp án C. Đáp án: C
Câu 10 [379642]: Vào thời điểm nào trong khoảng thời gian từ 2 đến 3 giờ, kim giờ và kim phút tạo với nhau một góc bằng 50°?
A, 2 giờ 25 phút.
B, 2 giờ 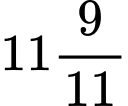 phút.
phút.
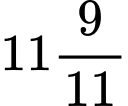 phút.
phút.C, 2 giờ 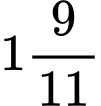 phút.
phút.
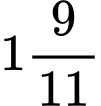 phút.
phút.D, 2 giờ 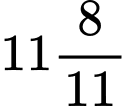 phút.
phút.
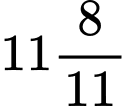 phút.
phút.
Ta có góc giữa kim giờ và kim phút là 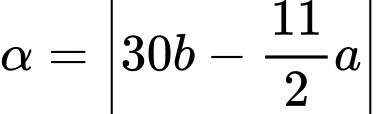
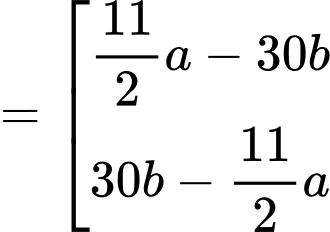
Trong đó: a = phút và b = giờ.
Ở đây b = 2 và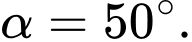
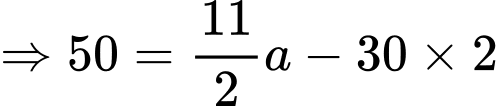 hoặc
hoặc 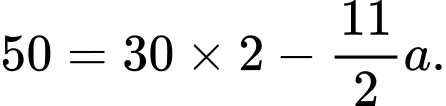
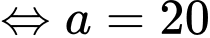 phút hoặc
phút hoặc 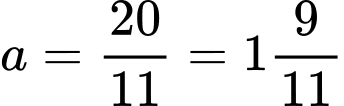 phút.
phút.
Kết hợp với đáp án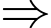 tại thời điểm 2 giờ
tại thời điểm 2 giờ 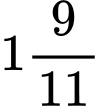 phút kim giờ tạo với kim phút 1 góc bằng
phút kim giờ tạo với kim phút 1 góc bằng 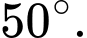
Chọn đáp án C. Đáp án: C
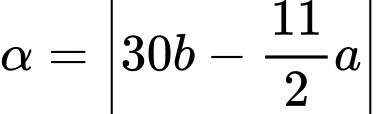
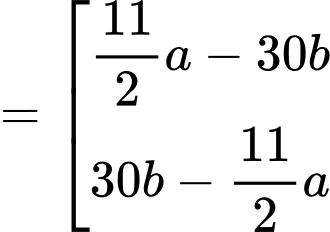
Trong đó: a = phút và b = giờ.
Ở đây b = 2 và
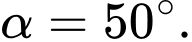
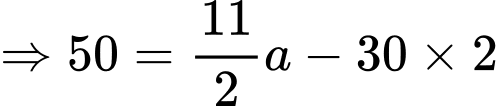 hoặc
hoặc 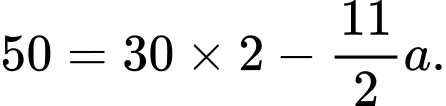
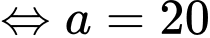 phút hoặc
phút hoặc 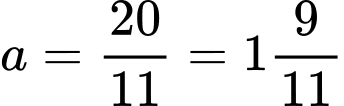 phút.
phút.Kết hợp với đáp án
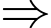 tại thời điểm 2 giờ
tại thời điểm 2 giờ 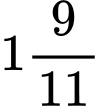 phút kim giờ tạo với kim phút 1 góc bằng
phút kim giờ tạo với kim phút 1 góc bằng 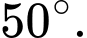
Chọn đáp án C. Đáp án: C
Câu 11 [379651]: Ngày 1 tháng 1 năm 2012 là Chủ Nhật thì ngày đầu tiên của năm 2016 rơi vào
A, Thứ sáu.
B, Chủ nhật.
C, Thứ Tư.
D, Thứ Bảy.
Từ năm 2012 đến năm 2016 có 4 năm. Trong đó có năm 2012 là năm nhuận còn lại không phải là năm nhuận.
Vậy năm 2012 có 2 ngày lẻ còn các năm còn lại có 1 ngày lẻ.
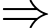 Có tổng 5 ngày lẻ
Có tổng 5 ngày lẻ 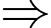 Ngày 1 tháng 1 năm 2012 là thứ Sáu.
Ngày 1 tháng 1 năm 2012 là thứ Sáu.
Chọn đáp án A. Đáp án: A
Vậy năm 2012 có 2 ngày lẻ còn các năm còn lại có 1 ngày lẻ.
 Có tổng 5 ngày lẻ
Có tổng 5 ngày lẻ  Ngày 1 tháng 1 năm 2012 là thứ Sáu.
Ngày 1 tháng 1 năm 2012 là thứ Sáu.
Chọn đáp án A. Đáp án: A
Câu 12 [379653]: Ngày 4 tháng 6 năm 2001 là ngày thứ mấy?
A, Thứ Hai.
B, Thứ Ba.
C, Thứ Tư.
D, Thứ Năm.
Tách năm 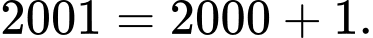
Vì năm 2000 không có ngày lẻ (do cứ 400 năm sẽ 0 có ngày lẻ) Dư 1 năm lẻ.
Dư 1 năm lẻ.
 Từ ngày 1 tháng 1 năm 2001 đến ngày 4 tháng 6 năm 2006 có
Từ ngày 1 tháng 1 năm 2001 đến ngày 4 tháng 6 năm 2006 có 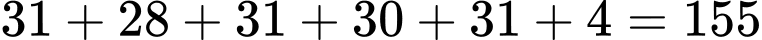 ngày (22 tuần dư 1 ngày).
ngày (22 tuần dư 1 ngày).
 Ngày 4 tháng 6 năm 2001 là ngày thứ Hai.
Ngày 4 tháng 6 năm 2001 là ngày thứ Hai.
Chọn đáp án A. Đáp án: A
Vì năm 2000 không có ngày lẻ (do cứ 400 năm sẽ 0 có ngày lẻ)
 Dư 1 năm lẻ.
Dư 1 năm lẻ. Từ ngày 1 tháng 1 năm 2001 đến ngày 4 tháng 6 năm 2006 có
Từ ngày 1 tháng 1 năm 2001 đến ngày 4 tháng 6 năm 2006 có 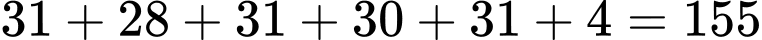 ngày (22 tuần dư 1 ngày).
ngày (22 tuần dư 1 ngày). Ngày 4 tháng 6 năm 2001 là ngày thứ Hai.
Ngày 4 tháng 6 năm 2001 là ngày thứ Hai.Chọn đáp án A. Đáp án: A
Câu 13 [289548]: Hai định dạng ngày khác nhau, tức là DD/MM/YY và MM/DD/YY phổ biến ở hầu hết các quốc gia. (Ví dụ: ngày 6 tháng 9 năm 1960 được viết là 6/9/60 ở định dạng DD/MM/YY và 9/6/60 ở định dạng MM/DD/YY). Nếu không biết ngày đó được viết dưới định dạng nào sẽ gây nhầm lẫn với người đọc. Hãy cho biết trong một năm có bao nhiêu ngày được viết thỏa mãn hai định dạng mà gây nhầm lẫn với người đọc?
A, 12 ngày.
B, 30 ngày.
C, 132 ngày.
D, 144 ngày.
Chọn đáp án C.
Những ngày viết gây nhầm lẫn cho người đọc là những ngày có ngày và tháng khác nhau, đồng thời ngày đó phải nhỏ hơn hoặc bằng ngày 12 (vì 1 năm chỉ có 12 tháng).
Số ngày trong 1 năm được viết thỏa mãn 2 định dạng là: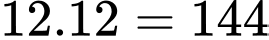 ngày. (1 năm có 12 tháng, mỗi tháng có 12 ngày được viết thỏa mãn đinh).
ngày. (1 năm có 12 tháng, mỗi tháng có 12 ngày được viết thỏa mãn đinh).
Số ngày trong 1 năm được viết thỏa mãn 2 định dạng mà không gây nhầm lẫn với người đọc là: 12 ngày.
Ví dụ: Ngày 01 tháng 01 năm 1960, được viết thỏa mãn 2 định dạng 01/01/60 nên dù người đọc nghĩ theo định dạng nào cũng sẽ đúng ngày.
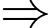 Số ngày trong 1 năm được viết thỏa mãn 2 định dạng mà gây nhầm lẫn với người đọc là:
Số ngày trong 1 năm được viết thỏa mãn 2 định dạng mà gây nhầm lẫn với người đọc là: 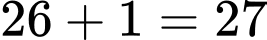 ngày. Đáp án: C
ngày. Đáp án: C
Những ngày viết gây nhầm lẫn cho người đọc là những ngày có ngày và tháng khác nhau, đồng thời ngày đó phải nhỏ hơn hoặc bằng ngày 12 (vì 1 năm chỉ có 12 tháng).
Số ngày trong 1 năm được viết thỏa mãn 2 định dạng là:
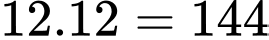 ngày. (1 năm có 12 tháng, mỗi tháng có 12 ngày được viết thỏa mãn đinh).
ngày. (1 năm có 12 tháng, mỗi tháng có 12 ngày được viết thỏa mãn đinh).Số ngày trong 1 năm được viết thỏa mãn 2 định dạng mà không gây nhầm lẫn với người đọc là: 12 ngày.
Ví dụ: Ngày 01 tháng 01 năm 1960, được viết thỏa mãn 2 định dạng 01/01/60 nên dù người đọc nghĩ theo định dạng nào cũng sẽ đúng ngày.
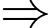 Số ngày trong 1 năm được viết thỏa mãn 2 định dạng mà gây nhầm lẫn với người đọc là:
Số ngày trong 1 năm được viết thỏa mãn 2 định dạng mà gây nhầm lẫn với người đọc là: 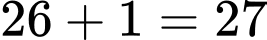 ngày. Đáp án: C
ngày. Đáp án: C
Câu 14 [379662]: Ngày cuối cùng của một thế kỷ không thể vào thứ mấy?
A, Thứ Sáu.
B, Thứ Tư.
C, Thứ Hai.
D, Thứ Ba.
Cứ 100 năm có 5 ngày lẻ  Ngày cuối cùng của thế kỷ đầu tiên là Thứ Sáu.
Ngày cuối cùng của thế kỷ đầu tiên là Thứ Sáu.
Cứ 200 năm có 3 ngày lẻ Ngày cuối cùng của thế kỷ thứ hai là Thứ Tư.
Ngày cuối cùng của thế kỷ thứ hai là Thứ Tư.
Cứ 300 năm có 1 ngày lẻ Ngày cuối cùng của thế kỷ thứ ba là Thứ Hai.
Ngày cuối cùng của thế kỷ thứ ba là Thứ Hai.
Cứ 400 năm có 0 ngày lẻ (vì năm thứ 400 là năm nhuận) Ngày cuối cùng của thế kỷ thứ tư là Chủ Nhật.
Ngày cuối cùng của thế kỷ thứ tư là Chủ Nhật.
 Ngày cuối cùng của một thế kỷ có thể là thứ Sáu, thứ Tư, thứ Hai hoặc Chủ nhật; không thể là Thứ Ba, Thứ Năm và Thứ Bảy.
Ngày cuối cùng của một thế kỷ có thể là thứ Sáu, thứ Tư, thứ Hai hoặc Chủ nhật; không thể là Thứ Ba, Thứ Năm và Thứ Bảy.
Chọn đáp án D.Đáp án: D
 Ngày cuối cùng của thế kỷ đầu tiên là Thứ Sáu.
Ngày cuối cùng của thế kỷ đầu tiên là Thứ Sáu.Cứ 200 năm có 3 ngày lẻ
 Ngày cuối cùng của thế kỷ thứ hai là Thứ Tư.
Ngày cuối cùng của thế kỷ thứ hai là Thứ Tư.Cứ 300 năm có 1 ngày lẻ
 Ngày cuối cùng của thế kỷ thứ ba là Thứ Hai.
Ngày cuối cùng của thế kỷ thứ ba là Thứ Hai.Cứ 400 năm có 0 ngày lẻ (vì năm thứ 400 là năm nhuận)
 Ngày cuối cùng của thế kỷ thứ tư là Chủ Nhật.
Ngày cuối cùng của thế kỷ thứ tư là Chủ Nhật. Ngày cuối cùng của một thế kỷ có thể là thứ Sáu, thứ Tư, thứ Hai hoặc Chủ nhật; không thể là Thứ Ba, Thứ Năm và Thứ Bảy.
Ngày cuối cùng của một thế kỷ có thể là thứ Sáu, thứ Tư, thứ Hai hoặc Chủ nhật; không thể là Thứ Ba, Thứ Năm và Thứ Bảy.Chọn đáp án D.Đáp án: D
Câu 15 [379656]: Thứ Hai rơi vào những ngày nào trong tháng 10 năm 1994?
A, 4, 11, 18, 25.
B, 2, 9, 16, 23.
C, 1, 8, 15, 22.
D, 3, 10, 17, 24, 31.
Tách năm 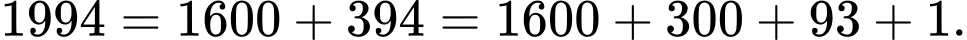
Vì 1600 năm không có ngày lẻ (cứ 400 năm không có ngày lẻ); 300 năm có 1 ngày lẻ (100 năm có 5 ngày lẻ).
Phân tích: 93 năm = 23 năm nhuận + 70 năm không nhuận
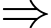 Số ngày lẻ trong 93 năm =
Số ngày lẻ trong 93 năm = 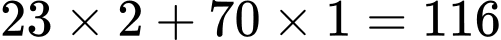 ngày ( 16 tuần, dư 4 ngày).
ngày ( 16 tuần, dư 4 ngày).
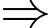 Từ ngày 1 tháng 1 năm 1994 đến ngày 1 tháng 10 năm 1994 là:
Từ ngày 1 tháng 1 năm 1994 đến ngày 1 tháng 10 năm 1994 là:
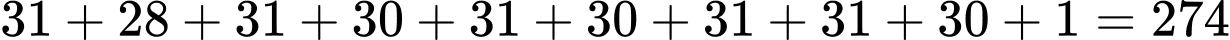 ngày (39 tuần dư 1 ngày).
ngày (39 tuần dư 1 ngày).
Tổng số ngày lẻ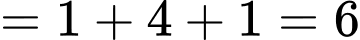 ngày.
ngày.
>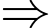 Thứ 2 đầu tiên trong tháng 10 năm 1994 là ngày 3 tháng 10.
Thứ 2 đầu tiên trong tháng 10 năm 1994 là ngày 3 tháng 10.
Vậy ngày 3, 10, 17, 24, 31 là thứ 2 trong tháng 10.
Chọn đáp án D. Đáp án: D
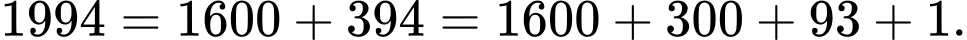
Vì 1600 năm không có ngày lẻ (cứ 400 năm không có ngày lẻ); 300 năm có 1 ngày lẻ (100 năm có 5 ngày lẻ).
Phân tích: 93 năm = 23 năm nhuận + 70 năm không nhuận
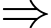 Số ngày lẻ trong 93 năm =
Số ngày lẻ trong 93 năm = 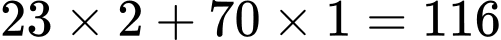 ngày ( 16 tuần, dư 4 ngày).
ngày ( 16 tuần, dư 4 ngày).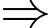 Từ ngày 1 tháng 1 năm 1994 đến ngày 1 tháng 10 năm 1994 là:
Từ ngày 1 tháng 1 năm 1994 đến ngày 1 tháng 10 năm 1994 là: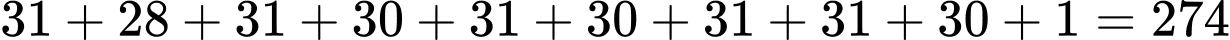 ngày (39 tuần dư 1 ngày).
ngày (39 tuần dư 1 ngày).Tổng số ngày lẻ
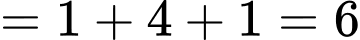 ngày.
ngày.>
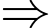 Thứ 2 đầu tiên trong tháng 10 năm 1994 là ngày 3 tháng 10.
Thứ 2 đầu tiên trong tháng 10 năm 1994 là ngày 3 tháng 10.Vậy ngày 3, 10, 17, 24, 31 là thứ 2 trong tháng 10.
Chọn đáp án D. Đáp án: D
Câu 16 [289201]: Lớp 7A đứng ngoài sân, lớp trưởng cho các bạn xếp thành 4 hàng, mỗi hàng có số học sinh bằng nhau. Khi vào lớp, số học sinh xếp thành bàn 3 hoặc 5 thì vừa đủ. Lớp 7A có bao nhiêu học sinh?
A, 15 học sinh.
B, 30 học sinh.
C, 45 học sinh.
D, 60 học sinh.
Gọi $n$ là số học sinh lớp 7A.
Dựa vào giả thiết:
• “Lớp trưởng cho các bạn xếp thành $4$ hàng, mỗi hàng có số học sinh bằng nhau.”
$\Rightarrow $ $n$ chia $4$ dư $1.$ (1)
• “Khi vào lớp, số học sinh xếp thành bàn $3$ hoặc $5$ thì vừa đủ.”
$\Rightarrow $ $n$ chia hết cho $3$ và $5.$ (2)
Từ (1) và (2) và các đáp án $\Rightarrow x=45.$ Chọn đáp án C.
Đáp án: C
Dựa vào giả thiết:
• “Lớp trưởng cho các bạn xếp thành $4$ hàng, mỗi hàng có số học sinh bằng nhau.”
$\Rightarrow $ $n$ chia $4$ dư $1.$ (1)
• “Khi vào lớp, số học sinh xếp thành bàn $3$ hoặc $5$ thì vừa đủ.”
$\Rightarrow $ $n$ chia hết cho $3$ và $5.$ (2)
Từ (1) và (2) và các đáp án $\Rightarrow x=45.$ Chọn đáp án C.
Đáp án: C
Câu 17 [289756]: Một học sinh đang chuẩn bị cho kỳ thi của mình. Học sinh thắp hai ngọn nến có chiều dài bằng nhau, một cây nến dày hơn cây nến kia. Cây nến dày được thiết kế để tồn tại trong năm giờ trong khi cây nến mỏng được thiết kế để tồn tại trong ba giờ. Sau khi học xong, học sinh thấy được cây nến dày dài gấp 3 lần cây nến mỏng. Người học sinh đã học dưới ánh nến bao lâu?
A, 60 phút.
B, 75 phút.
C, 90 phút.
D, 150 phút.
Chọn đáp án D.
Gọi chiều dài mỗi cây nến ban đầu là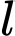
Thời gian học sinh học dưới ánh nến là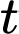 giờ.
giờ.
Chiều dài của cây nến dày sau khi học xong là: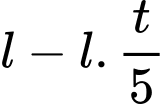
Chiều dài của cây nến mỏng sau khi học xong là: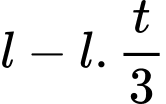
Vì sau khi học xong, học sinh thấy được cây nến dày dài gấp 3 lần cây nến mỏng nên ta có:
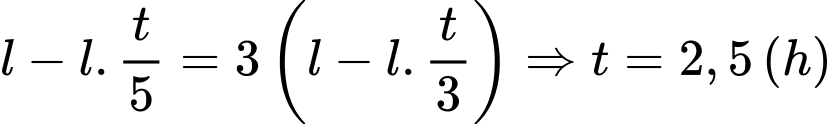
Vậy học sinh đã học dưới ánh nến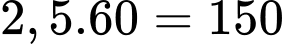 (phút). Đáp án: D
(phút). Đáp án: D
Gọi chiều dài mỗi cây nến ban đầu là
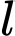
Thời gian học sinh học dưới ánh nến là
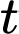 giờ.
giờ.
Chiều dài của cây nến dày sau khi học xong là:
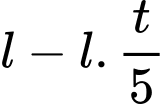
Chiều dài của cây nến mỏng sau khi học xong là:
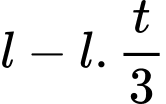
Vì sau khi học xong, học sinh thấy được cây nến dày dài gấp 3 lần cây nến mỏng nên ta có:
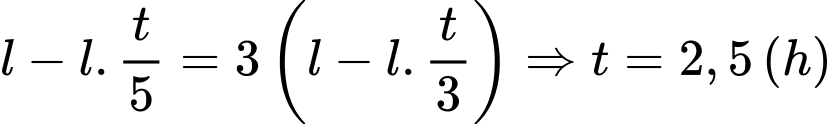
Vậy học sinh đã học dưới ánh nến
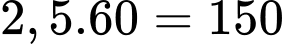 (phút). Đáp án: D
(phút). Đáp án: D
Câu 18 [379668]: Chỉ dùng bình 4 lít và bình 6 lít, lượng nước nào sau đây không đo được? (Giả sử có nguồn cung cấp nước vô hạn)
A, 2 lít.
B, 3 lít.
C, 8 lít.
D, Nhiều hơn một trong các đáp án trên.
Chọn đáp án B.
Ta có thể đo được 2 lít và 8 lít bằng cách:
Quy trình được trình bày dưới bảng sau:
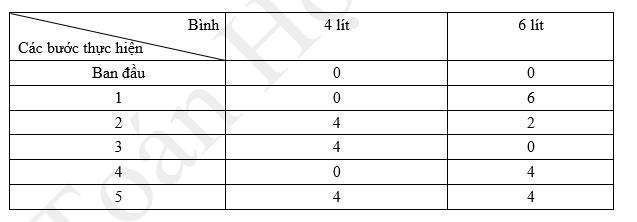
Do đó không thể đo được 3 lít. Đáp án: B
Ta có thể đo được 2 lít và 8 lít bằng cách:
Quy trình được trình bày dưới bảng sau:

Do đó không thể đo được 3 lít. Đáp án: B
Câu 19 [290565]: Vào năm 1940, một nhà toán học cho biết ông ta được 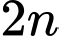 tuổi vào năm
tuổi vào năm 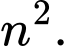 Ông cũng cho biết vào năm
Ông cũng cho biết vào năm 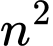 nếu lấy tổng số tuổi cộng với tháng sinh sẽ ra kết quả là bình phương ngày sinh của ông. Hãy cho biết ông sinh vào tháng nào?
nếu lấy tổng số tuổi cộng với tháng sinh sẽ ra kết quả là bình phương ngày sinh của ông. Hãy cho biết ông sinh vào tháng nào?
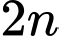 tuổi vào năm
tuổi vào năm 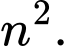 Ông cũng cho biết vào năm
Ông cũng cho biết vào năm 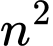 nếu lấy tổng số tuổi cộng với tháng sinh sẽ ra kết quả là bình phương ngày sinh của ông. Hãy cho biết ông sinh vào tháng nào?
nếu lấy tổng số tuổi cộng với tháng sinh sẽ ra kết quả là bình phương ngày sinh của ông. Hãy cho biết ông sinh vào tháng nào? A, Tháng 6.
B, Tháng 8.
C, Tháng 10.
D, Tháng 12.
Chọn đáp án D.
Ta có: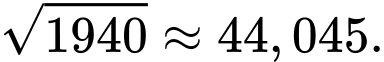
Nếu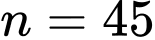 thì vào năm
thì vào năm 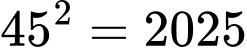 nhà toán học này
nhà toán học này 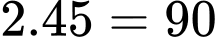 tuổi.
tuổi.
Có nghĩa là: Ông sinh vào năm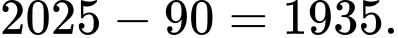 Vậy vào năm 1940, ông ta mới được 5 tuổi (không logic, vì 5 tuổi không trở thành nhà toán học được).
Vậy vào năm 1940, ông ta mới được 5 tuổi (không logic, vì 5 tuổi không trở thành nhà toán học được).
Tương tự, với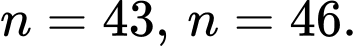 Nếu
Nếu 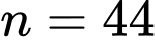 thì vào năm
thì vào năm 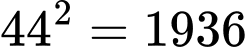 nhà toán học này
nhà toán học này 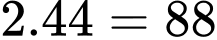 tuổi.
tuổi.
Có nghĩa là: Ông sinh vào năm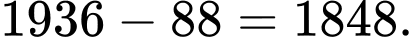 Vậy vào năm 1940, ông ta 92 tuổi (thỏa mãn).
Vậy vào năm 1940, ông ta 92 tuổi (thỏa mãn).
Vào năm 1936, nếu lấy tổng số tuổi cộng với tháng sinh sẽ ra kết quả là bình phương ngày sinh của ông (tháng và ngày sinh đều phải là số tự nhiên) và năm đó, ông 88 tuổi Nhà toán học này sinh vào ngày 10 tháng 12 năm 1848. Đáp án: D
Ta có:
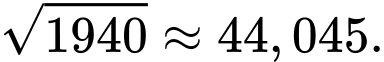
Nếu
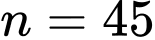 thì vào năm
thì vào năm 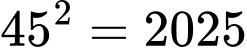 nhà toán học này
nhà toán học này 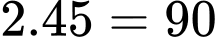 tuổi.
tuổi.Có nghĩa là: Ông sinh vào năm
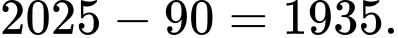 Vậy vào năm 1940, ông ta mới được 5 tuổi (không logic, vì 5 tuổi không trở thành nhà toán học được).
Vậy vào năm 1940, ông ta mới được 5 tuổi (không logic, vì 5 tuổi không trở thành nhà toán học được).Tương tự, với
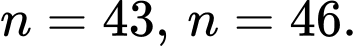 Nếu
Nếu 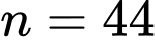 thì vào năm
thì vào năm 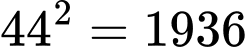 nhà toán học này
nhà toán học này 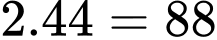 tuổi.
tuổi.Có nghĩa là: Ông sinh vào năm
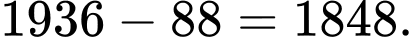 Vậy vào năm 1940, ông ta 92 tuổi (thỏa mãn).
Vậy vào năm 1940, ông ta 92 tuổi (thỏa mãn).Vào năm 1936, nếu lấy tổng số tuổi cộng với tháng sinh sẽ ra kết quả là bình phương ngày sinh của ông (tháng và ngày sinh đều phải là số tự nhiên) và năm đó, ông 88 tuổi Nhà toán học này sinh vào ngày 10 tháng 12 năm 1848. Đáp án: D
Câu 20 [379670]: A, B, C, D, E và F là 6 chữ số khác nhau và khác 0, thỏa mãn 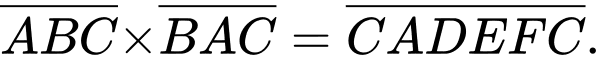 Biết rằng
Biết rằng 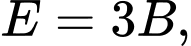
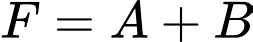 và
và 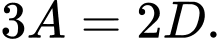 Giá trị của C là
Giá trị của C là
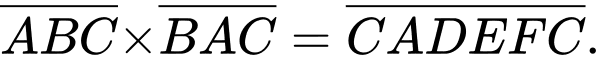 Biết rằng
Biết rằng 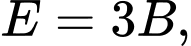
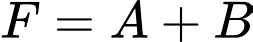 và
và 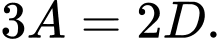 Giá trị của C là
Giá trị của C là A, 1.
B, 5.
C, 7.
D, 4.
Chọn đáp án A.
Ta có: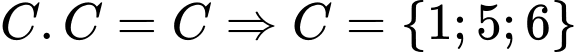
Kết hợp đáp án
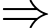 Loại đáp án C và D và giá trị
Loại đáp án C và D và giá trị 
Vì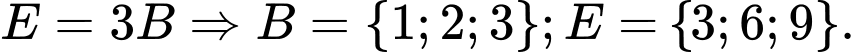
Vì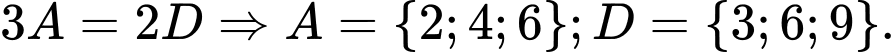
Kết hợp với dữ kiện: A, B, C, D, E và F là 6 chữ số khác nhau và khác 0 và các phép thử ta có duy nhất 1 trường hợp thỏa mãn: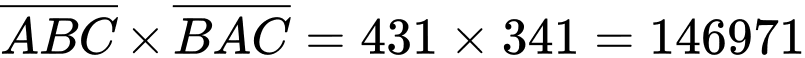
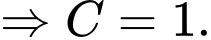 Đáp án: A
Đáp án: A
Ta có:
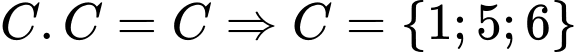
Kết hợp đáp án
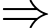 Loại đáp án C và D và giá trị
Loại đáp án C và D và giá trị 
Vì
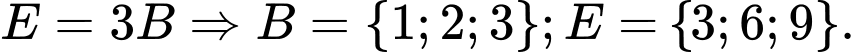
Vì
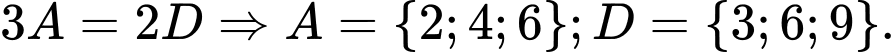
Kết hợp với dữ kiện: A, B, C, D, E và F là 6 chữ số khác nhau và khác 0 và các phép thử ta có duy nhất 1 trường hợp thỏa mãn:
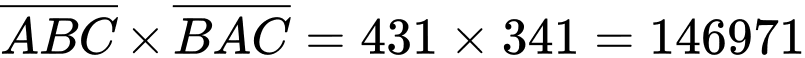
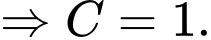 Đáp án: A
Đáp án: A